Intelligent Analysis Algorithm for Satellite Health under Time-Varying and Extremely High Thermal Loads
Abstract
1. Introduction
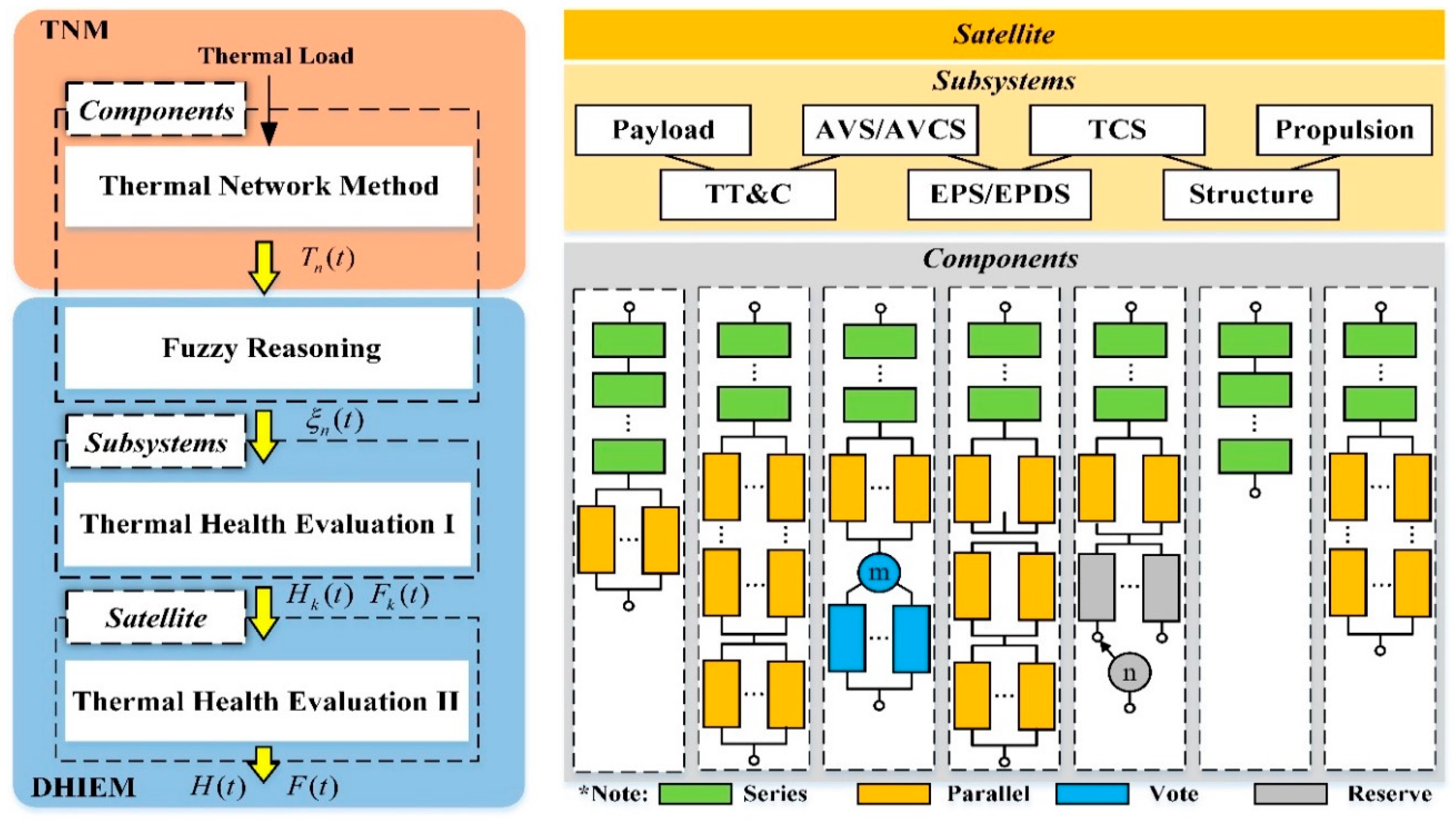
2. Dynamic Health Intelligent Evaluation Model
2.1. Principle Description and Evaluation Index
2.1.1. Definition of Evaluation Index
- Failure Probability :
- Health Degree :
- Failure Factor :
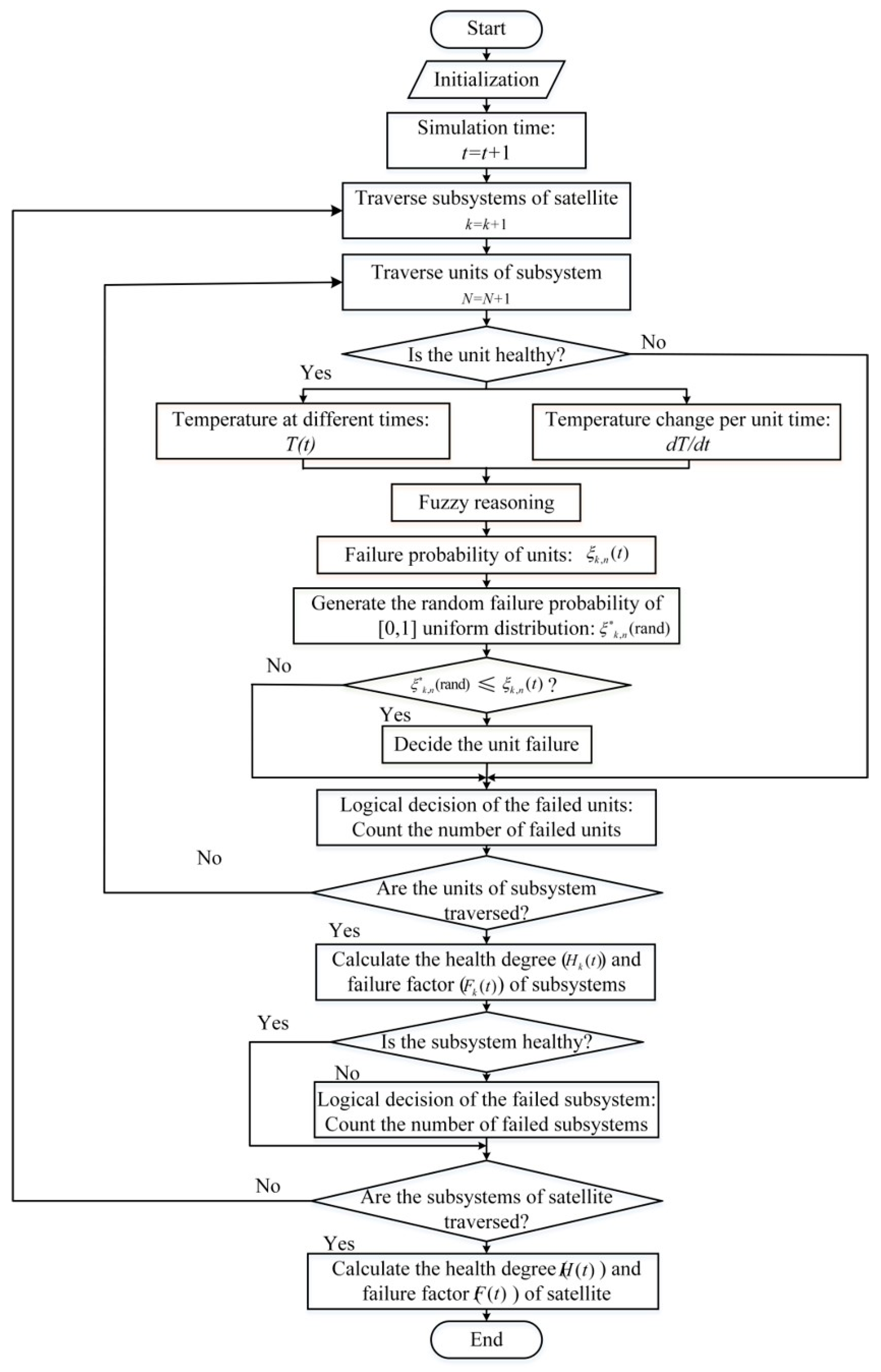
2.1.2. Principle Description
2.2. Component Temperature Dynamic Modeling
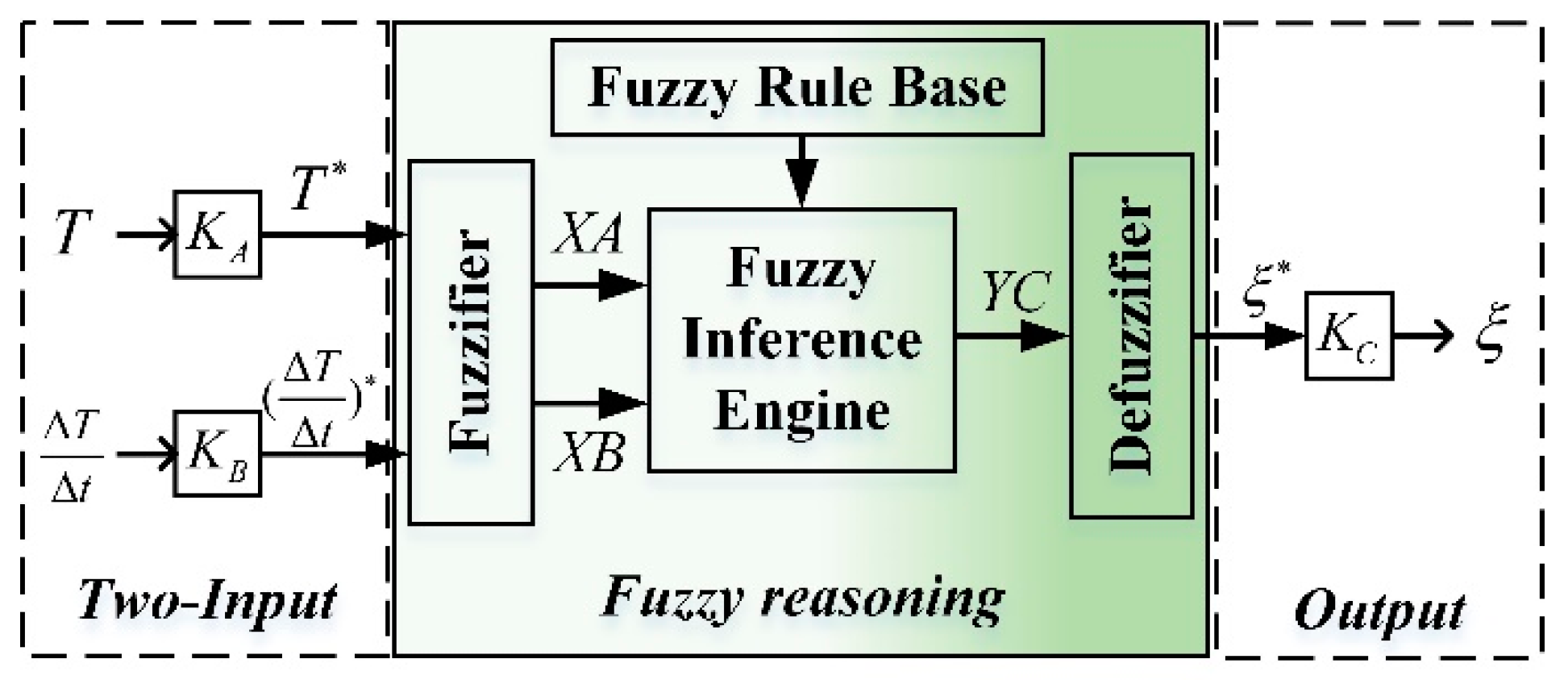
2.3. Component Failure Probability Fuzzy Modeling
2.3.1. Fuzzy Reasoning
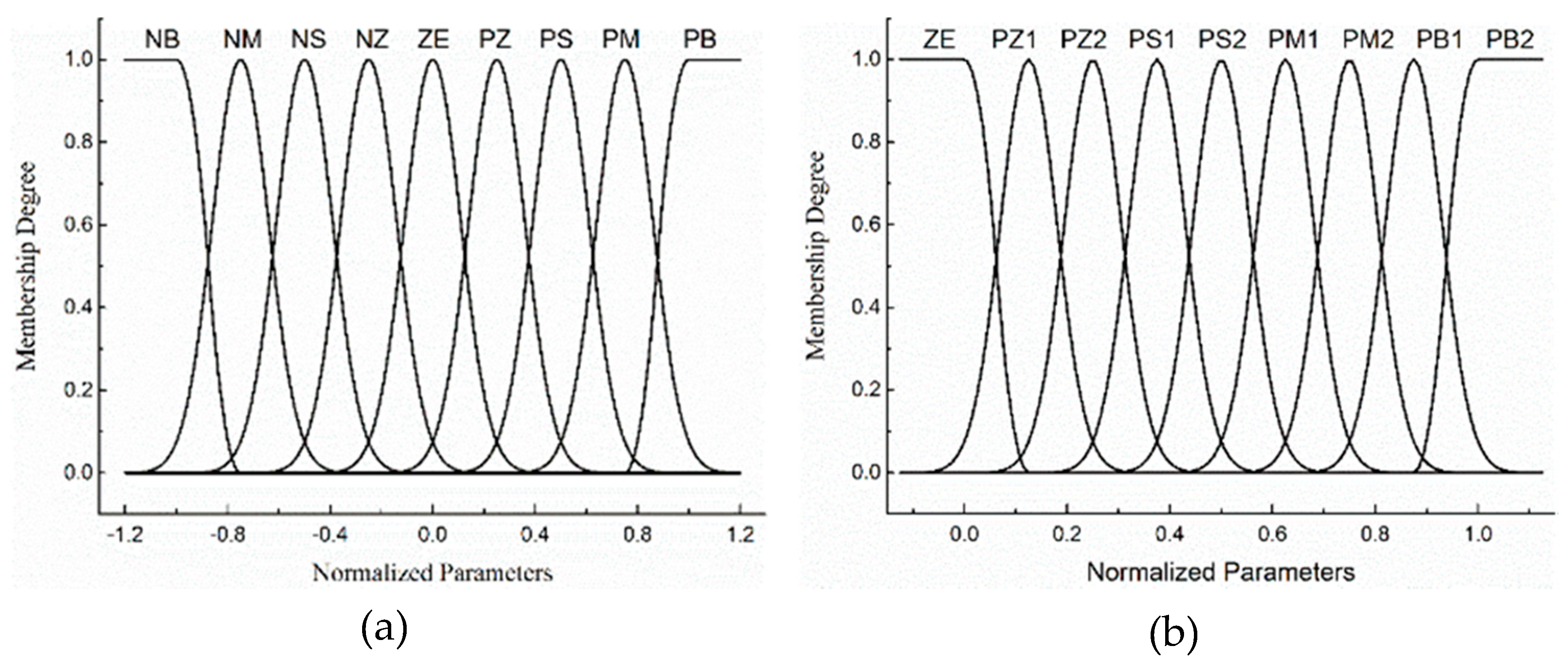
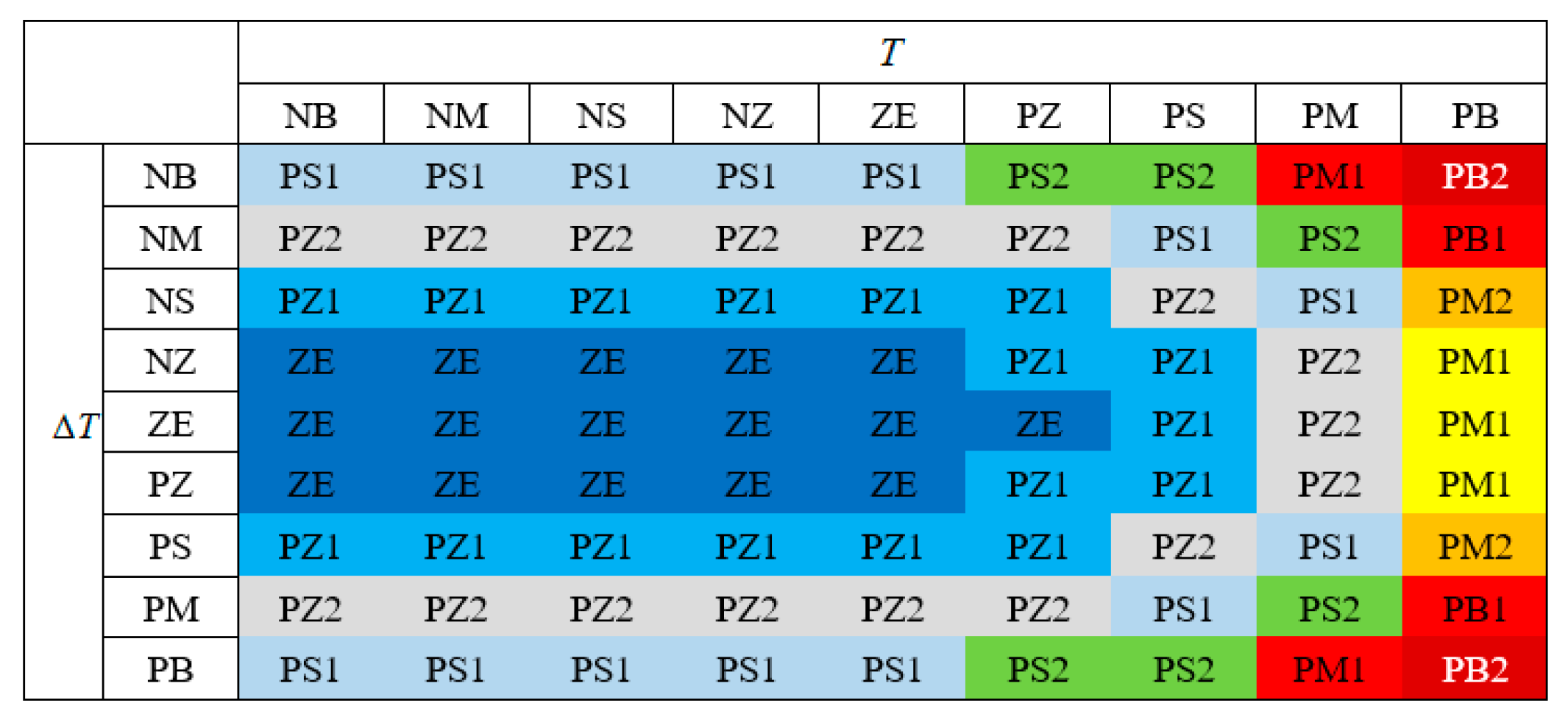
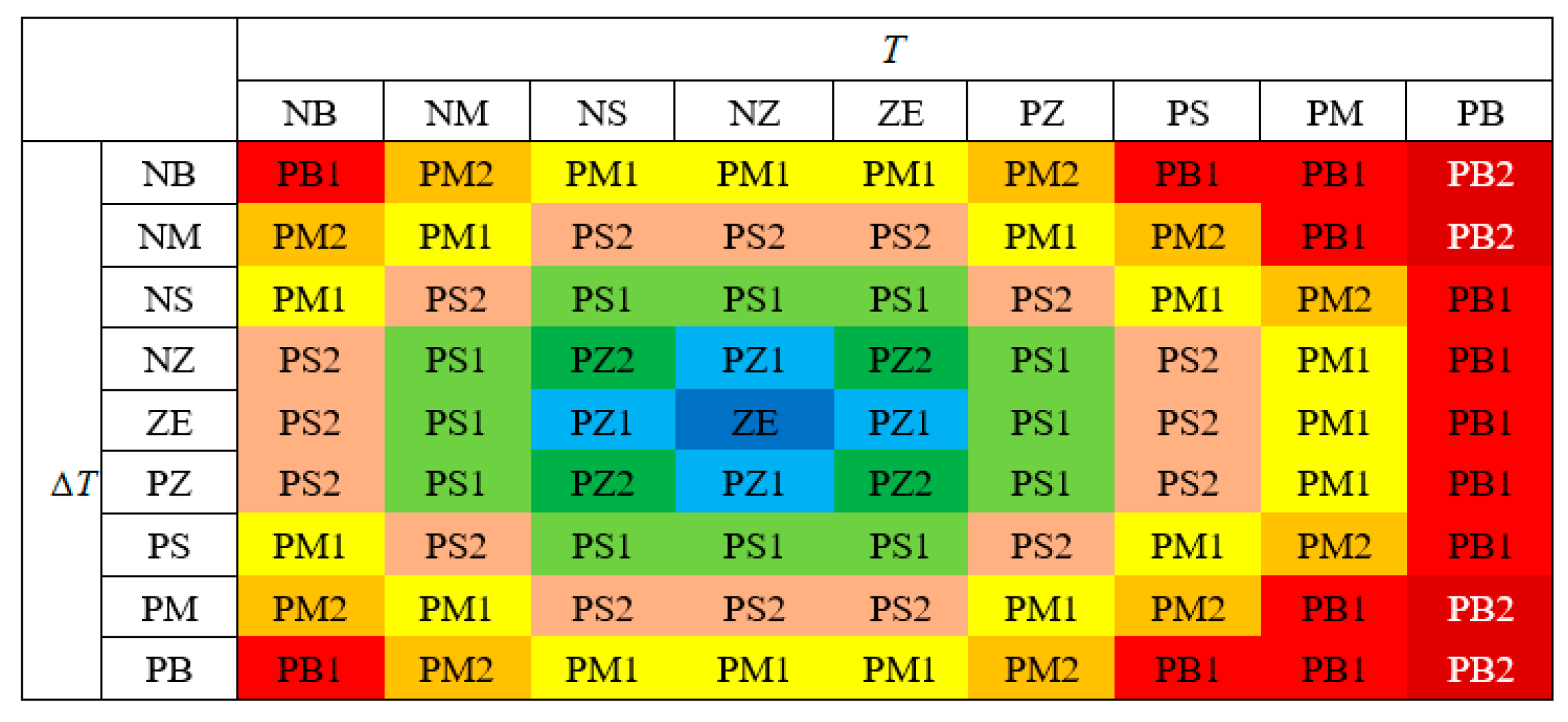
2.3.2. Fuzzy Rule Design
2.4. System Health Dynamic Evaluation Modeling
3. Results and Discussion
3.1. Cases Design
3.1.1. Parameters Setting for Normal Orbital Operation
3.1.2. Design of Thermal Damage Conditions
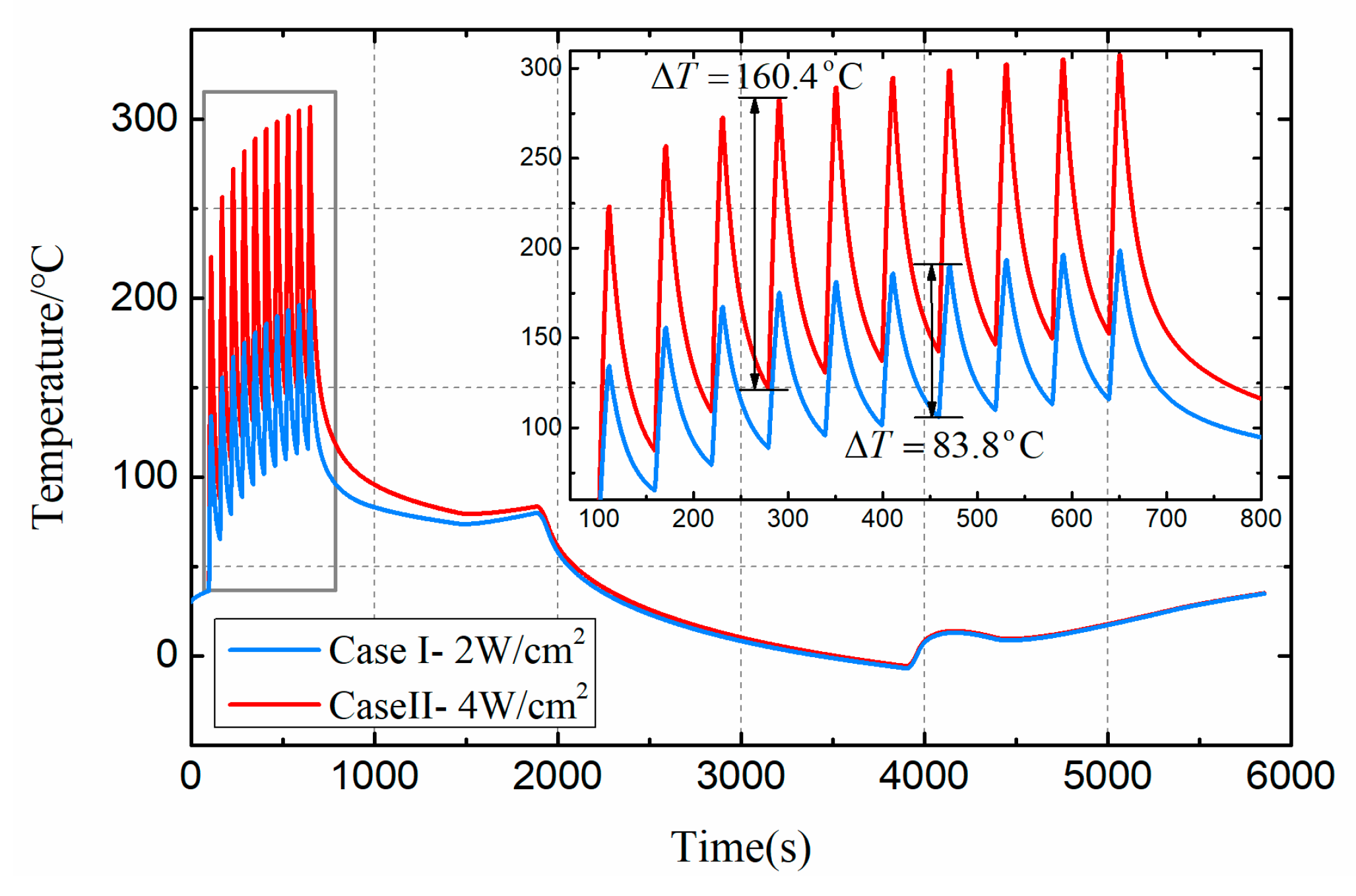
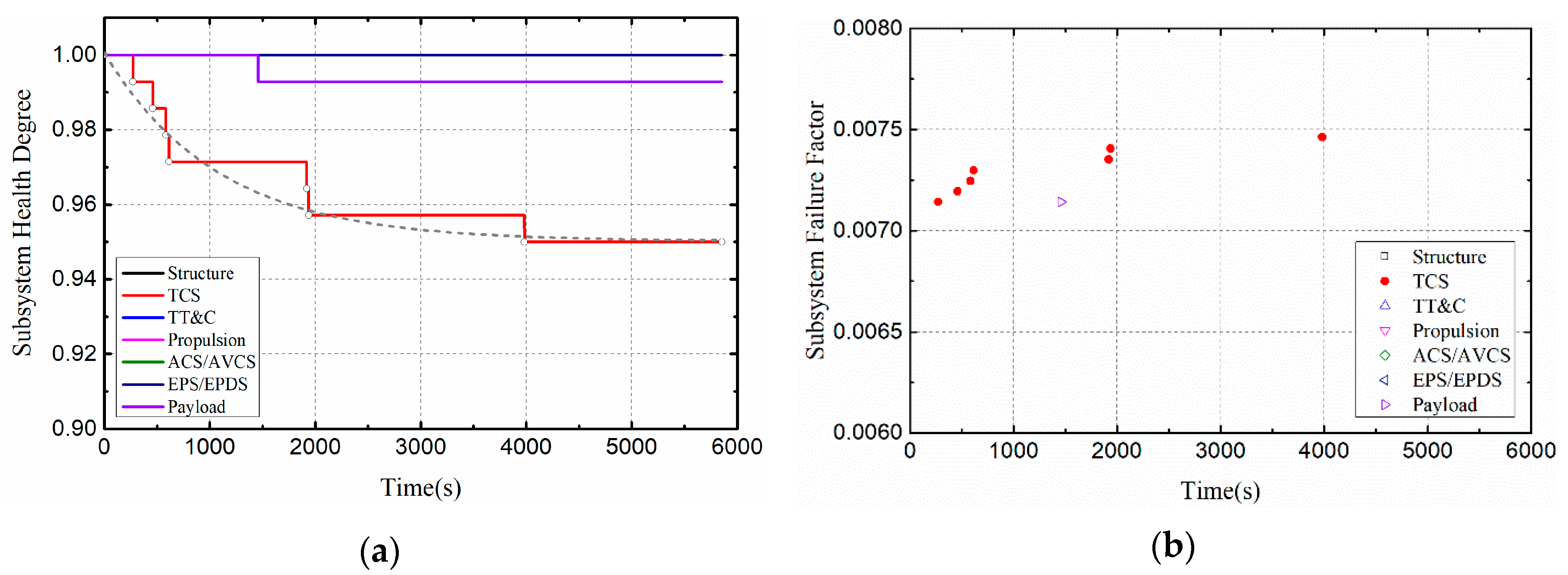
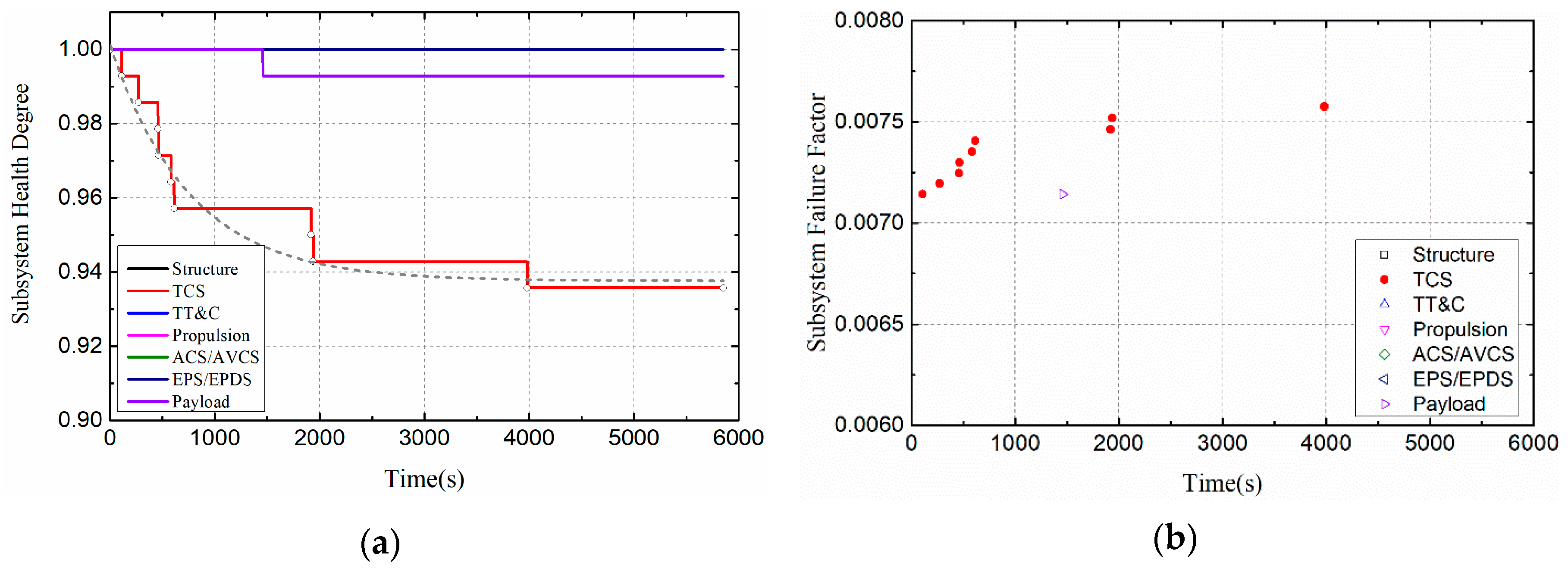
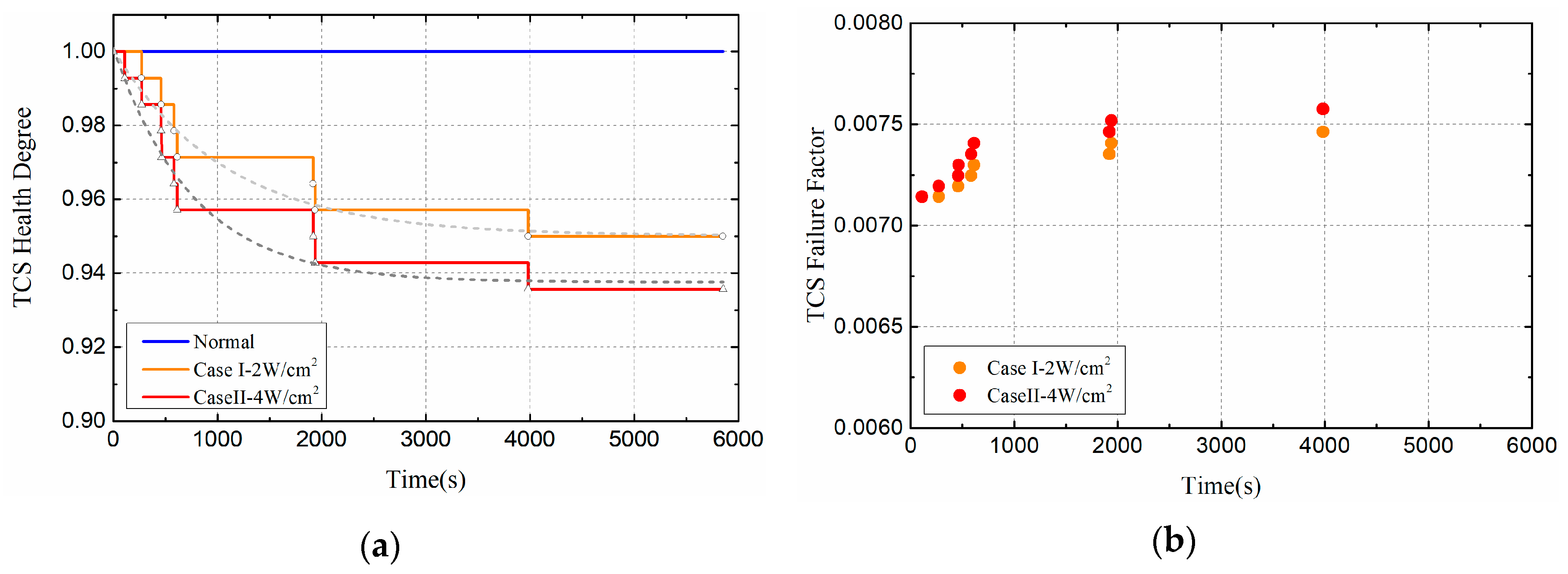
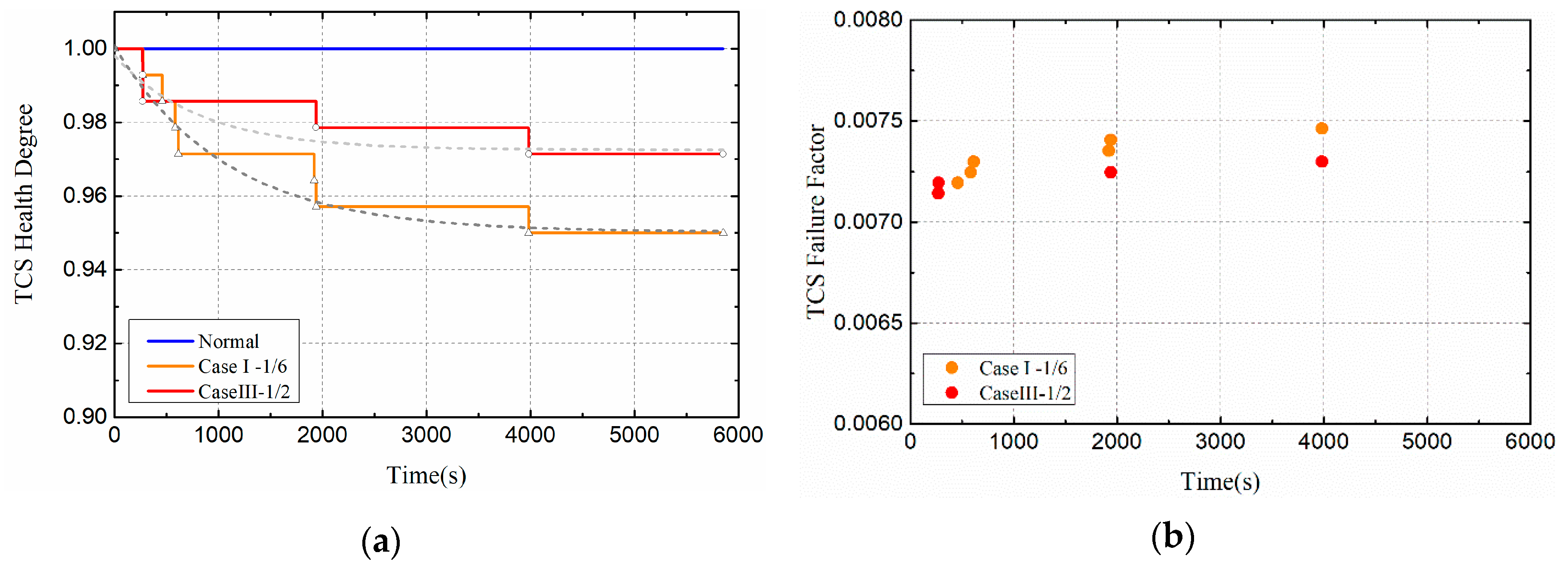
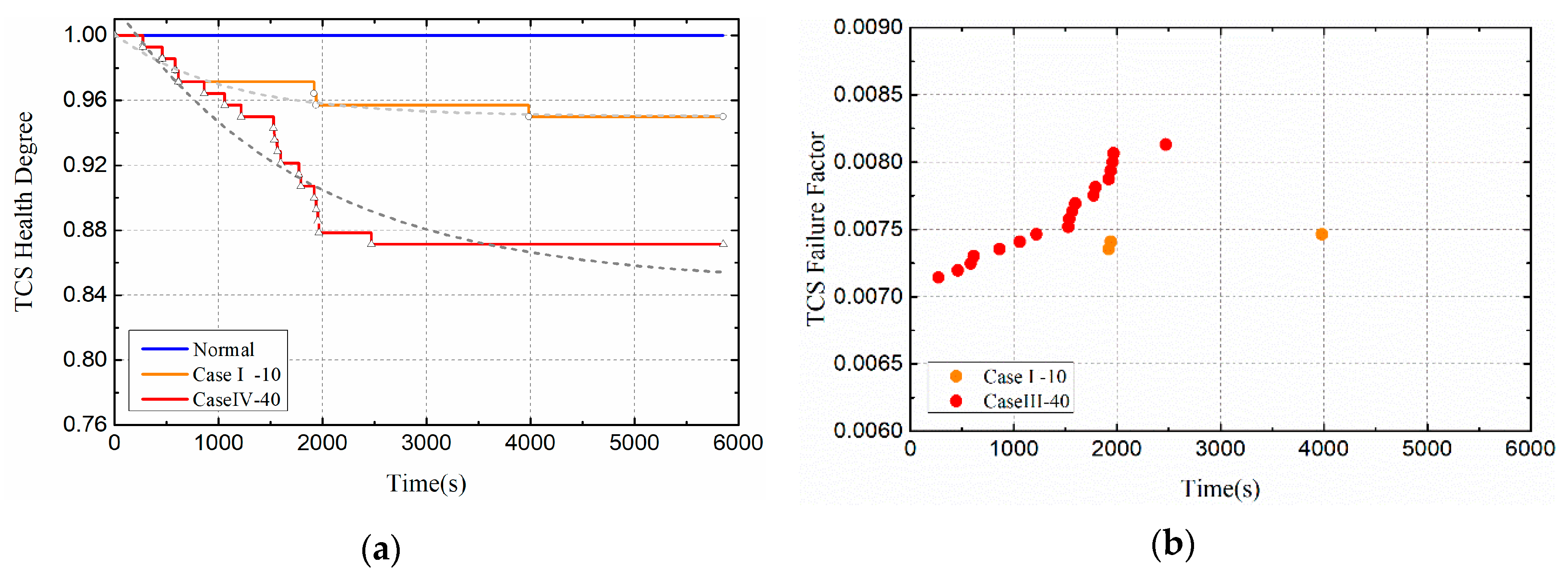
3.2. Effects of Thermal Load Amplitude on Satellite Health
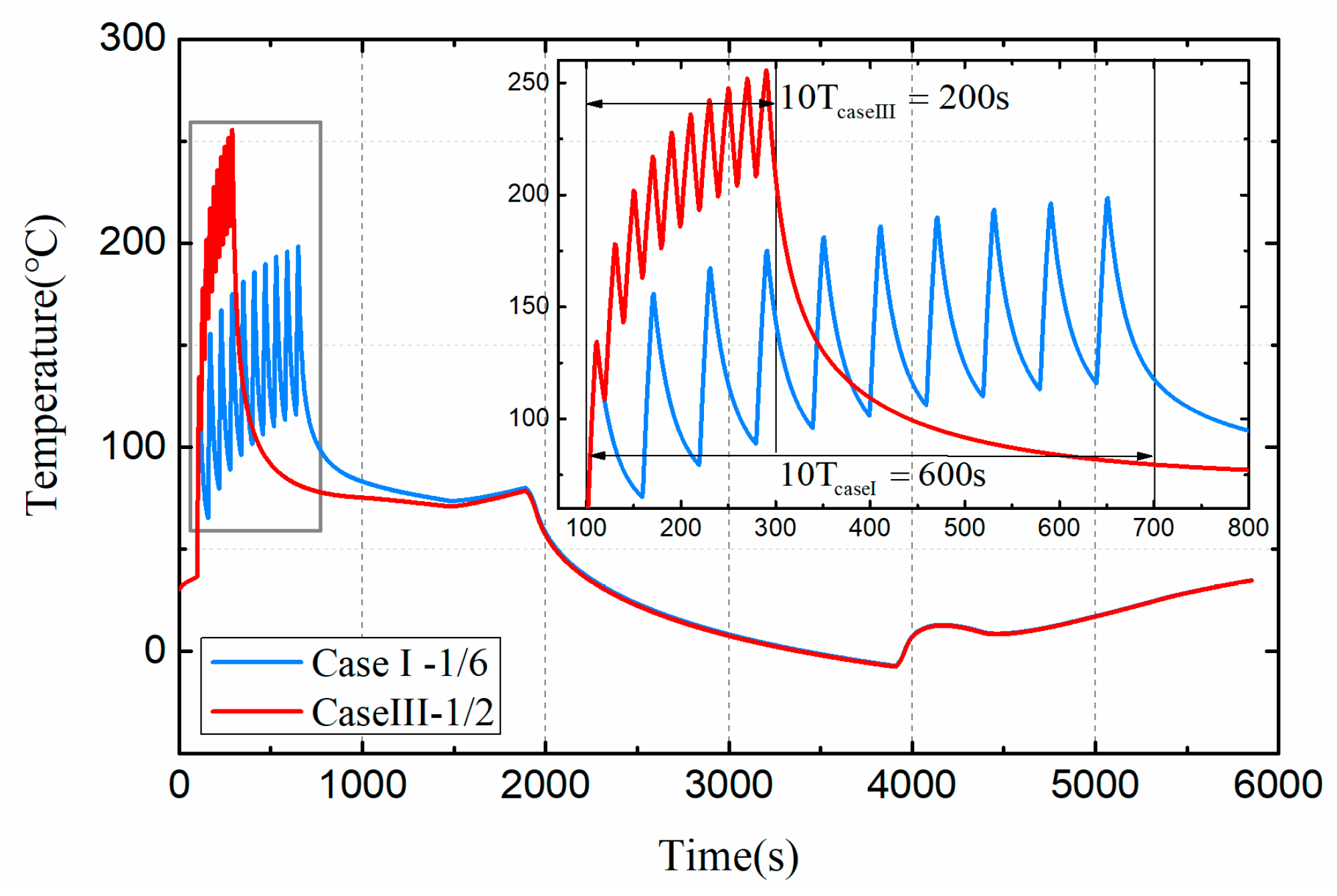
3.3. Effects of Thermal Load Duty Ratio on Satellite Health
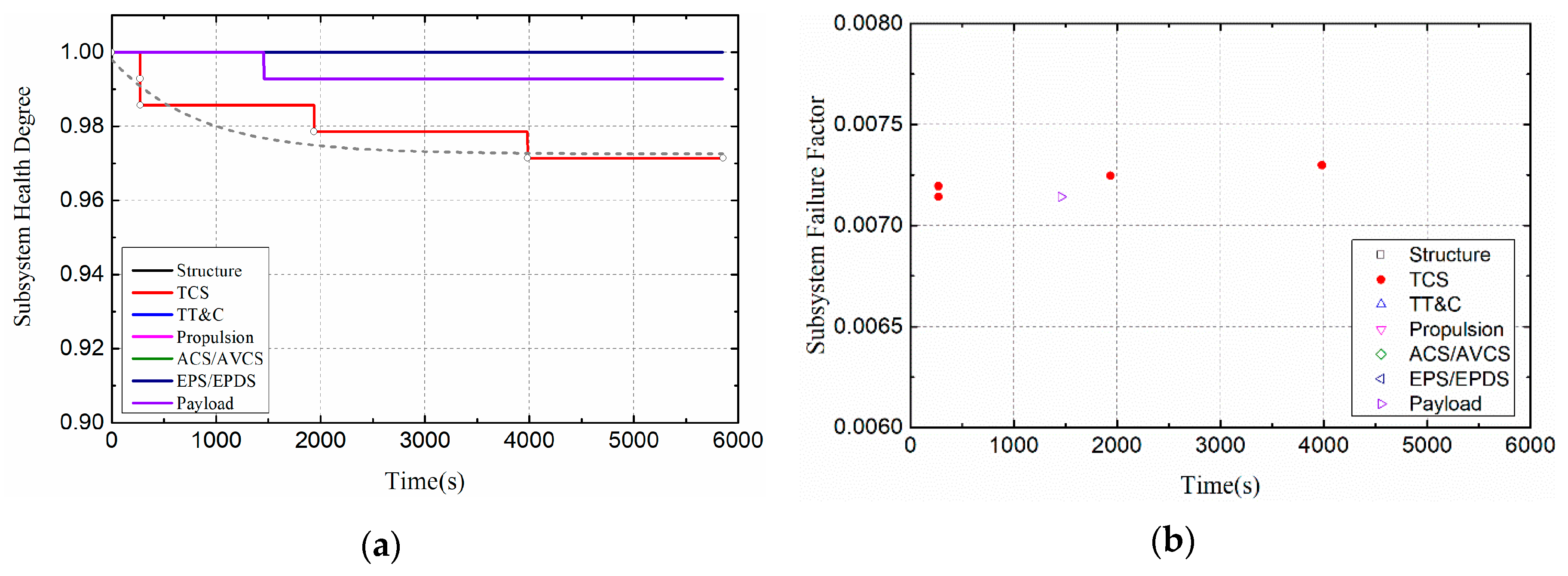
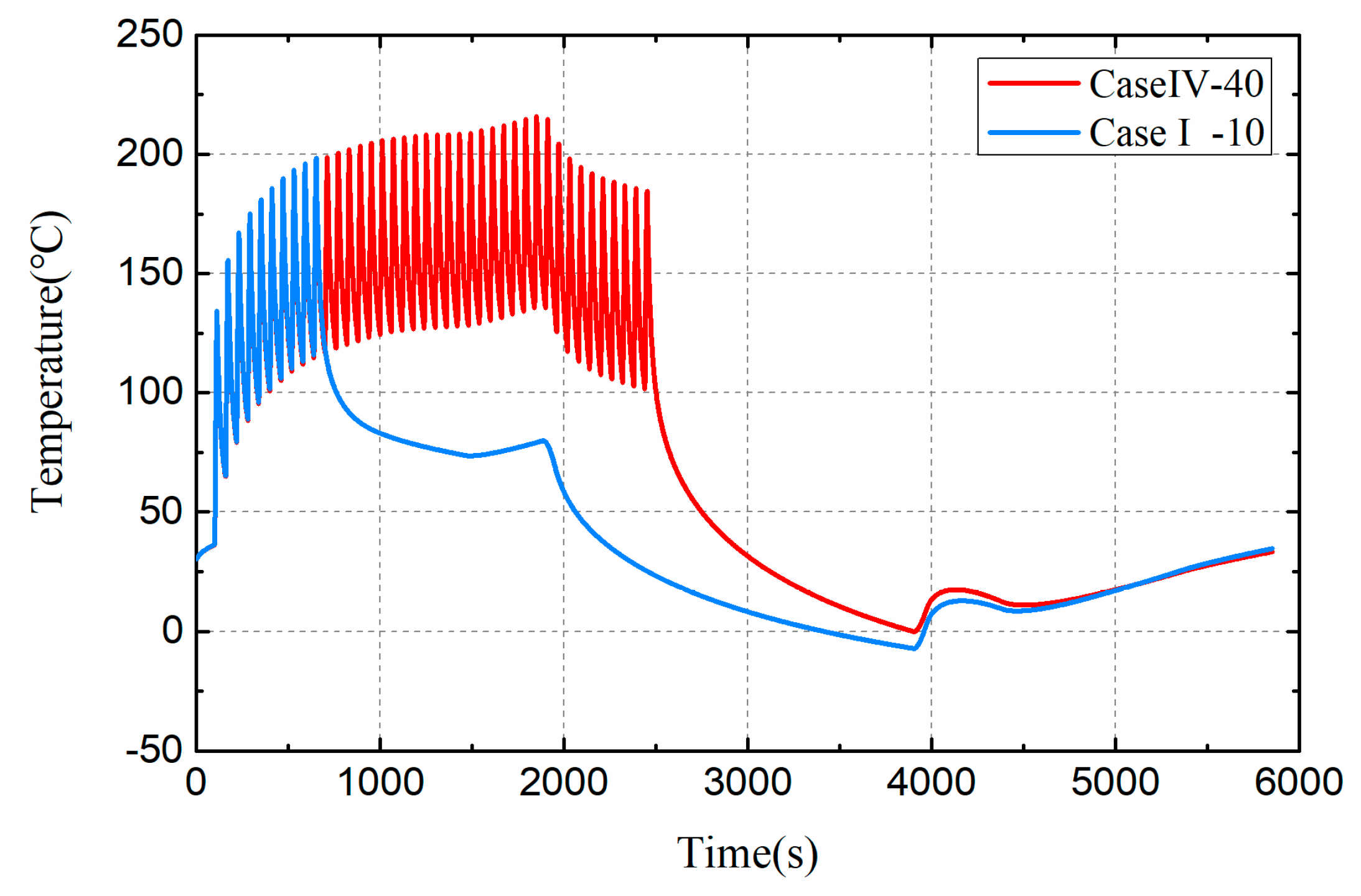
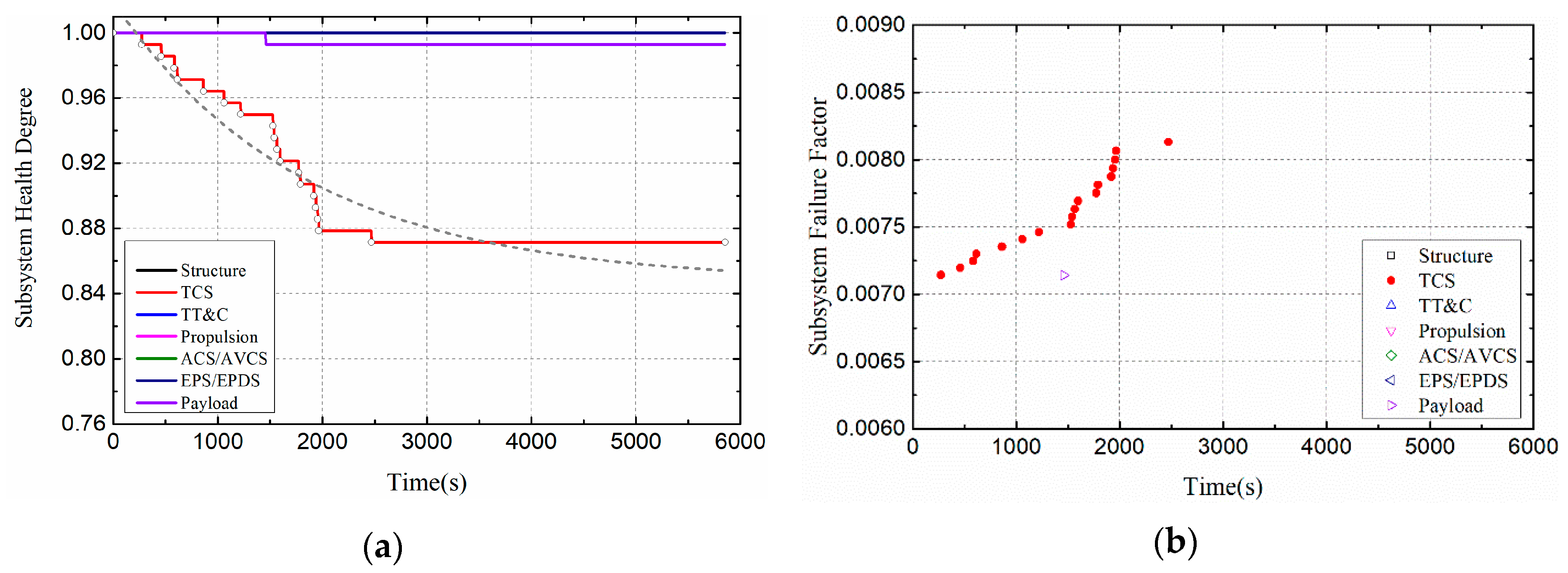
3.4. Effects of Thermal Load Cycle on Satellite Health
4. Conclusions
- The fuzziness of the relationship between temperature and failure probability is considered, and the relationship between temperature and failure probability is quantitatively described by intelligent analysis method (fuzzy reasoning).
- The model can quickly and accurately evaluate the effects of different thermal conditions on satellite health. The health deterioration of the system is characterized by the change of health degree and failure factor.
- Multi-period, high heat flux density, and low duty ratio have great influence on satellite health.
Author Contributions
Funding
Conflicts of Interest
References
- Chudoba, B.; Coleman, G.; Gonzalez, L.; Haney, E.; Oza, A.; Ricketts, V. Orbital transfer vehicle (OTV) system sizing study for manned GEO satellite servicing. Aeronaut. J. 2016, 120, 573–599. [Google Scholar] [CrossRef]
- Seo, H.S.; Rhee, J.; Han, E.S.; Kim, I.S. Thermal failure of the LM117 regulator under harsh space thermal environments. Aerosp. Sci. Technol. 2013, 27, 49–56. [Google Scholar] [CrossRef]
- Barcena, J.; Maudes, J.; Vellvehi, M.; Jorda, X.; Obieta, I.; Guraya, C.; Bilbao, L.; Jimenez, C.; Merveille, C.; Coleto, J. Innovative packaging solution for power and thermal management of wide-bandgap semiconductor devices in space applications. Acta Astronaut. 2008, 62, 422–430. [Google Scholar] [CrossRef]
- Wang, J.X.; Li, Y.Z.; Li, J.X.; Li, C.; Zhang, Y.; Ning, X.W. A gas-atomized spray cooling system integrated with an ejector loop: Ejector modeling and thermal performance analysis. Energy Convers. Manag. 2019, 180, 106–118. [Google Scholar] [CrossRef]
- Swanson, T.D.; Birur, G.C. NASA thermal control technologies for robotic spacecraft. Appl. Therm. Eng. 2003, 23, 1055–1065. [Google Scholar] [CrossRef]
- Yang, C.; Hou, X.; Wang, L. Thermal design, analysis and comparison on three concepts of space solar power satellite. Acta Astronaut. 2017, 137, 382–402. [Google Scholar] [CrossRef]
- Palla, C.; Peroni, M.; Kingston, J. Failure analysis of satellite subsystems to define suitable de-orbit devices. Acta Astronaut. 2016, 128, 343–349. [Google Scholar] [CrossRef][Green Version]
- Gonzalo, J.; Domínguez, D.; Lopez, D. On the challenge of a century lifespan satellite. Prog. Aerosp. Sci. 2014, 70, 28–41. [Google Scholar] [CrossRef]
- Kim, S.Y.; Castet, J.F.; Saleh, J.H. Spacecraft electrical power subsystem: Failure behavior, reliability, and multi-state failure analyses. Reliab. Eng. Syst. Saf. 2012, 98, 55–65. [Google Scholar] [CrossRef]
- Tafazoli, M. A study of on-orbit spacecraft failures. Acta Astronaut. 2009, 64, 195–205. [Google Scholar] [CrossRef]
- Pecht, M.; Kang, W.C. A critique of Mil-Hdbk-217E reliability prediction methods. IEEE Trans. Reliab. 1988, 37, 453–457. [Google Scholar] [CrossRef]
- Bensoussan, A.; Suhir, E.; Henderson, P.; Zahir, M. A unified multiple stress reliability model for microelectronic devices-Application to 1.55 μm DFB laser diode module for space validation. Microelectron. Reliab. 2015, 55, 1729–1735. [Google Scholar] [CrossRef]
- Castet, J.F.; Saleh, J.H. Satellite Reliability: Statistical Data Analysis and Modeling. J. Spacecr. Rocket. 2009, 46, 1065–1076. [Google Scholar] [CrossRef]
- Lee, W.S. Fault tree analysis, methods, and applications: A review. IEEE Trans. Reliab. 1985, 34, 194–203. [Google Scholar] [CrossRef]
- De Queiroz Souza, R.; Álvares, A.J. FMEA and FTA analysis for application of the reliability centered maintenance methodology: Case study on hydraulic turbines. ABCM Symp. Ser. Mechatron. 2008, 3, 803–812. [Google Scholar]
- Wu, J.; Yan, S.; Xie, L. Reliability analysis method of a solar array by using fault tree analysis and fuzzy reasoning Petrinet. Acta Astronaut. 2011, 69, 960–968. [Google Scholar] [CrossRef]
- Achutuni, R.; Menzel, P. Space systems considerations in the design of advanced geostationary operational environmental satellites. Adv. Space Res. 1999, 23, 1377–1384. [Google Scholar] [CrossRef]
- Akita, T.; Takaki, R.; Shima, E. A new adaptive estimation method of spacecraft thermal mathematical model with an ensemble Kalman filter. Acta Astronaut. 2012, 73, 144–155. [Google Scholar] [CrossRef]
- Pérez-Grande, I.; Sanz-Andrés, A.; Guerra, C.; Alonso, G. Analytical study of the thermal behaviour and stability of a small satellite. Appl. Therm. Eng. 2009, 29, 2567–2573. [Google Scholar] [CrossRef]
- Li, Y.Z.; Lee, K.M. Thermohydraulic Dynamics and Fuzzy Coordination Control of a Microchannel Cooling Network for Space Electronics. IEEE Trans. Ind. Electron. 2011, 58, 700–708. [Google Scholar] [CrossRef]
- Qian, X.; Zhang, Y.; Gendeel, M. State Rules Mining and Probabilistic Fault Analysis for 5 MW Offshore Wind Turbines. Energies 2019, 12, 2046. [Google Scholar] [CrossRef]
| (a) | (b) | ||||
| Fuzzy Sets | Ranks | Linguistic Values | Fuzzy Sets | Ranks | Linguistic Values |
| NB | −4 | Negative big | ZE | 0 | Zero |
| NM | −3 | Negative medium | PZ1 | 1 | Positive zero 1 |
| NS | −2 | Negative small | PZ2 | 2 | Positive zero 2 |
| NZ | −1 | Negative zero | PS1 | 3 | Positive small 1 |
| ZE | 0 | Zero | PS2 | 4 | Positive small 2 |
| PZ | 1 | Positive zero | PM1 | 5 | Positive medium 1 |
| PS | 2 | Positive small | PM2 | 6 | Positive medium 2 |
| PM | 3 | Positive medium | PB1 | 7 | Positive big 1 |
| PB | 4 | Positive big | PB2 | 8 | Positive big 2 |
| Parameters | Value |
|---|---|
| Solar incident angle | 17.23 °C |
| Orbit altitude | 641.65 km |
| Average of solar radiation | 1354 W/m2 |
| Albedo | 0.35 |
| Earth infrared radiation | 221.484 W/m2 |
| Space temperature | 4 K |
| Cases | Amplitude | Duty Ratio | Cycle |
|---|---|---|---|
| I | 2 W/cm2 | 1/6 (Heat 10 s; Cool 50 s) | 10 |
| II | 4 W/cm2 | 1/6 (Heat 10 s; Cool 50 s) | 10 |
| III | 2 W/cm2 | 1/2 (Heat 10 s; Cool 10 s) | 10 |
| IV | 2 W/cm2 | 1/6 (Heat 10 s; Cool 50 s) | 40 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, E.-H.; Li, Y.-Z.; Li, T.-T.; Li, J.-X.; Zhai, Z.-Z.; Li, T. Intelligent Analysis Algorithm for Satellite Health under Time-Varying and Extremely High Thermal Loads. Entropy 2019, 21, 983. https://doi.org/10.3390/e21100983
Li E-H, Li Y-Z, Li T-T, Li J-X, Zhai Z-Z, Li T. Intelligent Analysis Algorithm for Satellite Health under Time-Varying and Extremely High Thermal Loads. Entropy. 2019; 21(10):983. https://doi.org/10.3390/e21100983
Chicago/Turabian StyleLi, En-Hui, Yun-Ze Li, Tian-Tian Li, Jia-Xin Li, Zhuang-Zhuang Zhai, and Tong Li. 2019. "Intelligent Analysis Algorithm for Satellite Health under Time-Varying and Extremely High Thermal Loads" Entropy 21, no. 10: 983. https://doi.org/10.3390/e21100983
APA StyleLi, E.-H., Li, Y.-Z., Li, T.-T., Li, J.-X., Zhai, Z.-Z., & Li, T. (2019). Intelligent Analysis Algorithm for Satellite Health under Time-Varying and Extremely High Thermal Loads. Entropy, 21(10), 983. https://doi.org/10.3390/e21100983





