Entropy Generation in Cu-Al2O3-H2O Hybrid Nanofluid Flow over a Curved Surface with Thermal Dissipation
Abstract
1. Introduction
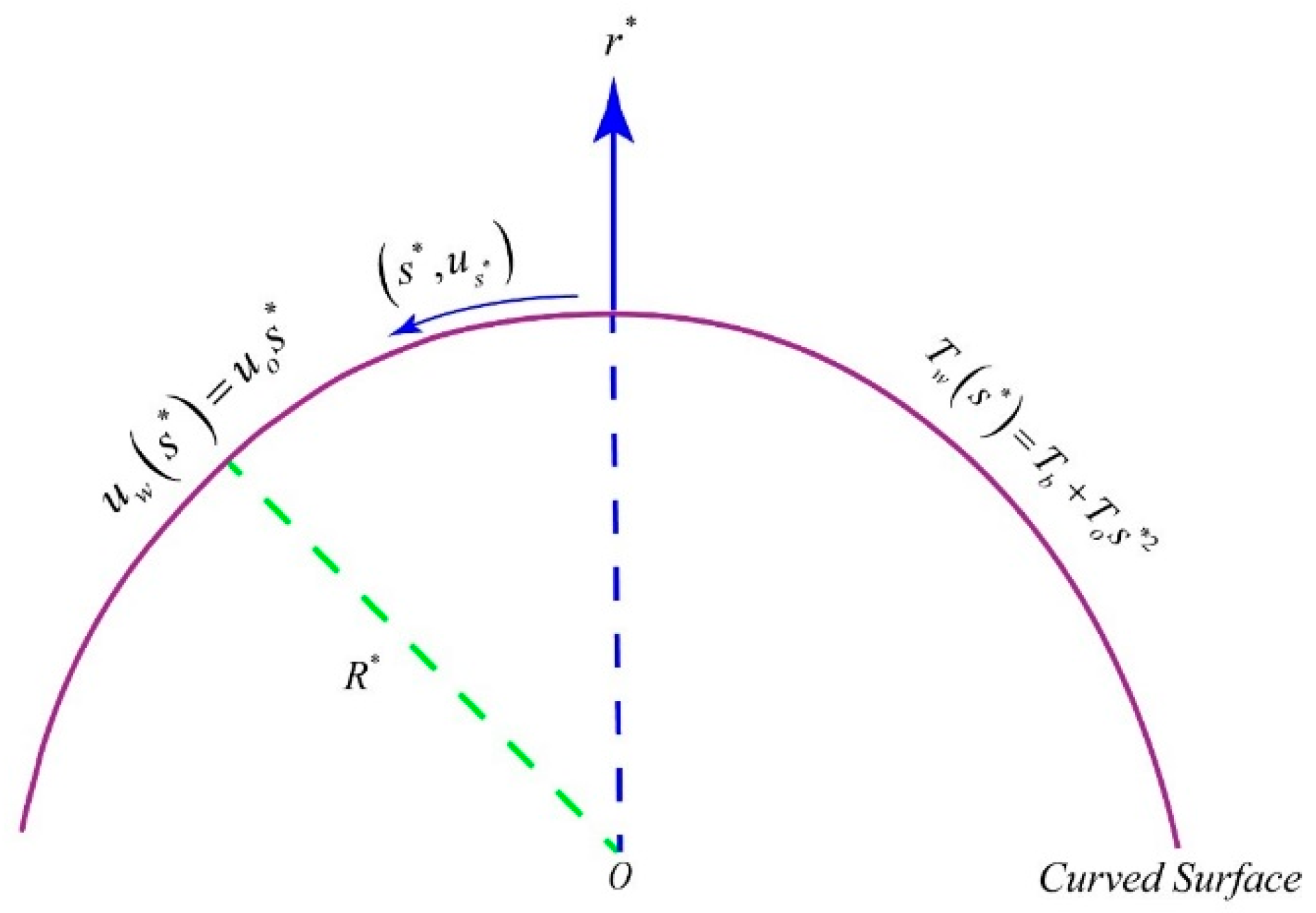
2. Model Formulation
2.1. Thermophysical Properties
2.1.1. Effective Density of Regular and Hybrid Nanoliquid
2.1.2. Effective Heat Capacitance of Regular and Hybrid Nanoliquids
2.1.3. Effective Thermal Conductivity of Regular and Hybrid Nanoliquids
2.1.4. Effective Dynamic Viscosity of Regular and Hybrid Nanoliquids
3. Entropy Generation Minimization (EGM)
4. Results and Discussion
5. Concluding Remarks
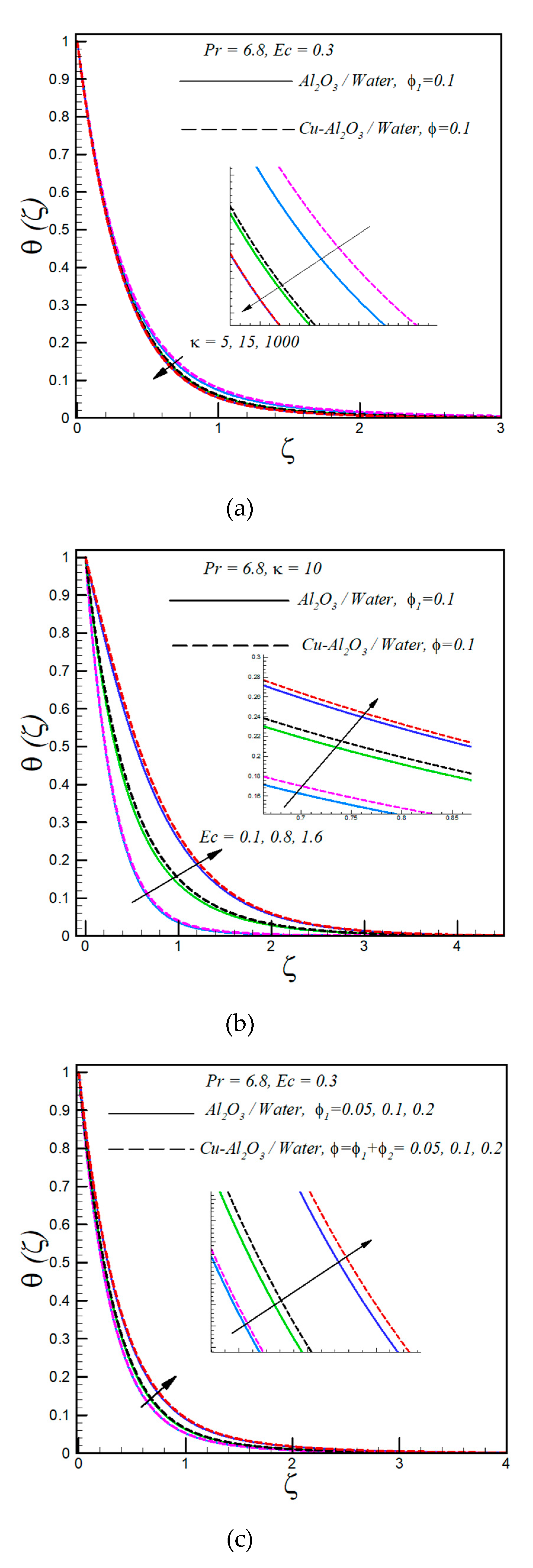
- An increment in the dimensionless radius of curvature leads to suppression of the temperature profile.
- An increment in the Eckert number and solid volume fraction of nanoparticles leads to boosting the temperature profile.
- A high rate of heat transfer is observed in hybrid nanofluid as compare to regular nanofluid.
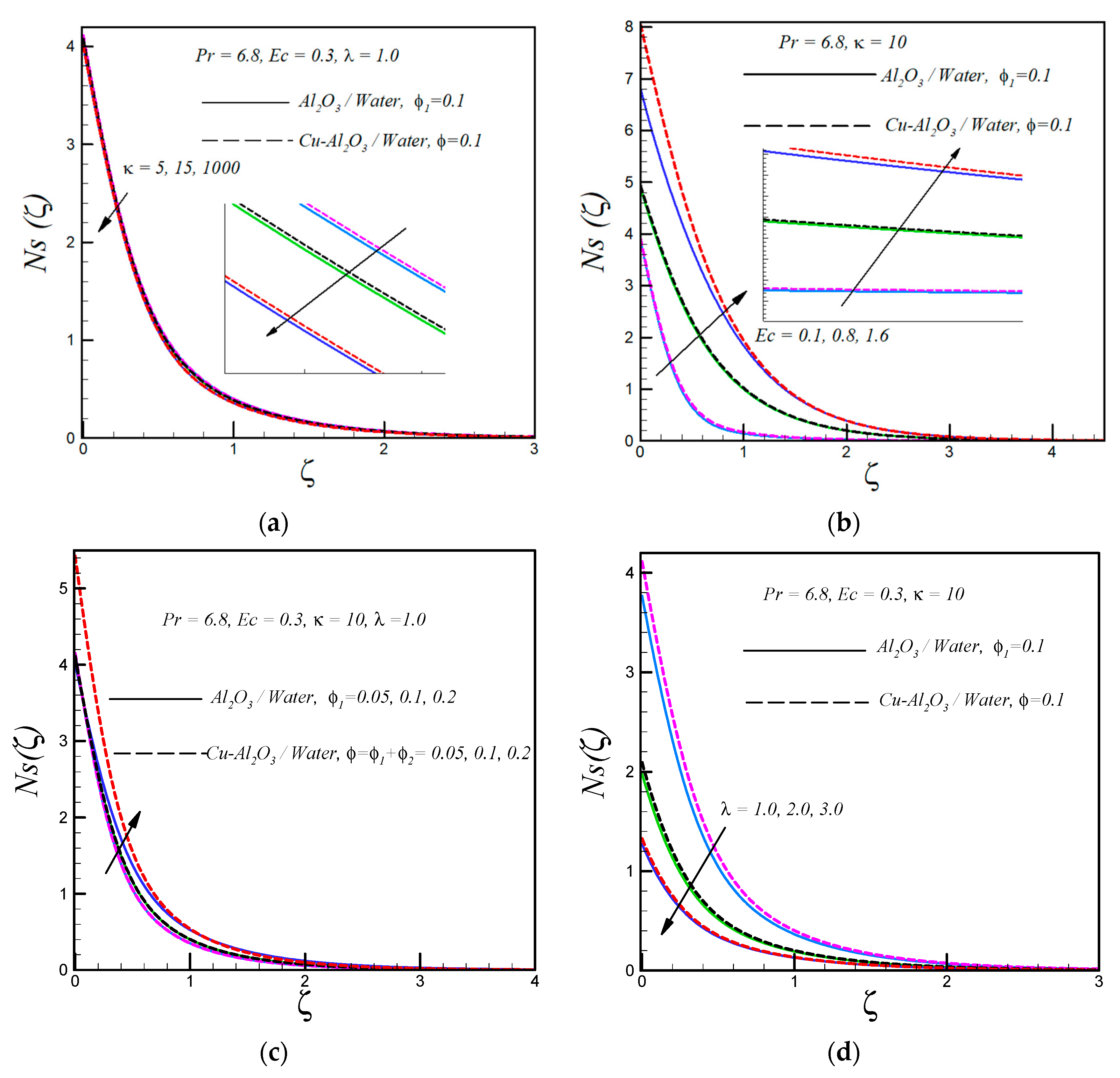
- The entropy generation profile is suppressed by rising values of the temperature difference parameter.
- Under the same circumstances, the rate of entropy generation is less in a flow over a flat surface as compared to the curved surface.
- The entropy generation Ns enhances with rising values of the solid volume fraction and the Eckert number.
- Less entropy is generated in the flow of regular nanofluid as compare to hybrid nanofluid.
- The entropy generation Ns is maximum at the solid boundary.
Author Contributions
Funding
Conflicts of Interest
References
- Bejan, A. The Method of Entropy Generation Minimization. In Energy and the Environment; Springer: Berlin, Germany, 1999; pp. 11–22. [Google Scholar]
- Butt, A.S.; Tufail, M.N.; Ali, A.; Dar, A. Theoretical investigation of entropy generation effects in nanofluid flow over an inclined stretching cylinder. Int. J. Exergy 2019, 28, 126–157. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Bagheri, S.; Momoniat, E.; Freidoonimehr, N. Entropy analysis of convective MHD flow of third grade non-Newtonian fluid over a stretching sheet. Ain Shams Eng. J. 2017, 8, 77–85. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Rashidi, M.M.; Ganji, D.D. Effect of non-uniform magnetic field on forced convection heat transfer of Fe3O4-water nanofluid. Comput. Methods Appl. Mech. Eng. 2015, 294, 299–312. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Nasiri, M.; Shadloo, M.S.; Yang, Z. Entropy Generation in a Circular Tube Heat Exchanger Using Nanofluids: Effects of Different Modeling Approaches. Heat Transf. Eng. 2017, 38, 853–866. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Abelman, S.; Mehr, N.F. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. Int. J. Heat Mass Transf. 2013, 62, 515–525. [Google Scholar] [CrossRef]
- Makinde, O.D. Second Law Analysis for Variable Viscosity Hydromagnetic Boundary Layer Flow with Thermal Radiation and Newtonian Heating. Entropy 2011, 13, 1446–1464. [Google Scholar] [CrossRef]
- Makinde, O.D.; Tshehla, M.S. Irreversibility analysis of MHD mixed convection channel flow of nanofluid with suction and injection. Glob. J. Pure Appl. Math. 2017, 13, 4851–4867. [Google Scholar]
- Butt, A.S.; Ali, A.; Mehmood, A. Entropy Generation Effects in Cu Water Nano Fluid Flow and Heat Transfer Over a Radially Stretching Surface. J. Nanofluids 2016, 5, 471–478. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M. Entropy generation and heat transfer in boundary layer flow over a thin needle moving in a parallel stream in the presence of non-linear Rosseland radiation. Int. J. Therm. Sci. 2018, 123, 117–128. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Tayebi, T.; Chamkha, A.J.; Hashim, I. Effect of rotating solid cylinder on entropy generation and convective heat transfer in a wavy porous cavity heated from below. Int. Commun. Heat Mass Transf. 2018, 95, 197–209. [Google Scholar] [CrossRef]
- Gebhart, B. Effects of viscous dissipation in natural convection. J. Fluid Mech. 1962, 14, 225–232. [Google Scholar] [CrossRef]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer: Berlin, Germany, 2016. [Google Scholar]
- Hsiao, K.-L. Conjugate heat transfer of magnetic mixed convection with radiative and viscous dissipation effects for second-grade viscoelastic fluid past a stretching sheet. Appl. Therm. Eng. 2007, 27, 1895–1903. [Google Scholar] [CrossRef]
- Lin, Y.; Zheng, L.; Chen, G. Unsteady flow and heat transfer of pseudo-plastic nanoliquid in a finite thin film on a stretching surface with variable thermal conductivity and viscous dissipation. Powder Technol. 2015, 274, 324–332. [Google Scholar] [CrossRef]
- Yazdi, M.H.; Hashim, I.; Sopian, K. Bin Slip boundary layer flow of a power-law fluid over moving permeable surface with viscous dissipation and prescribed surface temperature. Int. Rev. Mech. Eng. 2014, 8, 502–510. [Google Scholar]
- Hsiao, K.-L. Multimedia physical feature for unsteady MHD mixed convection viscoelastic fluid over a vertical stretching sheet with viscous dissipation. Int. J. Phys. Sci. 2012, 7, 2515–2524. [Google Scholar]
- Sreenivasulu, P.; Poornima, T.; Reddy, N.B. Thermal Radiation Effects on MHD Boundary Layer Slip Flow Past a permeable Exponential Stretching Sheet in the Presence of Joule Heating and Viscous Dissipation. J. Appl. Fluid Mech. 2016, 9, 267–278. [Google Scholar] [CrossRef]
- Makinde, O.D. Analysis of Sakiadis flow of nanofluids with viscous dissipation and Newtonian heating. Appl. Math. Mech. 2012, 33, 1545–1554. [Google Scholar] [CrossRef]
- Hsiao, K.-L. Combined electrical MHD heat transfer thermal extrusion system using Maxwell fluid with radiative and viscous dissipation effects. Appl. Therm. Eng. 2017, 112, 1281–1288. [Google Scholar] [CrossRef]
- Xiao, B.; Wang, W.; Zhang, X.; Long, G.; Fan, J.; Chen, H.; Deng, L. A novel fractal solution for permeability and Kozeny-Carman constant of fibrous porous media made up of solid particles and porous fibers. Powder Technol. 2019, 349, 92–98. [Google Scholar] [CrossRef]
- Liang, M.; Liu, Y.; Xiao, B.; Yang, S.; Wang, Z.; Han, H. An analytical model for the transverse permeability of gas diffusion layer with electrical double layer effects in proton exchange membrane fuel cells. Int. J. Hydrog. Energy 2018, 43, 17880–17888. [Google Scholar] [CrossRef]
- Long, G.; Liu, S.; Xu, G.; Wong, S.-W.; Chen, H.; Xiao, B. A Perforation-Erosion Model for Hydraulic-Fracturing Applications. SPE Prod. Oper. 2018, 33, 770–783. [Google Scholar] [CrossRef]
- Hashim, I.; Alsabery, A.I.; Sheremet, M.A.; Chamkha, A.J. Numerical investigation of natural convection of Al2O3-water nanofluid in a wavy cavity with conductive inner block using Buongiorno’s two-phase model. Adv. Powder Technol. 2019, 30, 399–414. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Gedik, E.; Chamkha, A.J.; Hashim, I. Effects of two-phase nanofluid model and localized heat source/sink on natural convection in a square cavity with a solid circular cylinder. Comput. Methods Appl. Mech. Eng. 2019, 346, 952–981. [Google Scholar] [CrossRef]
- Boulahia, Z.; Wakif, A.; Chamkha, A.J.; Amanulla, C.H.; Sehaqui, R. Effects of Wavy Wall Amplitudes on Mixed Convection Heat Transfer in a Ventilated Wavy Cavity Filled by Copper-Water Nanofluid Containing a Central Circular Cold Body. J. Nanofluids 2019, 8, 1170–1178. [Google Scholar] [CrossRef]
- Shenoy, A.; Sheremet, M.; Pop, I. Convective Flow and Heat Transfer from Wavy Surfaces: Viscous Fluids, Porous Media, and Nanofluids; CRC Press: Boca Raton, FL, USA, 2016; ISBN 9781315350653. [Google Scholar]
- Hsiao, K.-L. To promote radiation electrical MHD activation energy thermal extrusion manufacturing system efficiency by using Carreau-Nanofluid with parameters control method. Energy 2017, 130, 486–499. [Google Scholar] [CrossRef]
- Devi, S.U.M.A.; Devi, S.P.A. Heat transfer enhancement of Cu-Al2O3/water hybrid nanofluid flow over a stretching sheet. J. Niger. Math. Soc. 2017, 36, 419–433. [Google Scholar]
- Gorla, R.S.R.; Siddiqa, S.; Mansour, M.A.; Rashad, A.M.; Salah, T. Heat source/sink effects on a hybrid nanofluid-filled porous cavity. J. Thermophys. Heat Transf. 2017, 31, 847–857. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Khan, N.A.; Hamdani, M. Heat Transfer Analysis of Cu-Al2O3-Water and Cu-Al2O3-Kerosene Oil Hybrid Nanofluids in the Presence of Frictional Heating: Using 3-Stage Lobatto IIIA Formula. J. Nanofluids 2019, 8, 885–891. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Miroshnichenko, I.V.; Sheremet, M.A. Numerical analysis of unsteady conjugate natural convection of hybrid water-based nanofluid in a semicircular cavity. J. Therm. Sci. Eng. Appl. 2017, 9, 41004. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Saleem, S. Second law analysis of three dimensional dissipative flow of hybrid nanofluid. J. Nanofluids 2018, 7, 1272–1280. [Google Scholar] [CrossRef]
- Das, S.; Chakraborty, S.; Jana, R.N.; Makinde, O.D. Entropy Analysis of Nanofluid Flow Over a Convectively Heated Radially Stretching Disk Embedded in a Porous Medium. J. Nanofluids 2016, 5, 48–58. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A.; Mehmood, A. Numerical investigation of magnetic field effects on entropy generation in viscous flow over a stretching cylinder embedded in a porous medium. Energy 2016, 99, 237–249. [Google Scholar] [CrossRef]
- Roşca, N.C.; Pop, I. Unsteady boundary layer flow over a permeable curved stretching/shrinking surface. Eur. J. Mech. 2015, 51, 61–67. [Google Scholar] [CrossRef]
| Properties | Base Fluid (Water) | Al2O3 (Aluminum Oxide) | Cu (Copper) |
|---|---|---|---|
| 4179 | 765 | 385 | |
| 0.613 | 40 | 401 | |
| 997.1 | 3970 | 8933 | |
| 6.8 | - | - |
| Present Numerical Results | ||
|---|---|---|
| Bvp4c | RKFM | |
| 5 | 1.157632 | 1.157631 |
| 10 | 1.073487 | 1.073488 |
| 20 | 1.035610 | 1.035609 |
| 30 | 1.023531 | 1.023531 |
| 40 | 1.017588 | 1.017586 |
| 50 | 1.014048 | 1.014049 |
| 100 | 1.007039 | 1.007038 |
| 200 | 1.003554 | 1.003564 |
| 1000 | 1.000798 | 1.000799 |
| Rosca and Pop [36] | Present Results | |
|---|---|---|
| 5 | 1.15076 | 1.1576312 |
| 10 | 1.07172 | 1.0734886 |
| 20 | 1.03501 | 1.0356098 |
| 30 | 1.02315 | 1.0235310 |
| 40 | 1.01729 | 1.0175866 |
| 50 | 1.01380 | 1.0140492 |
| 100 | 1.00687 | 1.0070384 |
| 200 | 1.00342 | 1.0035641 |
| 1000 | 1.00068 | 1.0007993 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afridi, M.I.; Alkanhal, T.A.; Qasim, M.; Tlili, I. Entropy Generation in Cu-Al2O3-H2O Hybrid Nanofluid Flow over a Curved Surface with Thermal Dissipation. Entropy 2019, 21, 941. https://doi.org/10.3390/e21100941
Afridi MI, Alkanhal TA, Qasim M, Tlili I. Entropy Generation in Cu-Al2O3-H2O Hybrid Nanofluid Flow over a Curved Surface with Thermal Dissipation. Entropy. 2019; 21(10):941. https://doi.org/10.3390/e21100941
Chicago/Turabian StyleAfridi, Muhammad Idrees, Tawfeeq Abdullah Alkanhal, Muhammad Qasim, and Iskander Tlili. 2019. "Entropy Generation in Cu-Al2O3-H2O Hybrid Nanofluid Flow over a Curved Surface with Thermal Dissipation" Entropy 21, no. 10: 941. https://doi.org/10.3390/e21100941
APA StyleAfridi, M. I., Alkanhal, T. A., Qasim, M., & Tlili, I. (2019). Entropy Generation in Cu-Al2O3-H2O Hybrid Nanofluid Flow over a Curved Surface with Thermal Dissipation. Entropy, 21(10), 941. https://doi.org/10.3390/e21100941






