AKL-ABC: An Automatic Approximate Bayesian Computation Approach Based on Kernel Learning
Abstract
1. Introduction
- We propose a novel automatic ABC approach for computing posterior estimates avoiding any tuning procedure of free parameters. In detail, a Mahalanobis distance is optimized through a CKA-based algorithm to code the simulation and parameter space matching and an information theoretic learning (ITL)-based method to learn the kernel bandwidth. Furthermore, a graph representation is carried out to highlight local dependencies utilizing a local neighborhood selection (LNS).
- The mathematical models regarding AKL-ABC are described and enhanced (including the CKA and LNS coupling with ABC through kernel machines and graph theory).
- The experiments are expanded and explained in detail considering well-known challenging databases.
- A free parameter analysis is provided to show the performance of our AKL-ABC as an automatic approximate inference method.
2. Related Work
2.1. Summary Statistics-Based Approaches
2.2. Weighting-Based Techniques
2.3. Regression-Adjustment Methods
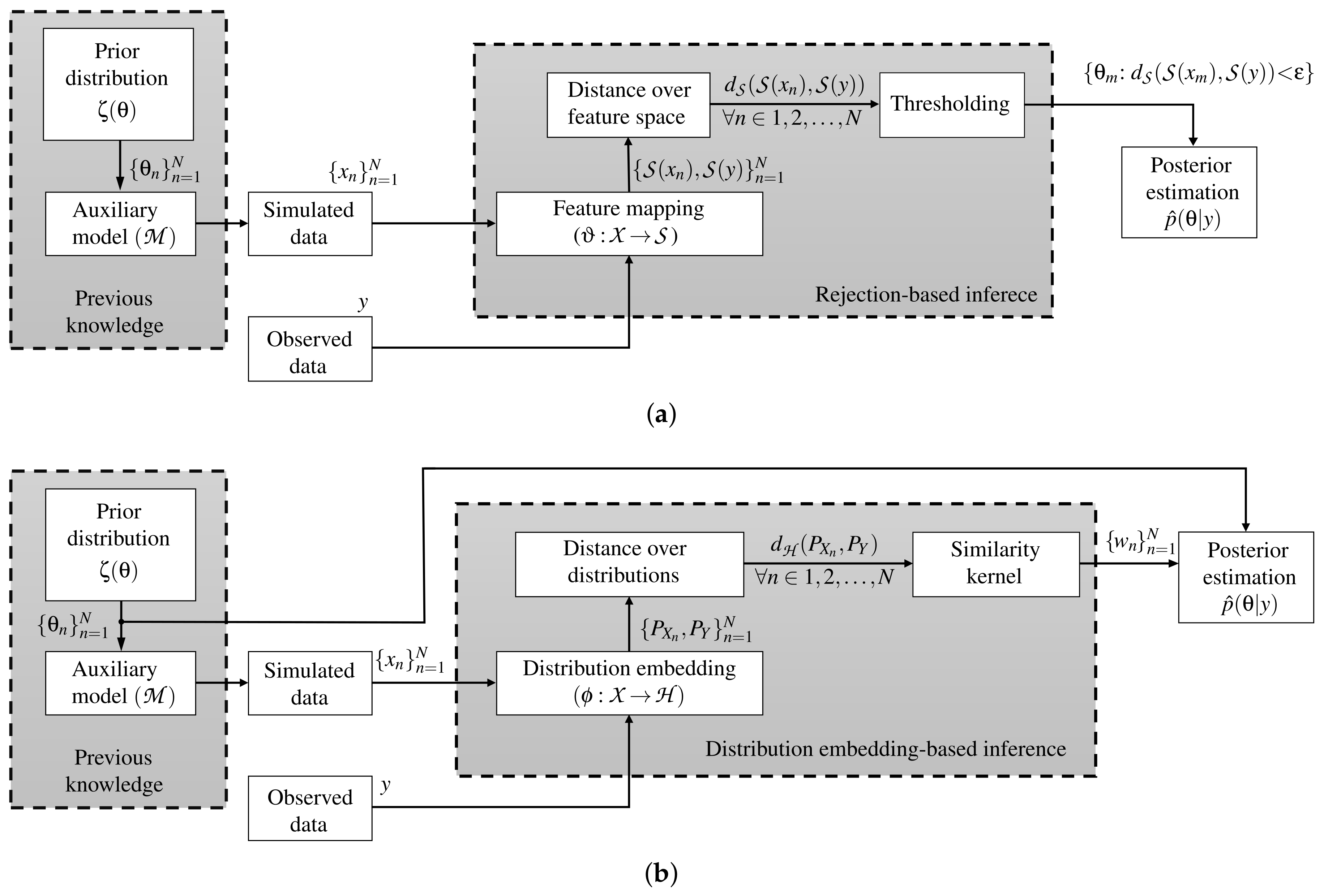
3. Materials and Methods
3.1. ABC Fundamentals
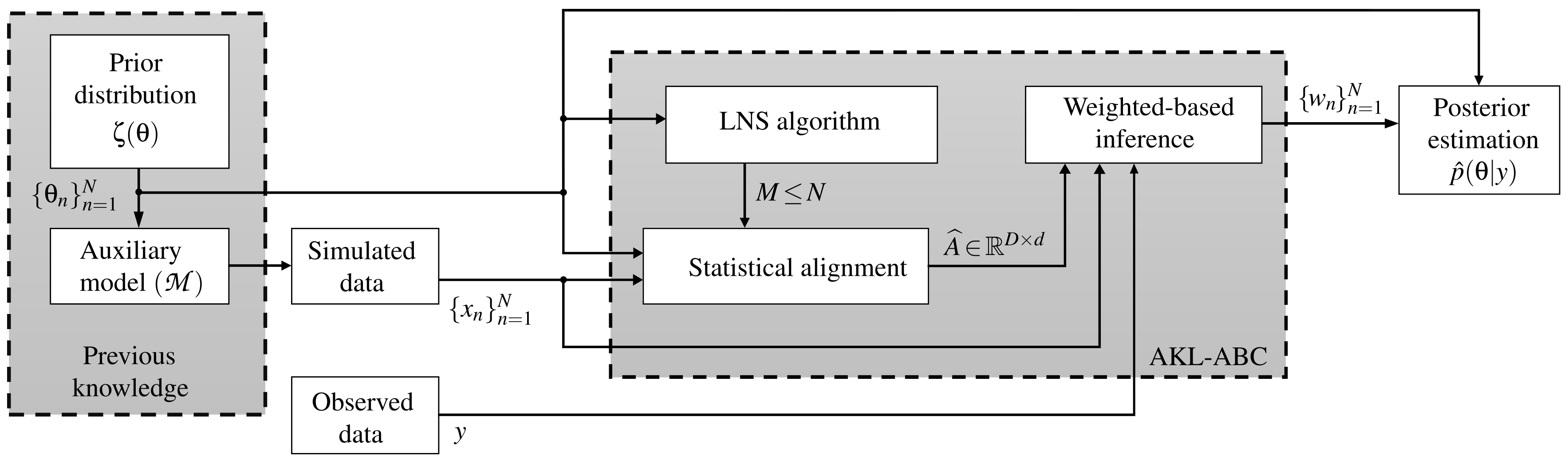
3.2. Automatic ABC Based on Kernel Learning
3.2.1. Kernel Learning in the Context of ABC
3.2.2. Tuning Through Nearest Neighbors Based on Graph Theory
| Algorithm 1 AKL-ABC algorithm | |
| Input: Observed data: y, prior: , mapping: . | |
| Output: Posterior estimation: | |
| Kernel learning stage: | |
| 1: | ▹ Draw training data. |
| 2: | ▹ Highlight local dependencies in using LNS. |
| 3: | ▹ Compute the CKA based on and |
| Inference stage: | |
| 4: | ▹ Draw simulated data. |
| 5: | ▹ Project features of observed data |
| 6: for do | |
| 7: | ▹ ▹ Project features of simulated data |
| 8: | ▹ Compute the n-th weight value. |
| 9: end for | |
| 10: | ▹ Normalize the weights |
| 10: | ▹ Approximate the posterior. |
3.3. Theoretical Aspects of AKL-ABC
4. Experimental Setup
4.1. Datasets and Quality Assessment
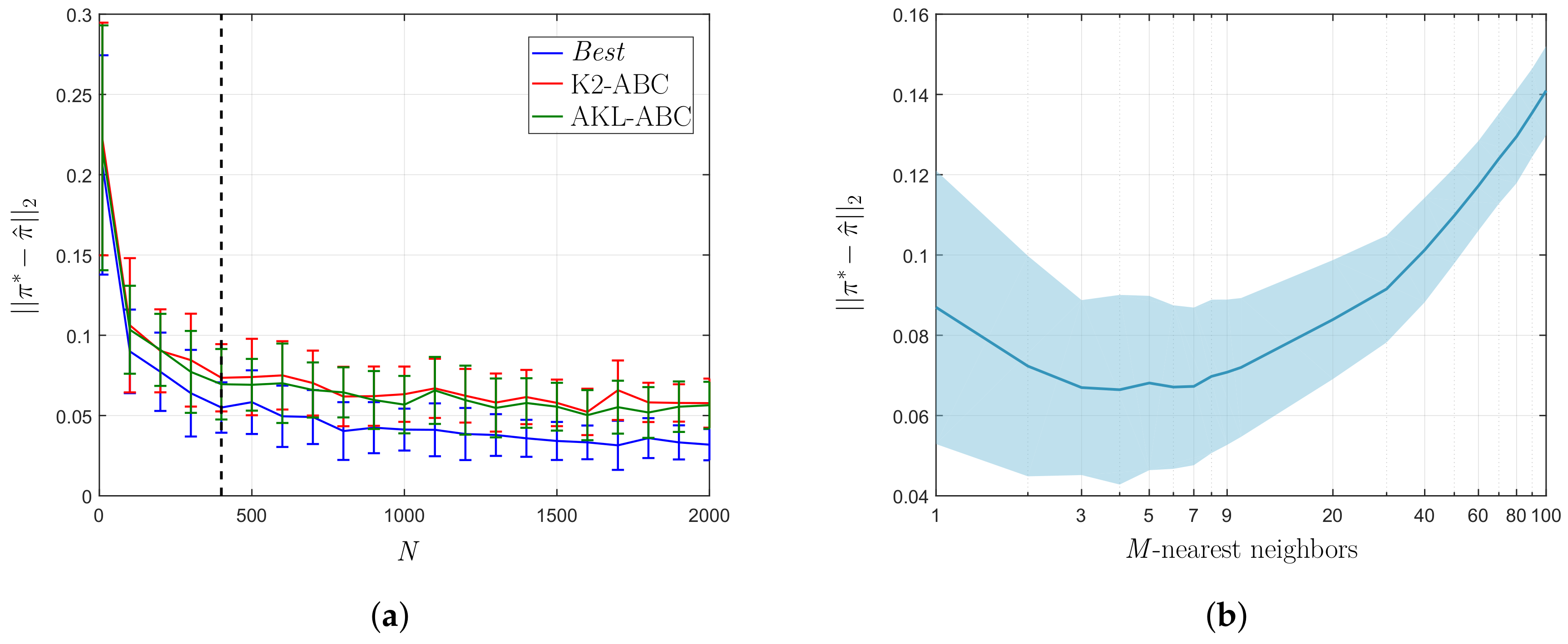
4.2. AKL-ABC Training and Method Comparison
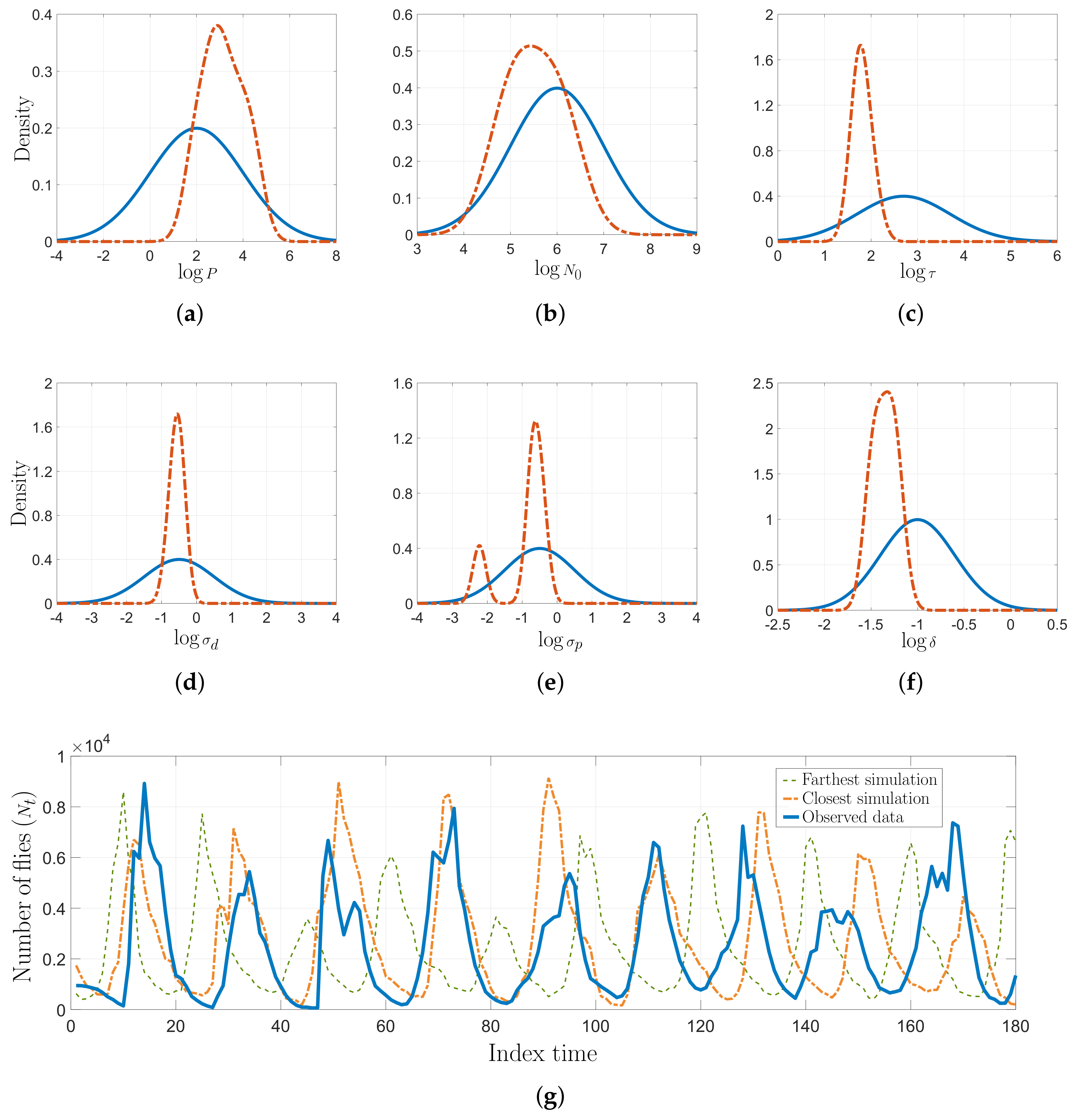
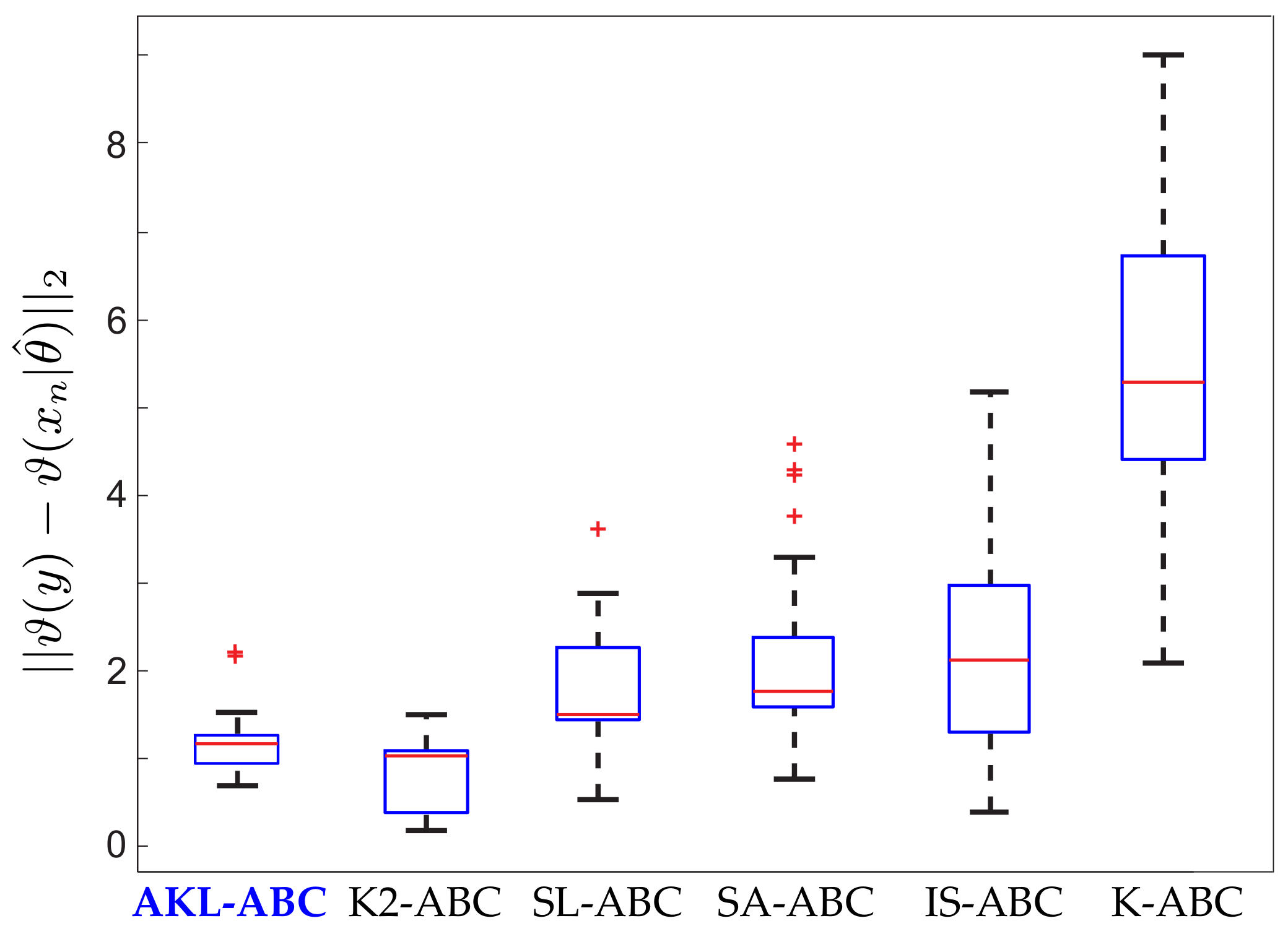
5. Results and Discussion
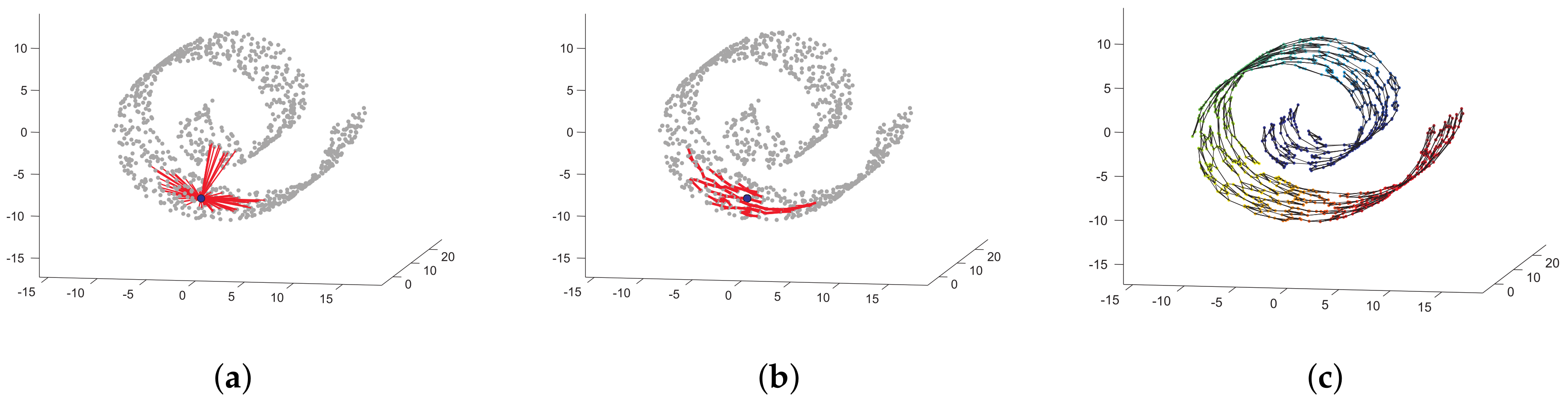
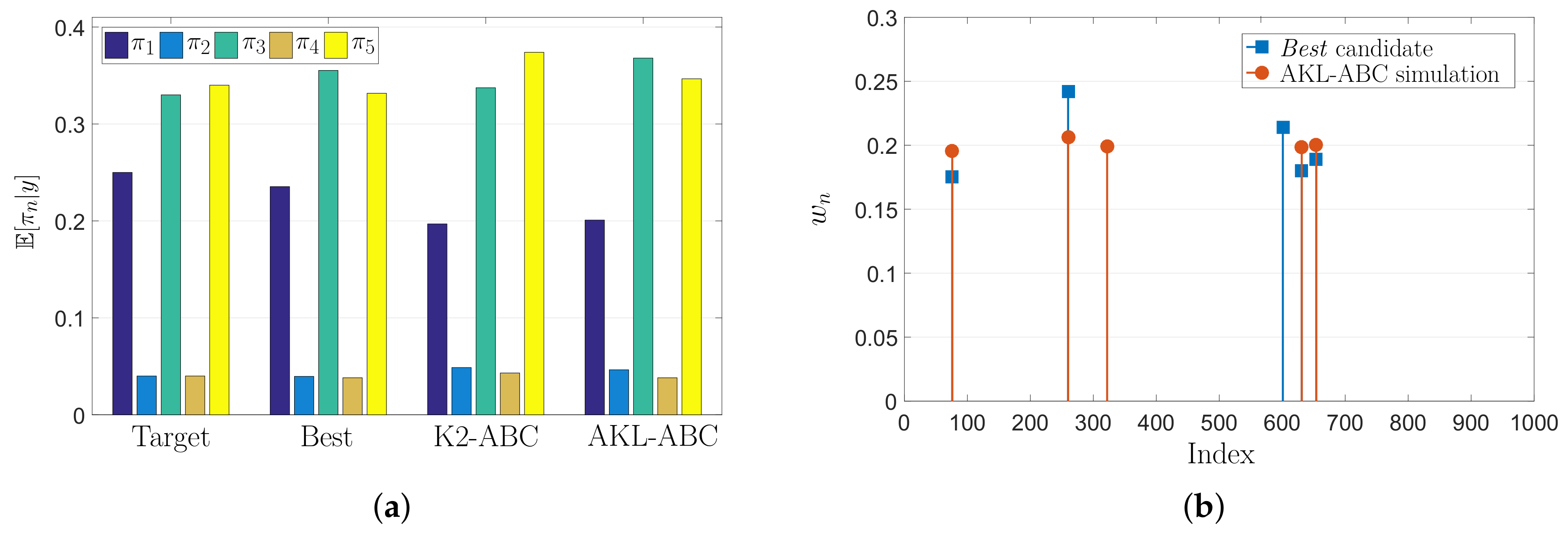
5.1. Toy Problem Results
5.2. Real Dataset Results
5.3. Computational Tractability
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Symbol | Description |
| Parameter space | |
| Simulations space | |
| Feature space | |
| Reproducing Kernel Hilbert Space (RKHS) | |
| n-th prior sample | |
| n-th simulation | |
| y | Observed data |
| Representation weight associated to the n-th prior sample | |
| Projection of the n-th simulation | |
| Set of the M-nearest neighbors of according to the LNS algorithm | |
| Set of the M-nearest neighbors of projected features of the observed data | |
| Auxiliary model | |
| Feature mapping | |
| Mapping function associated to the RHKS | |
| Kernel function | |
| Gaussian kernel | |
| Similarity kernel | |
| Statistical alignment between two kernel matrices | |
| -order Information Potencial | |
| Distance between prior samples | |
| Distance between simulations | |
| Distance between features of simulations | |
| Distance between distributions in an RKHS | |
| Euclidean distance | |
| Prior distribution | |
| Posterior distribution | |
| Likelihood function | |
| Conditional distribution associated to simulations | |
| Distribution of the n-th simulation | |
| Distribution of the observed data | |
| Kernel matrix over prior samples | |
| Kernel matrix over features of simulations | |
| Projection matrix for the Centered Kernel Alignment (CKA) | |
| Sample covariance matrix of prior samples | |
| Feature matrix of simulations | |
| Threshold for rejection ABC | |
| Gaussian kernel bandwidths | |
| M | M-nearest neighbors according to the LNS algorithm |
| number of iterations performed by the LNS algorithm | |
| G | number of iterations required by the gradient-descent method in AKL-ABC |
| Step sizes for gradient descent rules |
Appendix A. Local Neighborhood Selection (LNS) Algorithm
- Compute the Euclidean distance for all points in .
- Construct the minimal connected neighborhood graph of the given dataset by the M-nearest neighbors method (MNN) fixing the smallest neighborhood size . Check the full connectivity of the graph by using the Breadth-first search (BFS) [39]. If the graph is not full connected, update and start again this step.
- Compute the geodesic distance over by using the Dijistra’s algorithm [39].
- Define , where is the number of edges in and N the number of samples in .
- Set the vector , with . The vector contains the possible values of m for each .
- For each define the sets and , with . Each element in and corresponds to the nearest neighbors of () according to the Euclidean and geodesic distances, respectively.
- Calculate the linearity conservation matrix , which analyses the similarity of the neighborhoods obtained by and , taking into account the patch size. Each element of can be computed as, , where calculates the cardinality of a set and the complement.
- Initially, for each define the set . Verify the equality , where is the i-th row vector of . If the equality is fulfilled, then update .
- Define for each as .
- Smooth to obtain similar properties in surrounding neighborhoods according to , where is a vector with the sizes of the neighborhoods of each element in (set with the first nearest neighbors of according to the Euclidean distance, ).
- Store all the values into the vector .
- Remove the outliers in (see [40]), and replace them by the average of the elements in , which were not identified as outliers.
- Each element in contains the number of nearest neighbors for each .
References
- Wasserman, L. Models, Statistical Inference and Learning. In All of Statistics: A Concise Course in Statistical Inference; Springer: New York, NY, USA, 2004; pp. 87–96. [Google Scholar] [CrossRef]
- Thijssen, J. A Concise Introduction to Statistical Inference; Chapman and Hall/CRC: London, UK, 2016. [Google Scholar]
- Casella, G.; Berger, R.L. Statistical Inference; Duxbury: Pacific Grove, CA, USA, 2002; Volume 2. [Google Scholar]
- Bickel, P.; Klaassen, C.; Ritov, Y.; Wellner, J. Efficient and Adaptive Estimation for Semiparametric Models; Johns Hopkins Series in the Mathematical Sciences; Springer: New York, NY, USA, 1998. [Google Scholar]
- Box, G.E.; Tiao, G.C. Bayesian Inference in Statistical Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 40. [Google Scholar]
- Meeker, W.Q.; Hahn, G.J.; Escobar, L.A. Statistical Intervals: A Guide for Practitioners and Researchers; John Wiley & Sons: Hoboken, NJ, USA, 2017; Volume 541. [Google Scholar]
- Toni, T.; Welch, D.; Strelkowa, N.; Ipsen, A.; Stumpf, M. Approximate Bayesian computation scheme for parameter inference and model selection in dynamical systems. J. R. Soc. Interface 2009, 6, 187–202. [Google Scholar] [CrossRef] [PubMed]
- Pritchard, J.K.; Seielstad, M.T.; Perez-Lezaun, A.; Feldman, M.W. Population growth of human Y chromosomes: A study of Y chromosome microsatellites. Mol. Biol. Evol. 1999, 16, 1791–1798. [Google Scholar] [CrossRef] [PubMed]
- Liepe, J.; Kirk, P.; Filippi, S.; Toni, T.; Barnes, C.; Stumpf, M. A framework for parameter estimation and model selection from experimental data in systems biology using approximate Bayesian computation. Nat. Protoc. 2014, 9, 439–456. [Google Scholar] [CrossRef] [PubMed]
- Holden, P.B.; Edwards, N.R.; Hensman, J.; Wilkinson, R.D. ABC for Climate: Dealing with Expensive Simulators. In Handbook of Approximate Bayesian Computation; CRC Press: Boca Raton, FL, USA, 2018; Chapter 19. [Google Scholar] [CrossRef]
- Fasiolo, M.; Wood, S.N. Approximate methods for dynamic ecological models. arXiv 2015, arXiv:1511.02644. [Google Scholar]
- Fan, Y.; Meikle, S.R.; Angelis, G.; Sitek, A. ABC in nuclear imaging. In Handbook of Approximate Bayesian Computation; CRC Press: Boca Raton, FL, USA, 2018; Chapter 25. [Google Scholar] [CrossRef]
- Wawrzynczak, A.; Kopka, P. Approximate Bayesian Computation for Estimating Parameters of Data-Consistent Forbush Decrease Model. Entropy 2018, 20, 622. [Google Scholar] [CrossRef]
- Turner, B.M.; Zandt, T.V. A tutorial on approximate Bayesian computation. J. Math. Psychol. 2012, 56, 69–85. [Google Scholar] [CrossRef]
- Hainy, M.; Müller, W.G.; Wynn, H.P. Learning Functions and Approximate Bayesian Computation Design: ABCD. Entropy 2014, 16, 4353–4374. [Google Scholar] [CrossRef]
- Fearnhead, P.; Prangle, D. Constructing summary statistics for approximate Bayesian computation: semi-automatic approximate Bayesian computation [with Discussion]. J. R. Stat. Soc. Ser. (Stat. Methodol.) 2012, 74, 419–474. [Google Scholar] [CrossRef]
- Joyce, P.; Marjoram, P. Approximately sufficient statistics and bayesian computation. Stat. Appl. Genet. Mol. Biol. 2008, 7. [Google Scholar] [CrossRef]
- Wood, S. Statistical inference for noisy nonlinear ecological dynamic systems. Nature 2010, 466, 1102–1104. [Google Scholar] [CrossRef]
- Gleim, A.; Pigorsch, C. Approximate Bayesian Computation with Indirect Summary Statistics. Available online: http://ect-pigorsch.mee.uni-bonn.de/data/research/papers (accessed on 10 July 2019).
- Park, M.; Jitkrittum, W.; Sejdinovic, D. K2-ABC: Approximate Bayesian Computation with Kernel Embeddings. In Proceedings of the 19th International Conference on Artificial Intelligence and Statistics, Cadiz, Spain, 9–11 May 2016; Gretton, A., Robert, C.C., Eds.; PMLR: Cadiz, Spain, 2016; Volume 51, pp. 398–407. [Google Scholar]
- González-Vanegas, W.; Alvarez-Meza, A.; Orozco-Gutierrez, Á. Sparse Hilbert Embedding-Based Statistical Inference of Stochastic Ecological Systems. In Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications; Mendoza, M., Velastín, S., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 255–262. [Google Scholar]
- Cortes, C.; Mohri, M.; Rostamizadeh, A. Algorithms for Learning Kernels Based on Centered Alignment. J. Mach. Learn. Res. 2012, 13, 795–828. [Google Scholar]
- González-Vanegas, W.; Álvarez-Meza, A.; Orozco-Gutiérrez, A. An Automatic Approximate Bayesian Computation Approach Using Metric Learning. In Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications; Vera-Rodriguez, R., Fierrez, J., Morales, A., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 12–19. [Google Scholar]
- Beaumont, M.A. Approximate Bayesian Computation. Annu. Rev. Stat. Its Appl. 2019, 6, 379–403. [Google Scholar] [CrossRef]
- Prangle, D. Summary statistics in approximate Bayesian computation. In Handbook of Approximate Bayesian Computation; CRC Press: Boca Raton, FL, USA, 2018; Chapter 5. [Google Scholar] [CrossRef]
- Pigorsch, E.G.C. Approximate Bayesian Computation with Indirect Summary Statistics. Technical Report. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.665.5503 (accessed on 19 September 2019).
- Nakagome, S.; Fukumizu, K.; Mano, S. Kernel approximate Bayesian computation in population genetic inferences. Stat. Appl. Genet. Mol. Biol. 2013, 12, 667–678. [Google Scholar] [CrossRef] [PubMed]
- Mitrovic, J.; Sejdinovic, D.; Teh, Y.W. DR-ABC: Approximate Bayesian Computation with Kernel-Based Distribution Regression. In Machine Learning Research, Proceedings of the 33rd International Conference on Machine Learning; Balcan, M.F., Weinberger, K.Q., Eds.; PMLR: New York, NY, USA, 2016; Volume 48, pp. 1482–1491. [Google Scholar]
- Meeds, E.; Welling, M. GPS-ABC: Gaussian Process Surrogate Approximate Bayesian Computation. arXiv 2014, arXiv:1401.2838. [Google Scholar]
- Jiang, B.; Wu, T.Y.; Zheng, C.; Wong, W.H. Learning summary statistic for approximate bayesian computation via deep neural network. Stat. Sin. 2017, 27, 1595–1618. [Google Scholar]
- Creel, M. Neural nets for indirect inference. Econom. Stat. 2017, 2, 36–49. [Google Scholar] [CrossRef]
- Alvarez-Meza, A.M.; Orozco-Gutierrez, A.; Castellanos-Dominguez, G. Kernel-Based Relevance Analysis with Enhanced Interpretability for Detection of Brain Activity Patterns. Front. Neurosci. 2017, 11, 550. [Google Scholar] [CrossRef]
- Brockmeier, A.J.; Choi, J.S.; Kriminger, E.G.; Francis, J.T.; Principe, J.C. Neural Decoding with Kernel-Based Metric Learning. Neural Comput. 2014, 26, 1080–1107. [Google Scholar] [CrossRef]
- Álvarez-Meza, A.M.; Cárdenas-Peña, D.; Castellanos-Dominguez, G. Unsupervised Kernel Function Building Using Maximization of Information Potential Variability. In Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications; Bayro-Corrochano, E., Hancock, E., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 335–342. [Google Scholar]
- Álvarez Meza, A.; Valencia-Aguirre, J.; Daza-Santacoloma, G.; Castellanos-Domínguez, G. Global and local choice of the number of nearest neighbors in locally linear embedding. Pattern Recognit. Lett. 2011, 32, 2171–2177. [Google Scholar] [CrossRef]
- Cristianini, N.; Shawe-Taylor, J.; Elisseeff, A.; Kandola, J.S. On Kernel-Target Alignment. In Advances in Neural Information Processing Systems 14; Dietterich, T.G., Becker, S., Ghahramani, Z., Eds.; MIT Press: Cambridge, MA, USA, 2002; pp. 367–373. [Google Scholar]
- Shimazaki, H.; Shinomoto, S. Kernel bandwidth optimization in spike rate estimation. J. Comput. Neurosci. 2010, 29, 171–182. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, H.; He, P.; Chen, W.; Liu, X.; Gao, J.; Han, J. On the Variance of the Adaptive Learning Rate and Beyond. arXiv 2019, arXiv:1908.03265. [Google Scholar]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach, 3rd ed.; Series in Artificial Intelligence; Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Rencher, A.C. Methods of Multivariate Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2003; Volume 492. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Vanegas, W.; Álvarez-Meza, A.; Hernández-Muriel, J.; Orozco-Gutiérrez, Á. AKL-ABC: An Automatic Approximate Bayesian Computation Approach Based on Kernel Learning. Entropy 2019, 21, 932. https://doi.org/10.3390/e21100932
González-Vanegas W, Álvarez-Meza A, Hernández-Muriel J, Orozco-Gutiérrez Á. AKL-ABC: An Automatic Approximate Bayesian Computation Approach Based on Kernel Learning. Entropy. 2019; 21(10):932. https://doi.org/10.3390/e21100932
Chicago/Turabian StyleGonzález-Vanegas, Wilson, Andrés Álvarez-Meza, José Hernández-Muriel, and Álvaro Orozco-Gutiérrez. 2019. "AKL-ABC: An Automatic Approximate Bayesian Computation Approach Based on Kernel Learning" Entropy 21, no. 10: 932. https://doi.org/10.3390/e21100932
APA StyleGonzález-Vanegas, W., Álvarez-Meza, A., Hernández-Muriel, J., & Orozco-Gutiérrez, Á. (2019). AKL-ABC: An Automatic Approximate Bayesian Computation Approach Based on Kernel Learning. Entropy, 21(10), 932. https://doi.org/10.3390/e21100932




