Orthogonal Chaotic Binary Sequences Based on Bernoulli Map and Walsh Functions
Abstract
:1. Introduction
2. Preliminaries
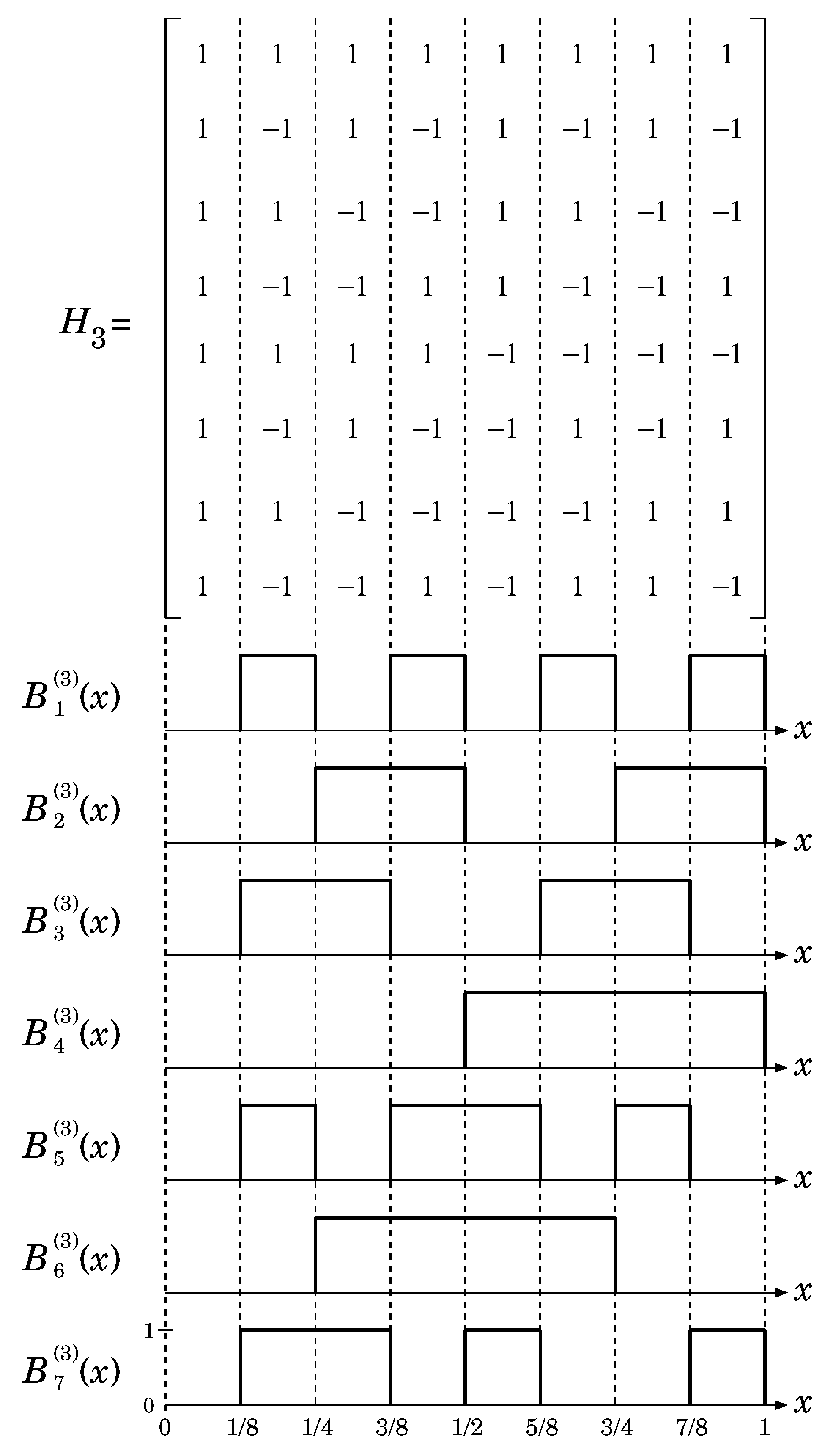
3. Hadamard Matrix and Walsh Functions
4. Orthogonal Chaotic Binary Sequences
5. Conclusions
Funding
Conflicts of Interest
References
- Kohda, T.; Tsuneda, A. Statistics of chaotic binary sequences. IEEE Trans. Inf. Theory 1997, 43, 104–112. [Google Scholar] [CrossRef]
- Kohda, T.; Tsuneda, A. Design of sequences of i.i.d. p-ary random variables. In Proceedings of the 1997 IEEE International Symposium on Information Theory, Ulm, Germany, 6–7 July 1997; p. 17. [Google Scholar]
- Kennedy, M.; Setti, G.; Rovatti, R. Chaotic Electronics in Telecommunications; CRC Press: New York, NY, USA, 2000. [Google Scholar]
- Stojanovski, T.; Kocarev, L. Chaos-based random number generators—Part I: analysis. IEEE Trans. Circuits Syst. I 2001, 48, 281–288. [Google Scholar] [CrossRef]
- Stojanovski, T.; Pihl, J.; Kocarev, L. Chaos-based random umber generators—Part II: practical realization. IEEE Trans. Circuits Syst. I 2001, 48, 382–385. [Google Scholar] [CrossRef]
- Bernardini, R.; Cortelazzo, G. Tools for designing chaotic systems for secure random number generation. IEEE Trans. Circuits Syst. I 2001, 48, 552–564. [Google Scholar] [CrossRef]
- Gerosa, A.; Bernardini, R.; Pietri, S. A fully integrated chaotic system for the generation of truly random numbers. IEEE Trans. Circuits Syst. I 2001, 49, 993–1000. [Google Scholar] [CrossRef]
- Fort, A.; Cortigiani, F.; Rocchi, S.; Vignoli, V. Very high-speed true random noise generator. Analog Integr. Circuits Process. 2003, 34, 97–105. [Google Scholar] [CrossRef]
- Kyaw, T.N.N.; Tsuneda, A. Generation of chaos-based random bit sequences with prescribed auto-correlations by post-processing using linear feedback shift registers. NOLTA 2017, 8, 224–234. [Google Scholar] [CrossRef]
- Demir, K.; Ergün, S. An analysis of deterministic chaos as an entropy source for random number generators. Entropy 2018, 20, 957. [Google Scholar] [CrossRef]
- Li, C.; Feng, B.; Li, S.; Kurths, J.; Chen, G. Dynamic analysis of digital chaotic maps via state-mapping networks. IEEE Trans. Circuits Syst. I 2019, 66, 2322–2335. [Google Scholar] [CrossRef]
- Tsuneda, A. Orthogonal chaotic binary sequences based on Walsh functions. In Proceedings of the Second International Workshop on Sequence Design and Its Applications in Communications, Shimonoseki, Japan, 10–14 October 2005. [Google Scholar]
- Beauchamp, K.G. Walsh Functions and Their Applications; Academic Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Davies, A.C. On the definition and generation of Walsh functions. IEEE Trans. Comput. 1972, 100, 187–189. [Google Scholar] [CrossRef]
- Geadah, Y.A.; Corinthios, M.J.G. Natural, dyadic, and sequency order algorithms and processors for the Walsh-Hadamard transform. IEEE Trans. Comput. 1977, C-26, 435–442. [Google Scholar] [CrossRef]
- Golubov, B.; Efimov, A.; Skvortsov, V. Walsh Series and Transforms; Springer: Berlin/Heidelberger, Germany, 1991. [Google Scholar]
- Wang, X.; Liang, X.; Zheng, J.; Zhou, H. Fast detection and segmentation of partial image blur based on discrete Walsh-Hadamard transform. Signal Process.-Image Commun. 2019, 70, 47–56. [Google Scholar] [CrossRef]
- Lasota, A.; Mackey, M.C. Chaos, Fractals, and Noise; Springer: Berlin/Heidelberger, Germany, 1994. [Google Scholar]
- Tsuneda, A.; Kuga, Y.; Inoue, T. New maximal-period sequences using extended nonlinear feedback shift registers based on chaotic maps. IEICE Trans. Fundamentals 2001, E85-A, 1327–1332. [Google Scholar]
- Golomb, S.W. Shift Register Sequences; revised ed.; Aegean Park Press: Laguna Hills, CA, USA, 1982. [Google Scholar]

| Binary Function | Evaluation Result |
|---|---|
| balanced and i.i.d. | |
| balanced and i.i.d. | |
| balanced and i.i.d. | |
| balanced and i.i.d. | |
| balanced and i.i.d. | |
| balanced and i.i.d. | |
| balanced and i.i.d. | |
| balanced and i.i.d. |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsuneda, A. Orthogonal Chaotic Binary Sequences Based on Bernoulli Map and Walsh Functions. Entropy 2019, 21, 930. https://doi.org/10.3390/e21100930
Tsuneda A. Orthogonal Chaotic Binary Sequences Based on Bernoulli Map and Walsh Functions. Entropy. 2019; 21(10):930. https://doi.org/10.3390/e21100930
Chicago/Turabian StyleTsuneda, Akio. 2019. "Orthogonal Chaotic Binary Sequences Based on Bernoulli Map and Walsh Functions" Entropy 21, no. 10: 930. https://doi.org/10.3390/e21100930
APA StyleTsuneda, A. (2019). Orthogonal Chaotic Binary Sequences Based on Bernoulli Map and Walsh Functions. Entropy, 21(10), 930. https://doi.org/10.3390/e21100930





