Enhanced Negative Nonlocal Conductance in an Interacting Quantum Dot Connected to Two Ferromagnetic Leads and One Superconducting Lead
Abstract
:1. Introduction
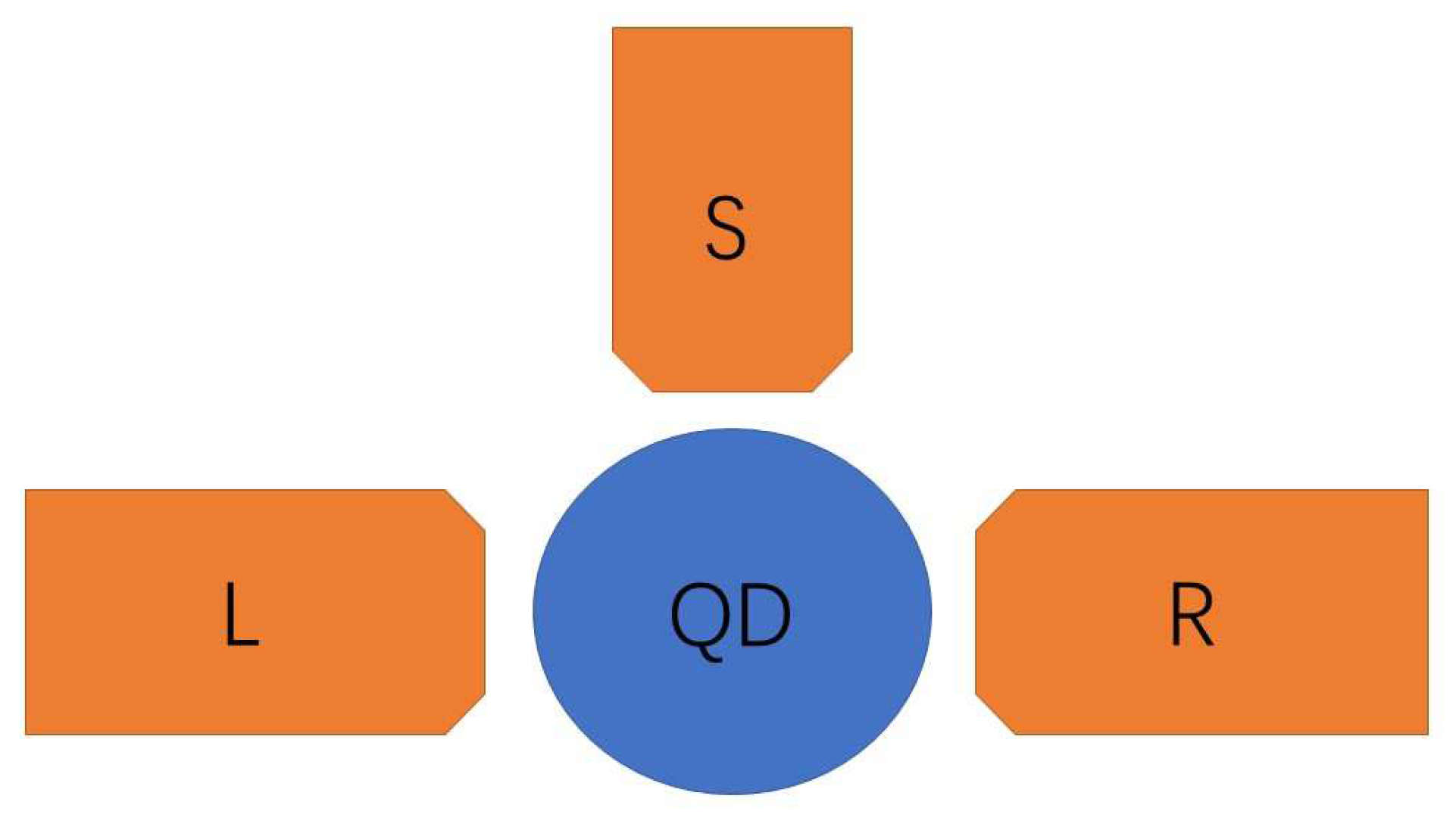
2. Model and Theoretical Formulation
2.1. Model Hamiltonian
2.2. Self-Consistent Equations
2.3. The Current and Linear Conductance
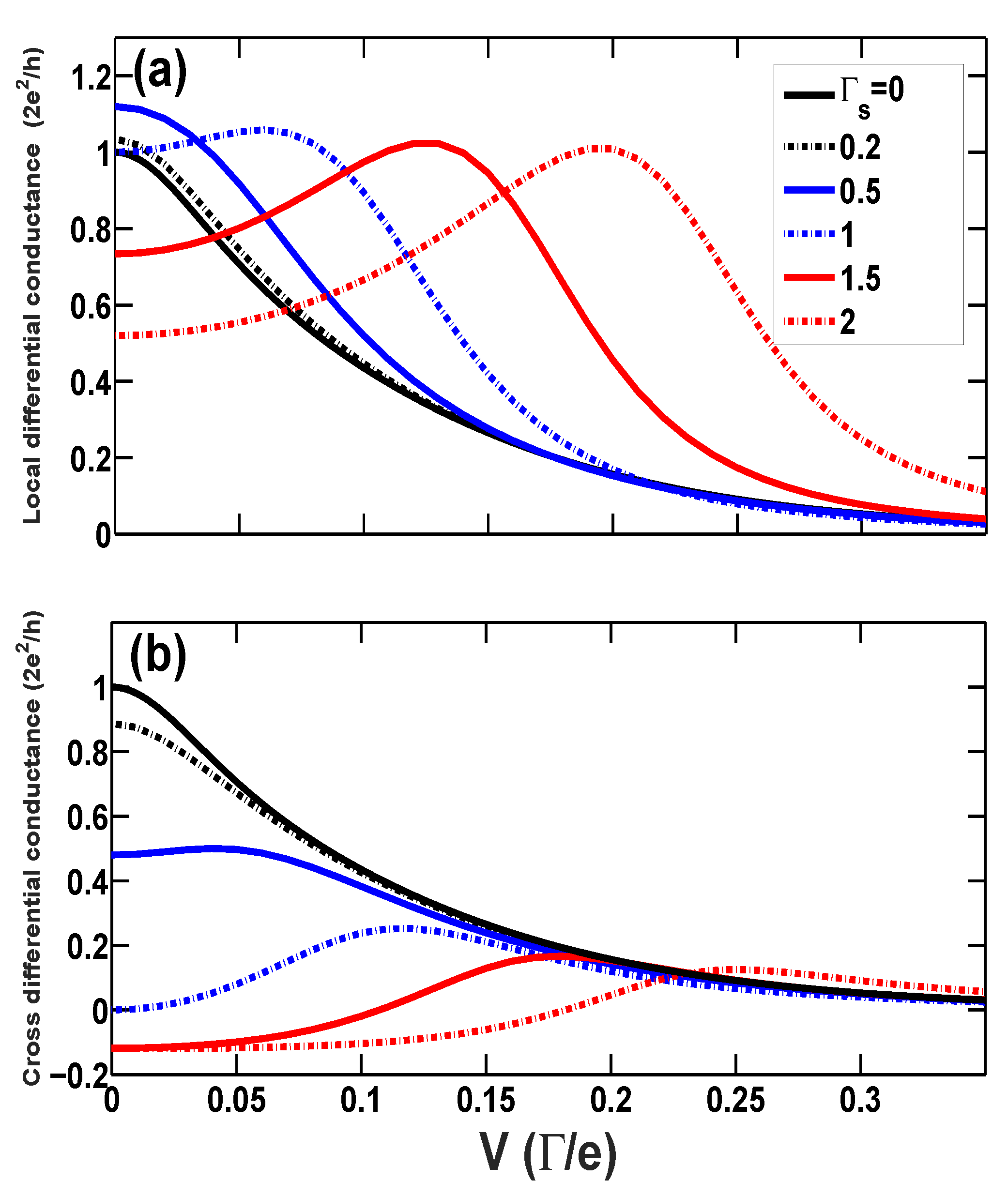
3. Result and Discussion
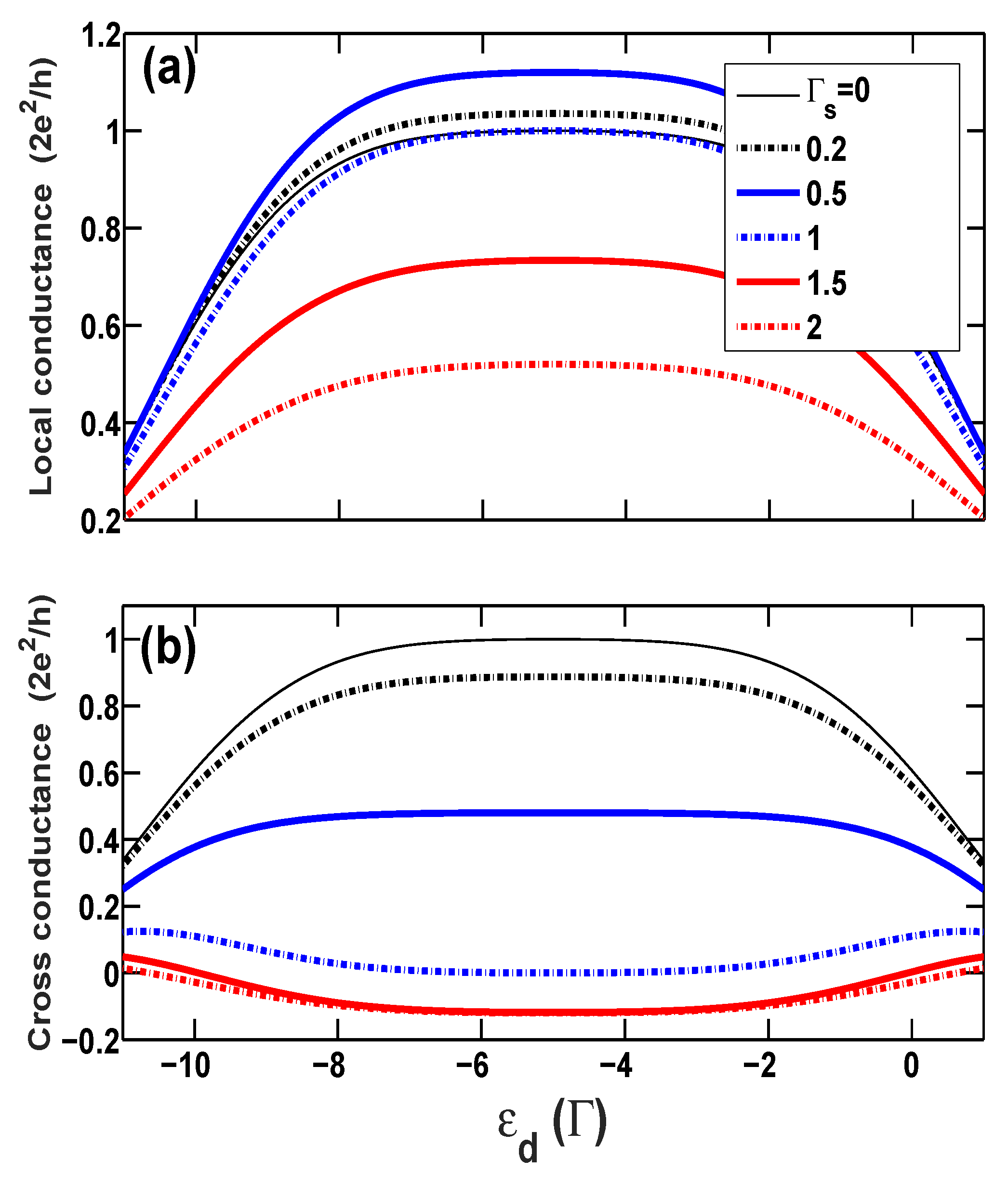
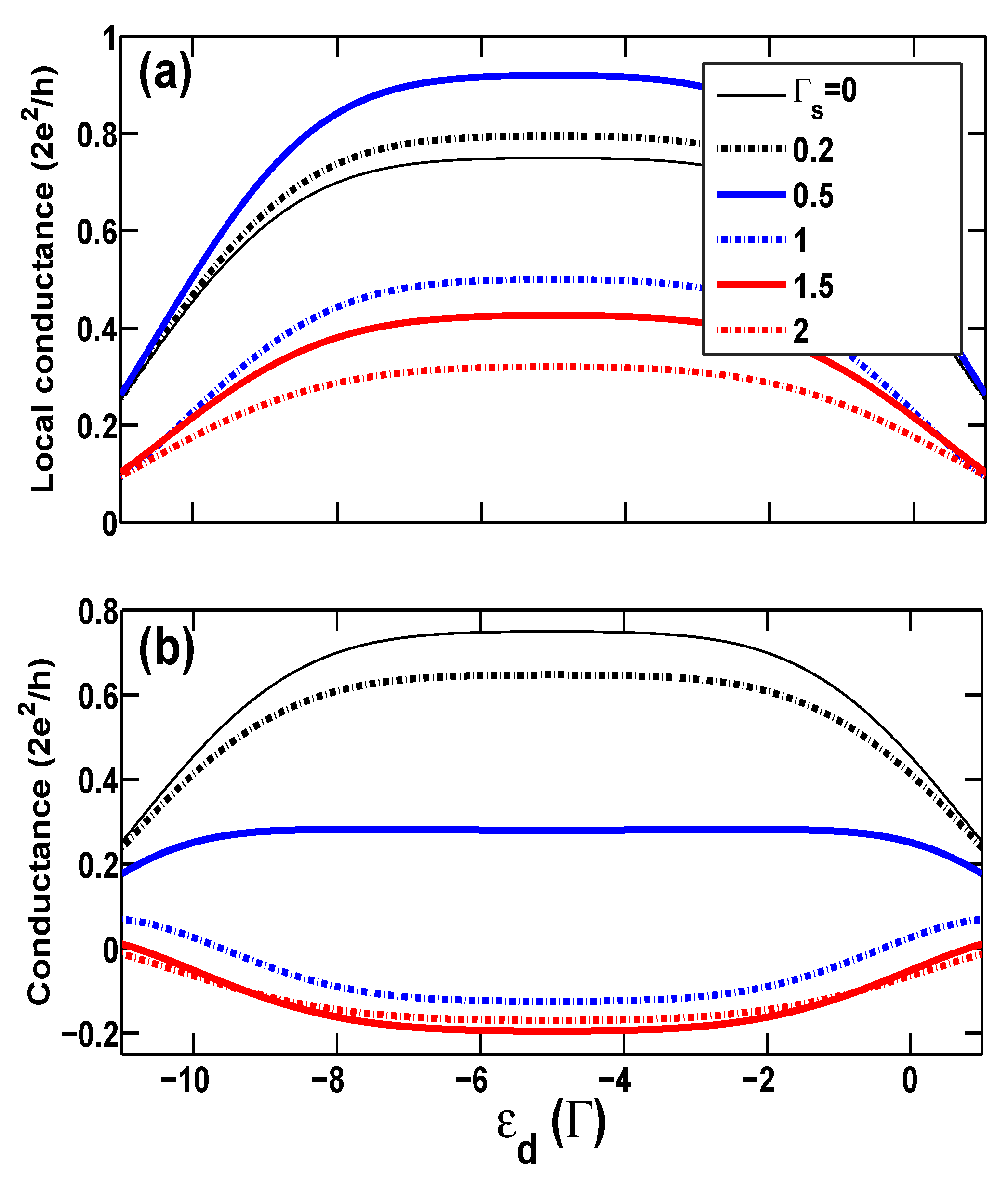
3.1. Linear Local and Cross Conductances
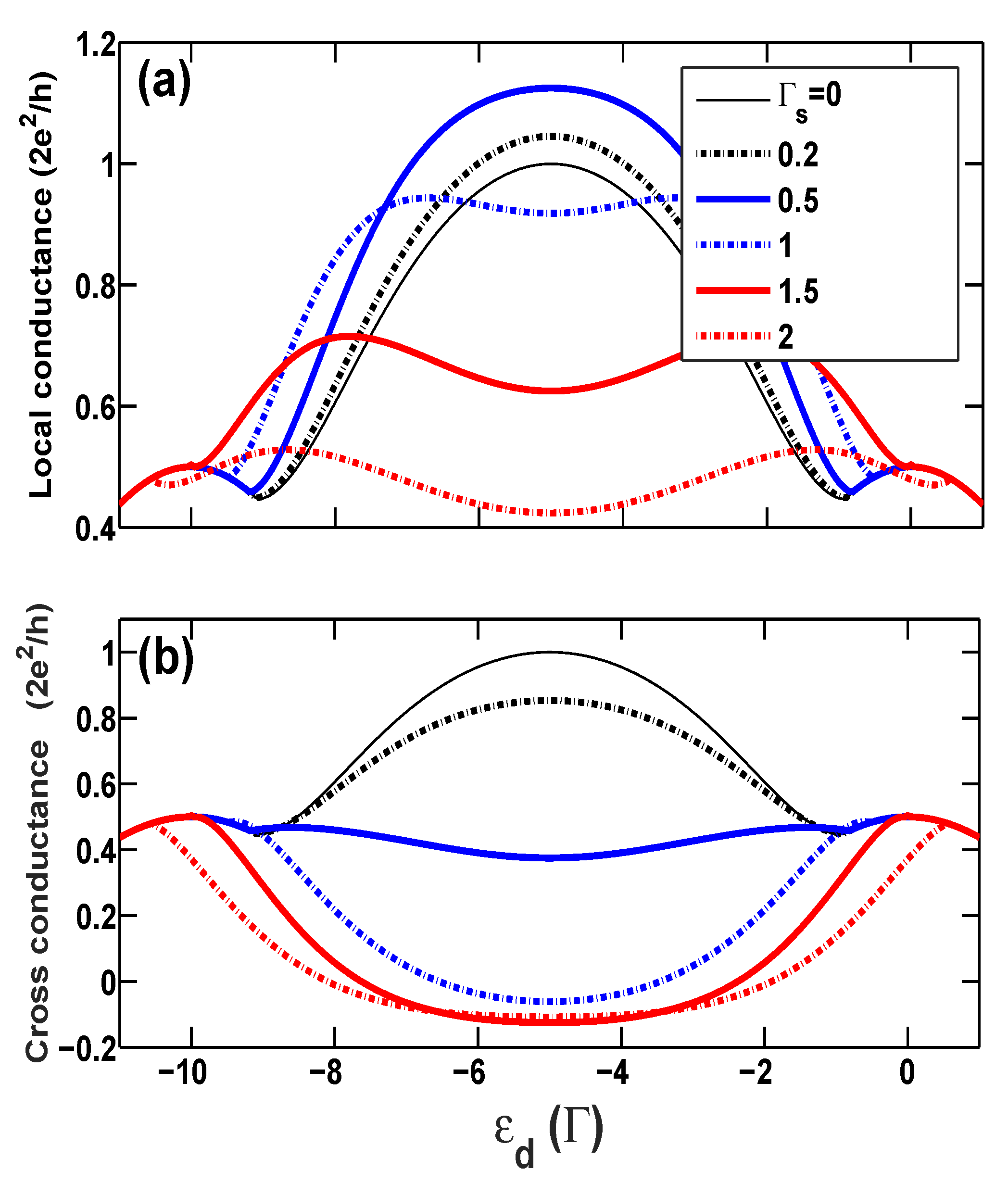
3.2. Nonlinear Local and Cross Conductances
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Buitelaar, M.R.; Nussbaumer, T.; Schönenberger, C. Quantum Dot in the Kondo Regime Coupled to Superconductors. Phys. Rev. Lett. 2002, 89, 256801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Russo, S.; Kroug, M.; Klapwijk, T.M.; Morpurgo, A.F. Experimental Observation of Bias-Dependent Nonlocal Andreev Reflection. Phys. Rev. Lett. 2005, 95, 027002. [Google Scholar] [CrossRef] [PubMed]
- Cadden-Zimansky, P.; Chandrasekhar, V. Nonlocal Correlations in Normal-Metal Superconducting Systems. Phys. Rev. Lett. 2006, 97, 237003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jarillo-Herrero, P.; Van Dam, J.A.; Kouwenhoven, L.P. Quantum supercurrent transistors in carbon nanotubes. Nature 2006, 439, 953. [Google Scholar] [CrossRef] [PubMed]
- Van Dam, J.A.; Nazarov, Y.V.; Bakkers, E.P.; De Franceschi, S.; Kouwenhoven, L.P. Supercurrent reversal in quantum dots. Nature 2006, 442, 667. [Google Scholar] [CrossRef] [PubMed]
- Sand-Jespersen, T.; Paaske, J.; Andersen, B.M.; Grove-Rasmussen, K.; Jørgensen, H.I.; Aagesen, M.; Sørensen, C.B.; Lindelof, P.E.; Flensberg, K.; Nygård, J. Kondo-Enhanced Andreev Tunneling in InAs Nanowire Quantum Dots. Phys. Rev. Lett. 2007, 99, 126603. [Google Scholar] [CrossRef] [Green Version]
- Hofstetter, L.; Csonka, S.; Nygård, J.; Schönenberger, C. Cooper pair splitter realized in a two-quantum-dot Y-junction. Nature 2009, 461, 960. [Google Scholar] [CrossRef]
- Grove-Rasmussen, K.; Jørgensen, H.I.; Andersen, B.M.; Paaske, J.; Jespersen, T.S.; Nygård, J.; Flensberg, K.; Lindelof, P.E. Superconductivity-enhanced bias spectroscopy in carbon nanotube quantum dots. Phys. Rev. B 2009, 79, 134518. [Google Scholar] [CrossRef] [Green Version]
- Franceschi, S.D.; Kouwenhoven, L.; Schönenberger, C.; Wernsdorfer, W. Hybrid superconductor-quantum dot devices. Nat. Nanotechnol. 2010, 5, 703. [Google Scholar] [CrossRef]
- Franke, K.J.; Schulze, G.; Pascual, J.I. Competition of Superconducting Phenomena and Kondo Screening at the Nanoscale. Science 2011, 332, 940–944. Available online: https://science.sciencemag.org/content/332/6032/940.full.pdf (accessed on 11 October 2019). [CrossRef]
- Dirks, T.; Hughes, T.L.; Lal, S.; Uchoa, B.; Chen, Y.F.; Chialvo, C.; Goldbart, P.M.; Mason, N. Transport through Andreev bound states in a graphene quantum dot. Nat. Phys. 2011, 7, 386. [Google Scholar] [CrossRef]
- Schindele, J.; Baumgartner, A.; Schönenberger, C. Near-Unity Cooper Pair Splitting Efficiency. Phys. Rev. Lett. 2012, 109, 157002. [Google Scholar] [CrossRef] [PubMed]
- Braunecker, B.; Burset, P.; Levy Yeyati, A. Entanglement Detection from Conductance Measurements in Carbon Nanotube Cooper Pair Splitters. Phys. Rev. Lett. 2013, 111, 136806. [Google Scholar] [CrossRef] [PubMed]
- Lee, E.J.H.; Jiang, X.; Houzet, M.; Aguado, R.; Lieber, C.M.; Franceschi, S.D. Spin-resolved Andreev levels and parity crossings in hybrid superconductor Csemiconductor nanostructures. Nat. Nanotechnol. 2014, 9, 79. [Google Scholar] [CrossRef]
- Deacon, R.S.; Oiwa, A.; Sailer, J.; Baba, S.; Kanai, Y.; Shibata, K.; Hirakawa, K.; Tarucha, S. Cooper pair splitting in parallel quantum dot Josephson junctions. Nat. Commun. 2015, 6, 7446. [Google Scholar] [CrossRef]
- Ruby, M.; Pientka, F.; Peng, Y.; von Oppen, F.; Heinrich, B.W.; Franke, K.J. Tunneling Processes into Localized Subgap States in Superconductors. Phys. Rev. Lett. 2015, 115, 087001. [Google Scholar] [CrossRef]
- Fülöp, G.; Domínguez, F.; d’Hollosy, S.; Baumgartner, A.; Makk, P.; Madsen, M.H.; Guzenko, V.A.; Nygård, J.; Schönenberger, C.; Levy Yeyati, A.; et al. Magnetic Field Tuning and Quantum Interference in a Cooper Pair Splitter. Phys. Rev. Lett. 2015, 115, 227003. [Google Scholar] [CrossRef]
- Albrecht, S.M.; Higginbotham, A.P.; Madsen, M.; Kuemmeth, F.; Jespersen, T.S.; Nygård, J.; Krogstrup, P.; Marcus, C.M. Exponential protection of zero modes in Majorana islands. Nature 2016, 531, 206. [Google Scholar] [CrossRef]
- Ruby, M.; Peng, Y.; von Oppen, F.; Heinrich, B.W.; Franke, K.J. Orbital Picture of Yu-Shiba-Rusinov Multiplets. Phys. Rev. Lett. 2016, 117, 186801. [Google Scholar] [CrossRef]
- Lutchyn, R.M.; Sau, J.D.; Das Sarma, S. Majorana Fermions and a Topological Phase Transition in Semiconductor-Superconductor Heterostructures. Phys. Rev. Lett. 2010, 105, 077001. [Google Scholar] [CrossRef] [Green Version]
- Cuevas, J.C.; Levy Yeyati, A.; Martín-Rodero, A. Kondo effect in normal-superconductor quantum dots. Phys. Rev. B 2001, 63, 094515. [Google Scholar] [CrossRef] [Green Version]
- Eldridge, J.; Pala, M.G.; Governale, M.; König, J. Superconducting proximity effect in interacting double-dot systems. Phys. Rev. B 2010, 82, 184507. [Google Scholar] [CrossRef]
- Golubev, D.S.; Zaikin, A.D. Shot noise and Coulomb effects on nonlocal electron transport in normal-metal/superconductor/normal-metal heterostructures. Phys. Rev. B 2010, 82, 134508. [Google Scholar] [CrossRef]
- Martín-Rodero, A.; Yeyati, A.L. Josephson and Andreev transport through quantum dots. Adv. Phys. 2011, 60, 899–958. [Google Scholar] [CrossRef] [Green Version]
- Yamada, Y.; Tanaka, Y.; Kawakami, N. Interplay of Kondo and superconducting correlations in the nonequilibrium Andreev transport through a quantum dot. Phys. Rev. B 2011, 84, 075484. [Google Scholar] [CrossRef]
- Moghaddam, A.G.; Governale, M.; König, J. Driven superconducting proximity effect in interacting quantum dots. Phys. Rev. B 2012, 85, 094518. [Google Scholar] [CrossRef]
- Koga, A. Quantum Monte Carlo study of nonequilibrium transport through a quantum dot coupled to normal and superconducting leads. Phys. Rev. B 2013, 87, 115409. [Google Scholar] [CrossRef]
- Kiršanskas, G.; Goldstein, M.; Flensberg, K.; Glazman, L.I.; Paaske, J. Yu-Shiba-Rusinov states in phase-biased superconductor–quantum dot–superconductor junctions. Phys. Rev. B 2015, 92, 235422. [Google Scholar] [CrossRef]
- Žitko, R. Spectral properties of Shiba subgap states at finite temperatures. Phys. Rev. B 2016, 93, 195125. [Google Scholar] [CrossRef] [Green Version]
- Beckmann, D.; Weber, H.B.; Löhneysen, H.V. Evidence for Crossed Andreev Reflection in Superconductor-Ferromagnet Hybrid Structures. Phys. Rev. Lett. 2004, 93, 197003. [Google Scholar] [CrossRef] [Green Version]
- Hofstetter, L.; Geresdi, A.; Aagesen, M.; Nygård, J.; Schönenberger, C.; Csonka, S. Ferromagnetic Proximity Effect in a Ferromagnet–Quantum-Dot–Superconductor Device. Phys. Rev. Lett. 2010, 104, 246804. [Google Scholar] [CrossRef] [PubMed]
- Martinek, J.; Utsumi, Y.; Imamura, H.; Barnaś, J.; Maekawa, S.; König, J.; Schön, G. Kondo Effect in Quantum Dots Coupled to Ferromagnetic Leads. Phys. Rev. Lett. 2003, 91, 127203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pasupathy, A.N.; Bialczak, R.C.; Martinek, J.; Grose, J.E.; Donev, L.A.K.; McEuen, P.L.; Ralph, D.C. The Kondo Effect in the Presence of Ferromagnetism. Science 2004, 306, 86–89. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hauptmann, J.R.; Paaske, J.; Lindelof, P.E. Electric-field-controlled spin reversal in a quantum dot with ferromagnetic contacts. Nat. Phys. 2008, 4, 373. [Google Scholar] [CrossRef]
- Gaass, M.; Hüttel, A.K.; Kang, K.; Weymann, I.; von Delft, J.; Strunk, C. Universality of the Kondo Effect in Quantum Dots with Ferromagnetic Leads. Phys. Rev. Lett. 2011, 107, 176808. [Google Scholar] [CrossRef] [Green Version]
- Dong, B.; Cui, H.L.; Liu, S.Y.; Lei, X.L. Kondo-type transport through an interacting quantum dot coupled to ferromagnetic leads. J. Phys.-Condes. Matter 2003, 15, 8435–8444. [Google Scholar] [CrossRef]
- Choi, M.S.; Sánchez, D.; López, R. Kondo Effect in a Quantum Dot Coupled to Ferromagnetic Leads: A Numerical Renormalization Group Analysis. Phys. Rev. Lett. 2004, 92, 056601. [Google Scholar] [CrossRef] [Green Version]
- Sánchez, D.; López, R.; Samuelsson, P.; Büttiker, M. Andreev drag effect in ferromagnetic-normal-superconducting systems. Phys. Rev. B 2003, 68, 214501. [Google Scholar] [CrossRef] [Green Version]
- Weymann, I.; Wójcik, K.P. Andreev transport in a correlated ferromagnet-quantum-dot-superconductor device. Phys. Rev. B 2015, 92, 245307. [Google Scholar] [CrossRef]
- Futterer, D.; Governale, M.; Pala, M.G.; König, J. Nonlocal Andreev transport through an interacting quantum dot. Phys. Rev. B 2009, 79, 054505. [Google Scholar] [CrossRef] [Green Version]
- Futterer, D.; Governale, M.; König, J. Generation of pure spin currents by superconducting proximity effect in quantum dots. EPL (Europhys. Lett.) 2010, 91, 47004. [Google Scholar] [CrossRef]
- Sothmann, B.; Futterer, D.; Governale, M.; König, J. Probing the exchange field of a quantum-dot spin valve by a superconducting lead. Phys. Rev. B 2010, 82, 094514. [Google Scholar] [CrossRef]
- Weymann, I.; Trocha, P. Superconducting proximity effect and zero-bias anomaly in transport through quantum dots weakly attached to ferromagnetic leads. Phys. Rev. B 2014, 89, 115305. [Google Scholar] [CrossRef]
- Michałek, G.; Bułka, B.R.; Domański, T.; Wysokiński, K.I. Interplay between direct and crossed Andreev reflections in hybrid nanostructures. Phys. Rev. B 2013, 88, 155425. [Google Scholar] [CrossRef]
- Michałek, G.; Domański, T.; Bułka, B.R.; Wysokiński, K.I. Novel non-local effects in three-terminal hybrid devices with quantum dot. Sci. Rep. 2015, 5, 14572. [Google Scholar] [CrossRef] [Green Version]
- Kotliar, G.; Ruckenstein, A.E. New Functional Integral Approach to Strongly Correlated Fermi Systems: The Gutzwiller Approximation as a Saddle Point. Phys. Rev. Lett. 1986, 57, 1362–1365. [Google Scholar] [CrossRef]
- Schönhammer, K. Variational results as saddle-point approximations: The Anderson impurity model. Phys. Rev. B 1990, 42, 2591–2593. [Google Scholar] [CrossRef]
- Aguado, R.; Langreth, D.C. Out-of-Equilibrium Kondo Effect in Double Quantum Dots. Phys. Rev. Lett. 2000, 85, 1946–1949. [Google Scholar] [CrossRef] [Green Version]
- Dong, B.; Lei, X.L. Kondo effect and antiferromagnetic correlation in transport through tunneling-coupled double quantum dots. Phys. Rev. B 2002, 65, 241304. [Google Scholar] [CrossRef] [Green Version]
- Dong, B.; Lei, X.L. Kondo-type transport through a quantum dot under magnetic fields. Phys. Rev. B 2001, 63, 235306. [Google Scholar] [CrossRef]
- Dong, B.; Lei, X.L. Kondo-type transport through a quantum dot: a new finite-Uslave-boson mean-field approach. J. Phys.-Condes. Matter 2001, 13, 9245–9258. [Google Scholar] [CrossRef]
- Ma, J.; Dong, B.; Lei, X.L. Spin-Polarized Transport Through a Quantum Dot Coupled to Ferromagnetic Leads: Kondo Correlation Effect. Commun. Theor. Phys. 2005, 43, 341–348. [Google Scholar] [CrossRef] [Green Version]
- Bergeret, F.S.; Yeyati, A.L.; Martín-Rodero, A. Interplay between Josephson effect and magnetic interactions in double quantum dots. Phys. Rev. B 2006, 74, 132505. [Google Scholar] [CrossRef] [Green Version]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.; Dong, B.; Lei, X.-L. Enhanced Negative Nonlocal Conductance in an Interacting Quantum Dot Connected to Two Ferromagnetic Leads and One Superconducting Lead. Entropy 2019, 21, 1003. https://doi.org/10.3390/e21101003
Lee C, Dong B, Lei X-L. Enhanced Negative Nonlocal Conductance in an Interacting Quantum Dot Connected to Two Ferromagnetic Leads and One Superconducting Lead. Entropy. 2019; 21(10):1003. https://doi.org/10.3390/e21101003
Chicago/Turabian StyleLee, Cong, Bing Dong, and Xiao-Lin Lei. 2019. "Enhanced Negative Nonlocal Conductance in an Interacting Quantum Dot Connected to Two Ferromagnetic Leads and One Superconducting Lead" Entropy 21, no. 10: 1003. https://doi.org/10.3390/e21101003
APA StyleLee, C., Dong, B., & Lei, X.-L. (2019). Enhanced Negative Nonlocal Conductance in an Interacting Quantum Dot Connected to Two Ferromagnetic Leads and One Superconducting Lead. Entropy, 21(10), 1003. https://doi.org/10.3390/e21101003




