Description of Transfer Processes in a Locally Nonequilibrium Medium
Abstract
1. Introduction
2. Transfer Processes in an Equilibrium Medium
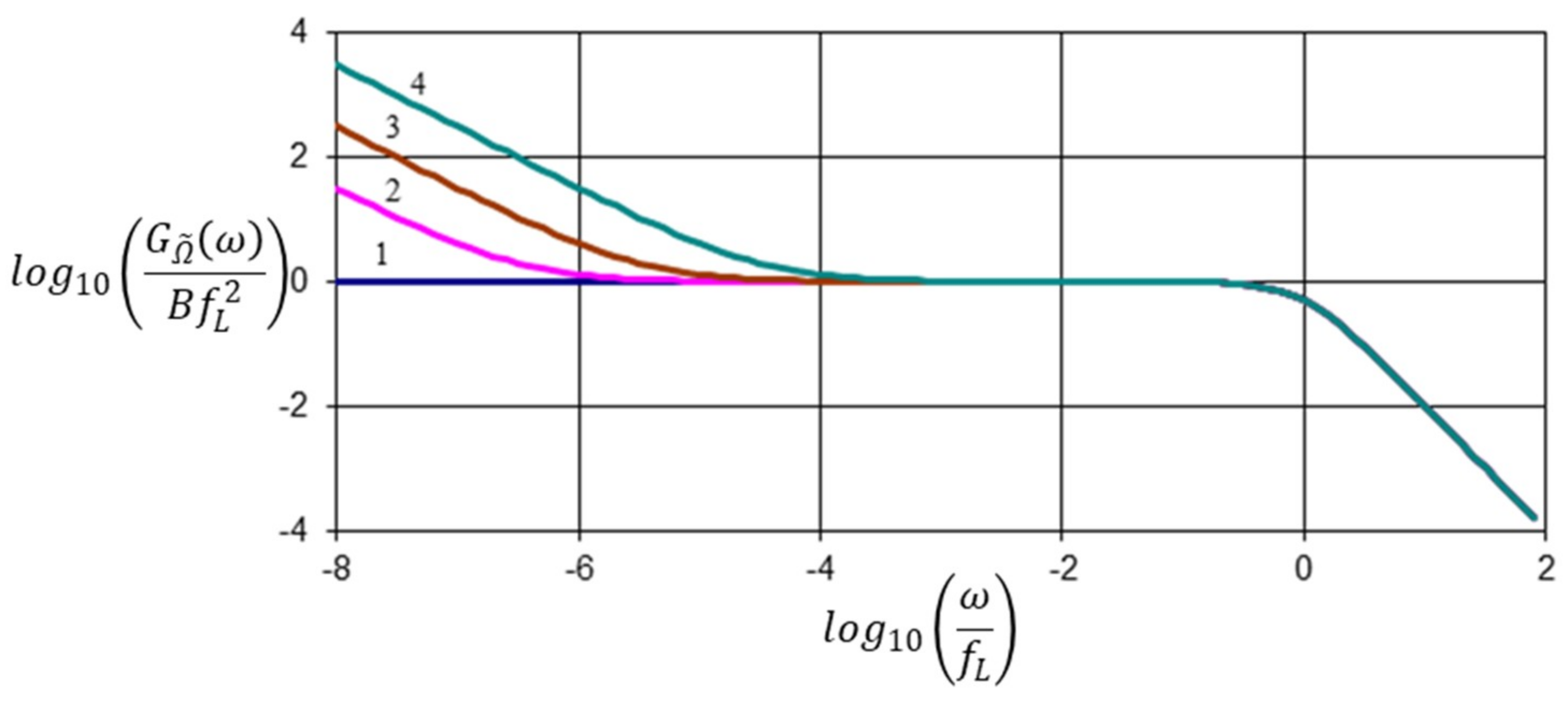
3. Transfer Processes in a Nonequilibrium Medium
4. Conclusions
Funding
Conflicts of Interest
References
- Glansdorff, P.; Prigogine, I. Thermodynamic Theory of Structure, Stability and Fluctuations; Wiley Interscience: London, UK, 1971. [Google Scholar]
- Sobolev, S.L. Local non-equilibrium transport models. Phys.-Uspekhi 1997, 40, 1043–1053. [Google Scholar] [CrossRef]
- Jou, D.; Casas-Vazquez, J.; Lebon, G. Extended Irreversible Thermodynamics, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Morozov, A.N. Flicker-noise in a locally nonequilibrium medium. JETP Lett. 2018, 107, 798–799. [Google Scholar] [CrossRef]
- Bochkov, G.N.; Kuzovlev, Y.E. New aspects in 1/f noise studies. Sov. Phys. Uspekhi 1983, 26, 829–844. [Google Scholar] [CrossRef]
- Kuzovlev, Y.E. Why nature needs 1/f noise. Phys.-Uspekhi 2015, 58, 719–729. [Google Scholar] [CrossRef]
- Hooge, F.N. 1/f noise sources. IEEE Trans. Electron. Devices 1994, 41, 1926–1935. [Google Scholar] [CrossRef]
- Kogan, S.H. Low-frequency current noise with a 1/f spectrum in solids. Sov. Phys. Uspekhi 1985, 28, 170–195. [Google Scholar] [CrossRef]
- Hooge, F.N.; Gaal, J.L. Fluctuations with a 1/f spectrum in the conductance of ionic solutions and in the voltage of concentration cells. Philips Res. Rep. 1971, 26, 77–90. [Google Scholar]
- Bezrukov, S.M.; Pustovoit, M.A.; Sibilev, A.I.; Drabkin, G.M. Large-scale conductance fluctuations in solutions of strong electrolytes. Phys. B Condens. Matter 1989, 159, 388–398. [Google Scholar] [CrossRef]
- Van den Berg, R.J.; De Vos, A.; De Goede, J. Electrical noise in solutions of hydrochloric acid in ethanol. Phys. Lett. A 1989, 139, 249–252. [Google Scholar] [CrossRef]
- Marchesoni, F.; Taloni, A. Subdiffusion and long-time anticorrelations in a stochastic single file. Phys. Rev. Lett. 2006, 97, 106101. [Google Scholar] [CrossRef]
- Morozov, A.N. Use of the theory of non-Markovian processes in the description of Brownian motion. JETP 1996, 82, 703–708. [Google Scholar]
- Lisy, V.; Tothova, J.; Glod, L. On the correlation properties of thermal noise in fluids. Int. J. Thermophys. 2013, 34, 629–641. [Google Scholar] [CrossRef]
- Hauge, E.H.; Martin-Lof, A. Fluctuating hydrodynamics and Brownian motion. J. Stat. Phys. 1973, 7, 259–281. [Google Scholar] [CrossRef]
- Volkov, V.S.; Leonov, A.I. Non-Markovian Brownian motion in a viscoelastic fluid. J. Chem. Phys. 1996, 104, 5922–5931. [Google Scholar] [CrossRef]
- Mainardi, F.; Mura, A.; Tampieri, F. Brownian motion and anomalous diffusion revisited via a fractional Langevin equation. Mod. Probl. Stat. Phys. 2009, 8, 3–23. [Google Scholar]
- Morozov, A.N.; Skripkin, A.V. Spherical particle Brownian motion in viscous medium as non-Markovian random process. Phys. Lett. A 2011, 375, 4113–4115. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Evangelista, L.R.; Lenzi, M.K.; Ribeiro, H.V.; de Oliveira, E.C. Solutions for a non-Markovian diffusion equation. Phys. Lett. A 2010, 374, 4193–4198. [Google Scholar] [CrossRef]
- Mura, A.; Taqqu, M.S.; Mainardi, F. Non-Markovian diffusion equations and processes: Analysis and simulations. Phys. A Stat. Mech. Appl. 2008, 387, 5033–5064. [Google Scholar] [CrossRef]
- Prehl, J.; Bold, F.; Hoffmann, K.H.; Essex, C. Symmetric fractional diffusion and entropy production. Entropy 2016, 18, 275. [Google Scholar] [CrossRef]
- Fuentes, M.A.; Cáceres, M.O. Computing the non-linear anomalous diffusion equation from first principles. Phys. Lett. A 2008, 372, 1236–1239. [Google Scholar] [CrossRef]
- Vishnevskaya, G.P.; Frolova, E.N.; Yulmetyev, R.M. Manifestation of liquid-state and solid-state properties in electron relaxation of paramagnetic ions in solutions: Non-Markovian processes. Phys. Solid State 2002, 44, 1055–1060. [Google Scholar] [CrossRef]
- Khalvashi, E.K. Non-Markovian theory of electron paramagnetic resonance in localized and quasi-localized electron spins via an example of manganites with colossal magnetoresistance. J. Exp. Theor. Phys. 2005, 100, 398–409. [Google Scholar] [CrossRef]
- Li, J.-G.; Zu, J.; Shao, B. Factorization law for entanglement evolution of two qubits in non-Markovian pure dephasing channels. Phys. Lett. A 2011, 375, 2300–2304. [Google Scholar] [CrossRef]
- Adamian, G.G.; Antonenko, N.V.; Kanokov, Z.; Sargsyan, V.V. Quantum non-Markovian stochastic equations. Theor. Math. Phys. 2005, 145, 1443–1456. [Google Scholar] [CrossRef]
- Stockburger, J.T.; Grabert, H. Non-Markovian quantum state diffusion. Chem. Phys. 2001, 268, 249–256. [Google Scholar] [CrossRef]
- Iwamatsu, A.; Ogawa, Y.; Mitsumori, Y.; Minami, F. Non-Markovian dephasing of excitons in Gaas quantum wells. J. Lumin. 2006, 119–120, 487–491. [Google Scholar] [CrossRef]
- Sargsyan, V.V.; Kanokov, Z.; Adamian, G.G.; Antonenko, N.V. Quantum non-Markovian Langevin equations and transport coefficients. Phys. At. Nucl. 2005, 68, 2009–2021. [Google Scholar] [CrossRef]
- Shushin, A.I. Non-Markovian stochastic Liouville equation and anomalous quantum relaxation kinetics. J. Exp. Theor. Phys. 2005, 101, 577–583. [Google Scholar] [CrossRef][Green Version]
- Xia, H. Non-Markovian Velocity Diffusion in Plasma Turbulence. Ph.D. Thesis, Texas Tech University, Lubbock, TX, USA, 1994; p. 2029. [Google Scholar]
- Kustova, E.; Giordano, D. Cross-coupling effects in chemically non-equilibrium viscous compressible flows. Chem. Phys. 2011, 379, 83–91. [Google Scholar] [CrossRef]
- Klimontovich, Y.L. Turbulent Motion and the Structure of Chaos: A New Approach to the Statistical Theory of Open Systems; Springer: Dordrecht, The Netherlands, 1991. [Google Scholar]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morozov, A.N. Description of Transfer Processes in a Locally Nonequilibrium Medium. Entropy 2019, 21, 9. https://doi.org/10.3390/e21010009
Morozov AN. Description of Transfer Processes in a Locally Nonequilibrium Medium. Entropy. 2019; 21(1):9. https://doi.org/10.3390/e21010009
Chicago/Turabian StyleMorozov, Andrey N. 2019. "Description of Transfer Processes in a Locally Nonequilibrium Medium" Entropy 21, no. 1: 9. https://doi.org/10.3390/e21010009
APA StyleMorozov, A. N. (2019). Description of Transfer Processes in a Locally Nonequilibrium Medium. Entropy, 21(1), 9. https://doi.org/10.3390/e21010009



