Information Entropy of Tight-Binding Random Networks with Losses and Gain: Scaling and Universality
Abstract
1. Introduction
1.1. Network Model with Losses and Gain
1.2. Previous Work
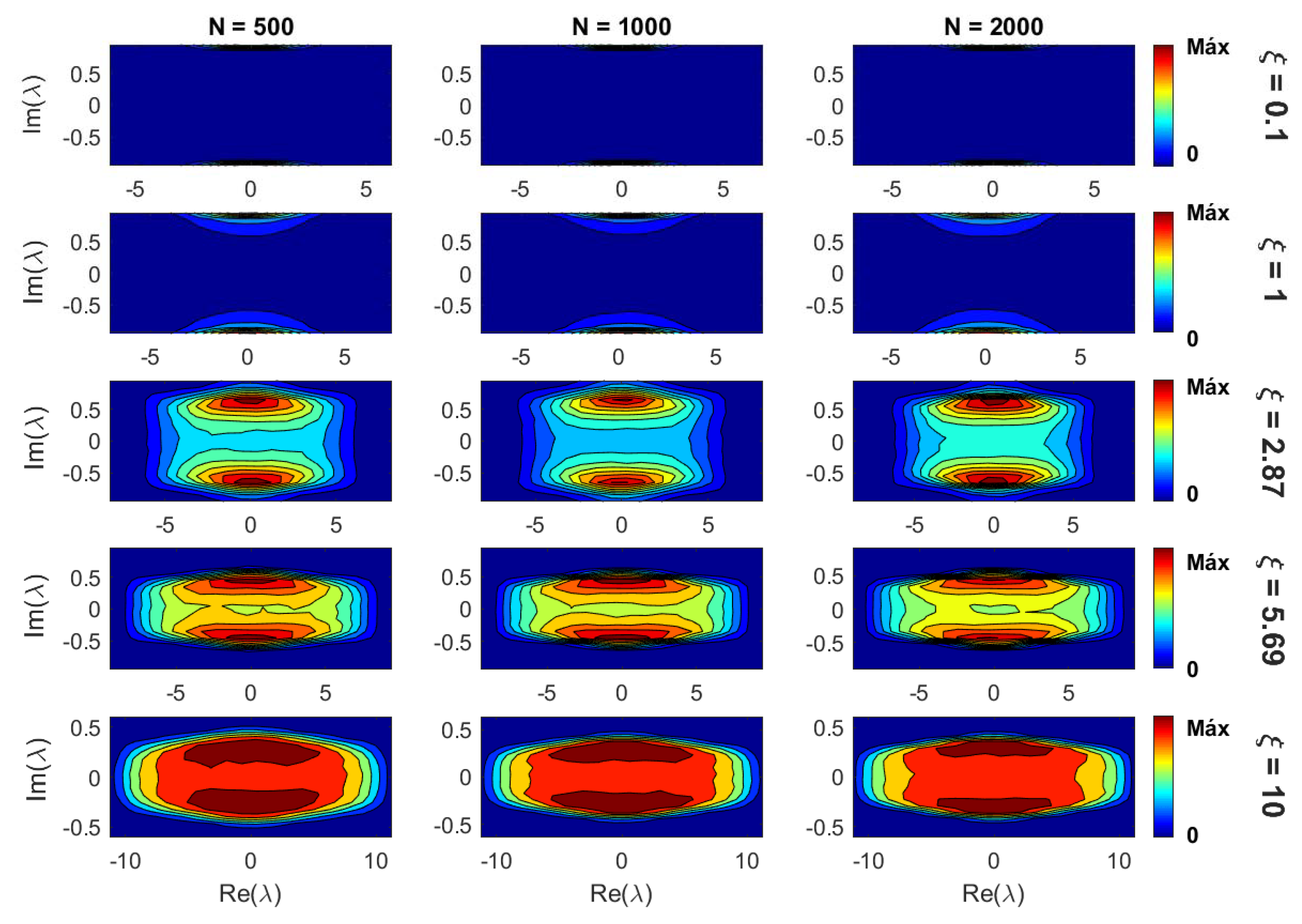
2. Results
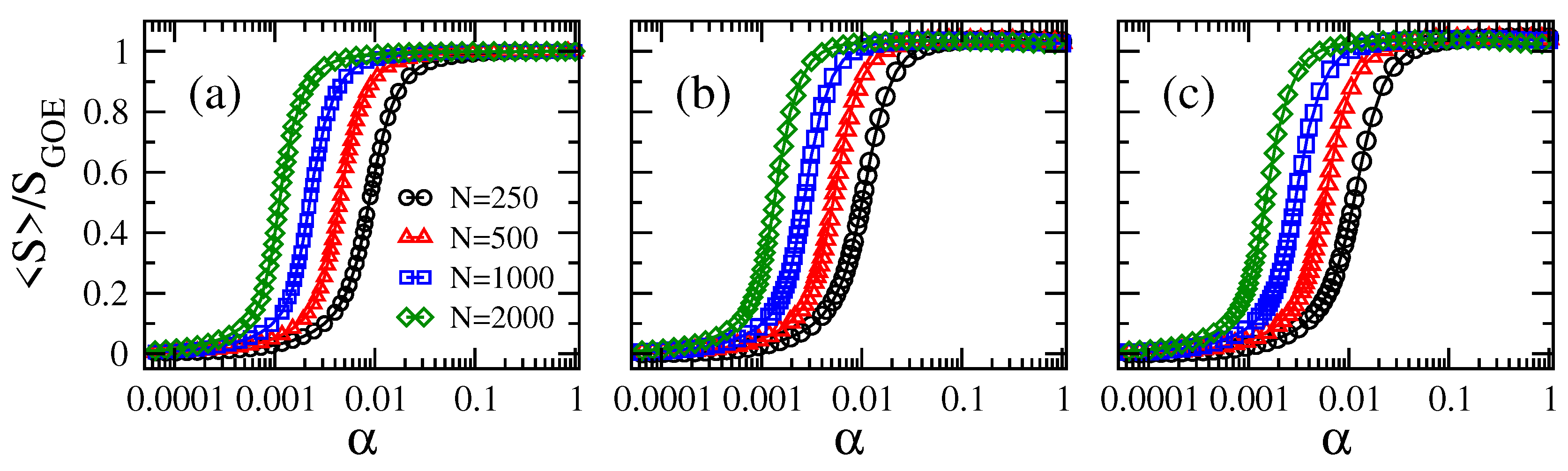
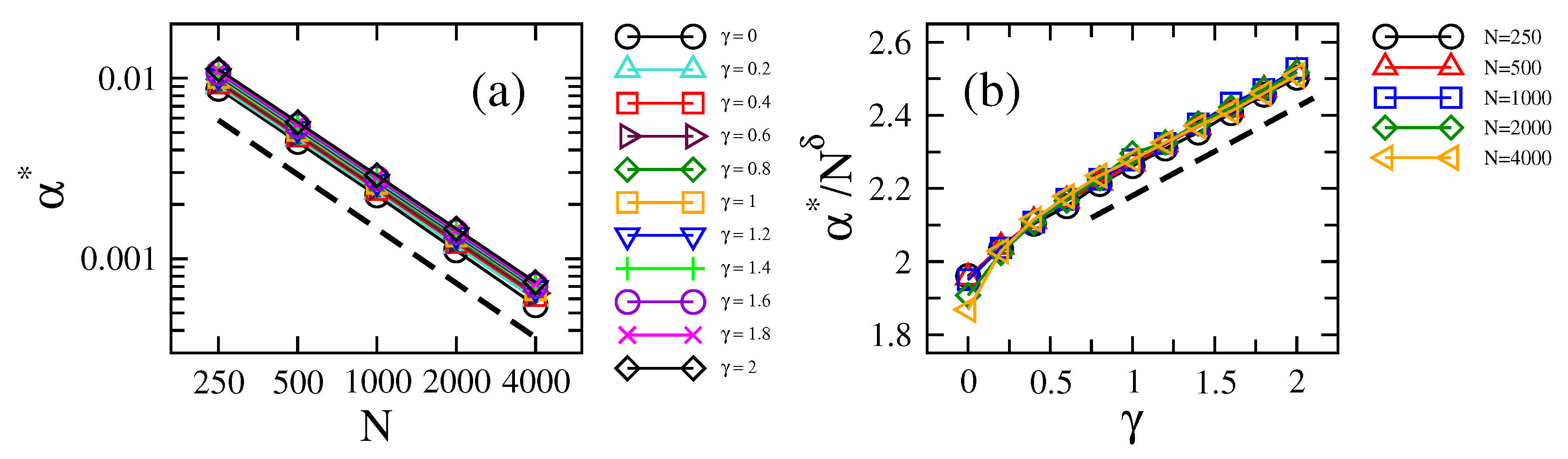
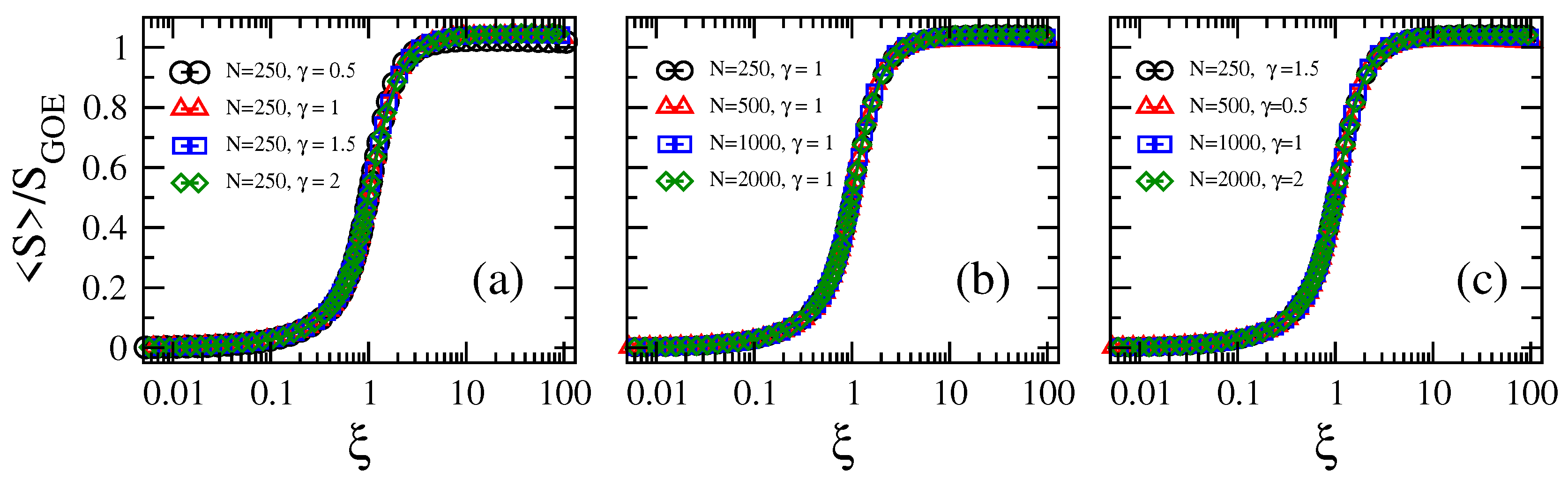
2.1. Scaling of Information Entropy
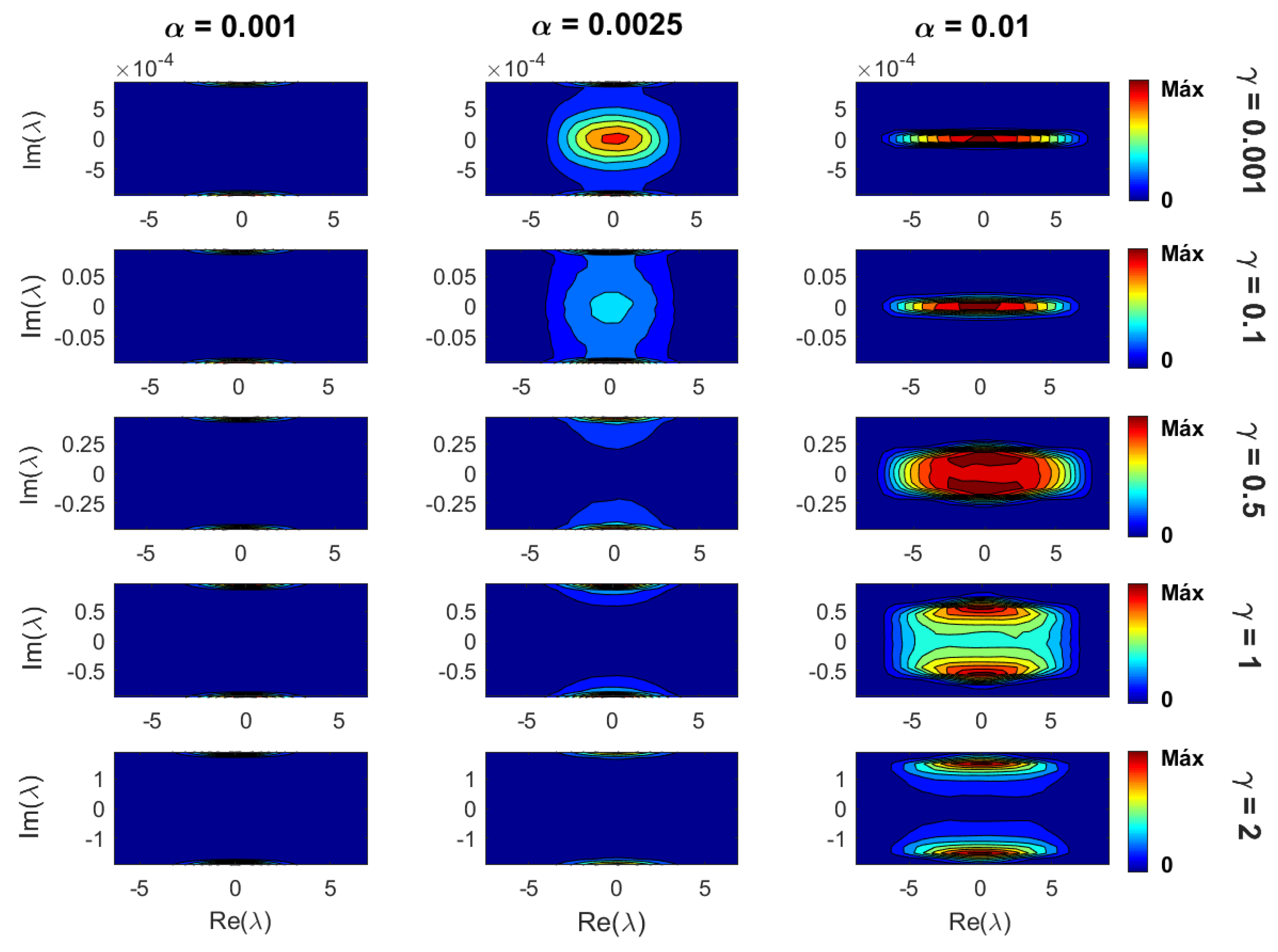
2.2. Eigenvalue Properties
3. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Newman, M.E.J. Networks: An Introduction; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Anderson, P.W. Absence of diffusion in certain random lattices. Phys. Rev. 1958, 109, 1492–1505. [Google Scholar] [CrossRef]
- Jackson, A.D.; Mejia-Monasterio, C.; Rupp, T.; Saltzer, M.; Wilke, T. Spectral ergodicity and normal modes in ensembles of sparse matrices. Nucl. Phys. A 2001, 687, 405–434. [Google Scholar] [CrossRef]
- Goringe, C.M.; Bowler, D.R.; Hernandez, E. Tight-binding modelling of materials. Rep. Prog. Phys. 1997, 60, 1447–1512. [Google Scholar] [CrossRef]
- Martinez-Mendoza, A.J.; Alcazar-Lopez, A.; Mendez-Bermudez, J.A. Scattering and transport properties of tight-binding random networks. Phys. Rev. E 2013, 88, 122126. [Google Scholar] [CrossRef] [PubMed]
- Biroli, G.; Ribeiro-Teixeira, A.C.; Tarzia, M. Difference between level statistics, ergodicity and localization transitions on the Bethe lattice. arXiv, 2012; arXiv:1211.7334. [Google Scholar]
- De Luca, A.; Altshuler, B.L.; Kravtsov, V.E.; Scardicchio, A. Anderson localization on the Bethe lattice: Nonergodicity of extended states. Phys. Rev. Lett. 2014, 113, 046806. [Google Scholar] [CrossRef] [PubMed]
- Tikhonov, K.S.; Mirlin, A.D.; Skvortsov, M.A. Anderson localization and ergodicity on random regular graphs. Phys. Rev. B 2016, 94, 220203(R). [Google Scholar] [CrossRef]
- Tikhonov, K.S.; Mirlin, A.D. Fractality of wave functions on a Cayley tree: Difference between tree and locally treelike graph without boundary. Phys. Rev. B 2016, 94, 184203. [Google Scholar] [CrossRef]
- Garcia-Mata, I.; Giraud, O.; Georgeot, B.; Martin, J.; Dubertrand, R.; Lemarie, G. Scaling theory of the Anderson transition in random graphs: Ergodicity and universality. Phys. Rev. Lett. 2017, 118, 166801. [Google Scholar] [CrossRef]
- Metz, F.L.; Perez-Castillo, I. Level compressibility for the Anderson model on regular random graphs and the eigenvalue statistics in the extended phase. Phys. Rev. B 2017, 96, 064202. [Google Scholar] [CrossRef]
- Sonner, M.; Tikhonov, K.S.; Mirlin, A.D. Multifractality of wave functions on a Cayley tree: From root to leaves. Phys. Rev. B 2017, 96, 214204. [Google Scholar] [CrossRef]
- Tikhonov, K.S.; Mirlin, A.D. Statistics of eigenstates near the localization transition on random regular graphs. arXiv, 2012; arXiv:1810.11444. [Google Scholar] [CrossRef]
- Jahnke, L.; Kantelhardt, J.W.; Berkovits, R.; Havlin, S. Wave localization in complex networks with high clustering. Phys. Rev. Lett. 2008, 101, 175702. [Google Scholar] [CrossRef] [PubMed]
- Mendez-Bermudez, J.A.; Ferraz-de-Arruda, G.; Rodrigues, F.A.; Moreno, Y. Scaling properties of multilayer random networks. Phys. Rev. E 2017, 96, 012307. [Google Scholar] [CrossRef] [PubMed]
- Mendez-Bermudez, J.A.; Alcazar-Lopez, A.; Martinez-Mendoza, A.J.; Rodrigues, F.A.; Peron, T.K.D.M. Universality in the spectral and eigenvector properties of random networks. Phys. Rev. E 2015, 91, 032122. [Google Scholar] [CrossRef]
- Gera, R.; Alonso, L.; Crawford, B.; House, J.; Mendez-Bermudez, J.A.; Knuth, T.; Miller, R. Identifying network structure similarity using spectral graph theory. Appl. Net. Sci. 2018, 3, 2. [Google Scholar] [CrossRef]
- Metha, M.L. Random Matrices; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Mahaux, C.; Weidenmüller, H.A. Shell Model Approach to Nuclear Reactions; North-Holland: Amsterdam, The Netherlands, 1969. [Google Scholar]
- Sokolov, V.V.; Zelevinsky, V.G. Dynamics and statistics of unstable quantum states. Nucl. Phys. A 1989, 504, 562–588. [Google Scholar] [CrossRef]
- Sokolov, V.V.; Zelevinsky, V.G. On a statistical theory of overlapping resonances. Phys. Lett. B 1988, 202, 10–14. [Google Scholar] [CrossRef]
- Sokolov, V.V.; Zelevinsky, V.G. Collective dynamics of unstable quantum states. Ann. Phys. (N. Y.) 1992, 216, 323–350. [Google Scholar] [CrossRef]
- Rotter, I. A continuum shell model for the open quantum mechanical nuclear system. Rep. Prog. Phys. 1991, 54, 635–682. [Google Scholar] [CrossRef]
- Weiss, M.; Mendez-Bermudez, J.A.; Kottos, T. Resonance width distribution for high dimensional random media. Phys. Rev. B 2006, 73, 045103. [Google Scholar] [CrossRef]
- Herrera-Gonzalez, I.F.; Mendez-Bermudez, J.A.; Izrailev, F.M. Transport through quasi-one-dimensional wires with correlated disorder. Phys. Rev. E 2014, 90, 042115. [Google Scholar] [CrossRef] [PubMed]
- Herrera-Gonzalez, I.F.; Mendez-Bermudez, J.A.; Izrailev, F.M. Distribution of S-matrix poles for one-dimensional disordered wires. arXiv, 2016; arXiv:1810.06166. [Google Scholar]
- Celardo, G.L.; Biella, A.; Kaplan, L.; Borgonovi, F. Interplay of superradiance and disorder in the Anderson Model. Fortschr. Phys. 2013, 61, 250. [Google Scholar] [CrossRef]
- Chavez, N.C.; Mattiotti, F.; Mendez-Bermudez, J.A.; Borgonovi, F.; Celardo, G.L. Real and imaginary energy gaps: A comparison between single excitation Superradiance and Superconductivity. arXiv, 2018; arXiv:1805.03153. [Google Scholar]
- El-Ganainy, R.; Makris, K.G.; Khajavikhan, M.; Musslimani, Z.H.; Rotter, S.; Christodoulides, D.N. Non-Hermitian physics and PT symmetry. Nat. Phys. 2018, 14, 11–19. [Google Scholar] [CrossRef]
- Vazquez-Candanedo, O.; Hernandez-Herrejon, J.C.; Izrailev, F.M.; Christodoulides, D.N. Gain- or loss-induced localization in one-dimensional PT-symmetric tight-binding models. Phys. Rev. A 2014, 89, 013832. [Google Scholar] [CrossRef]
- Mendez-Bermudez, J.A.; Ferraz-de-Arruda, G.; Rodrigues, F.A.; Moreno, Y. Diluted banded random matrices: Scaling behavior of eigenvector and spectral properties. J. Phys. A Math. Theor. 2017, 50, 495205. [Google Scholar] [CrossRef]
- Alonso, L.; Mendez-Bermudez, J.A.; Gonzalez-Melendrez, A.; Moreno, Y. Weighted random-geometric and random-rectangular graphs: Spectral and eigenvector properties of the adjacency matrix. J. Complex Netw. 2018, 6, 753. [Google Scholar] [CrossRef]
- Mirlin, A.D.; Fyodorov, Y.V. Universality of level correlation function of sparse random matrices. J. Phys. A Math. Gen. 1991, 24, 2273–2286. [Google Scholar] [CrossRef]
- Evangelou, S.N. A numerical study of sparse random matrices. J. Stat. Phys. 1992, 69, 361–383. [Google Scholar] [CrossRef]
- Evangelou, S.N.; Economou, E.N. Spectral density singularities, level statistics, and localization in a sparse random matrix ensemble. Phys. Rev. Lett. 1992, 68, 361–364. [Google Scholar] [CrossRef] [PubMed]
- Fyodorov, Y.V.; Mirlin, A.D. Localization in ensemble of sparse random matrices. Phys. Rev. Lett. 1991, 67, 2049–2052. [Google Scholar] [CrossRef] [PubMed]
- Rogers, T.; Castillo, I.P. Cavity approach to the spectral density of non-Hermitian sparse matrices. Phys. Rev. E 2009, 79, 012101. [Google Scholar] [CrossRef] [PubMed]
- Giraud, O.; Georgeot, B.; Shepelyansky, D.L. Delocalization transition for the Google matrix. Phys. Rev. E 2009, 80, 026107. [Google Scholar] [CrossRef] [PubMed]
- Georgeot, B.; Giraud, O.; Shepelyansky, D.L. Spectral properties of the Google matrix of the World Wide Web and other directed networks. Phys. Rev. E 2010, 81, 056109. [Google Scholar] [CrossRef] [PubMed]
- Jalan, S.; Zhu, G.; Li, B. Spectral properties of directed random networks with modular structure. Phys. Rev. E 2011, 84, 046107. [Google Scholar] [CrossRef]
- Neri, I.; Metz, F.L. Spectra of Sparse Non-Hermitian Random Matrices: An Analytical Solution. Phys. Rev. Lett. 2012, 109, 030602. [Google Scholar] [CrossRef]
- Wood, P.M. Universality and the circular law for sparse random matrices. Ann. Appl. Prob. 2012, 22, 1266–1300. [Google Scholar] [CrossRef]
- Ye, B.; Qiu, L.; Wanga, X.; Guhr, T. Spectral statistics in directed complex networks and universality of the Ginibre ensemble. Commun. Nonlinear Sci. Numer. Simulat. 2015, 20, 1026–1032. [Google Scholar] [CrossRef]
- Neri, I.; Metz, F.L. Eigenvalue outliers of Non-Hermitian random matrices with a local tree structure. Phys. Rev. Lett. 2016, 117, 224101. [Google Scholar] [CrossRef] [PubMed]
- Allesina, S.; Tang, S. The stability-complexity relationship at age 40: A random matrix perspective. Popul. Ecol. 2015, 57, 63–75. [Google Scholar] [CrossRef]
- Cook, N.A. Spectral Properties of Non-Hermitian Random Matrices. Ph.D. Thesis, University of California, Los Angeles, CA, USA, 2016. [Google Scholar]
- Izrailev, F.M. Simple models of quantum chaos: Spectrum and eigenfunctions. Phys. Rep. 1990, 196, 299–392. [Google Scholar] [CrossRef]
- Zhu, G.; Yang, H.; Yin, C.; Li, B. Localizations on complex networks. Phys. Rev. E 2008, 77, 066113. [Google Scholar] [CrossRef]
- Gong, L.; Tong, P. von Neumann entropy and localization-delocalization transition of electron states in quantum small-world networks. Phys. Rev. E 2006, 74, 056103. [Google Scholar] [CrossRef] [PubMed]
- Jalan, S.; Solymosi, N.; Vattay, G.; Li, B. Random matrix analysis of localization properties of gene coexpression network. Phys. Rev. E 2010, 81, 046118. [Google Scholar] [CrossRef] [PubMed]
- Menichetti, G.; Remondini, D.; Panzarasa, P.; Mondragon, R.J.; Bianconi, G. Weighted multiplex networks. PLoS ONE 2014, 9, e97857. [Google Scholar] [CrossRef]
- Brody, T.A.; Flores, J.; French, J.B.; Mello, P.A.; Pandey, A.; Wong, S.S.M. Random-matrix physics: Spectrum and strength fluctuations. Rev. Mod. Phys. 1981, 53, 385–479. [Google Scholar] [CrossRef]
- Volya, A.; Zelevinsky, V. Super-radiance and open quantum systems. AIP Conf. Proc. 2005, 777, 229–249. [Google Scholar] [CrossRef]
- Celardo, G.L.; Kaplan, L. Superradiance transition in one-dimensional nanostructures: An effective non-Hermitian Hamiltonian formalism. Phys. Rev. B 2009, 79, 155108. [Google Scholar] [CrossRef]
- Celardo, G.L.; Smith, A.M.; Sorathia, S.; Zelevinsky, V.G.; Sen’kov, R.A.; Kaplan, L. Transport through nanostructures with asymmetric coupling to the leads. Phys. Rev. B 2010, 82, 165437. [Google Scholar] [CrossRef]
- Celardo, G.L.; Izrailev, F.M.; Sorathia, S.; Zelevinsky, V.G.; Berman, G.P. Continuum shell model: From Ericson to conductance fluctuations. AIP Conf. Proc. 2008, 995, 75–84. [Google Scholar] [CrossRef]
- Scully, M.O.; Svidzinsky, A.A. The Lamb shift–Yesterday, today, and tomorrow. Science 2010, 328, 1239–1241. [Google Scholar] [CrossRef] [PubMed]
- Dicke, R.H. Coherence in spontaneous radiation processes. Phys. Rev. 1954, 93, 99–110. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Martínez, C.T.; Méndez-Bermúdez, J.A. Information Entropy of Tight-Binding Random Networks with Losses and Gain: Scaling and Universality. Entropy 2019, 21, 86. https://doi.org/10.3390/e21010086
Martínez-Martínez CT, Méndez-Bermúdez JA. Information Entropy of Tight-Binding Random Networks with Losses and Gain: Scaling and Universality. Entropy. 2019; 21(1):86. https://doi.org/10.3390/e21010086
Chicago/Turabian StyleMartínez-Martínez, C. T., and J. A. Méndez-Bermúdez. 2019. "Information Entropy of Tight-Binding Random Networks with Losses and Gain: Scaling and Universality" Entropy 21, no. 1: 86. https://doi.org/10.3390/e21010086
APA StyleMartínez-Martínez, C. T., & Méndez-Bermúdez, J. A. (2019). Information Entropy of Tight-Binding Random Networks with Losses and Gain: Scaling and Universality. Entropy, 21(1), 86. https://doi.org/10.3390/e21010086





