The Effect of Cognitive Resource Competition Due to Dual-Tasking on the Irregularity and Control of Postural Movement Components
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants and Measurement Procedures
2.2. Data Analysis
2.2.1. Pre-Processing
2.2.2. Kinematic Principal Component Analysis
2.2.3. Measures of Postural Control
2.3. Validity Considerations and Cross-Validation
2.4. Statistics
3. Results
3.1. PCA Results
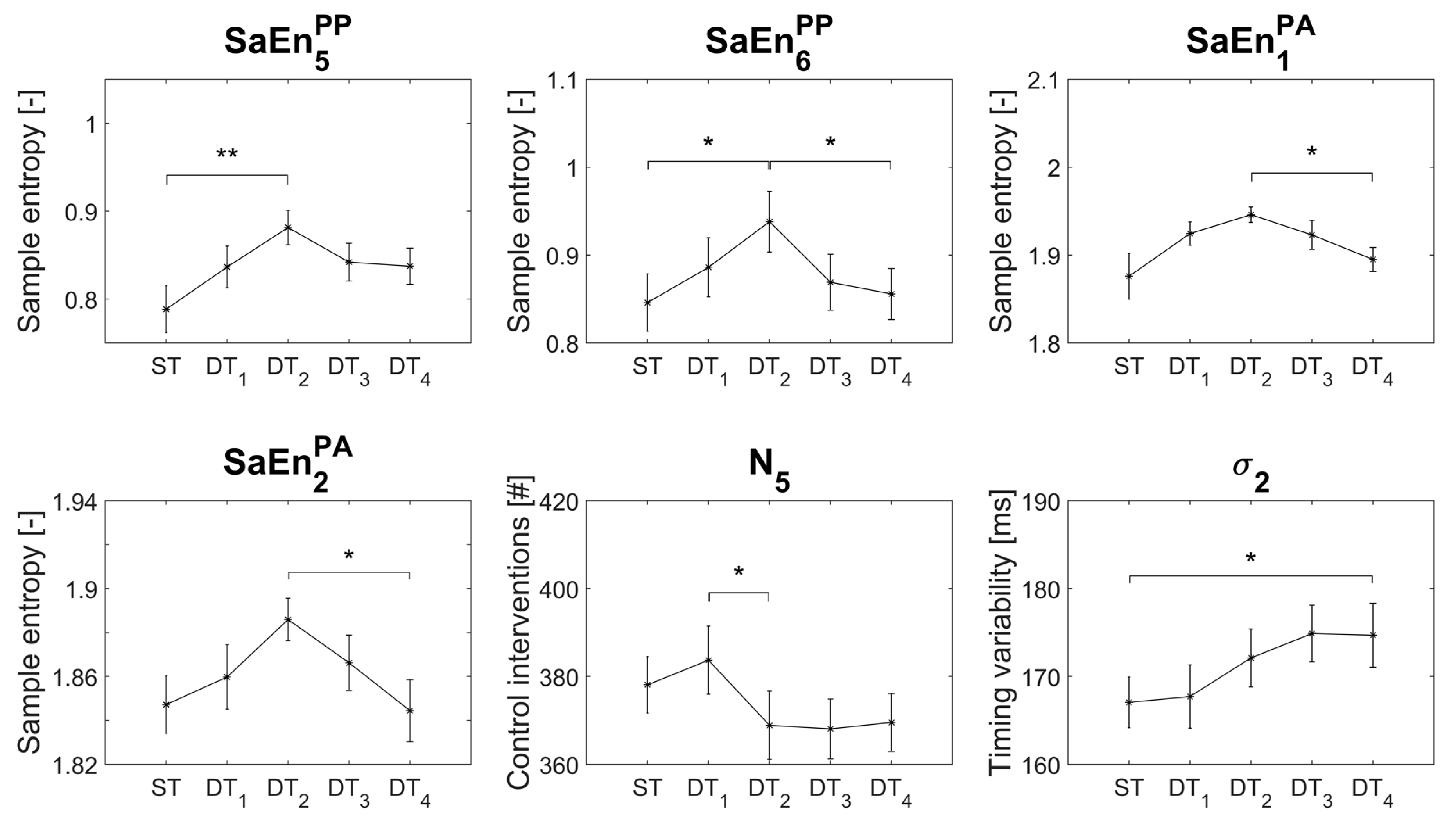
3.2. Dual-Tasking Effects (n-back)
3.3. Interaction Effects
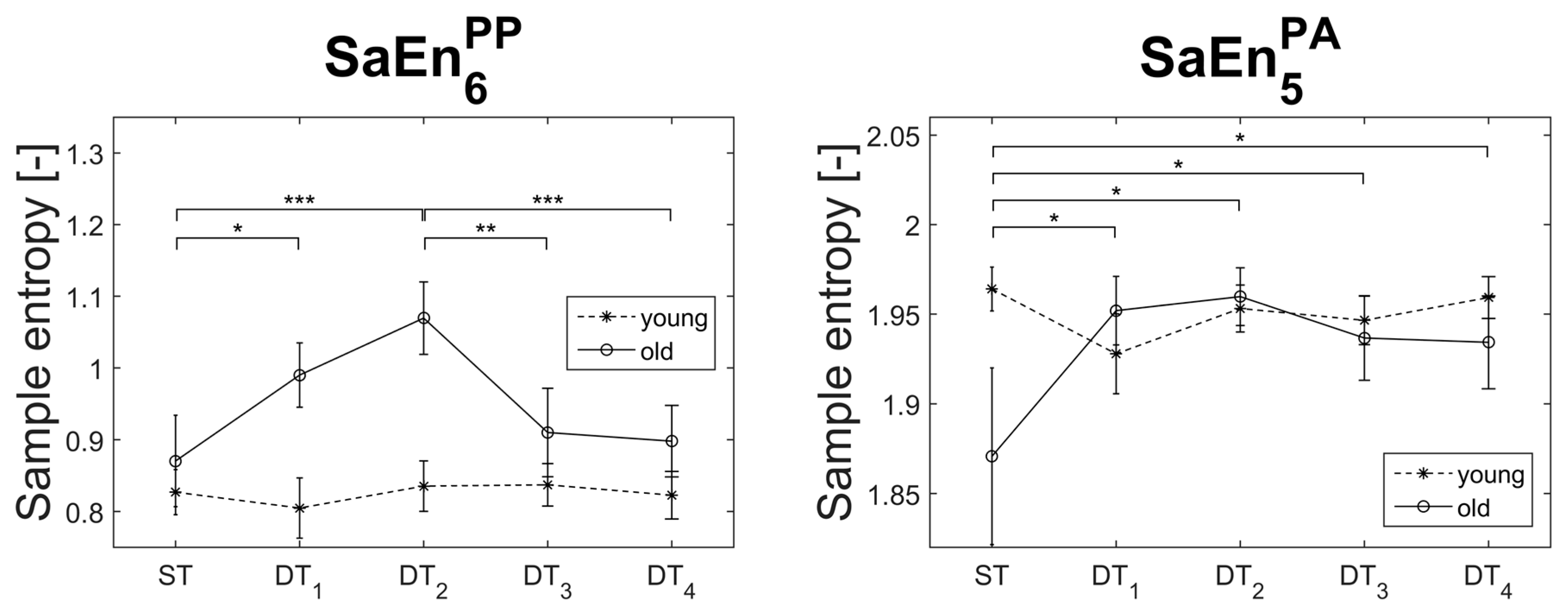
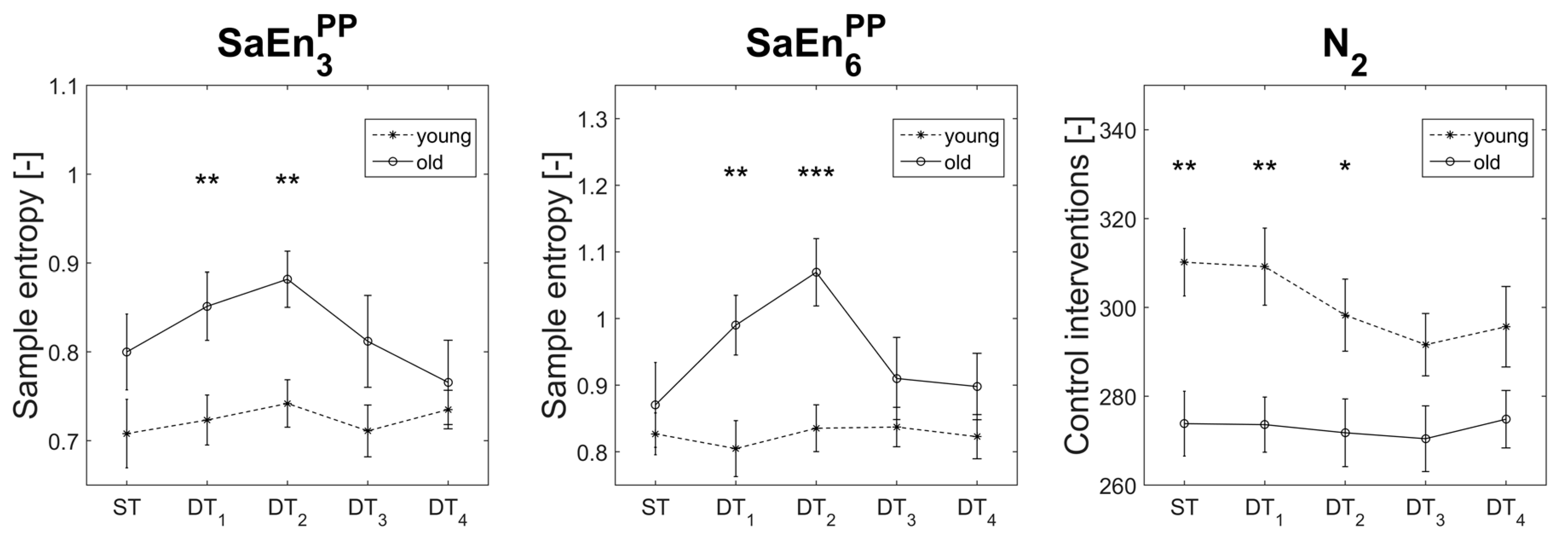
3.4. Age Effects between Subjects
4. Discussion
4.1. Dual-Tasking Effects
4.2. Age-DT Interaction Effects
4.3. Age Effects
4.4. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Woollacott, M.; Shumway-Cook, A. Attention and the control of posture and gait: A review of an emerging area of research. Gait Posture 2002, 16, 1–14. [Google Scholar] [CrossRef]
- Bronstein, A.M. Multisensory integration in balance control. Handb. Clin. Neurol. 2016, 137, 57–66. [Google Scholar] [PubMed]
- Kaliuzhna, M.; Ferrè, E.R.; Herbelin, B.; Blanke, O.; Haggard, P. Multisensory effects on somatosensation: A trimodal visuo-vestibular-tactile interaction. Sci. Rep. 2016, 6, 26301. [Google Scholar] [CrossRef] [PubMed]
- Bringoux, L.; Scotto Di Cesare, C.; Borel, L.; Macaluso, T.; Sarlegna, F.R. Do Visual and Vestibular Inputs Compensate for Somatosensory Loss in the Perception of Spatial Orientation? Insights from a Deafferented Patient. Front. Hum. Neurosci. 2016, 10, 181. [Google Scholar] [CrossRef] [PubMed]
- Teasdale, N.; Simoneau, M. Attentional demands for postural control: The effects of aging and sensory reintegration. Gait Posture 2001, 14, 203–210. [Google Scholar] [CrossRef]
- Redfern, M.S.; Yardley, L.; Bronstein, A.M. Visual influences on balance. J. Anxiety Disord. 2001, 15, 81–94. [Google Scholar] [CrossRef]
- Woollacott, M.H. Systems contributing to balance disorders in older adults. J. Gerontol. Ser. A Biol. Sci. Med. Sci. 2000, 55, M424–M428. [Google Scholar] [CrossRef]
- Pellecchia, G.L. Postural sway increases with attentional demands of concurrent cognitive task. Gait Posture 2003, 18, 29–34. [Google Scholar] [CrossRef]
- Melzer, I.; Benjuya, N.; Kaplanski, J. Age-related changes of postural control: Effect of cognitive tasks. Gerontology 2001, 47, 189–194. [Google Scholar] [CrossRef] [PubMed]
- Vander Velde, T.; Woollacott, M. Non-visual spatial tasks reveal increased interactions with stance postural control. Brain Res. 2008, 1208, 95–102. [Google Scholar] [CrossRef] [PubMed]
- Bustillo-Casero, P.; Villarrasa-Sapiña, I.; García-Massó, X. Effects of dual task difficulty in motor and cognitive performance: Differences between adults and adolescents. Hum. Mov. Sci. 2017, 55, 8–17. [Google Scholar] [CrossRef] [PubMed]
- Riley, M.A.; Baker, A.A.; Schmit, J.M.; Weaver, E. Effects of visual and auditory short-term memory tasks on the spatiotemporal dynamics and variability of postural sway. J. Mot. Behav. 2005, 37, 311–324. [Google Scholar] [CrossRef] [PubMed]
- Stins, J.F.; Roerdink, M.; Beek, P.J. To freeze or not to freeze? Affective and cognitive perturbations have markedly different effects on postural control. Hum. Mov. Sci. 2011, 30, 190–202. [Google Scholar] [CrossRef] [PubMed]
- Polskaia, N.; Richer, N.; Dionne, E.; Lajoie, Y. Continuous cognitive task promotes greater postural stability than an internal or external focus of attention. Gait Posture 2015, 41, 454–458. [Google Scholar] [CrossRef] [PubMed]
- Huxhold, O.; Li, S.-C.; Schmiedek, F.; Lindenberger, U. Dual-tasking postural control: Aging and the effects of cognitive demand in conjunction with focus of attention. Brain Res. Bull. 2006, 69, 294–305. [Google Scholar] [CrossRef] [PubMed]
- Potvin-Desrochers, A.; Richer, N.; Lajoie, Y. Cognitive tasks promote automatization of postural control in young and older adults. Gait Posture 2017, 57, 40–45. [Google Scholar] [CrossRef] [PubMed]
- Lacour, M.; Bernard-Demanze, L.; Dumitrescu, M. Posture control, aging, and attention resources: Models and posture-analysis methods. Neurophysiol. Clin. Clin. Neurophysiol. 2008, 38, 411–421. [Google Scholar] [CrossRef]
- Vuillerme, N.; Nafati, G. How attentional focus on body sway affects postural control during quiet standing. Psychol. Res. 2007, 71, 192–200. [Google Scholar] [CrossRef]
- Wulf, G.; Mercer, J.; McNevin, N.; Guadagnoli, M.A. Reciprocal influences of attentional focus on postural and suprapostural task performance. J. Mot. Behav. 2004, 36, 189–199. [Google Scholar] [CrossRef]
- Donker, S.F.; Roerdink, M.; Greven, A.J.; Beek, P.J. Regularity of center-of-pressure trajectories depends on the amount of attention invested in postural control. Exp. Brain Res. 2007, 181, 1–11. [Google Scholar] [CrossRef]
- Stins, J.F.; Michielsen, M.E.; Roerdink, M.; Beek, P.J. Sway regularity reflects attentional involvement in postural control: Effects of expertise, vision and cognition. Gait Posture 2009, 30, 106–109. [Google Scholar] [CrossRef] [PubMed]
- Cavanaugh, J.T.; Guskiewicz, K.M.; Giuliani, C.; Marshall, S.; Mercer, V.S.; Stergiou, N. Recovery of postural control after cerebral concussion: New insights using approximate entropy. J. Athl. Train. 2006, 41, 305–313. [Google Scholar] [PubMed]
- Schmit, J.M.; Regis, D.I.; Riley, M.A. Dynamic patterns of postural sway in ballet dancers and track athletes. Exp. Brain Res. 2005, 163, 370–378. [Google Scholar] [CrossRef] [PubMed]
- Borg, F.G.; Laxåback, G. Entropy of balance—Some recent results. J. Neuroeng. Rehabil. 2010, 7, 38. [Google Scholar] [CrossRef] [PubMed]
- Winter, D.A.; Prince, F.; Frank, J.S.; Powell, C.; Zabjek, K.F. Unified theory regarding A/P and M/L balance in quiet stance. J. Neurophysiol. 1996, 75, 2334–2343. [Google Scholar] [CrossRef] [PubMed]
- Cavanaugh, J.T.; Mercer, V.S.; Stergiou, N. Approximate entropy detects the effect of a secondary cognitive task on postural control in healthy young adults: A methodological report. J. Neuroeng. Rehabil. 2007, 4, 42. [Google Scholar] [CrossRef] [PubMed]
- Ladislao, L.; Rabini, R.A.; Ghetti, G.; Fioretti, S. Approximate entropy on posturographic data of diabetic subjects with peripheral neuropathy. Gait Posture 2008, 28, S6–S7. [Google Scholar] [CrossRef]
- Santarcangelo, E.L.; Scattina, E.; Carli, G.; Balocchi, R.; Macerata, A.; Manzoni, D. Modulation of the postural effects of cognitive load by hypnotizability. Exp. Brain Res. 2009, 194, 323–328. [Google Scholar] [CrossRef]
- Haran, F.J.; Keshner, E.A. Sensory Reweighting as a Method of Balance Training for Labyrinthine Loss. J. Neurol. Phys. Ther. 2008, 32, 186. [Google Scholar] [CrossRef]
- De Beaumont, L.; Mongeon, D.; Tremblay, S.; Messier, J.; Prince, F.; Leclerc, S.; Lassonde, M.; Théoret, H. Persistent motor system abnormalities in formerly concussed athletes. J. Athl. Train. 2011, 46, 234–240. [Google Scholar] [CrossRef]
- Gao, J.; Hu, J.; Buckley, T.; White, K.; Hass, C. Shannon and Renyi entropies to classify effects of Mild Traumatic Brain Injury on postural sway. PLoS ONE 2011, 6, e24446. [Google Scholar] [CrossRef] [PubMed]
- Sosnoff, J.J.; Broglio, S.P.; Shin, S.; Ferrara, M.S. Previous Mild Traumatic Brain Injury and Postural-Control Dynamics. J. Athl. Train. 2011, 46, 85–91. [Google Scholar] [CrossRef] [PubMed]
- Haid, T.; Federolf, P. Human Postural Control: Assessment of Two Alternative Interpretations of Center of Pressure Sample Entropy through a Principal Component Factorization of Whole-Body Kinematics. Entropy 2018, 20, 30. [Google Scholar] [CrossRef]
- Federolf, P.A. A novel approach to study human posture control: “Principal movements” obtained from a principal component analysis of kinematic marker data. J. Biomech. 2016, 49, 364–370. [Google Scholar] [CrossRef] [PubMed]
- Todorov, E.; Jordan, M.I. Optimal feedback control as a theory of motor coordination. Nat. Neurosci. 2002, 5, 1226–1235. [Google Scholar] [CrossRef] [PubMed]
- Zago, M.; Pacifici, I.; Lovecchio, N.; Galli, M.; Federolf, P.A.; Sforza, C. Multi-segmental movement patterns reflect juggling complexity and skill level. Hum. Mov. Sci. 2017, 54, 144–153. [Google Scholar] [CrossRef] [PubMed]
- Daffertshofer, A.; Lamoth, C.J.C.; Meijer, O.G.; Beek, P.J. PCA in studying coordination and variability: A tutorial. Clin. Biomech. 2004, 19, 415–428. [Google Scholar] [CrossRef]
- Troje, N.F. Decomposing biological motion: A framework for analysis and synthesis of human gait patterns. J. Vis. 2002, 2, 371–387. [Google Scholar] [CrossRef]
- Promsri, A.; Haid, T.; Werner, I.; Federolf, P. Influence of lower-limb dominance on coordinative movement structures observed during single-leg balancing on a multiaxial unstable surface. Gait Posture 2018. [Google Scholar] [CrossRef]
- Haid, T.H.; Doix, A.-C.M.; Nigg, B.M.; Federolf, P.A. Age Effects in Postural Control Analyzed via a Principal Component Analysis of Kinematic Data and Interpreted in Relation to Predictions of the Optimal Feedback Control Theory. Front. Aging Neurosci. 2018, 10, 22. [Google Scholar] [CrossRef]
- Promsri, A.; Haid, T.; Federolf, P. How does lower limb dominance influence postural control movements during single leg stance? Hum. Mov. Sci. 2018, 58, 165–174. [Google Scholar] [CrossRef] [PubMed]
- Gløersen, Ø.; Federolf, P. Predicting Missing Marker Trajectories in Human Motion Data Using Marker Intercorrelations. PLoS ONE 2016, 11, e0152616. [Google Scholar] [CrossRef] [PubMed]
- Federolf, P.A. A Novel Approach to Solve the “Missing Marker Problem” in Marker-Based Motion Analysis That Exploits the Segment Coordination Patterns in Multi-Limb Motion Data. PLoS ONE 2013, 8, e78689. [Google Scholar] [CrossRef] [PubMed]
- Rine, R.M.; Schubert, M.C.; Whitney, S.L.; Roberts, D.; Redfern, M.S.; Musolino, M.C.; Roche, J.L.; Steed, D.P.; Corbin, B.; Lin, C.-C.; et al. Vestibular function assessment using the NIH Toolbox. Neurology 2013, 80, S25–S31. [Google Scholar] [CrossRef] [PubMed]
- Coquart, J.B.J.; Garcin, M. Knowledge of the endpoint: Effect on perceptual values. Int. J. Sports Med. 2008, 29, 976–979. [Google Scholar] [CrossRef] [PubMed]
- Gløersen, Ø.; Myklebust, H.; Hallén, J.; Federolf, P. Technique analysis in elite athletes using principal component analysis. J. Sports Sci. 2017, 36, 229–237. [Google Scholar] [CrossRef] [PubMed]
- Defense Technical Information Center. DTIC ADA304353: Anthropometry and Mass Distribution for Human Analogues, Volume I: Military Male Aviators; Naval Biodynamics Laboratory: New Orleans, LA, USA, 1988. [Google Scholar]
- Estrada, L.; Torres, A.; Sarlabous, L.; Jané, R. Influence of Parameter Selection in Fixed Sample Entropy of Surface Diaphragm Electromyography for Estimating Respiratory Activity. Entropy 2017, 19, 460. [Google Scholar] [CrossRef]
- Kanekar, N.; Lee, Y.-J.; Aruin, A.S. Frequency analysis approach to study balance control in individuals with multiple sclerosis. J. Neurosci. Methods 2014, 222, 91–96. [Google Scholar] [CrossRef] [PubMed]
- Bro, R.; Kjeldahl, K.; Smilde, A.K.; Kiers, H.A.L. Cross-validation of component models: A critical look at current methods. Anal. Bioanal. Chem. 2008, 390, 1241–1251. [Google Scholar] [CrossRef] [PubMed]
- Camacho, J.; Ferrer, A. Cross-validation in PCA models with the element-wise k-fold (ekf) algorithm: Theoretical aspects. J. Chemom. 2012, 26, 361–373. [Google Scholar] [CrossRef]
- Diana, G.; Tommasi, C. Cross-validation methods in principal component analysis: A comparison. Stat. Methods Appl. 2002, 11, 71–82. [Google Scholar] [CrossRef]
- Deviterne, D.; Gauchard, G.C.; Jamet, M.; Vançon, G.; Perrin, P.P. Added cognitive load through rotary auditory stimulation can improve the quality of postural control in the elderly. Brain Res. Bull. 2005, 64, 487–492. [Google Scholar] [CrossRef] [PubMed]
- Gill, J.; Allum, J.H.J.; Carpenter, M.G.; Held-Ziolkowska, M.; Adkin, A.L.; Honegger, F.; Pierchala, K. Trunk Sway Measures of Postural Stability During Clinical Balance Tests: Effects of Age. J. Gerontol. Ser. A 2001, 56, M438–M447. [Google Scholar] [CrossRef]
- Allum, J.H.J.; Adkin, A.L.; Carpenter, M.G.; Held-Ziolkowska, M.; Honegger, F.; Pierchala, K. Trunk sway measures of postural stability during clinical balance tests: Effects of a unilateral vestibular deficit. Gait Posture 2001, 14, 227–237. [Google Scholar] [CrossRef]
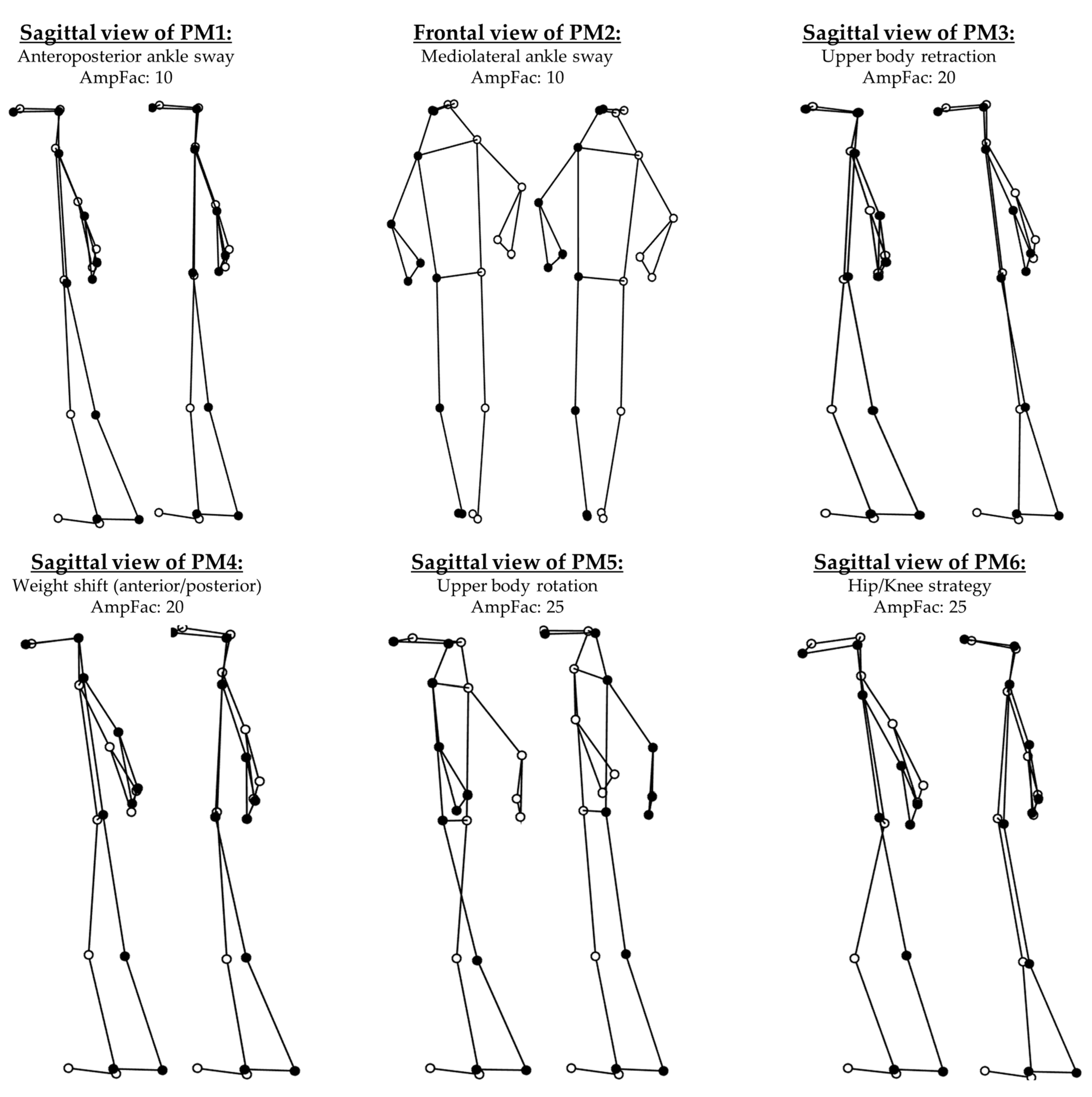
| k | EV [%] | Effects | Main Strategy (Directions) | Specifications/Additional Features |
|---|---|---|---|---|
| 1 | 51.1 | PA | Ankle (anterior/posterior) | No visible motions in the rest of the body. |
| 2 | 26.5 | PA, σ | Ankle (medial/lateral) | No visible motions in the rest of the body. |
| 3 | 9.7 | Upper body (retraction) | Upper body leans back. Front knee (flexion/extension). | |
| 4 | 3.9 | Weight shift (anterior/posterior) | Upper body shifted from over one foot to over the other. | |
| 5 | 2.6 | PP, N | Upper body rotation | No visible motions in the rest of the body. |
| 6 | 1.9 | PP, N | Hip/Knee strategy | Flexion/extension in both hip and knee. |
| Nk | σk | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p | p | p | p | |||||||||
| PM1 | 0.062 1 | 0.06 | 0.64 | 0.016 *,2 | 0.09 | 0.76 | 0.147 1 | 0.04 | 0.50 | 0.190 2 | 0.04 | 0.37 |
| PM2 | 0.228 | 0.04 | 0.45 | 0.028 * | 0.07 | 0.76 | 0.082 | 0.05 | 0.62 | 0.024 * | 0.07 | 0.77 |
| PM3 | 0.054 | 0.06 | 0.68 | 0.101 2 | 0.05 | 0.53 | 0.363 1 | 0.03 | 0.33 | 0.403 | 0.03 | 0.03 |
| PM4 | 0.128 1 | 0.05 | 0.53 | 0.082 | 0.05 | 0.62 | 0.147 | 0.04 | 0.52 | 0.116 | 0.05 | 0.56 |
| PM5 | 0.003 ** | 0.10 | 0.92 | 0.303 1 | 0.03 | 0.34 | 0.011 *,1 | 0.09 | 0.83 | 0.216 1 | 0.04 | 0.42 |
| PM6 | 0.017 * | 0.07 | 0.80 | 0.099 2 | 0.05 | 0.52 | 0.030 * | 0.07 | 0.75 | 0.065 1 | 0.06 | 0.64 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haid, T.; Federolf, P. The Effect of Cognitive Resource Competition Due to Dual-Tasking on the Irregularity and Control of Postural Movement Components. Entropy 2019, 21, 70. https://doi.org/10.3390/e21010070
Haid T, Federolf P. The Effect of Cognitive Resource Competition Due to Dual-Tasking on the Irregularity and Control of Postural Movement Components. Entropy. 2019; 21(1):70. https://doi.org/10.3390/e21010070
Chicago/Turabian StyleHaid, Thomas, and Peter Federolf. 2019. "The Effect of Cognitive Resource Competition Due to Dual-Tasking on the Irregularity and Control of Postural Movement Components" Entropy 21, no. 1: 70. https://doi.org/10.3390/e21010070
APA StyleHaid, T., & Federolf, P. (2019). The Effect of Cognitive Resource Competition Due to Dual-Tasking on the Irregularity and Control of Postural Movement Components. Entropy, 21(1), 70. https://doi.org/10.3390/e21010070






