A Programmable Mechanical Maxwell’s Demon
Abstract
1. Introduction
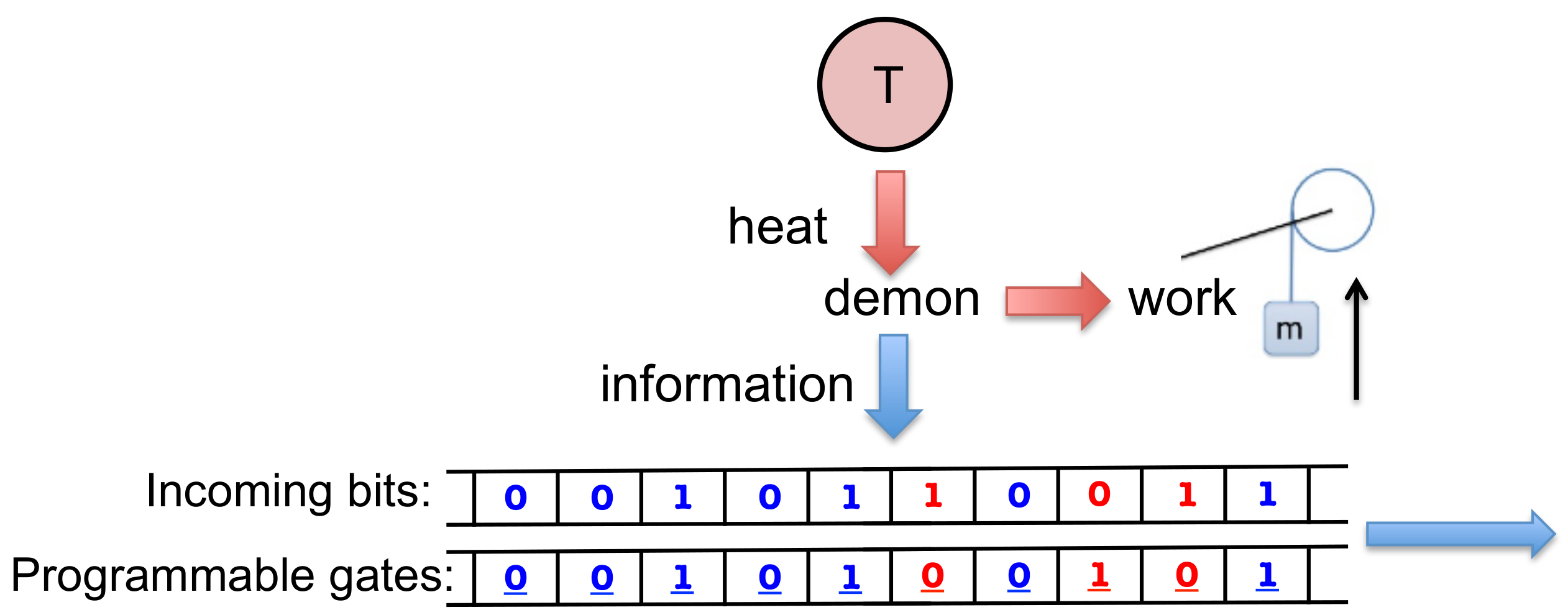
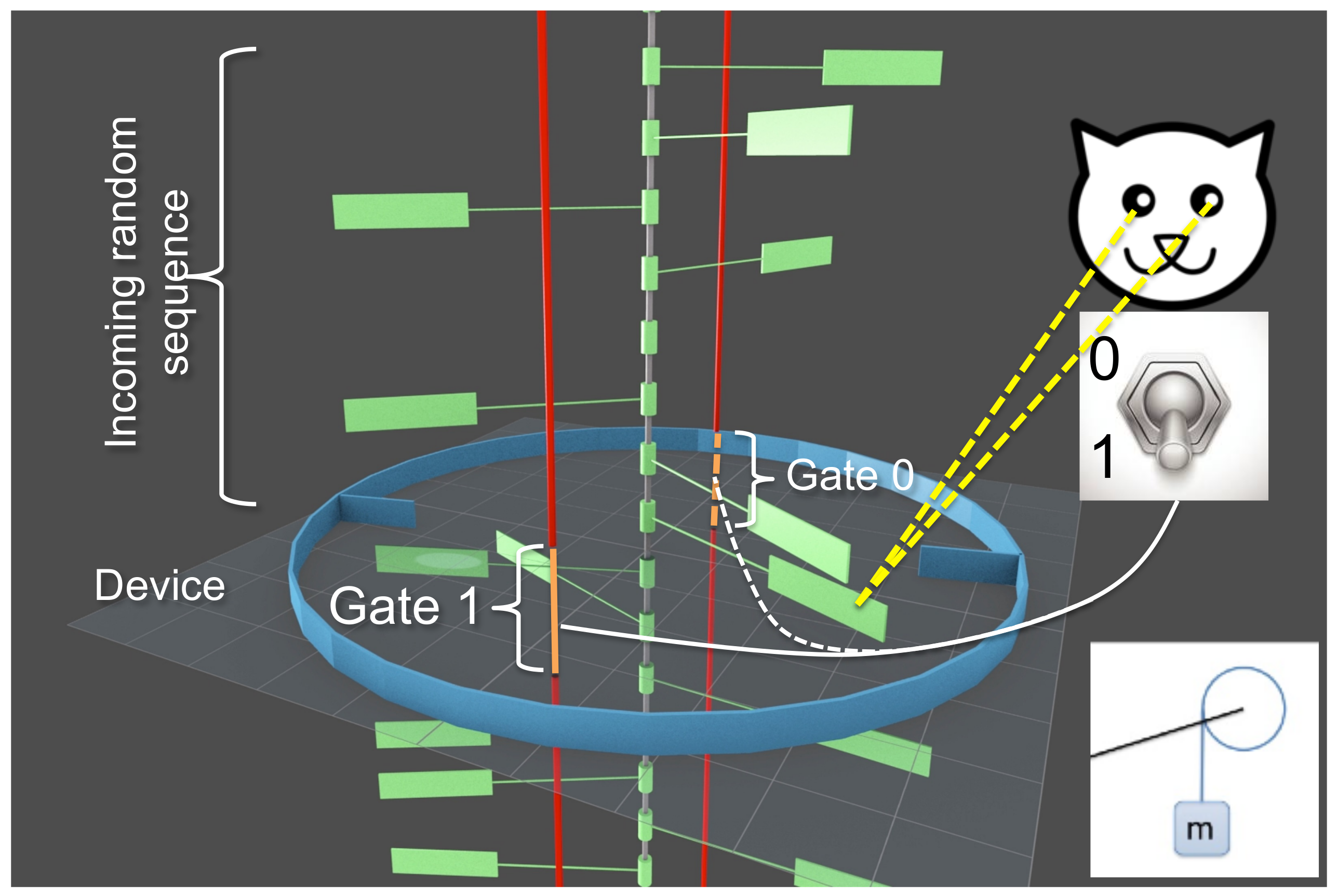
2. Programmable Maxwell’s Demon
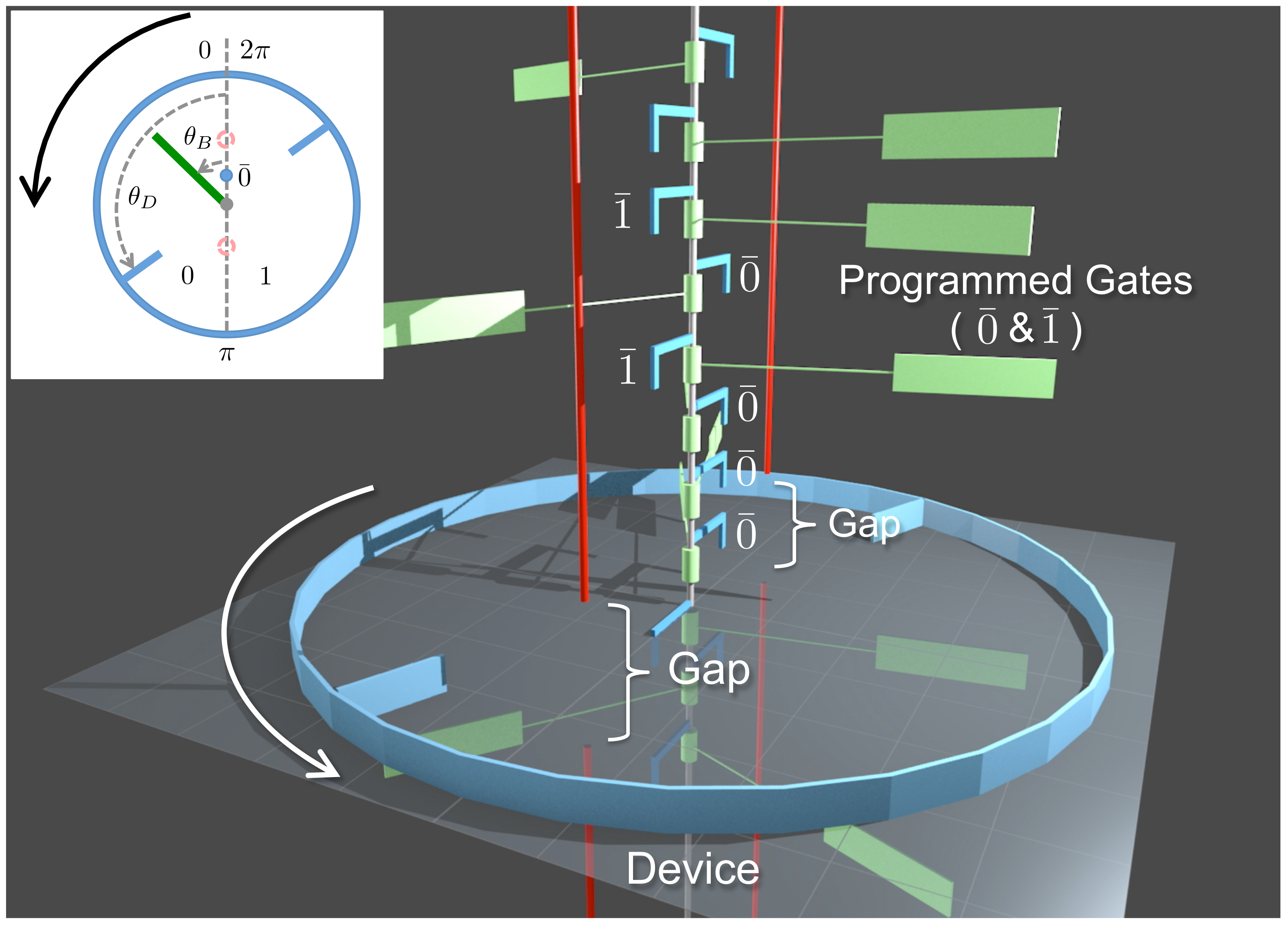
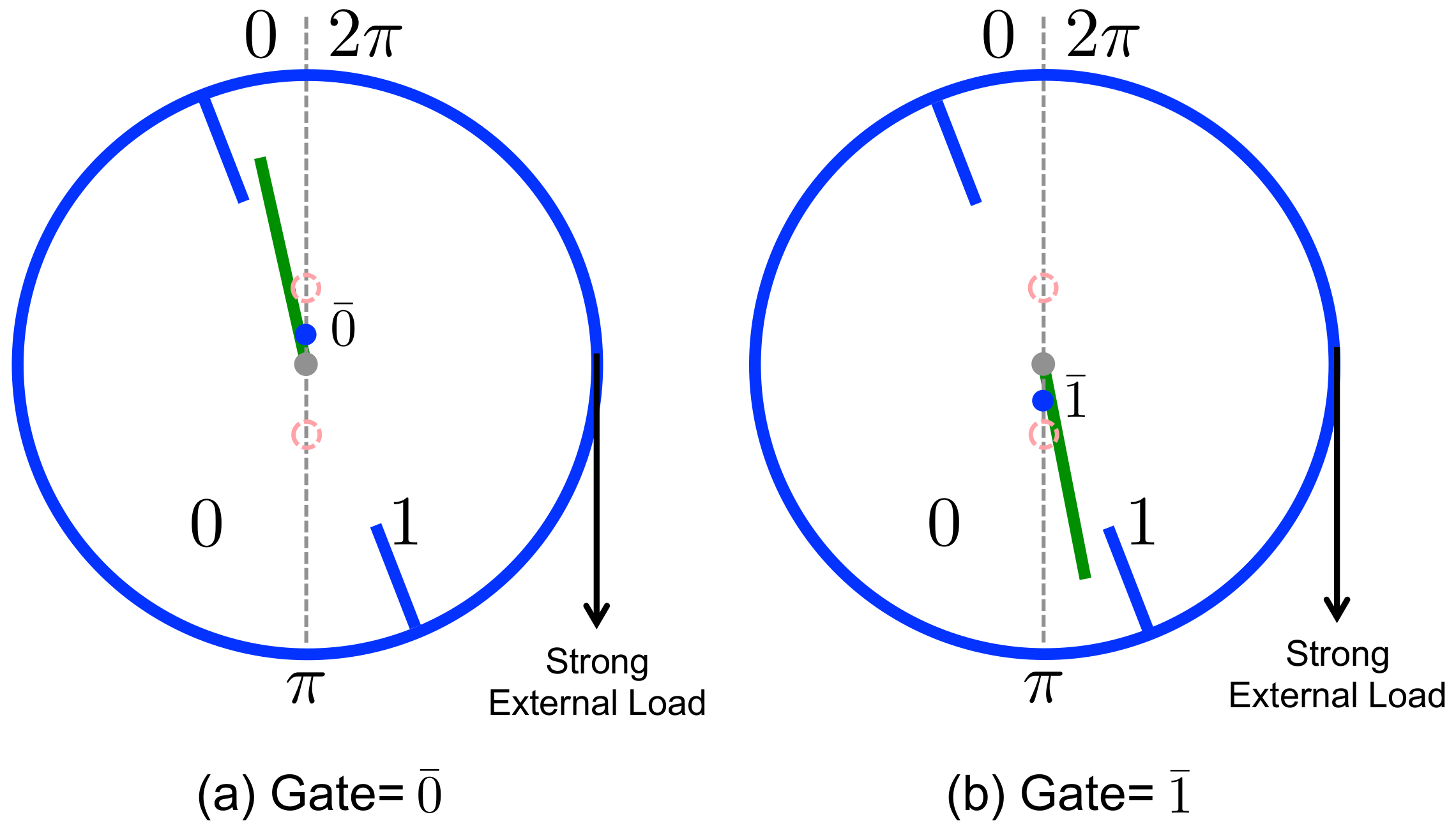
2.1. Components and Basic Design
2.2. Memory Register—A Sequence of Bits
2.3. Work Reservoir—A Mass that Can Be Raised or Lowered
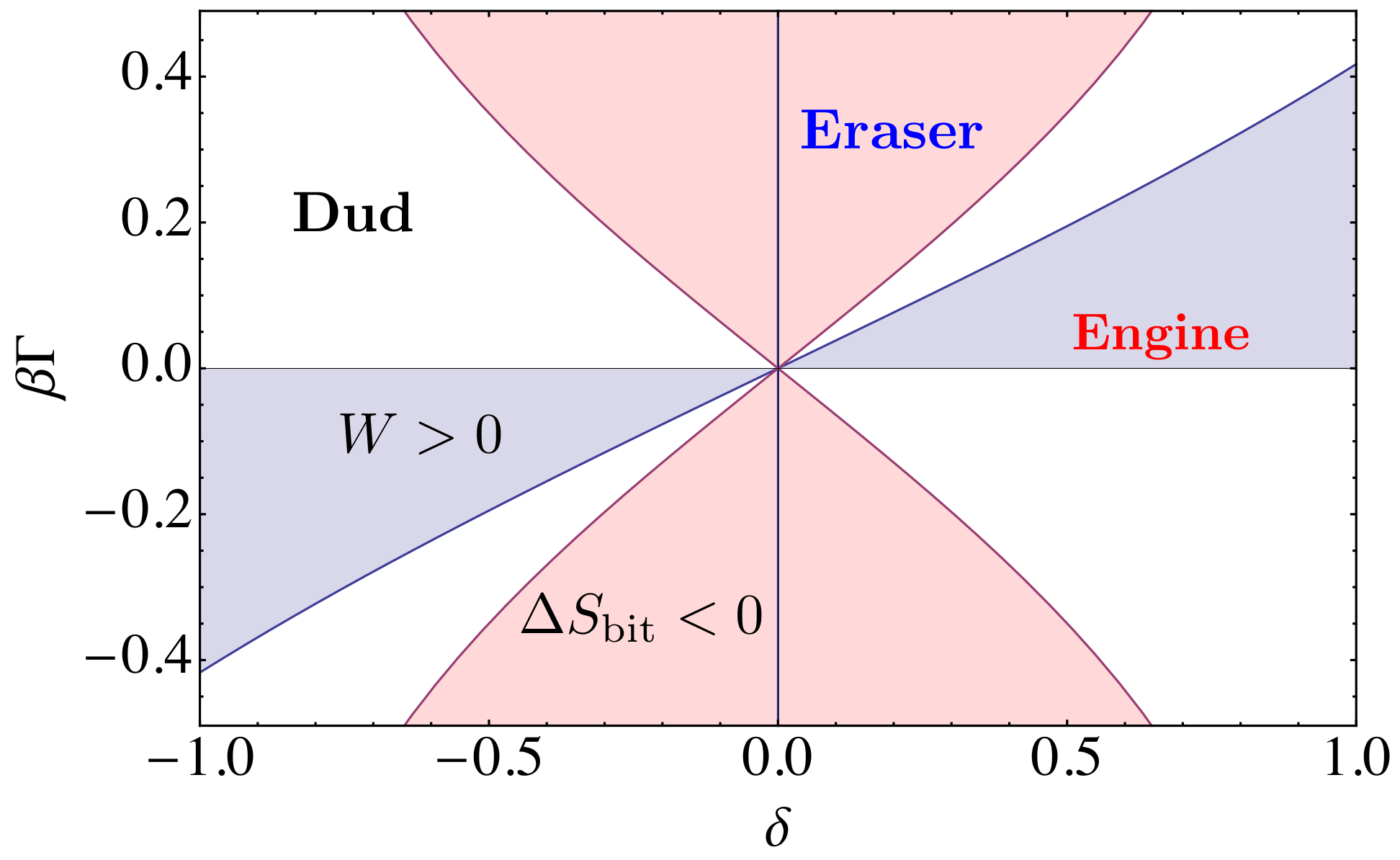
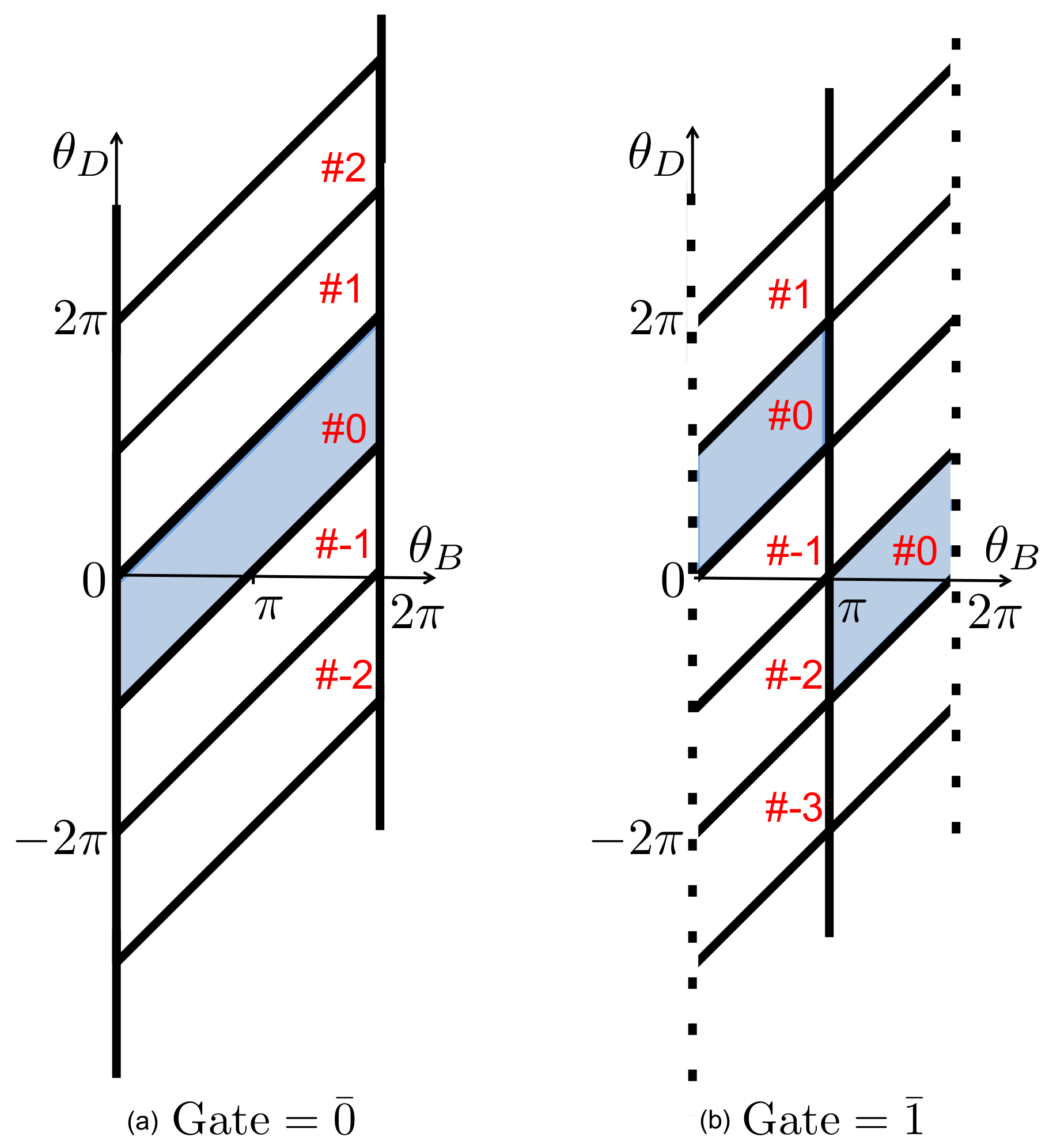
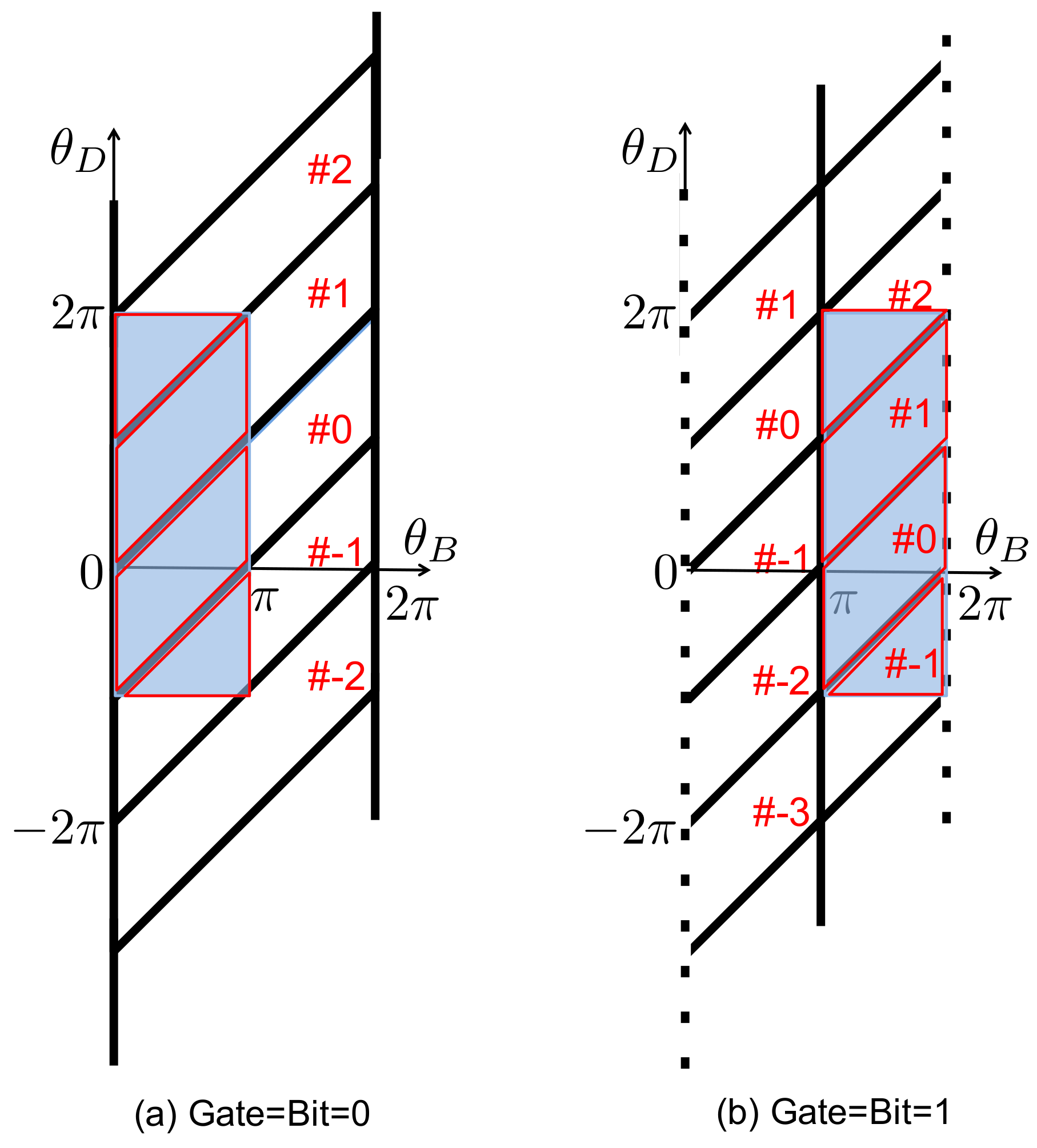
3. Operational Modes of the Programmable Demon
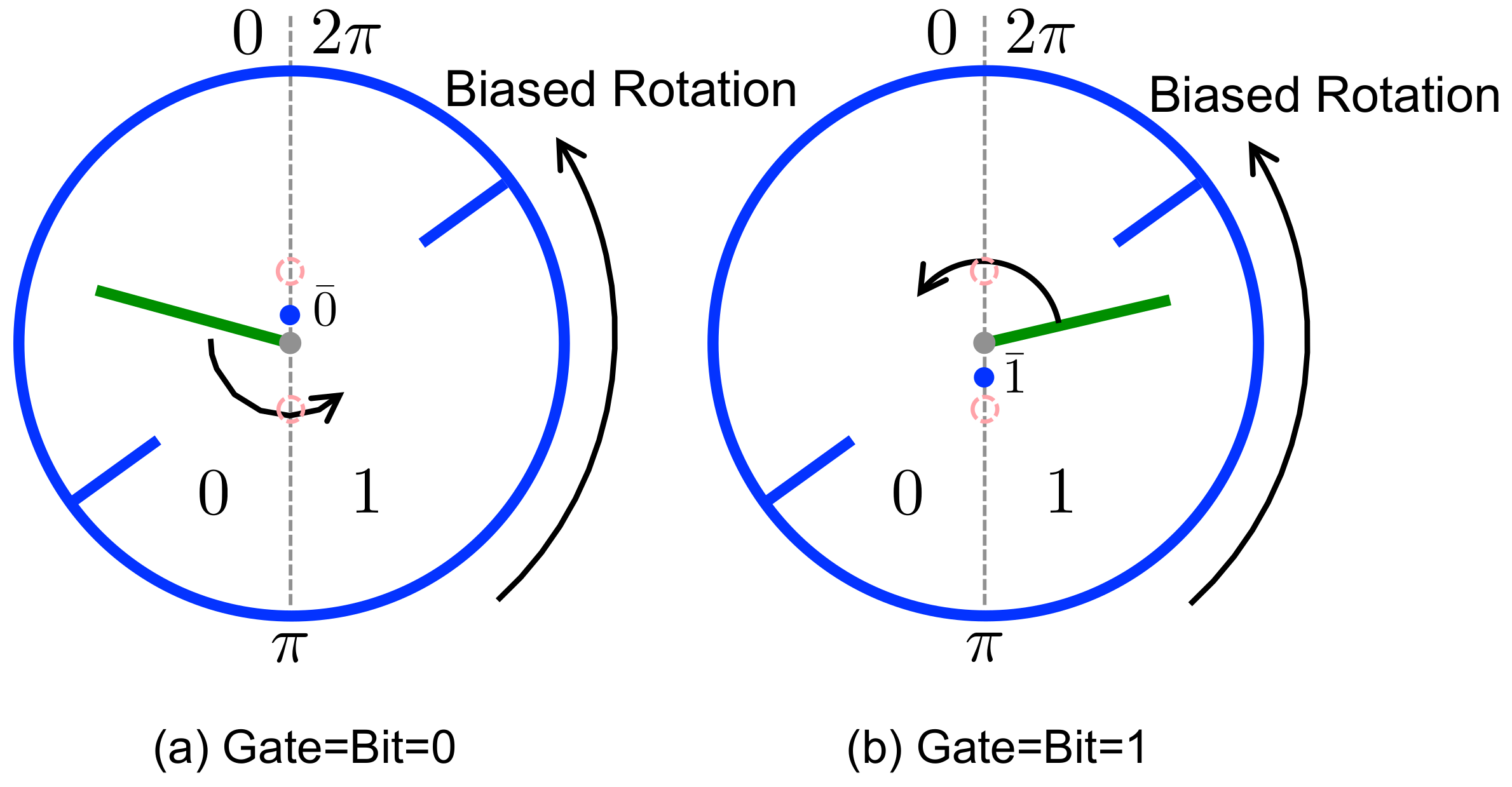
3.1. Engine Mode
3.2. Eraser Mode
3.3. Dud Mode
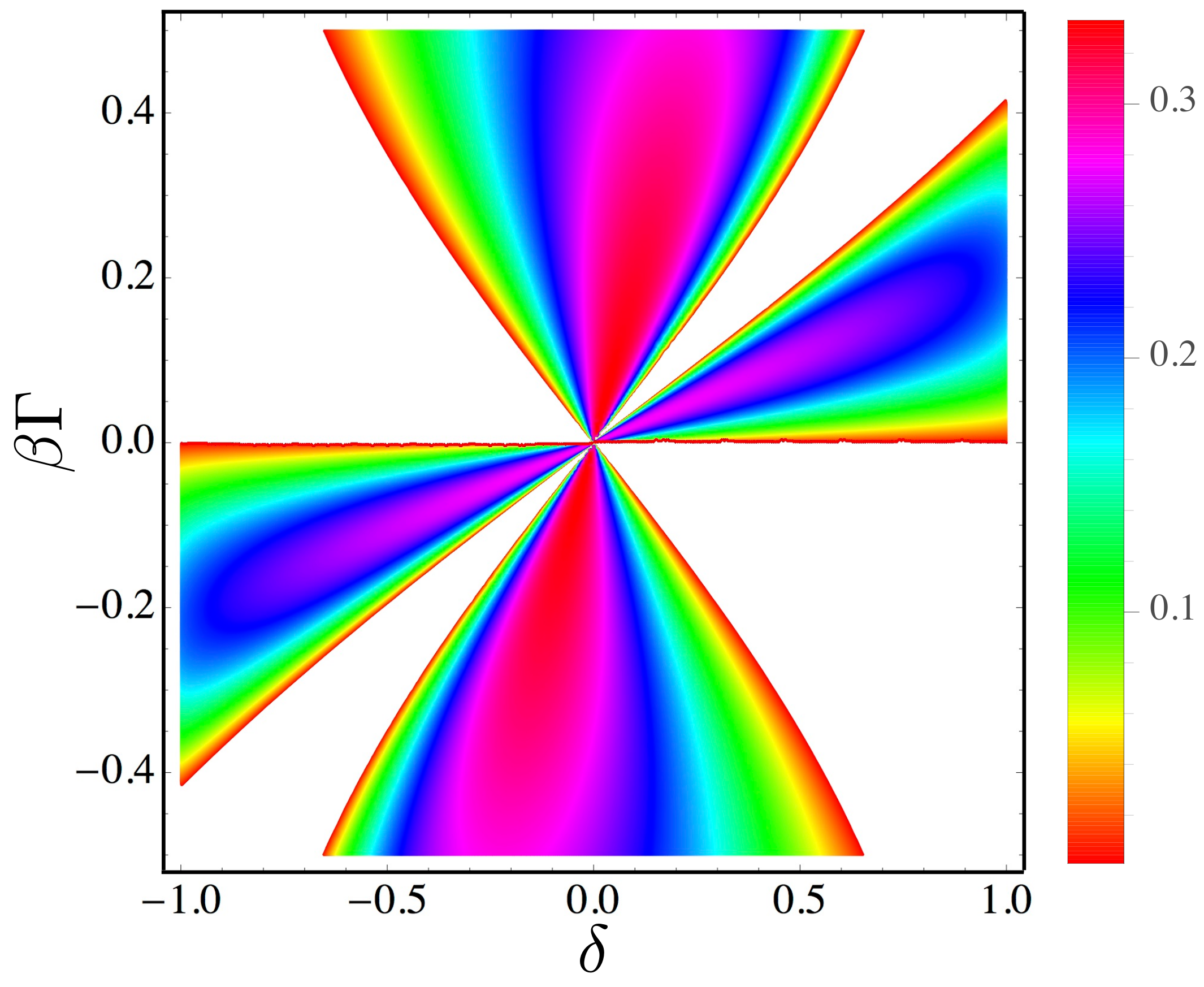
4. Numerical and Analytical Results
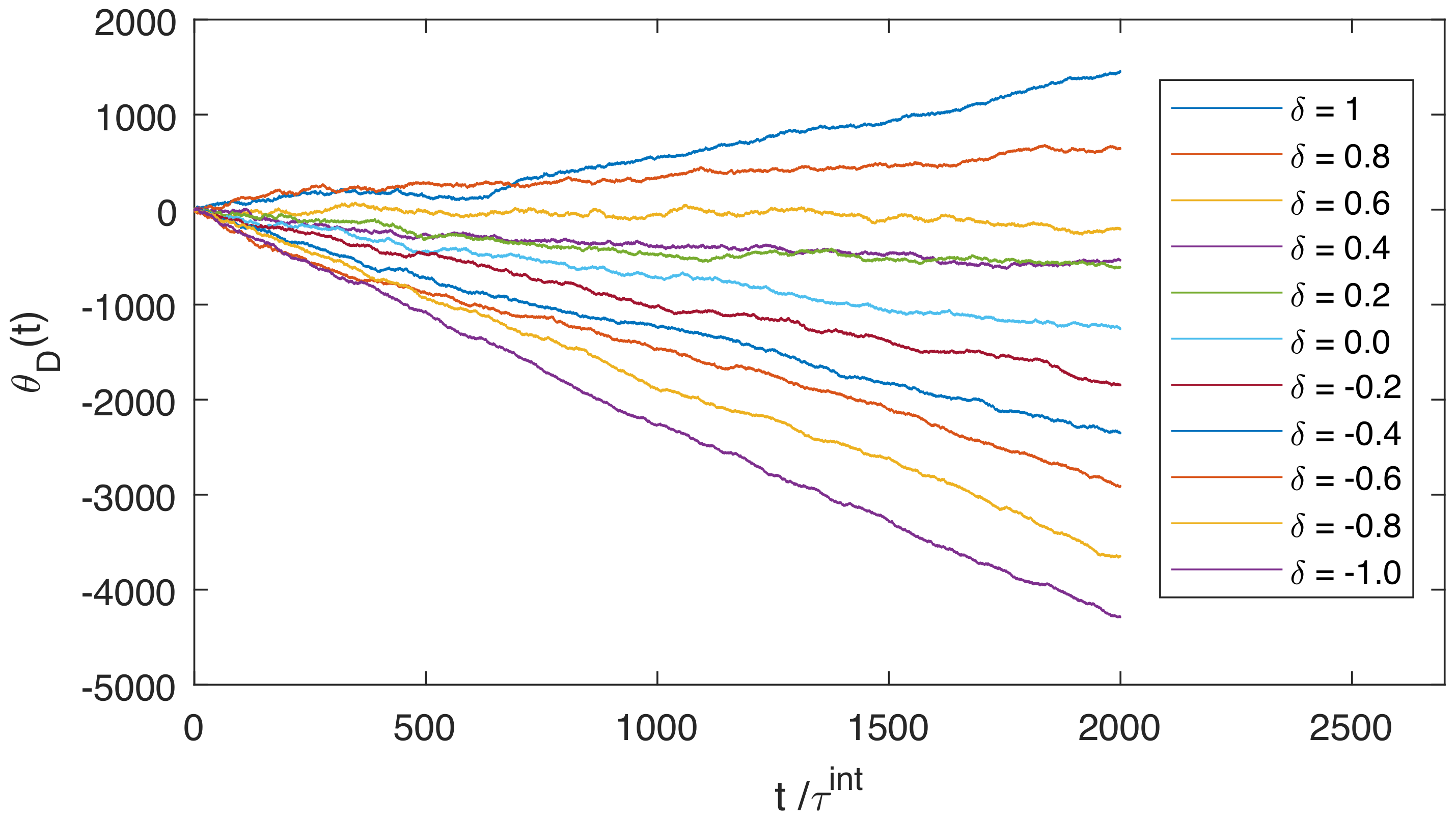
4.1. Numerical Simulations
4.2. Analytical Results for the Slow-Moving Limit
4.3. Second Law of Thermodynamics in the Slow Moving Limit
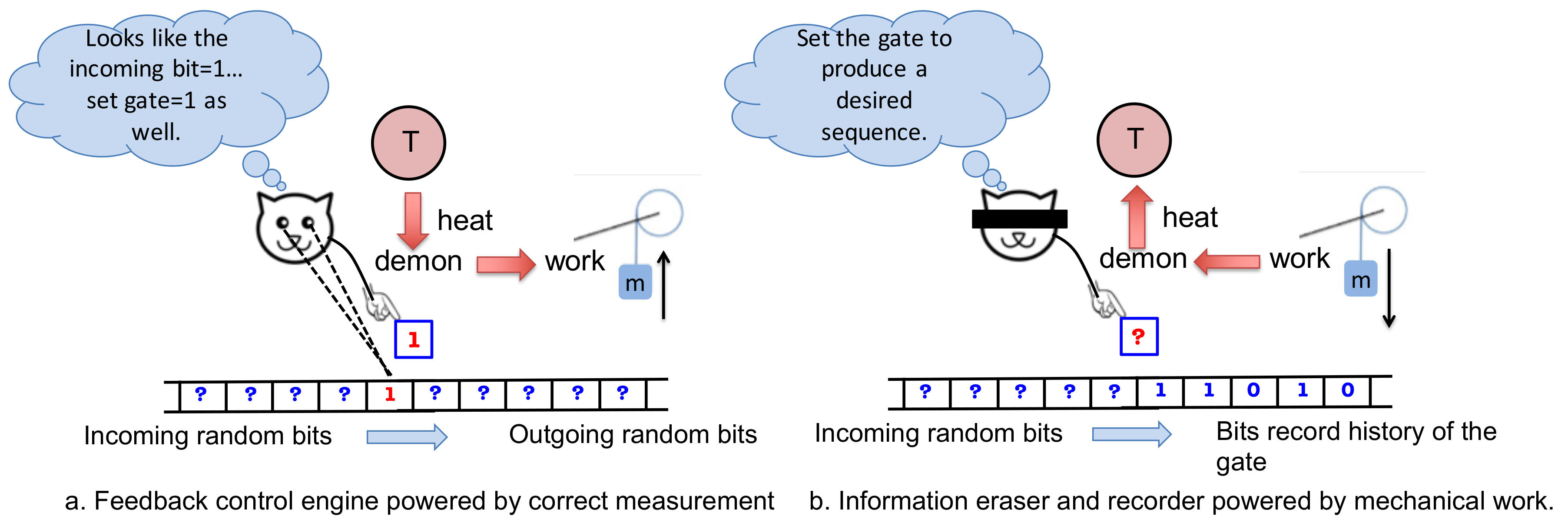
5. Our Machine As a Feedback-Controlled Device
5.1. Feedback-Controlled Engine
5.2. The Second Law of Thermodynamics with Feedback Control
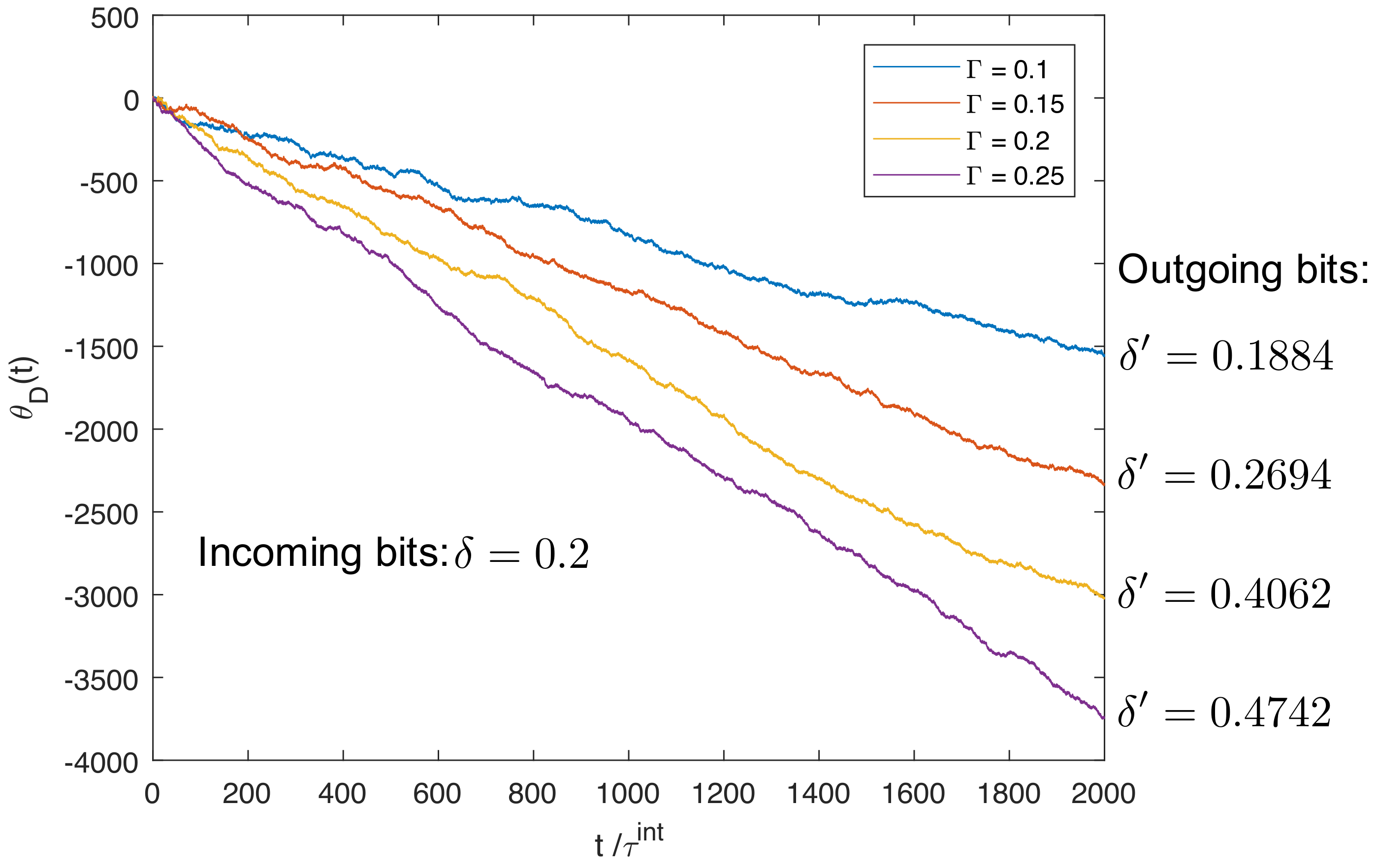
5.3. Feedback-Controlled Information Recorder
6. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Work Delivered Per Interaction Interval
Appendix B. Compatibility with the Second Law of Thermodynamics
References
- Maxwell, J.C. The Scientific Letters and Papers of James Clerk Maxwell; Cambridge University Press: Cambridge, UK, 1995; Volume 2, pp. 1862–1873. [Google Scholar]
- Smoluchowski, M. Experimentell nachweisbare, der üblichen Thermodynamik widersprechende Molekularphänomene [Experimentally verifiable phenomena of molecules contradicting usual thermodynamics]. Physikalische Zeitschrift 1912, 13, 1069–1080. (In German) [Google Scholar]
- Feynman, R.P.; Leighton, R.B.; Sands, M. The Feynman Lectures on Physics; Addison-Wesley: Reading, MA, USA, 1966. [Google Scholar]
- Landauer, R. Irreversibility and Heat Generation in the Computing Process. IBM J. Res. Dev. 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Penrose, O. Foundations of Statistical Mechanics; Pergamon Press: Oxford, UK, 1970; Volume 42. [Google Scholar]
- Bennett, C.H. Logical Reversibility of Computation. IBM J. Res. Dev. 1973, 17, 525–532. [Google Scholar] [CrossRef]
- Bennett, C.H. Dissipation-error tradeoff on proofreading. BioSystems 1979, 11, 85–91. [Google Scholar] [CrossRef]
- Jarzynski, C. Nonequilibrium Equality for Free Energy Differences. Phys. Rev. Lett. 1997, 78, 2690–2693. [Google Scholar] [CrossRef]
- Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 1999, 60, 2721. [Google Scholar] [CrossRef]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Progr. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef]
- Collin, D.; Ritort, F.; Jarzynski, C.; Smith, S.B.; Tinoco, I., Jr.; Bustamante, C. Verification of the Crooks fluctuation theorem and recovery of RNA folding free energies. Nature 2005, 437, 231–234. [Google Scholar] [CrossRef]
- Kay, E.R.; Leigh, D.A.; Zerbetto, F. Synthetic molecular motors and mechanical machines. Angew. Chem. Int. Ed. 2007, 46, 72–191. [Google Scholar] [CrossRef]
- Kim, K.H.; Qian, H. Fluctuation theorems for a molecular refrigerator. Phys. Rev. E 2007, 75, 022102. [Google Scholar] [CrossRef]
- Gavrilov, M.; Chétrite, R.; Bechhoefer, J. Direct measurement of weakly nonequilibrium system entropy is consistent with Gibbs–Shannon form. Proc. Natl. Acad. Sci. USA 2017, 114, 11097–11102. [Google Scholar] [CrossRef] [PubMed]
- Serreli, V.; Lee, C.F.; Kay, E.R.; Leigh, D.A. A molecular information ratchet. Nature 2007, 445, 523–527. [Google Scholar] [CrossRef] [PubMed]
- Bérut, A.; Arakelyan, A.; Petrosyan, A.; Ciliberto, S.; Dillenschneider, R.; Lutz, E. Experimental verification of Landauer’s principle linking information and thermodynamics. Nature 2012, 483, 187–189. [Google Scholar] [CrossRef]
- Koski, J.V.; Maisi, V.F.; Pekola, J.P.; Averin, D.V. Experimental realization of a Szilard engine with a single electron. Proc. Natl. Acad. Sci. USA 2014, 111, 13786–13789. [Google Scholar] [CrossRef]
- Koski, J.V.; Kutvonen, A.; Khaymovich, I.M.; Ala-Nissila, T.; Pekola, J.P. On-Chip Maxwell’s Demon as an Information-Powered Refrigerator. Phys. Rev. Lett. 2015, 115, 260602. [Google Scholar] [CrossRef] [PubMed]
- Camati, P.A.; Peterson, J.P.; Batalhao, T.B.; Micadei, K.; Souza, A.M.; Sarthour, R.S.; Oliveira, I.S.; Serra, R.M. Experimental rectification of entropy production by Maxwell’s demon in a quantum system. Phys. Rev. Lett. 2016, 117, 240502. [Google Scholar] [CrossRef] [PubMed]
- Toyabe, S.; Sagawa, T.; Ueda, M.; Muneyuki, E.; Sano, M. Experimental demonstration of information-to-energy conversion and validation of the generalized Jarzynski equality. Nat. Phys. 2010, 6, 988–992. [Google Scholar] [CrossRef]
- Serra-Garcia, M.; Foehr, A.; Molerón, M.; Lydon, J.; Chong, C.; Daraio, C. Mechanical autonomous stochastic heat engine. Phys. Rev. Lett. 2016, 117, 010602. [Google Scholar] [CrossRef] [PubMed]
- Chida, K.; Desai, S.; Nishiguchi, K.; Fujiwara, A. Power generator driven by Maxwell’s demon. Nat. Commun. 2017, 8, 15310. [Google Scholar] [CrossRef]
- Elouard, C.; Herrera-Martí, D.; Huard, B.; Auffèves, A. Extracting Work from Quantum Measurement in Maxwell’s Demon Engines. Phys. Rev. Lett. 2017, 118, 260603. [Google Scholar] [CrossRef]
- Cottet, N.; Jezouin, S.; Bretheau, L.; Campagne-Ibarcq, P.; Ficheux, Q.; Anders, J.; Auffèves, A.; Azouit, R.; Rouchon, P.; Huard, B. Observing a quantum Maxwell demon at work. Proc. Natl. Acad. Sci. USA 2017, 114, 7561–7564. [Google Scholar] [CrossRef] [PubMed]
- Zurek, W.H. Thermodynamic cost of computation, algorithmic complexity and the information metric. Nature 1989, 341, 119–124. [Google Scholar] [CrossRef]
- Leff, H.; Rex, A.F. Maxwell’s Demon 2 Entropy, Classical and Quantum Information, Computing; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Sagawa, T.; Ueda, M. Generalized Jarzynski equality under nonequilibrium feedback control. Phys. Rev. Lett. 2010, 104, 090602. [Google Scholar] [CrossRef] [PubMed]
- Sagawa, T.; Ueda, M. Nonequilibrium thermodynamics of feedback control. Phys. Rev. E 2012, 85, 021104. [Google Scholar] [CrossRef] [PubMed]
- Deffner, S.; Jarzynski, C. Information Processing and the Second Law of Thermodynamics: An Inclusive, Hamiltonian Approach. Phys. Rev. X 2013, 3, 041003. [Google Scholar] [CrossRef]
- Sagawa, T.; Ueda, M. Role of mutual information in entropy production under information exchanges. New J. Phys. 2013, 15, 125012. [Google Scholar] [CrossRef]
- Horowitz, J.M.; Esposito, M. Thermodynamics with continuous information flow. Phys. Rev. X 2014, 4, 031015. [Google Scholar] [CrossRef]
- Barato, A.; Seifert, U. Unifying three perspectives on information processing in stochastic thermodynamics. Phys. Rev. Lett. 2014, 112, 090601. [Google Scholar] [CrossRef]
- Parrondo, J.M.R.; Horowitz, J.M.; Sagawa, T. Thermodynamics of information. Nat. Phys. 2015, 11, 131–139. [Google Scholar] [CrossRef]
- Lu, Z.; Mandal, D.; Jarzynski, C. Engineering Maxwell’s demon. Phys. Today 2014, 67, 60–61. [Google Scholar] [CrossRef]
- Szilard, L. über die Entropieverminderung in einem thermodynamischen System bei Eingriffen intelligenter Wesen. Z. Physik 1929, 53, 840–856. (In German) [Google Scholar] [CrossRef]
- Cao, F.J.; Feito, M.; Touchette, H. Information and flux in a feedback controlled Brownian ratchet. Phys. A Stat. Mech. Appl. 2009, 388, 113–119. [Google Scholar] [CrossRef]
- Vaikuntanathan, S.; Jarzynski, C. Modeling Maxwell’s demon with a microcanonical Szilard engine. Phys. Rev. E 2011, 83, 061120. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.W.; Sagawa, T.; de Liberato, S.; Ueda, M. Quantum Szilard engine. Phys. Rev. Lett. 2011, 106, 070401. [Google Scholar] [CrossRef] [PubMed]
- Mandal, D.; Jarzynski, C. Work and information processing in a solvable model of Maxwell’s demon. Proc. Natl. Acad. Sci. USA 2012, 109, 11641–11645. [Google Scholar] [CrossRef] [PubMed]
- Tu, Y. The nonequilibrium mechanism for ultrasensitivity in a biological switch: Sensing by Maxwell’s demons. Proc. Natl. Acad. Sci. USA 2008, 105, 11737–11741. [Google Scholar] [CrossRef] [PubMed]
- Mehta, P.; Schwab, D.J. Energetic costs of cellular computation. Proc. Natl. Acad. Sci. USA 2012. [Google Scholar] [CrossRef]
- Mandal, D.; Quan, H.T.; Jarzynski, C. Maxwell’s refrigerator: an exactly solvable model. Phys. Rev. Lett. 2013, 111, 030602. [Google Scholar] [CrossRef]
- Deffner, S. Information-driven current in a quantum Maxwell demon. Phys. Rev. E 2013, 88, 062128. [Google Scholar] [CrossRef]
- Strasberg, P.; Schaller, G.; Brandes, T.; Esposito, M. Thermodynamics of a physical model implementing a Maxwell demon. Phys. Rev. Lett. 2013, 110, 040601. [Google Scholar] [CrossRef]
- Barato, A.C.; Seifert, U. An autonomous and reversible Maxwell’s demon. EPL (Europhys. Lett.) 2013, 101, 60001. [Google Scholar] [CrossRef]
- Chapman, A.; Miyake, A. How an autonomous quantum Maxwell demon can harness correlated information. Phys. Rev. E 2015, 92, 062125. [Google Scholar] [CrossRef] [PubMed]
- Boyd, A.B.; Mandal, D.; Crutchfield, J.P. Identifying functional thermodynamics in autonomous Maxwellian ratchets. New J. Phys. 2016, 18, 023049. [Google Scholar] [CrossRef]
- Ouldridge, T.E.; Govern, C.C.; ten Wolde, P.R. Thermodynamics of computational copying in biochemical systems. Phys. Rev. X 2017, 7, 021004. [Google Scholar] [CrossRef]
- Givant, S.; Halmos, P. Introduction to Boolean Algebras; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Bennett, C.H. Notes on Landauer’s Principle, Reversible Computation, and Maxwell’s Demon. Stud. Hist. Philos. Mod. Phys. 2003, 34, 501–510. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Sagawa, T.; Ueda, M. Fluctuation theorem with information exchange: Role of correlations in stochastic thermodynamics. Phys. Rev. Lett. 2012, 109, 180602. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Z.; Jarzynski, C. A Programmable Mechanical Maxwell’s Demon. Entropy 2019, 21, 65. https://doi.org/10.3390/e21010065
Lu Z, Jarzynski C. A Programmable Mechanical Maxwell’s Demon. Entropy. 2019; 21(1):65. https://doi.org/10.3390/e21010065
Chicago/Turabian StyleLu, Zhiyue, and Christopher Jarzynski. 2019. "A Programmable Mechanical Maxwell’s Demon" Entropy 21, no. 1: 65. https://doi.org/10.3390/e21010065
APA StyleLu, Z., & Jarzynski, C. (2019). A Programmable Mechanical Maxwell’s Demon. Entropy, 21(1), 65. https://doi.org/10.3390/e21010065




