Fourier Transform on the Homogeneous Space of 3D Positions and Orientations for Exact Solutions to Linear PDEs
Abstract
1. Introduction
1.1. Structure of the Article
- We construct —the Fourier transform on the quotient , in Equation (44).
- The matrix representations for , explicit inversion and Plancherel formulas are shown in Theorem 1.
- The explicit spectral decompositions of PDE evolutions for -stable Lévy process on , in the Fourier domains of both and , are shown in Theorem 2; here, the new spectral decomposition in the Fourier domain of is simpler and involves ordinary spherical harmonics.
- The quantification of monotonic increase of entropy of PDE solutions for -stable Lévy processes on for in terms of Fisher information matrices is shown in Proposition 1.
- the exact formulas for the probability kernels of -stable Lévy processes on , in Theorem 3. This also includes new formulas for the heat kernels (the case ), that are more efficient than the heat kernels presented in previous work [40].
- Simple formulation and verifications (Monte-Carlo simulations) of discrete random walks for -stable Lévy processes on in Proposition 3. The corresponding SDEs are in Appendix A.
1.2. Introduction to the Fourier Transform on the Homogeneous Space of Positions and Orientations
- 1.
- is a homomorphism;
- 2.
- for all ; and
- 3.
- there does not exist a closed subspace V of other than such that .
1.3. Introduction to the PDEs of Interest on the Quotient
1.4. Reformulation of the PDE on the Lie Group
1.5. Increase of Entropy for the Diffusion System () and the Poisson System () on
1.6. A Preview on the Spectral Decomposition of the PDE Evolution Operator and the Inclusion of
2. Symmetries of the PDEs of Interest
2.1. PDE Symmetries
2.2. Obtaining the Kernels with from the Kernels with
3. The Fourier Transform on
- (1)
- For s = 0 or m = 0, they coincide with standard spherical harmonics Yl,m, cf. ([89], eq.4.32):
- (2)
- They have a specific rotation transformation property in view of Equation (32):
- (3)
- For each s ∈ fixed, they form a complete orthonormal basis for 2(S2):
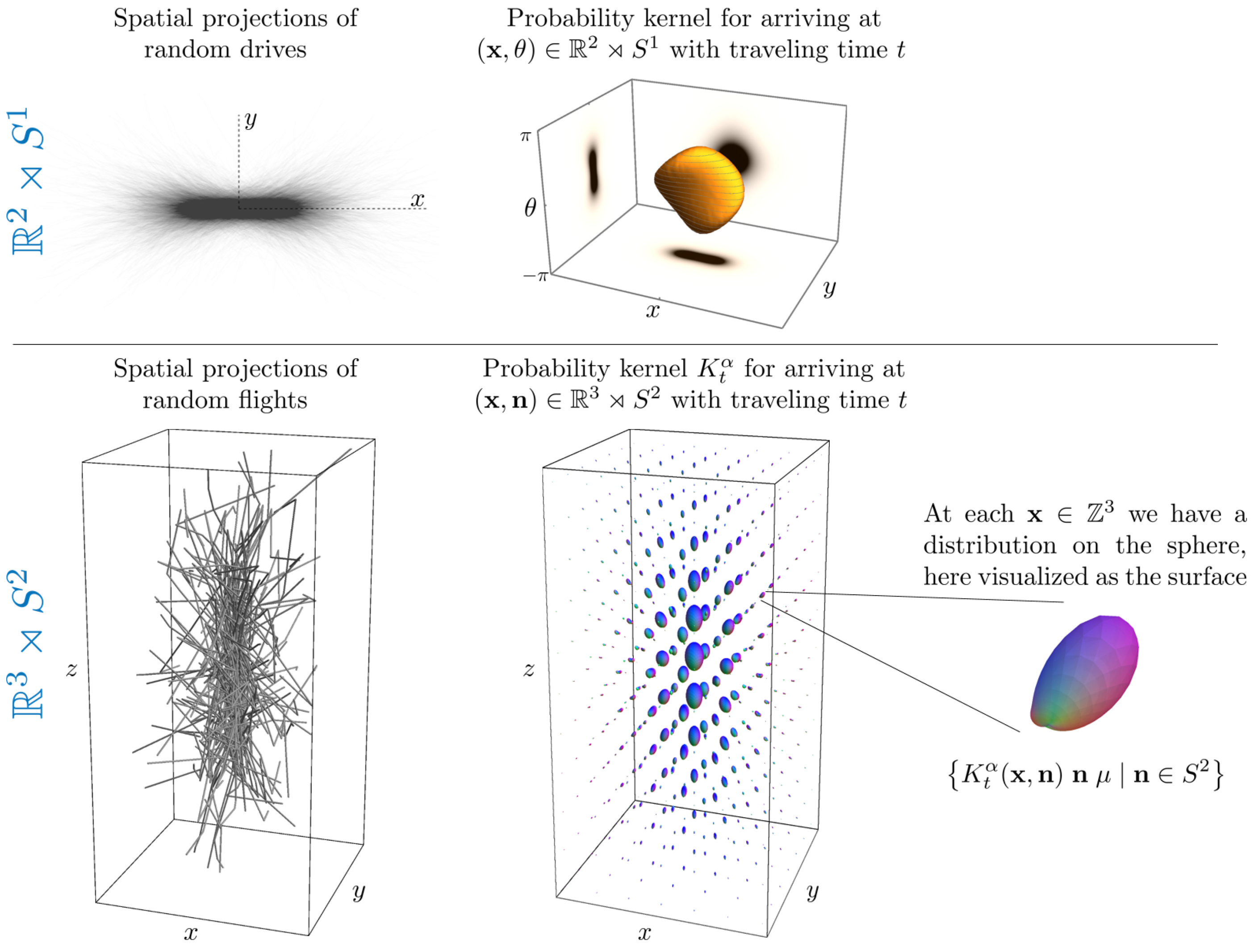
4. A Specific Fourier Transform on the Homogeneous Space of Positions and Orientations
4.1. The Homogeneous Space
4.2. Fourier Transform on
- 1.
- it relates to a unique function via ;
- 2.
- the matrix coefficientsrelative to the modified spherical harmonic basis vanish if ; and
- 3.
- the matrix coefficientsrelative to the modified spherical harmonic basis vanish if or .
5. Application of the Fourier Transform on for Explicit Solutions of the Fokker–Planck PDEs of -stable Lévy Processes on
5.1. Exact Kernel Representations by Spectral Decomposition in the Fourier Domain
5.1.1. Eigenfunctions and Preliminaries
5.1.2. The Explicit Spectral Decomposition of the Evolution Operators
- In the Fourier domain of the homogeneous space of positions and orientations, we have:
- We extend these results to the kernels of PDE in Equation (6), which are Forward-Kolmogorov equations of -stable Lévy process with .
- We provide a structured alternative formula via the transform characterized in Theorem 1.
- Via conjugation with :
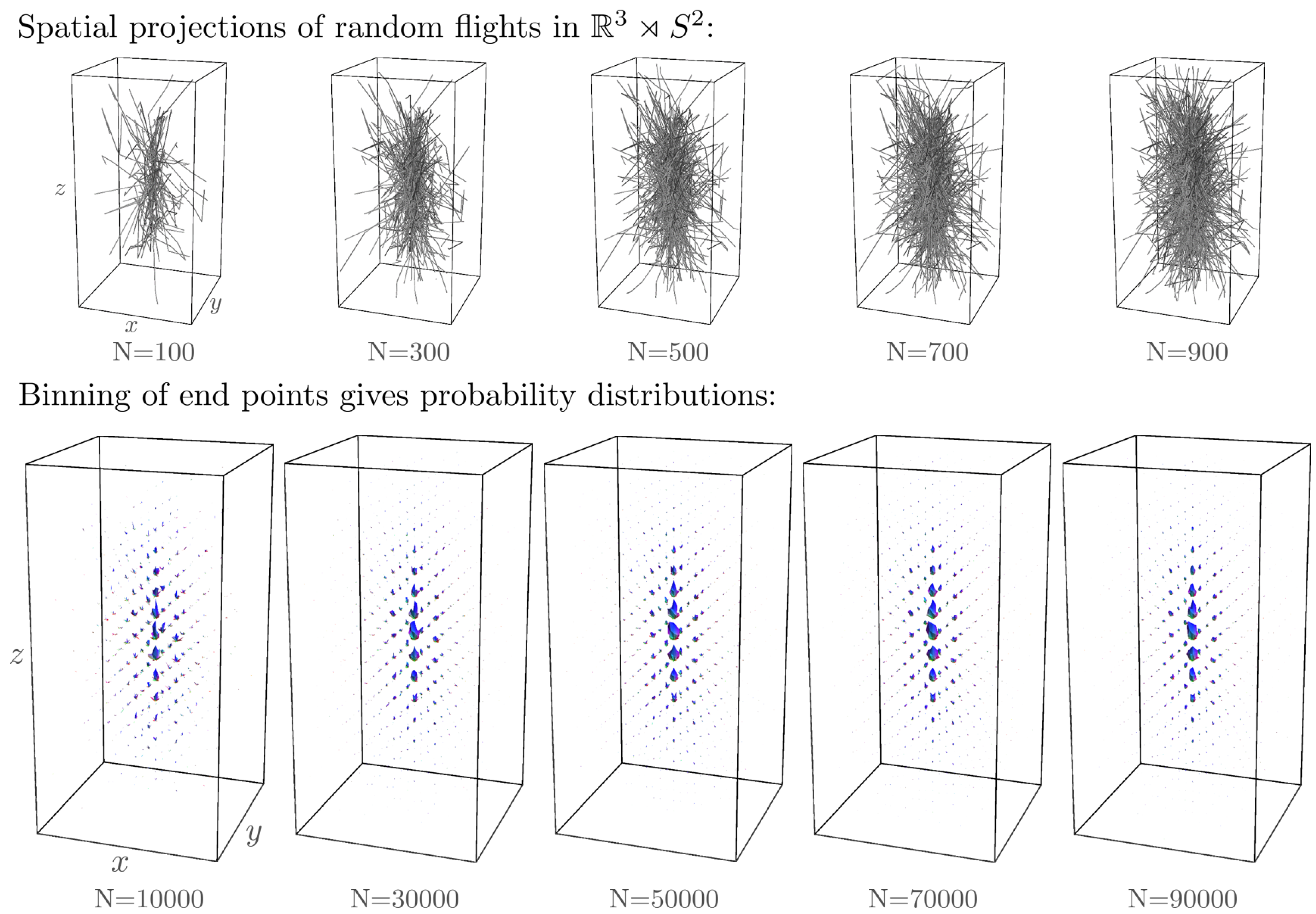
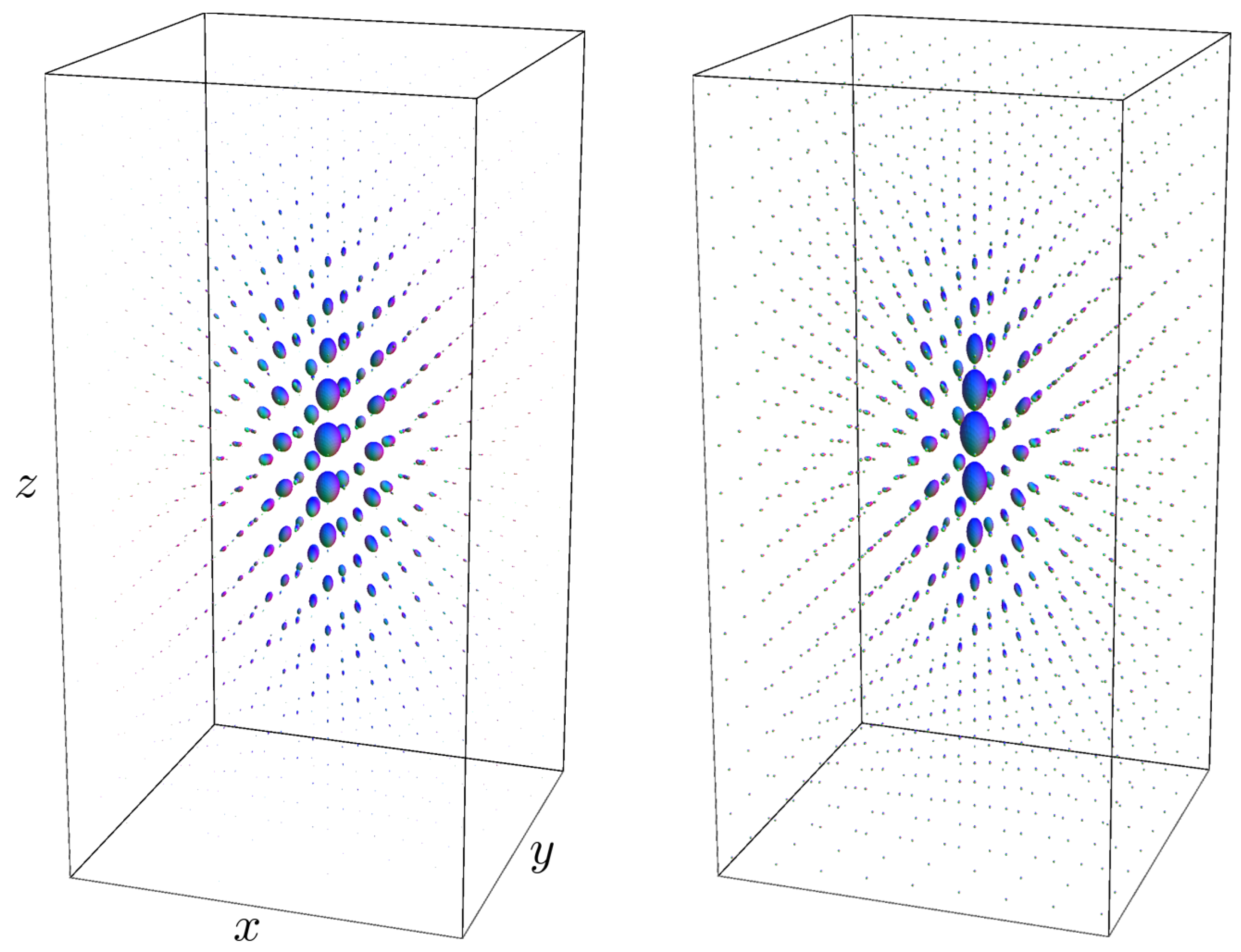
5.2. Monte-Carlo Approximations of the Kernels
5.3. Comparison of Monte-Carlo Approximations of the Kernels to the Exact Solutions
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| UIR | Unitary Irreducible Representation | |
| G | The rigid body motions group | Equation (1) |
| The reference axis | Equation (3) | |
| H | The subgroup that stabilizes | Equation (3) |
| The homogeneous space of positions and orientations | Equation (3) | |
| The spatial Fourier transform of U | Equation (18) | |
| The Fourier transform | Equation (43) | |
| Parameter of the -Stable processes (indexing fractional power of the generator) | Equation (10) |
| Rotation angle around reference axis | Remark 7 | |
| UIR of | Equation (32) | |
| the action on the quotient corresponding to | Definition 7 | |
| The probability kernel on G | Equation (26) | |
| The probability kernel on | Equation (27) | |
| Solution of the PDE on G | Equation (10) | |
| Solution of the PDE on | Equation (6) | |
| Evolution generator of the PDE on G | Equation (11) | |
| Evolution generator of the PDE on | Equation (7) | |
| Any rotation that maps onto | Remark 2 | |
| A counter-clockwise rotation about axis with angle | Remark 2 | |
| Lévy Processes on | Definition A1 | |
| Lévy Processes on | Equation (A4) | |
| The kernel relating and | Equation (77) | |
| The ordinary spherical harmonics | Proposition 2 | |
| The modified spherical harmonics according to [4] | Proposition 2 | |
| The generalized spherical harmonics according to [40] | Definition 10 | |
| The spheroidal wave basis function for | Definition 11 | |
| ZYZ Euler angles. | Equation (A12) |
Appendix A. Probability Theory
Appendix A.1. Lévy Processes on R 3 ⋊S 2
- 1.
- For any and , the variables , , …, are independent.
- 2.
- The distribution of does not depend on .
- 3.
- almost surely.
- 4.
- It is stochastically continuous, i.e., , .Here, .
Appendix A.2. SDE Formulation of α-Stable Lévy Processes on
Appendix A.2.1. From the Diffusion Case α = 1 to the General Case α ∈ (0,1]
Appendix A.2.2. α-Stability of the Lévy Process
Appendix B. Left-Invariant Vector Fields on SE(3) via Two Charts
References
- Zettl, A. Sturm-Liouville Theory; Mathematical Surveys and Monographs; American Mathematical Society: Providence, RI, USA, 2005; Volume 121. [Google Scholar]
- Kato, T. Operators in Hilbert spaces. In Perturbation Theory for Linear Operators; Classics in Mathematics; Springer: Berlin/Heidelberg, Germany, 1976; pp. 251–308. [Google Scholar]
- Rudin, W. Functional Analysis, 2nd ed.; McGraw-Hill, Inc.: New York, NY, USA, 1991. [Google Scholar]
- Chirikjian, G.S.; Kyatkin, A.B. Engineering Applications of Noncommutative Harmonic Analysis: With Emphasis on Rotation and Motion Groups; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Chirikjian, G.S. Stochastic Models, Information Theory, and Lie Groups: Analytic Methods and Modern Applications; Springer Science & Business Media: Berlin, Germany, 2011; Volume 2. [Google Scholar]
- Saccon, A.; Aguiar, A.P.; Hausler, A.J.; Hauser, J.; Pascoal, A.M. Constrained motion planning for multiple vehicles on SE(3). In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 5637–5642. [Google Scholar]
- Henk Nijmeijer, A.V.D.S. Nonlinear Dynamical Control Systems; Springer: Berlin/Heidelberg, Germany, 1990; p. 426. [Google Scholar]
- Ali, S.; Antoine, J.; Gazeau, J. Coherent States, Wavelets and Their Generalizations; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Bekkers, E.; Lafarge, M.; Veta, M.; Eppenhof, K.; Pluim, J.; Duits, R. Roto-Translation Covariant Convolutional Networks for Medical Image Analysis. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2018; Springer International Publishing: Cham, Switzerland, 2018; pp. 440–448. [Google Scholar]
- Bekkers, E.; Loog, M.; ter Haar Romeny, B.; Duits, R. Template matching via densities on the roto-translation group. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 452–466. [Google Scholar] [CrossRef] [PubMed]
- Cohen, T.S.; Geiger, M.; Weiler, M. Intertwiners between Induced Representations (with Applications to the Theory of Equivariant Neural Networks). arXiv, 2018; arXiv:1803.10743. [Google Scholar]
- Cohen, T.; Welling, M. Group equivariant convolutional networks. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 2990–2999. [Google Scholar]
- Sifre, L.; Mallat, S. Rotation, scaling and deformation invariant scattering for texture discrimination. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1233–1240. [Google Scholar]
- Duits, R.; Felsberg, M.; Granlund, G.; ter Haar Romeny, B. Image Analysis and Reconstruction using a Wavelet Transform Constructed from a Reducible Representation of the Euclidean Motion Group. Int. J. Comput. Vis. 2006, 72, 79–102. [Google Scholar] [CrossRef]
- Citti, G.; Sarti, A. A Cortical Based Model of Perceptual Completion in the Roto-Translation Space. J. Math. Imaging Vis. 2006, 24, 307–326. [Google Scholar] [CrossRef]
- Duits, R.; Fuehr, H.; Janssen, B.; Florack, L.; van Assen, H. Evolution equations on Gabor transforms and their applications. ACHA 2013, 35, 483–526. [Google Scholar] [CrossRef]
- Prandi, D.; Gauthier, J.P. A Semidiscrete Version of the Citti-Petitot-Sarti Model as a Plausible Model for Anthropomorphic Image Reconstruction and Pattern Recognition; Springer International Publishing: Cham, Switzerland, 2018; p. 113. [Google Scholar]
- Janssen, M.H.J.; Janssen, A.J.E.M.; Bekkers, E.J.; Bescós, J.O.; Duits, R. Design and Processing of Invertible Orientation Scores of 3D Images. J. Math. Imaging Vis. 2018, 60, 1427–1458. [Google Scholar] [CrossRef]
- Boscain, U.; Duplaix, J.; Gauthier, J.; Rossi, F. Anthropomorphic Image Reconstruction via Hypoelliptic Diffusion. SIAM J. Control Optim. 2012, 50, 1309–1336. [Google Scholar] [CrossRef]
- Schur, I. Vorlesungen über Invariantentheorie; P. Noordhoff: Groningen, The Netherlands, 1968. [Google Scholar]
- Dieudonné, J. Treatise on Analysis; Academic Press: New York, NY, USA, 1977; Volume V. [Google Scholar]
- Folland, G.B. A Course in Abstract Harmonic Analysis; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Agrachev, A.; Boscain, U.; Gauthier, J.P.; Rossi, F. The intrinsic hypoelliptic Laplacian and its heat kernel on unimodular Lie groups. J. Funct. Anal. 2009, 256, 2621–2655. [Google Scholar] [CrossRef]
- Führ, H. Abstract Harmonic Analysis of Continuous Wavelet Transforms; Springer Science & Business Media: Berlin, Germany, 2005. [Google Scholar]
- Mackey, G.W. Imprimitivity for Representations of Locally Compact Groups I. Proc. Natl. Acad. Sci. USA 1949, 35, 537–545. [Google Scholar] [CrossRef] [PubMed]
- Sugiura, M. Unitary Representations and Harmonic Analysis: An Introduction; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Dixmier, J. C*-algebras; North Holland: Amsterdam, Switzerland, 1981. [Google Scholar]
- Ghaani Farashani, A. Operator-valued Fourier transforms over homogeneous spaces of compact groups. Groups Geom. Dyn. 2017, 11, 1437–1467. [Google Scholar] [CrossRef]
- Ghaani Farashani, A. Poisson summation formulas over homogeneous spaces of compact groups. Anal. Math. Phys. 2017, 4, 493–508. [Google Scholar] [CrossRef]
- Ghaani Farashani, A. Plancherel (trace) formulas over homogeneous spaces of compact groups. Can. Math. Bull. 2017, 60, 111–121. [Google Scholar] [CrossRef]
- Ghaani Farashahi, A. Relative Fourier transforms over canonical homogeneous spaces of semi-direct product groups with abelian normal factor. J. Korean Math. Soc. 2017, 54, 117–139. [Google Scholar] [CrossRef]
- Gaveau, B. Principe de moindre action, propagation de la chaleur et estimees sous elliptiques sur certains groupes nilpotents. Acta Math. 1977, 139, 95–153. [Google Scholar] [CrossRef]
- Duits, R.; van Almsick, M. The explicit solutions of linear left-invariant second order stochastic evolution equations on the 2D Euclidean motion group. Q. Appl. Math. 2008, 66, 27–67. [Google Scholar] [CrossRef]
- Duits, R.; Franken, E. Line Enhancement and Completion via Linear Left Invariant Scale Spaces on SE(2); SSVM; Springer: Berlin/Heidelberg, Germany, 2009; pp. 795–807. [Google Scholar]
- Duits, R.; van Almsick, M. The Explicit Solutions of Linear Left-Invariant Second Order Stochastic Evolution Equations on the 2D-Euclidean Motion Group; Technical Report CASA-Report, nr.43; Department of Mathematics and Computer Science, Eindhoven University of Technology: Eindhoven, The Netherlands, 2005; 37p, Available online: http://www.win.tue.nl/analysis/reports/rana05-43.pdf (accessed on 14 December 2005).
- Duits, R.; Franken, E. Left-invariant parabolic evolutions on SE(2) and contour enhancement via invertible orientation scores Part II: Nonlinear left-invariant diffusions on invertible orientation scores. Q. Appl. Math. 2010, 68, 293–331. [Google Scholar] [CrossRef]
- Zhang, J.; Duits, R.; Sanguinetti, G.; ter Haar Romeny, B.M. Numerical Approaches for Linear Left-invariant Diffusions on SE(2), their Comparison to Exact Solutions, and their Applications in Retinal Imaging. Numer. Methods Theory Appl. 2016, 9, 1–50. [Google Scholar] [CrossRef]
- Mumford, D. Elastica and Computer Vision. In Algebraic Geometry and its Applications; Springer: New York, NY, USA, 1994; pp. 491–506. [Google Scholar]
- Petitot, J. The neurogeometry of pinwheels as a sub-Riemannian contact structure. J. Physiol. Paris 2003, 97, 265–309. [Google Scholar] [CrossRef] [PubMed]
- Portegies, J.M.; Duits, R. New exact and numerical solutions of the (convection–)diffusion kernels on SE(3). Differ. Geom. Appl. 2017, 53, 182–219. [Google Scholar] [CrossRef]
- Chirikjian, G. Degenerate Diffusions and Harmonic Analysis on SE(3): A Tutorial. In Stochastic Geometric Mechanics; Albeverio, S., Cruzeiro, A., Holm, D., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 77–99. [Google Scholar]
- Park, W.; Liu, Y.; Zhou, Y.; Moses, M.; Chirikjian, G. Kinematic State Estimation and Motion Planning for Stochastic Nonholonomic Systems Using the Exponential Map. Robotica 2008, 26, 419–434. [Google Scholar] [CrossRef] [PubMed]
- Chirikjian, G.; Wang, Y. Conformational Statistics of Stiff Macromolecules as Solutions to PDEs on the Rotation and Motion Groups. Phys. Rev. E 2000, 62, 880–892. [Google Scholar] [CrossRef]
- Portegies, J. PDEs on the Lie Group SE(3). Ph.D. Thesis, Department of Mathematics and Computer Science, Eindhoven University of Technology, Eindhoven, The Netherlands, 2018. Available online: www.bmia.bmt.tue.nl/people/RDuits/PHD/Jorg.pdf (accessed on 12 March 2018).
- Portegies, J.M.; Fick, R.H.J.; Sanguinetti, G.R.; Meesters, S.P.L.; Girard, G.; Duits, R. Improving Fiber Alignment in HARDI by Combining Contextual PDE Flow with Constrained Spherical Deconvolution. PLoS ONE 2015, 10, e0138122. [Google Scholar] [CrossRef] [PubMed]
- Momayyez-Siahkal, P.; Siddiqi, K. 3D Stochastic Completion Fields for Fiber Tractography. In Proceedings of the 2009 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Miami, FL, USA, 20–25 June 2009; pp. 178–185. [Google Scholar]
- Skibbe, H.; Reisert, M. Spherical Tensor Algebra: A Toolkit for 3D Image Processing. J. Math. Imaging Vis. 2017, 58, 349–381. [Google Scholar] [CrossRef]
- Meesters, S.; Ossenblok, P.; Wagner, L.; Schijns, O.; Boon, P.; Florack, L.; Vilanova, A.; Duits, R. Stability metrics for optic radiation tractography: Towards damage prediction after resective surgery. J. Neurosci. Methods 2017, 288, 34–44. [Google Scholar] [CrossRef] [PubMed]
- Reisert, M.; Kiselev, V.G. Fiber Continuity: An Anisotropic Prior for ODF Estimation. IEEE Trans. Med. Imaging 2011, 30, 1274–1283. [Google Scholar] [CrossRef] [PubMed]
- Prčkovska, V.; Rodrigues, P.; Duits, R.; Haar Romenij, B.T.; Vilanova, A. Extrapolating fiber crossings from DTI data: Can we infer similar fiber crossings as in HARDI? In Proceedings of the Workshop on Computational Diffusion MRI, MICCA, Beijing, China, 16 January 2010. [Google Scholar]
- Iijima, T. Basic Theory of Pattern Observation; Papers of Technical Group on Automata and Automatic Control, IECE: Chiba, Japan, 1959. [Google Scholar]
- Koenderink, J.J. The structure of images. Biol. Cybern. 1984, 50, 363–370. [Google Scholar] [CrossRef] [PubMed]
- ter Haar Romeny, B.M. Front-End Vision and Multi-Scale Image Analysis: Multi-Scale Computer Vision Theory and Applications, Written in Mathematica; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Weickert, J. Anisotropic Diffusion in Image Processing; ECMI, B.G. Teubner: Stuttgart, Germany, 1998. [Google Scholar]
- Duits, R.; Burgeth, B. Scale Spaces on Lie Groups. In SSVM; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4485, pp. 300–312. [Google Scholar]
- Benoist, Y.; Quint, J.F. Central limit theorem for linear groups. Ann. Probab. 2016, 44, 1306–1340. [Google Scholar] [CrossRef]
- Pilte, M.; Bonnabel, S.; Barbaresco, F. Maneuver Detector for Active Tracking Update Rate Adaptation. In Proceedings of the 2018 19th International Radar Symposium (IRS), Bonn, Germany, 20–22 June 2018; pp. 1–10. [Google Scholar]
- Berger, J.; Neufeld, A.; Becker, F.; Lenzen, F.; Schnörr, C. Second Order Minimum Energy Filtering on SE(3) with Nonlinear Measurement Equations. In Scale Space and Variational Methods in Computer Vision; Aujol, J.F., Nikolova, M., Papadakis, N., Eds.; Springer: Cham, Switzerland, 2015; pp. 397–409. [Google Scholar]
- Oksendal, B. Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Hsu, E. Stochastic Analysis on Manifolds; Contemporary Mathematics; American Mathematical Society: Providence, RI, USA, 2002. [Google Scholar]
- Feller, W. An Introduction to Probability Theory and Its Applications; Wiley Series in Probability and Mathematical Statistics; Wiley: Hoboken, NJ, USA, 1966; Volume II. [Google Scholar]
- Felsberg, M.; Duits, R.; Florack, L. The Monogenic Scale Space on a Bounded Domain and its Applications. In Scale Space Methods in Computer Vision. Scale-Space 2003; Lecture Notes of Computer Science; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2695, pp. 209–224. [Google Scholar]
- Duits, R.; Felsberg, M.; Florack, L.M.J. α Scale Spaces on a Bounded Domain. In Scale Space Methods in Computer Vision. Scale-Space 2003; Lecture Notes of Computer Science; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2695, pp. 494–510. [Google Scholar]
- Duits, R.; Florack, L.; Graaf, J.D.; Romeny, B.T.H. On the Axioms of Scale Space Theory. J. Math. Imaging Vis. 2004, 20, 267–298. [Google Scholar] [CrossRef]
- Pedersen, K.S.; Duits, R.; Nielsen, M. On α Kernels, Lévy Processes, and Natural Image Statistics. In Scale Space and PDE Methods in Computer Vision; Kimmel, R., Sochen, N.A., Weickert, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 468–479. [Google Scholar]
- Yosida, K. Functional Analysis; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Winkels, M.; Cohen, T.S. 3D G-CNNs for Pulmonary Nodule Detection. arXiv, 2018; arXiv:1804.04656. [Google Scholar]
- Worrall, D.; Brostow, G. CubeNet: Equivariance to 3D Rotation and Translation. arXiv, 2018; arXiv:1804.04458. [Google Scholar]
- Weiler, M.; Geiger, M.; Welling, M.; Boomsma, W.; Cohen, T. 3D Steerable CNNs: Learning Rotationally Equivariant Features in Volumetric Data. arXiv, 2018; arXiv:1807.02547. [Google Scholar]
- Montobbio, N.; Sarti, A.; Citti, G. A metric model for the functional architecture of the visual cortex. arXiv, 2018; arXiv:1807.02479. [Google Scholar]
- Oyallon, E.; Mallat, S.; Sifre, L. Generic deep networks with wavelet scattering. arXiv, 2013; arXiv:1312.5940. [Google Scholar]
- Kanti, V.; Mardia, P.E.J. Directional Statistics; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 1999. [Google Scholar]
- Wu, L. Chapter 3 Modeling Financial Security Returns Using Lévy Processes. In Handbooks in Operations Research and Management Science; Birge, J.R., Linetsky, V., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; Volume 15, pp. 117–162. [Google Scholar]
- Belkic, D.D.; Belkic, K. Signal Processing in Magnetic Resonance Spectroscopy with Biomedical Applications; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Chirikjian, G. Information-theoretic inequalities on unimodular Lie groups. J. Geom. Mech. 2010, 2, 119–158. [Google Scholar] [CrossRef] [PubMed]
- Barbaresco, F. Higher Order Geometric Theory of Information and Heat Based on Poly-Symplectic Geometry of Souriau Lie Groups Thermodynamics and Their Contextures: The Bedrock for Lie Group Machine Learning. Entropy 2018, 20, 840. [Google Scholar] [CrossRef]
- Akian, M.; Quadrat, J.; Viot, M. Bellman processes. Lect. Notes Control Inf. Sci. 1994, 199, 302–311. [Google Scholar]
- Schmidt, M.; Weickert, J. Morphological Counterparts of Linear Shift-Invariant Scale-Spaces. J. Math. Imaging Vis. 2016, 56, 352–366. [Google Scholar] [CrossRef]
- Hörmander, L. Hypoelliptic second order differential equations. Acta Math. 1967, 119, 147–171. [Google Scholar] [CrossRef]
- Misiorek, A.; Weron, R. Heavy-Tailed Distributions in VaR Calculations. In Handbook of Computational Statistics: Concepts and Methods; Gentle, J.E., Härdle, W.K., Mori, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1025–1059. [Google Scholar]
- Felsberg, M.; Sommer, G. The Monogenic Scale-Space: A Unifying Approach to Phase-Based Image Processing in Scale-Space. J. Math. Imaging Vis. 2004, 21, 5–26. [Google Scholar] [CrossRef]
- Kanters, F.; Florack, L.; Duits, R.; Platel, B.; ter Haar Romeny, B. ScaleSpaceViz: α-Scale spaces in practice. Pattern Recognit. Image Anal. 2007, 17, 106–116. [Google Scholar] [CrossRef]
- Duits, R.; Franken, E. Left-invariant parabolic evolutions on SE(2) and contour enhancement via invertible orientation scores Part I: Linear left-invariant diffusion equations on SE(2). Q. Appl. Math. 2010, 68, 255–292. [Google Scholar] [CrossRef]
- Duits, R.; Franken, E. Left-Invariant Diffusions on the Space of Positions and Orientations and their Application to Crossing-Preserving Smoothing of HARDI images. Int. J. Comput. Vis. 2011, 92, 231–264. [Google Scholar] [CrossRef]
- Duits, R.; Dela Haije, T.; Creusen, E.; Ghosh, A. Morphological and Linear Scale Spaces for Fiber Enhancement in DW-MRI. J. Math. Imaging Vis. 2012, 46, 326–368. [Google Scholar] [CrossRef]
- Duits, R.; Bekkers, E.; Mashtakov, A. Fourier Transform on the Homogeneous Space of 3D Positions and Orientations for Exact Solutions to PDEs. arXiv, 2018; arXiv:1811.00363. [Google Scholar]
- Portegies, J.; Sanguinetti, G.; Meesters, S.; Duits, R. New Approximation of a Scale Space Kernel on SE(3) and Applications in Neuroimaging. In SSVM; Aujol, J.F., Nikolova, M., Papadakis, N., Eds.; Number 9087 in LNCS; Springer International Publishing: Cham, Switzerland, 2015; pp. 40–52. [Google Scholar]
- Arendt, W.; Bukhvalov, A.V. Integral representation of resolvent and semigroups. Forum Math. 1994, 6, 111–137. [Google Scholar] [CrossRef]
- Griffiths, D. Introduction to Quantum Mechanics; Prentice-Hall: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Wigner, E. Gruppentheorie und ihre Anwendungen auf die Quantenmechanik der Atomspektren. In Braunschweig: Vieweg Verlag; 1931 Translated into English by Griffin, J.J.; Group Theory and Its Application to the Quantum Mechanics of Atomic Spectra; Academic Press: New York, NY, USA, 1959. [Google Scholar]
- Margenau, H.; Murphy, G.M. The Mathematics of Physics and Chemistry; David Van Nostrand: New York, NY, USA, 1956. [Google Scholar]
- ter Elst, A.F.M.; Robinson, D.W. Weighted Subcoercive Operators on Lie Groups. J. Funct. Anal. 1998, 157, 88–163. [Google Scholar] [CrossRef]
- Dong, H.; Chirikjian, G. A Comparison of Gaussian and Fourier Methods for Degenerate Diffusions on SE(2). In Proceedings of the 2015 IEEE Conference on Decision and Control, Osaka, Japan, 15–18 December 2015; pp. 15–18. [Google Scholar]
- Meesters, S.P.L.; Sanguinetti, G.R.; Garyfallidis, E.; Portegies, J.M.; Duits, R. Fast Implementations of Contextual PDE’S for HARDI Data Processing in DIPY; Abstract. Presented at 24th ISMRM Annual Meeting and Exhibition, Singapore, 7–13 May 2016; pp. 1–4. [Google Scholar]
- Chirikjian, G. Group Theory and Biomolecular Conformation, I.: Mathematical and computational models. J. Phys. Condens. Matter 2010, 22, 323103. [Google Scholar] [CrossRef] [PubMed]
- Pinsky, M.A. Isotropic transport process on a Riemannian manifold. Trans. Am. Math. Soc. 1976, 218, 353–360. [Google Scholar] [CrossRef]
- Prčkovska, V.; Andorra, M.; Villoslada, P.; Martinez-Heras, E.; Duits, R.; Fortin, D.; Rodrigues, P.; Descoteaux, M. Contextual Diffusion Image Post-processing Aids Clinical Applications. In Visualization and Processing of Higher Order Descriptors for Multi-Valued Data; Hotz, I., Schultz, T., Eds.; Mathematics and Visualization; Springer International Publishing: Cham, Switzerland, 2015; pp. 353–377. [Google Scholar] [CrossRef]
- Meesters, S.P.L.; Sanguinetti, G.R.; Garyfallidis, E.; Portegies, J.M.; Ossenblok, P.; Duits, R. Cleaning Output of Tractography via Fiber to Bundle Coherence, a New Open Source Implementation; Abstract. Presented at Organization for Human Brain Mapping Annual Meeting, Geneve, Switzerland, 26–30 June 2016. [Google Scholar]
- Liao, M. Lévy Processes in Lie Groups; Cambridge Tracts in Mathematics, Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Duits, R.; Ghosh, A.; Dela Haije, T.C.J.; Mashtakov, A. On Sub-Riemannian Geodesics in SE(3) Whose Spatial Projections do not Have Cusps. J. Dyn. Control Syst. 2016, 22, 771–805. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duits, R.; Bekkers, E.J.; Mashtakov, A. Fourier Transform on the Homogeneous Space of 3D Positions and Orientations for Exact Solutions to Linear PDEs. Entropy 2019, 21, 38. https://doi.org/10.3390/e21010038
Duits R, Bekkers EJ, Mashtakov A. Fourier Transform on the Homogeneous Space of 3D Positions and Orientations for Exact Solutions to Linear PDEs. Entropy. 2019; 21(1):38. https://doi.org/10.3390/e21010038
Chicago/Turabian StyleDuits, Remco, Erik J. Bekkers, and Alexey Mashtakov. 2019. "Fourier Transform on the Homogeneous Space of 3D Positions and Orientations for Exact Solutions to Linear PDEs" Entropy 21, no. 1: 38. https://doi.org/10.3390/e21010038
APA StyleDuits, R., Bekkers, E. J., & Mashtakov, A. (2019). Fourier Transform on the Homogeneous Space of 3D Positions and Orientations for Exact Solutions to Linear PDEs. Entropy, 21(1), 38. https://doi.org/10.3390/e21010038





