How to Construct a Combined S-CO2 Cycle for Coal Fired Power Plant?
Abstract
1. Introduction
2. System Description and Methods
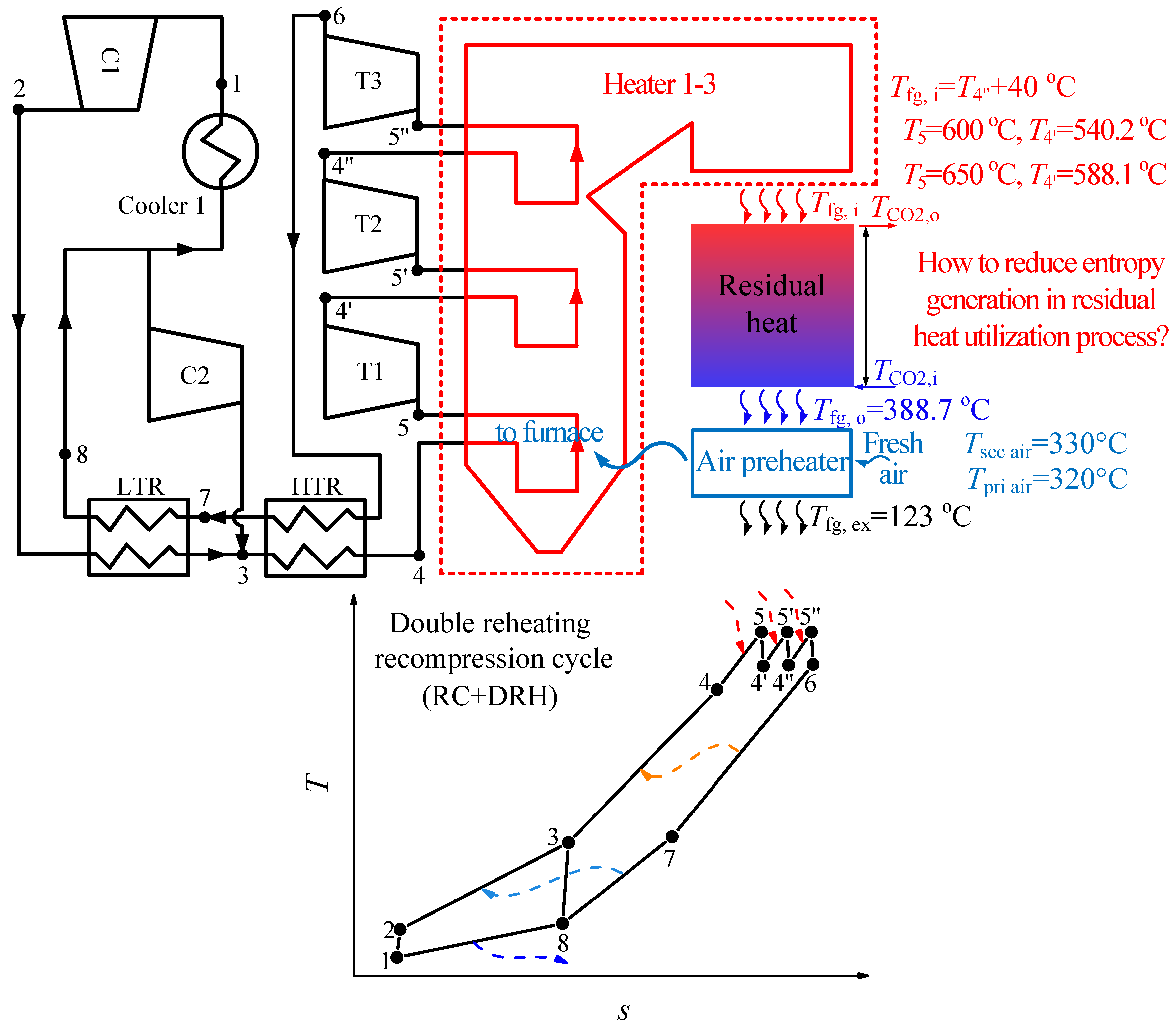
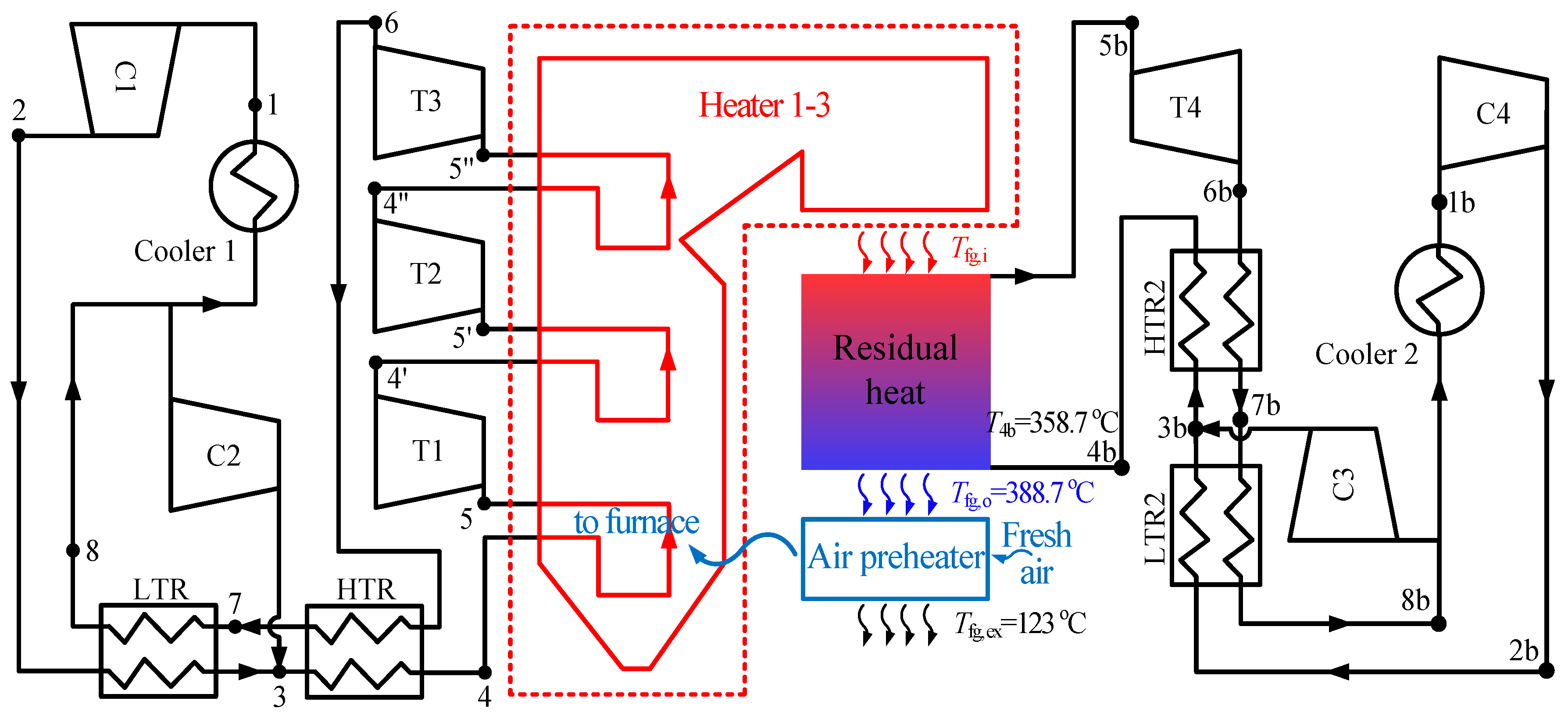
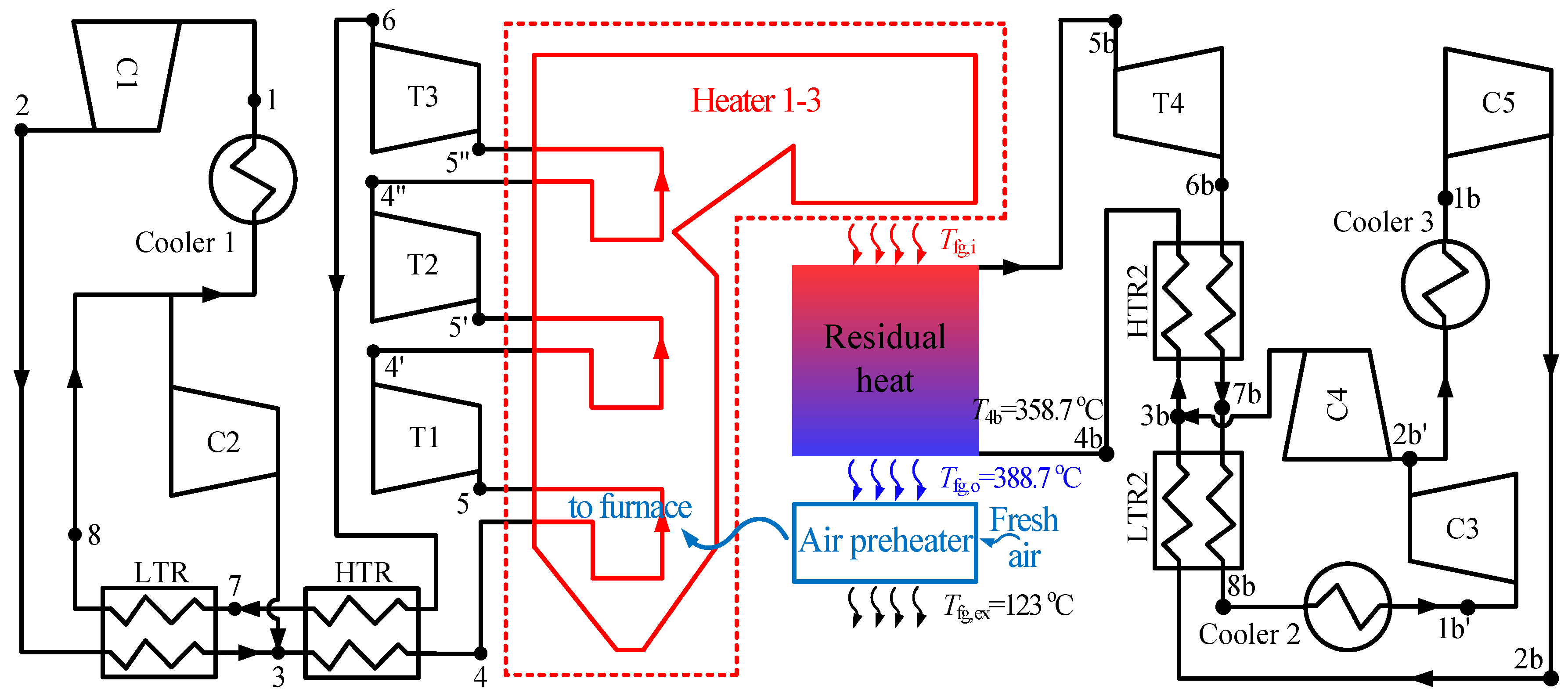
2.1. S-CO2 Cycle Description
2.2. Thermodynamic Model for S-CO2 Cycle
2.3. Calculation Method of Residual Heat
3. Results and Discussion
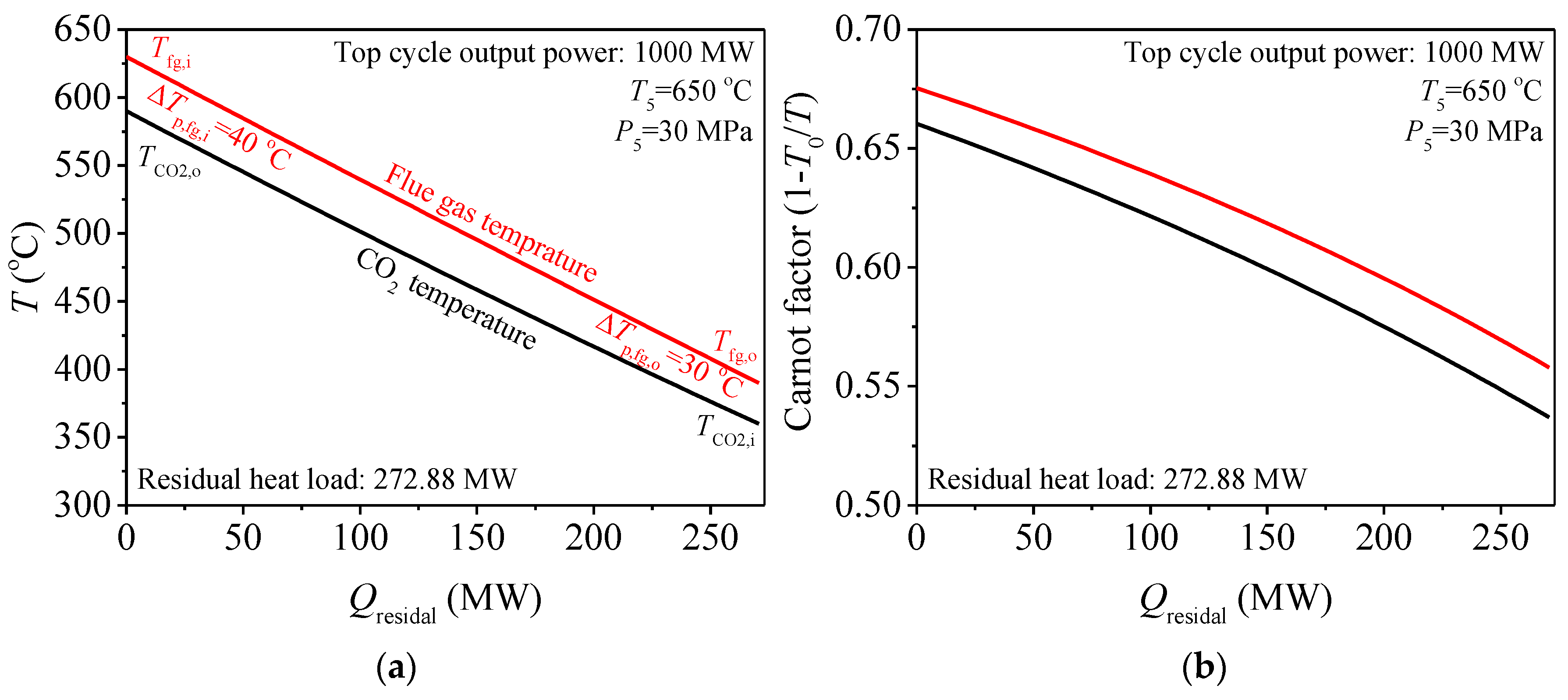
3.1. Causes of Residual Heat Problem
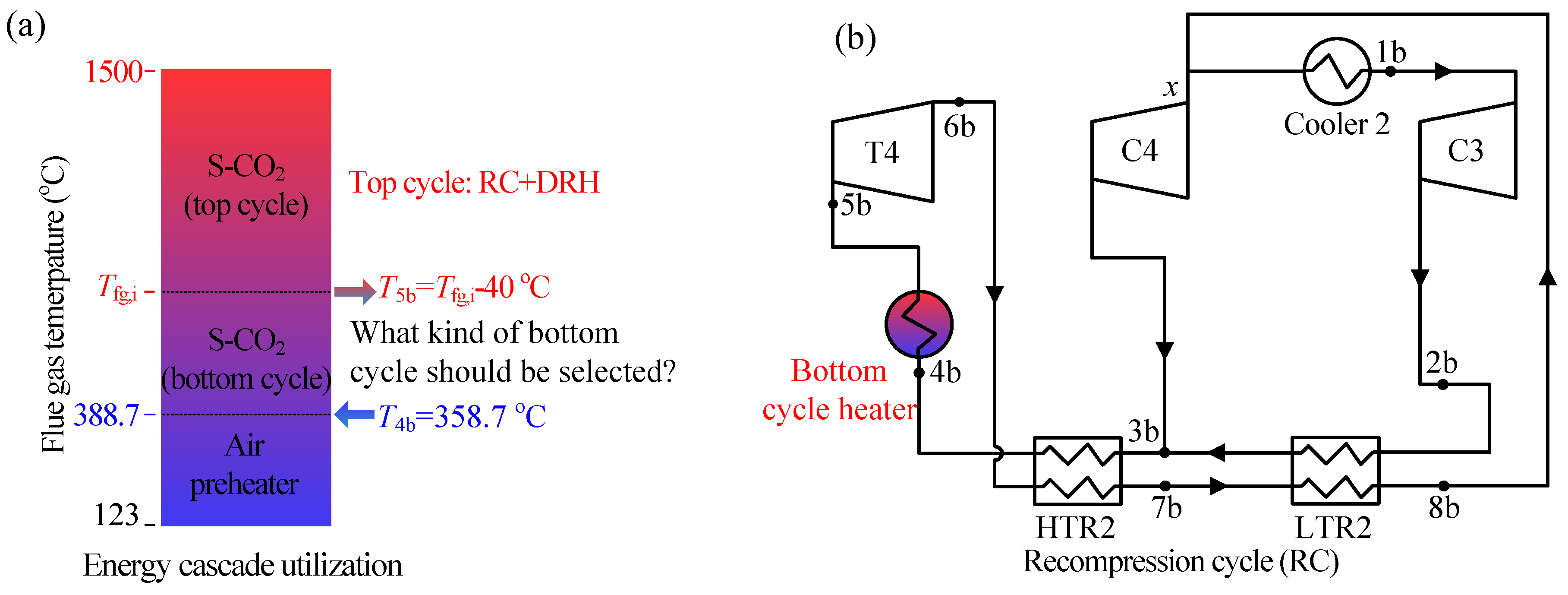
3.2. Exergy Destruction Control Strategy during Residual Heat Recovery
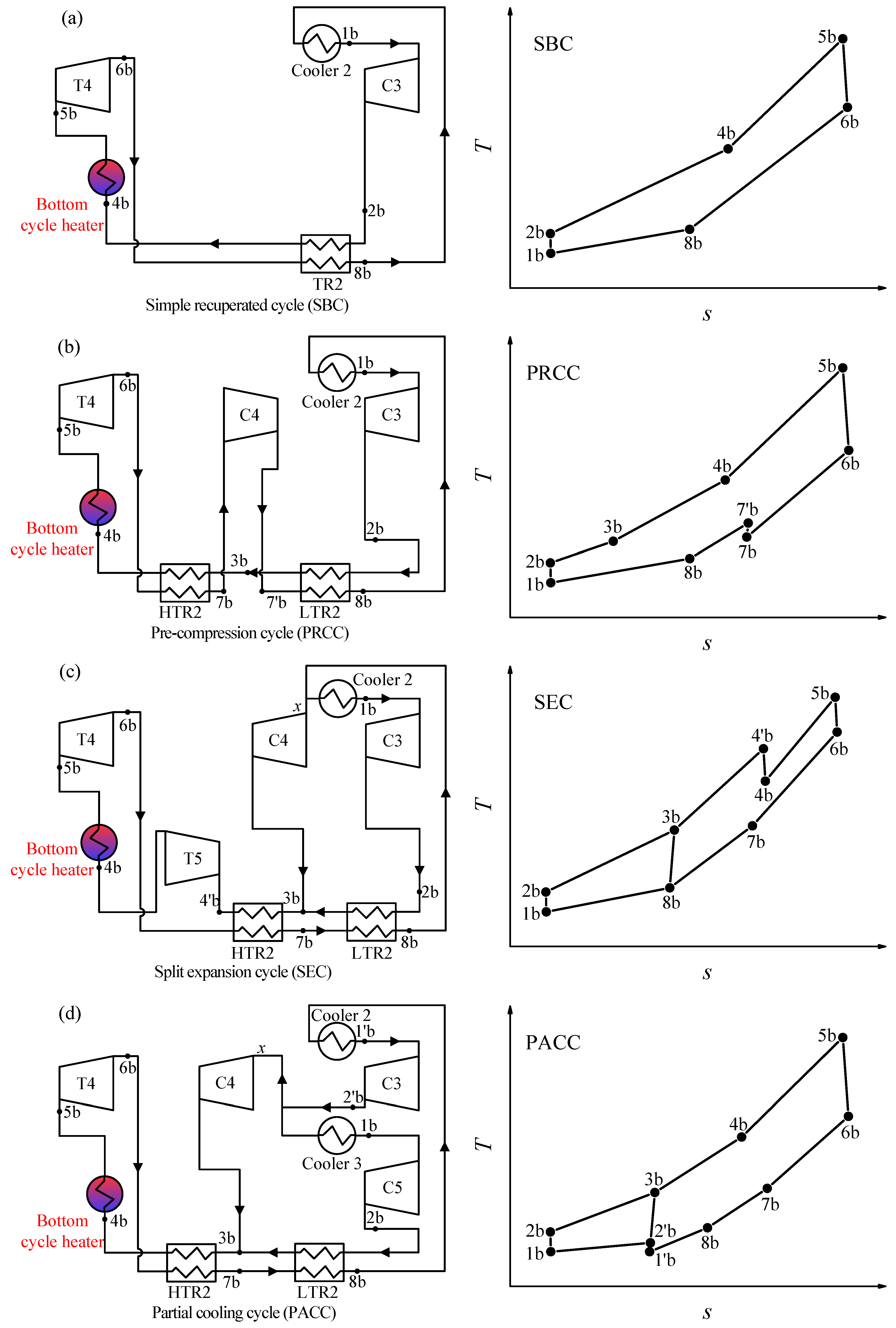
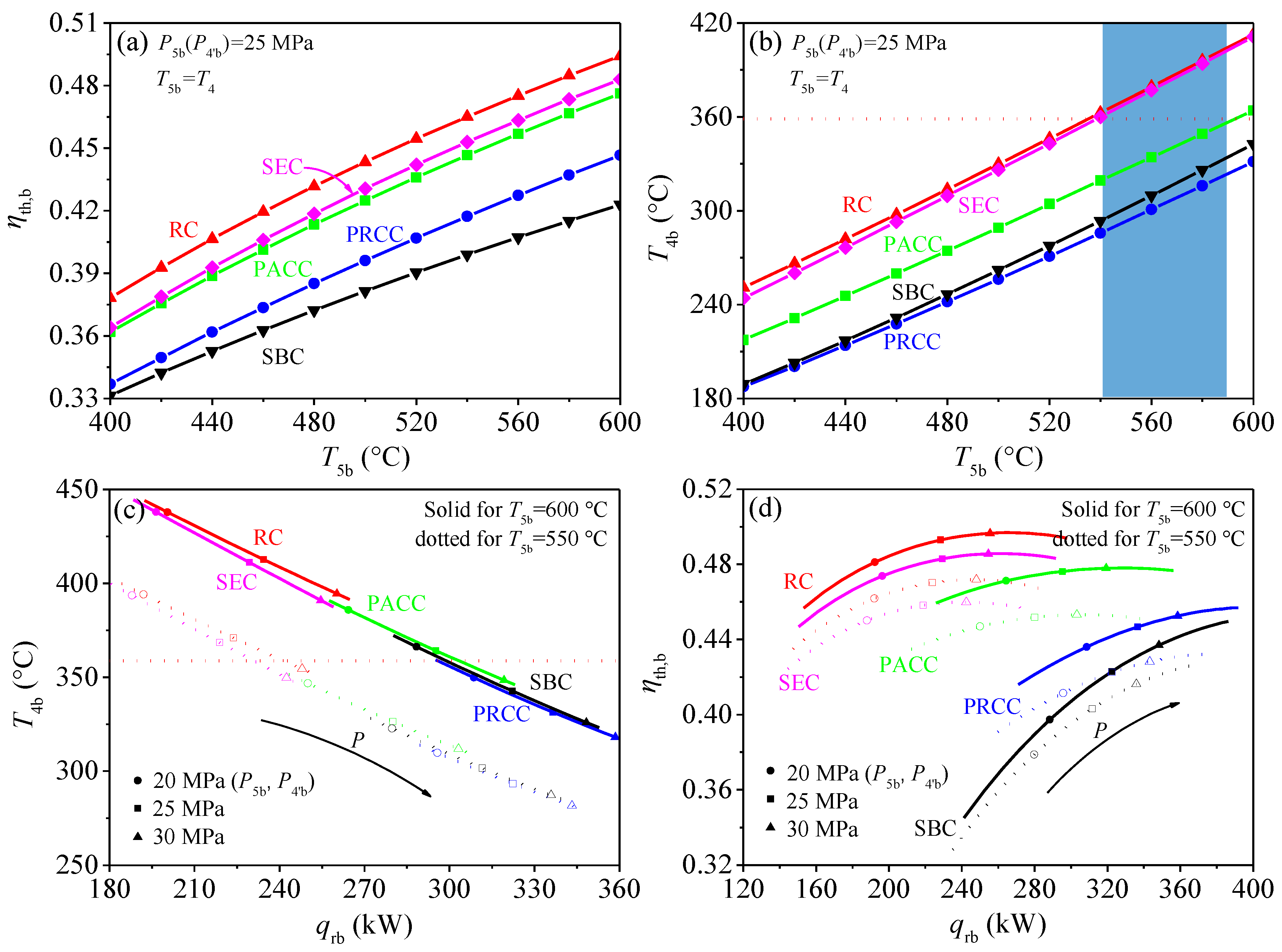
3.3. Analysis of Five S-CO2 Bottom Cycle
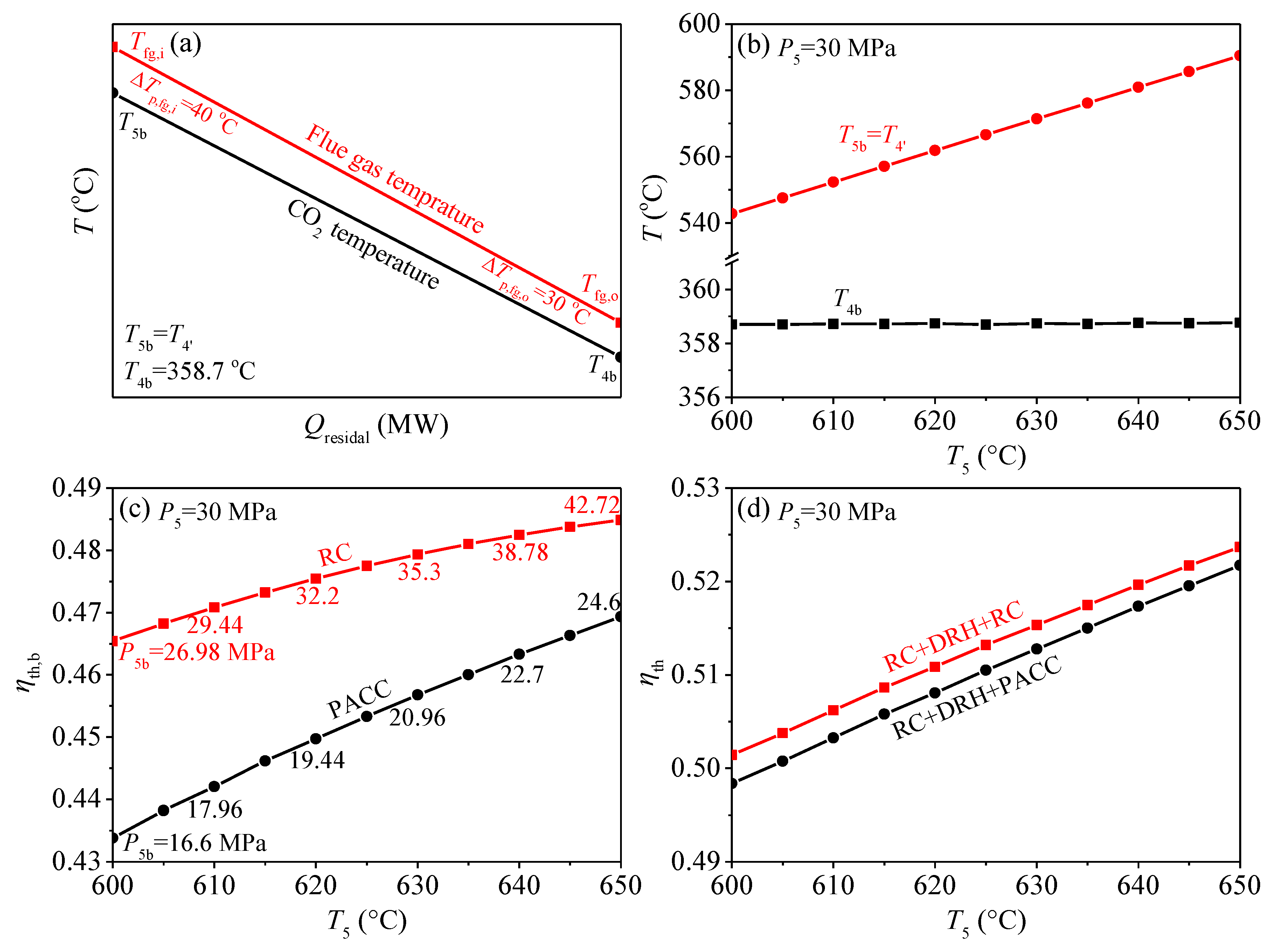
3.4. Analysis of Two Combined S-CO2 Cycles
4. Conclusions
- The exergy destruction control strategy during residual heat recovery is proposed which can be set as the boundary condition for different bottom cycles comparison. The purpose of this strategy is to ensure that the exergy destruction in residual heat absorption process is equal and minimum when comparing different bottom cycles.
- Five S-CO2 bottom cycles are simulated. It is shown that different S-CO2 cycles exhibit different characteristics. In order to ensure the exergy destruction control strategy during residual heat recovery, CO2 temperature at the inlet of bottom cycle heater (T4b) should be adjusted by tuning the turbine inlet pressure of bottom cycle (P5b).
- When the top cycle is a double reheating recompression cycle (RC + DRH), the recompression cycle (RC) and partial cooling cycle (PACC) are suitable as the bottom cycle due to their better performance. Meanwhile, the RC + DRH + RC and RC + DRH + PACC are suitable for different temperature regions. It is recommended that when turbine inlet temperature of top cycle (T5) is 600–630 °C, RC + DRH + RC is more suitable, when T5 is 630–650 °C, RC + DRH + PACC should be proposed.
Author Contributions
Funding
Conflicts of Interest
References
- Conti, J.; Holtberg, P.; Diefenderfer, J.; LaRose, A.; Turnure, J.T.; Westfall, L. International Energy Outlook 2016 with Projections to 2040; Office of Energy Analysis; USDOE Energy Information Administration (EIA): Washington, DC, USA, 2016. [Google Scholar]
- Sathre, R.; Gustavsson, L.; Le Truong, N. Climate effects of electricity production fuelled by coal, forest slash and municipal solid waste with and without carbon capture. Energy 2017, 122, 711–723. [Google Scholar] [CrossRef]
- Liu, Z.; Guan, D.; Wei, W.; Davis, S.J.; Ciais, P.; Bai, J.; Peng, S.; Zhang, Q.; Hubacek, K.; Marland, G. Reduced carbon emission estimates from fossil fuel combustion and cement production in China. Nature 2015, 524, 335. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; He, Y.; Zhu, H. Integration between supercritical CO2 Brayton cycles and molten salt solar power towers: A review and a comprehensive comparison of different cycle layouts. Appl. Energy 2017, 195, 819–836. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Q.; Lei, J.; Han, W.; Jin, H. Investigation of thermodynamic performances for two-stage recompression supercritical CO2 Brayton cycle with high temperature thermal energy storage system. Energy Convers. Manag. 2018, 165, 477–487. [Google Scholar] [CrossRef]
- Wang, K.; He, Y. Thermodynamic analysis and optimization of a molten salt solar power tower integrated with a recompression supercritical CO2 Brayton cycle based on integrated modeling. Energy Convers. Manag. 2017, 135, 336–350. [Google Scholar] [CrossRef]
- Linares Hurtado, J.I.; Cantizano González, A.; Arenas Pinilla, E.M.; Moratilla Soria, B.Y.; Martín Palacios, V.; Batet Miracle, L. Recuperated versus single-recuperator re-compressed supercritical CO2 Brayton power cycles for DEMO fusion reactor based on dual coolant lithium lead blanket. Energy 2017, 140, 307–317. [Google Scholar] [CrossRef]
- Ahn, Y.; Lee, J.I. Study of various Brayton cycle designs for small modular sodium-cooled fast reactor. Nucl. Eng. Des. 2014, 276, 128–141. [Google Scholar] [CrossRef]
- Moisseytsev, A.; Sienicki, J.J. Investigation of alternative layouts for the supercritical carbon dioxide Brayton cycle for a sodium-cooled fast reactor. Nucl. Eng. Des. 2009, 239, 1362–1371. [Google Scholar] [CrossRef]
- Kim, M.S.; Ahn, Y.; Kim, B.; Lee, J.I. Study on the supercritical CO2 power cycles for landfill gas firing gas turbine bottoming cycle. Energy 2016, 111, 893–909. [Google Scholar] [CrossRef]
- Kim, Y.M.; Sohn, J.L.; Yoon, E.S. Supercritical CO2 Rankine cycles for waste heat recovery from gas turbine. Energy 2017, 118, 893–905. [Google Scholar] [CrossRef]
- Hou, S.; Wu, Y.; Zhou, Y.; Yu, L. Performance analysis of the combined supercritical CO2 recompression and regenerative cycle used in waste heat recovery of marine gas turbine. Energy Convers. Manag. 2017, 151, 73–85. [Google Scholar] [CrossRef]
- Angelino, G. Carbon dioxide condensation cycles for power production. J. Eng. Power 1968, 90, 287–295. [Google Scholar] [CrossRef]
- Bae, S.J.; Ahn, Y.; Lee, J.; Lee, J.I. Various supercritical carbon dioxide cycle layouts study for molten carbonate fuel cell application. J. Power Sources 2014, 270, 608–618. [Google Scholar] [CrossRef]
- Dostál, V.; Driscoll, M.J.; Hejzlar, P. A Supercritical Carbon Dioxide Cycle for Next Generation Nuclear Reactors. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2004. [Google Scholar]
- Baik, S.; Kim, S.G.; Lee, J.; Lee, J.I. Study on CO2–water printed circuit heat exchanger performance operating under various CO2 phases for S-CO2 power cycle application. Appl. Therm. Eng. 2017, 113, 1536–1546. [Google Scholar] [CrossRef]
- Nikitin, K.; Kato, Y.; Ngo, L. Printed circuit heat exchanger thermal–hydraulic performance in supercritical CO2 experimental loop. Int. J. Refrig. 2006, 29, 807–814. [Google Scholar] [CrossRef]
- Xu, J.; Sun, E.; Li, M.; Liu, H.; Zhu, B. Key issues and solution strategies for supercritical carbon dioxide coal fired power plant. Energy 2018, 157, 227–246. [Google Scholar] [CrossRef]
- Le Moullec, Y. Conceptual study of a high efficiency coal-fired power plant with CO2 capture using a supercritical CO2 Brayton cycle. Energy 2013, 49, 32–46. [Google Scholar] [CrossRef]
- Zhou, L.; Xu, G.; Zhao, S.; Xu, C.; Yang, Y. Parametric analysis and process optimization of steam cycle in double reheat ultra-supercritical power plants. Appl. Therm. Eng. 2016, 99, 652–660. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, H.; Han, W.; Bai, W.; Yang, Y.; Yao, M.; Wang, Y. Improved design of supercritical CO2 Brayton cycle for coal-fired power plant. Energy 2018, 155, 1–14. [Google Scholar] [CrossRef]
- Park, S.; Kim, J.; Yoon, M.; Rhim, D.; Yeom, C. Thermodynamic and economic investigation of coal-fired power plant combined with various supercritical CO2 Brayton power cycle. Appl. Therm. Eng. 2018, 130, 611–623. [Google Scholar] [CrossRef]
- Bai, Z.; Zhang, G.; Li, Y.; Xu, G.; Yang, Y. A supercritical CO2 Brayton cycle with a bleeding anabranch used in coal-fired power plants. Energy 2018, 142, 731–738. [Google Scholar] [CrossRef]
- Mecheri, M.; Le Moullec, Y. Supercritical CO2 Brayton cycles for coal-fired power plants. Energy 2016, 103, 758–771. [Google Scholar] [CrossRef]
- Chen, S.; Soomro, A.; Yu, R.; Hu, J.; Sun, Z.; Xiang, W. Integration of chemical looping combustion and supercritical CO2 cycle for combined heat and power generation with CO2 capture. Energy Convers. Manag. 2018, 167, 113–124. [Google Scholar] [CrossRef]
- Johnson, G.A.; McDowell, M.W.; O’Connor, G.M.; Sonwane, C.G.; Subbaraman, G. Supercritical CO2 cycle development at pratt and whitney rocketdyne. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; pp. 1015–1024. [Google Scholar]
- McClung, A.; Brun, K.; Delimont, J. Comparison of supercritical carbon dioxide cycles for oxy-combustion. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015; pp. V9T–V36T. [Google Scholar]
- Sun, E.; Xu, J.; Li, M.; Liu, G.; Zhu, B. Connected-top-bottom-cycle to cascade utilize flue gas heat for supercritical carbon dioxide coal fired power plant. Energy Convers. Manag. 2018, 172, 138–154. [Google Scholar] [CrossRef]
- Basu, P.; Kefa, C.; Jestin, L. Boilers and Burners: Design and Theory; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP; Version 9.1; National Institute of Standards and Technology, Standard Reference Data Program: Gaithersburg, MD, USA, 2013. Available online: http://www.nist.gov/srd/nist23.cfm (accessed on 27 November 2018).
- Bejan, A.; Mamut, E. (Eds.) Thermodynamic Optimization of Complex Energy Systems; Springer Science & Business Media: Berlin, Germany, 2012; Volume 69. [Google Scholar]
- Li, Q.; Liu, Z. Thermal Economy Calculation and Analysis of Thermal Power Plant; China Electric Power Press: Beijing, China, 2008. (In Chinese) [Google Scholar]
- Wang, L.; Deng, L.; Tang, C.; Fan, Q.; Wang, C.; Che, D. Thermal deformation prediction based on the temperature distribution of the rotor in rotary air-preheater. Appl. Therm. Eng. 2015, 90, 478–488. [Google Scholar] [CrossRef]
- Yu, C.; Xu, J.; Sun, Y. Transcritical pressure Organic Rankine Cycle (ORC) analysis based on the integrated-average temperature difference in evaporators. Appl. Therm. Eng. 2015, 88, 2–13. [Google Scholar] [CrossRef]
- Mafi, M.; Amidpour, M.; Naeynian, S.M.M. Comparison of low temperature mixed refrigerant cycles for separation systems. Int. J. Energy Res. 2009, 33, 358–377. [Google Scholar] [CrossRef]
- Khennich, M.; Sorin, M.; Galanis, N. Equivalent Temperature-Enthalpy Diagram for the Study of Ejector Refrigeration Systems. Entropy 2014, 16, 2669–2685. [Google Scholar] [CrossRef]
- Linnhoff, B.; Dhole, V.R. Shaftwork targets for low temperature process design. Chem. Eng. Sci. 1992, 4, 2081–2091. [Google Scholar] [CrossRef]
| Parameters | Values |
|---|---|
| Turbine inlet temperature (T5) | 600–650 °C |
| Turbine inlet pressure (P5) | 30 MPa |
| Turbine isentropic efficiency (ηt,s) | 93% |
| Compressor C1 inlet temperature (T1) | 32 °C |
| Compressor C1 inlet pressure (P1) | 7.6 MPa |
| Compressors isentropic efficiency (ηc,s) | 89% |
| Pressure drops in LTR and HTR (ΔP) | 0.1 MPa |
| LTR and HTR pinch temperature difference (ΔTLTR or ΔTHTR) | 10 °C |
| Primary air temperature (Tpri air) | 320 °C |
| Primary air temperature at the inlet of air preheater (Tpri air,in) | 31 °C |
| Primary air flow rate ratio (αpri) | 19% |
| Secondary air temperature (Tsec air) | 330 °C |
| Secondary air temperature at the inlet of air preheater (Tsec air,in) | 23 °C |
| Secondary air flow rate ratio (αsec) | 81% |
| Excess air coefficient (αair) | 1.2 |
| Exit flue gas temperature (Tfg, ex) | 123 °C |
| Environment temperature | 20 °C |
| Pinch temperature between Tfg,4 and T4 (∆Tp,4) | 40 °C |
| Pipeline efficiency (ηp) | 99% |
| Power generator efficiency (ηg) | 98.5% |
| Variable/Parameter | Values |
|---|---|
| Turbine inlet temperature (T5b) | 400–600 °C |
| Turbine inlet pressure (P5b) | 15–45 MPa |
| Turbine isentropic efficiency (ηt,s) | 93% |
| Compressor inlet temperature (T1b) | 32 °C |
| LP compressor inlet pressure (P1b) | 7.6 MPa |
| Compressors isentropic efficiency (ηc,s) | 89% |
| Pressure drop of each component except the boiler (ΔP) | 0.1 MPa |
| Pressure drop of the boiler (ΔPb) | 0.2 MPa |
| LTR2 and HTR2 pinch temperature difference (ΔTLTR2 or ΔTHTR2) | 10 °C |
| Car | Har | Oar | Nar | Sar | Aar | Mar | Vdaf | Qf |
|---|---|---|---|---|---|---|---|---|
| 61.70 | 3.67 | 8.56 | 1.12 | 0.60 | 8.80 | 15.55 | 34.73 | 23442 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, E.; Hu, H.; Li, H.; Liu, C.; Xu, J. How to Construct a Combined S-CO2 Cycle for Coal Fired Power Plant? Entropy 2019, 21, 19. https://doi.org/10.3390/e21010019
Sun E, Hu H, Li H, Liu C, Xu J. How to Construct a Combined S-CO2 Cycle for Coal Fired Power Plant? Entropy. 2019; 21(1):19. https://doi.org/10.3390/e21010019
Chicago/Turabian StyleSun, Enhui, Han Hu, Hangning Li, Chao Liu, and Jinliang Xu. 2019. "How to Construct a Combined S-CO2 Cycle for Coal Fired Power Plant?" Entropy 21, no. 1: 19. https://doi.org/10.3390/e21010019
APA StyleSun, E., Hu, H., Li, H., Liu, C., & Xu, J. (2019). How to Construct a Combined S-CO2 Cycle for Coal Fired Power Plant? Entropy, 21(1), 19. https://doi.org/10.3390/e21010019





