Measuring Integrated Information: Comparison of Candidate Measures in Theory and Simulation
Abstract
1. Introduction
- integration, i.e., the system behaves as one; and
- segregation, i.e., the parts of the system behave independently.
2. Methods
2.1. Notation, Convention and Preliminaries
- ,
- , and
- for any injective functions .
2.2. Integrated Information Measures
2.2.1. Overview
- Whole-minus-sum integrated information, ;
- Integrated stochastic interaction, ;
- Integrated synergy, ;
- Decoder-based integrated information, ;
- Geometric integrated information, ; and
- Causal density, CD.
2.2.2. Minimum Information Partition
2.2.3. Whole-Minus-Sum Integrated Information
- For discrete variables:
- For continuous, linear-Gaussian variables:
- For continuous variables with an arbitrary distribution, we must resort to the nearest-neighbour methods introduced by [24]. See reference for details.
2.2.4. Integrated Stochastic Interaction
- For discrete variables:
- For continuous, linear-Gaussian variables:
- For continuous variables with an arbitrary distribution, we must resort to the nearest-neighbour methods introduced by [24]. See reference for details.
2.2.5. Integrated Synergy
- For discrete variables: (following Griffith and Koch’s [30] PID scheme)
- For continuous, linear-Gaussian variables:
- For continuous variables with an arbitrary distribution: unknown.
2.2.6. Decoder-Based Integrated Information
- For discrete variables:
- For continuous, linear-Gaussian variables: (see appendix for details)
- For continuous variables with an arbitrary distribution: unknown.
2.2.7. Geometric Integrated Information
- For discrete variables: numerically optimise the objective subject to the constraints
- For continuous, linear-Gaussian variables: numerically optimise the objectivewhere , and subject to the constraints
- For continuous variables with an arbitrary distribution: unknown.
2.2.8. Causal Density
- For discrete variables:
- For continuous, linear-Gaussian variables:
- For continuous variables with an arbitrary distribution, we must resort to the nearest-neighbour methods introduced by [24]. See reference for details.
2.2.9. Other Measures
3. Results
- Whole-minus-sum integrated information, ,
- Integrated stochastic interaction, ,
- Decoder-based integrated information, ,
- Geometric integrated information, ,
- Integrated synergy, ,
- Causal density, CD.
- Time-delayed mutual information (TDMI), ; and
- Average absolute correlation , defined as the average absolute value of the non-diagonal entries in the system’s correlation matrix.
3.1. Key Quantities for Computing the Integrated Information Measures
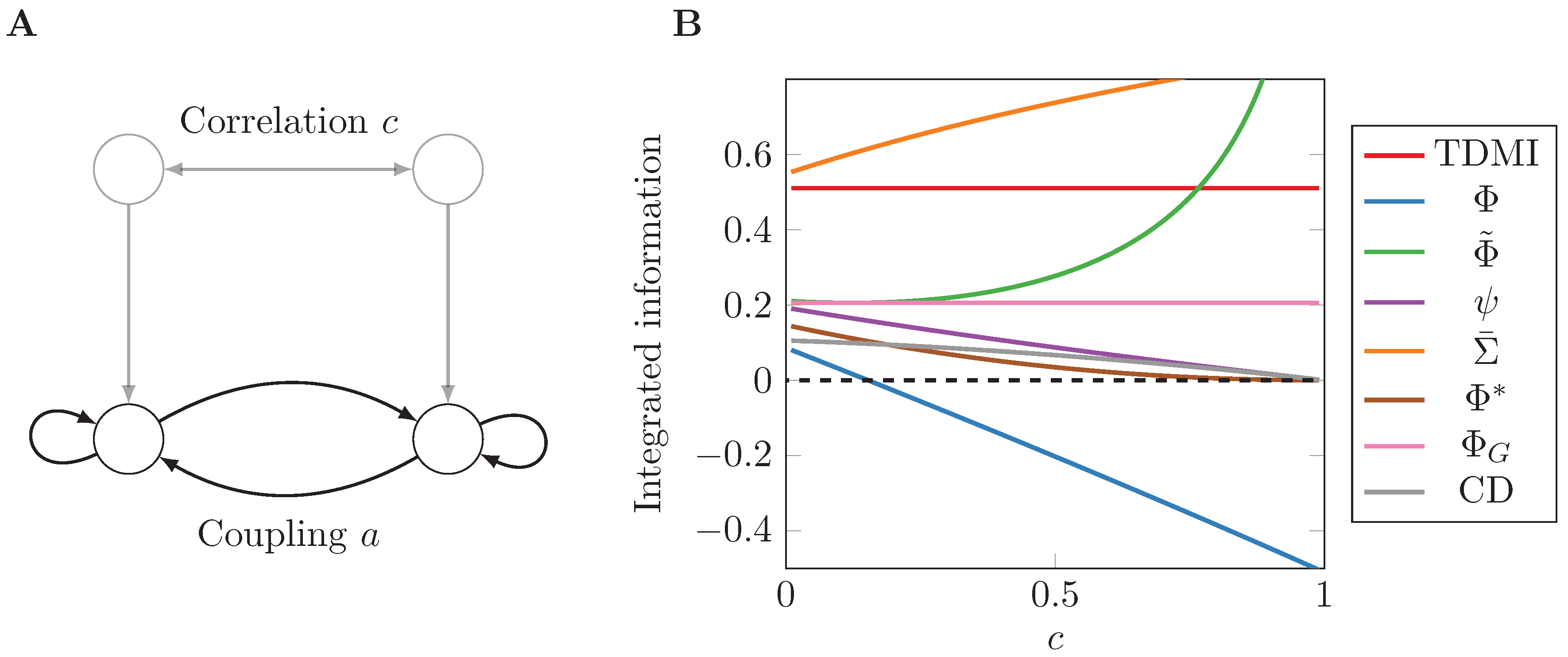
3.2. Two-Node Network
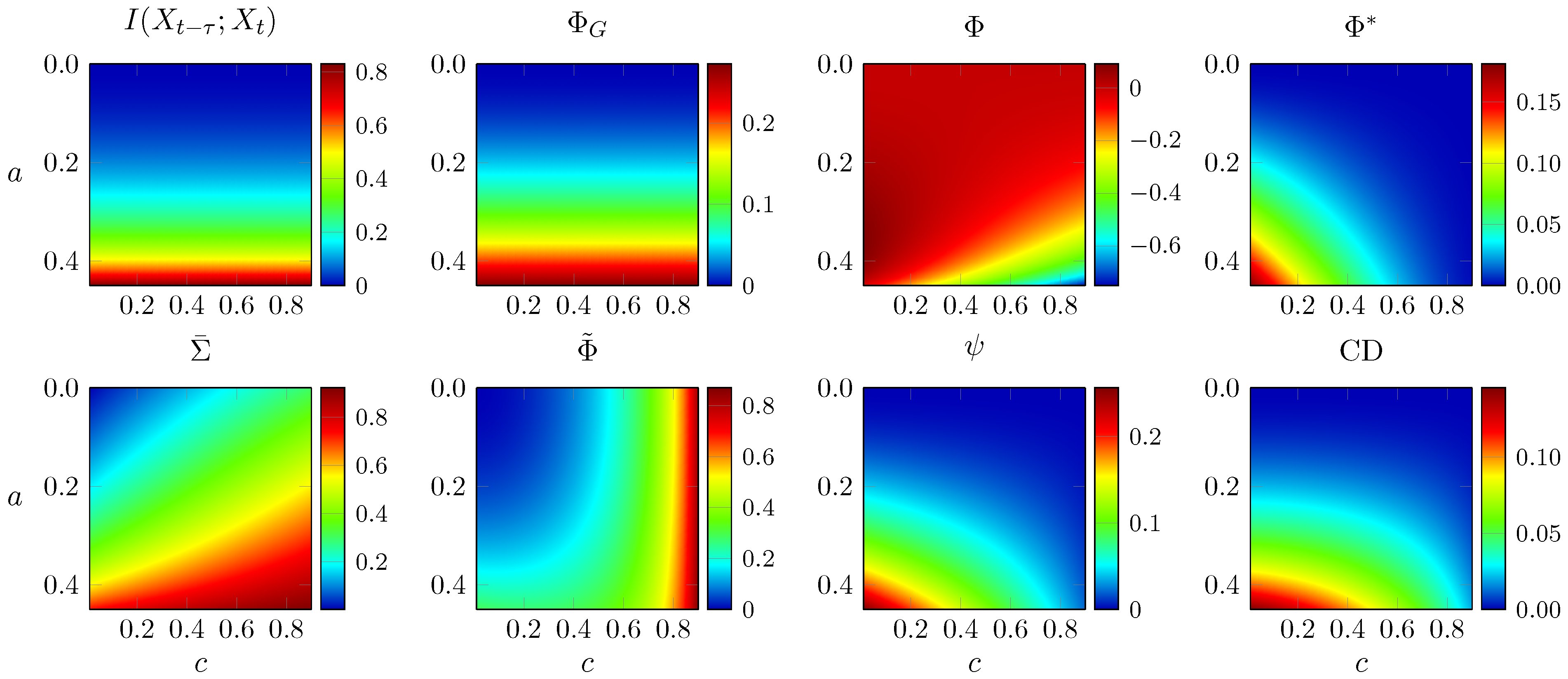
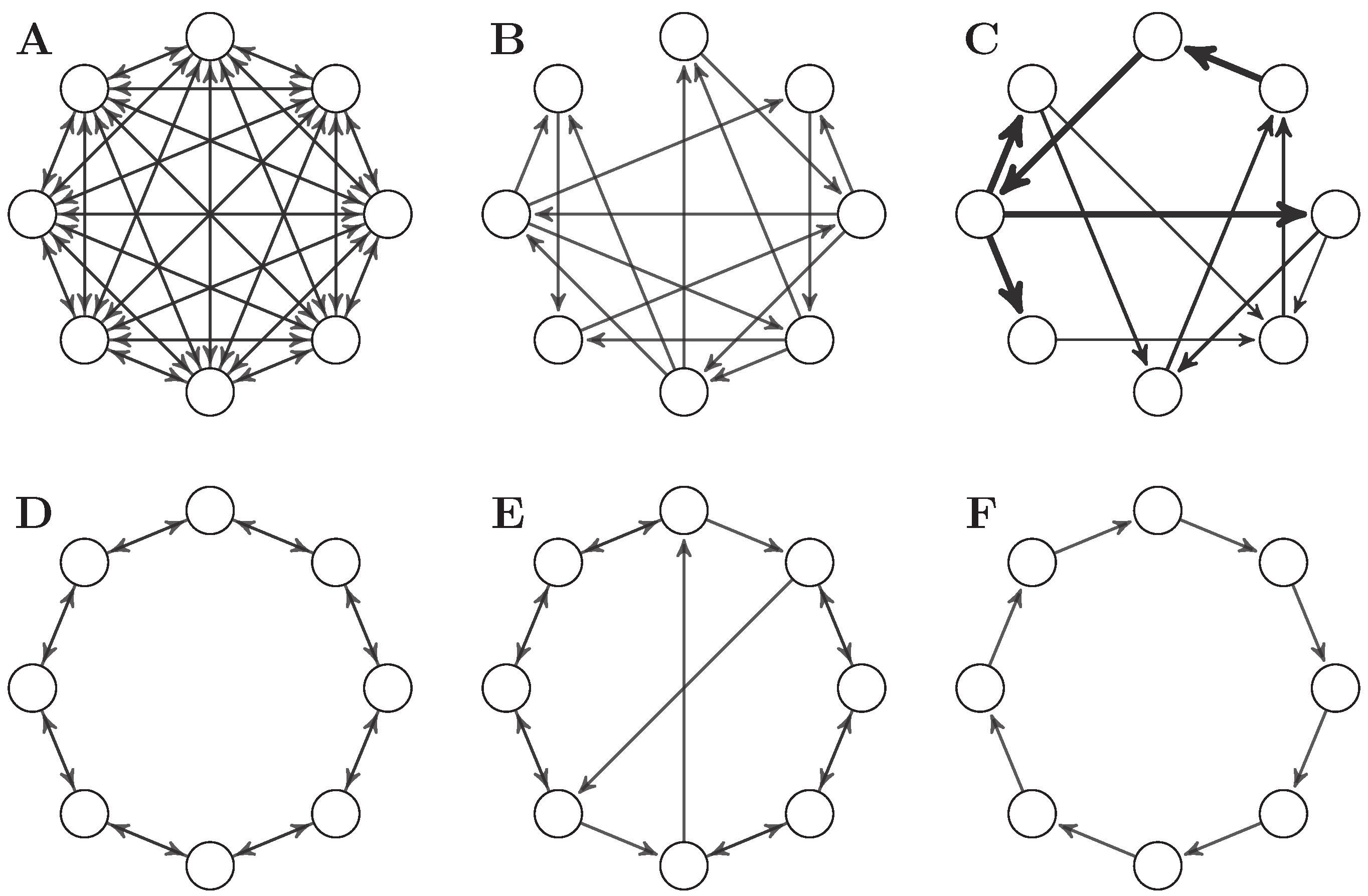
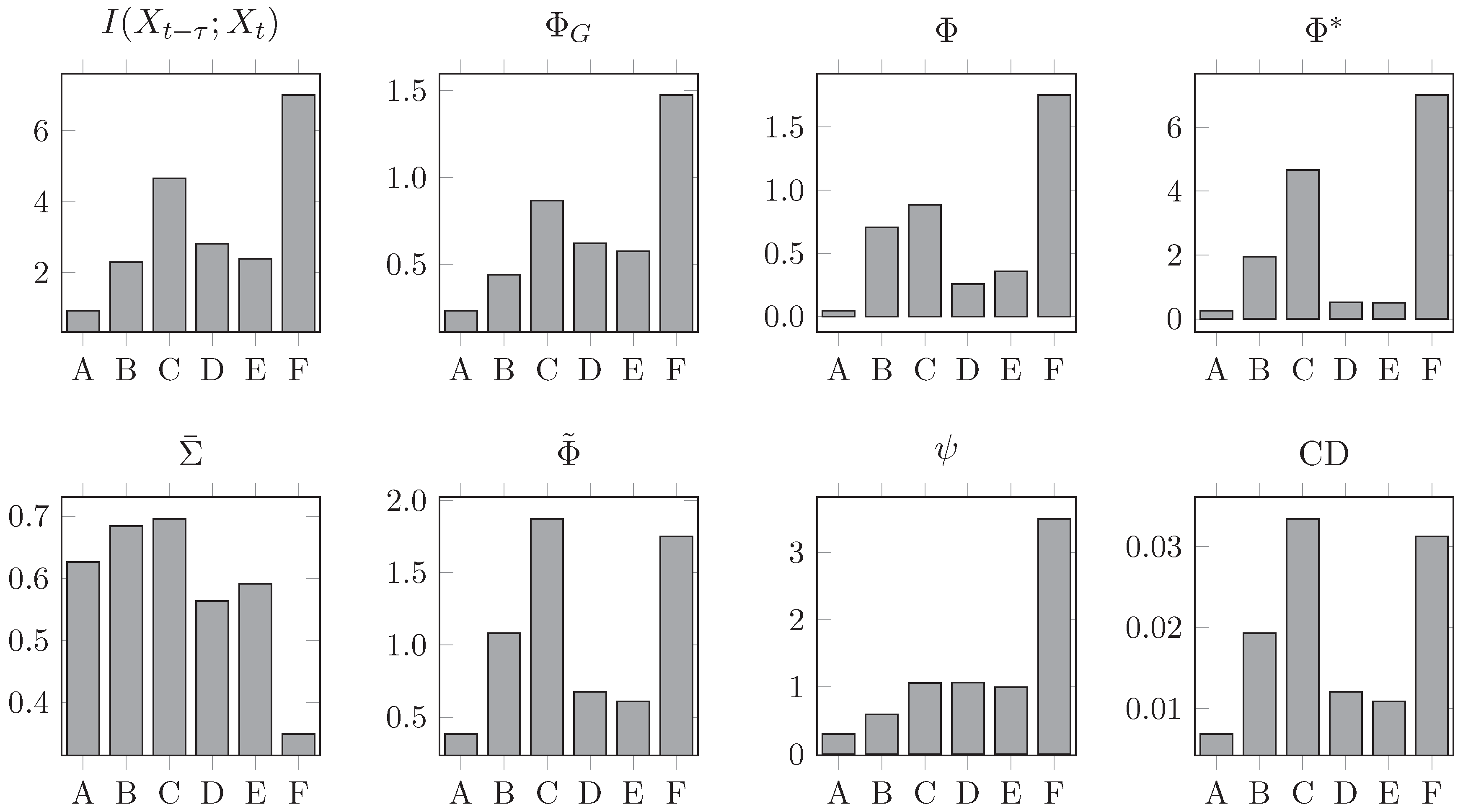
3.3. Eight-Node Networks
- A
- A fully connected network without self-loops.
- B
- The -optimal binary network presented in [2].
- C
- The -optimal weighted network presented in [2].
- D
- A bidirectional ring network.
- E
- A “small-world” network, formed by introducing two long-range connections to a bidirectional ring network.
- F
- A unidirectional ring network.
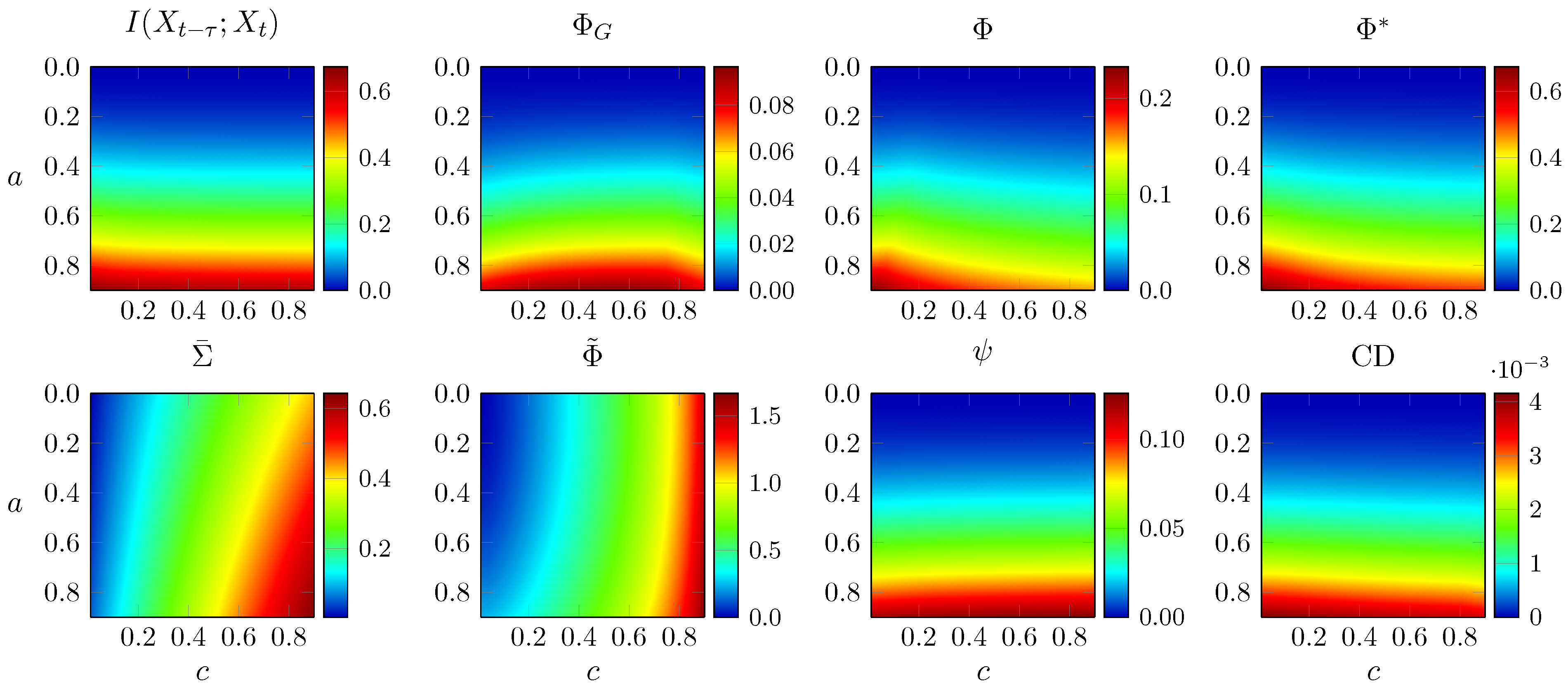
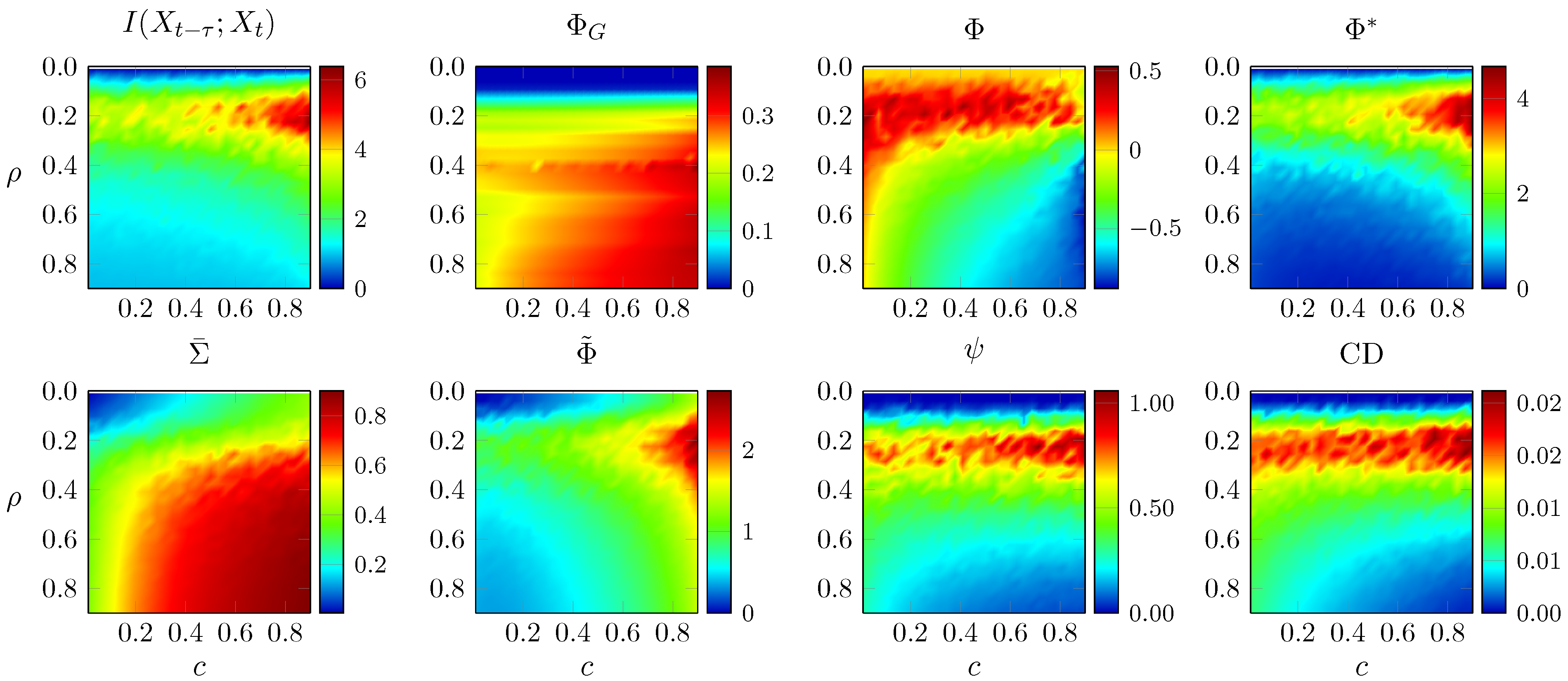
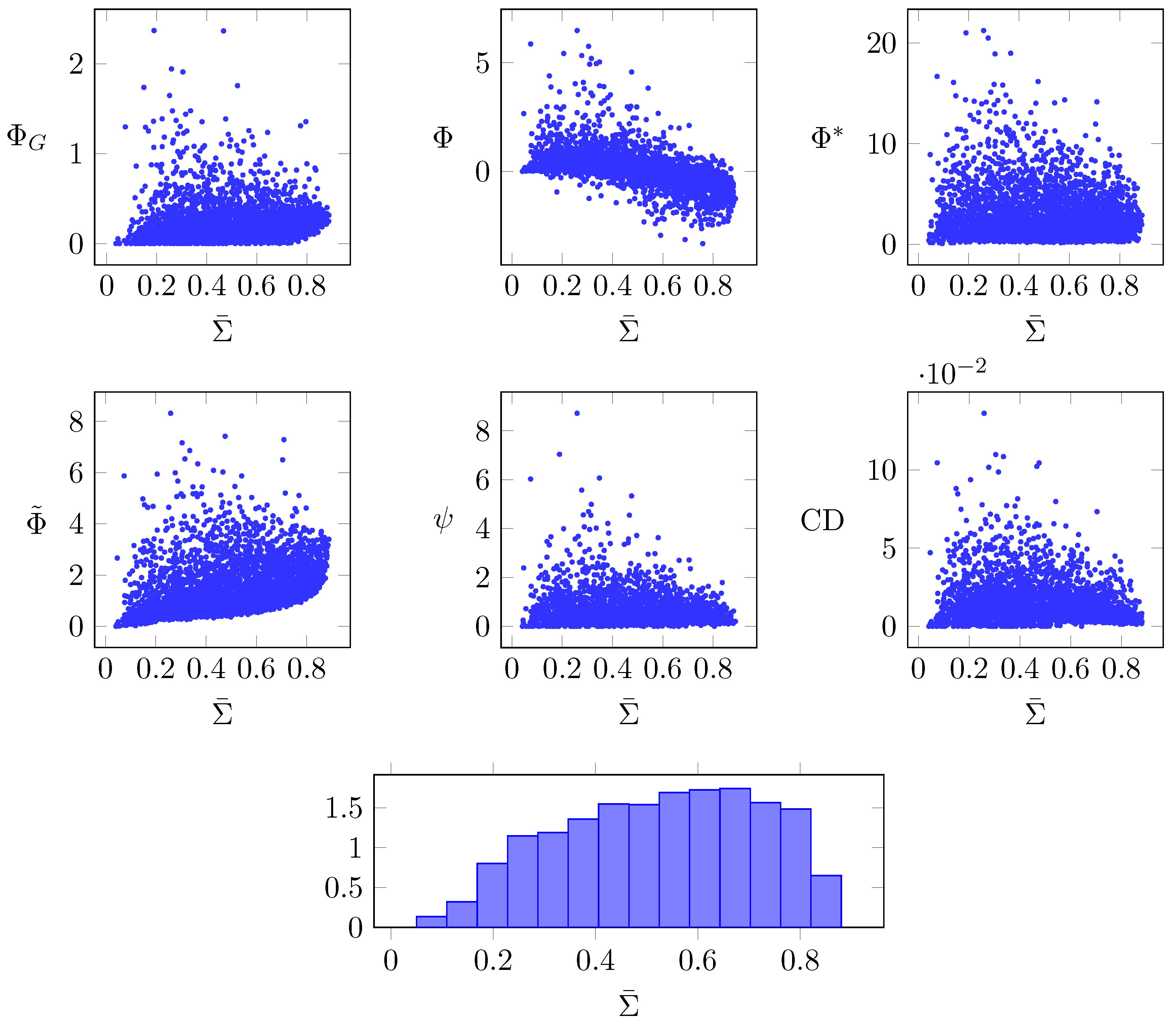
3.4. Random Networks
4. Discussion
4.1. Partition Selection
4.2. Continuous Variables and the Linear Gaussian Assumption
4.3. Empirical as Opposed to Maximum Entropy Distribution
5. Final Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Derivation and Concavity Proof of I *
Appendix A.1. Derivation of I * in Gaussian Systems
Appendix A.2. (β) Is Concave in β in Gaussian Systems
- An affine function preserves concavity, in the sense that a linear combination of convex (concave) functions is also convex (concave).
- A non-negative weighted sum preserves concavity. Since , the outer integral in Equation (A20) preserves concavity,
Appendix B. Bounds on Causal Density
Appendix C. Properties of Integrated Information Measures
- MI-1
- ,
- MI-2
- ,
- MI-3
- for any injective functions ,
Appendix C.1. Whole-Minus-Sum Integrated Information Φ
- Time-symmetric
- Follows from (MI-1).
- Non-negative
- Proof by example. If , we have .
- Rescaling-invariant
- Follows from (MI-3) when Balduzzi and Tononi’s [12] normalisation factor is not used.
- Bounded by TDMI
- Follows from (MI-2).
Appendix C.2. Integrated Stochastic Interaction
- Time-symmetric
- Follows from , which can be proved starting from the system temporal joint entropy
- Non-negative
- Follows from the fact that is an M-projection (see Reference [4]).
- Rescaling-invariant
- Follows from the non-invariance of differential entropy [18] (regardless of whether a normalisation factor is used).
- Bounded by TDMI
- Proof by counterexample. In the two-node AR process of the main text as , although TDMI remains finite.
Appendix C.3. Integrated Synergy ψ
- Time-symmetric
- Proof by counterexample—for the AR system with
Appendix C.4. Decoder-Based Integrated Information Φ*
- Non-negative
- Follows from , proven in Reference [36].
- Rescaling-invariant
- Assume that the measure is computed on a time series of rescaled data , where A is a diagonal matrix with positive real numbers. Then, its covariance is related to the covariance of the original time series as . We can analogously calculate and easily verify that all A’s cancel out, proving the invariance.
- Bounded by TDMI
- Follows from , proven in Reference [36].
Appendix C.5. Geometric Integrated Information ΦG
- Time-symmetric
- Follows from the symmetry in the constraints that define the manifold of restricted models Q [4].
- Non-negative
- Follows from the fact that is an M-projection [4].
- Rescaling-invariant
- Given a Gaussian distribution p with covariance , its M-projection in Q is another Gaussian with covariance . Given a new distribution formed by rescaling some of the variables in p, the M-projection of is a Gaussian with covariance with A a diagonal positive matrix (see above), which satisfies and therefore is invariant to rescaling.
- Bounded by TDMI
- TDMI can be defined as the M-projection of the full model p to a manifold of restricted models [4]. The bound follows from the fact that .
Appendix C.6. Causal Density
- Time-symmetric
- Follows from the non-symmetry of transfer entropy [61].
- Non-negative
- Re-writing CD as a sum of conditional MI terms, follows from (MI-2).
- Rescaling-invariant
- Follows from (MI-3).
- Bounded by TDMI
- Proven in S2 Appendix.
References
- Holland, J. Complexity: A Very Short Introduction; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Barrett, A.B.; Seth, A.K. Practical measures of integrated information for time-series data. PLoS Comput. Biol. 2011, 7, e1001052. [Google Scholar] [CrossRef] [PubMed]
- Griffith, V. A principled infotheoretic ϕ-like measure. arXiv, 2014; arXiv:1401.0978. [Google Scholar]
- Oizumi, M.; Tsuchiya, N.; Amari, S.-I. A unified framework for information integration based on information geometry. arXiv, 2015; arXiv:1510.04455. [Google Scholar]
- Oizumi, M.; Amari, S.-I.; Yanagawa, T.; Fujii, N.; Tsuchiya, N. Measuring integrated information from the decoding perspective. arXiv, 2015; arXiv:1505.04368. [Google Scholar]
- Toker, D.; Sommer, F.T. Great than the sum: Integrated information in large brain networks. arXiv, 2017; arXiv:1708.02967. [Google Scholar]
- Mediano, P.A.M.; Farah, J.C.; Shanahan, M.P. Integrated information and metastability in systems of coupled oscillators. arXiv, 2016; arXiv:1606.08313. [Google Scholar]
- Tagliazucchi, E. The signatures of conscious access and its phenomenology are consistent with large-scale brain communication at criticality. Conscious. Cogn. 2017, 55, 136–147. [Google Scholar] [CrossRef] [PubMed]
- Oizumi, M.; Albantakis, L.; Tononi, G. From the phenomenology to the mechanisms of consciousness: Integrated information theory 3.0. PLoS Comput. Biol. 2014, 10, e1003588. [Google Scholar] [CrossRef] [PubMed]
- Tononi, G.; Sporns, O.; Edelman, G.M. A measure for brain complexity: Relating functional segregation and integration in the nervous system. Proc. Natl. Acad. Sci. USA 1994, 91, 5033–5037. [Google Scholar] [CrossRef] [PubMed]
- Sporns, O. Complexity. Scholarpedia 2007, 2, 1623. [Google Scholar] [CrossRef]
- Balduzzi, D.; Tononi, G. Integrated information in discrete dynamical dystems: Motivation and theoretical framework. PLoS Comput. Biol. 2008, 4, e1000091. [Google Scholar] [CrossRef] [PubMed]
- Seth, A.K.; Barrett, A.B.; Barnett, L. Causal density and integrated information as measures of conscious level. Philos. Trans. A 2011, 369, 3748–3767. [Google Scholar] [CrossRef] [PubMed]
- Granger, C.W.J. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424. [Google Scholar] [CrossRef]
- Seth, A.K.; Izhikevich, E.; Reeke, G.N.; Edelman, G.M. Theories and measures of consciousness: An extended framework. Proc. Natl. Acad. Sci. USA 2006, 103, 10799–10804. [Google Scholar] [CrossRef] [PubMed]
- Kanwal, M.S.; Grochow, J.A.; Ay, N. Comparing information-theoretic measures of complexity in Boltzmann machines. Entropy 2017, 19, 310. [Google Scholar] [CrossRef]
- Tegmark, M. Improved measures of integrated information. arXiv, 2016; arXiv:1601.02626. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements Information Theory; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- The formal derivation of the differential entropy proceeds by considering the entropy of a discrete variable with k states, and taking the k→∞ limit. The result is the differential entropy plus a divergent term that is usually dropped and is ultimately responsible for the undesirable properties of differential entropy. In the case of I(X;Y) the divergent terms for the various entropies involved cancel out, restoring the useful properties of its discrete counterpart.
- Although the origins of causal density go as back as 1969, it hasn’t been until the last decade that it has found its way into neuroscience. The paper referenced in the table acts as a modern review of the properties and behaviour of causal density. This measure is somewhat distinct from the others, but is still a measure of complexity based on information dynamics between the past and current state; therefore its inclusion here will be useful.
- Krohn, S.; Ostwald, D. Computing integrated information. arXiv, 2016; arXiv:1610.03627. [Google Scholar]
- The c and e here stand respectively for cause and effect. Without an initial condition, here that the uniform distribution holds at time 0, there would be no well-defined probability distribution for these states. Further, Markovian dynamics are required for these probability distributions to be well-defined; for non-Markovian dynamics, a longer chain of initial states would have to be specified, going beyond just that at time 0.
- Barrett, A.B. An exploration of synergistic and redundant information sharing in static and dynamical gaussian systems. arXiv, 2014; arXiv:1411.2832. [Google Scholar]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed]
- Ay, N. Information geometry on complexity and stochastic interaction. Entropy 2015, 17, 2432–2458. [Google Scholar] [CrossRef]
- Wiesner, K.; Gu, M.; Rieper, E.; Vedral, V. Information-theoretic bound on the energy cost of stochastic simulation. arXiv, 2011; arXiv:1110.4217. [Google Scholar]
- Williams, P.L.; Beer, R.D. Nonnegative decomposition of multivariate information. arXiv, 2010; arXiv:1004.2515. [Google Scholar]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J. Shared information—New insights and problems in decomposing information in complex systems. In Proceedings of the European Conference on Complex Systems 2012; Gilbert, T., Kirkilionis, M., Nicolis, G., Eds.; Springer: Berlin, Germany, 2012. [Google Scholar]
- Barrett’s derivation of the MMI-PID, which follows Williams and Beer and Griffith and Koch’s procedure, gives this formula when the target is univariate. We generalise the formula here to the case of multivariate target in order to render ψ computable for Gaussians. This formula leads to synergy being the extra information contributed by the weaker source given the stronger source was previously known.
- Griffith, V.; Koch, C. Quantifying synergistic mutual information. arXiv, 2012; arXiv:1205.4265. [Google Scholar]
- Rosas, F.; Ntranos, V.; Ellison, C.; Pollin, S.; Verhelst, M. Understanding interdependency through complex information sharing. Entropy 2016, 18, 38. [Google Scholar] [CrossRef]
- Ince, R.A.A. Measuring multivariate redundant information with pointwise common change in surprisal. Entropy 2017, 19, 318. [Google Scholar] [CrossRef]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying unique information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Kay, J.W.; Ince, R.A.A. Exact partial information decompositions for Gaussian systems based on dependency constraints. arXiv, 2018; arXiv:1803.02030. [Google Scholar]
- Latham, P.E.; Nirenberg, S. Synergy, redundancy, and independence in population codes, revisited. J. Neurosci. 2005, 25, 5195–5206. [Google Scholar] [CrossRef] [PubMed]
- Merhav, N.; Kaplan, G.; Lapidoth, A.; Shitz, S.S. On information rates for mismatched decoders. IEEE Trans. Inf. Theory 1994, 40, 1953–1967. [Google Scholar] [CrossRef]
- Oizumi, M.; Ishii, T.; Ishibashi, K.; Hosoya, T.; Okada, M. Mismatched decoding in the brain. J. Neurosci. 2010, 30, 4815–4826. [Google Scholar] [CrossRef]
- Amari, S.-I.; Nagaoka, H. Methods of Information Geometry; American Mathematical Society: Providence, RI, USA, 2000. [Google Scholar]
- Amari, S.-I. Information geometry in optimization, machine learning and statistical inference. Front. Electr. Electron. Eng. China 2010, 5, 241–260. [Google Scholar] [CrossRef]
- Boyd, S.S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Seth, A.K. Causal connectivity of evolved neural networks during behavior. Netw. Comput. Neural Syst. 2005, 16, 35–54. [Google Scholar] [CrossRef]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Granger causality and transfer entropy are equivalent for Gaussian variables. Phys. Rev. Lett. 2009, 103, 238701. [Google Scholar] [CrossRef] [PubMed]
- Barnett, L.; Seth, A.K. Behaviour of granger causality under filtering: Theoretical invariance and practical application. J. Neurosci. Methods 2011, 201, 404–419. [Google Scholar] [CrossRef] [PubMed]
- Lindner, M.; Vicente, R.; Priesemann, V.; Wibral, M. TRENTOOL: A matlab open source toolbox to analyse information flow in time series data with transfer entropy. BMC Neurosci. 2011, 12, 119. [Google Scholar] [CrossRef] [PubMed]
- Lizier, J.T.; Heinzle, J.; Horstmann, A.; Haynes, J.-D.; Prokopenko, M. Multivariate information-theoretic measures reveal directed information structure and task relevant changes in fMRI connectivity. J. Comput. Neurosci. 2010, 30, 85–107. [Google Scholar] [CrossRef] [PubMed]
- Mediano, P.A.M.; Shanahan, M.P. Balanced information storage and transfer in modular spiking neural networks. arXiv, 2017; arXiv:1708.04392. [Google Scholar]
- Barnett, L.; Seth, A.K. The MVGC multivariate granger causality toolbox: A new approach to granger-causal inference. J. Neurosci. Methods 2014, 223, 50–68. [Google Scholar] [CrossRef] [PubMed]
- Lütkepohl, H. New Introduction to Multiple Time Series Analysis; Springer: New York, NY, USA, 2005. [Google Scholar]
- According to an anonymous reviewer, ΦG does decrease with noise correlation in discrete systems, although in this article we focus exclusively in Gaussian systems.
- Note that in Figure 5 the Φ-optimal networks B and C score much less than simpler network F. This is because all networks have been scaled to a spectral radius of 0.9—when the networks are normalised to a spectral radius of 0.5, as in the original paper, then B and C are, as expected, the networks with highest Φ.
- Humphries, M.D.; Gurney, K. Network ‘small-world-ness:’ A quantitative method for determining canonical network equivalence. PLoS ONE 2008, 3, e0002051. [Google Scholar] [CrossRef] [PubMed]
- Yin, H.; Benson, A.R.; Leskovec, J. Higher-order clustering in networks. arXiv, 2017; arXiv:1704.03913. [Google Scholar]
- The small-world index of a network is defined as the ratio between its clustering coefficient and its mean minimum path length, normalised by the expected value of these measures on a random network of the same density. Since the networks we consider are small and sparse, we use the 4th order cliques (instead of triangles, which are 3rd order cliques) to calculate the clustering coefficient.
- Tononi, G.; Sporns, O. Measuring information integration. BMC Neurosci. 2003, 4, 31. [Google Scholar] [CrossRef]
- Toker, D.; Sommer, F. Moving past the minimum information partition: How to quickly and accurately calculate integrated information. arXiv, 2016; arXiv:1605.01096. [Google Scholar]
- Hidaka, S.; Oizumi, M. Fast and exact search for the partition with minimal information loss. arXiv, 2017; arXiv:1708.01444. [Google Scholar]
- Arsiwalla, X.D.; Verschure, P.F.M.J. Integrated information for large complex networks. In Proceedings of the 2013 International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 4–9 August 2013; pp. 1–7. [Google Scholar]
- Dayan, P.; Abbott, L.F. Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Wang, Q.; Kulkarni, S.R.; Verdu, S. Divergence estimation for multidimensional densities via k-nearest-neighbor distances. IEEE Trans. Inf. Theory 2009, 55, 2392–2405. [Google Scholar] [CrossRef]
- Barrett, A.B.; Barnett, L. Granger causality is designed to measure effect, not mechanism. Front. Neuroinform. 2013, 7, 6. [Google Scholar] [CrossRef]
- Wibral, M.; Vicente, R.; Lizier, J.T. (Eds.) Directed Information Measures in Neuroscience; Understanding Complex Systems; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
| Measure | Description | Reference |
|---|---|---|
| Information lost after splitting the system | [12] | |
| Uncertainty gained after splitting the system | [2] | |
| Synergistic predictive information between parts of the system | [3] | |
| Past state decoding accuracy lost after splitting the system | [5] | |
| Information-geometric distance to system with disconnected parts | [4] | |
| CD | Average pairwise directed information flow | [13] |
| CD | ||||||
|---|---|---|---|---|---|---|
| Time-symmetric | ✓ | ✓ | ✕ | ? | ✓ | ✕ |
| Non-negative | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Invariant to variable rescaling | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ |
| Upper-bounded by time-delayed mutual information | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ |
| Known estimators for arbitrary real-valued systems | ✓ | ✓ | ✕ | ✕ | ✕ | ✓ |
| Closed-form expression in discrete and Gaussian systems | ✓ | ✓ | ✓ | ✕ | ✕ | ✓ |
| Measure | Ranking | |||||
|---|---|---|---|---|---|---|
| F | C | D | E | B | A | |
| F | C | D | E | B | A | |
| F | C | B | E | D | A | |
| F | C | B | E | D | A | |
| C | B | A | E | D | F | |
| C | F | B | D | E | A | |
| F | C | D | E | B | A | |
| CD | C | F | B | D | E | A |
| SWI | C | E | B | A | D | F |
| Measure | Summary of Results |
|---|---|
| Erratic behaviour, negative when nodes are strongly correlated. | |
| Mostly reflects noise input correlation, not sensitive to changes in coupling. | |
| Reflects both segregation and integration. | |
| Reflects both segregation and integration. | |
| Mostly reflects changes in coupling, not sensitive to noise input correlation. | |
| CD | Reflects both segregation and integration. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mediano, P.A.M.; Seth, A.K.; Barrett, A.B. Measuring Integrated Information: Comparison of Candidate Measures in Theory and Simulation. Entropy 2019, 21, 17. https://doi.org/10.3390/e21010017
Mediano PAM, Seth AK, Barrett AB. Measuring Integrated Information: Comparison of Candidate Measures in Theory and Simulation. Entropy. 2019; 21(1):17. https://doi.org/10.3390/e21010017
Chicago/Turabian StyleMediano, Pedro A.M., Anil K. Seth, and Adam B. Barrett. 2019. "Measuring Integrated Information: Comparison of Candidate Measures in Theory and Simulation" Entropy 21, no. 1: 17. https://doi.org/10.3390/e21010017
APA StyleMediano, P. A. M., Seth, A. K., & Barrett, A. B. (2019). Measuring Integrated Information: Comparison of Candidate Measures in Theory and Simulation. Entropy, 21(1), 17. https://doi.org/10.3390/e21010017





