Noise Reduction Method of Underwater Acoustic Signals Based on CEEMDAN, Effort-To-Compress Complexity, Refined Composite Multiscale Dispersion Entropy and Wavelet Threshold Denoising
Abstract
1. Introduction
2. Basic Theory
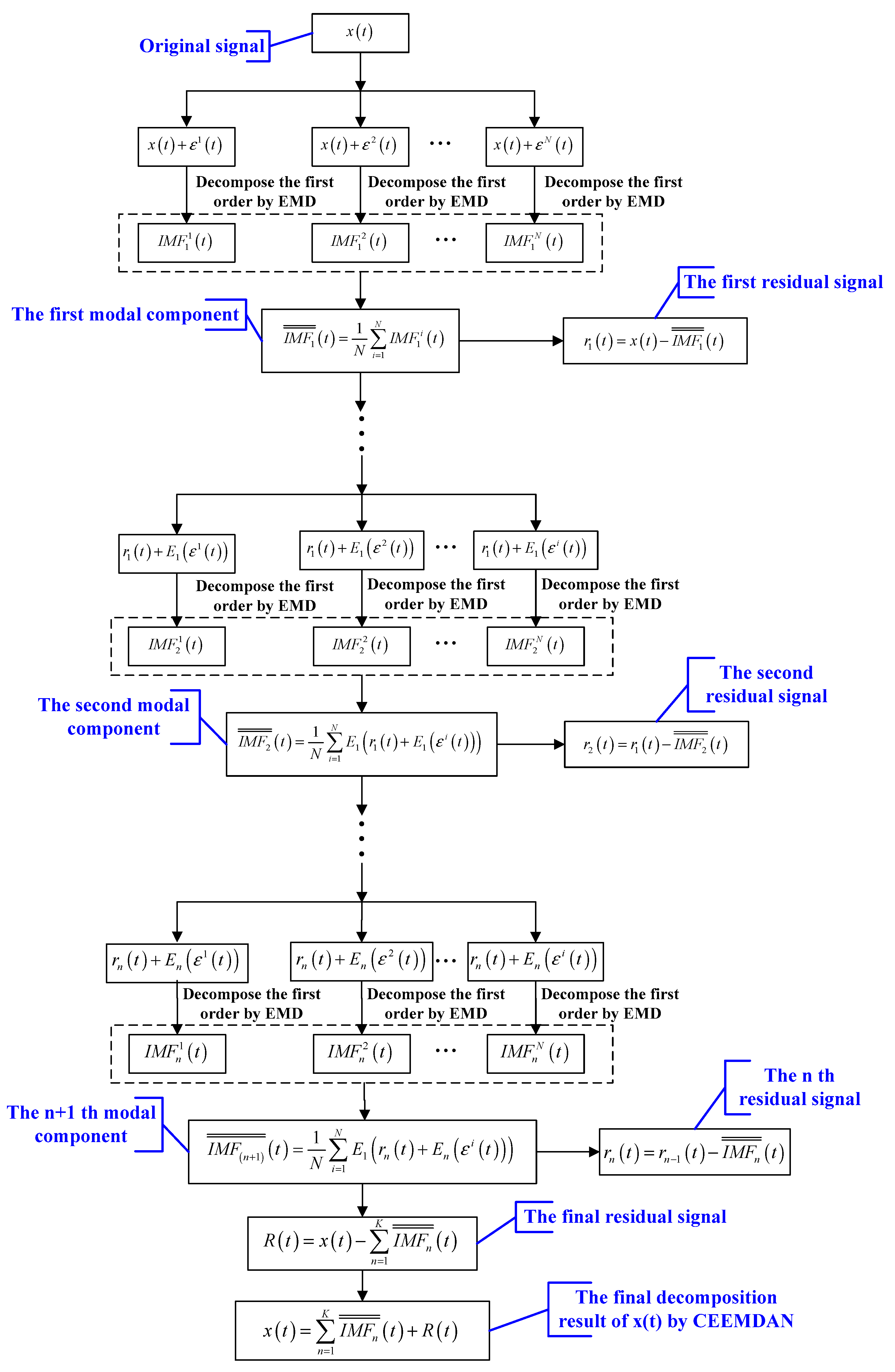
2.1. Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN)
2.1.1. EEMD
2.1.2. CEEMDAN
2.2. Effort-To-Compress Complexity (ETC)
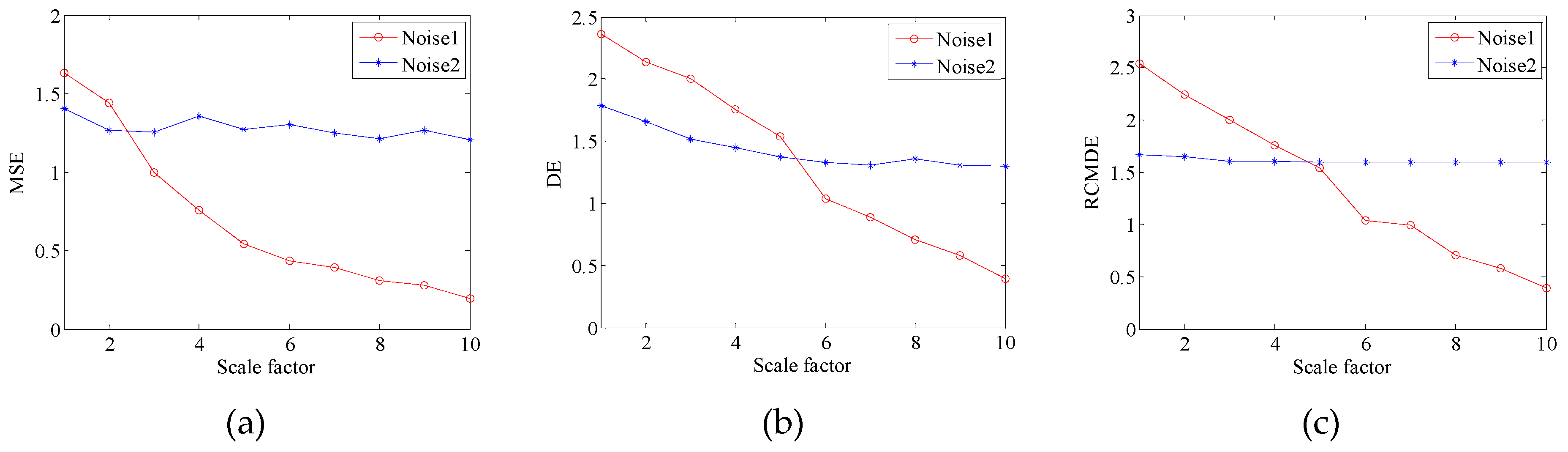
2.3. Refined Composite Multiscale Dispersion Entropy (RCMDE)
2.3.1. Dispersion Entropy (DE)
2.3.2. Multiscale Dispersion Entropy (MDE)
2.3.3. Refined Composite Multiscale Dispersion Entropy (RCMDE)
2.4. Wavelet Threshold Denoising
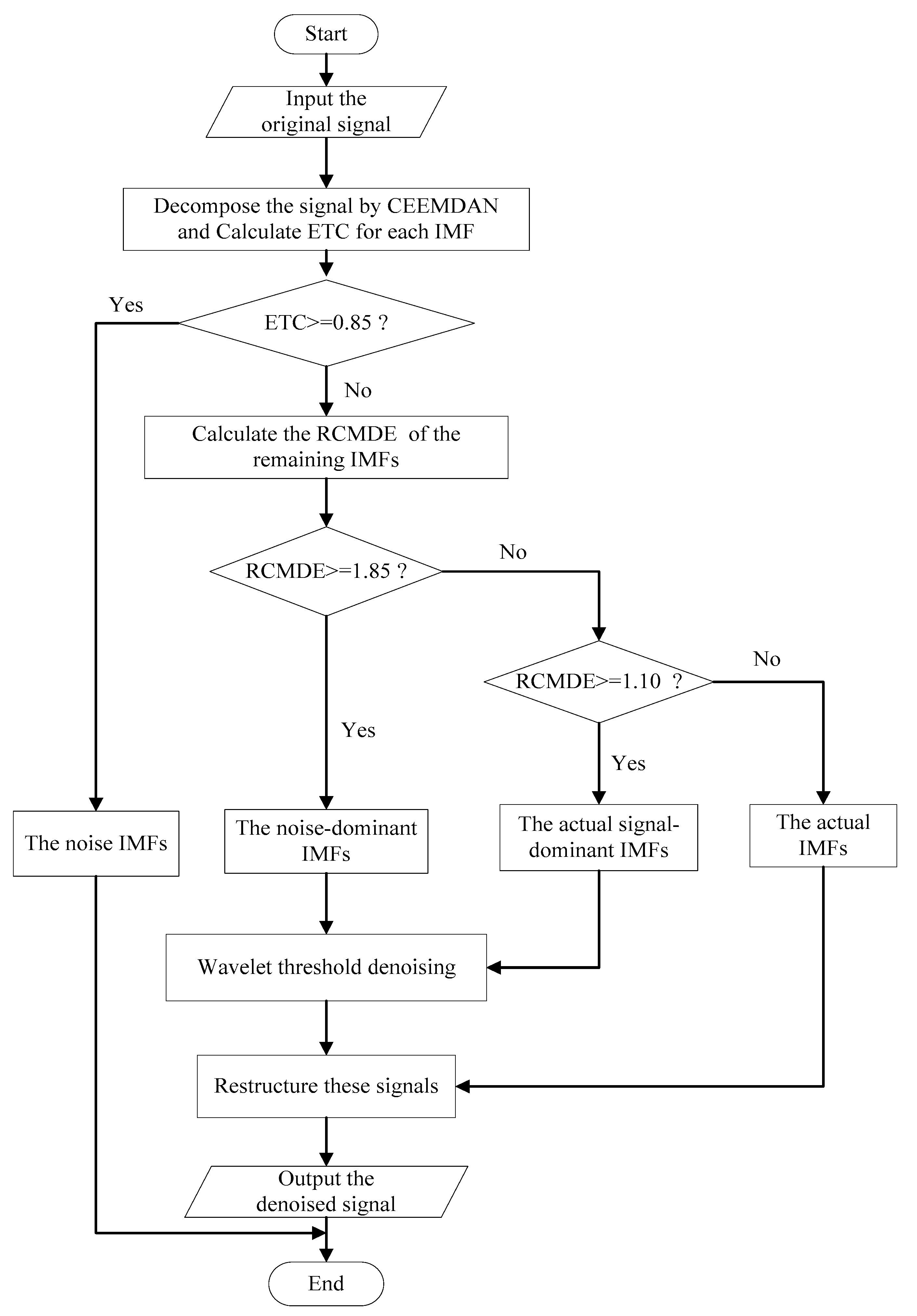
3. The Proposed Noise Reduction Algorithm
3.1. The Proposed Noise Reduction Algorithm
3.2. Evaluation Method of Chaotic Time Series
3.2.1. Signal-To-Noise Ratio (SNR)
3.2.2. Root Mean Square Error (RMSE)
3.2.3. Correlation Dimension
3.2.4. Noise Intensity
3.2.5. Lyapunov Exponent
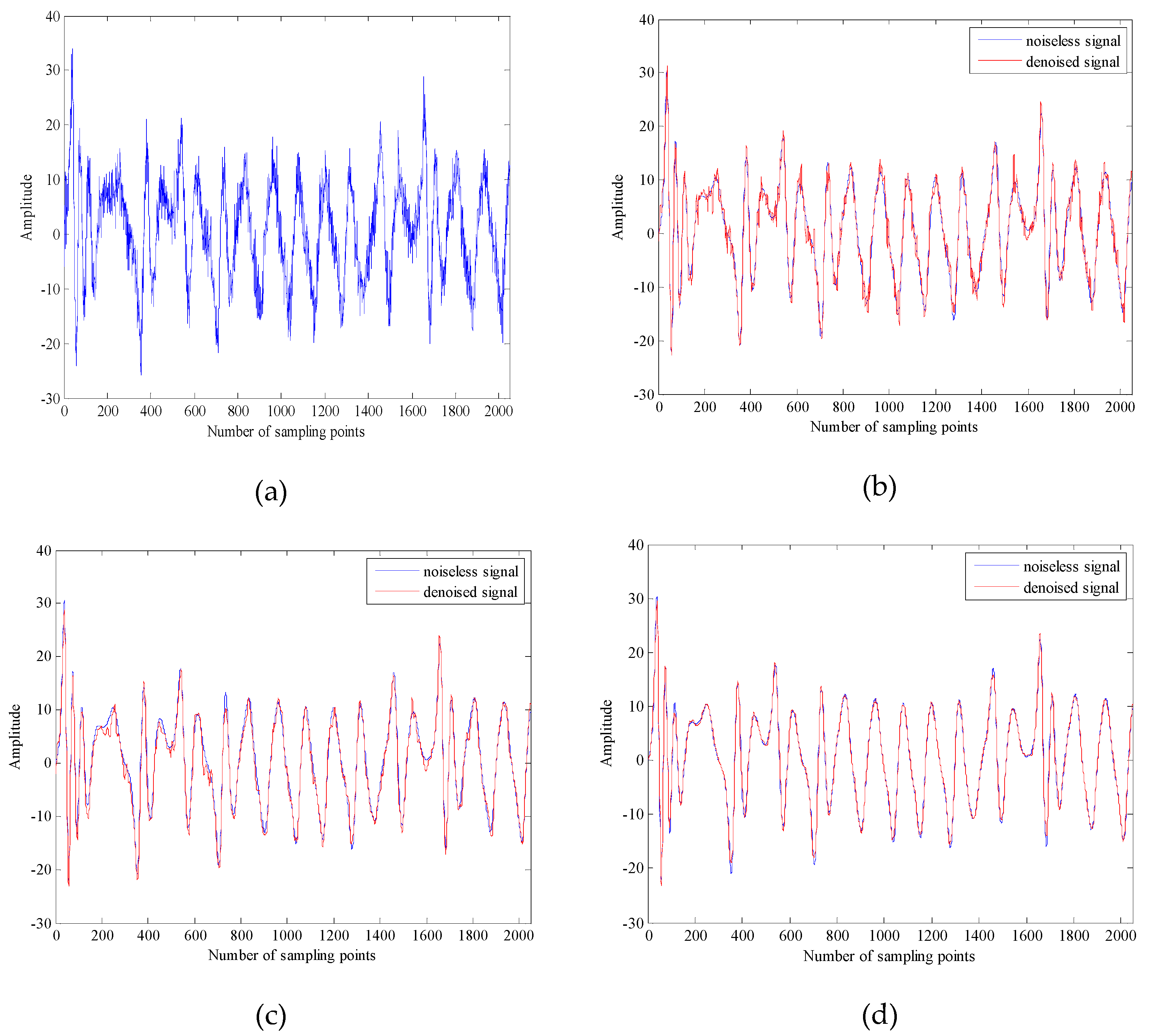
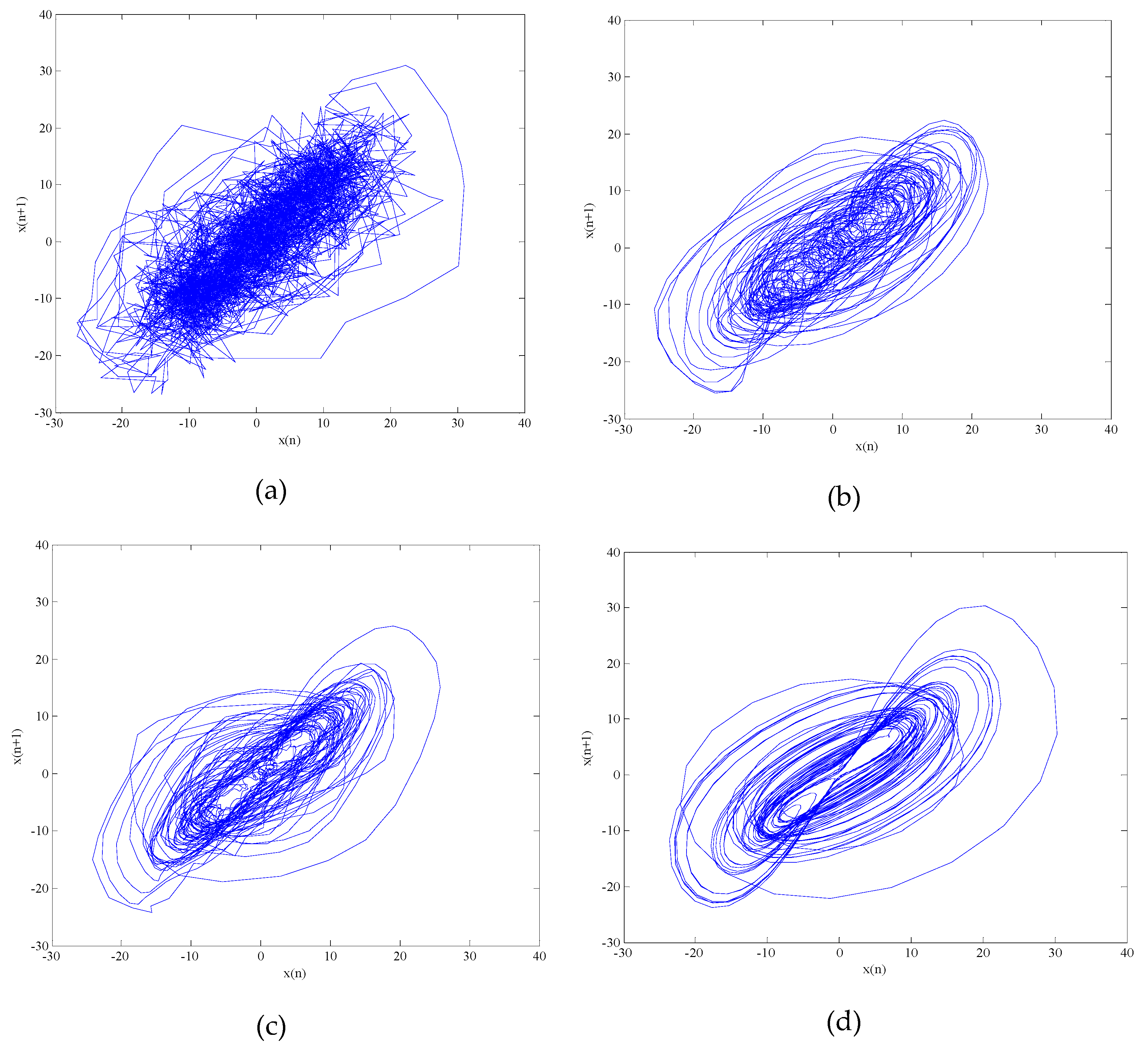
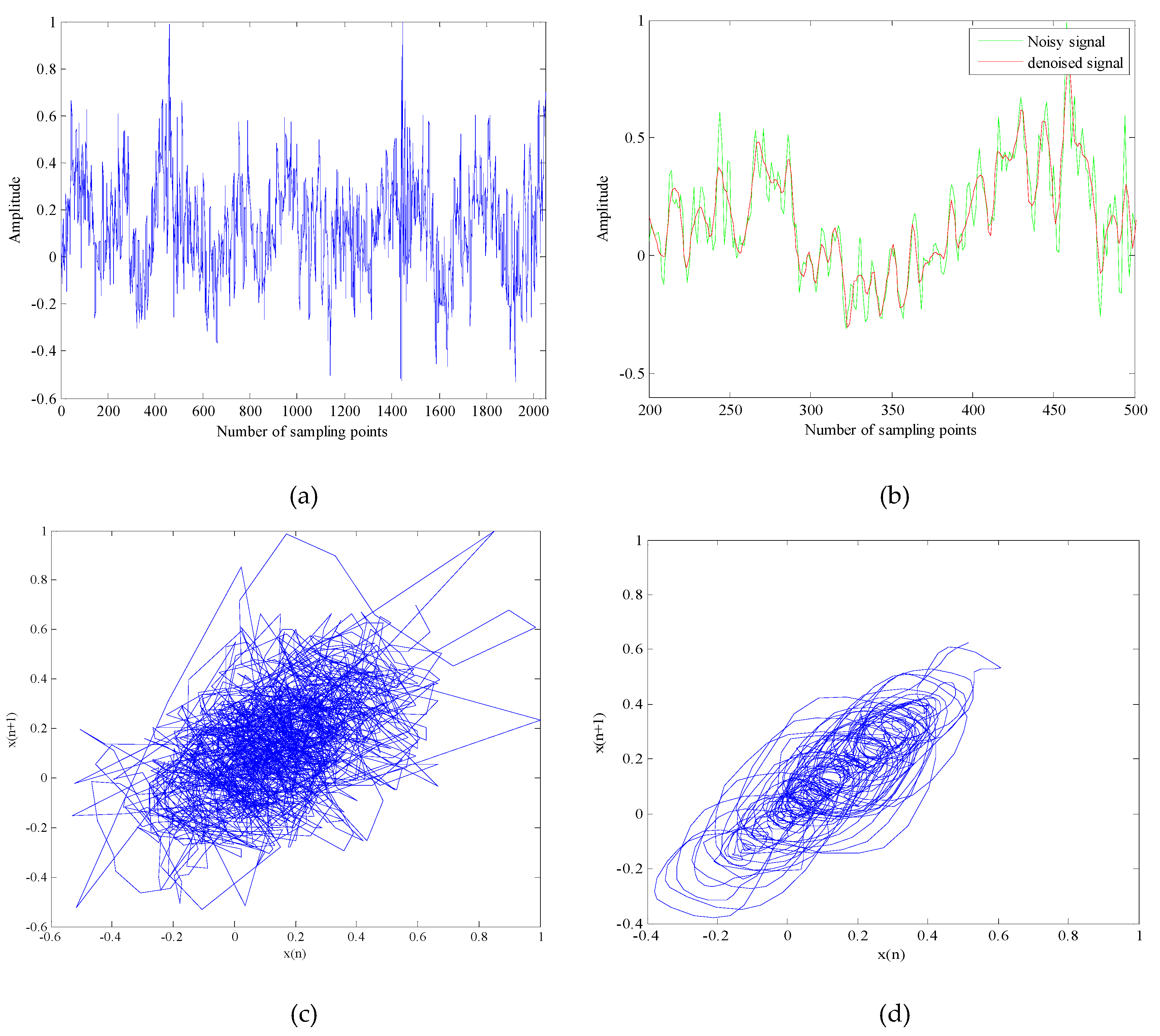
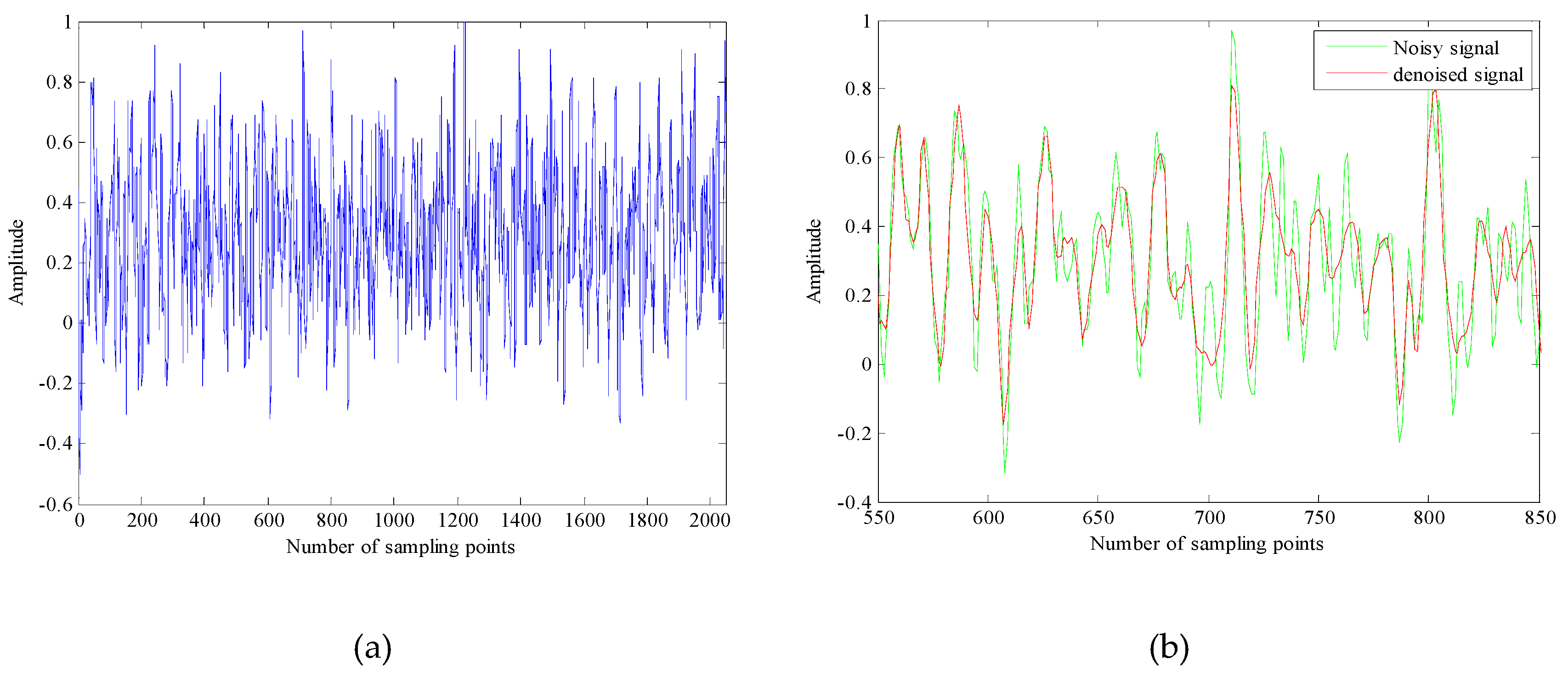
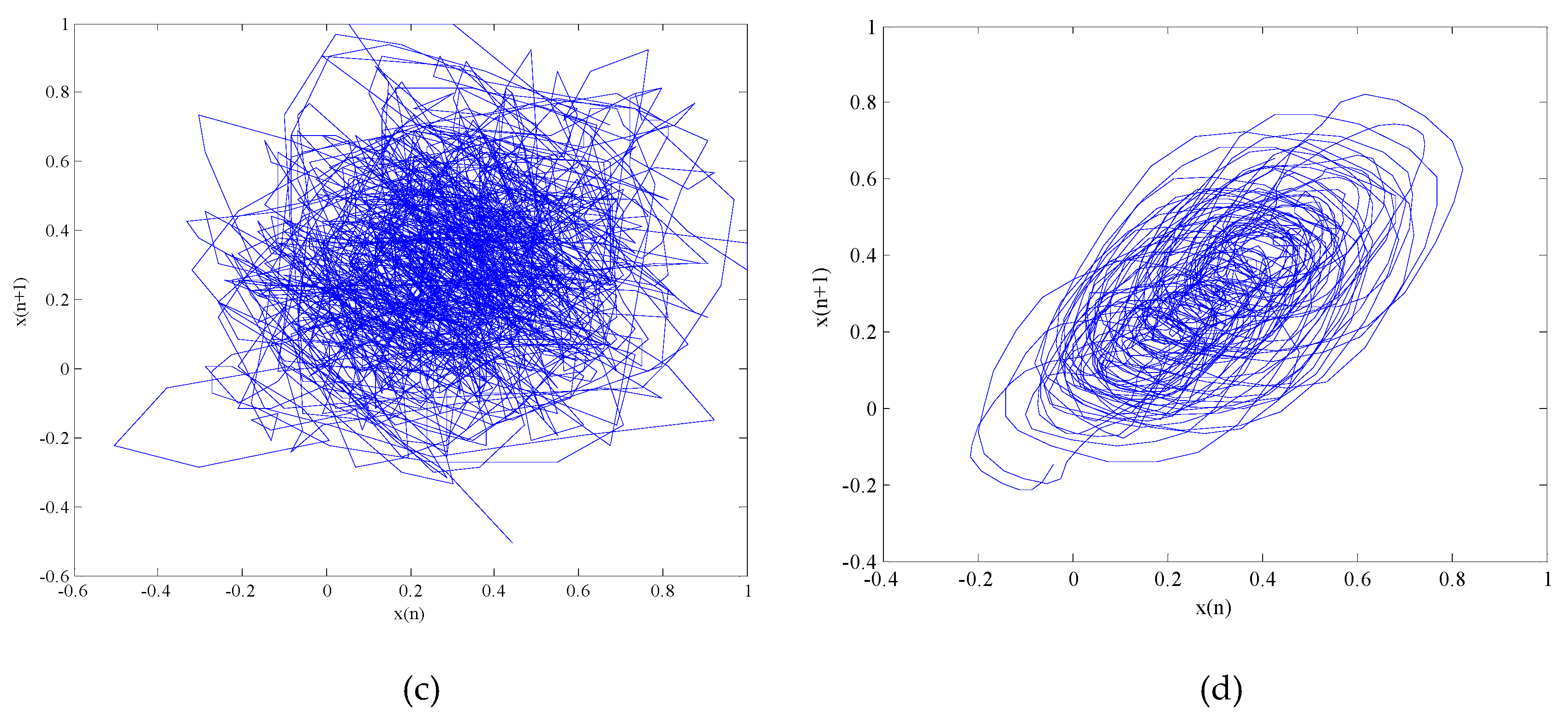
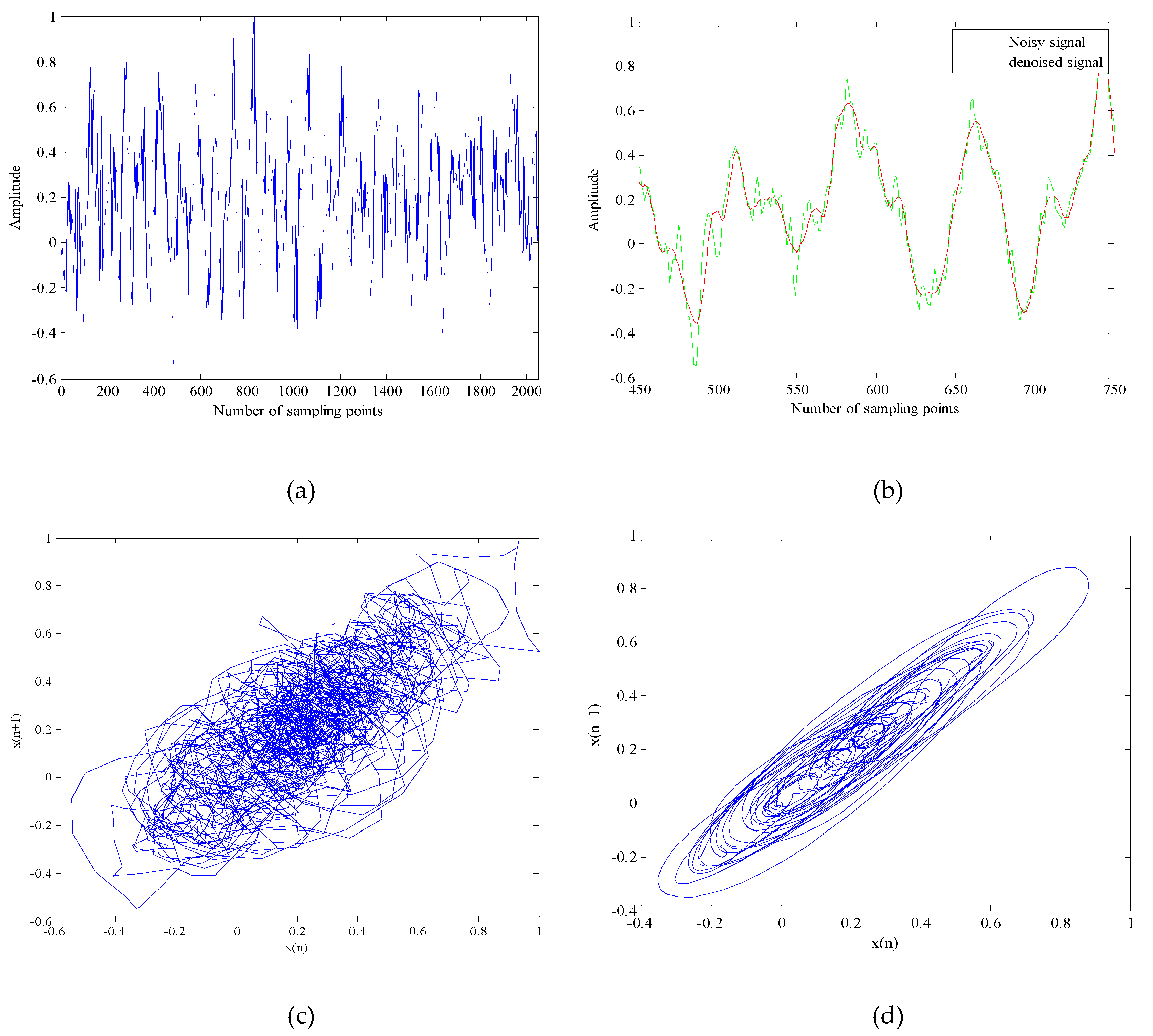
4. The Chaotic Signal Denoising Experiment
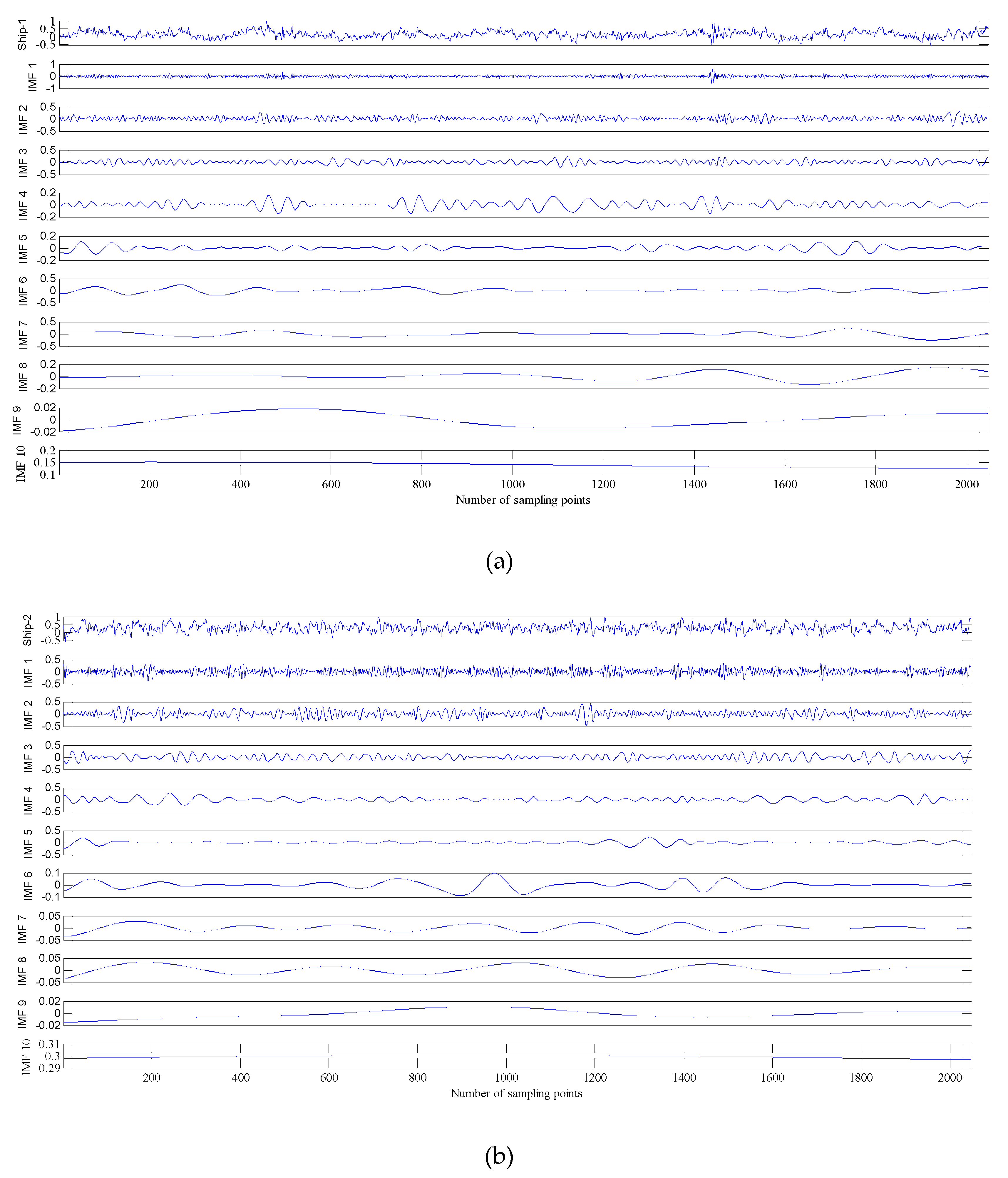
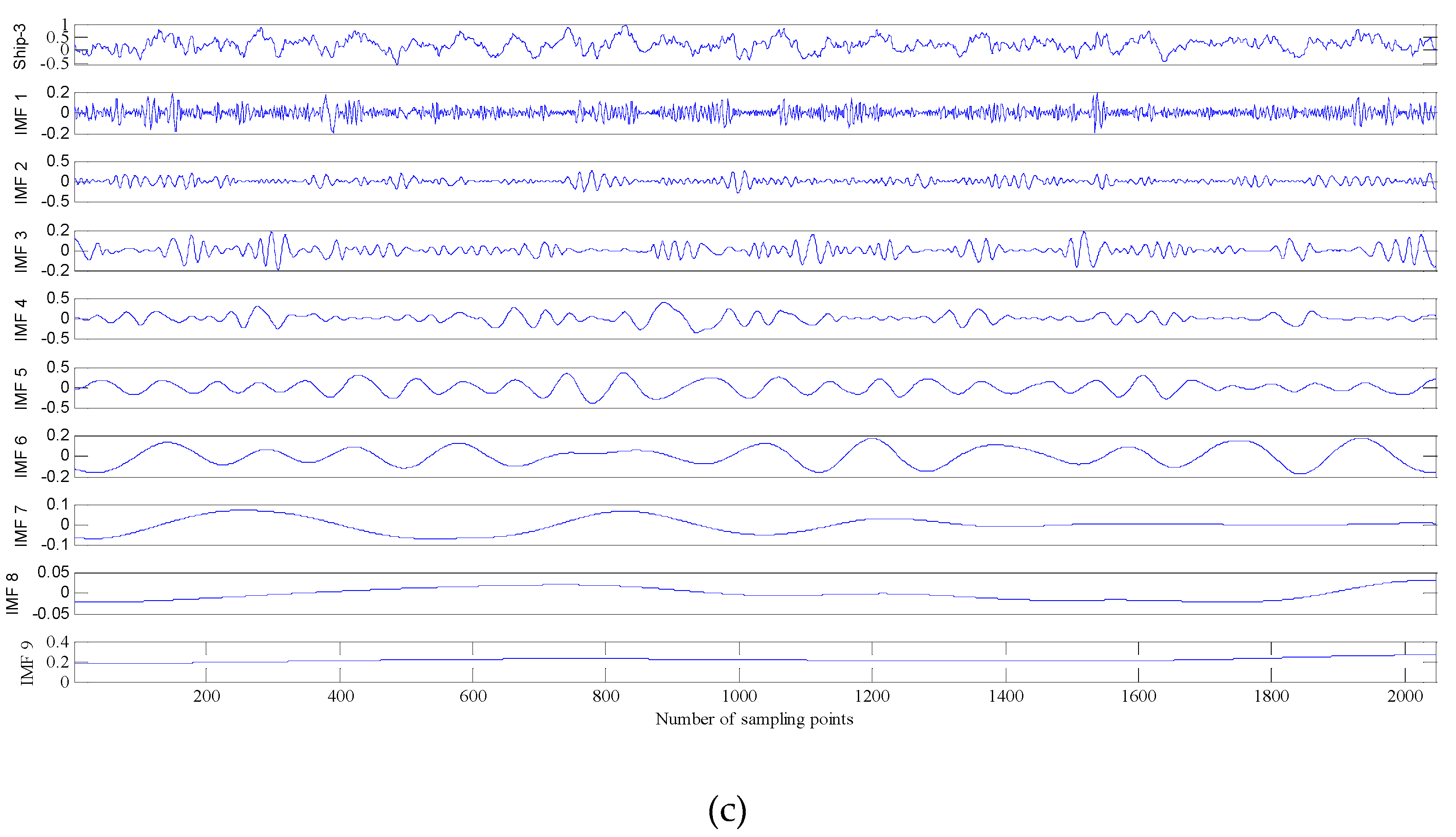
5. The Underwater Acoustic Signals Denoising Experiment
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Yang, H.; Li, Y.A.; Li, G.H. Noise reduction method of ship radiated noise with ensemble empirical mode decomposition of adaptive noise. Noise Control Eng. J. 2016, 64, 230–242. [Google Scholar]
- Li, Y.; Li, Y.; Chen, X.; Yu, J. Denoising and feature extraction algorithms using NPE combined with VMD and their applications in ship-radiated noise. Symmetry 2017, 9, 256. [Google Scholar] [CrossRef]
- Zheng, H.M.; Li, Y.A.; Chen, L. Noise reduction of ship signals based on the local projective algorithm. J. Northwest. Polytech. Univ. 2011, 29, 569–574. [Google Scholar]
- Liu, X.Z.; Wu, M.H.; Liu, M. Underwater acoustic signal noise reduction method based on LCD-ICA. J. Naval Aeronaut. Astronaut. Univ. 2016, 31, 518–522. [Google Scholar]
- Zhou, S.Z.; Zeng, X.Y.; Wang, L. Dynamic threshold orthogonal matching pursuit method for underwater acoustic signal denoising. Tech. Acoust. 2017, 36, 378–382. [Google Scholar]
- Li, Y.X.; Li, Y.A.; Chen, X.; Yu, J. Research on ship-radiated noise denoising using secondary variational mode decomposition and correlation coefficient. Sensors 2018, 18, 48. [Google Scholar]
- Chen, Z.; Li, Y.A.; Liang, H.T.; Yu, J. Hierarchical cosine similarity entropy for feature extraction of ship-radiated noise. Entropy 2018, 20, 425. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shi, H.H.; Zheng, Q.A.; Yen, N.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Damaševičius, R.; Napoli, C.; Sidekerskienė, T.; Woźniak, M. IMF mode demixing in EMD for jitter analysis. J. Comput. Sci. 2017, 22, 240–252. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Lei, R.; Pengjian, S. Fractional empirical mode decomposition energy entropy based on segmentation and its application to the electrocardiograph signal. Nonlinear Dyn. 2018, 94, 1669–1687. [Google Scholar]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Li, J.; Li, Q. Medium term electricity load forecasting based on CEEMDAN, permutation entropy and ESN with leaky integrator neurons. Electr. Mach. Control 2015, 19, 70–80. [Google Scholar]
- Kuai, M.; Cheng, G.; Pang, Y.; Li, Y. Research of planetary gear fault diagnosis based on permutation entropy of CEEMDAN and ANFIS. Sensors 2018, 18, 782. [Google Scholar] [CrossRef] [PubMed]
- Azami, H.; Rostaghi, M.; Fernández, A.; Escudero, J. Dispersion entropy for the analysis of resting-state MEG regularity in Alzheimer’s disease. In Proceedings of the 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 6417–6420. [Google Scholar]
- Zhang, W.; Qu, Z.; Zhang, K.; Mao, W.; Ma, Y.; Fan, X. A combined model based on CEEMDAN and modified flower pollination algorithm for wind speed forecasting. Energ. Convers. Manag. 2017, 136, 439–451. [Google Scholar] [CrossRef]
- He, Z.J.; Zhou, Z.X. Fault diagnosis of roller bearings based on ELMD sample entropy and Boosting-SVM. J. Vib. Shock 2016, 35, 190–195. [Google Scholar]
- Bandt, C.; Pompe, B. Permutation entropy: a natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Li, Y.X.; Li, Y.A.; Chen, Z.; Chen, X. Feature extraction of ship-radiated noise based on permutation entropy of the intrinsic mode function with the highest energy. Entropy 2016, 18, 393. [Google Scholar] [CrossRef]
- Chen, T.; Ju, S.; Yuan, X.; Elhoseny, M.; Ren, F.; Fan, M.; Chen, Z. Emotion recognition using empirical mode decomposition and approximation entropy. Comput. Electr. Eng. 2018, 72, 383–392. [Google Scholar] [CrossRef]
- Morabito, F.C.; Labate, D.; La Foresta, F.; Bramanti, A.; Morabito, G.; Palamara, I. Multivariate multi-scale permutation entropy for complexity analysis of alzheimer’s disease EEG. Entropy 2012, 14, 1186–1202. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Chen, X.; Yu, J. A novel feature extraction method for ship-radiated noise based on variational mode decomposition and multi-scale permutation entropy. Entropy 2017, 19, 342. [Google Scholar]
- Wu, Y.; Shang, P.J.; Li, Y.L. Modified generalized multiscale sample entropy and surrogate data analysis for financial time series. Nonlinear Dyn. 2018, 92, 1335–1350. [Google Scholar] [CrossRef]
- Rostaghi, M.; Azami, H. Dispersion entropy: a measure for time series analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Azami, H.; Rostaghi, M.; Abásolo, D.; Escudero, J. Refined composite multiscale dispersion entropy and its application to biomedical signals. IEEE Trans. Bio-Med. Eng. 2017, 64, 2872–2879. [Google Scholar]
- Li, C.Z.; Zheng, J.D.; Pan, H.Y.; Liu, Q.Y. Fault Diagnosis Method of Rolling Bearing Based on Refined Composite Multiscale Dispersion Entropy and SVM. Available online: http://kns.cnki.net/kcms/detail/42.1294.TH.20180917.1541.002.html (accessed on 17 September 2018).
- Liu, H.; Mi, X.W.; Li, Y.F. Comparison of two new intelligent wind speed forecasting approaches based on Wavelet packet decomposition, complete ensemble empirical mode decomposition with adaptive noise and artificial neural networks. Energ. Conv. Manag. 2018, 155, 188–200. [Google Scholar] [CrossRef]
- Zhu, M.; Duan, Z.S.; Guo, B.L.; Wang, M. Application of CEEMDAN combined with LMS algorithm in signal denoising of bearings. Noise Vib. Control 2018, 38, 144–149. [Google Scholar]
- Li, Y.X.; Li, Y.A.; Chen, X.; Yu, J.; Yang, H.; Wang, L. A new underwater acoustic signal denoising technique based on CEEMDAN, mutual information, permutation entropy and wavelet threshold denoising. Entropy 2018, 20, 563. [Google Scholar] [CrossRef]
- Balasubramanian, K.; Nagaraj, N. Aging and cardiovascular complexity: effect of the length of RR tachograms. PeerJ 2016, 4, e2755. [Google Scholar] [CrossRef]
- Nagaraj, N.; Balasubramanian, K. Dynamical complexity of short and noisy time series. Eur. Phys. J. Spec. Top. 2017, 26, 2191–2204. [Google Scholar] [CrossRef]
- Nagaraj, N.; Balasubramanian, K.; Dey, S. A new complexity measure for time series analysis and classification. Eur. Phys. J. Spec. Top. 2013, 222, 847–860. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Coarse-graining approaches in univariate multiscale sample and dispersion entropy. Entropy 2018, 20, 138. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Improved multiscale permutation entropy for biomedical signal analysis: interpretation and application to electroencephalogram recordings. Biomed. Signal Process. Control 2016, 23, 28–41. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Amplitude- and fluctuation-based dispersion entropy. Entropy 2018, 20, 210. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Tong, S.G.; Cong, F.Y.; Xu, J. Research of feature extraction method based on sparse reconstruction and multiscale dispersion entropy. Appl. Sci. 2018, 8, 888. [Google Scholar] [CrossRef]
- Azami, H.; Kinneylang, E.; Ebied, A.; Fernández, A.; Escudero, J. Multiscale dispersion entropy for the regional analysis of resting-state magnetoencephalogram complexity in alzheimer’s disease. In Proceedings of the 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Seogwipo, Korea, 11–15 July 2017; pp. 3182–3185. [Google Scholar]
- Xiao, M.H.; Wen, K.; Zhang, C.Y.; Zhao, X.; Wei, W.; Wu, D. Research on fault feature extraction method of rolling bearing based on NMD and wavelet threshold denoising. Shock Vib. 2018, 2018, 9495265. [Google Scholar] [CrossRef]
- Figlus, T.; STAŃCZYK, M. Diagnosis of the wear of gears in the gearbox using the wavelet packet transform. Metalurgija 2014, 53, 673–676. [Google Scholar]
- Wang, J.L.; Wei, Q.X.; Zhao, L.Q.; Yu, T.; Han, R. An improved empirical mode decomposition method using second generation wavelets interpolation. Digit. Signal Process. 2018, 79, 164–174. [Google Scholar] [CrossRef]
- Wang, L.B.; Zhang, X.D.; Wang, X.L. Chaotic signal denoising method based on independent component analysis and empirical mode decomposition. Acta Phys. Sin 2013, 62, 050201. [Google Scholar]
- Rosenstein, M.T.; Collins, J.J.; Luca, C.J.D. A practical method for calculating largest Lyapunov exponents from small data set. Phys. D Nonlinear Phenomen. 1993, 65, 117–134. [Google Scholar] [CrossRef]
- Li, Y.B.; Xie, S.Y.; Zhao, J.; Liu, C.; Xie, X.Z. Improved GP algorithm for the analysis of sleep stages based on grey model. Scienceasia 2017, 43, 312–318. [Google Scholar] [CrossRef][Green Version]
| SNR/dB | EMD_MSE_WSTD | EEMD_DE_WSTD | CEEMDAN_ETC_RCMDE_WSTD | |||
|---|---|---|---|---|---|---|
| SNR/dB | RMSE | SNR/dB | RMSE | SNR/dB | RMSE | |
| −10 | 2.4455 | 0.9591 | 3.7687 | 0.7750 | 4.4430 | 0.6691 |
| 0 | 8.5354 | 0.7234 | 11.0066 | 0.5883 | 13.1377 | 0.4850 |
| 10 | 16.3106 | 0.4117 | 18.8902 | 0.3119 | 22.1273 | 0.2556 |
| 20 | 24.7166 | 0.2448 | 26.5438 | 0.1756 | 31.4315 | 0.0807 |
| Signals | Maximum Lyapunov Exponent | Correlation Dimension | Noise Intensity |
|---|---|---|---|
| Chens signal (SNR = 10 dB) | 0.3487 | 2.4369 | 0.2538 |
| EMD_MSE_WSTD | 0.2973 | 2.1702 | 0.2071 |
| EEMD_DE_WSTD | 0.2142 | 1.8960 | 0.1875 |
| CEEMDAN_ETC_RCMDE_WSTD | 0.1418 | 1.4542 | 0.1442 |
| Underwater Acoustic Signals | Noise IMFs | Noise-Dominant IMFs | Real Signal-Dominant IMFs | Real IMFs |
|---|---|---|---|---|
| Ship-1 | IMF1 | IMF2, IMF3 | IMF4, IMF5, IMF6, IMF7 | IMF8, IMF9, IMF10 |
| Ship-2 | IMF1 | IMF2, IMF3, IMF4 | IMF5, IMF6, IMF7, IMF8 | IMF9, IMF10 |
| Ship-3 | IMF1 | IMF2, IMF3 | IMF4, IMF5, IMF6 | IMF7, IMF8, IMF9, IMF10 |
| Underwater Acoustic Signals | Parameters | Before Noise Reduction | EMD_MSE_WSTD | EEMD_DE_WSTD | CEEMDAN_ETC_RCMDE_WSTD |
|---|---|---|---|---|---|
| Ship-1 | Correlation Dimension | 1.7821 | 1.6698 | 1.5356 | 1.4906 |
| Noise Intensity | 0.2250 | 0.1401 | 0.0977 | 0.0703 | |
| PE | 1.5525 | 1.0854 | 0.8366 | 0.6758 | |
| RCMDE | 2.5232 | 1.2350 | 0.9800 | 0.4492 | |
| Ship-2 | Correlation Dimension | 1.6751 | 1.5405 | 1.3438 | 1.2004 |
| Noise Intensity | 0.2354 | 0.1380 | 0.1037 | 0.0893 | |
| PE | 1.6001 | 0.9055 | 0.7686 | 0.5359 | |
| RCMDE | 2.3280 | 1.2022 | 0.6991 | 0.3658 | |
| Ship-3 | Correlation Dimension | 1.6869 | 1.4772 | 1.2355 | 1.1890 |
| Noise Intensity | 0.2512 | 0.1545 | 0.1221 | 0.0927 | |
| PE | 1.5466 | 0.9495 | 0.6792 | 0.5004 | |
| RCMDE | 2.1359 | 1.0304 | 0.6751 | 0.3047 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Guan, Q.; Yang, H. Noise Reduction Method of Underwater Acoustic Signals Based on CEEMDAN, Effort-To-Compress Complexity, Refined Composite Multiscale Dispersion Entropy and Wavelet Threshold Denoising. Entropy 2019, 21, 11. https://doi.org/10.3390/e21010011
Li G, Guan Q, Yang H. Noise Reduction Method of Underwater Acoustic Signals Based on CEEMDAN, Effort-To-Compress Complexity, Refined Composite Multiscale Dispersion Entropy and Wavelet Threshold Denoising. Entropy. 2019; 21(1):11. https://doi.org/10.3390/e21010011
Chicago/Turabian StyleLi, Guohui, Qianru Guan, and Hong Yang. 2019. "Noise Reduction Method of Underwater Acoustic Signals Based on CEEMDAN, Effort-To-Compress Complexity, Refined Composite Multiscale Dispersion Entropy and Wavelet Threshold Denoising" Entropy 21, no. 1: 11. https://doi.org/10.3390/e21010011
APA StyleLi, G., Guan, Q., & Yang, H. (2019). Noise Reduction Method of Underwater Acoustic Signals Based on CEEMDAN, Effort-To-Compress Complexity, Refined Composite Multiscale Dispersion Entropy and Wavelet Threshold Denoising. Entropy, 21(1), 11. https://doi.org/10.3390/e21010011





