Reply to “Comment on ‘Glass Transition, Crystallization of Glass-Forming Melts, and Entropy”’ by Zanotto and Mauro
Abstract
1. Introduction
2. Main Topics of Controversy
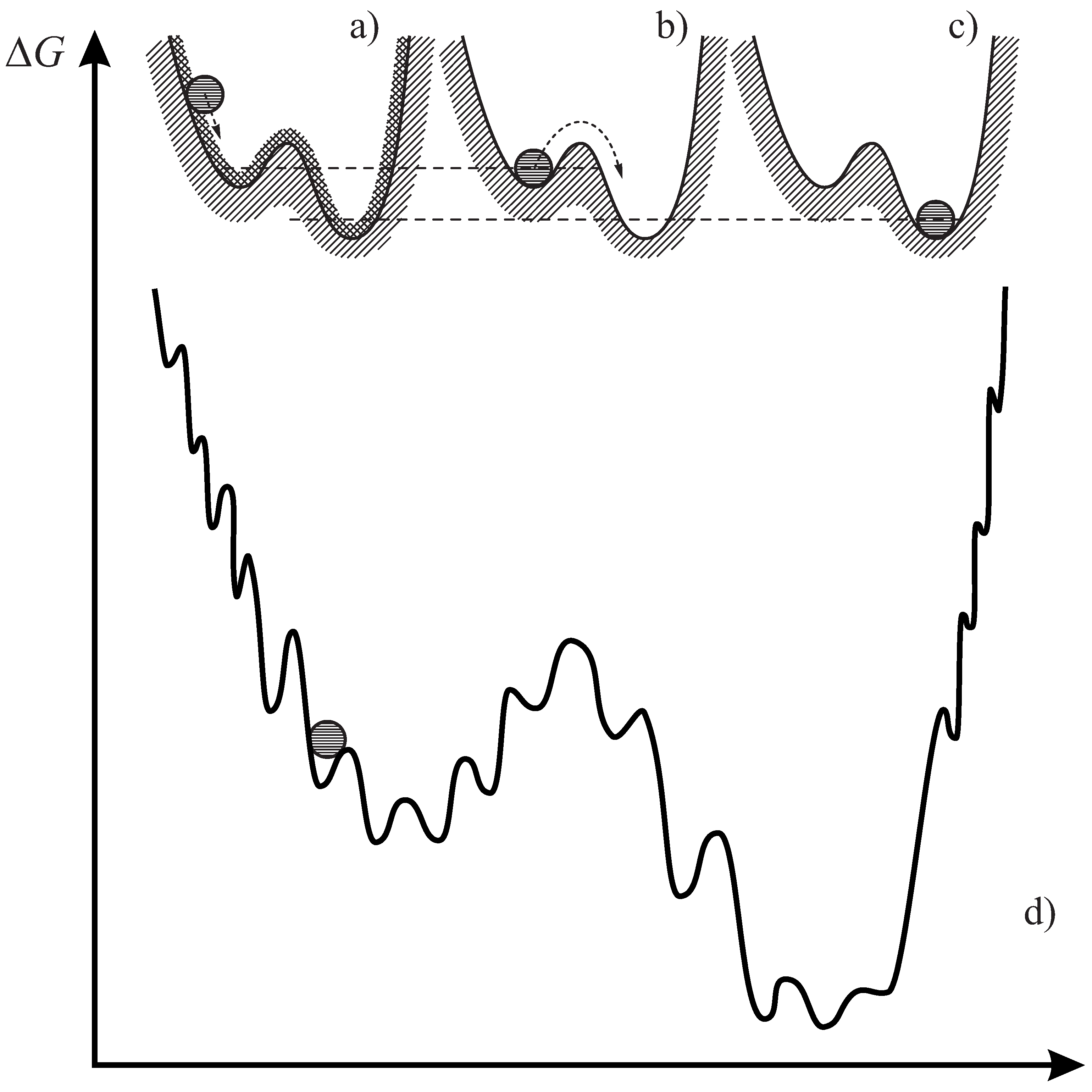
2.1. Definition of Glass and the Glass Transition
2.2. Greek Philosophy and Kinetic Criteria of Glass Formation
2.3. Flow vs. Relaxation
2.4. Temperature Dependence of the Viscosity
2.5. Crystallization
2.6. Broken Ergodicity and Entropy
3. Final Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Schmelzer, J.W.P.; Tropin, T.V. Glass transition, crystallization of glass-forming melts, and entropy. Entropy 2018, 20, 103. [Google Scholar] [CrossRef]
- Zanotto, E.D.; Mauro, J.C. Comment on “Glass transition, crystallization of glass-forming melts, and entropy” by Schmelzer and Tropin. [Entropy 20, 103 (2018)]. Entropy 2018. present volume. [Google Scholar]
- Zanotto, E.D.; Mauro, J.C. The glassy state of matter: Its definition and ultimate fate. J. Non-Cryst. Solids 2017, 471, 490–495. [Google Scholar] [CrossRef]
- Gutzow, I.S.; Schmelzer, J.W.P. The Vitreous State: Thermodynamics, Structure, Rheology, and Crystallization, 1st ed.; Springer: Berlin, Germany, 1995; 2nd enlarged ed.; Springer: Heidelberg, Germany, 2013. [Google Scholar]
- Androsch, R.; Schick, C.; Schmelzer, J.W.P. Sequence of enthalpy relaxation, homogeneous nucleation, and crystal growth in glassy Polyamide 6. Eur. Polym. J. 2014, 53, 100–108. [Google Scholar] [CrossRef]
- Androsch, R.; Zhuravlev, E.; Schmelzer, J.W.P.; Schick, C. Relaxation and crystal nucleation in polymer glasses. Eur. Polym. J. 2018, 102, 195–208. [Google Scholar] [CrossRef]
- Kelton, K.F.; Greer, A.L. Nucleation in Condensed Matter: Applications in Materials and Biology; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Schmelzer, J.W.P.; Schick, C. Dependence of Crystallization Processes of Glass-forming Melts on Prehistory: A Theoretical Approach to a Quantitative Treatment. Phys. Chem. Glasses Eur. J. Glass Sci. Technol. 2012, B53, 99–106. [Google Scholar]
- Schmelzer, J.W.P.; Gutzow, I.S. Glasses and the Glass Transition; WILEY-VCH: Berlin/Weinheim, Germany, 2011. [Google Scholar]
- Goldstein, M. Viscous Liquids and the Glass Transition: A Potential Energy Barrier Picture. J. Chem. Phys. 1969, 51, 3728–3739. [Google Scholar] [CrossRef]
- Davies, R.O.; Jones, G.O. Thermodynamic and kinetic properties of glasses. Adv. Phys. 1953, 2, 370–410. [Google Scholar] [CrossRef]
- Gutzow, I.; Grigorova, T.; Avramov, I.; Schmelzer, J.W.P. Generic phenomenology of vitrification and relaxation and the Kohlrausch and Maxwell equations. Phys. Chem. Glasses 2002, 43C, 477–486. [Google Scholar]
- Nemilov, S.V.; Johari, G.P. A mechanism for spontaneous relaxation of glass at room temperature. Philos. Mag. 2003, 83, 3117–3132. [Google Scholar] [CrossRef]
- Golubkov, V.V.; Porai-Koshitz, E.A. Thermal expansion and glass-transition of borate melts. Glass Phys. Chem. 1991, 17, 796–809. [Google Scholar]
- Bokov, N.A.; Golubkov, V.V. Temperature Dependences of the Density of Borate Glasses in Equilibrium States at Temperatures below the Glass Transition Point. Glass Phys. Chem. 2008, 34, 527–533. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, B.A.; Bai, H.Y.; Wang, W.H. Evolution of hidden localized flow during glass-to-liquid transition in metallic glass. Nat. Commun. 2014, 5, 5823. [Google Scholar] [CrossRef] [PubMed]
- Perez-De-Eulate, N.G.; Cangialosi, D. Double Mechanism for Structural Recovery of Polystyrene Nanospheres. Macromolecules 2018, 51, 3299–3307. [Google Scholar] [CrossRef]
- Ediger, M.D.; Harrowell, P. Perspective: Supercooled liquids and glasses. J. Chem. Phys. 2012, 137, 080901. [Google Scholar] [CrossRef] [PubMed]
- Reiner, M. The Deborah number. Phys. Today 1964, 17, 62. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P. Kinetic criteria of glass formation and the pressure dependence of the glass transition temperature. J. Chem. Phys. 2012, 136, 074512. [Google Scholar] [CrossRef] [PubMed]
- Zanotto, E.D. Do cathedral glasses flow? Am. J. Phys. 1998, 66, 392–395. [Google Scholar] [CrossRef]
- Zanotto, E.D.; Gupta, P.K. Do cathedral glasses flow? Additional remarks. Am. J. Phys. 1999, 67, 260–262. [Google Scholar] [CrossRef]
- Ediger, M.D.; Angell, C.A.; Nagel, S.R. Supercooled Liquids and Glasses. J. Phys. Chem. 1996, 100, 13200–13212. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Tropin, T.V. Kinetic criteria of glass-formation, pressure dependence of the glass-transition temperature, and the Prigogine-Defay ratio. J. Non-Cryst. Solids 2015, 407, 170–178. [Google Scholar] [CrossRef]
- Tanaka, H. Relation between Thermodynamics and Kinetics of Glass-Forming Liquids. Phys. Rev. Lett. 2003, 90, 055701. [Google Scholar] [CrossRef] [PubMed]
- Gallino, I.; Schroers, J.; Busch, R. Kinetic and thermodynamic studies of the fragility of bulk metallic glass forming liquids. J. Appl. Phys. 2010, 108, 063501. [Google Scholar] [CrossRef]
- Martinez-Garcia, J.C.; Rzoska, S.J.; Drzozd-Rzoska, A.; Martinez-Garcia, J. A universal description of ultraslow glass dynamics. Nat. Commun. 2013, 4, 1823. [Google Scholar] [CrossRef] [PubMed]
- Mauro, J.C.; Yue, Y.; Ellison, A.J.; Gupta, P.K.; Allan, D.C. Viscosity of glass-forming liquids. PNAS 2009, 106, 19780–19784. [Google Scholar] [CrossRef] [PubMed]
- Waterton, S.C. The viscosity-temperature relationship and some inferences on the nature of molten and of plastic glass. J. Soc. Glass Technol. 1932, 16, 244–249. [Google Scholar]
- Martinez-Garcia, J.C.; Rzoska, S.J.; Drzozd-Rzoska, A.; Martinez-Garcia, J.; Mauro, J.C. Divergent dynamics and the Kauzmann temperature in glass forming systems. Sci. Rep. 2014, 4, 5160. [Google Scholar] [CrossRef] [PubMed]
- Kauzmann, W. The Nature of the Glassy State and the Behavior of Liquids at Low Temperatures. Chem. Rev. 1948, 43, 219–256. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Abyzov, A.S.; Fokin, V.M.; Schick, C. Kauzmann paradox and the crystallization of glass-forming melts. J. Non-Cryst. Solids 2017, in press. [Google Scholar] [CrossRef]
- Pedersen, U.R.; Schroeder, T.B.; Dyre, J.C. Phase Diagram of Kob-Andersen-Type Binary Lennard-Jones Mixtures. Phys. Rev. Lett. 2018, 120, 165501. [Google Scholar] [CrossRef] [PubMed]
- Berthier, L.; Ediger, M.D. Facets of glass physics. Phys. Today 2016, 69, 41–46. [Google Scholar] [CrossRef]
- Stevenson, J.D.; Wolynes, P.G. The Ultimate Fate of Supercooled Liquids. J. Phys. Chem. 2011, A115, 3713–3719. [Google Scholar] [CrossRef] [PubMed]
- Fokin, V.M.; Yuritsyn, N.S.; Zanotto, E.D.; Schmelzer, J.W.P. Homogeneous crystal nucleation in silicate glasses: A 40 years perspective. J. Non-Cryst. Solids 2006, 352, 2681–2714. [Google Scholar] [CrossRef]
- Zanotto, E.D. Fundamentals of Crystal Nucleation in Glasses, Advanced School on Glasses and Glass-Ceramics, São Carlos, Brazil, 1–9 August 2015. Available online: https://www.youtube.com/watch?v=k4StIrP1CsA (accessed on 1 September 2018).
- Johari, G.P. On resolving the statistical and calorimetric entropies of glass and non-crystalline solids, and the residual entropy problem. Thermochim. Acta 2010, 500, 111–118. [Google Scholar] [CrossRef]
- Mauro, J.C.; Loucks, R.J.; Sabyasachi, S. Heat capacity, enthalpy fluctuations, and configurational entropy in broken ergodic systems. J. Chem. Phys. 2010, 133, 164503. [Google Scholar] [CrossRef] [PubMed]
- Johari, G.P. Comment on “Heat capacity, enthalpy fluctuations, and configurational entropy in broken ergodic systems”. [J. Chem. Phys. 133, 164503 (2010)]. J. Chem. Phys. 2011, 134, 147101. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, M. On the reality of residual entropies of glasses and disordered crystals. J. Chem. Phys. 2008, 128, 154510. [Google Scholar] [CrossRef] [PubMed]
- Gujrati, P.D. Hierarchy of Relaxation Times and Residual Entropy: A Non-equilibrium Approach. Entropy 2018, 20, 149. [Google Scholar] [CrossRef]
- Nemilov, S.V. On the Possibility of Calculating Entropy, Free Energy, and Enthalpy of Vitreous Substances. Entropy 2018, 20, 187. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmelzer, J.W.P.; Tropin, T.V. Reply to “Comment on ‘Glass Transition, Crystallization of Glass-Forming Melts, and Entropy”’ by Zanotto and Mauro. Entropy 2018, 20, 704. https://doi.org/10.3390/e20090704
Schmelzer JWP, Tropin TV. Reply to “Comment on ‘Glass Transition, Crystallization of Glass-Forming Melts, and Entropy”’ by Zanotto and Mauro. Entropy. 2018; 20(9):704. https://doi.org/10.3390/e20090704
Chicago/Turabian StyleSchmelzer, Jürn W. P., and Timur V. Tropin. 2018. "Reply to “Comment on ‘Glass Transition, Crystallization of Glass-Forming Melts, and Entropy”’ by Zanotto and Mauro" Entropy 20, no. 9: 704. https://doi.org/10.3390/e20090704
APA StyleSchmelzer, J. W. P., & Tropin, T. V. (2018). Reply to “Comment on ‘Glass Transition, Crystallization of Glass-Forming Melts, and Entropy”’ by Zanotto and Mauro. Entropy, 20(9), 704. https://doi.org/10.3390/e20090704





