On Differences between Deterministic and Stochastic Models of Chemical Reactions: Schlögl Solved with ZI-Closure
Abstract
1. Background
2. Zero-Information Closure Scheme
3. Results
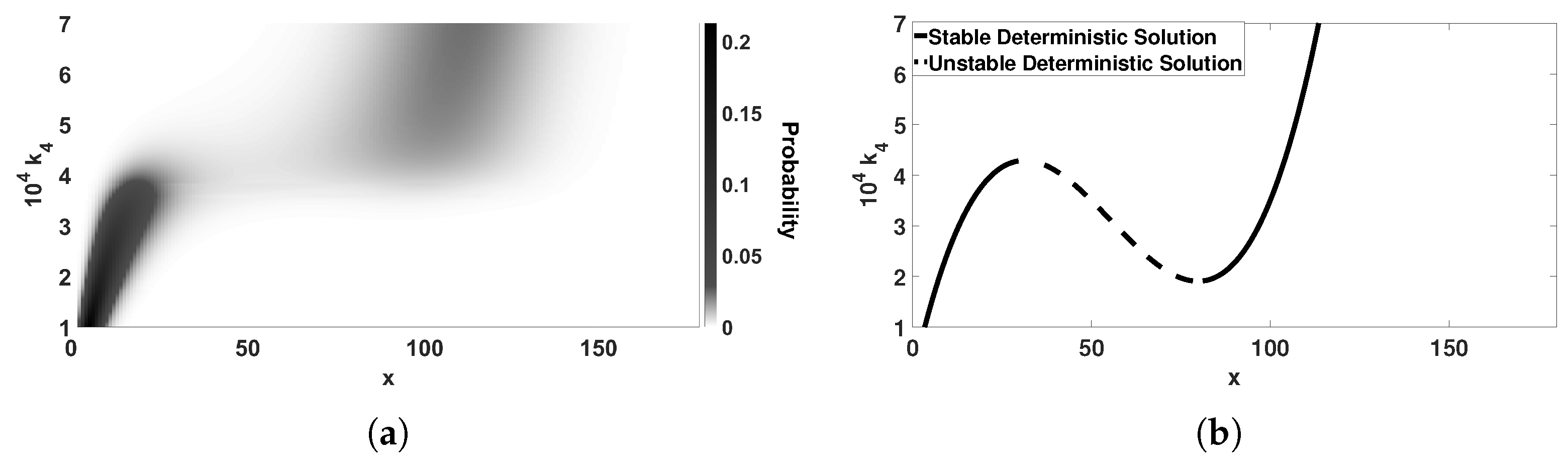
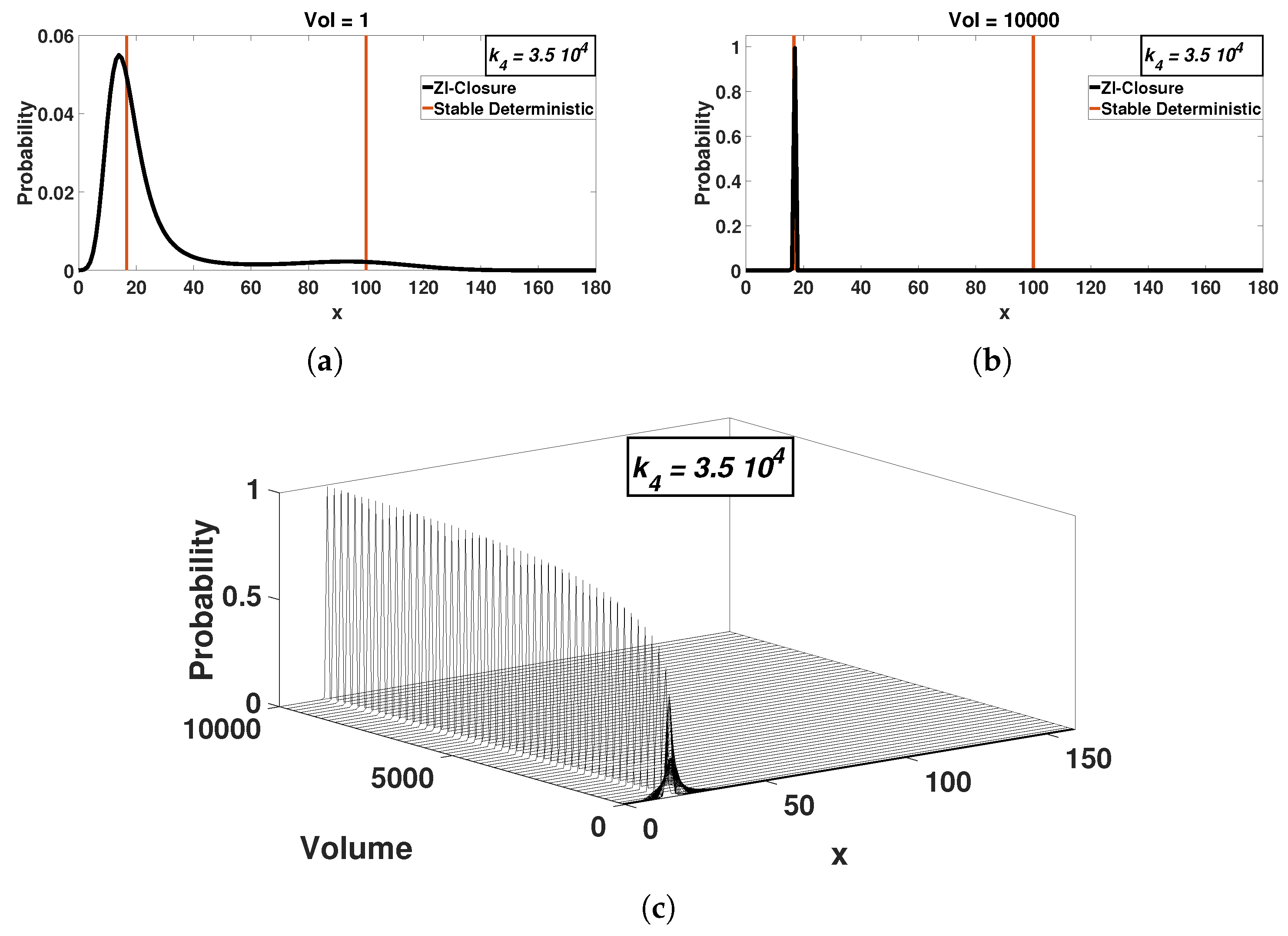
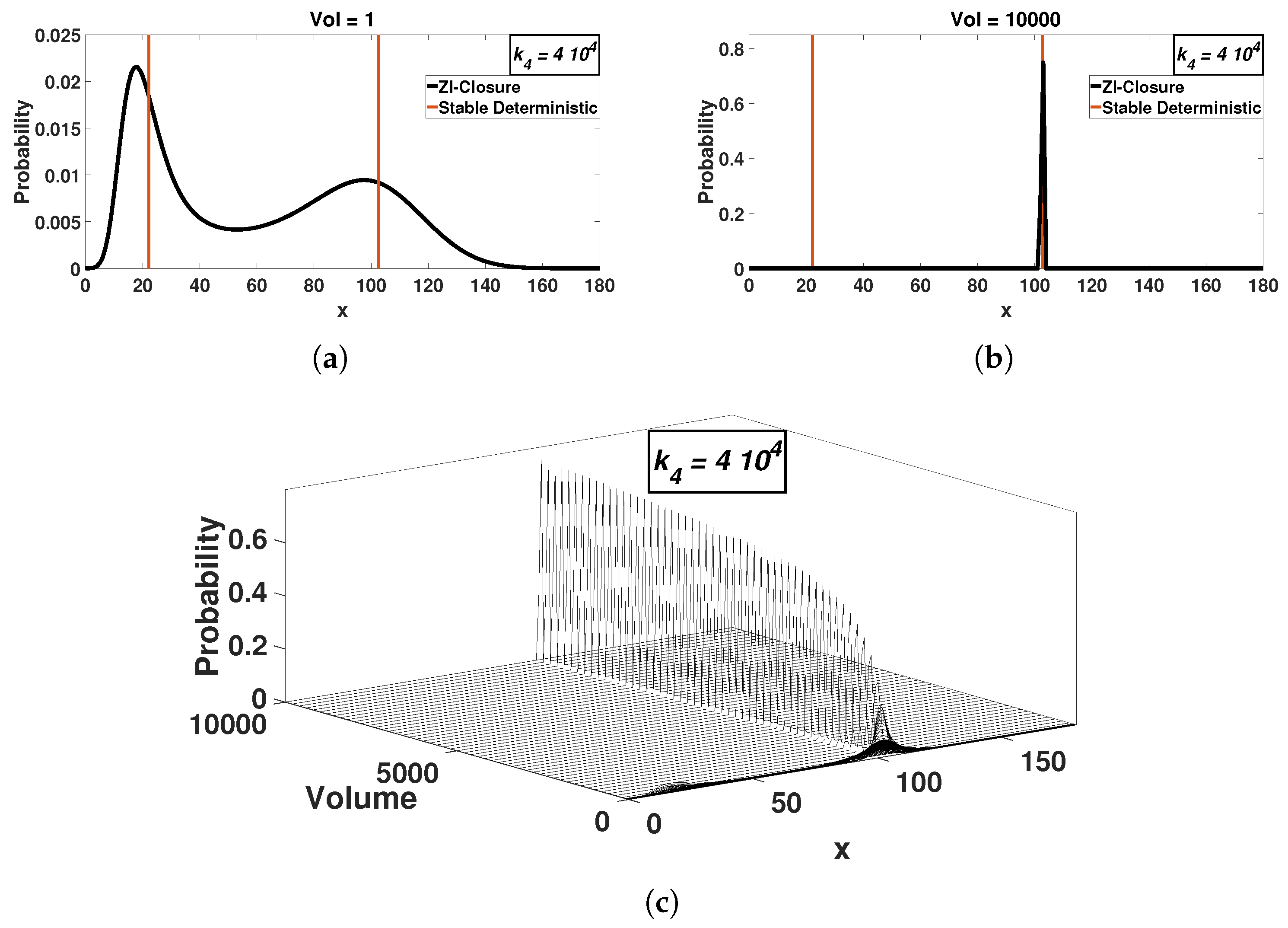
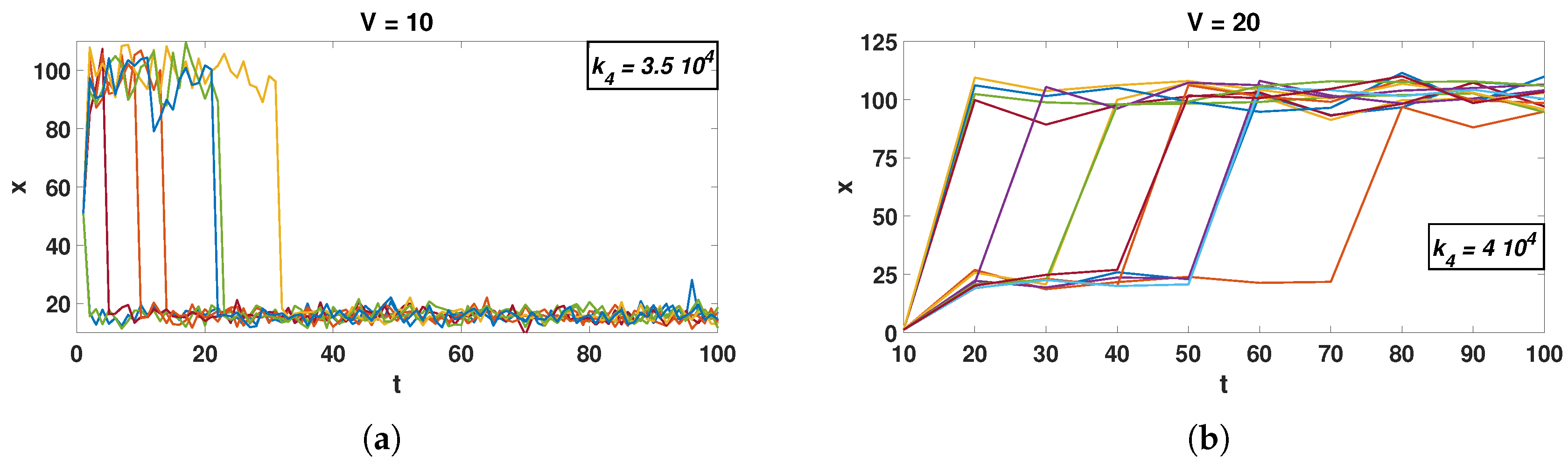
3.1. Bimodality Collapse for Mesoscopic Systems
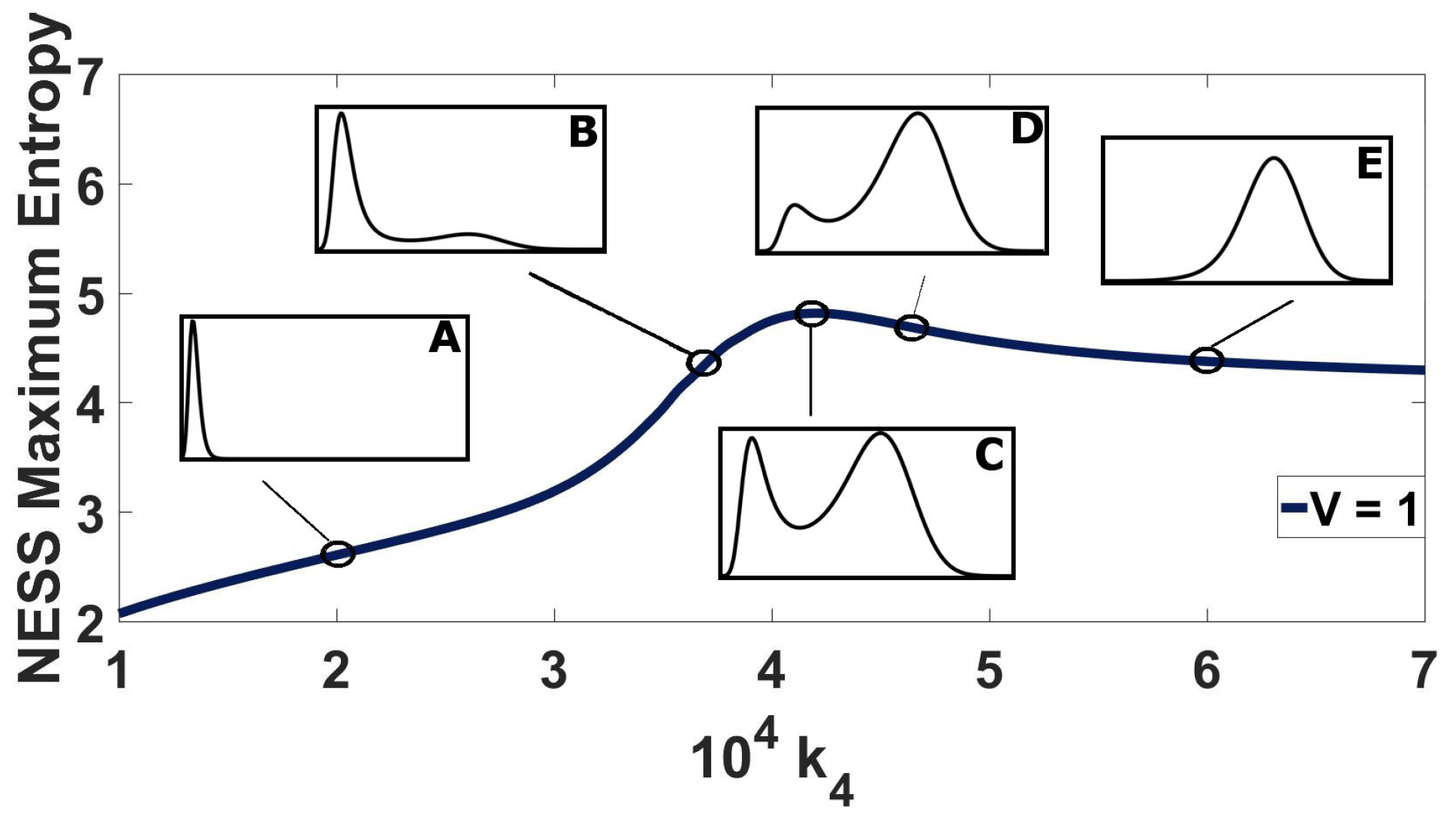
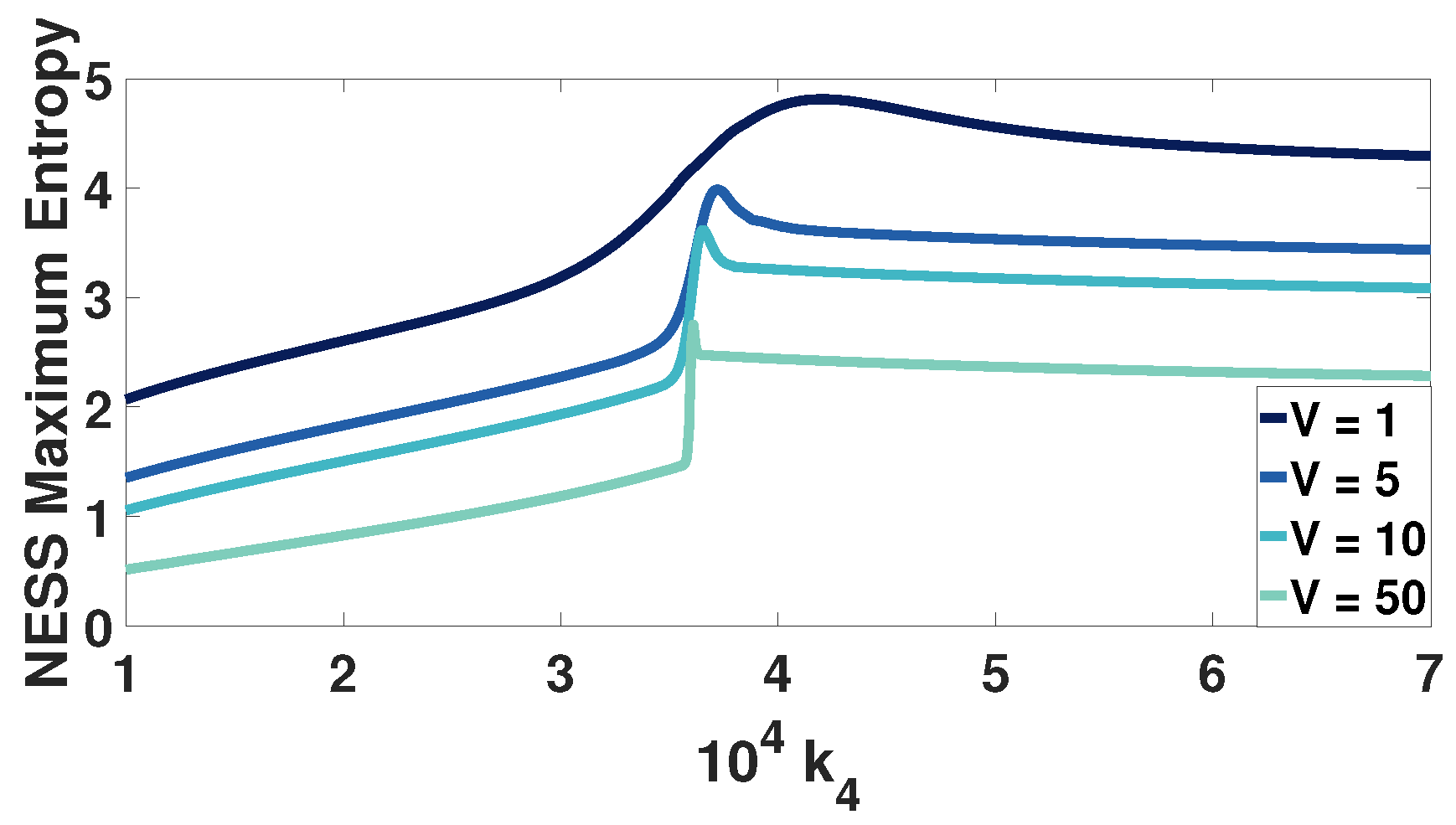
3.2. Entropy of NESS Systems
4. Discussion
5. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
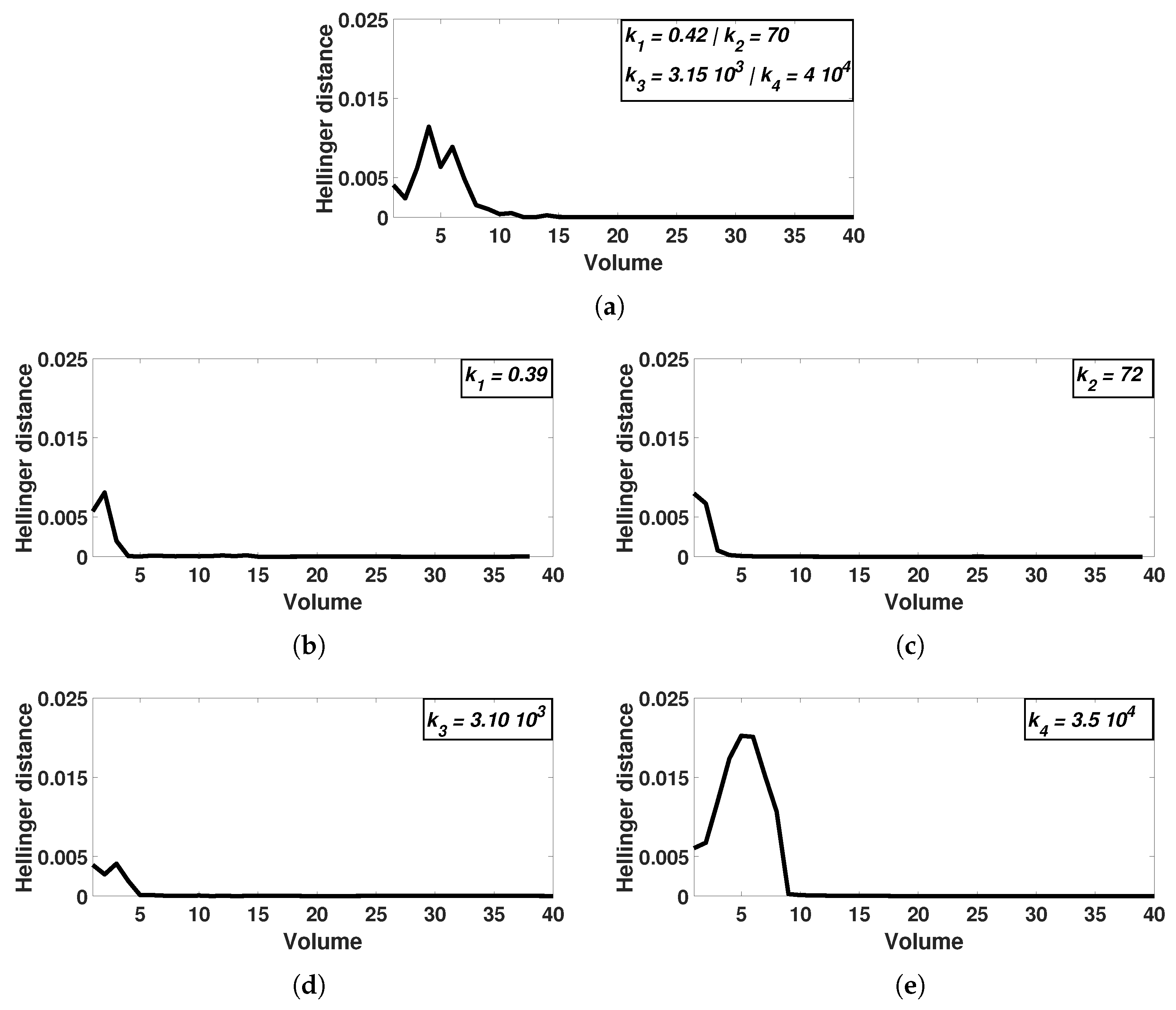
Appendix A. ZI-Closure Accuracy
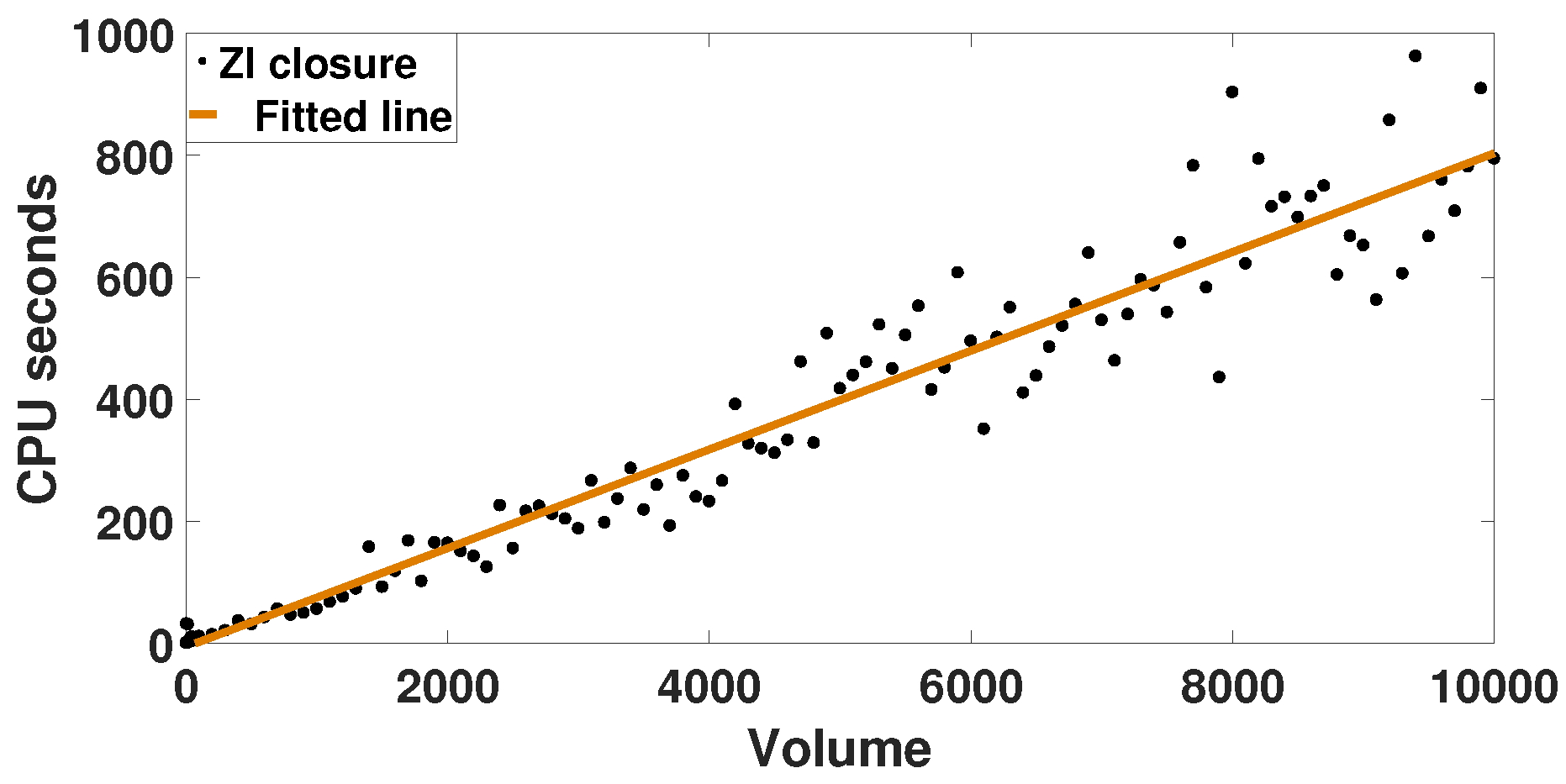
| Volume | 1 | 10 | 20 | 30 | 40 | 44 |
|---|---|---|---|---|---|---|
References
- Voit, E.O.; Martens, H.A.; Omholt, S.W. 150 Years of the Mass Action Law. PLoS Comput. Biol. 2015, 11, e1004012. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, D.T. Markov Processes, an Introduction for Physical Scientists; Academic Press Inc.: San Diego, CA, USA, 1992. [Google Scholar]
- McQuarrie, D. Stochastic approach to chemical kinetics. J. Appl. Probab. 1967, 4, 413–478. [Google Scholar] [CrossRef]
- Kurtz, T.G. Limit theorems and diffusion approximations for density dependent Markov chains. Math. Prog. Stud. 1976, 5, 67–78. [Google Scholar]
- Kurtz, T.G. Strong approximation theorems for density dependent Markov chains. Stoch. Process. Appl. 1978, 6, 223–240. [Google Scholar] [CrossRef]
- Malek Mansour, M.; Van Den Broeck, C.; Nicolis, G.; Turner, J.W. Asymptotic properties of Markovian master equations. Ann. Phys. 1981, 131, 283–313. [Google Scholar] [CrossRef]
- Leung, H.K. Metastable states in a nonlinear stochastic model. Phys. Rev. A 1984, 30, 2609. [Google Scholar] [CrossRef]
- Vellela, M.; Qian, H. A quasistationary analysis of a stochastic chemical reaction: Keizer’s paradox. Bull. Math. Biol. 2007, 69, 1727–1746. [Google Scholar] [CrossRef] [PubMed]
- Ebeling, W.; Schimansky-Geier, L. Stochastic dynamics of a bistable reaction system. Physica A 1979, 98, 587–600. [Google Scholar] [CrossRef]
- Van Kampen, N.G. Stochastic Processes in Physics and Chemistry; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Schlögl, F. On thermodynamics near a steady state. Z. Phys. 1971, 248, 446–458. [Google Scholar] [CrossRef]
- Nicolis, G.; Turner, J.W. Effects of fluctuations on bifurcation phenomena. Ann. N. Y. Acad. Sci. 1979, 316, 251–262. [Google Scholar] [CrossRef]
- Matheson, I.; Walls, D.F.; Gardiner, C.W. Stochastic models of first-order nonequilibrium phase transitions in chemical reactions. J. Stat. Phys. 1975, 12, 21–34. [Google Scholar] [CrossRef]
- Smadbeck, P.; Kaznessis, Y.N. A closure scheme for chemical master equations. Proc. Natl. Acad. Sci. USA 2013, 110, 14261–14265. [Google Scholar] [CrossRef] [PubMed]
- Ge, H.; Qian, H. Physical origins of entropy production, free energy dissipation, and their mathematical representations. Phys. Rev. E 2010, 81, 051133. [Google Scholar] [CrossRef] [PubMed]
- Ross, J.; Fernandez Villaverde, A. Thermodynamics and Fluctuations Far From Equilibrium. Entropy 2010, 12, 2199–2243. [Google Scholar] [CrossRef]
- Sakaguchi, H. Creation and Reproduction of Model Cells with Semipermeable Membrane. J. R. Soc. Jpn. 2009, 78, 014801. [Google Scholar] [CrossRef]
- Suchorski, Y.; Wrobel, R.; Becker, S. CO Oxidation on a CeOx/Pt(111) Inverse Model Catalyst Surface: Catalytic Promotion and Tuning of Kinetic Phase Diagrams. J. Phys. Chem. C 2008, 112, 20012–20017. [Google Scholar] [CrossRef]
- Ross, J. Thermodynamics and Fluctuations Far from Equilibrium; Springer Series in Chemical Physics; Springer: New York, NY, USA, 2008. [Google Scholar]
- Zhu, P. Associated relaxation time and intensity correlation function of a bistable system driven by cross-correlation additive and multiplicative coloured noise sources. Eur. Phys. J. B 2007, 55, 447–452. [Google Scholar] [CrossRef]
- Gaspard, P. Hamiltonian dynamics, nanosystems, and nonequilibrium statistical mechanics. Physica A 2006, 369, 201–246. [Google Scholar] [CrossRef]
- Leda, M.; Kawczynski, A. On the variety of traveling fronts in one-variable multistable reaction-diffusion systems. J. Phys. Chem. A 2006, 110, 7882–7887. [Google Scholar] [CrossRef] [PubMed]
- Berdau, M.; Yelenin, G.G.; Karpowicz, A.; Ehsasi, M.; Christmann, K.; Block, J.H. Macroscopic and mesoscopic characterization of a bistable reaction system:CO oxidation on Pt(111) surface. J. Chem. Phys. 1999, 110, 11551–11573. [Google Scholar] [CrossRef]
- Guidi, G.M.; Goldbeter, A. Bistability without hysteresis in chemical reaction systems. J. Phys. Chem. A 1997, 101, 9367–9376. [Google Scholar] [CrossRef]
- Ptashne, M. A Genetic Switch: Phage Lambda Revisited; Cold Spring Harbor Laboratory Press: New York, NY, USA, 2004. [Google Scholar]
- Gardner, T.S.; Cantor, C.R.; Collins, J.J. Construction of a genetic toggle switch in Escherichia coli. Nature 2000, 403, 339–342. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.C.; Ferguson, E.L. Spatial bistability of Dpp-receptor interactions during Drosophila dorsal-ventral patterning. Nature 2005, 434, 229–234. [Google Scholar] [CrossRef] [PubMed]
- Angeli, D.; Ferrell, J.E., Jr.; Sontag, D. Detection of multistability, bifurcations, and hysteresis in a large class of biological positive-feedback systems. Proc. Natl. Acad. Sci. USA 2004, 101, 1822–1827. [Google Scholar] [CrossRef] [PubMed]
- Artyomov, M.N.; Das, J.; Kardar, M.; Chakraborty, A.K. Purely stochastic binary decisions in cell signaling models without underlying deterministic bistabilities. Proc. Natl. Acad. Sci. USA 2007, 104, 18958–18963. [Google Scholar] [CrossRef] [PubMed]
- Hasty, J.; McMillen, D.; Isaacs, F.; Collins, J.J. Computational studies of gene regulatory networks: In numero molecular biology. Nat. Rev. Genet. 2001, 2, 268–279. [Google Scholar] [CrossRef] [PubMed]
- Wilhelm, T. The smallest chemical reaction system with bistability. BMC Syst. Biol. 2009, 3, 90. [Google Scholar] [CrossRef] [PubMed]
- Schnoerr, D.; Sanguinetti, G.; Grima, R. Approximation and inference methods for stochastic biochemical kinetics—A tutorial review. J. Phys. A 2007, 50, 093001. [Google Scholar] [CrossRef]
- Grima, R. A study of the accuracy of moment-closure approximations for stochastic chemical kinetics. J. Chem. Phys. 2012, 136, 154105. [Google Scholar] [CrossRef] [PubMed]
- Grima, R.; Thomas, P.; Straube, A.V. How accurate are the nonlinear chemical Fokker-Planck and chemical Langevin equations? J. Chem. Phys. 2011, 135, 084103. [Google Scholar] [CrossRef] [PubMed]
- Constantino, P.H.; Vlysidis, M.; Smadbeck, P.; Kaznessis, Y.N. Modeling stochasticity in biochemical reaction networks. J. Phys. D Appl. Phys. 2016, 49, 093001. [Google Scholar] [CrossRef]
- Constantino, P.H.; Kaznessis, Y.N. Maximum entropy prediction of non-equilibrium stationary distributions for stochastic reaction networks with oscillatory dynamics. Chem. Eng. Sci. 2017, 171, 139–148. [Google Scholar] [CrossRef]
- Sotiropoulos, V.; Kaznessis, Y.N. Analytical derivation of moment equations in stochastic chemical kinetics. Chem. Eng. Sci. 2011, 66, 268–277. [Google Scholar] [CrossRef] [PubMed]
- Smadbeck, P.; Kaznessis, Y.N. Efficient moment matrix generation for arbitrary chemical networks. Chem. Eng. Sci. 2012, 84, 612–618. [Google Scholar] [CrossRef] [PubMed]
- Andreychenko, A.; Bortolussi, L.; Grima, R.; Thomas, P.; Wolf, V. Distribution Approximations for the Chemical Master Equation: Comparison of the Method of Moments and the System Size Expansion. In Modeling Cellular Systems; Springer International Publishing AG: Cham, Switzerland, 2017; pp. 39–66. [Google Scholar]
- Kapur, J.N. Maximum-Entropy Models in Science and Engineering; New Age International Publishers: New Delhi, India, 1989. [Google Scholar]
- Ge, H.; Qian, H. Thermodynamic Limit of a Nonequilibrium Steady State: Maxwell-Type Construction for a Bistable Biochemical System. Phys. Rev. Lett. 2009, 103, 148103. [Google Scholar] [CrossRef] [PubMed]
- Ge, H.; Qian, H. Non-equilibrium phase transition in mesoscopic biochemical systems: from stochastic to nonlinear dynamics and beyond. J. R. Soc. Interface 2011, 8, 107–116. [Google Scholar] [CrossRef] [PubMed]
- Vellela, M.; Qian, H. Stochastic dynamics and non-equilibrium thermodynamics of a bistable chemical system: The Schlögl model revisited. J. R. Soc. Interface 2009, 6, 925–940. [Google Scholar] [CrossRef] [PubMed]
- Duncan, A.; Liao, S.; Vejchodský, T.; Erban, R.; Grima, R. Noise-induced multistability in chemical systems: Discrete versus continuum modeling. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2015, 91, 042111. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, D.T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 1976, 22, 403–434. [Google Scholar] [CrossRef]
- Prigogine, I. Moderation et Transformations Irreversibles des Systemes Ouverts. Bull. Cl. Sci. Acad. R. Belg. 1945, 31, 600–606. [Google Scholar]
- Keizer, J.; Fox, R.F. Qualms regarding the range of validity of the glansdorff-prigogine criterion for stability of non-equilibrium States. Proc. Natl. Acad. Sci. USA 1974, 71, 192–196. [Google Scholar] [CrossRef] [PubMed]
- Glansdorff, P.; Nicolis, G.; Prigogine, I. The thermodynamic stability theory of non-equilibrium States. Proc. Natl. Acad. Sci. USA 1974, 71, 197–199. [Google Scholar] [CrossRef] [PubMed]
- Callen, H.B. Principle of Minimum Entropy Production. Phys. Rev. 1957, 105, 360. [Google Scholar] [CrossRef]
- Jaynes, E.T. The minimum entropy production principle. Annu. Rev. Phys. Chem. 1980, 31, 579–601. [Google Scholar] [CrossRef]
- Smadbeck, P.; Kaznessis, Y.N. On a theory of stability for nonlinear stochastic chemical reaction networks. J. Chem. Phys. 2015, 142, 184101. [Google Scholar] [CrossRef] [PubMed]
- Van der Vaart, A.W. Asymptotic Statistics; Cambridge Series in Statistical and Probabilistic Mathematics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vlysidis, M.; Kaznessis, Y.N. On Differences between Deterministic and Stochastic Models of Chemical Reactions: Schlögl Solved with ZI-Closure. Entropy 2018, 20, 678. https://doi.org/10.3390/e20090678
Vlysidis M, Kaznessis YN. On Differences between Deterministic and Stochastic Models of Chemical Reactions: Schlögl Solved with ZI-Closure. Entropy. 2018; 20(9):678. https://doi.org/10.3390/e20090678
Chicago/Turabian StyleVlysidis, Michail, and Yiannis N. Kaznessis. 2018. "On Differences between Deterministic and Stochastic Models of Chemical Reactions: Schlögl Solved with ZI-Closure" Entropy 20, no. 9: 678. https://doi.org/10.3390/e20090678
APA StyleVlysidis, M., & Kaznessis, Y. N. (2018). On Differences between Deterministic and Stochastic Models of Chemical Reactions: Schlögl Solved with ZI-Closure. Entropy, 20(9), 678. https://doi.org/10.3390/e20090678




