Transpiration and Viscous Dissipation Effects on Entropy Generation in Hybrid Nanofluid Flow over a Nonlinear Radially Stretching Disk
Abstract
:1. Introduction
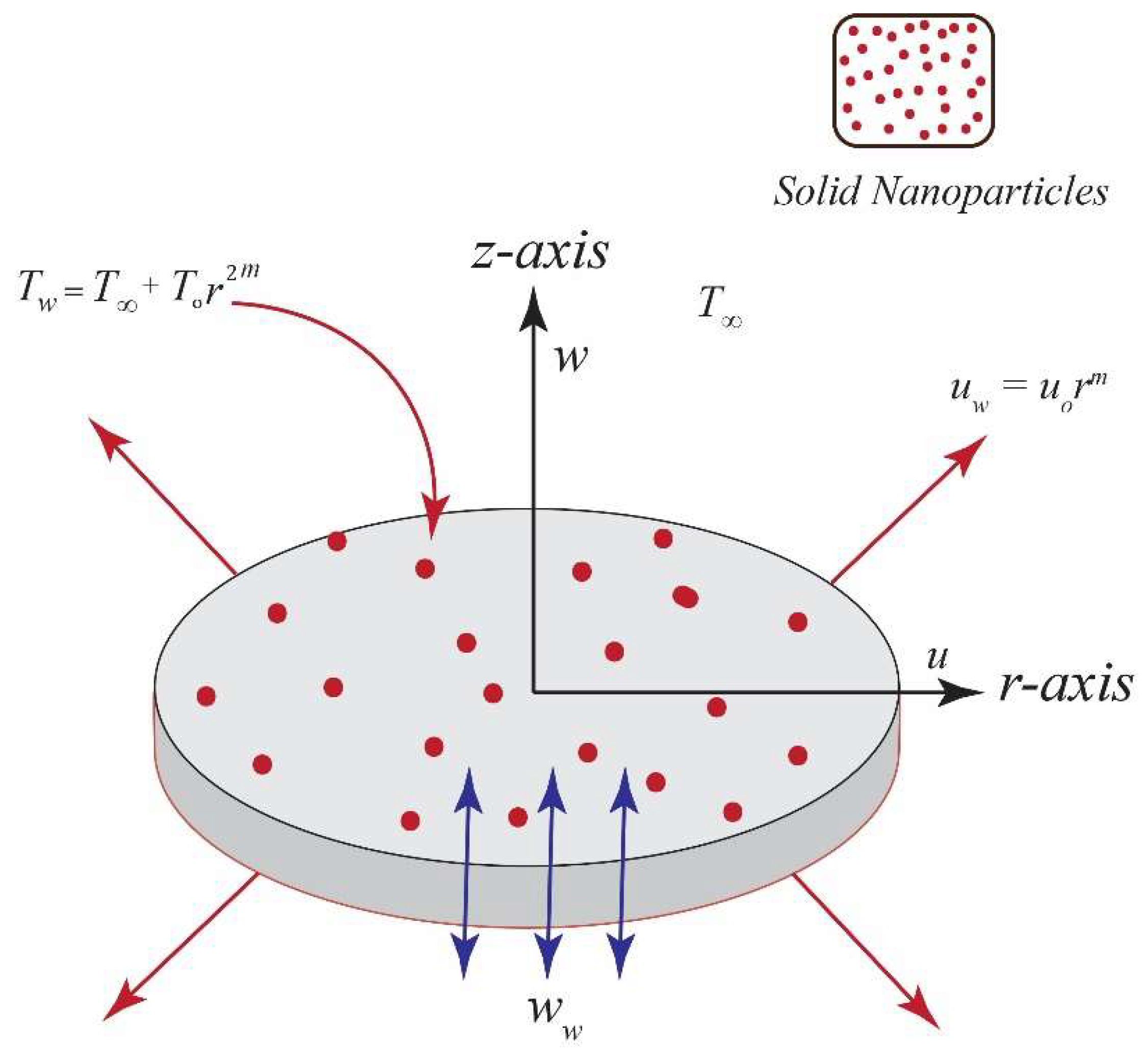
2. The Mathematical Model
2.1. Thermophysical Properties of Hybrid Nanofluid
2.1.1. Effective Density
2.1.2. Effective Heat Capacitance
2.1.3. Effective Thermal Conductivity
2.1.4. Effective Dynamic Viscosity
2.2. Similarity Transformations
2.3. Entropy Generation
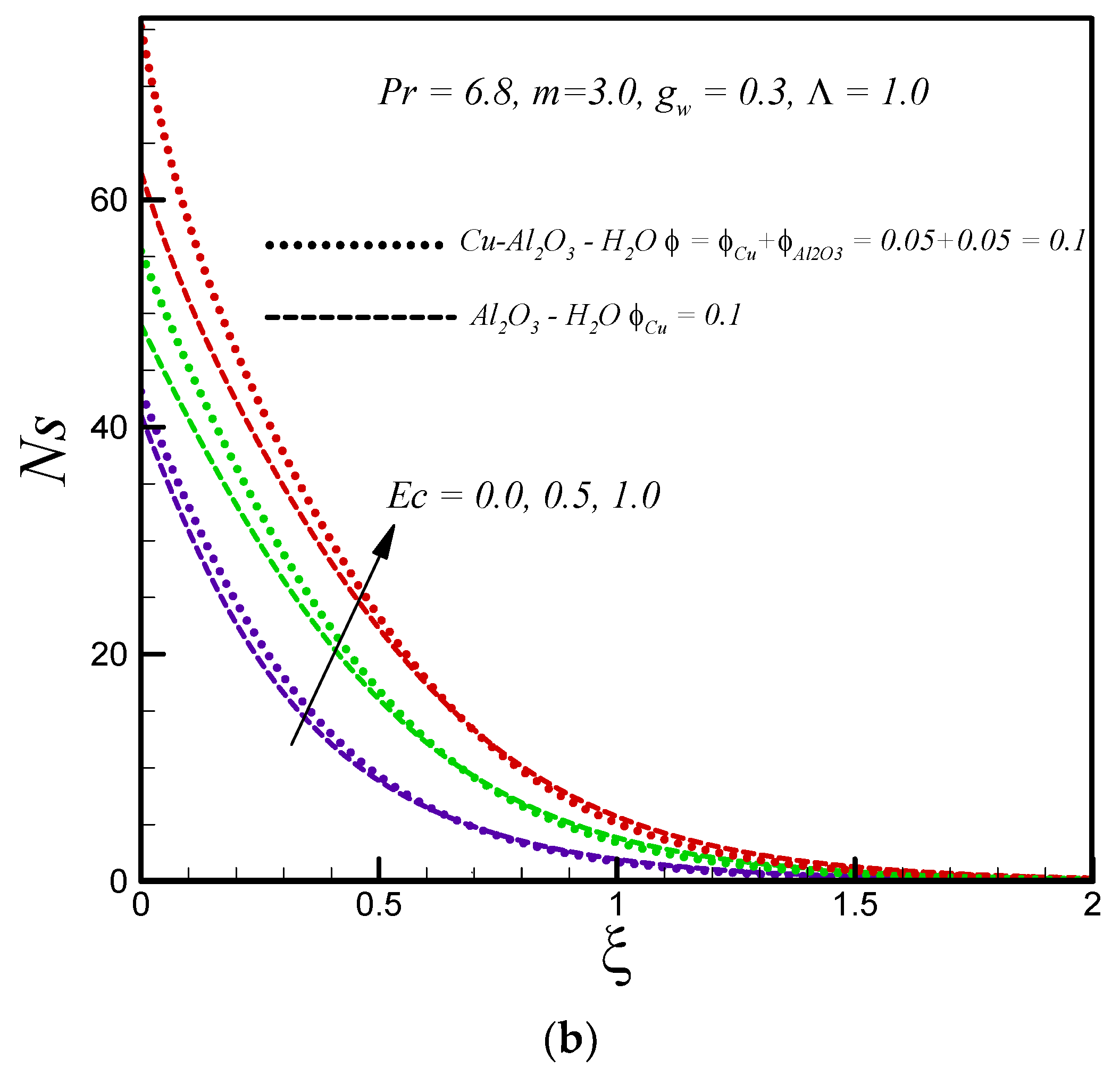
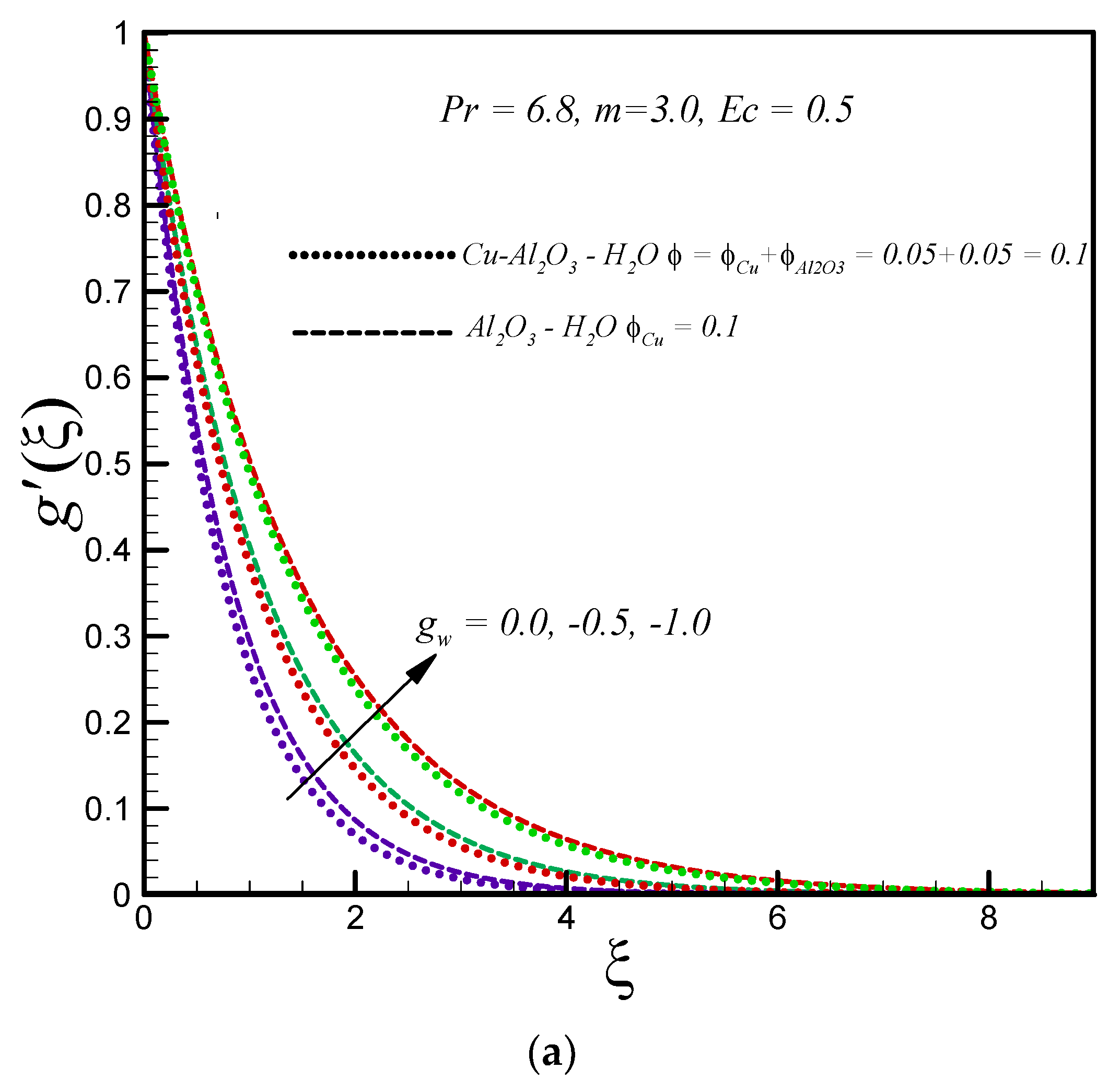
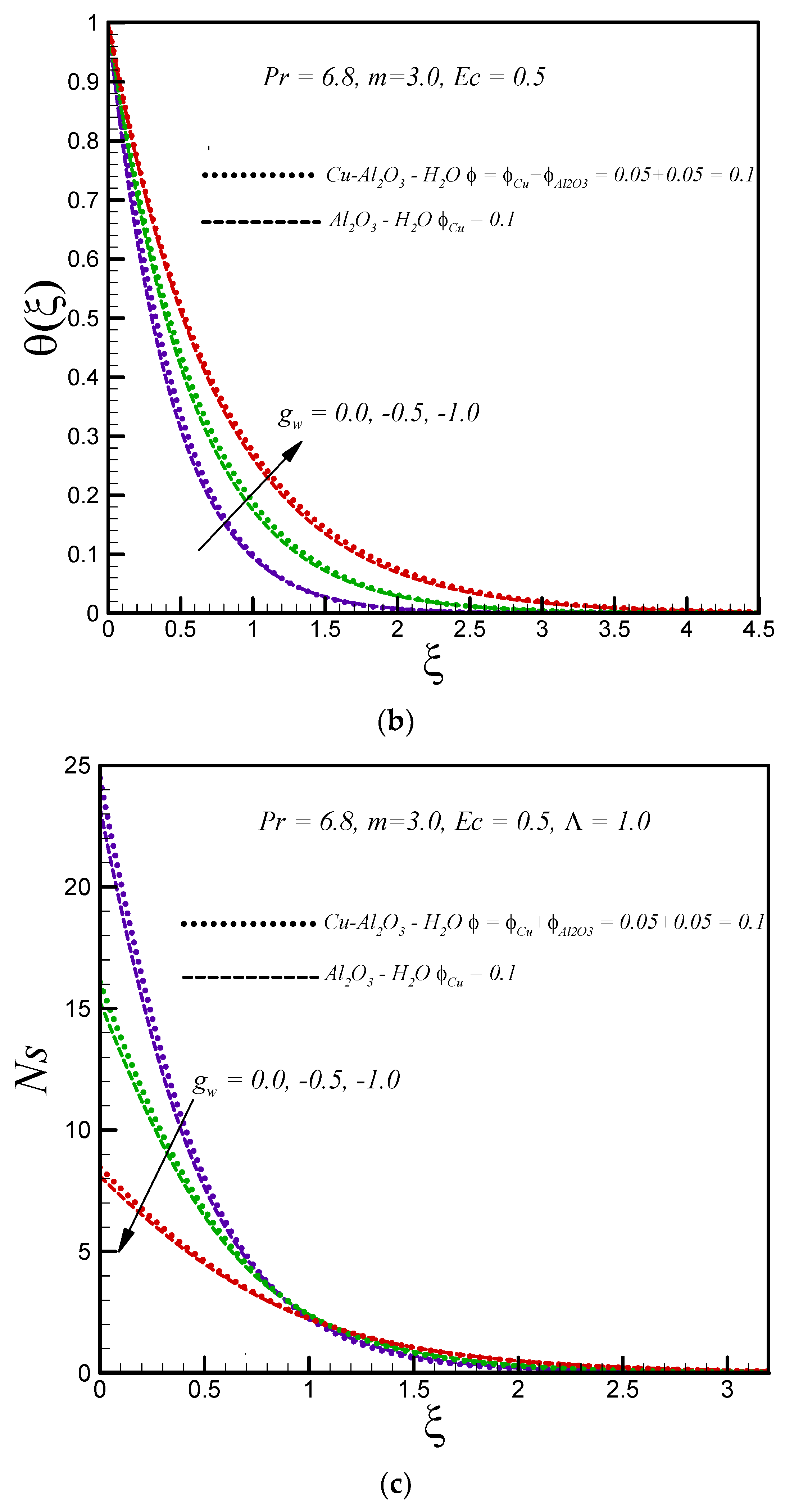
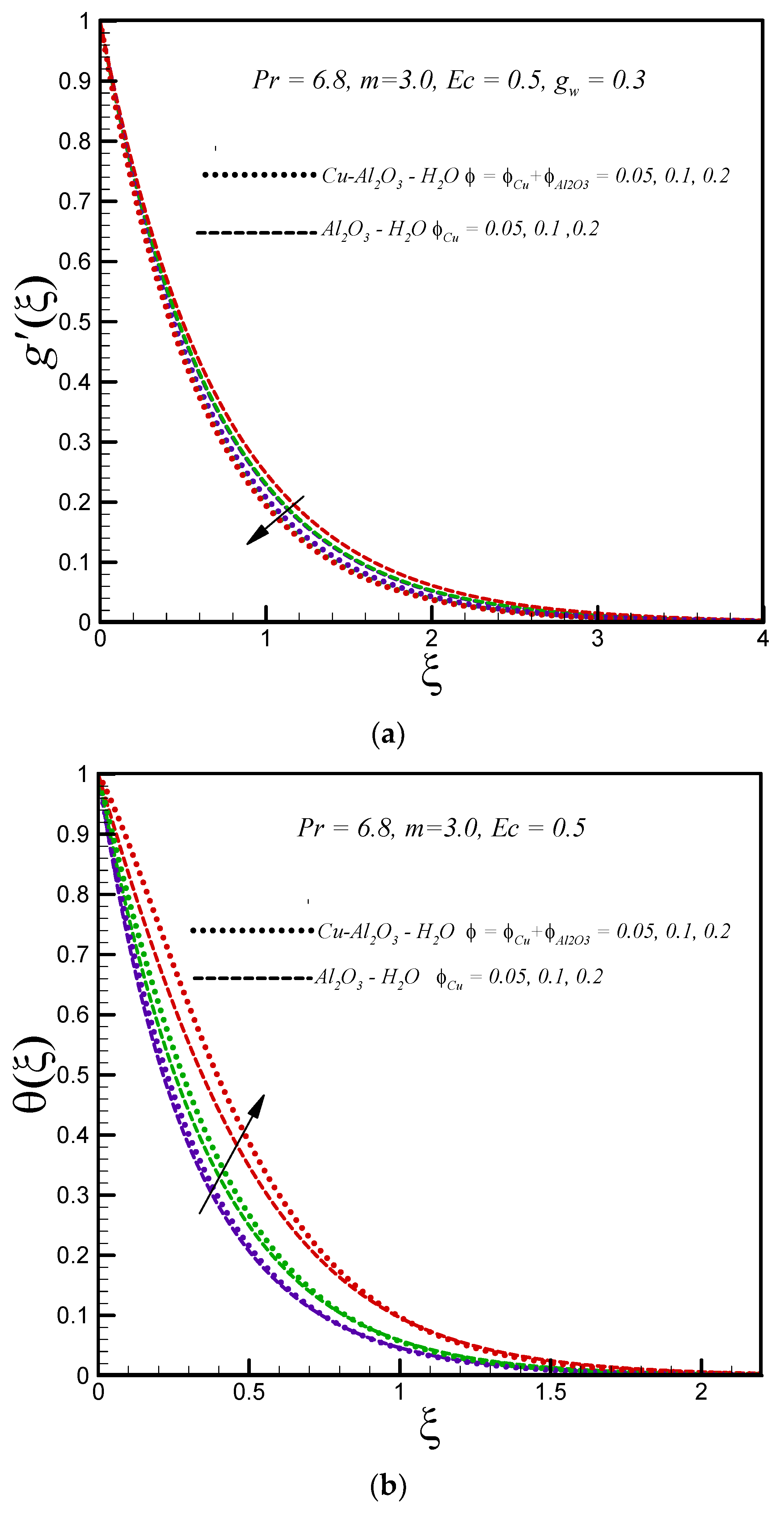
3. Numerical Results and Discussions
4. Concluding Remarks
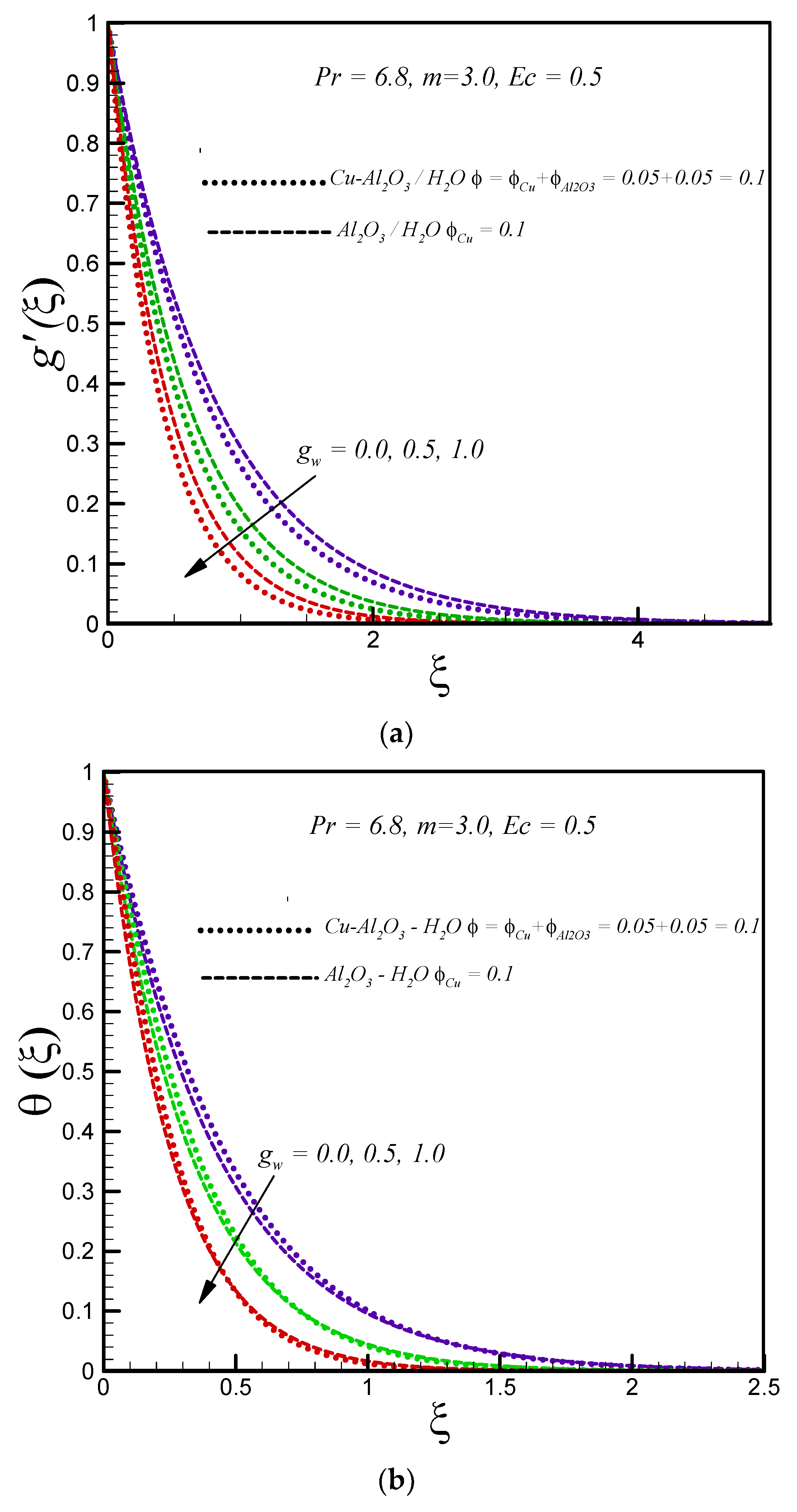
- The velocity and temperature profile of regular and hybrid nanofluids decrease with increasing suction.
- The thermal boundary layer is thick for a hybrid nanofluid in comparison to a regular nanofluid.
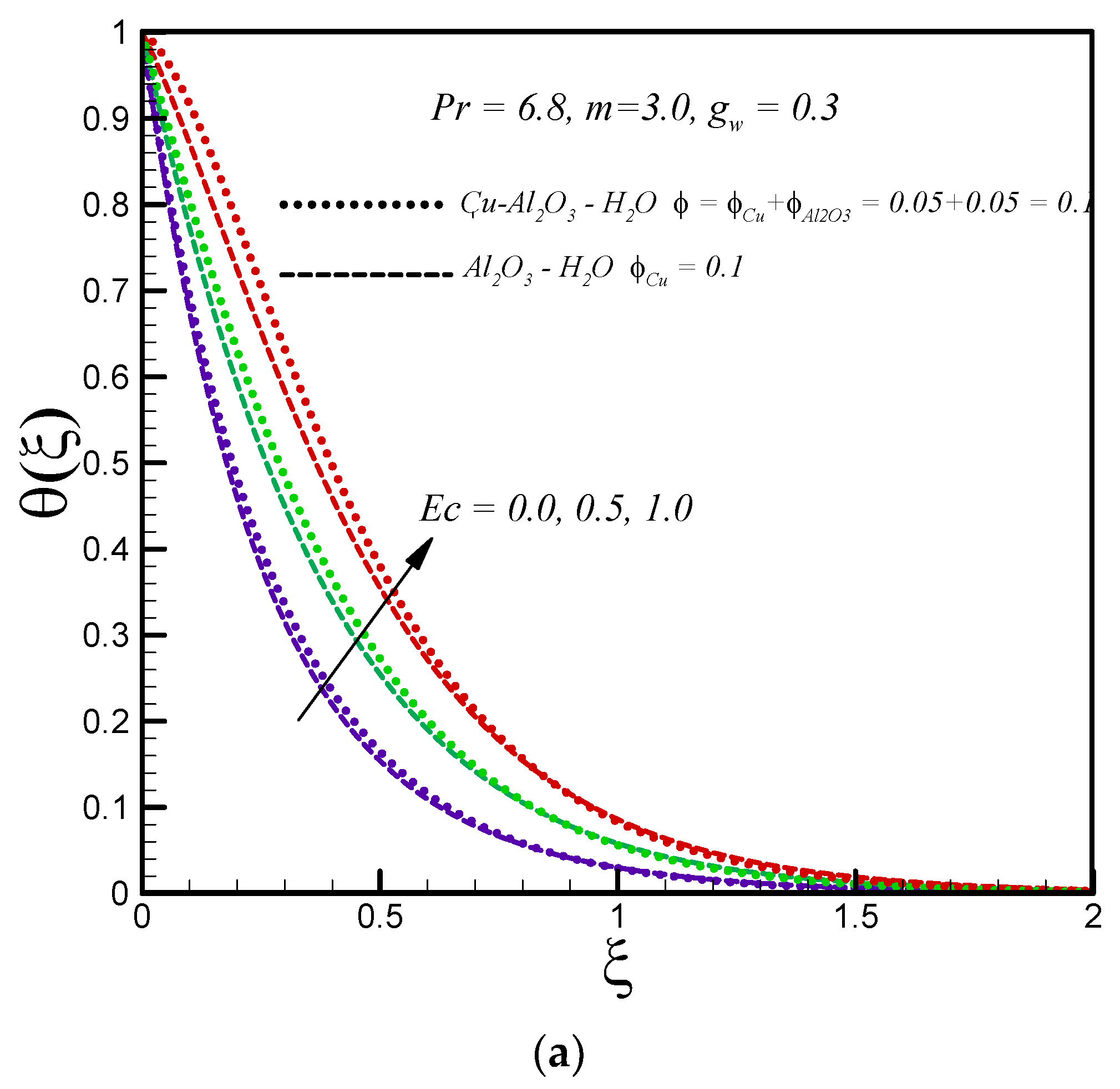
- Increasing values of Eckert number, nanoparticle volume fraction, and injection result in a rise in temperature distribution for both the regular and hybrid nanofluid.
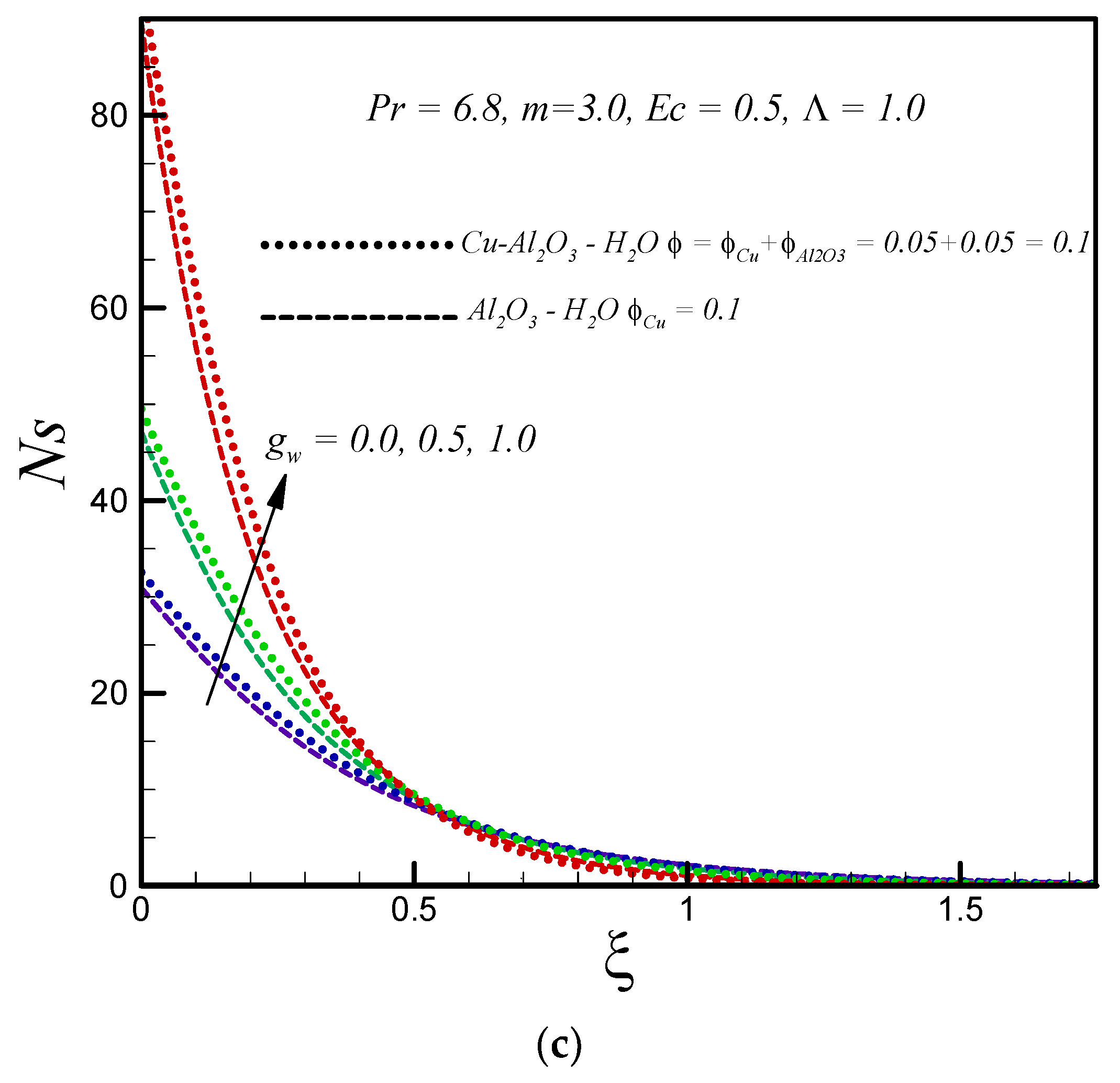
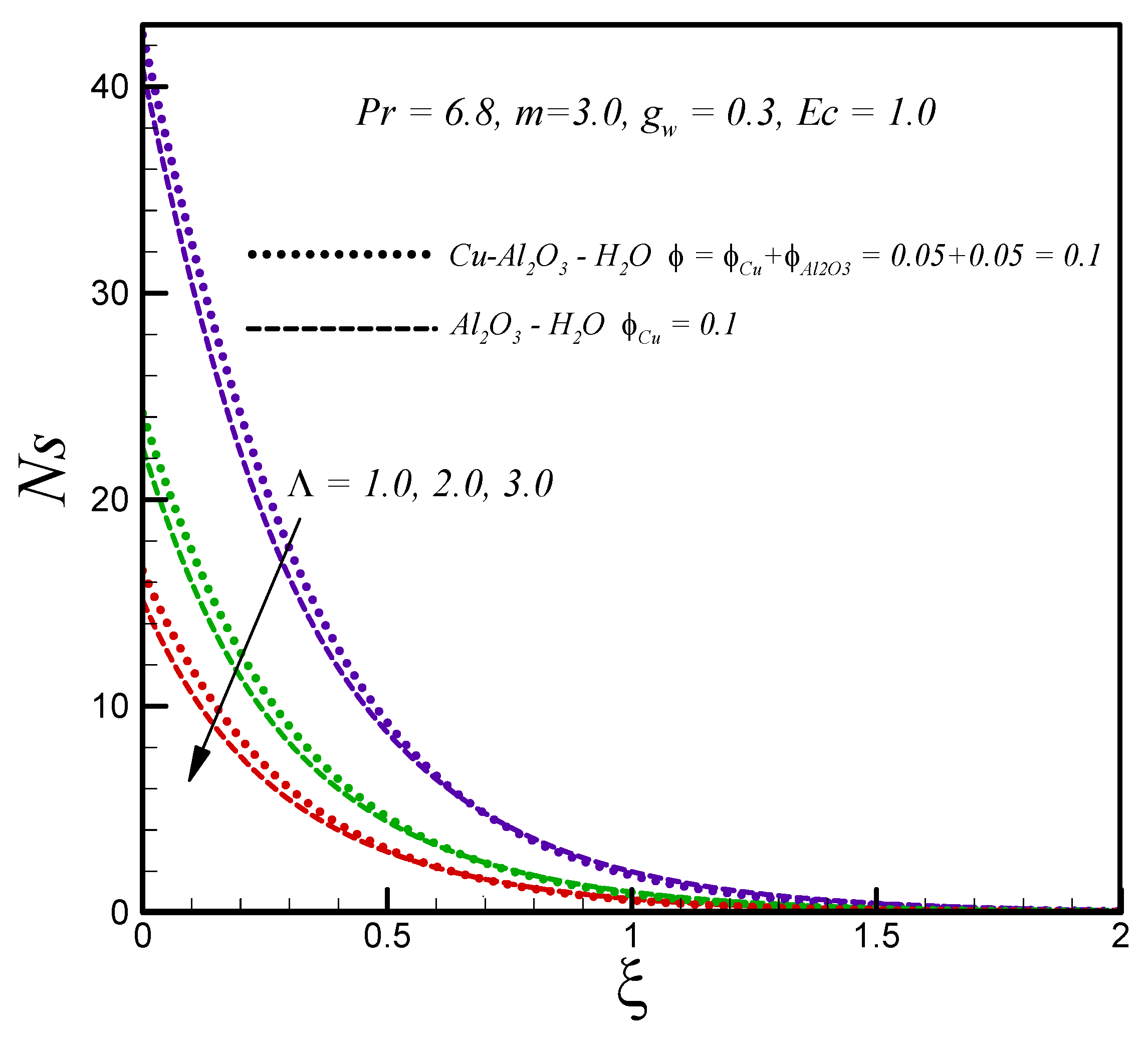
- Entropy generation increases with rising values of suction, Eckert number, and nanoparticle volume fraction for both types of nanofluid.
- Entropy generation in the hybrid nanofluid Cu–Al2O3–H2O is higher than regular nanofluid Al2O3–H2O.
- A reduction in entropy generation is observed with increasing temperature difference and injection.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bejan, A. A study of entropy generation in fundamental convective heat transfer. ASME J. Heat Transf. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Reddy, G.J.; Kumar, M.; Kethireddy, B.; Chamkha, A.J. Colloidal study of unsteady magnetohydrodynamic couple stress fluid flow over an isothermal vertical flat plate with entropy heat generation. J. Mol. Liq. 2018, 252, 169–179. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M. Entropy generation and heat transfer in boundary layer flow over a thin needle moving in a parallel stream in the presence of nonlinear Rosseland radiation. Int. J. Therm. Sci. 2018, 123, 117–128. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M. Entropy generation in three-dimensional flow of dissipative fluid. Int. J. Appl. Comput. Math. 2018, 16, 1–11. [Google Scholar] [CrossRef]
- Khan, A.; Karim, F.; Khan, I.; Ali, F.; Khan, D. Irreversibility analysis in unsteady flow over a vertical plate with arbitrary wall shear stress and ramped wall temperature. Results Phys. 2018, 8, 1283–1290. [Google Scholar] [CrossRef]
- Rashad, A.M.; Armaghani, T.; Chamkha, A.J.; Mansour, M.A. Entropy Generation and MHD natural convection of a nanofluid in an inclined square porous cavity: Effects of a heat sink and source size and location. Chin. J. Phys. 2018, 56, 193–211. [Google Scholar] [CrossRef]
- Qasim, M.; Afridi, M.I. Effects of energy dissipation and variable thermal conductivity on entropy generation rate in mixed convection flow. ASME J. Therm. Sci. Eng. Appl. 2017. [Google Scholar] [CrossRef]
- Khan, A.; Khan, I.; Ali, F.; Shafie, S. A note on entropy generation in MHD flow over a vertical plate embedded in a porous medium with arbitrary shear stress and ramped temperature. J. Porous Media 2016, 19, 175–187. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M. Comparative study and entropy generation analysis of Cu–H2O and Ag–H2O nanofluids flow over a slendering stretching surface. J. Nanofluids 2018, 7, 783–790. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A. A computational study of entropy generation and magnetohydrodynamic flow and heat transfer over an unsteady stretching permeable sheet. Eur. Phys. J. Plus 2014, 129, 1–13. [Google Scholar]
- Das, S.; Jana, R.N.; Makinde, O.D. Entropy generation in hydromagnetic and thermal boundary layer flow due to radial stretching sheet with Newtonian heating. J. Heat Mass Transf. Res. 2015, 2, 51–61. [Google Scholar]
- Khan, N.A.; Aziz, S.; Ullah, S. Entropy generation on MHD flow of Powell-Eyring fluid between radially stretching rotating disk with diffusion-thermo and thermo-diffusion effects. Acta Mech. Autom. 2017, 11, 20–32. [Google Scholar] [CrossRef]
- Khan, N.A.; Naz, F.; Sultan, F. Entropy generation analysis and effects of slip conditions on micropolar fluid flow due to a rotating disk. Open Eng. 2017, 7, 185–198. [Google Scholar] [CrossRef] [Green Version]
- Gebhart, B. Effects of viscous dissipation in natural convection. J. Fluid Mech. 1962, 14, 225–235. [Google Scholar] [CrossRef]
- Partha, M.K.; Murthy, P.V.S.N.; Rajasekhar, G.P. Effect of viscous dissipation on the mixed convection heat transfer from an exponentially stretching surface. Heat Mass Transf. 2005, 41, 360–366. [Google Scholar] [CrossRef]
- Cortell, R. Effects of viscous dissipation and radiation on thermal boundary layer over a nonlinearly stretching sheet. Phys. Lett. A 2008, 372, 631–636. [Google Scholar] [CrossRef]
- Sreenivasulu, P.; Poornima, T.; Reddy, N.B. Thermal radiation effects on MHD boundary layer slip flow past a permeable exponential stretching sheet in the presence of Joule heating and viscous dissipation. J. Appl. Fluid Mech. 2016, 9, 267–278. [Google Scholar] [CrossRef]
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, San Francisco, CA, USA, 12–17 November 1995. [Google Scholar]
- Makinde, O.D. Effects of viscous dissipation and Newtonian heating on boundary-layer flow of nanofluids over a flat plate. Int. J. Numer. Methods Heat Fluid Flow 2013, 23, 1291–1303. [Google Scholar] [CrossRef]
- Hussanan, A.; Salleh, M.Z.; Khan, I.; Shafie, S. Convection heat transfer in micropolar nanofluids with oxide nanoparticles in water, kerosene and engine oil. J. Mol. Liq. 2017, 229, 482–488. [Google Scholar] [CrossRef]
- Sulochanan, C.; Ashwinkumar, G.P.; Sandeep, N. Boundary layer analysis of persistent moving horizontal needle in magnetohydrodynamic ferrofluid: A numerical study. Alex. Eng. J. 2017. [Google Scholar] [CrossRef]
- Reddy, P.S.; Chamkha, A.J. Heat and mass transfer characteristics of nanofluid over horizontal circular cylinder. Ain Shams Eng. J. 2016. [Google Scholar] [CrossRef]
- Hussanan, A.; Salleh, M.Z.; Khan, I. Microstructure and inertial characteristics of a magnetite ferrofluid over a stretching/shrinking sheet using effective thermal conductivity model. J. Mol. Liq. 2018, 225, 64–75. [Google Scholar] [CrossRef]
- Mutuku, W.N.; Makinde, O.D. Double stratification effects on heat and mass transfer in unsteady MHD nanofluid flow over a flat surface. Asia Pac. J. Comput. Eng. 2017, 4, 1–16. [Google Scholar] [CrossRef]
- Xiao, B.; Zhang, X.; Wang, W.; Long, G.; Chen, H.; Kang, H.; Ren, W. A fractal model for water flow through unsaturated porous rocks. Fractals 2018, 26, 1840015. [Google Scholar] [CrossRef]
- Hsiao, K.L. Nanofluid flow with multimedia physical features for conjugate mixed convection and radiation. Comput. Fluids 2014, 104, 1–8. [Google Scholar] [CrossRef]
- Long, G.; Xu, G. The effects of perforation erosion on practical hydraulic-fracturing applications. Soc. Pet. Eng. 2017, 22, 645–659. [Google Scholar] [CrossRef]
- Makinde, O.D. Free convection flow with thermal radiation and mass transfer past a moving vertical porous plate. Int. Commun. Heat Mass Transf. 2005, 32, 1411–1419. [Google Scholar] [CrossRef]
- Lin, Y.; Li, B.; Zheng, L.; Chen, G. Particle shape and radiation effects on Marangoni boundary layer flow and heat transfer of copper-water nanofluid driven by an exponential temperature. Powder Technol. 2016, 301, 379–386. [Google Scholar] [CrossRef]
- Lin, Y.; Zheng, L.; Li, B.; Ma, L. A new diffusion for laminar boundary layer flow of power law fluids past a flat surface with magnetic effect and suction or injection. Int. J. Heat Mass Transf. 2015, 90, 1090–1097. [Google Scholar] [CrossRef]
- Hsiao, K.L. Stagnation electrical MHD nanofluid mixed convection with slip boundary on a stretching sheet. Appl. Therm. Eng. 2016, 98, 580–861. [Google Scholar] [CrossRef]
- Cheng, C.Y. Free convection boundary layer flow over a horizontal cylinder of elliptic cross section in porous media saturated by a nanofluid. Int. J. Heat Mass Transf. 2012, 39, 931–936. [Google Scholar] [CrossRef]
- Devi, S.P.A.; Devi, S.S.U. Numerical investigation of hydromagnetic Cu–Al2O3/water hybrid nanofluid flow over a permeable stretching sheet with suction. Int. J. Nonlinear Sci. Numer. Simul. 2015, 17, 249–257. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Miroshnichenko, I.; Sheremet, M. Numerical analysis of unsteady conjugate natural convection of hybrid water-based nanofluid in a semicircular cavity. ASME J. Heat Transf. 2018, 140, 1–19. [Google Scholar] [CrossRef]
- Devi, S.P.A.; Devi, S.S.U. Numerical investigation of three dimensional Cu–Al2O3/water hybrid nanofluid flow over a stretching sheet with effecting Lorentz force subject to Newtonian heating. Can. J. Phys. 2016, 94, 490–496. [Google Scholar] [CrossRef]
- Olatundun, A.T.; Makinde, O.D. Analysis of Blasius flow of hybrid nanofluid over a convectively heated surface. Defect Diffus. Forum 2017, 377, 29–41. [Google Scholar] [CrossRef]

| Al2O3–Water | Cu–Al2O3–Water | |||||||
|---|---|---|---|---|---|---|---|---|
| R-K-Fehlberg Scheme | bvp4c | R-K-Fehlberg Scheme | Bvp4c | |||||
| 0.1 | −1.300363 | −2.398908 | −1.300361 | −2.398909 | −1.427521 | −2.045604 | −1.427521 | −2.045602 |
| 0.3 | −1.468136 | −2.670735 | −1.468135 | −2.670737 | −1.629400 | −2.185050 | −1.629401 | −1.629400 |
| 0.5 | −1.653273 | −2.968903 | −1.653271 | −2.968903 | −1.853650 | −2.333798 | −1.853651 | −1.853652 |
| 0.7 | −1.854387 | −3.292556 | −1.854387 | −3.292555 | −2.098183 | −2.496151 | −2.098182 | −2.098181 |
| 0.9 | −2.069710 | −3.639854 | −2.069711 | −3.639854 | −2.360413 | −2.674312 | −2.360413 | −2.360412 |
| Physical Properties | Base Fluid (Water) | ||
|---|---|---|---|
| - | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farooq, U.; Afridi, M.I.; Qasim, M.; Lu, D.C. Transpiration and Viscous Dissipation Effects on Entropy Generation in Hybrid Nanofluid Flow over a Nonlinear Radially Stretching Disk. Entropy 2018, 20, 668. https://doi.org/10.3390/e20090668
Farooq U, Afridi MI, Qasim M, Lu DC. Transpiration and Viscous Dissipation Effects on Entropy Generation in Hybrid Nanofluid Flow over a Nonlinear Radially Stretching Disk. Entropy. 2018; 20(9):668. https://doi.org/10.3390/e20090668
Chicago/Turabian StyleFarooq, Umer, Muhammad Idrees Afridi, Muhammad Qasim, and D. C. Lu. 2018. "Transpiration and Viscous Dissipation Effects on Entropy Generation in Hybrid Nanofluid Flow over a Nonlinear Radially Stretching Disk" Entropy 20, no. 9: 668. https://doi.org/10.3390/e20090668
APA StyleFarooq, U., Afridi, M. I., Qasim, M., & Lu, D. C. (2018). Transpiration and Viscous Dissipation Effects on Entropy Generation in Hybrid Nanofluid Flow over a Nonlinear Radially Stretching Disk. Entropy, 20(9), 668. https://doi.org/10.3390/e20090668






