Second Law Analysis of Dissipative Flow over a Riga Plate with Non-Linear Rosseland Thermal Radiation and Variable Transport Properties
Abstract
:1. Introduction
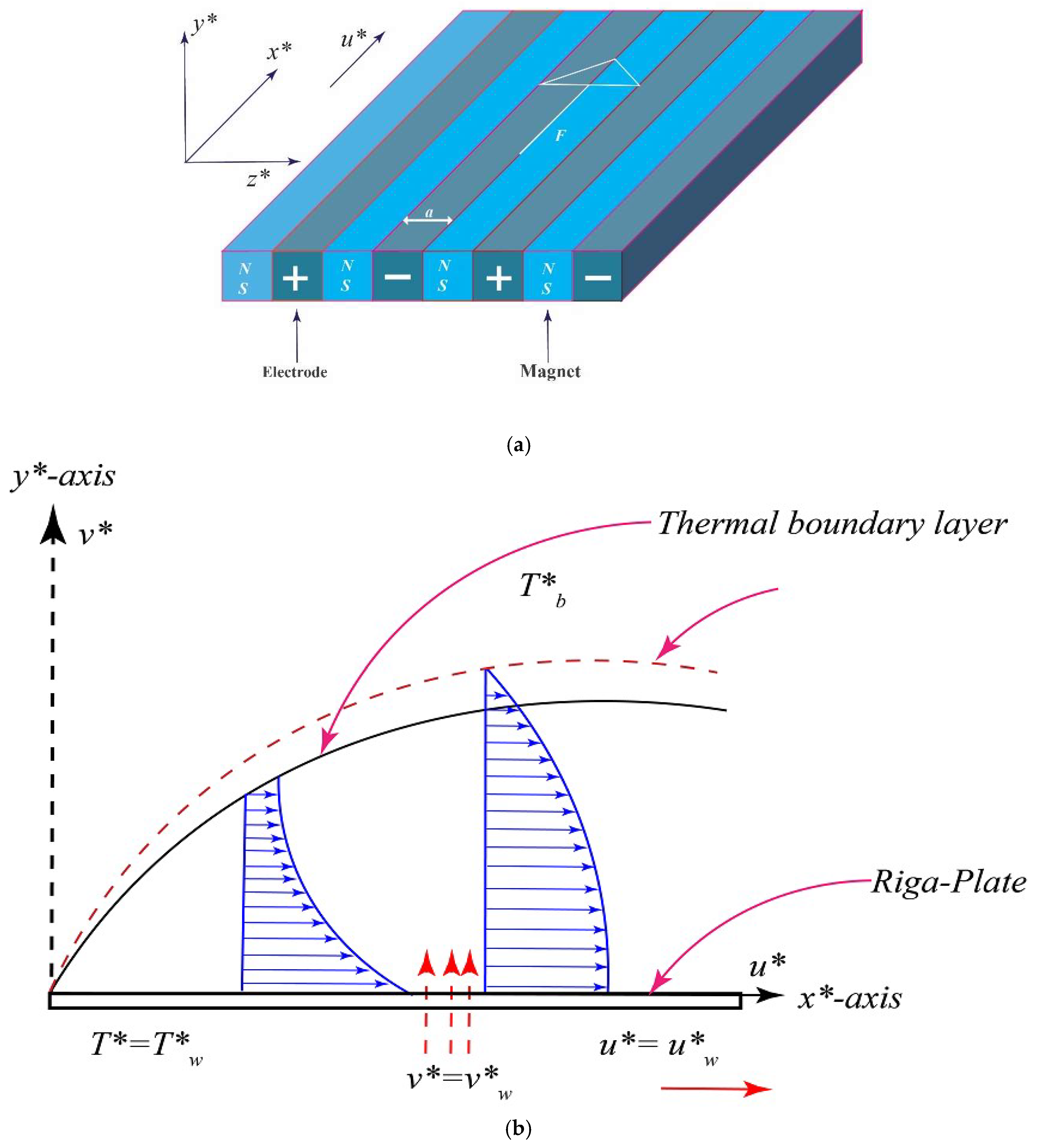
2. The Mathematical Model
3. Entropy Generation
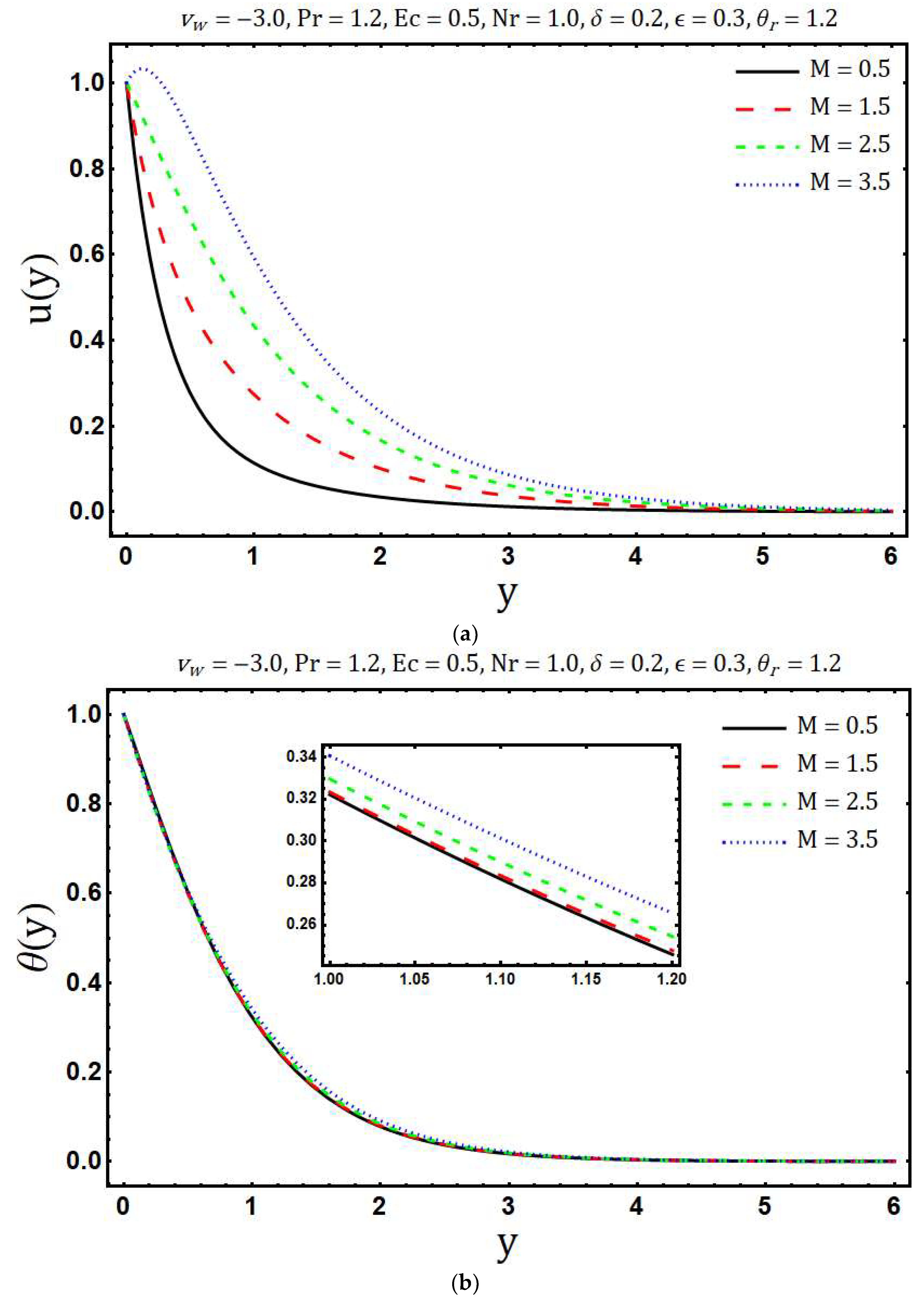
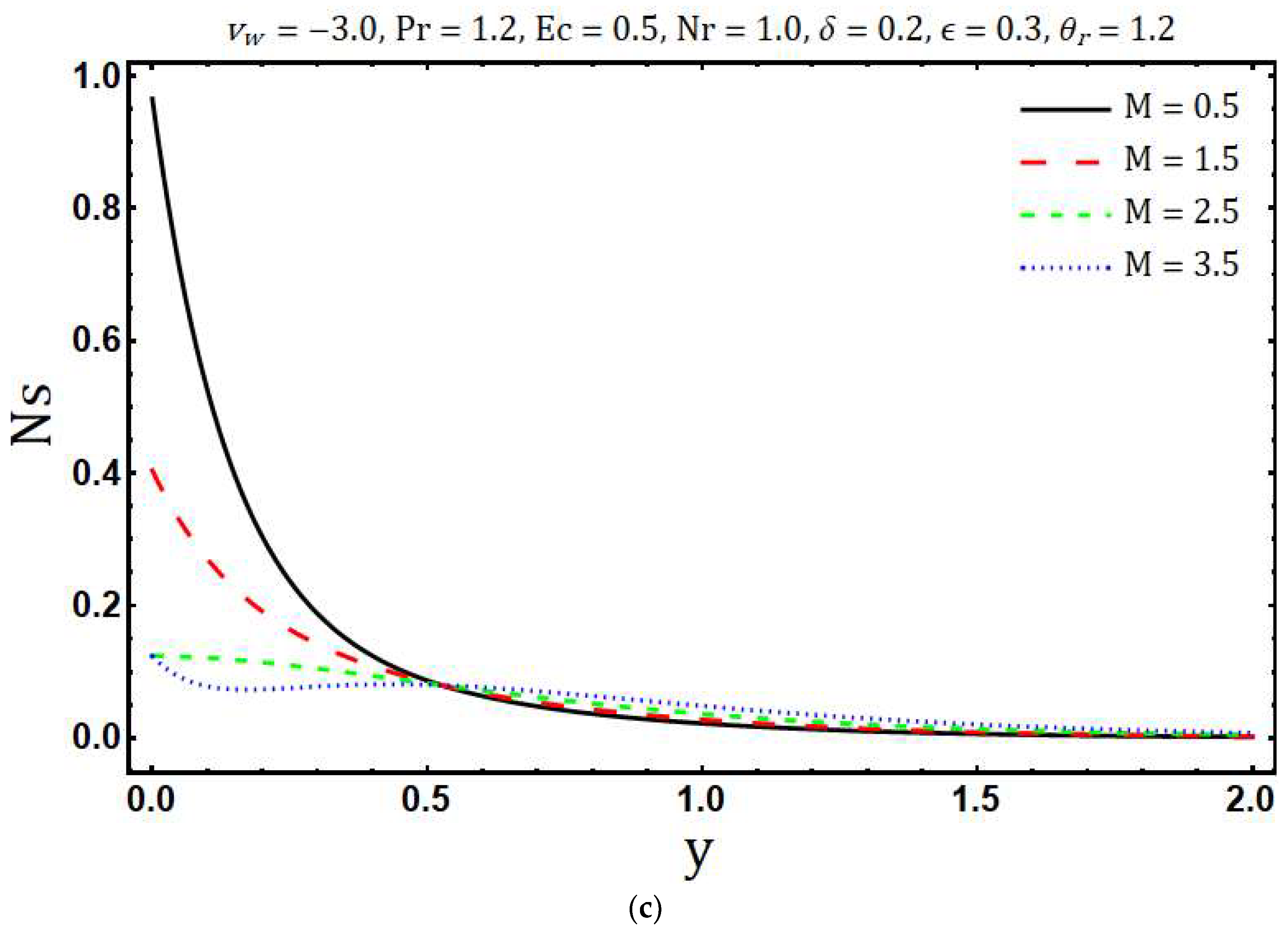
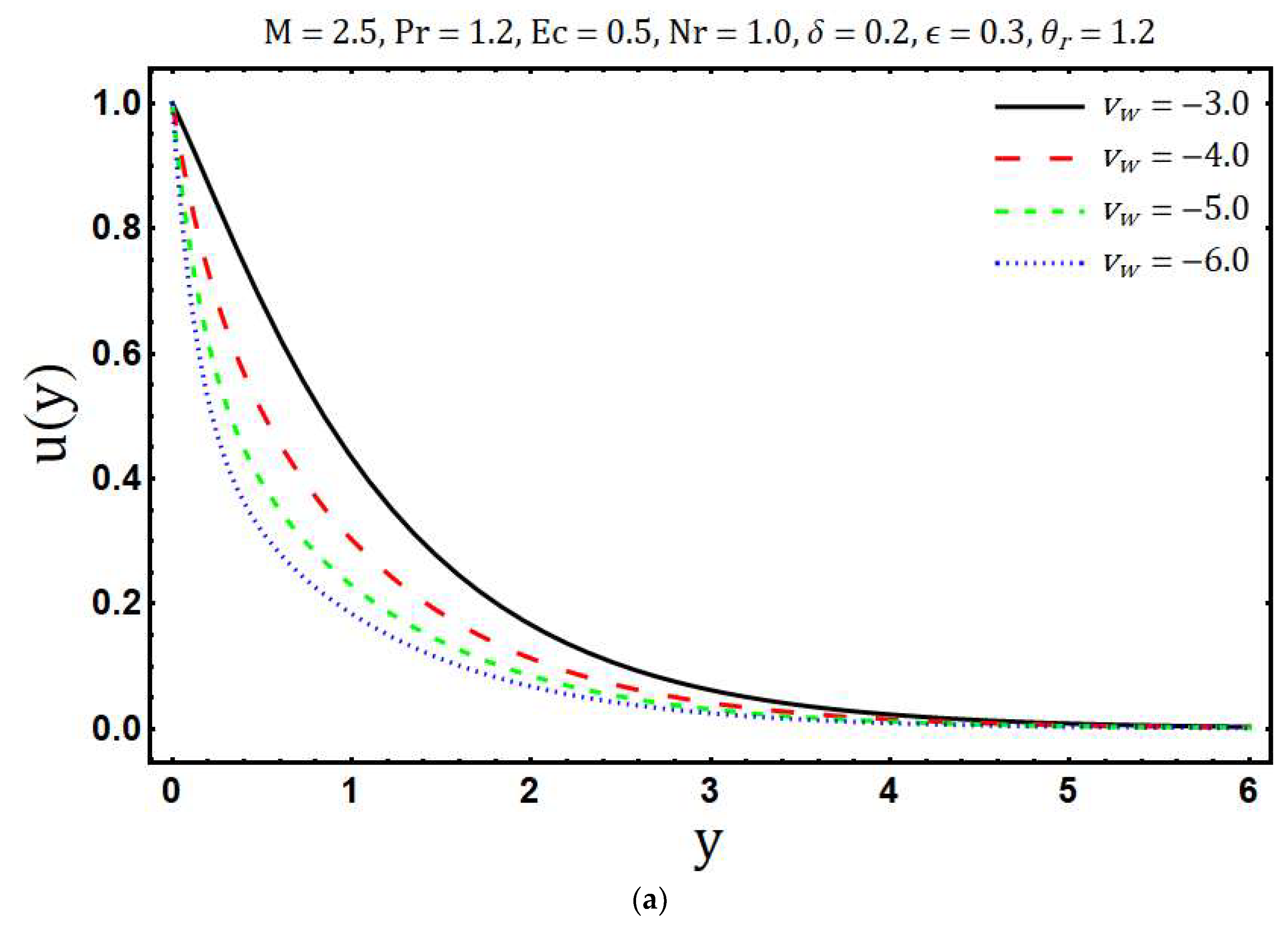
4. Results and Discussion
5. Concluding Remarks
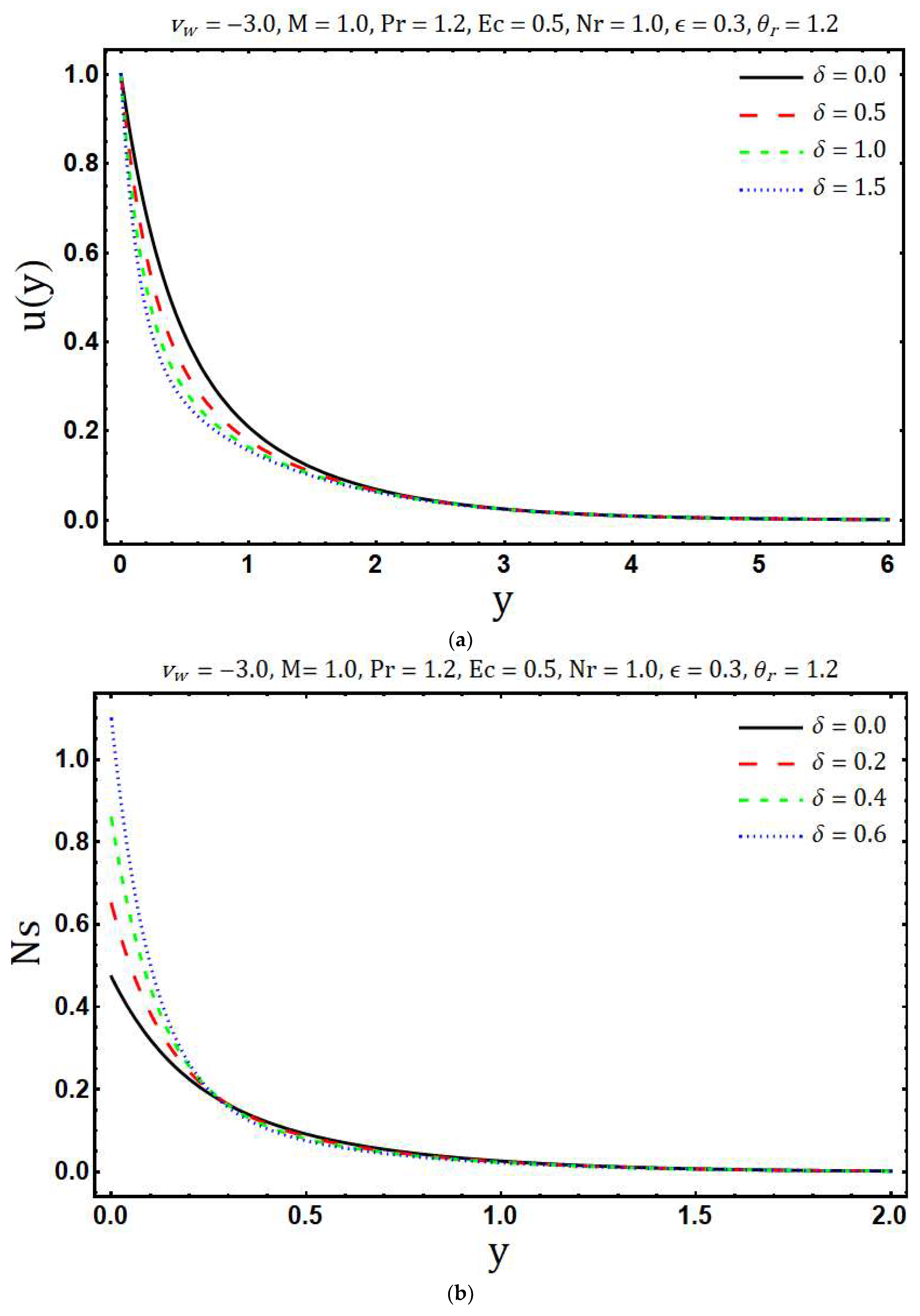
- Decay in the magnitude of velocity is found as the mass suction parameter and variable viscosity parameter increases while an enhancement in modified Hartmann number accelerates the fluid motion.
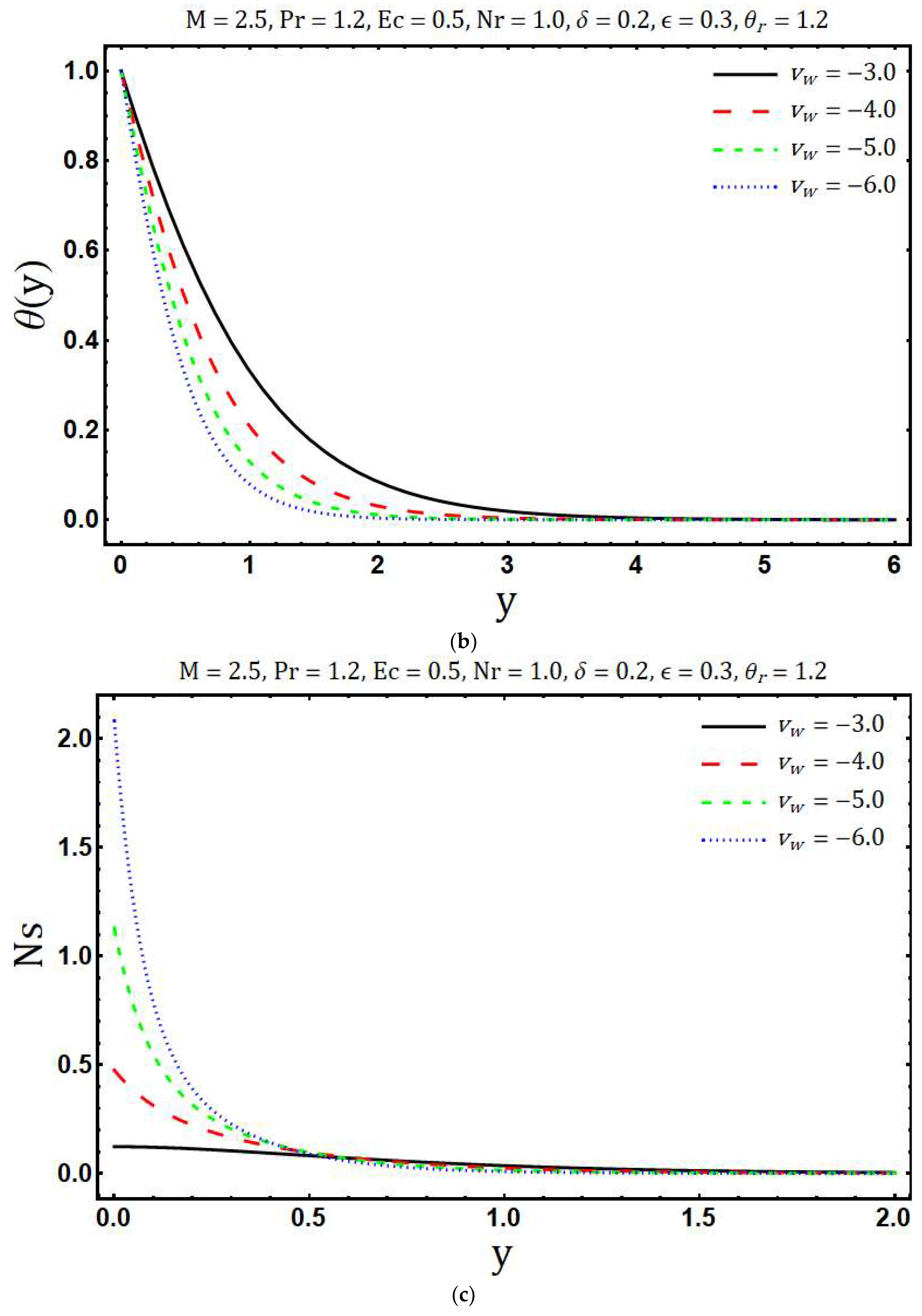
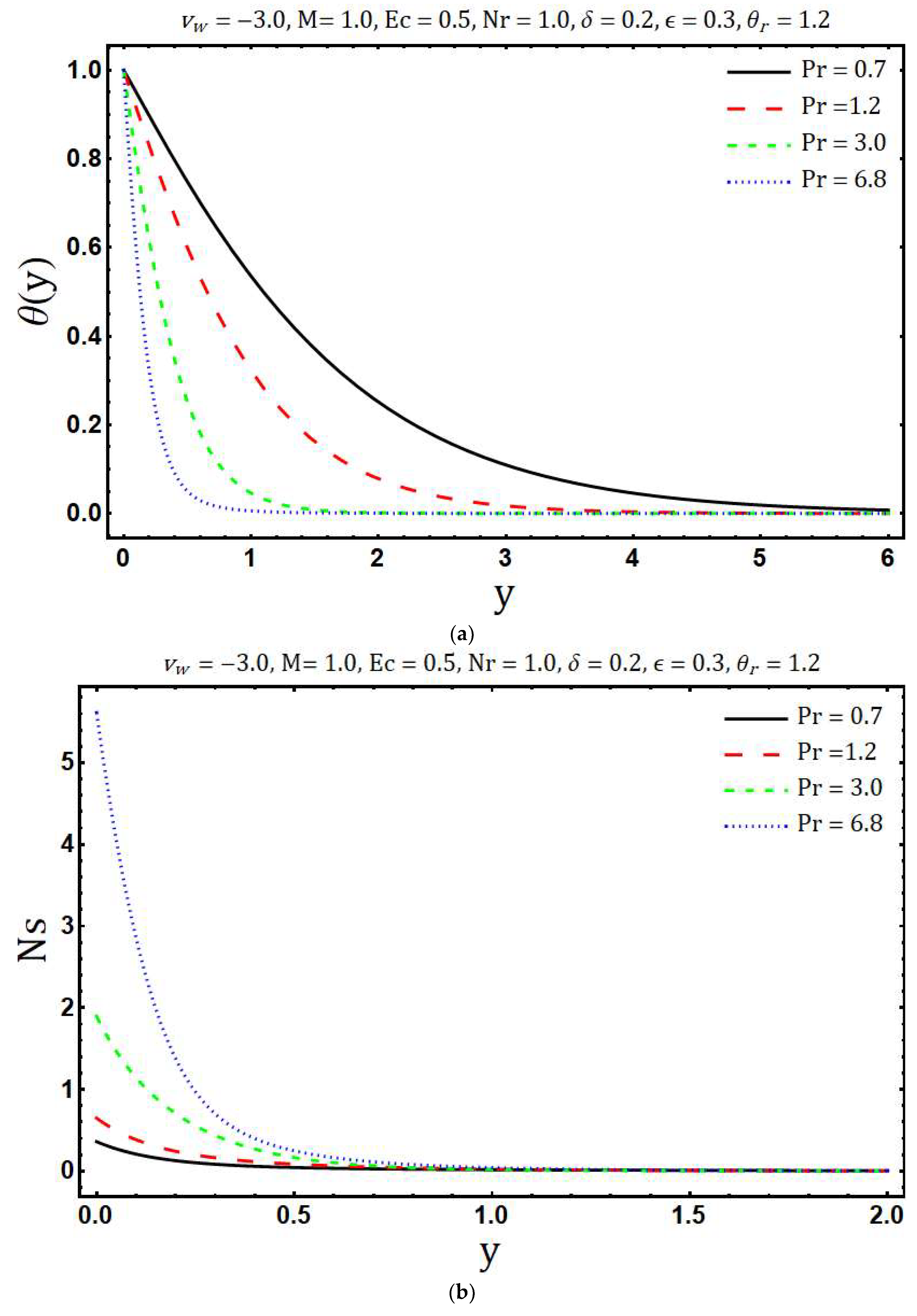
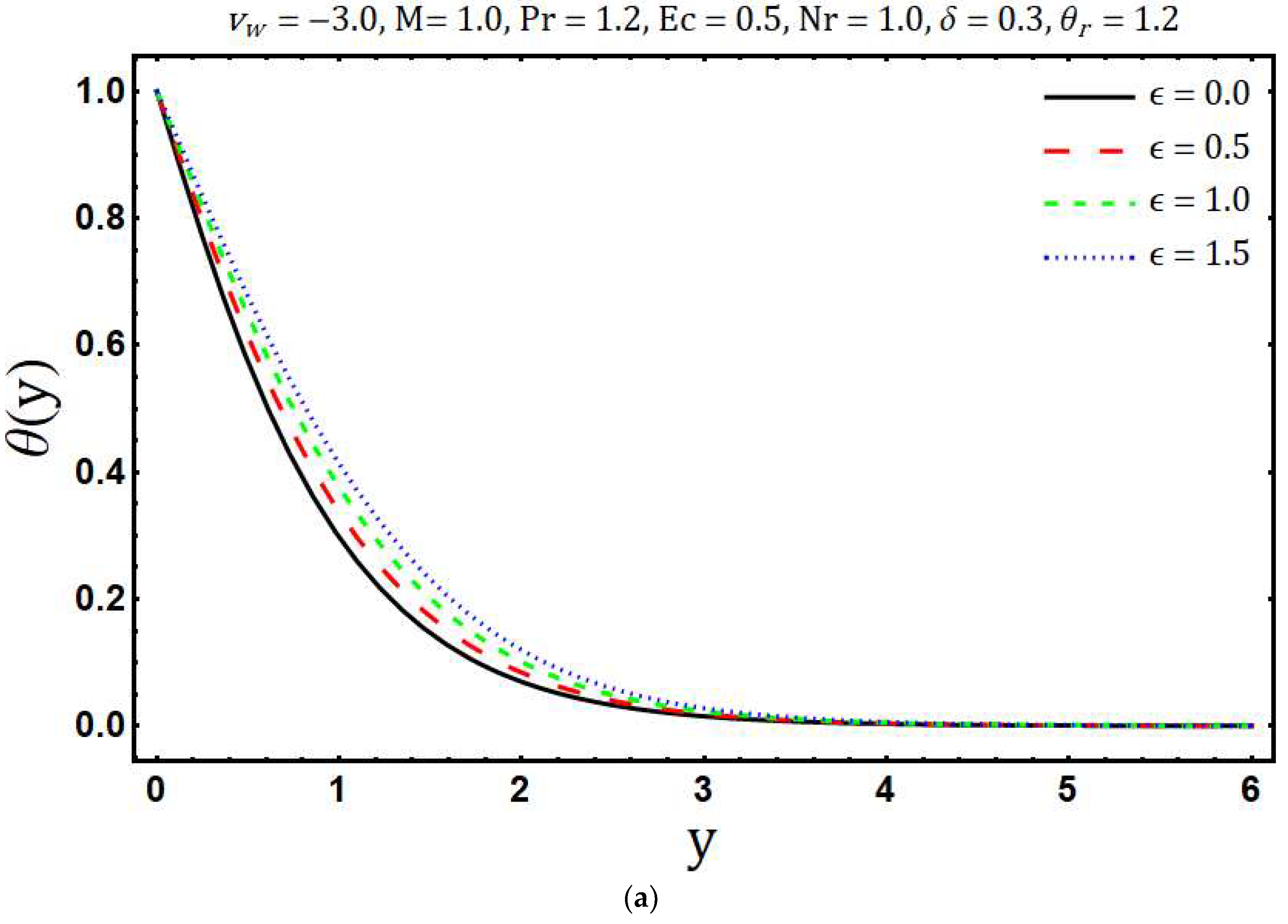
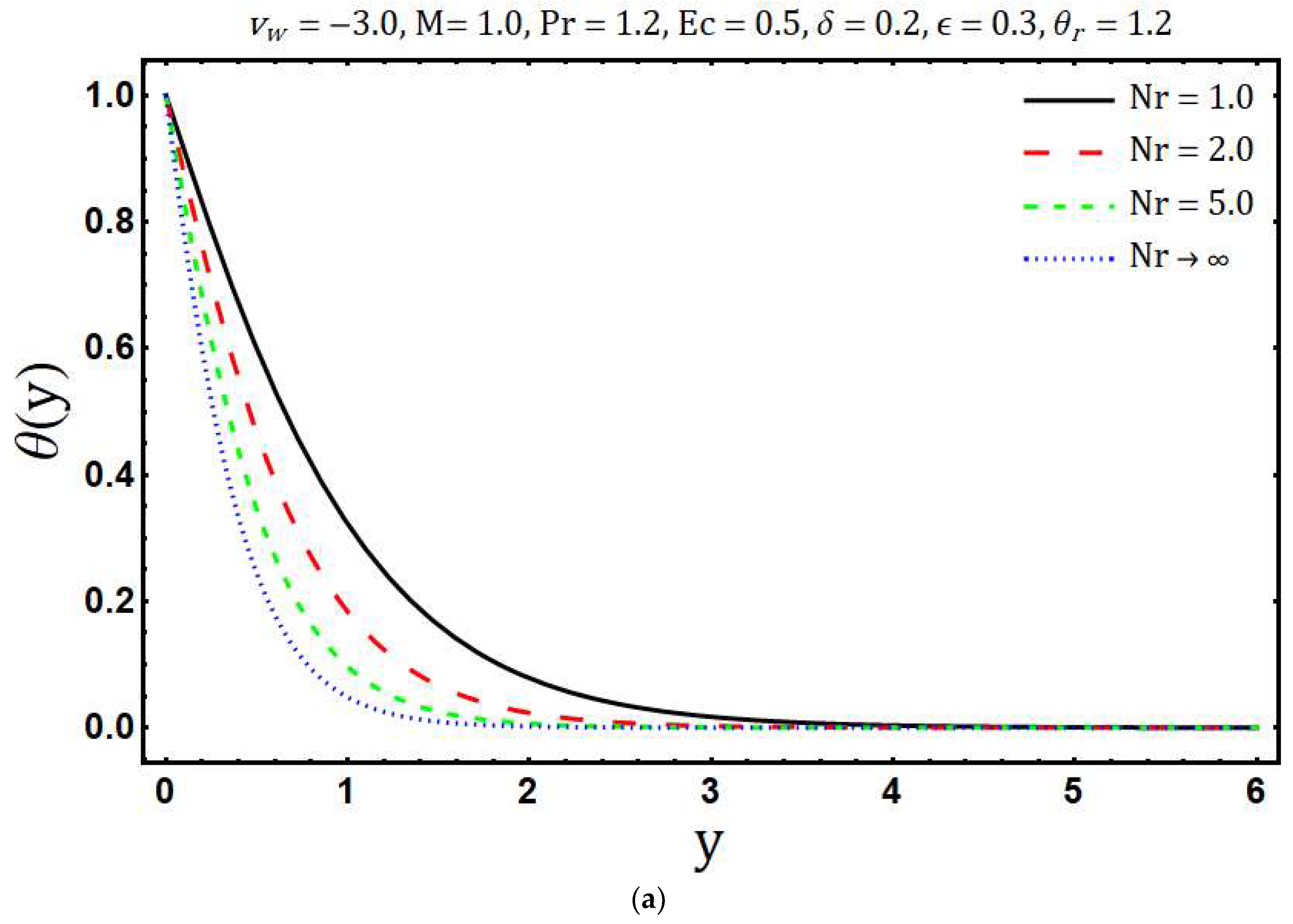
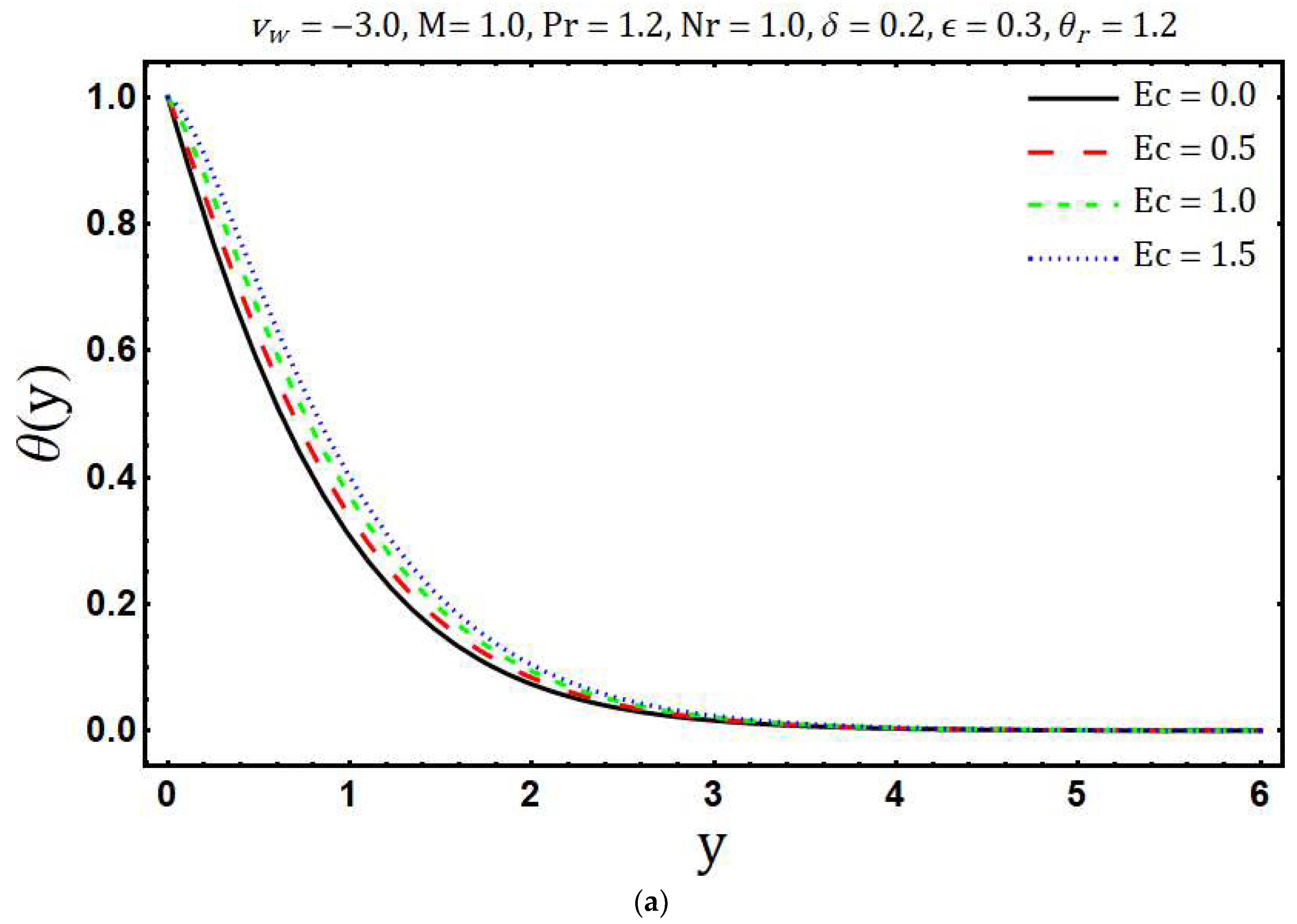
- Temperature increases with rising values of the Eckert number, heating parameter, and variable thermal conductivity while an opposite behavior has been observed for growing values of the mass suction parameter, Prandtl number, and radiation parameter .
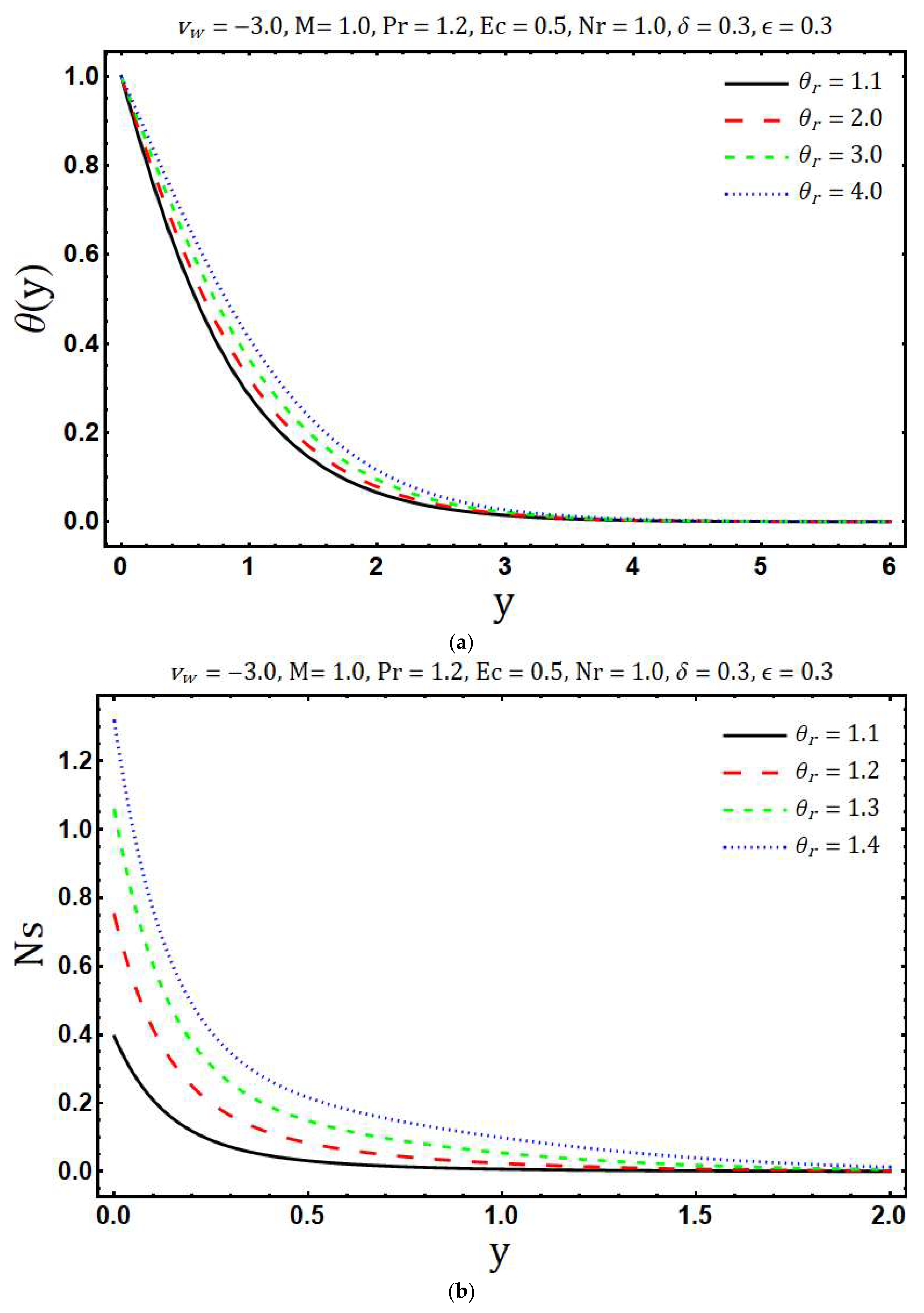
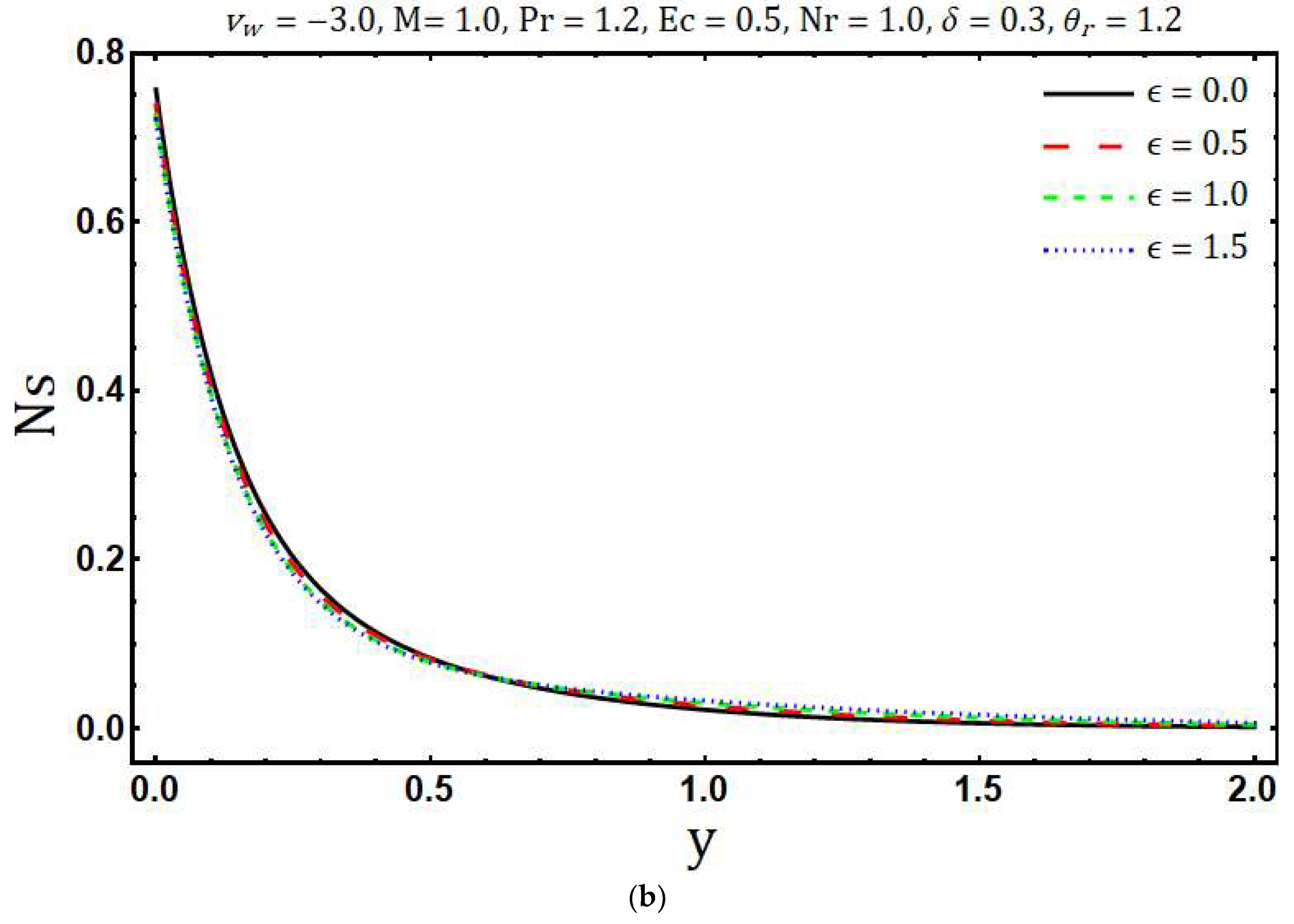
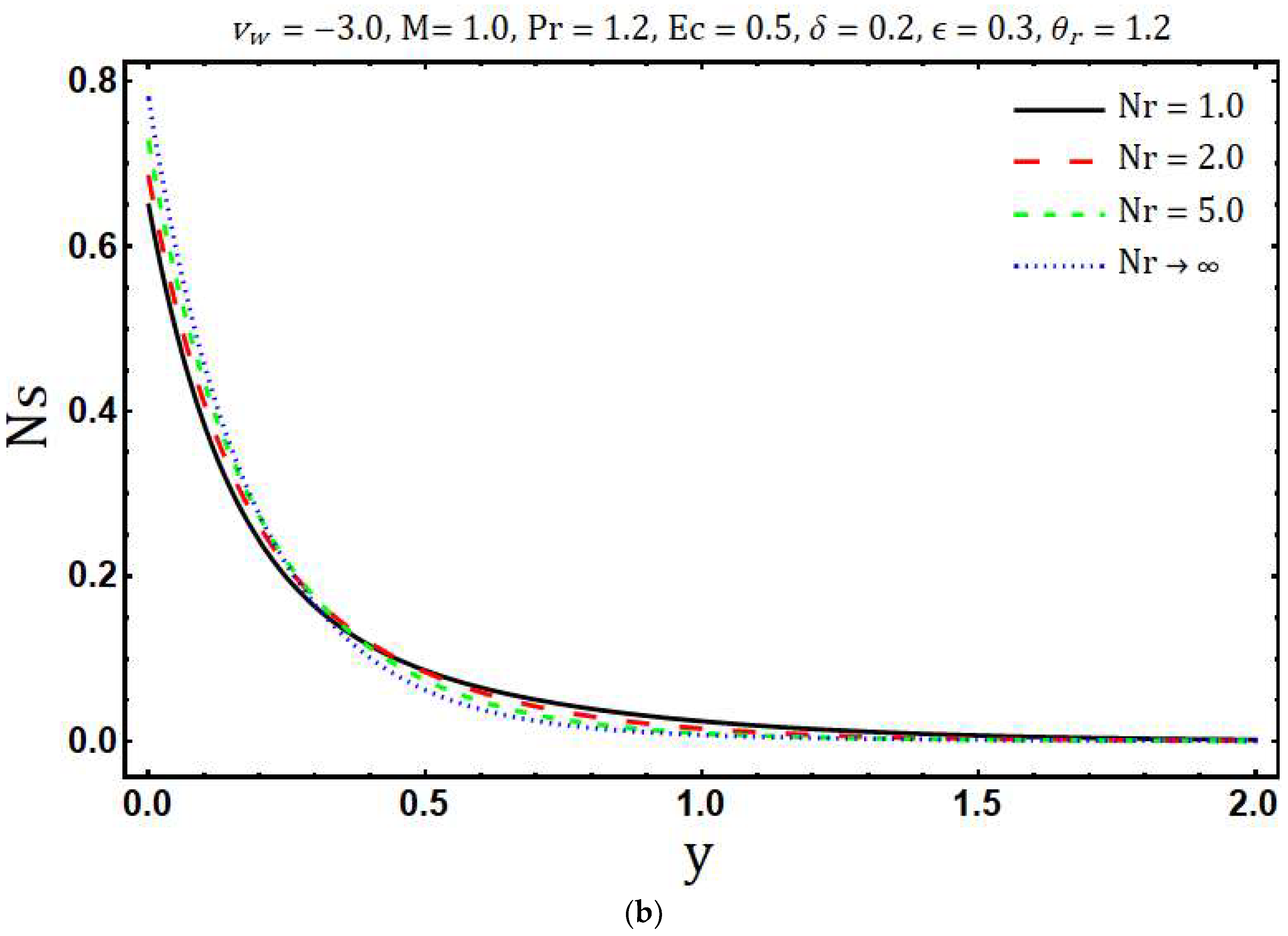
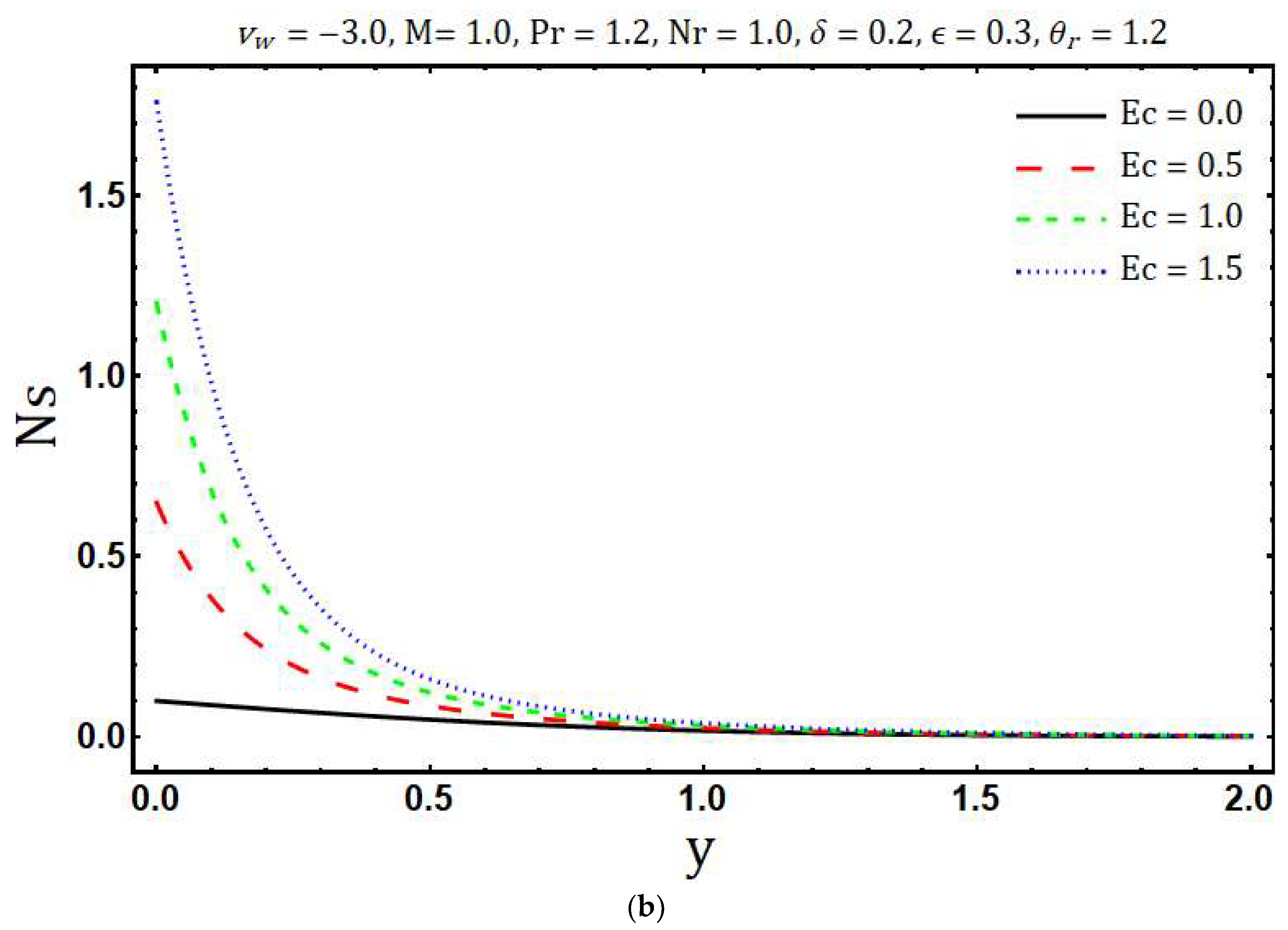
- The decrement in entropy generation is observed with increasing values of modified Hartmann number and variable thermal conductivity while increment in is observed with rising values of Prandtl number, radiation parameter, mass suction parameter, Eckert number, variable viscosity parameter and heating parameter.
- Maximum entropy is generated at the surface of Riga plate.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| with of electrodes and magnets | |
| specific heat at constant pressure | |
| Eckert number | |
| volumetric rate of entropy generation | |
| characteristic volumetric rate of entropy generation | |
| current density | |
| temperature dependent thermal conductivity | |
| thermal conductivity of fluid outside the boundary layer | |
| length unit | |
| magnetization of the magnets | |
| modified Hartmann number | |
| thermal radiation parameter | |
| entropy generation number | |
| Prandtl number | |
| fluid temperature | |
| temperature at the surface of Riga-plate | |
| ambient temperature | |
| horizontal velocity | |
| dimensionless horizontal velocity | |
| vertical component of velocity | |
| dimensionless vertical velocity | |
| horizontal coordinate | |
| dimensionless horizontal coordinate | |
| vertical coordinate | |
| dimensionless vertical coordinate | |
| Greek Symbols | |
| variable thermal conductivity parameter | |
| variable viscosity parameter | |
| dynamic viscosity | |
| dynamic viscosity of ambient fluid | |
| kinematic viscosity of ambient fluid | |
| fluid density | |
| dimensionless temperature | |
| heating parameter | |
| Subscripts | |
| condition on boundary | |
| condition outside the boundary layer |
References
- Gailitis, A.; Lielausis, O. On a possibility to reduce the hydrodynamic resistance of a plate in an electrolyte. Appl. Magnetohydrodyn. Rep. Phys. Inst. Riga 1961, 12, 143–146. [Google Scholar]
- Avilov, V.V. Electric and Magnetic Fields for the Riga Plate; Technical Report; FRZ: Rossendorf, Germany, 1998. [Google Scholar]
- Tsinober, A.B.; Shtern, A.G. Possibility of increasing the flow stability in a boundary layer by means of crossed electric and magnetic fields. Magnetohydrodynamics 1967, 3, 103–105. [Google Scholar]
- Pantokratoras, A. The Blasius and Sakiadis flow along a Riga-plate. Prog. Comput. Fluid Dyn. 2011, 11, 329–333. [Google Scholar] [CrossRef]
- Magyari, E.; Pantokratoras, A. Aiding and opposing mixed convection flows over the Riga-plate. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 3158–3167. [Google Scholar] [CrossRef]
- Ahmad, A.; Asghar, S.; Afzal, S. Flow of nanofluid past a Riga plate. J. Magn. Magn. Mater. 2016, 402, 44–48. [Google Scholar] [CrossRef]
- Ramesh, G.K.; Gireesha, B.J. Non-linear radiative flow of nanofluid past a moving/stationary Riga plate. Front. Heat Mass Transf. 2017, 9, 1–7. [Google Scholar] [CrossRef]
- Pantokratoras, A.; Magyari, E. EMHD free-convection boundary-layer flow from a Riga-plate. J. Eng. Math. 2009, 64, 303–315. [Google Scholar] [CrossRef]
- Pantokratoras, A.; Fang, T. Sakiadis flow with nonlinear Rosseland thermal radiation. Phys. Scr. 2012, 87, 015703. [Google Scholar] [CrossRef]
- Pantokratoras, A.; Fang, T. Blasius flow with nonlinear Rosseland thermal radiation. Meccanica 2014, 49, 1539–1545. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M. Entropy generation and heat transfer in boundary layer flow over a thin needle moving in a parallel stream in the presence of nonlinear Rosseland radiation. Int. J. Therm. Sci. 2018, 123, 117–128. [Google Scholar] [CrossRef]
- Sithole, H.; Mondal, H.; Sibanda, P. Entropy generation in a second grade magnetohydrodynamic nanofluid flow over a convectively heated stretching sheet with nonlinear thermal radiation and viscous dissipation. Res. Phys. 2018, 9, 1077–1085. [Google Scholar] [CrossRef]
- Babu, M.J.; Sandeep, N. Effect of nonlinear thermal radiation on non-aligned bio-convective stagnation point flow of a magnetic-nanofluid over a stretching sheet. Alex. Eng. J. 2016, 55, 1931–1939. [Google Scholar] [CrossRef]
- Ghadikolaei, S.S.; Hosseinzadeh, K.; Ganji, D.D.; Jafari, B. Nonlinear thermal radiation effect on magneto Casson nanofluid flow with Joule heating effect over an inclined porous stretching sheet. Case Stud. Therm. Eng. 2018, 12, 176–187. [Google Scholar] [CrossRef]
- Hossain, M.A.A.; Munir, M.S. Mixed convection flow from a vertical flat plate with temperature dependent viscosity. Int. J. Therm. Sci. 2000, 39, 173–183. [Google Scholar] [CrossRef]
- Khader, M.M.; Megahed, A.M. Approximate solutions for the flow and heat transfer due to a stretching sheet embedded in a porous medium with variable thickness, variable thermal conductivity and thermal radiation using Laguerre collocation method. Appl. Appl. Math. Int. J. 2015, 10, 817–834. [Google Scholar]
- Mureithi, E.W.; Mwaonanji, J.J.; Makinde, O.D. On the boundary layer flow over a moving surface in a fluid with temperature-dependent viscosity. Open J. Fluid Dyn. 2013, 3, 135–140. [Google Scholar] [CrossRef]
- Pal, D.; Mondal, H. Effects of temperature-dependent viscosity and variable thermal conductivity on MHD non-Darcy mixed convective diffusion of species over a stretching sheet. J. Egypt. Math. Soc. 2014, 22, 123–133. [Google Scholar] [CrossRef]
- Manjunatha, S.; Gireesha, B.J. Effects of variable viscosity and thermal conductivity on MHD flow and heat transfer of a dusty fluid. Ain Shams Eng. J. 2016, 7, 505–515. [Google Scholar] [CrossRef]
- Lin, Y.; Zheng, L.; Zhang, X. Radiation effects on Marangoni convection flow and heat transfer in pseudo-plastic non-Newtonian nanofluids with variable thermal conductivity. Int. J. Heat Mass Transf. 2014, 77, 708–716. [Google Scholar] [CrossRef]
- Hsiao, K.L. To Promote radiation electrical MHD activation Energy Thermal Extrusion Manufacturing System Efficiency by Using Carreau-Nanofluid with Parameters Control Method. Energy 2017, 130, 486–499. [Google Scholar] [CrossRef]
- Lin, Y.; Zheng, L.; Li, B.; Ma, L. A new diffusion for laminar boundary layer flow of power law fluids past a flat surface with magnetic effect and suction or injection. Int. J. Heat Mass Transf. 2015, 90, 1090–1097. [Google Scholar] [CrossRef]
- Olatundun, A.T.; Makinde, O.D. Analysis of Blasius flow of hybrid nanofluids over a convectively heated surface. Defect Diffus. Forum 2017, 377, 29–41. [Google Scholar] [CrossRef]
- Hsiao, K.L. Stagnation Electrical MHD Nanofluid Mixed Convection with Slip Boundary on a Stretching Sheet. Appl. Therm. Eng. 2016, 98, 850–861. [Google Scholar] [CrossRef]
- Seini, I.Y.; Makinde, O.D. Boundary layer flow near stagnation-points on a vertical surface with slip in the presence of transverse magnetic field. Int. J. Numer. Methods Heat Fluid Flow 2014, 24, 643–653. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization; CRC Press: New York, NY, USA, 1996. [Google Scholar]
- Bejan, A. The thermodynamic design of heat and mass transfer processes and devices. Heat Fluid Flow 1987, 8, 258–276. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Khan, I.; Shafie, S.; Alshomrani, A.S. Entropy generation in Magnetohydrodynamic mixed convection flow over an inclined stretching sheet. Entropy 2017, 19, 10. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Freidoonimehr, N. Analysis of entropy generation in MHD stagnation-point flow in porous media with heat transfer. Int. J. Comput. Methods Eng. Sci. Mech. 2014, 15, 345–355. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M. Entropy generation in three-dimensional flow of dissipative fluid. Int. J. Appl. Comput. Math. 2018, 16, 16. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Ismael, M.; Kasaeipoor, A.; Armaghani, T. Entropy generation and natural convection of CuO-Water nanofluid in C-shaped cavity under magnetic field. Entropy 2016, 18, 50. [Google Scholar] [CrossRef]
- Das, S.; Jana, R.N.; Chamkha, A.J. Entropy generation due to unsteady hydromagnetic Couette flow and heat transfer with asymmetric convective cooling in a rotating system. J. Math. Model. 2015, 3, 107–128. [Google Scholar]
- Butt, A.S.; Ali, A.; Tufail, N.; Mehmood, A. Entropy production in mixed convective magnetohydrodynamic flow of nanofluid over a linearly stretching sheet. J. Nanofluids 2017, 6, 379–389. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Shafie, S. Entropy generation in hydromagnetic boundary flow under the effects of frictional and Joule heating: Exact solutions. Eur. Phys. J. Plus 2017, 132, 3–11. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A. Entropy analysis of magnetohydrodynamic flow and heat transfer due to stretching cylinder. J. Taiwan Inst. Chem. Eng. 2014, 45, 780–786. [Google Scholar] [CrossRef]
| Shooting | bvp4c | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| −3.0 | 2.5 | 0.2 | 0.3 | 1.2 | 0.5 | 1.0 | 1.2 | ||
| −4.0 | |||||||||
| −5.0 | |||||||||
| −3.0 | 1.0 | ||||||||
| 2.0 | |||||||||
| 3.0 | |||||||||
| 2.5 | 0.0 | ||||||||
| 0.5 | |||||||||
| 1.0 | |||||||||
| 0.3 | 0.0 | ||||||||
| 0.5 | |||||||||
| 1.0 | |||||||||
| 0.3 | 0.7 | ||||||||
| 1.2 | |||||||||
| 3.0 | |||||||||
| 1.2 | 0.0 | ||||||||
| 0.3 | |||||||||
| 0.6 | |||||||||
| 0.5 | 1.0 | ||||||||
| 2.0 | |||||||||
| 5.0 | |||||||||
| 1.0 | 1.1 | ||||||||
| 1.2 | |||||||||
| 1.3 | |||||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afridi, M.I.; Qasim, M.; Hussanan, A. Second Law Analysis of Dissipative Flow over a Riga Plate with Non-Linear Rosseland Thermal Radiation and Variable Transport Properties. Entropy 2018, 20, 615. https://doi.org/10.3390/e20080615
Afridi MI, Qasim M, Hussanan A. Second Law Analysis of Dissipative Flow over a Riga Plate with Non-Linear Rosseland Thermal Radiation and Variable Transport Properties. Entropy. 2018; 20(8):615. https://doi.org/10.3390/e20080615
Chicago/Turabian StyleAfridi, Muhammad Idrees, Muhammad Qasim, and Abid Hussanan. 2018. "Second Law Analysis of Dissipative Flow over a Riga Plate with Non-Linear Rosseland Thermal Radiation and Variable Transport Properties" Entropy 20, no. 8: 615. https://doi.org/10.3390/e20080615
APA StyleAfridi, M. I., Qasim, M., & Hussanan, A. (2018). Second Law Analysis of Dissipative Flow over a Riga Plate with Non-Linear Rosseland Thermal Radiation and Variable Transport Properties. Entropy, 20(8), 615. https://doi.org/10.3390/e20080615






