Permutation Entropy Based on Non-Uniform Embedding
Abstract
1. Introduction
2. Preliminaries
2.1. Permutation Entropy
2.2. Non-Uniform Embedding
3. The Proposed Visualization Scheme for PE
- Determine the optimal embedding dimension D for a given time series.
- Set L (the upper range for all time lags). Determine the set of optimal time lags according to Equation (5).
- Repeat in lexicographical order and construct planar images of PE:
- Average all planar digital images of PE.
4. Computational Experiments
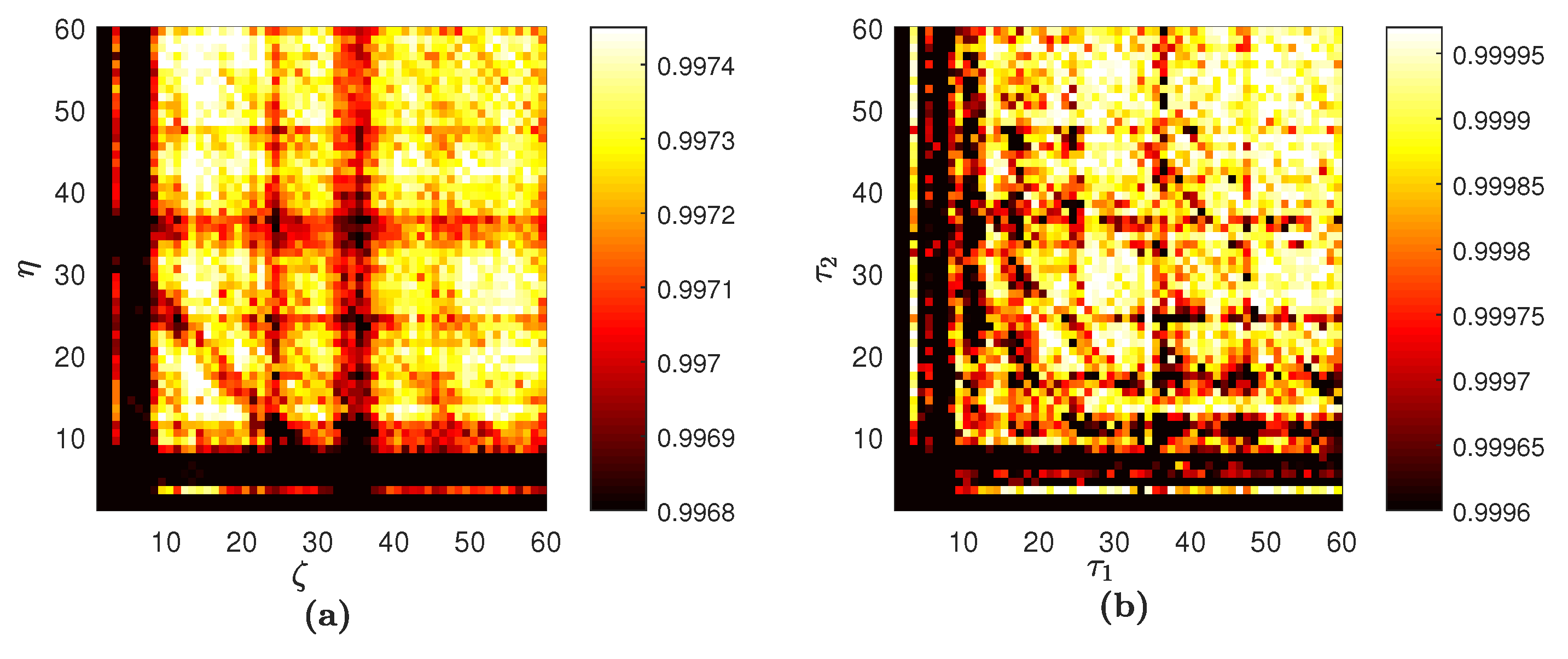
4.1. The Sine Wave
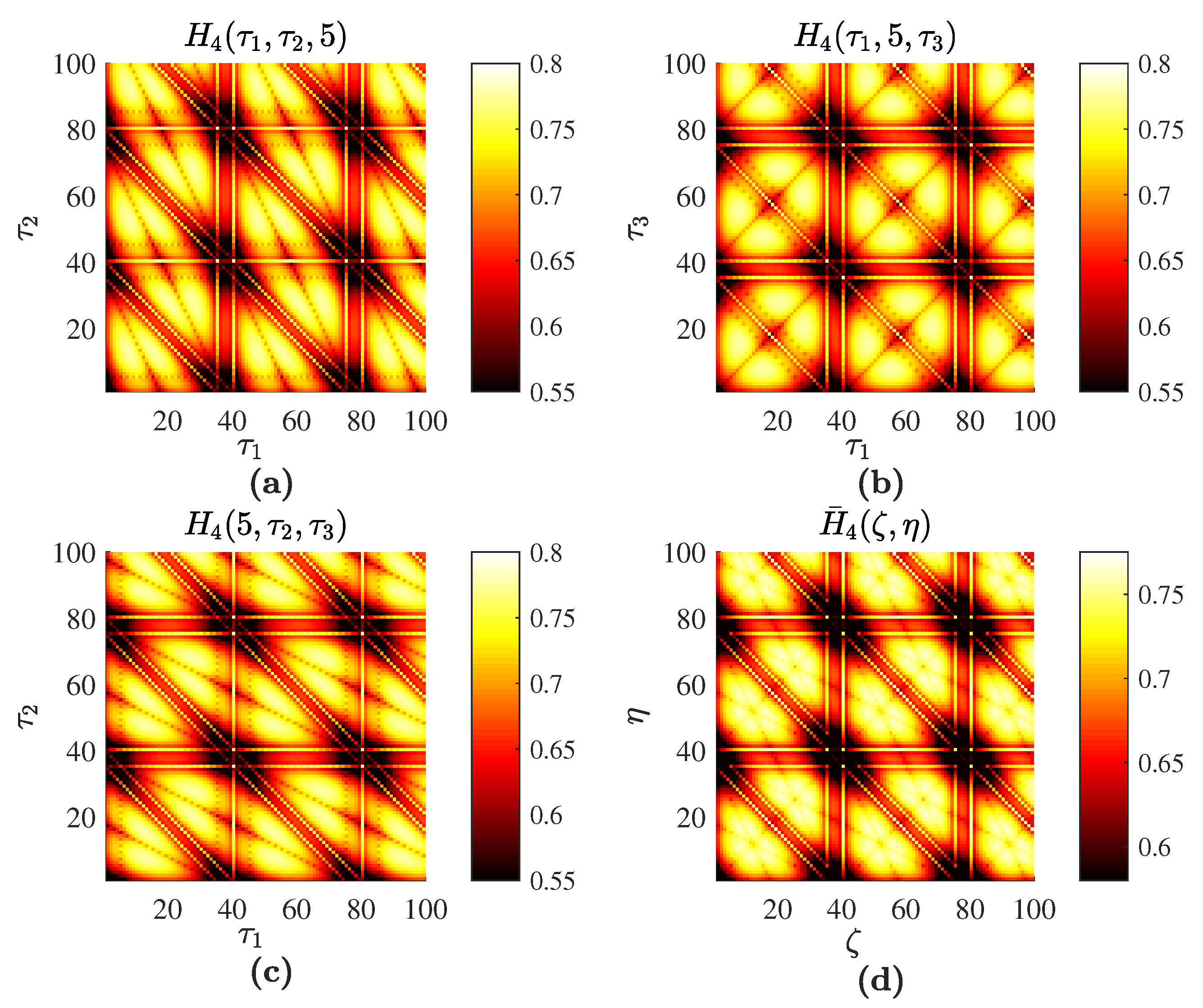
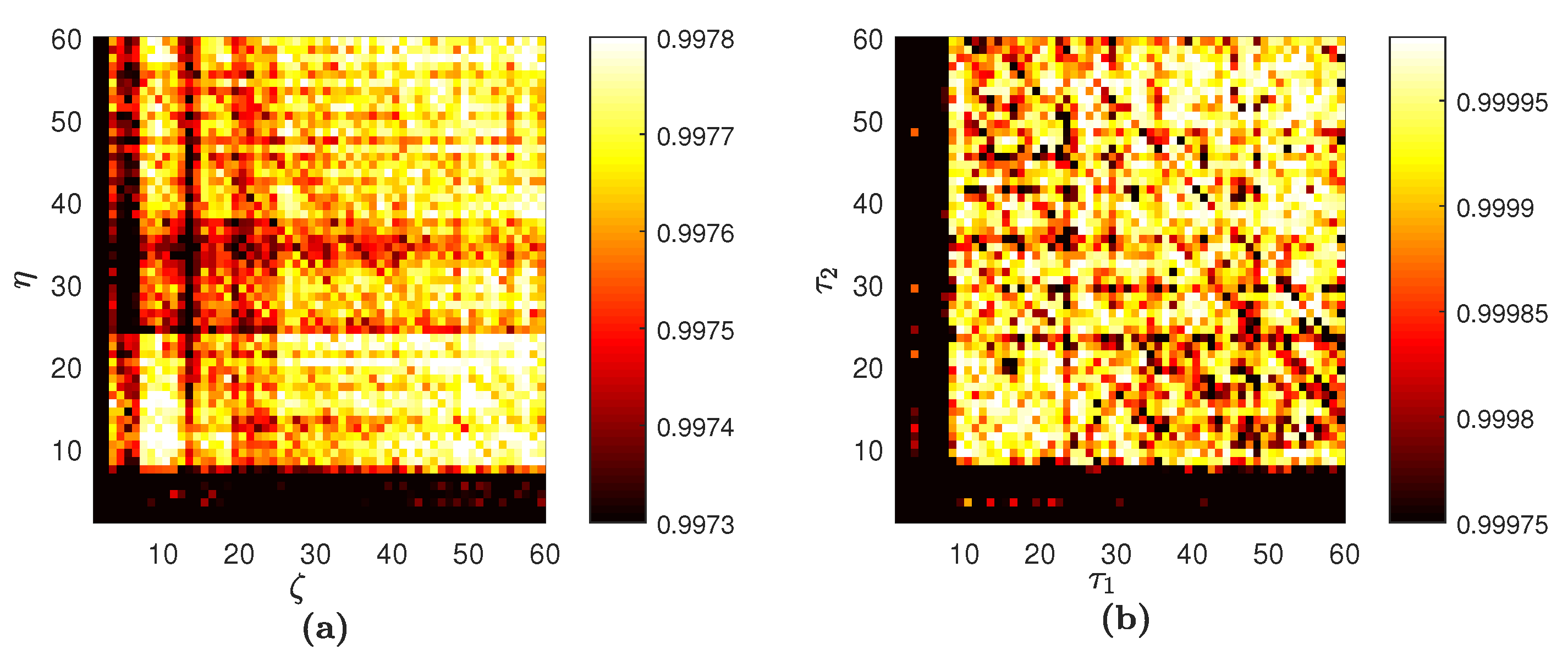
4.2. The Rössler Time Series
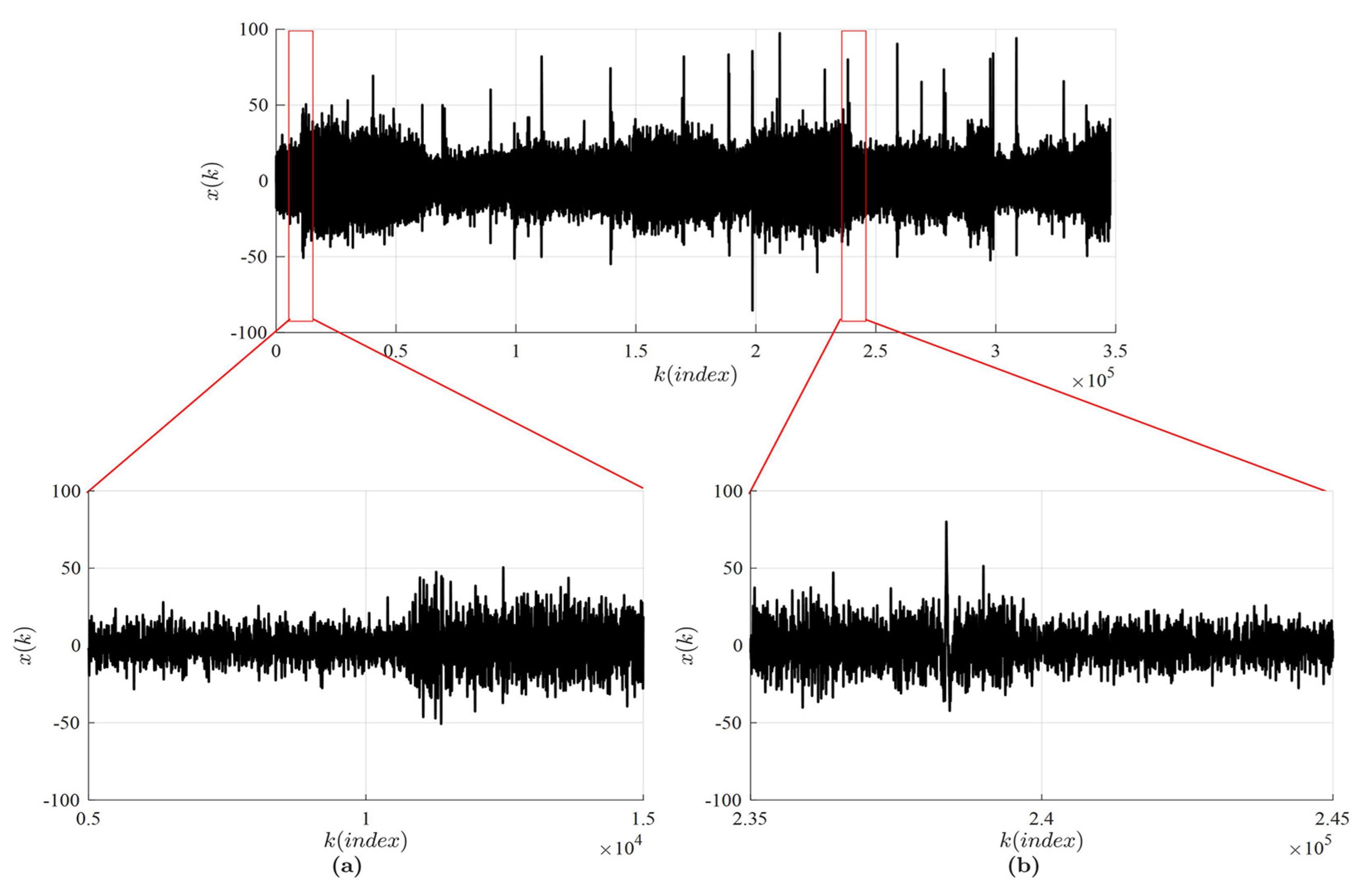
4.3. Real-World Time Series
5. Discussion
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PE | Permutation Entropy |
| FNN | False Nearest Neighbors |
| EEG | Electroencephalogram |
| BNCI | Brain/Neural Computer Interaction |
References
- Lempel, A.; Ziv, J. On the complexity of finite sequences. IEEE Trans. Inform. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Three approaches to the definition of the concept “quantity of information”. Probl. Peredachi Inf. 1965, 1, 3–11. [Google Scholar]
- Kaspar, F.; Schuster, H.G. Easily calculable measure for the complexity of spatiotemporal patterns. Phys. Rev. A 1987, 36, 842–848. [Google Scholar] [CrossRef]
- Farmer, D.J. Information dimension and the probabilistic structure of chaos. J. Phys. Sci. 1982, 37, 1304–1325. [Google Scholar] [CrossRef]
- Termonia, Y.; Alexandrowicz, Z. Fractal dimension of strange attractors from radius versus size of arbitrary clusters. Phys. Rev. Lett. 1983, 51, 1265–1268. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Walters, P. An Introduction to Ergodic Theory; Springer Publishing House: New York, NY, USA, 1982; p. 250. ISBN 978-0-387-95152-2. [Google Scholar]
- Stolz, I.; Keller, K. A general symbolic approach to Kolmogorov-Sinai entropy. Entropy 2017, 19, 675. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, 2039–2049. [Google Scholar] [CrossRef] [PubMed]
- Keller, K.; Unakafov, A.M.; Unakafova, V.A. Ordinal patterns. Entropy 2014, 16, 6212–6239. [Google Scholar] [CrossRef]
- Zhou, J.; Xiao, J.; Xiao, H.; Zhang, W.; Zhu, W.; Li, C. Multifault diagnosis for rolling element bearings based on intrinsic mode permutation entropy and ensemble optimal extreme learning machine. Adv. Mech. Eng. 2014, 6, 803–919. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Zunino, L.; Olivares, F.; Scholkmann, F.; Rosso, O.A. Permutation entropy based time series analysis: Equalities in the input signal can lead to false conclusions. Phys. Lett. A 2017, 381, 1883–1892. [Google Scholar] [CrossRef]
- Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutationentropy and its main biomedical and econophysicsapplications: A review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Li, Y.; Li, G.; Yang, Y.; Liang, X.; Xu, M. A fault diagnosis scheme for planetary gearboxes using adaptive multi-scale morphology filter and modified hierarchical permutation entropy. Mech. Syst. Signal Proccess 2018, 105, 319–337. [Google Scholar] [CrossRef]
- Unakafova, V.A.; Keller, K. Efficiently measuring complexity on the basis of real-world data. Entropy 2013, 15, 4392–4415. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Amplitude-aware permutation entropy: Illustration in spike detection and signal segmentation. Comput. Meth. Prog. Biomed. 2016, 128, 40–51. [Google Scholar] [CrossRef] [PubMed]
- Packard, N.H.; Crutchfield, J.P.; Farmer, J.D.; Shaw, R.S. Geometry from a time series. Phys. Rev. Lett. 1980, 45, 712–716. [Google Scholar] [CrossRef]
- Theiler, J. Estimating the fractal dimension of chaotic time series. Lincoln Lab. J. 1990, 3, 63–86. [Google Scholar]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Rand, D.A., Young, L.S., Eds.; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar] [CrossRef]
- Sauer, T.; Yorke, J.A.; Casdagli, M. Embedology. J. Stat. Phys. 1991, 65, 579–616. [Google Scholar] [CrossRef]
- Yap, H.L.; Eftekhari, A.; Wakin, M.B.; Rozell, C.J. A first analysis of the stability of takens’ embedding. In Proceedings of the IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, CA, USA, 3–5 December 2014; pp. 404–408. [Google Scholar] [CrossRef]
- Fraser, A.; Swinney, H. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Measuring the strangeness of strange attractors. Physical D 1983, 9, 189–208. [Google Scholar] [CrossRef]
- Buzug, T.; Pfister, G. Comparison of algorithms calculating optimal embedding parameters for delay time coordinates. Physical D 1992, 58, 127–137. [Google Scholar] [CrossRef]
- Buzug, T.; Pfister, G. Optimal delay time and embedding dimension for delay-time coordinates by analysis of the global static and local dynamical behavior of strange attractors. Phys. Rev. A 1992, 45, 7073–7084. [Google Scholar] [CrossRef] [PubMed]
- Casdagli, M.; Eubank, S.; Farmer, J.; Gibson, J. State space reconstruction in the presence of noise. Physical D 1991, 51, 52–98. [Google Scholar] [CrossRef]
- Bradley, E.; Kantz, H. Nonlinear time-series analysis revisited. Chaos 2015, 25, 097610. [Google Scholar] [CrossRef] [PubMed]
- Falconer, K. Box-counting dimension. In Fractal Geometry: Mathematical Foundation and Applications; John Wiley and Sons: Chichester, UK, 1990; pp. 27–43. ISBN 10: 0471922870. [Google Scholar]
- Grassberger, P.; Procaccia, I. Characterization of strange attractors. Phys. Rev. Lett. 1983, 50, 346–349. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Physical D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Pesin, Y. Characteristic Lyapunov exponents and smooth ergodic theory. Russ. Math. Surv. 1977, 32, 55–114. [Google Scholar] [CrossRef]
- Kennel, M.; Brown, R.; Abarbanel, H. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef] [PubMed]
- Abarbanel, H.D.I.; Brown, R.; Sidorowich, J.J.; Tsimring, L.S. The analysis of observed chaotic data in physical systems. Rev. Mod. Phys. 1993, 65, 1331–1392. [Google Scholar] [CrossRef]
- Huke, J.P.; Broomhead, D.S. Embedding theorems for non-uniformly sampled dynamical systems. Nonlinearity 2007, 20, 2205–2244. [Google Scholar] [CrossRef]
- Manabe, Y.; Chakraborty, B. A novel approach for estimation of optimal embedding parameters of nonlinear time series by structural learning of neural network. Neurocomputing 2007, 70, 1360–1371. [Google Scholar] [CrossRef]
- Small, M. Optimal time delay embedding for nonlinear time series modeling. arXiv, 2003; arXiv:0312011v1. [Google Scholar]
- Vitrano, J.B.; Povinelli, R.J. Selecting dimensions and delay values for a time-delay embedding using a genetic algorithm. In Proceedings of the GECCO’01 3rd Annual Conference on Genetic and Evolutionary Computation, San Francisco, CA, USA, 7–11 July 2001; pp. 1423–1430, ISBN 1-55860-774-9. [Google Scholar]
- Shen, M.; Chen, W.N.; Zhang, J.; Chung, H.S.H.; Kaynak, O. Optimal selection of parameters for nonuniform embedding of chaotic time series using ant colony optimization. IEEE Trans. Cybern. 2013, 43, 790–802. [Google Scholar] [CrossRef] [PubMed]
- Ragulskis, M.; Lukoseviciute, K. Non-uniform attractor embedding for time series forecasting by fuzzy inference systems. Neurocomputing 2009, 72, 2618–2626. [Google Scholar] [CrossRef]
- Lukoseviciute, K.; Ragulskis, M. Evolutionary algorithms for the selection of time lags for time series forecasting by fuzzy inference systems. Neurocomputing 2010, 73, 2077–2088. [Google Scholar] [CrossRef]
- Timofejeva, I.; Poskuviene, K.; Cao, M.S.; Ragulskis, M. Synchronization measure based on a geometric approach to attractor embedding using finite observation windows. Complexity 2018, 2018, 8259496. [Google Scholar] [CrossRef]
- Little, D.J.; Kane, D.M. Permutation entropy with vector embedding delays. Phy. Rev. E 2017, 96, 062205. [Google Scholar] [CrossRef] [PubMed]
- Rössler, O.E. An equation for continuous chaos. Phys. Lett. 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Letellier, C.; Messager, V. Influences on Otto E. Rössler’s earliest paper on chaos. Chaos 2010, 20, 3585–3616. [Google Scholar] [CrossRef]
- Amigo, J.M. Permutation Complexity in Dynamical Systems; Springer: Berlin, Germany, 2010; p. 280. ISBN 978-3-642-04083-2. [Google Scholar]
- Amigo, J.M.; Zambrano, S.; Sanjuan, M.A.F. Combinatorial detection of determinism in noisy time series. EPL 2008, 83, 60005. [Google Scholar] [CrossRef]
- BNCI Horizon 2020 Project Database. Available online: http://bnci-horizon-2020.eu/database/data-sets (accessed on 1 May 2018).
- Riedl, M.; Müller, A.; Wessel, N. Practical considerations of permutation entropy. Eur. Phys. J. Spec. Top. 2013, 222, 249–262. [Google Scholar] [CrossRef]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, M.; Poskuviene, K.; Alkayem, N.F.; Cao, M.; Ragulskis, M. Permutation Entropy Based on Non-Uniform Embedding. Entropy 2018, 20, 612. https://doi.org/10.3390/e20080612
Tao M, Poskuviene K, Alkayem NF, Cao M, Ragulskis M. Permutation Entropy Based on Non-Uniform Embedding. Entropy. 2018; 20(8):612. https://doi.org/10.3390/e20080612
Chicago/Turabian StyleTao, Mei, Kristina Poskuviene, Nizar Faisal Alkayem, Maosen Cao, and Minvydas Ragulskis. 2018. "Permutation Entropy Based on Non-Uniform Embedding" Entropy 20, no. 8: 612. https://doi.org/10.3390/e20080612
APA StyleTao, M., Poskuviene, K., Alkayem, N. F., Cao, M., & Ragulskis, M. (2018). Permutation Entropy Based on Non-Uniform Embedding. Entropy, 20(8), 612. https://doi.org/10.3390/e20080612








