We suppose that we are only allowed to see whether or not the MWC molecule is active or inactive, as would be true for most experimental observations of ligand-gated ion channels. This is a key constraint, as otherwise, the minimal generative model would be the minimal maximally predictive model and none of the discrepancies described here would arise. In what follows, we explore the effects of kinetic rates on intrinsic and functional computation.
3.1. Intrinsic Computation
If , then there is no “sync word”–that is, no string of observed past symbols that uniquely determines the underlying present state of the MWC molecule. (Note again that this would not be the case if we were allowed to observe the full state, and not just whether or not the MWC molecule is active or inactive.) This has important consequences for and for the process’ -machine.
To analyze
, we move to the discrete-time domain, so as to avoid the interpretational difficulties with differential entropy [
18]. By observing the process every
for
much smaller than any inherent time constant in the problem, the process is turned into a discrete-time process. The transition probabilities of this new process have corresponding labeled transition matrices
, which are approximated to lowest order in
by
, where
x is an emitted symbol:
and
The causal states correspond to the mixed states
defined by either
or
. When
, all
a’s and
b’s are allowed; there are an uncountable infinity of these causal states because there is no sync word. As such, the
-machine is uncountable and intractable, and statistical complexity is very likely infinite. However, when
, then only a countable set of
a’s and
b’s are allowed according to the discrete-time analogue of Theorem 1 of Ref. [
18]. In particular, the causal states are identified as both the present configuration (active or inactive) and the number of time steps since last configuration switch. As a result, the
-machine is countably infinite and tractable, and statistical complexity is finite, though it increases with
[
20].
This can be seen more directly by considering the mixed-state presentation’s box-counting dimension
when the process is turned into a discrete-time process with small time resolution
. We coarse-grain mixed-state simplex into cubes of side-length
, and count the number of non-empty boxes
, as described in Ref. [
17,
21]. The scaling of
with
reveals the box-counting dimension
of the mixed-state presentation, via
.
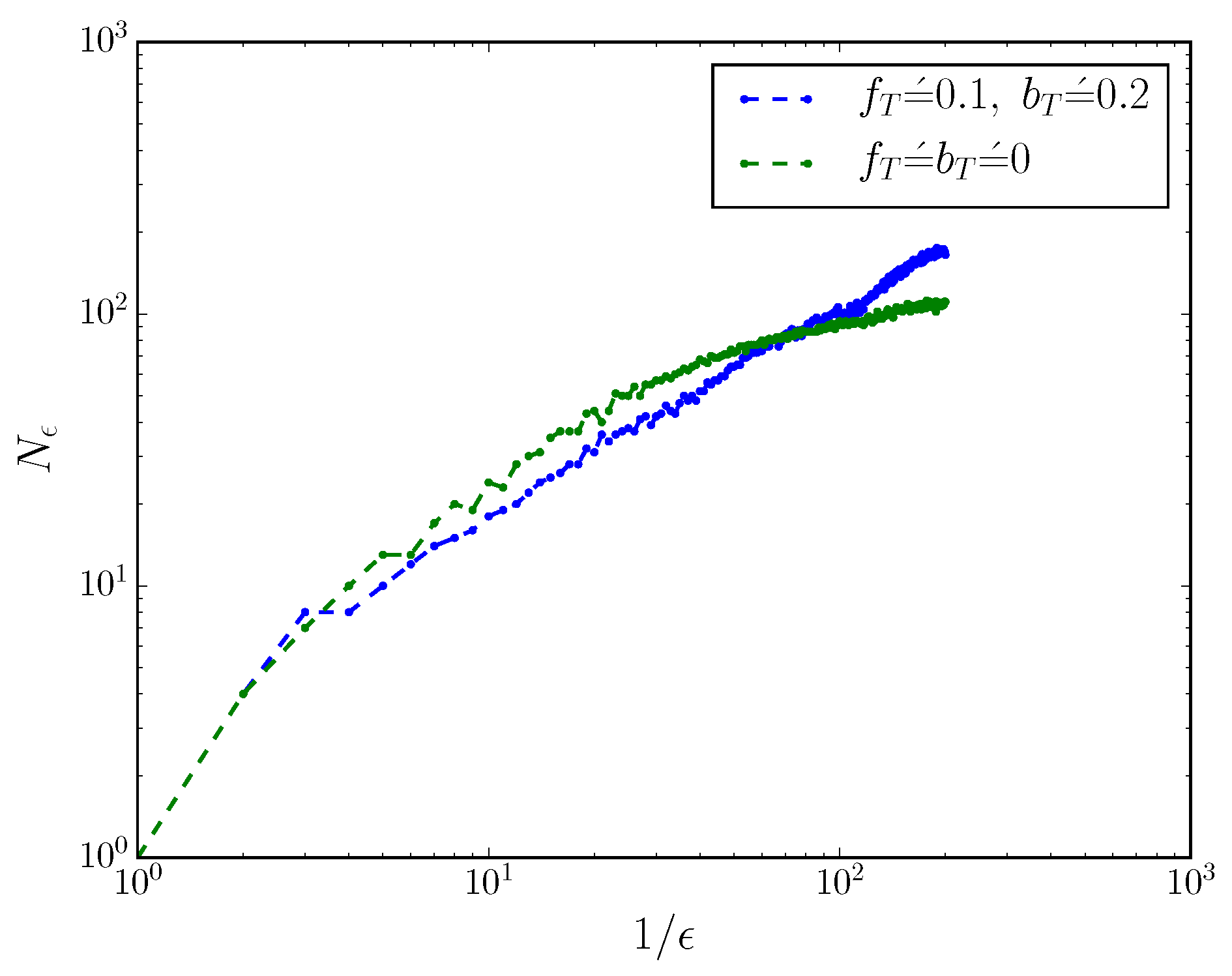
Figure 2 shows the scaling of
with
for an MWC molecule with and without
. When
,
; when
, the box-counting dimension
.
The reason for the former fact lies in Theorem 1 of Ref. [
18]. When
, the dynamic MWC molecule of
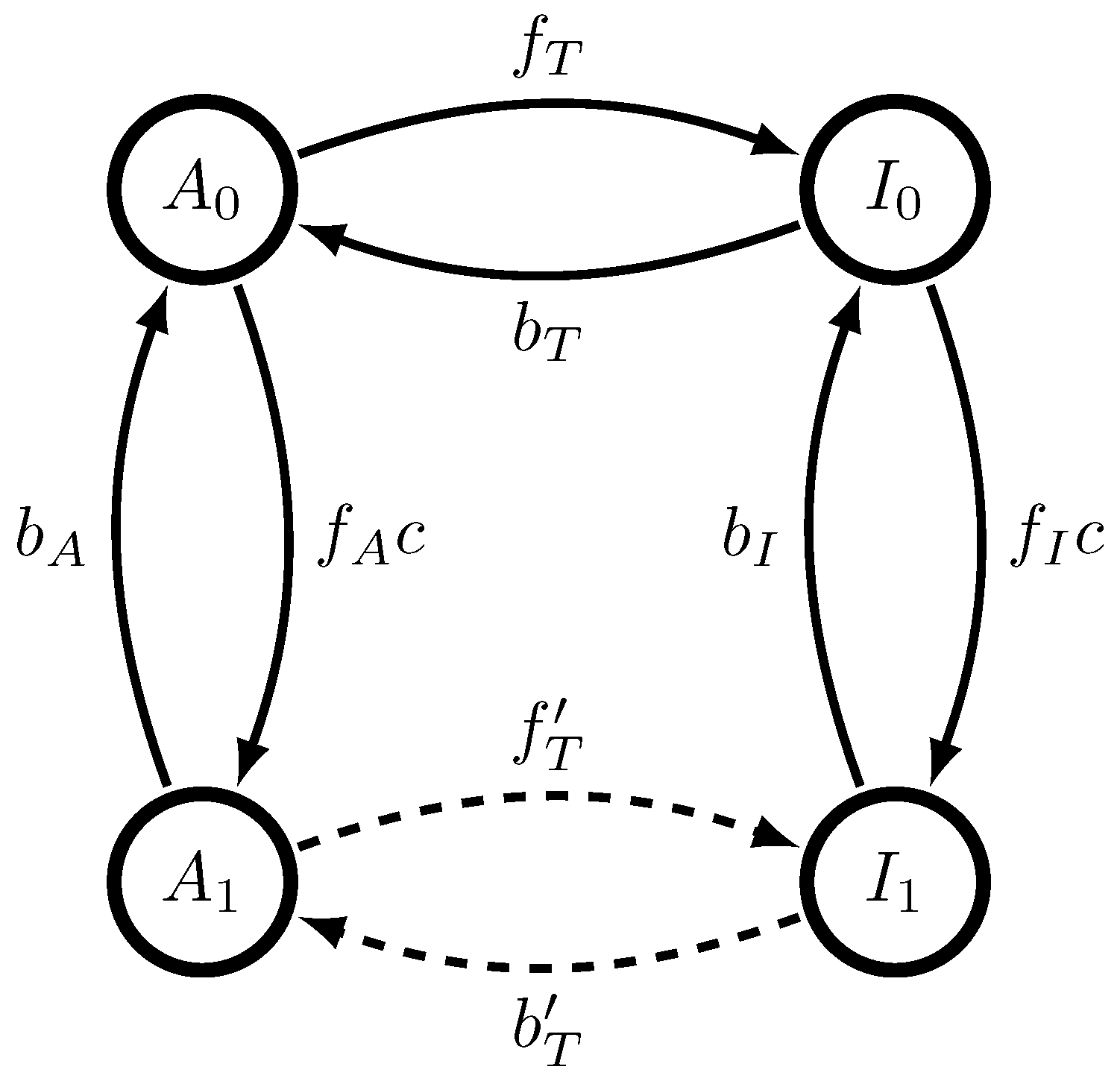
Figure 1 generates a semi-Markov process, a restricted version of the unifilar hidden semi-Markov processes analyzed in Ref. [
18]. This is true even when there is more than one ligand binding site. Causal states are characterized by
x, whether or not the MWC molecule is presently active, and
, the time since the MWC molecule last switched between activities. The now-tractable
-machine takes the form shown in
Figure 3.
In the continuous-time limit, which one can derive by considering the limit of the discrete-time process considered above with appropriate renormalization (e.g., compare Ref. [
20] to Ref. [
22]), all probability distributions over mixed states become probability density functions. Continuous-time statistical complexity can be defined using the entropy of mixed random variables [
18,
22], though differential entropy does have some troubling properties mentioned in those references. Given the analysis above, there is likely a singular limit in the continuous-time statistical complexity as the kinetic rates
tend to 0.
Not all structure-based characterizations of a process lack robustness in this way, as different structure-based metrics pick up on different kinds of structure. To show this, we now compare the statistical complexity
and the excess entropy
[
10,
11,
12] when
. (We calculate
of the continuous-time process, as the excess entropy of the discrete-time process converges to that of the continuous-time process in the
limit [
20].) The latter can be calculated via
[
23,
24], while
, and so calculation of both merely requires the joint distribution
. For that, we need
, the dwell time distributions of activity and inactivity. Note that emission of an
A implies that one has just landed in
, and similarly, emission of an
I implies that one has just landed in
. Hence,
is the first-passage time distribution to state
in which one starts in
; similarly,
is the first-passage time distribution to state
in which one starts in
. To aid with the calculation, we recall the labeled transition matrices of Equation (
5) when
. The matrix
includes only the transitions between various active conformations and the only transition from active to inactive,
. Therefore, the probability of not having stayed in active states given that one started in
after a time
t is given by
where
is the vector with elements
. Hence, the survival function
, the probability that one stays in the active conformation (one of
) after time
t given that one started in
, can be calculated via
After differentiation, we find that
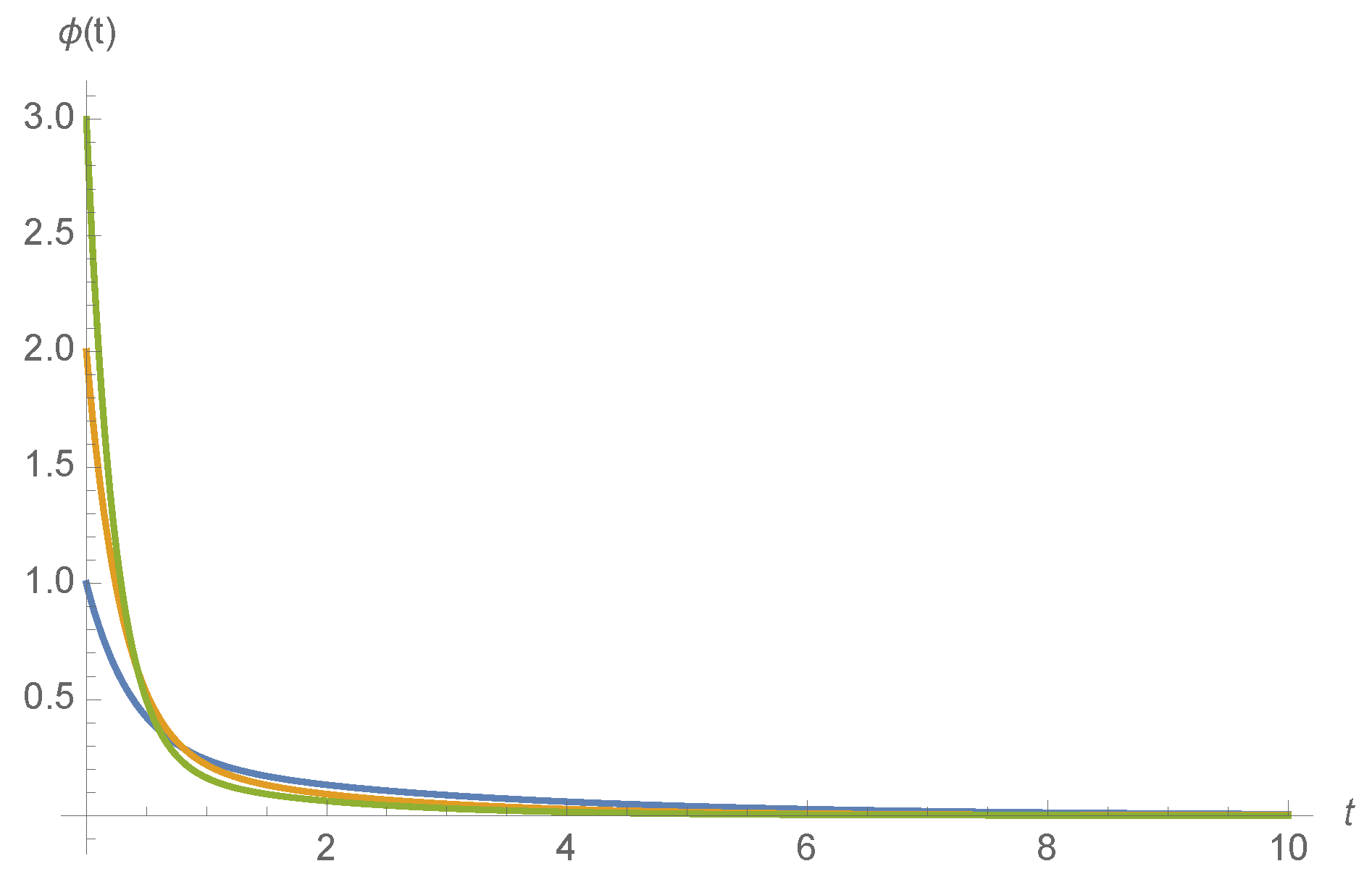
Examples of
for various ligand concentrations
c and kinetic rates are shown in
Figure 4.
From Lemma 1 of Ref. [
18], we find that the statistical complexity of this semi-Markov process is given by
where
,
, and
.
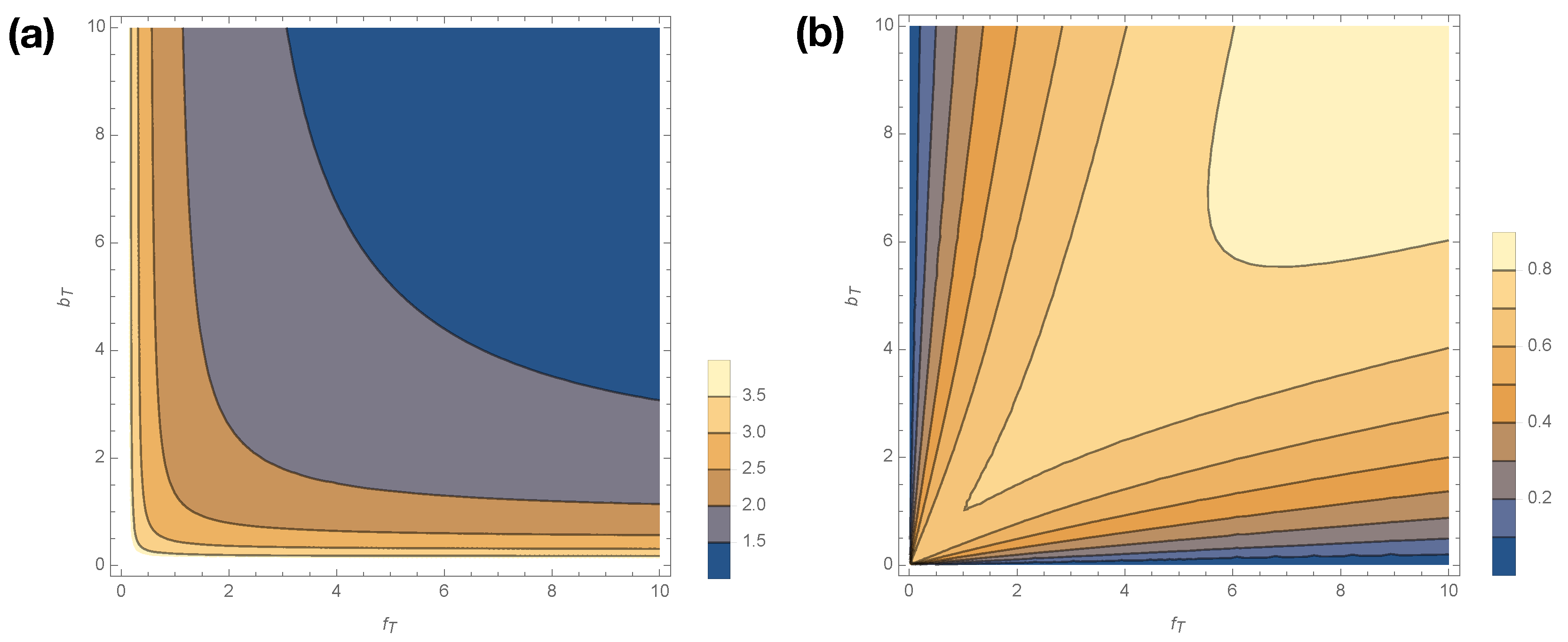
Figure 5 shows how
smoothly varies with changes in
for
. Statistical complexity is maximized at small kinetic rates,
; when those kinetic rates are small, dwell time distributions have longer tails, and the memory required to losslessly predict increases. Interestingly, if either
or
is exactly 0, then the generated process emits only
A or
I (see
Figure 1) and thus has
. In other words, the limits
are singular, as were the limits
.
We now wish to calculate
which is
[
23], and so
As a semi-Markov process is causally reversible, we have
as given in Equation (
10). Furthermore, the reverse-time causal states are the pair
(the time to next symbol and present symbol) while the forward-time causal states are still the pair
(the time since last symbol and present symbol) [
18], so that
almost surely, implying that
. Hence,
where
is just the present symbol. We then note that
as was derived in Ref. [
22] for a continuous-time renewal process, but the same derivation holds for the semi-Markov process. It is then straightforward to show that excess entropy is
where
Figure 5b shows how excess entropy
varies with
. Interestingly,
varies in opposition to
, attaining its lowest values at low values of
and
. Hence, the singular limits
that plague
are not singular limits for
. Nor are
singular limits for
, as arbitrarily small values of
lead to arbitrarily small perturbations to the trajectory distribution, and thus arbitrarily small perturbations to the mutual information between past and future.
How different would the results be for , i.e., when the number of binding sites of the MWC molecule exceeded 1? In short, we would expect the same qualitative trends and singular limits. In this more general case, we allow an active MWC molecule with k ligands bound to transition to an inactive MWC molecule with k ligands bound, and vice versa, both with rates and , as for . Meanwhile, also as for , the active MWC molecule with no ligands bound can transition to the inactive MWC molecule with no ligands bound with rate , and the reverse transition can occur with rate . The observed process for fixed ligand concentration would still be semi-Markov when , as was true for . Then, decreases in would lead to longer dwell times in active and inactive states, thereby increasing the statistical complexity ; and the dwell time distributions would become closer to exponential, decreasing the excess entropy . When become small but nonzero, all pasts are causal states, and so shoots to infinity, while (because it is a function of trajectory distributions) barely changes.
There are some well-known examples of how arbitrarily large
-machines can still have arbitrarily small excess entropies, e.g., the almost fair coin. Indeed, Ref. [
23] defined crypticity as the difference between statistical complexity
and excess entropy
. The dynamical MWC molecule described above adds another such example to the literature, finding not only that a familiar process can have arbitrarily large crypticity, but that
and
can be anti-correlated with respect to underlying kinetic rates, as is true for the process generated by the parametrized Simple Nonunifilar Source [
25]. There are also examples in the literature of processes with uncountable
-machines and nonzero box-counting dimensions of their mixed-state presentation, e.g., the Cantor process in Ref. [
26].
However, the dynamical MWC molecule is more than just an example of a process with potentially arbitrarily large crypticity or an uncountable -machine; it is also an example of how arbitrarily small changes to a generative model can lead to arbitrarily large changes in the causal structure of a process. Of course, it may be obvious to those familiar with intrinsic computation that sometimes, arbitrarily small perturbations in transition probabilities of a generative model can lead to arbitrarily large perturbations in -machine structure. However, to the author’s knowledge, the above MWC molecule example is the first such example in the literature.
3.2. Functional Computation
Monod-Wyman-Changeux (MWC) molecules have been used to model everything from ligand-gated ion channels to gene regulation [
8]. The functional computations that an MWC molecule is thought to perform include transduction of ligand concentration and low-pass filtering of input [
7].
Let
be the normalized eigenvector of eigenvalue 0 of matrix
, normalized so that
; and let
be the equilibrium probability of being in state
A. The MWC molecule’s ability to convey the ligand concentration via its activity is a static property, relying only on how the equilibrium distribution
varies with kinetic rates. An observer that can only see whether or not the MWC molecule is active can discern, to some extent, the external ligand concentration
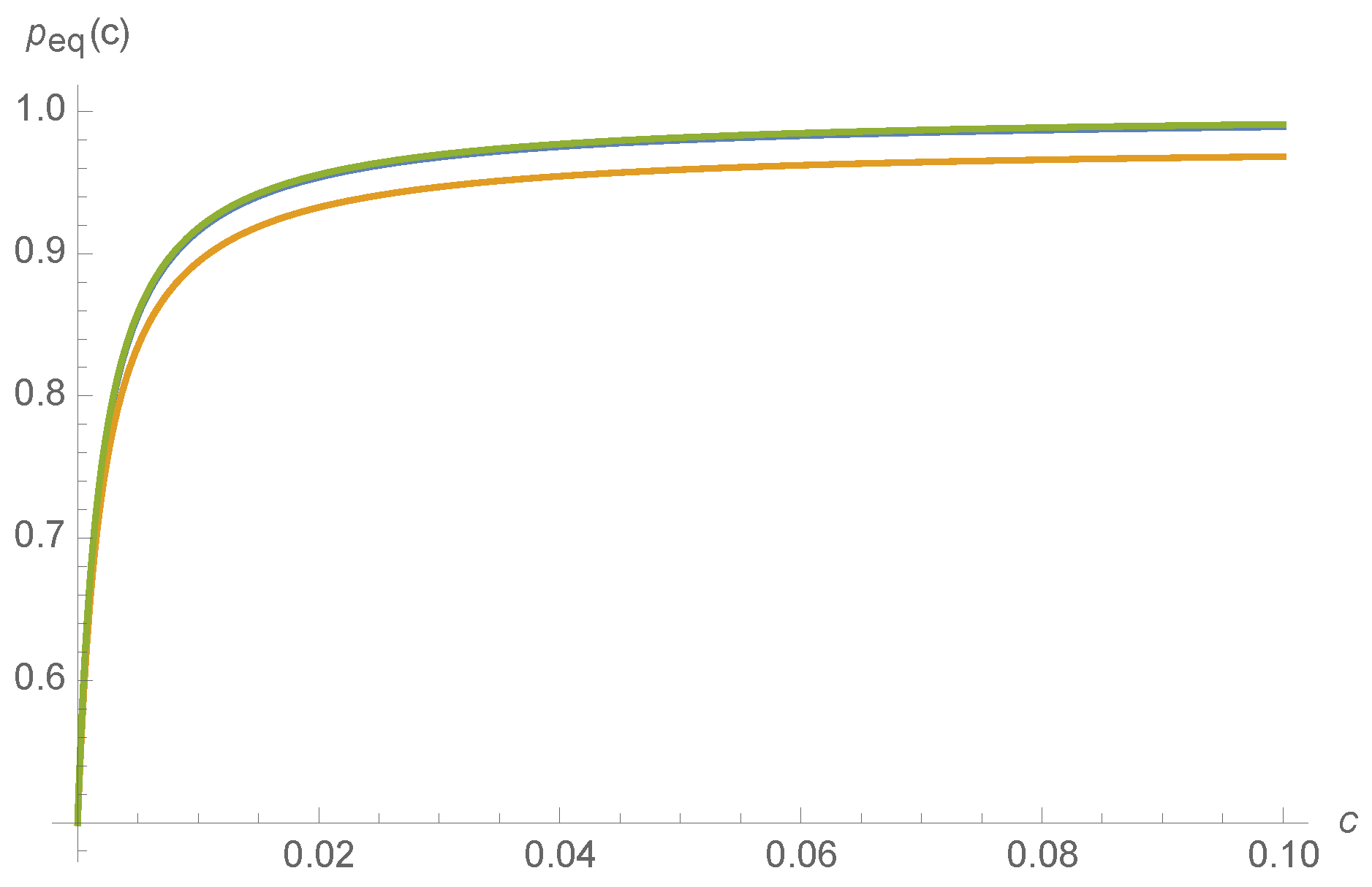
c. Such a situation might occur, for instance, for the nicotinic acetylcholine receptors at the neuromuscular junction that transduce information about whether or not a muscle fiber should seize, based on acetylcholine concentration. Though
in principle might be a non-smoothly varying function of
, a Mathematica calculation finds that
and thus
varies smoothly with kinetic rates
:
where the normalization constant is chosen so that
. The smooth variation of
with respect to
is depicted for a random choice of kinetic rates in
Figure 6.
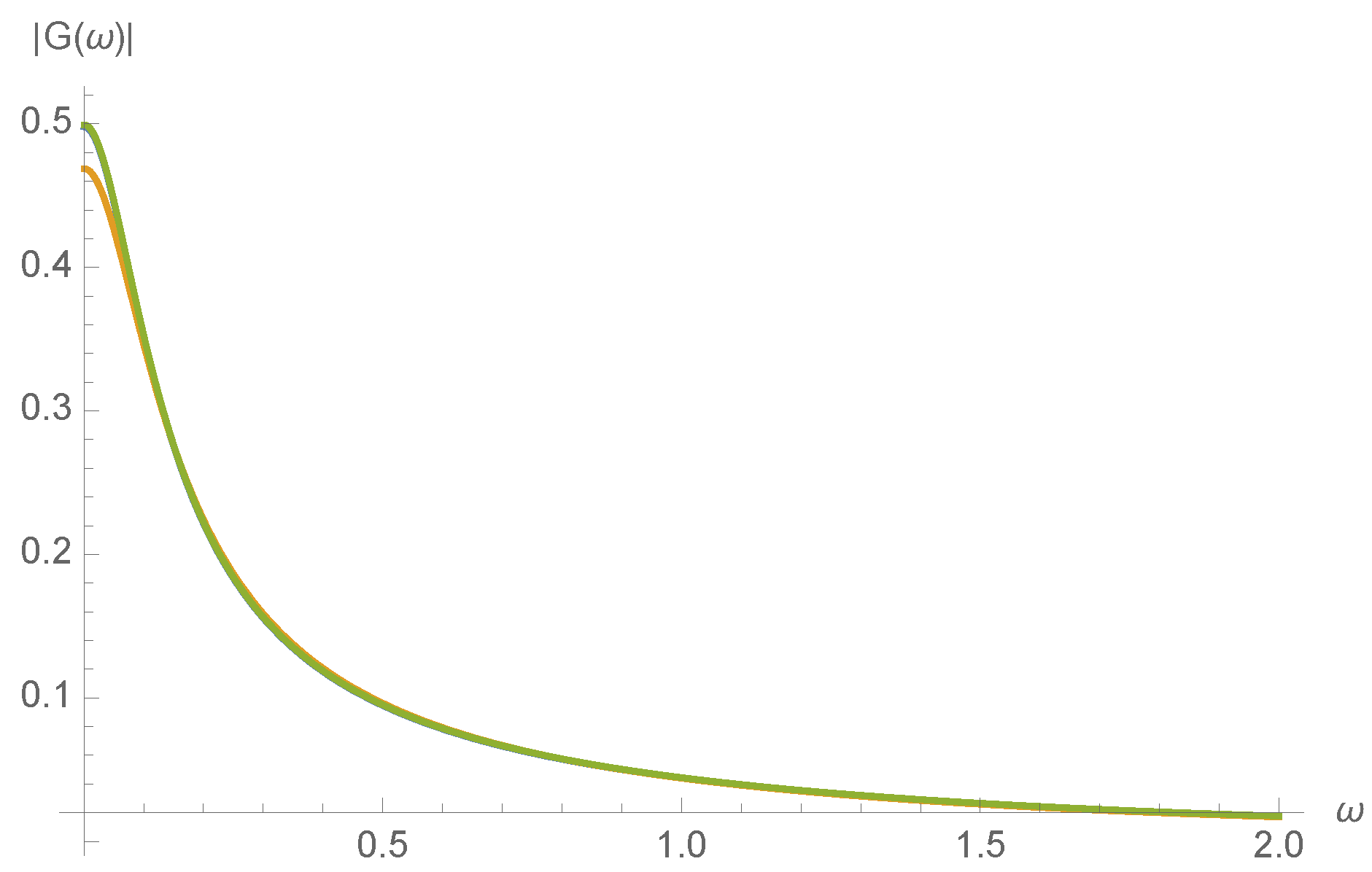
The MWC molecule is a low-pass filter of ligand concentration
c. Suppose that
, where
is small. Then
will also take the form
, where
is the transfer function. This transfer function therefore characterizes the dynamical response of the MWC molecule to fluctuations in the ligand concentration. From Equation 49 of Ref. [
8], we find that the transfer function
is
where
A series expansion not shown here confirms that
varies smoothly with kinetic rates
, as would be expected from the realization that all expressions in Equation (
18) are smoothly varying with
. To illustrate this, the magnitude of the transfer function,
, is plotted in
Figure 7 for a randomly chosen initial concentration of
.
Again, it is worth commenting on how these results would vary with larger
n, i.e., a larger number of potential ligands bound to the MWC molecule. We consider the dynamical model for this more complex MWC molecule as specified in
Section 3.1. Just as for the case when
, the eigenvector of eigenvalue 0 for this larger MWC molecule’s rate matrix is a continuous function of kinetic rates
and
; as a result, both the binding curve and the transfer function vary smoothly with these rates.