A Method for Measuring the Weak Value of Spin for Metastable Atoms
Abstract
1. Introduction
2. Details of the Experimental Apparatus to Determine Weak Values of Spin
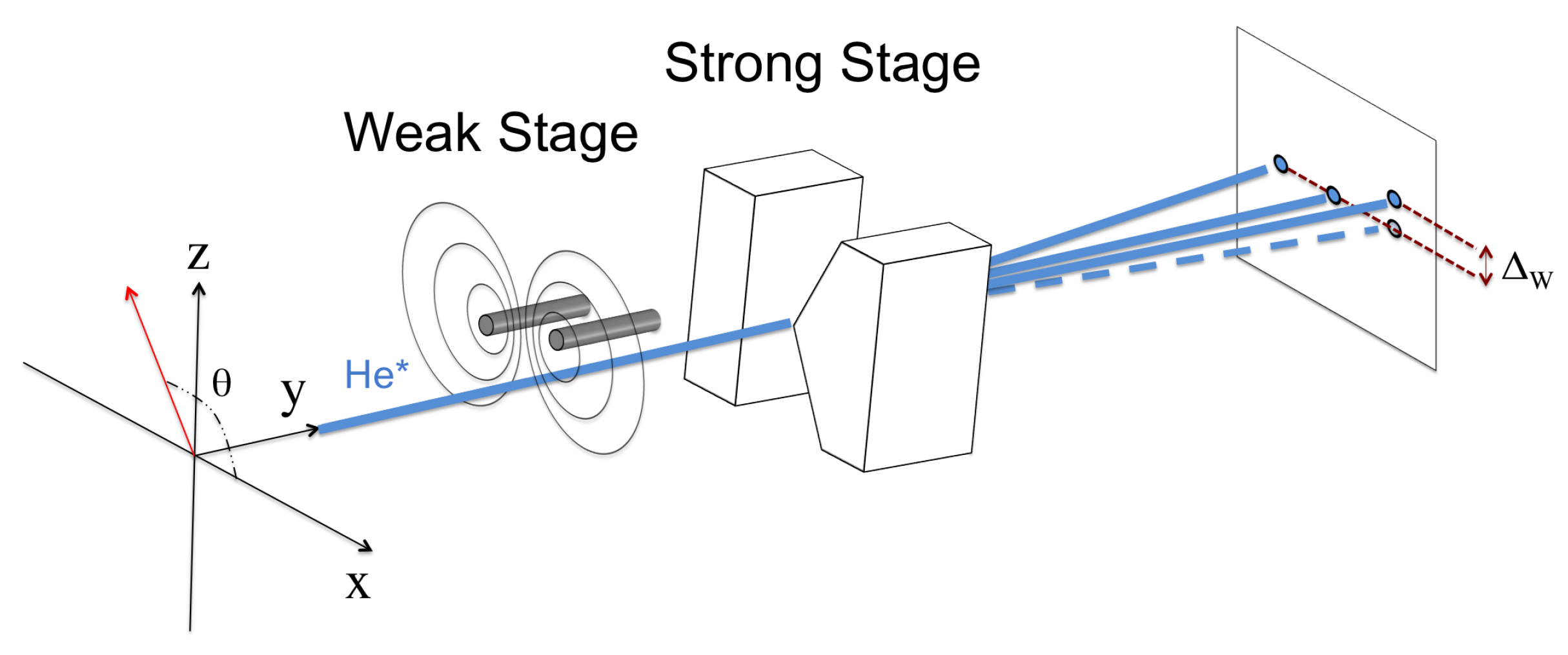
2.1. Overview
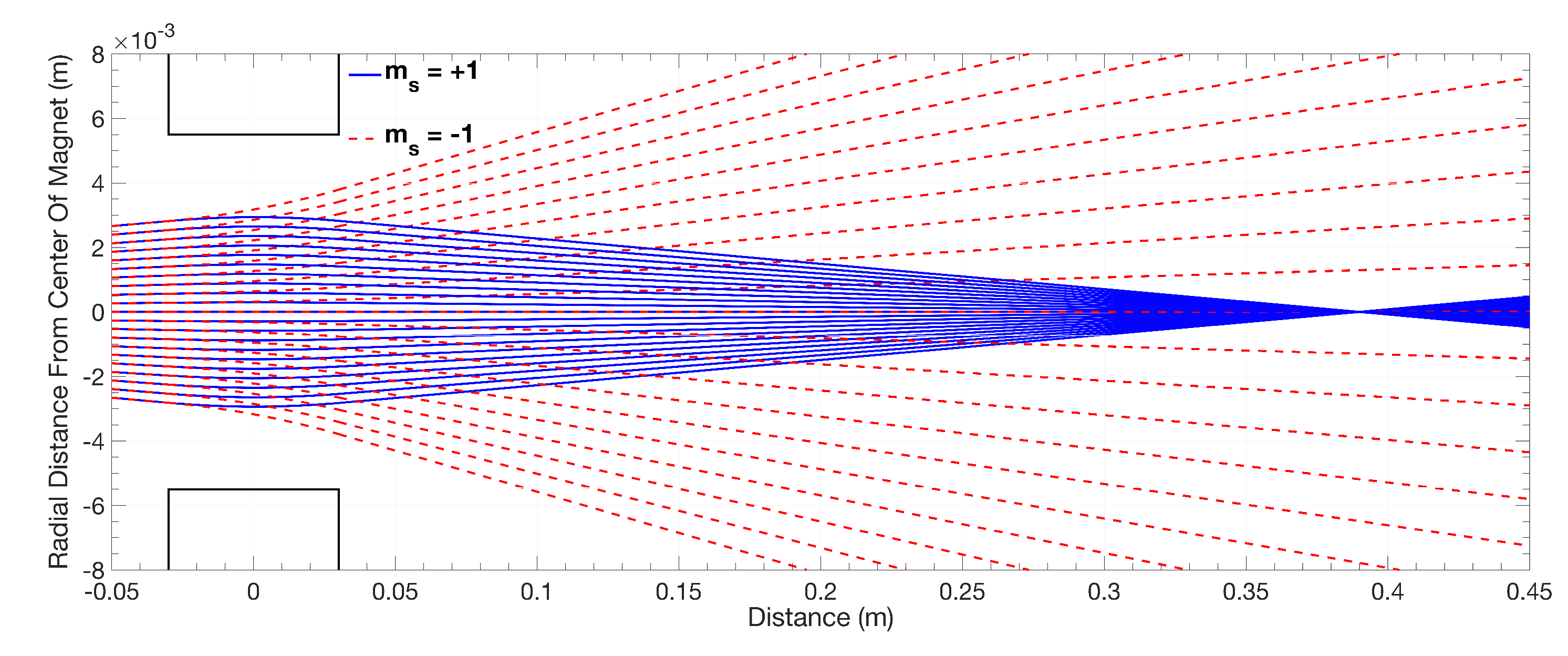
2.2. Stern–Gerlach Simulation Using the Impulse Approximation
2.3. Initial Conditions
2.4. Theory of the Weak Stage Process
2.5. Extracting the Weak Value of Spin
2.6. Free Evolution of the Gaussian Wave Packet at the Detector
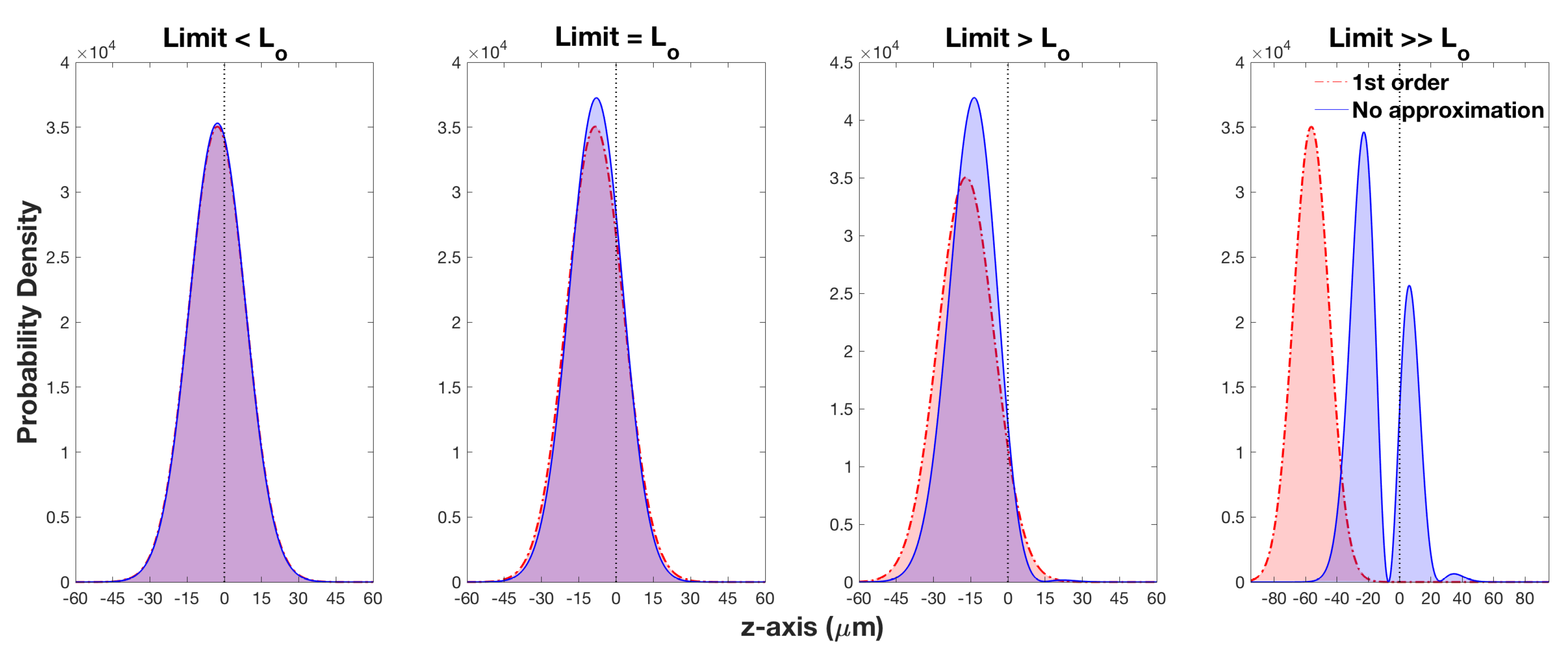
2.7. The Limit and Its Validity
3. Method for the Weak Measurement of Spin for Atomic Systems: Experimental Realisation
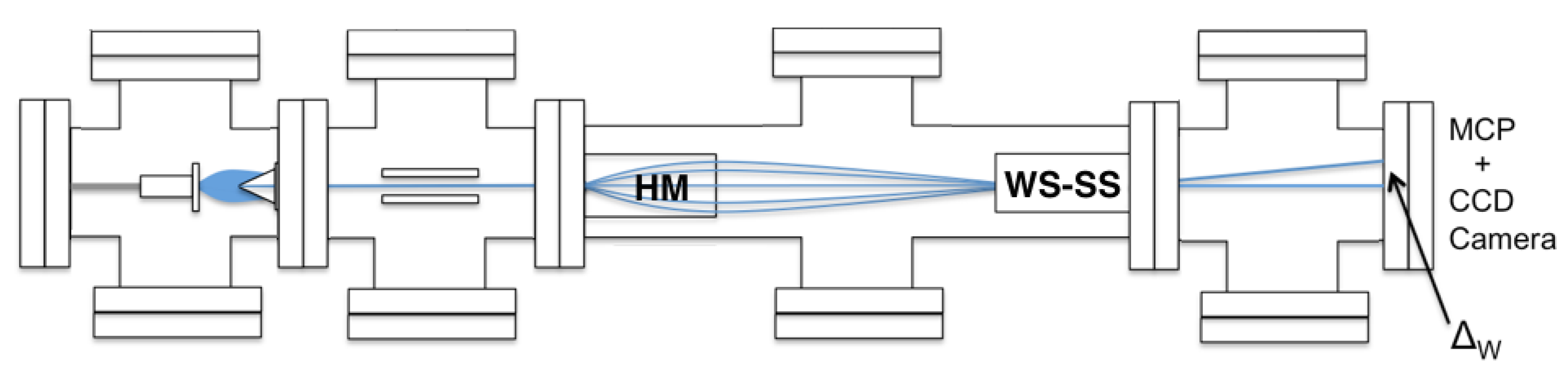
3.1. Schematic Lay-Out of the Apparatus
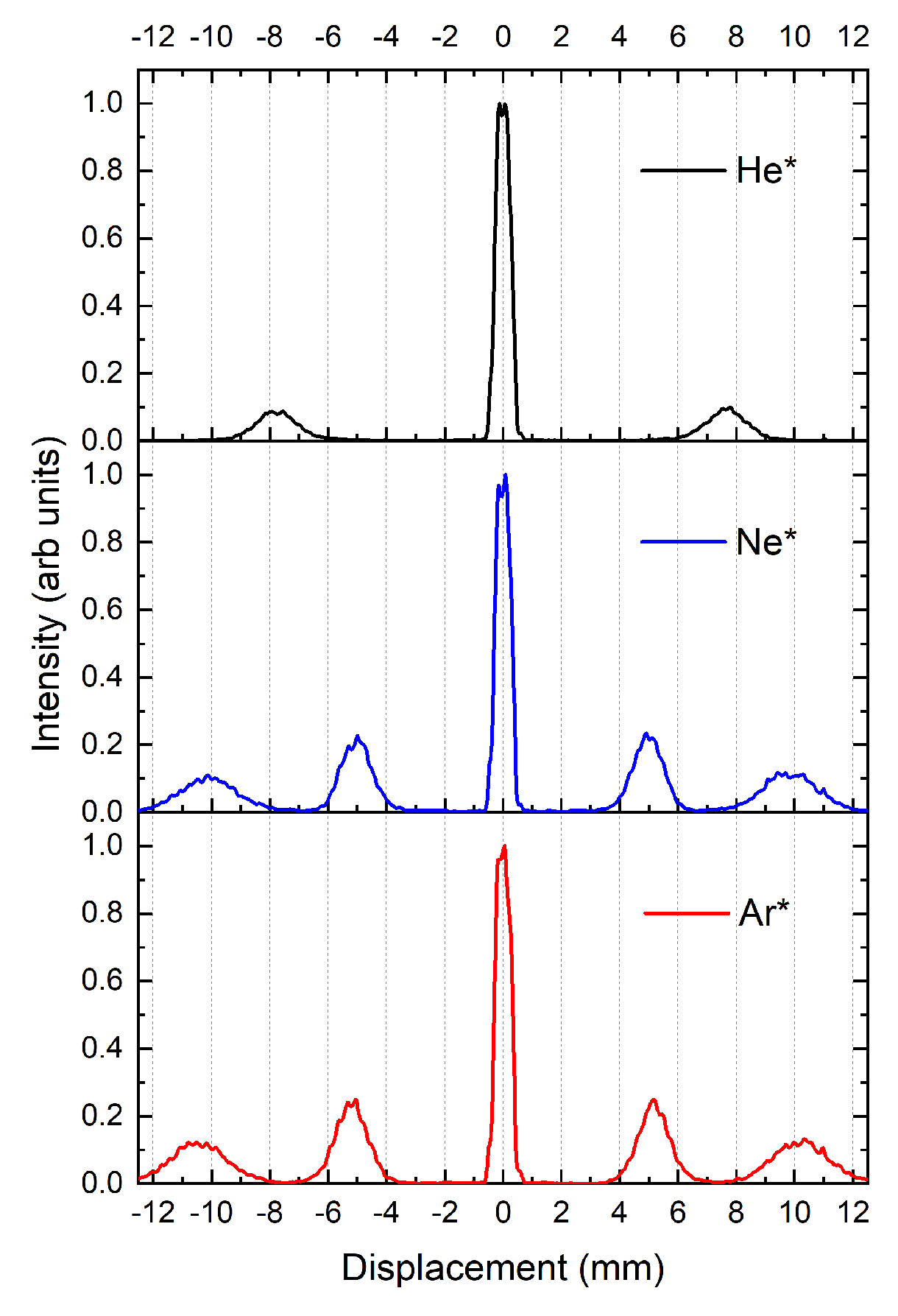
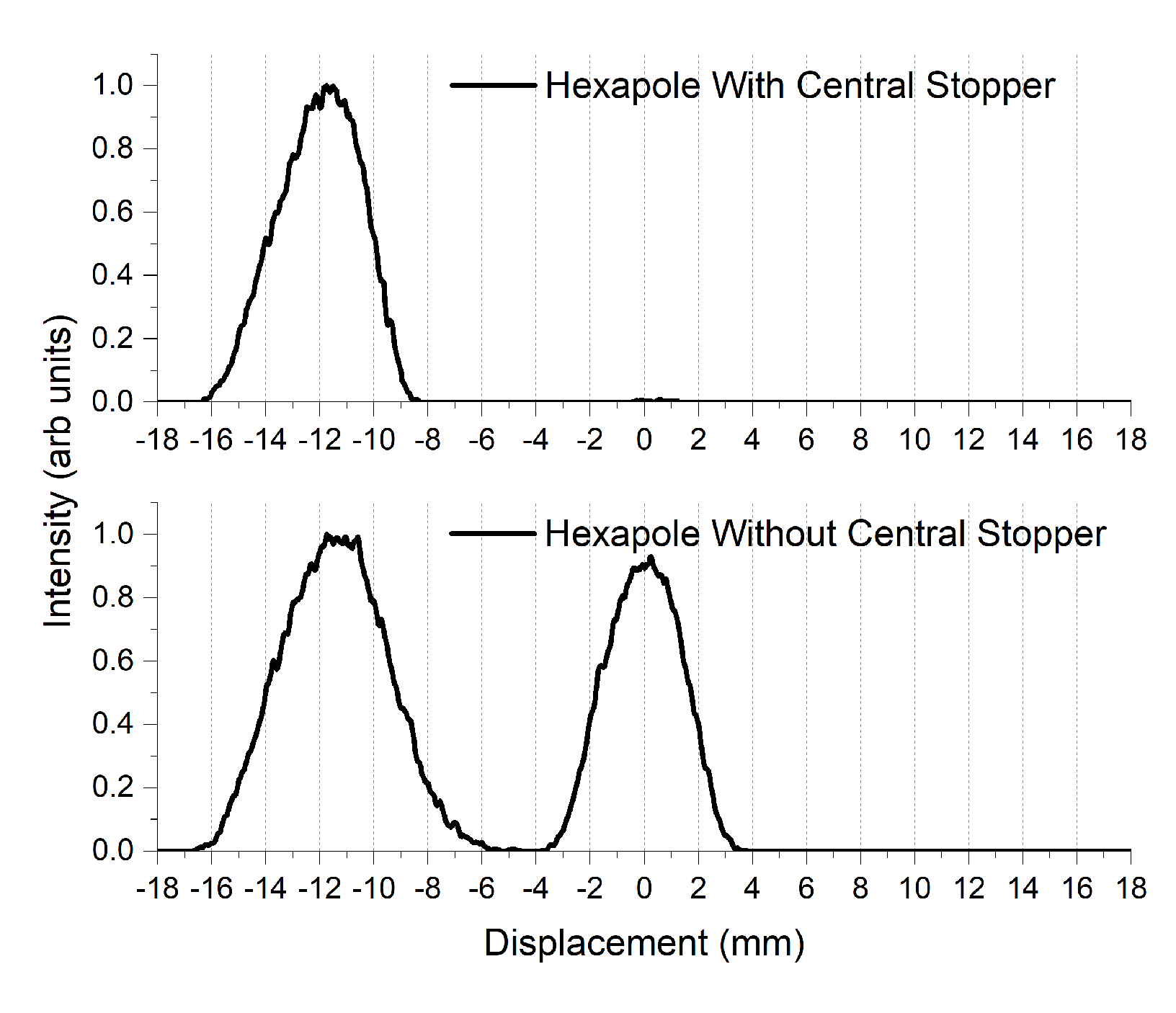
3.2. Experimental Data Confirming the Correct Functioning of the Last (Post-Selection) Stage
- It has a lifetime of approximately 8000 s [33], being unable to decay via electric dipole transitions and the Pauli exclusion principle, i.e., its decay is doubly forbidden. This lifetime is clearly large enough for the atoms to pass through all the stages of the apparatus before decaying. Furthermore, this allows scope for increasing the flight distance with no depreciable effects.
- Metastable helium atoms have an internal energy of 19.6 eV, the highest of any metastable noble gas species. Upon collision with any surface, it will easily ionise, and the emitted electron is observed with higher efficiency at the microchannel plate (MCP) detector.
3.3. The Functioning of the Hexapole Stage
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aharonov, Y.; Albert, D.Z.; Vaidman, L. How the Result of a Measurement of a Component of the Spin of a Spin-1/2 Particle Can Turn Out to be 100. Phys. Rev. Lett. 1988, 60, 1351–1354. [Google Scholar] [CrossRef] [PubMed]
- Aharonov, Y.; Vaidman, L. Properties of a quantum system during the time interval between two measurements. Phys. Rev. 1990, 41, 11–19. [Google Scholar] [CrossRef]
- Wiseman, H. Grounding Bohmian mechanics in weak values and Bayesianism. Phys. Lett. A 2003, 311, 285–291. [Google Scholar] [CrossRef]
- Leavens, C.R. Weak Measurements from the point of view of Bohmian Mechanics. Found. Phys. 2005, 35, 469–491. [Google Scholar] [CrossRef]
- Bohm, D.; Hiley, B.J. The Undivided Universe: An Ontological Interpretation of Quantum Mechanics; Routledge: London, UK, 1993. [Google Scholar]
- Flack, R.; Hiley, B.J. Feynman Paths and Weak Values. Entropy 2018, 20, 367. [Google Scholar] [CrossRef]
- Schwinger, J. The Theory of Quantum Fields III. Phys. Rev. 1953, 91, 728–740. [Google Scholar] [CrossRef]
- Feynman, R.P. Space-Time Approach to Non-Relativistic Quantum Mechanics. Rev. Mod. Phys. 1948, 20, 367–387. [Google Scholar] [CrossRef]
- Kocsis, S.; Braverman, B.; Ravets, S.; Stevens, M.J.; Mirin, R.P.; Shalm, L.K.; Steinberg, A.M. Observing the Average Trajectories of Single Photons in a Two-Slit Interferometer. Science 2011, 332, 1170–1173. [Google Scholar] [CrossRef] [PubMed]
- Hiley, B.J.; Aziz Mufti, A.H. The Ontological Interpretation of Quantum Field Theory Applied in a Cosmological Context, Fundamental Problems in Quantum Physics; Ferrero, M., van der Merwe, A., Eds.; Kluwer: Dordrecht, The Netherlands, 1995; pp. 141–156. [Google Scholar]
- Flack, R.; Hiley, B.J. Weak Values of Momentum of the Electromagnetic Field: Average Momentum Flow Lines, Not Photon Trajectories. arXiv 2016, arXiv:1611.06510. [Google Scholar]
- Mahler, D.H.; Rozema, L.A.; Fisher, K.; Vermeyden, L.; Resch, K.J.; Braverman, B.; Wiseman, H.M.; Steinberg, A.M. Measuring Bohm trajectories of entangled photons. In Lasers and Electro-Optics (CLEO); IEEE: Piscataway, NJ, USA, 2014; pp. 1–2. [Google Scholar]
- Bohm, D. A Suggested Interpretation of the Quantum Theory in Terms of Hidden Variables, II. Phys. Rev. 1952, 85, 180–193. [Google Scholar] [CrossRef]
- Bohm, D.; Hiley, B.J.; Kaloyerou, P.N. An Ontological Basis for the Quantum Theory: II-A Causal Interpretation of Quantum Fields. Phys. Rep. 1987, 144, 349–375. [Google Scholar] [CrossRef]
- Holland, P.R. The de Broglie-Bohm theory of motion and quantum field theory. Phys. Rep. 1993, 224, 95–150. [Google Scholar] [CrossRef]
- Kaloyerou, P.N. The Causal Interpretation of the Electromagnetic field. Phys. Rep. 1994, 244, 287–358. [Google Scholar] [CrossRef]
- Morley, J.; Edmunds, P.D.; Barker, P.F. Measuring the weak value of the momentum in a double slit interferometer. J. Phys. Conf. Ser. 2016, 701, 012030. [Google Scholar] [CrossRef]
- Sponar, S.; Denkmayr, T.; Geppert, H.; Lemmel, H.; Matzkin, A.; Tollaksen, J.; Hasegawa, Y. Weak values obtained in matter-wave interferometry. Phys. Rev. A 2014, 92, 062121. [Google Scholar] [CrossRef]
- Bohm, D.; Schiller, R.; Tiomno, J. A Causal Interpretation of the Pauli Equation (A). Nuovo Cim. Supp. 1955, 1, 48–66. [Google Scholar] [CrossRef]
- Bohm, D.; Schiller, R. A Causal Interpretation of the Pauli Equation (B). Nuovo Cim. Supp. 1955, 1, 67–91. [Google Scholar] [CrossRef]
- Hiley, B.J.; van Reeth, P. Quantum Trajectories: Real or Surreal? Entropy 2018, 20, 353. [Google Scholar] [CrossRef]
- Dewdney, C.; Holland, P.R.; Kyprianidis, A. What happens in a spin measurement? Phys. Lett. A 1986, 119, 259–267. [Google Scholar] [CrossRef]
- Dewdney, C.; Holland, P.R.; Kyprianidis, A. A Causal Account of Non-local Einstein-Podolsky-Rosen Spin Correlations. J. Phys. A Math. Gen. 1987, 20, 4717–4732. [Google Scholar] [CrossRef]
- Dewdney, C.; Holland, P.R.; Kyprianidis, A.; Vigier, J.-P. Spin and non-locality in quantum mechanics. Nature 1988, 336, 536–544. [Google Scholar] [CrossRef]
- Monachello, V.; Flack, R. The weak value of spin for atomic systems. J. Phys. Conf. Ser. 2016, 701, 012028. [Google Scholar] [CrossRef]
- Bohm, D. Quantum Theory; Prentice Hall: New York, NY, USA, 1951. [Google Scholar]
- Duck, I.M.; Stevenson, P.M.; Sudarshan, E.C.G. The sense in which a “weak measurement” of a spin-1/2 particle’s spin component yields a value 100. Phys. Rev. A 1989, 40, 2112–2117. [Google Scholar] [CrossRef]
- Ballentine, L.E. Quantum Mechanics: A Modern Development; World Scientific Publishing: New York, NY, USA, 1998. [Google Scholar]
- Pan, A.K.; Matzkin, A. Weak values in nonideal spin measurements: An exact treatment beyond the asymptotic regime. Phys. Rev. A 2012, 85, 022122. [Google Scholar] [CrossRef]
- Halfmann, T.; Koensgen, J.; Bergmann, K. A source for a high-intensity pulsed beam of metastable helium atoms. Meas. Sci. Technol. 2000, 11, 1510–1514. [Google Scholar] [CrossRef]
- Bleaney, B.I.; Bleaney, B. Electricity and Magnetism; Oxford University Press: London, UK, 1965. [Google Scholar]
- Baldwin, K. Metastable helium: Atom optics with nano-grenades. Contemp. Phys. 2005, 46, 105–120. [Google Scholar] [CrossRef]
- Hodgman, S.S.; Dall, R.G.; Byron, L.J.; Baldwin, K.G.H.; Buckman, S.J.; Truscott, A.G. Metastable helium: A new determination of the longest atomic excited-state lifetime. Phys. Rev. Lett. 2009, 103, 053002. [Google Scholar] [CrossRef] [PubMed]
- Halbach, K. Design of permanent multipole magnets with oriented rare earth cobalt material. Nuclear Instrum. Meth. 1980, 169, 1–10. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flack, R.; Monachello, V.; Hiley, B.; Barker, P. A Method for Measuring the Weak Value of Spin for Metastable Atoms. Entropy 2018, 20, 566. https://doi.org/10.3390/e20080566
Flack R, Monachello V, Hiley B, Barker P. A Method for Measuring the Weak Value of Spin for Metastable Atoms. Entropy. 2018; 20(8):566. https://doi.org/10.3390/e20080566
Chicago/Turabian StyleFlack, Robert, Vincenzo Monachello, Basil Hiley, and Peter Barker. 2018. "A Method for Measuring the Weak Value of Spin for Metastable Atoms" Entropy 20, no. 8: 566. https://doi.org/10.3390/e20080566
APA StyleFlack, R., Monachello, V., Hiley, B., & Barker, P. (2018). A Method for Measuring the Weak Value of Spin for Metastable Atoms. Entropy, 20(8), 566. https://doi.org/10.3390/e20080566





