Random k-Body Ensembles for Chaos and Thermalization in Isolated Systems
Abstract
1. Introduction
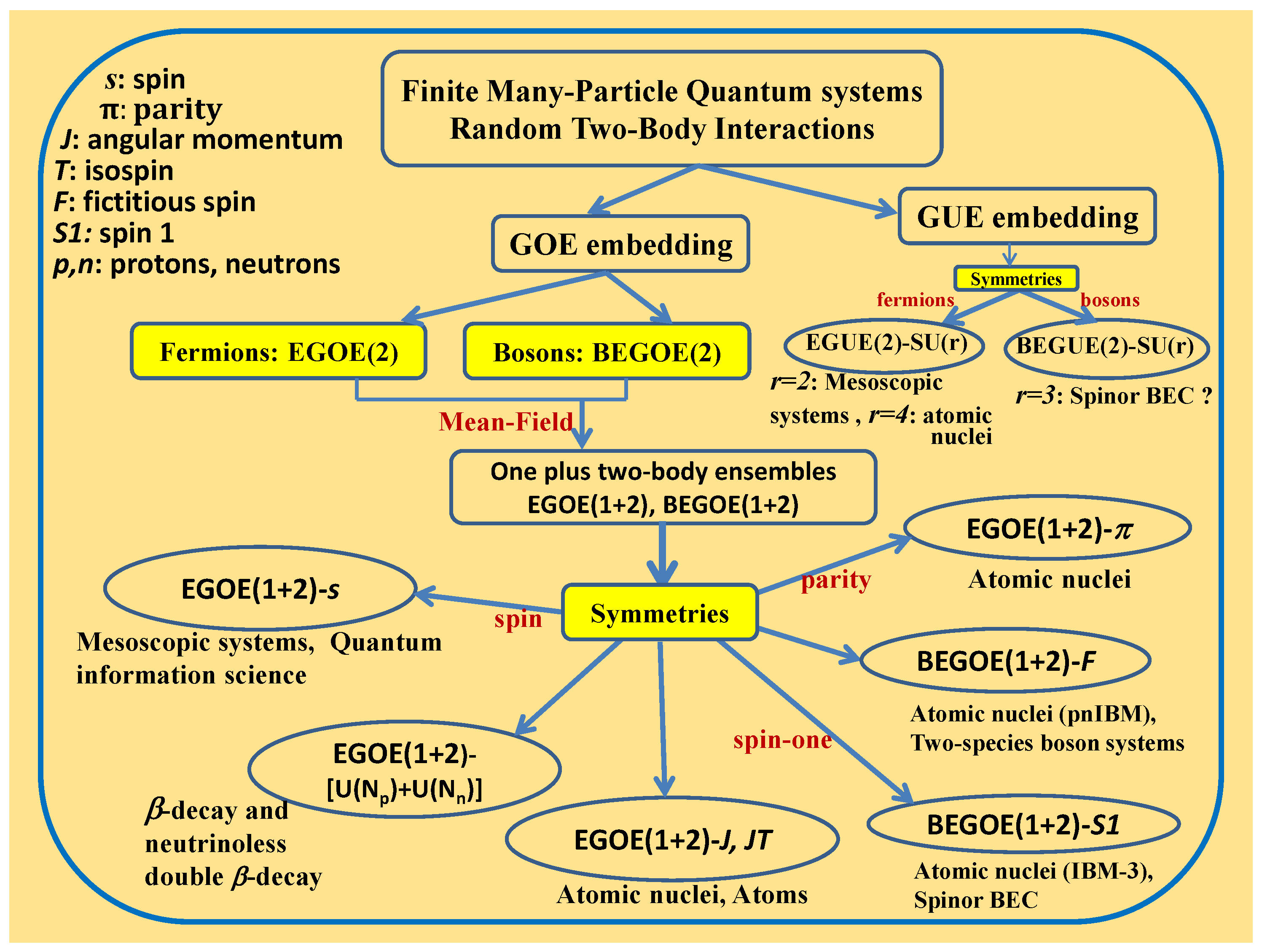
2. Random Matrix Ensembles with Symmetries for Fermi, Bose and Other Systems
2.1. Embedded Ensembles for Fermi and Bose Systems with Lie Symmetries
2.1.1. Ensembles for Fermion Systems
2.1.2. Ensembles for Boson Systems
2.2. Embedded Ensembles with Point Group Symmetries and Others
2.3. Ensembles for Majorana Fermions and Other Systems
3. Delocalization, Quench Dynamics and Thermalization in EE
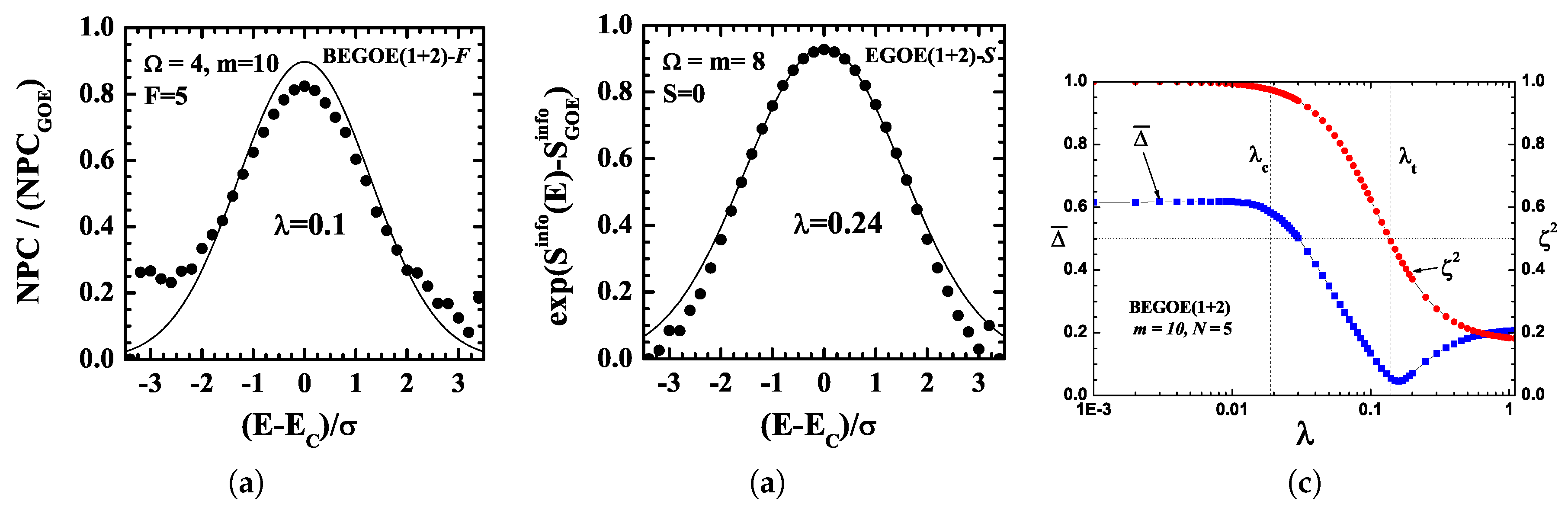
3.1. Localization–Delocalization Transitions and Thermalization
3.2. Relaxation Dynamics Following an Interaction Quench
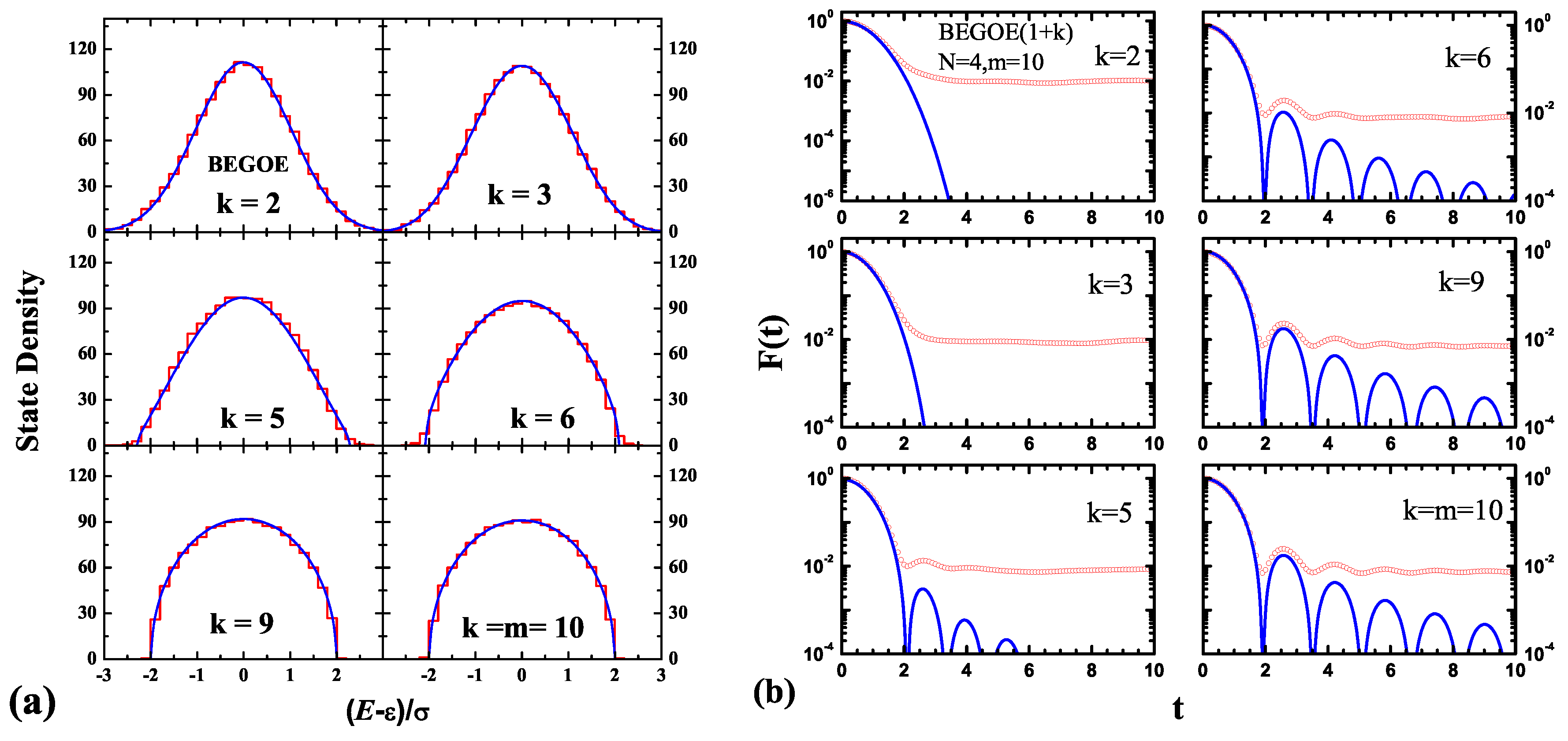
3.2.1. Eigenvalue Density for EE(k)
3.2.2. Survival Probability after an Interaction Quench
3.3. ETH and Ergodicity
4. Random Matrix Analysis of Weakly Interacting Trapped Bosons and Related Systems
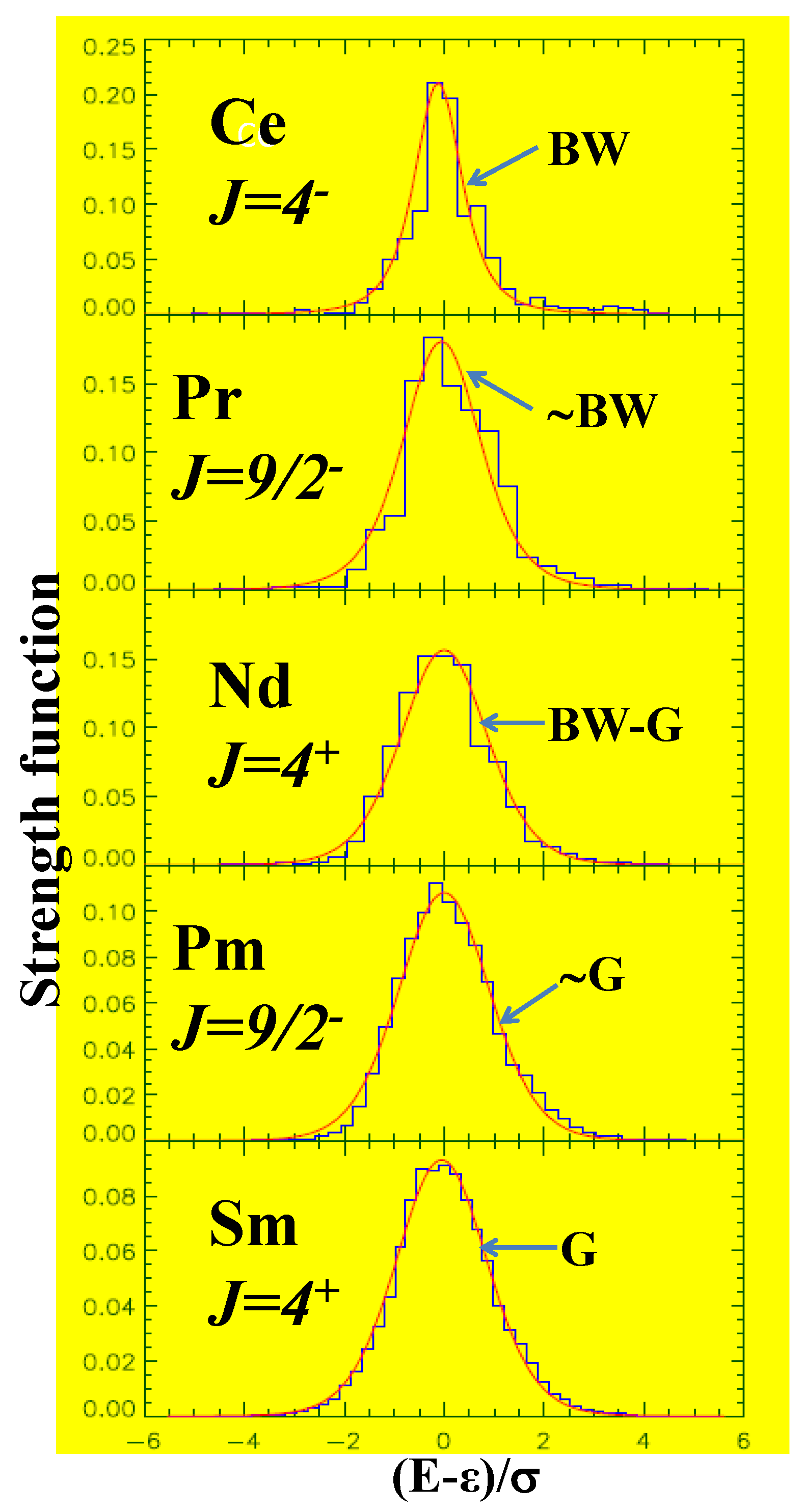
4.1. Results for Spectral Statistics Using GOE and Related Ensembles
4.1.1. Weakly-Interacting Trapped Boson Systems
4.1.2. Diffuse van der Waals Clusters
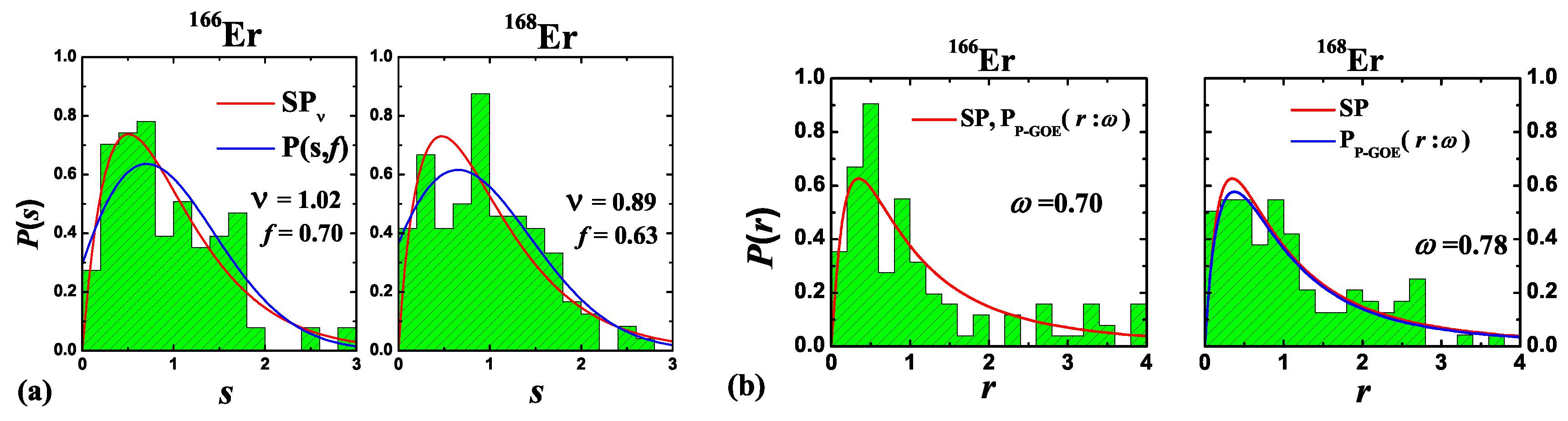
4.1.3. Molecular Resonances in Erbium Isotopes
4.2. Time Evolution, Quantum Chaos and Decoherence in Ultra-Cold Boson Systems
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Porter, C.E. Statistical Theories of Spectra: Fluctuations; Academic Press: New York, NY, USA, 1965. [Google Scholar]
- D’Alessio, L.; Kafri, Y.; Polkovnikov, A.; Rigol, M. From quantum chaos and eigenstate thermalization to statistical mechanics and thermodynamics. Adv. Phys. 2016, 65, 239–362. [Google Scholar] [CrossRef]
- Gogolin, C.; Eisert, J. Equilibration, thermalisation, and the emergence of statistical mechanics in closed quantum systems. Rep. Prog. Phys. 2016, 79, 056001. [Google Scholar] [CrossRef] [PubMed]
- Borgonovi, F.; Izrailev, F.M.; Santos, L.F.; Zelevinsky, V.G. Quantum chaos and thermalization in isolated systems of interacting particles. Phys. Rep. 2016, 626, 1–58. [Google Scholar] [CrossRef]
- Kota, V.K.B. Embedded Random Matrix Ensembles in Quantum physics; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Kota, V.K.B.; Chavda, N.D. Embedded random matrix ensembles from nuclear structure and their recent applications. Int. J. Mod. Phys. E 2018, 27, 1830001. [Google Scholar] [CrossRef]
- Mehta, M.L. Random Matrices, 3rd ed.; Elsevier B.V.: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Forrester, P.J. Log-Gases and Random Matrices; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Anderson, G.W.; Guionnet, A.; Zeitouni, O. An Introduction to Random Matrices; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Haake, F. Quantum Signatures of Chaos, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Akemann, G.; Baik, J.; di Francesco, P. (Eds.) The Oxford Handbook of Random Matrix Theory; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Brody, T.A.; Flores, J.; French, J.B.; Mello, P.A.; Pandey, A.; Wong, S.S. Random Matrix Physics: Spectrum and Strength Fluctuations. Rev. Mod. Phys. 1981, 53, 385–479. [Google Scholar] [CrossRef]
- Guhr, T.; Müller-Groeling, A.; Weidenmüller, H.A. Random-matrix theories in quantum physics: Common concepts. Phys. Rep. 1998, 299, 189–425. [Google Scholar] [CrossRef]
- Gómez, J.M.G.; Kar, K.; Kota, V.K.B.; Molina, R.A.; Relaño, A.; Retamosa, J. Many-Body Quantum Chaos: Recent Developments and Applications to Nuclei. Phys. Rep. 2011, 499, 103–226. [Google Scholar] [CrossRef]
- Mon, K.K.; French, J.B. Statistical properties of many-particle spectra. Ann. Phys. (N.Y.) 1975, 95, 90–111. [Google Scholar] [CrossRef]
- Benet, L.; Rupp, T.; Weidenmüller, H.A. Spectral properties of the k-body embedded Gaussian ensembles of random matrices. Ann. Phys. (N.Y.) 2001, 292, 67–94. [Google Scholar] [CrossRef]
- Papenbrock, T.; Weidenmüller, H.A. Random matrices and chaos in nuclear spectra. Rev. Mod. Phys. 2007, 79, 997–1013. [Google Scholar] [CrossRef]
- Kota, V.K.B. Embedded random matrix ensembles for complexity and chaos in finite interacting particle systems. Phys. Rep. 2001, 347, 223–288. [Google Scholar] [CrossRef]
- Vyas, M.; Kota, V.K.B.; Chavda, N.D. Transitions in eigenvalue and wavefunction structure in (1 + 2)-body random matrix ensembles with spin. Phys. Rev. E 2010, 81, 036212. [Google Scholar] [CrossRef] [PubMed]
- Chavda, N.D.; Kota, V.K.B. Localization-delocalization transitions in bosonic random matrix ensembles. Ann. Phys. (Berl.) 2017, 529, 1600287. [Google Scholar] [CrossRef]
- Haldar, S.K.; Chavda, N.D.; Vyas, M.; Kota, V.K.B. Fidelity decay and entropy production in many-particle systems after random interaction quench. J. Stat. Mech. Theor. Expt. 2016, 2016, 043101. [Google Scholar] [CrossRef]
- Kota, V.K.; Relaño, A.; Retamosa, J.; Vyas, M. Thermalization in the two-body random ensemble. J. Stat. Mech. Theor. Expt. 2011, 2011, P10028. [Google Scholar]
- Vyas, M. Non-equilibrium many-body dynamics following a quantum quench. AIP Conf. Proc. 2017, 1912, 020020. [Google Scholar]
- Magan, J.M. Random free fermions: An analytical example of eigenstate thermalization. Phys. Rev. Lett. 2016, 116, 030401. [Google Scholar] [CrossRef] [PubMed]
- Chakrabarti, B.; Biswas, A.; Kota, V.K.B.; Roy, K.; Haldar, S.K. Energy level statistics of interacting trapped bosons. Phys. Rev. A 2012, 86, 013637. [Google Scholar] [CrossRef]
- Roy, K.; Chakrabarti, B.; Biswas, A.; Kota, V.K.B.; Haldar, S.K. Spectral fluctuation and noise in the energy level statistics of interacting trapped bosons. Phys. Rev. E 2012, 85, 061119. [Google Scholar] [CrossRef] [PubMed]
- Haldar, S.K.; Chakrabarti, B.; Chavda, N.D.; Das, T.K.; Canuto, S.; Kota, V.K.B. Level-spacing statistics and spectral correlations in diffuse van der Waals clusters. Phys. Rev. A 2014, 89, 043607. [Google Scholar] [CrossRef]
- Roy, R.; Gammal, A.; Lekla, M.L.; Chakrabarti, B.; Kota, V.K.B. How to anticipate thermalization in an isolated quantum many-body system? In preparation.
- Lode, A.U.J.; Chakrabarti, B.; Kota, V.K.B. Many-body entropies, correlations, and emergence of statistical relaxation in interaction quench dynamics of ultracold bosons. Phys. Rev. A 2015, 92, 033622. [Google Scholar] [CrossRef]
- Small, R.A.; Müller, S. Particle diagrams and statistics of many-body random potentials. Ann. Phys. (N.Y.) 2015, 356, 269–298. [Google Scholar] [CrossRef]
- Asaga, T.; Benet, L.; Rupp, T.; Weidenmüller, H.A. Spectral properties of the k-body embedded Gaussian ensembles of random matrices for bosons. Ann. Phys. (N.Y.) 2002, 298, 229–247. [Google Scholar] [CrossRef]
- Dalton, B.J.; Ghanbari, S. Two mode theory of Bose-Einstein condensates: interferometry and the Josephson model. J. Mod. Opt. 2012, 59, 287–353. [Google Scholar] [CrossRef]
- Iachello, F.; van Isacker, P. The Interacting Boson-Fermion Model; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Kota, V.K.B. Group theoretical aspects of UB(6)⊗UF(20) symmetry limits of IBFM related to the UB(5) and OB(6) limits of IBM. Pramana-J. Phys. 1997, 48, 1035–1075. [Google Scholar] [CrossRef]
- Devi, Y.D.; Kota, V.K.B. Correspondence between SU(3)⊗U(2) limit of IBF2M and two quasi–particle Nilsson configurations. Phys. Lett. B 1994, 334, 253–258. [Google Scholar] [CrossRef]
- Kota, V.K.B.; Pramanik, U.D. Strong coupled and doubly decoupled bands in the SUBF(3)⊗UF(2j + 1) limit of interacting boson–fermion–fermion model. Z. Phys. A 1997, 358, 25–31. [Google Scholar] [CrossRef]
- Kota, V.K.B.; Pramanik, U.D. SU(3) coupling schemes for odd-odd nuclei in the interacting boson–fermion–fermion model with both odd proton and odd neutron in natural parity orbits. Eur. Phys. J. A 1998, 3, 243–253. [Google Scholar] [CrossRef]
- Iachello, F.; Levine, R.D. Algebraic Theory of Molecules; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Bijker, R.; Iachello, F. The algebraic cluster model: Structure of 16O. Nucl. Phys. A 2017, 957, 154–176. [Google Scholar] [CrossRef]
- Ortega, A.; Vyas, M.; Benet, L. Quantum efficiencies in finite disordered networks connected by many-body interactions. Ann. Phys. (Berl.) 2015, 527, 748–756. [Google Scholar] [CrossRef]
- Ortega, A.; Stegmann, T.; Benet, L. Efficient quantum transport in disordered interacting many-body networks. Phys. Rev. E 2016, 94, 042102. [Google Scholar] [CrossRef] [PubMed]
- Verbaarschot, J.J.M.; Wettig, T. Random matrix theory and chiral symmetry in QCD. Annu. Rev. Nucl. Part. Sci. 2000, 50, 343–410. [Google Scholar] [CrossRef]
- Altaland, A.; Zirnbauer, M.R. Nonstandered symmery classes in mesoscopic normal–superconding hybrid structures. Phy. Rev. B 1997, 55, 1142–1161. [Google Scholar] [CrossRef]
- Cotler, J.S.; Gur-Ari, G.; Hanada, M.; Polchinski, J.; Saad, P.; Shenker, S.H.; Stanford, D.; Streicher, A.; Tezuka, M. Black holes and random matrices. J. High Energy Phys. 2017, 5, 118. [Google Scholar] [CrossRef]
- Maldacena, J.; Stanford, D. Remarks on the Sachdev-Ye-Kitaev model. Phys. Rev. D 2016, 94, 106002. [Google Scholar] [CrossRef]
- Garcia-Garcia, A.M.; Verbaarschot, J.J.M. Spectral and thermodynamic properties of the Sachdev-Ye-Kitave model. Phys. Rev. D 2016, 94, 126010. [Google Scholar] [CrossRef]
- Garcia-Garcia, A.M.; Verbaarschot, J.J.M. Analytical spectral density of the Sachdev-Ye-Kitaev model at finite N. Phys. Rev. D 2017, 96, 066012. [Google Scholar] [CrossRef]
- Ismail, M.E.H.; Stanton, D.; Viennot, G. The combinatorics of q-Hermite polynomials and the Askey-Wilson Integral. Eur. J. Comb. 1987, 8, 379–392. [Google Scholar] [CrossRef]
- Bethe, H.A. An Attempt to Calculate the Number of Energy Levels of a Heavy Nucleus. Phys. Rev. 1936, 50, 332–341. [Google Scholar] [CrossRef]
- Magan, J.M. Decoherence and microscopic diffusion at the Sachdev-Ye-Kitaev model. arXiv 2017, arXiv:1612.06765v3. [Google Scholar]
- Vyas, M.; Seligman, T.H. Random Matrix Ensembles For Many-Body Quantum Systems. arXiv 2017, arXiv:1710.07712. [Google Scholar]
- Erdos, L.; Schroder, D. Phase transition in the density of states of quantum spin glasses. Math. Phys. Anal. Geom. 2014, 17, 441–464. [Google Scholar] [CrossRef]
- Borgonovi, F.; Izrailev, F.M. Localized thermal states. AIP Conf. Proc. 2017, 1912, 020003. [Google Scholar]
- Chavda, N.D.; Kota, V.K.B.; Potbhare, V. Thermalization in one- plus two-body ensembles for dense interacting boson systems. Phys. Lett. A 2012, 376, 2972–2976. [Google Scholar] [CrossRef]
- Kota, V.K.B.; Haq, R.U. Spectral Distributions in Nuclei and Statistical Spectroscopy; World Scientific: Singapore, 2010. [Google Scholar]
- Chirikov, B.V. An example of chaotic eigenstates in a complex atom. Phys. Lett. A 1985, 108, 68–70. [Google Scholar] [CrossRef]
- Angom, D.; Kota, V.K.B. Chaos and localization in the wavefunctions of complex atoms NdI, PmI and SmI. Phys. Rev. A 2005, 71, 042504. [Google Scholar] [CrossRef]
- Angom, D.; Ghosh, S.; Kota, V.K.B. Strength functions, entropies and duality in weakly to strongly interacting fermion systems. Phys. Rev. E 2004, 70, 016209. [Google Scholar] [CrossRef] [PubMed]
- Flambaum, V.V.; Gribakina, A.A.; Gribakin, G.F.; Ponomarev, A.V. Quantum chaos in many-body systems: What can we learn from the Ce atom. Physica D 1999, 131, 205–220. [Google Scholar] [CrossRef]
- Morrison, M.J.; Derevianko, A. Proposed search for T-odd, P-even interactions in spectra of chaotic atoms. Phys. Rev. A 2012, 86, 022115. [Google Scholar] [CrossRef]
- Greiner, M.; Mandel, O.; Hansch, T.W.; Bloch, I. Collapse and revival of the matter wave field of a Bose–Einstein condensate. Nature (London) 2002, 419, 51–54. [Google Scholar] [CrossRef] [PubMed]
- Friedenauer, A.; Schmitz, H.; Gluckert, J.T.; Schatz, D.P.A. Simulating a quantum magnet with trapped ions. Nat. Phys. 2008, 4, 757–761. [Google Scholar] [CrossRef]
- Ronzheimer, J.P.; Schreiber, M.; Braun, S.; Hodgman, S.S.; Langer, S.; McCulloch, I.P.; Heidrich-Meisner, F.; Bloch, I.; Schneider, U. Expansion dynamics of interacting bosons in homogeneous lattices in one and two dimensions. Phys. Rev. Lett. 2013, 110, 205301. [Google Scholar] [CrossRef] [PubMed]
- Jurcevic, P.; Lanyon, B.P.; Hauke, P.; Hempel, C.; Zoller, P.; Blatt, R.; Roos, C.F. Quasiparticle engineering and entanglement propagation in a quantum many-body system. Nature 2014, 511, 202–205. [Google Scholar] [CrossRef] [PubMed]
- Langen, T.; Geiger, R.; Schmiedmayer, J. Ultracold atoms Out of equilibrium. Ann. Rev. Condens. Matter Phys. 2015, 6, 201–217. [Google Scholar] [CrossRef]
- Riordan, J. The distribution of crossings of chords joining pairs of 2n points on a circle. Math. Comp. 1975, 29, 215–222. [Google Scholar]
- Touchard, J. Sur un probleme de configurations et sur les fractions continues. Can. J. Math. 1952, 4, 2–25. (In French) [Google Scholar] [CrossRef]
- Kota, V.K.B. SU(N) Wigner–Racah algebra for the matrix of second moments of embedded Gaussian unitary ensemble of random matrices. J. Math. Phys. 2005, 46, 033514. [Google Scholar] [CrossRef]
- Vyas, M. Some Studies on Two-Body Random Matrix Ensembles. Ph.D. Thesis, M.S. University of Baroda, Vadodara, India, 2011. [Google Scholar]
- Vyas, M.; Kota, V.K.B. Quenched quantum dynamics in few- to many-body systems using q-Hermite polynomials. arXiv 2018, arXiv:1805.00636. [Google Scholar]
- Rao, P.; Chavda, N.D. Fidelity decay and entropy production in k-body bosonic embedded ensembles. In preparation.
- Torres-Herrera, E.J.; Vyas, M.; Santos, L.F. General Features of the Relaxation Dynamics of Interacting Quantum Systems. New J. Phys. 2014, 16, 063010. [Google Scholar] [CrossRef]
- Torres-Herrera, E.J.; Karp, J.; Tavora, M.; Santos, L.F. Realistic Many-Body Quantum Systems vs. Full Random Matrices: Static and Dynamical Properties. Entropy 2016, 18, 359. [Google Scholar] [CrossRef]
- Santos, L.F.; Torres-Herrera, E.J. Analytical expressions for the evolution of many-body quantum systems quenched far from equilibrium. AIP Conf. Proc. 2017, 1912, 020015. [Google Scholar]
- Lauritzen, B.; Bortignon, P.F.; Broglia, R.A.; Zelevinsky, V.G. Limiting Value for the Width Controlling the Coupling of Collective Vibrations to the Compound Nucleus. Phys. Rev. Lett. 1995, 74, 5190–5193. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, S.; Lebowitz, J.L.; Tumulka, R.; Zanghi, N. Long-Time Behavior of Macroscopic Quantum Systems: Commentary Accompanying the English Translation of John Von Neumann’s 1929 Article on the Quantum Ergodic Theorem. Eur. Phys. J. H 2010, 35, 173–200. [Google Scholar] [CrossRef]
- Deutsch, J.M. Quantum statistical mechanics in a closed system. Phys. Rev. A 1991, 43, 2046–2049. [Google Scholar] [CrossRef] [PubMed]
- Srednicki, M. Chaos and quantum thermalization. Phys. Rev. E 1994, 50, 888–901. [Google Scholar] [CrossRef]
- Rigol, M.; Dunjko, V.; Olshanii, M. Thermalization and its mechanism for generic isolated quantum systems. Nature 2008, 452, 854–858. [Google Scholar] [CrossRef] [PubMed]
- Trotzky, S.; Chen, Y.A.; Flesch, A.; McCulloch, I.P.; Schollwöck, U.; Eisert, J.; Bloch, I. Probing the relaxation towards equilibrium in an isolated strongly correlated one-dimensional Bose gas. Nat. Phys. 2012, 8, 325–330. [Google Scholar] [CrossRef]
- Roy, K.; Chakrabarti, B.; Kota, V.K.B. Statistical properties of spectral fluctuations of N interacting bosons in an harmonic trap. Phys. Rev. E 2014, 90, 052137. [Google Scholar] [CrossRef] [PubMed]
- Roy, K.; Chakrabarti, B.; Kota, V.K.B. Spectral fluctuation and correlation structure of δn statistics in the spectra of interacting trapped bosons. Phys. Rev. E 2013, 87, 062101. [Google Scholar] [CrossRef] [PubMed]
- Roy, K.; Chakrabarti, B.; Chavda, N.D.; Kota, V.K.B.; Lekala, M.L.; Rampho, G.J. Spectral analysis of molecular resonances in Erbium isotopes: Are they close to semi-Poisson? Eur. Phys. Lett. 2017, 118, 46003. [Google Scholar] [CrossRef]
- Tomadin, A.; Mannella, R.; Wimberger, S. Many-body Landau-Zener tunneling in the Bose-Hubbard model. Phys. Rev. A 2008, 77, 013606. [Google Scholar] [CrossRef]
- Buonsante, P.; Wimberger, S. Engineering many-body quantum dynamics by disorder. Phys. Rev. A 2008, 77, 041606. [Google Scholar] [CrossRef]
- Parra-Murillo, C.A.; Madronero, J.; Wimberger, S. Two-band Bose-Hubbard model for many-body resonant tunneling in the Wannier-Stark system. Phys. Rev. A 2013, 88, 032119. [Google Scholar] [CrossRef]
- Fischer, D.; Hoffmann, D.; Wimberger, S. Spectral analysis of two-dimensional Bose-Hubbard models. Phys. Rev. A 2016, 93, 043620. [Google Scholar] [CrossRef]
- Anderson, M.H.; Ensher, J.R.; Matthews, M.R.; Wienman, C.E.; Cornell, E.A. Observation of Bose-Einstein Condensation in a Dilute Atomic Vapor. Science 1995, 269, 198–201. [Google Scholar] [CrossRef] [PubMed]
- Frisch, A.; Mark, M.; Aikawa, K.; Ferlaino, F.; Bohn, J.; Makrides, C.; Petrov, A.; Kotochigova, S. Quantum chaos in ultracold collisions of gas-phase erbium atoms. Nature 2014, 507, 475–479. [Google Scholar] [CrossRef] [PubMed]
- Mur-Petit, J.; Molina, R.A. Spectral statistics of molecular resonances in erbium isotopes: How chaotic are they? Phys. Rev. E 2015, 92, 042906. [Google Scholar] [CrossRef] [PubMed]
- Hernandez-Saldana, H.; Flores, J.; Seligman, T.H. Semi-Poisson statistics and beyond. Phys. Rev. E 1999, 60, 449–452. [Google Scholar] [CrossRef]
- Abul-Magd, A.Y.; Simbel, M.H. Nearest neighbor spacing distributions of low-lying levels of vibrational nuclei. Phys. Rev. C 1996, 54, 1675–1680. [Google Scholar] [CrossRef]
- Kota, V.K.B.; Sumedha, S. Transition curves for the variance of the nearest neighbor spacing distribution for Poisson to Gaussian orthogonal and unitary ensemble transitions. Phys. Rev. E 1999, 60, 3405–3408. [Google Scholar] [CrossRef]
- Chavda, N.D.; Kota, V.K.B. Probability Distribution of the Ratio of Consecutive Level Spacings in Interacting Particle Systems. Phys. Lett. A 2013, 377, 3009–3015. [Google Scholar] [CrossRef]
- Alon, O.E.; Streltsov, A.I.; Cederbaum, L.S. Multiconfigurational time-dependent Hartree method for bosons: Many-body dynamics of bosonic systems. Phys. Rev. A 2008, 77, 033613. [Google Scholar] [CrossRef]
- Streltsov, A.I.; Alon, O.E.; Cederbaum, L.S. General mapping for bosonic and fermionic operators in Fock space. Phys. Rev. A 2010, 81, 022124. [Google Scholar] [CrossRef]
- Lode, A.U.J.; Tsatsos, M.C. The Recursive Multiconfigurational Time-Dependent Hartree for Bosons Package (2014). Available online: http://ultracold.org (accessed on 8 November 2017).
- Szabowski, P.J. Multidimensional q-Normal and related distributions Markov case. Electron. J. Probab. 2010, 15, 1296–1318. [Google Scholar] [CrossRef]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kota, V.K.B.; Chavda, N.D. Random k-Body Ensembles for Chaos and Thermalization in Isolated Systems. Entropy 2018, 20, 541. https://doi.org/10.3390/e20070541
Kota VKB, Chavda ND. Random k-Body Ensembles for Chaos and Thermalization in Isolated Systems. Entropy. 2018; 20(7):541. https://doi.org/10.3390/e20070541
Chicago/Turabian StyleKota, Venkata Krishna Brahmam, and Narendra D. Chavda. 2018. "Random k-Body Ensembles for Chaos and Thermalization in Isolated Systems" Entropy 20, no. 7: 541. https://doi.org/10.3390/e20070541
APA StyleKota, V. K. B., & Chavda, N. D. (2018). Random k-Body Ensembles for Chaos and Thermalization in Isolated Systems. Entropy, 20(7), 541. https://doi.org/10.3390/e20070541



