Thermal Characteristics of Staggered Double-Layer Microchannel Heat Sink
Abstract
:1. Introduction
2. Numerical Analysis
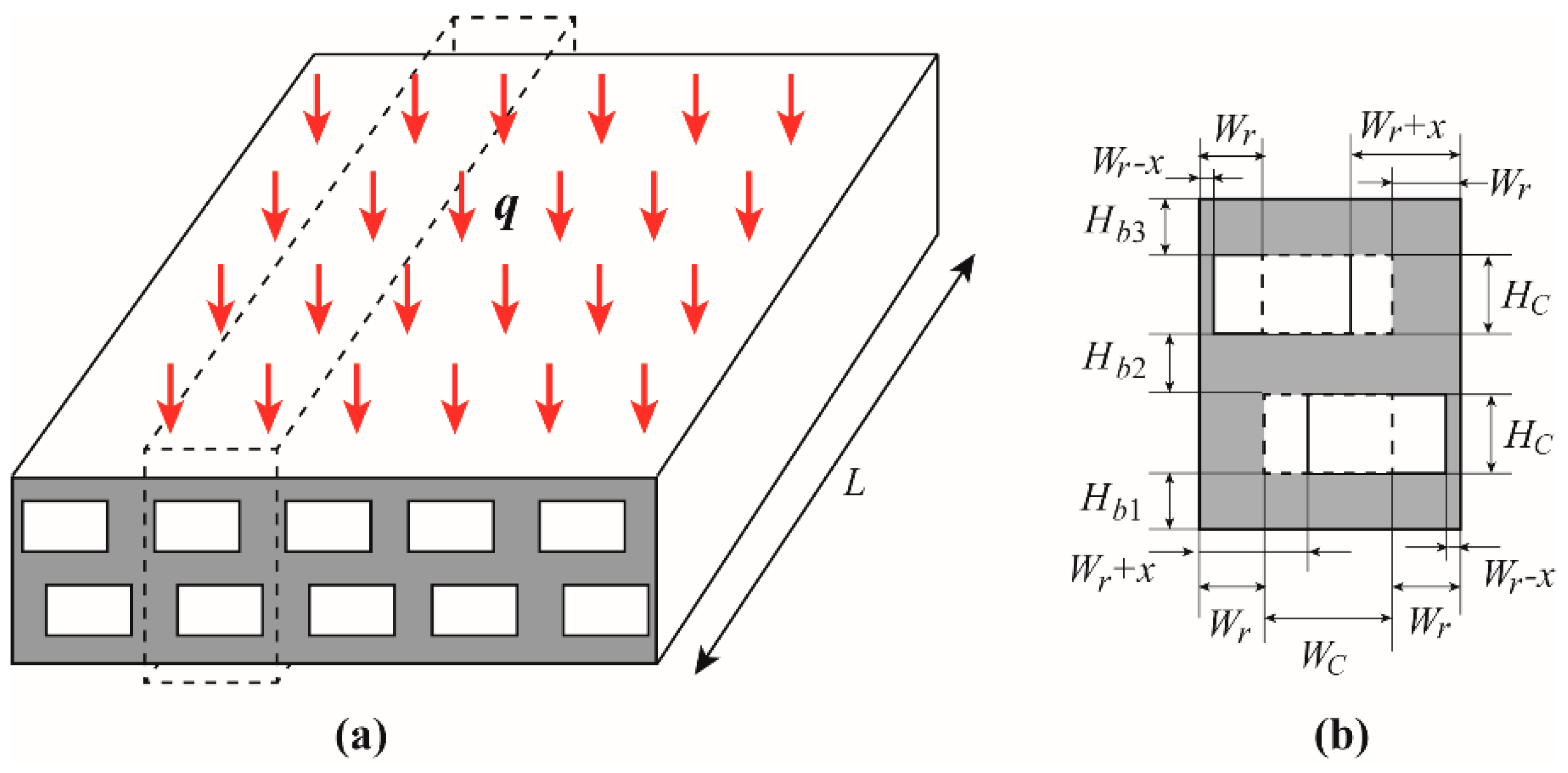
2.1. Description of the Staggered DLMCHS
2.2. Governing Equations
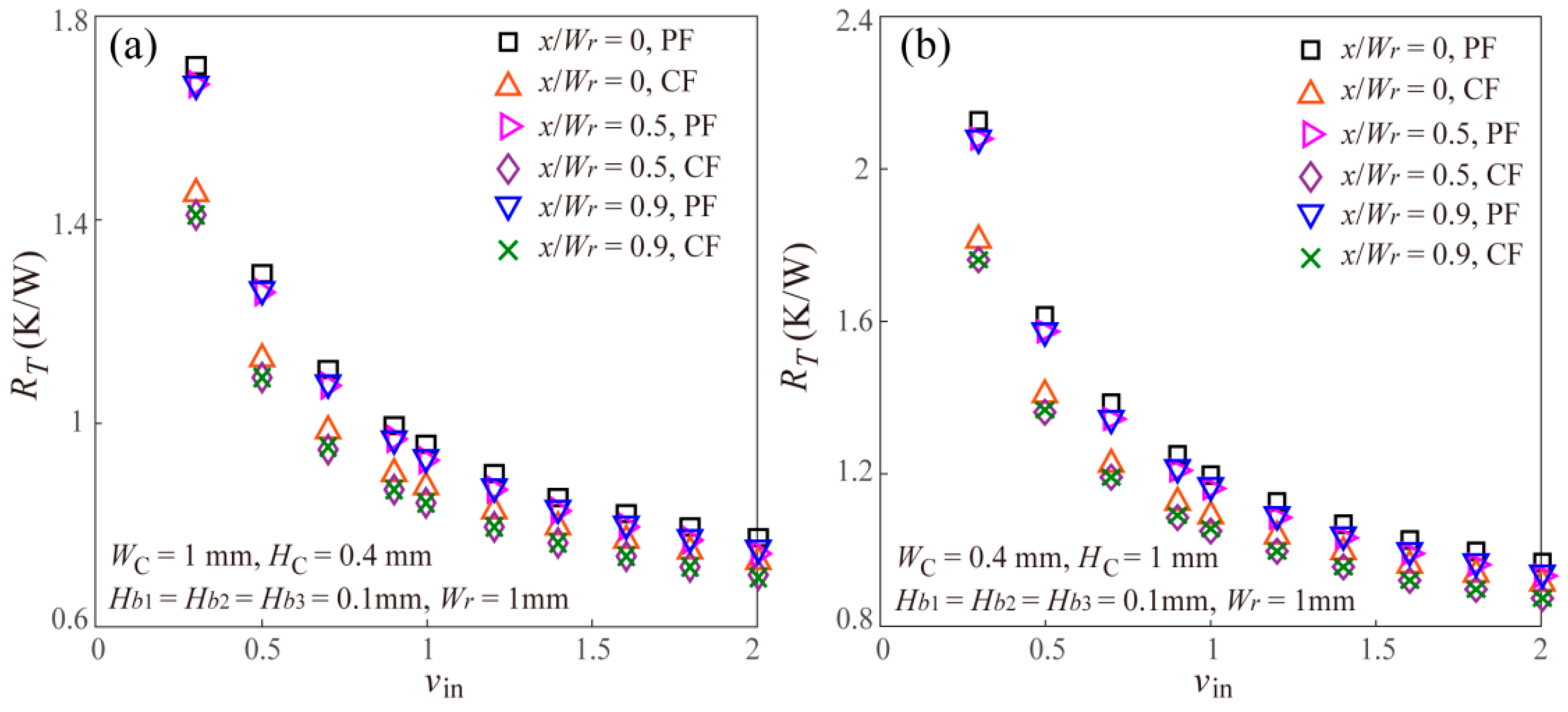
3. Results and Discussion
4. Conclusions
- (1)
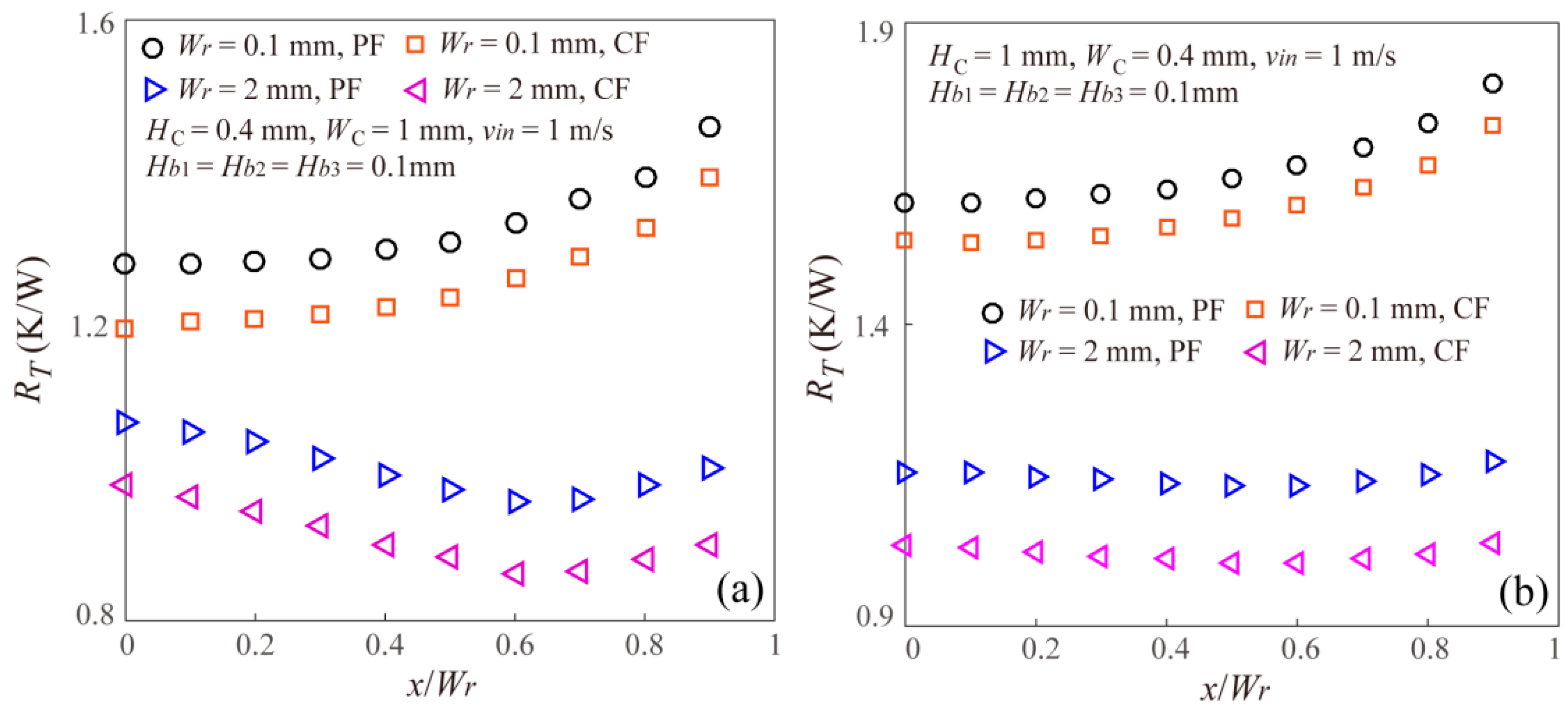
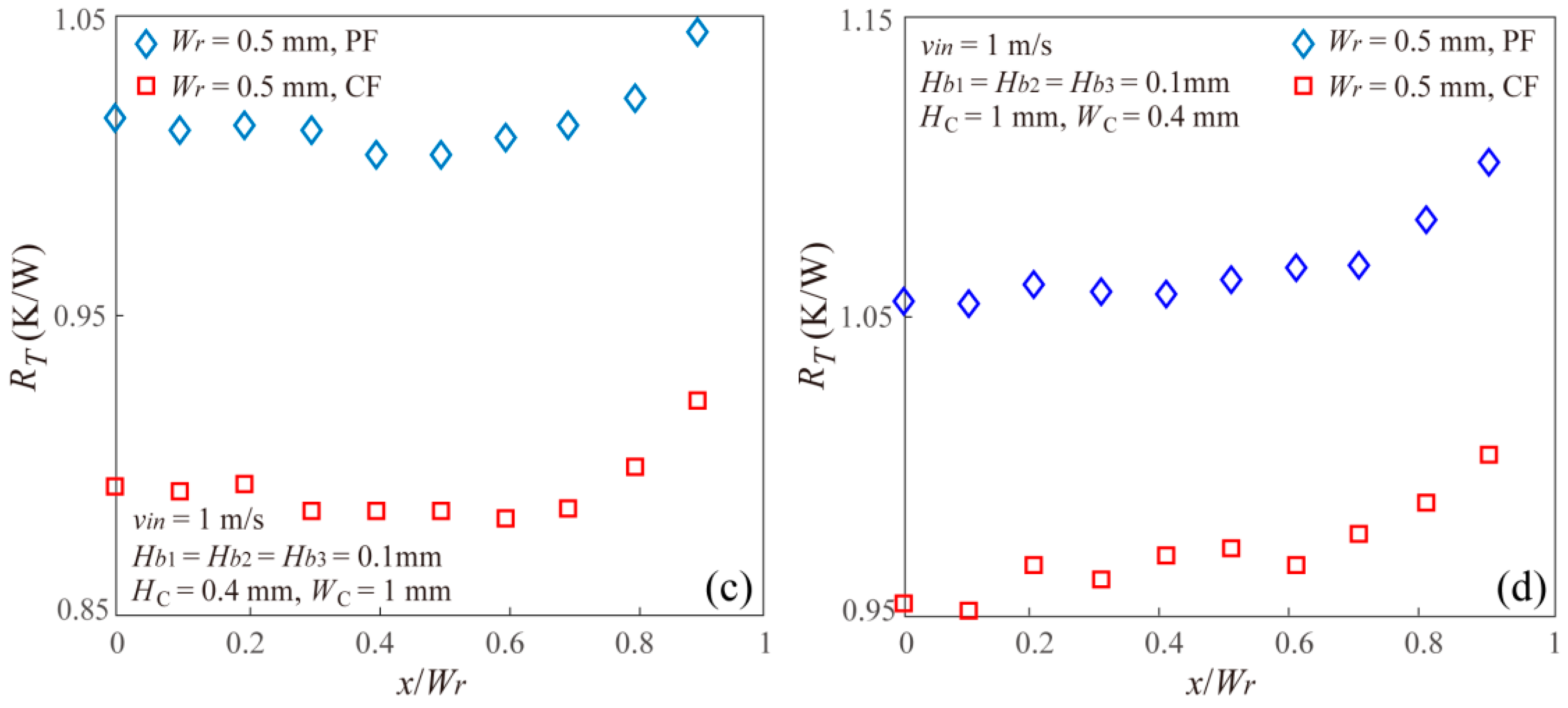
- The thermal resistance of the staggered DLMCHS increases with the increasing offset value when the vertical rib thickness is small enough, but decreases firstly and then increases as the offset value increases when the vertical rib thickness is large enough, which means there is an optimal offset value for the staggered DLMCHS to achieve a minimum thermal resistance when the vertical rib thickness is large enough.
- (2)
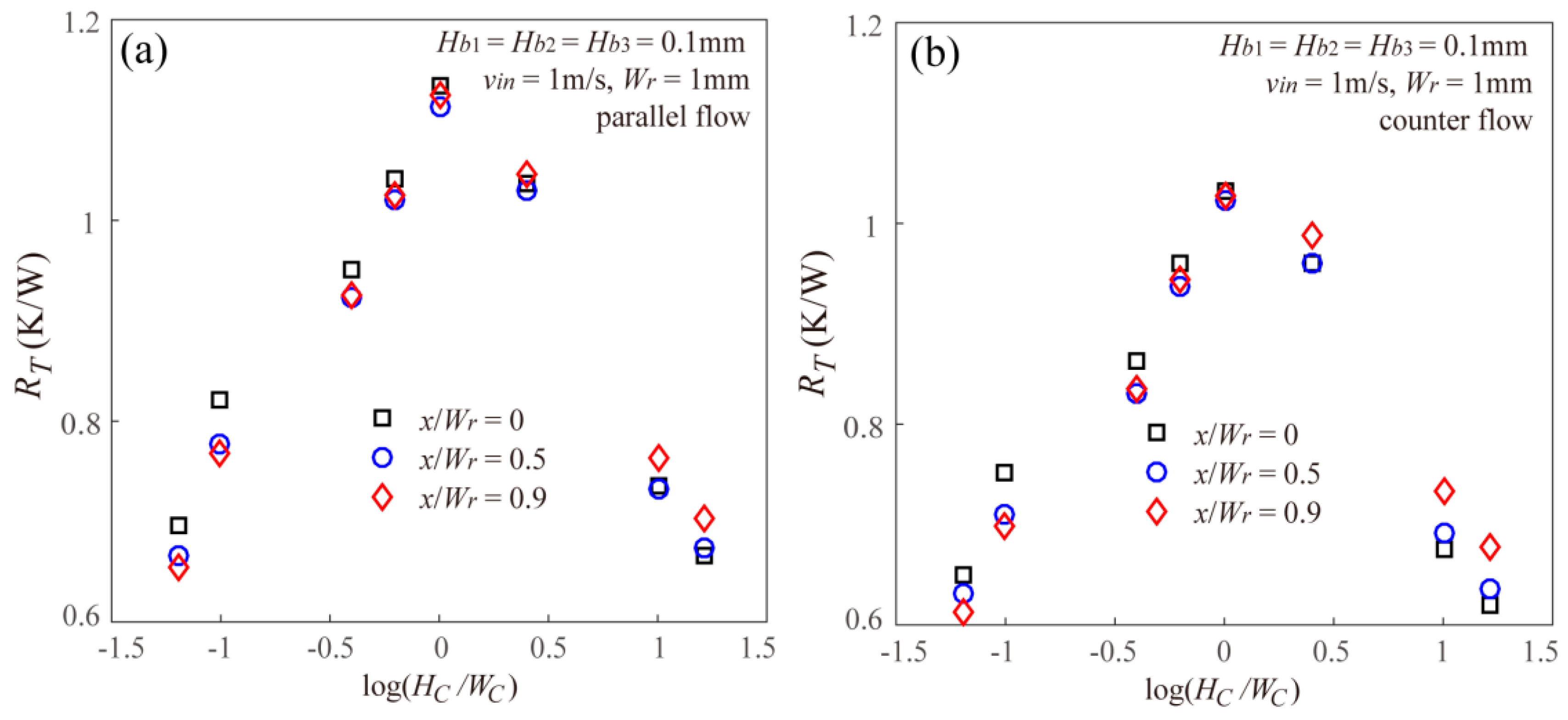
- The thermal resistance of the staggered DLMCHS shows a decreasing after increasing trend with the increasing microchannel aspect ratio under the constraint of a constant channel cross-sectional area. More important, the thermal resistance of the staggered DLMCHS decreases with the increasing offset when the aspect ratio is small enough, but increases with the increasing offset when the aspect ratio is large enough. This means that for the DLMCHS with a small microchannel aspect ratio, it is much easier for the offset between the upper layer and the lower layer to reduce the thermal resistance and improve the thermal performances of the DLMCHS.
- (3)
- The thermal resistance of the staggered DLMCHS decreases with the increasing inlet velocity.
Author Contributions
Funding
Conflicts of Interest
References
- Tuckerman, D.B.; Pease, R. High-performance heat sinking for VLSI. IEEE Electron. Device Lett. 1981, 2, 126–129. [Google Scholar] [CrossRef]
- Chen, Y.P.; Cheng, P. Heat transfer and pressure drop in fractal treelike microchannel nets. Int. J. Heat Mass Transf. 2002, 45, 2643–2648. [Google Scholar] [CrossRef]
- Pence, D.V. Reduced pumping power and wall temperature in microchannel heat sinks with fractal-like branching channel networks. Microscale Thermophys. Eng. 2003, 6, 319–330. [Google Scholar] [CrossRef]
- Wu, H.Y.; Cheng, P. An experimental study of convective heat transfer in silicon microchannels with different surface conditions. Int. J. Heat Mass Transf. 2003, 46, 2547–2556. [Google Scholar] [CrossRef]
- Gunnasegaran, P.; Mohammed, H.A.; Shuaib, N.H.; Saidur, R. The effect of geometrical parameters on heat transfer characteristics of microchannels heat sink with different shapes. Int. Commun. Heat Mass Transf. 2010, 37, 1078–1086. [Google Scholar] [CrossRef]
- Mohammed, H.A.; Gunnasegaran, P.; Shuaib, N.H. Influence of channel shape on the thermal and hydraulic performance of microchannel heat sink. Int. Commun. Heat Mass Transf. 2011, 38, 474–480. [Google Scholar] [CrossRef]
- Alfaryjat, A.A.; Mohammed, H.A.; Adam, N.M.; Ariffin, M.K.A.; Najafabadi, M.I. Influence of geometrical parameters of hexagonal, circular, and rhombus microchannel heat sinks on the thermohydraulic characteristics. Int. Commun. Heat Mass Transf. 2014, 52, 121–131. [Google Scholar] [CrossRef]
- Xia, G.D.; Jiang, J.; Wang, J.; Zhai, Y.L.; Ma, D.D. Effects of different geometric structures on fluid flow and heat transfer performance in microchannel heat sinks. Int. J. Heat Mass Transf. 2015, 80, 439–447. [Google Scholar] [CrossRef]
- Ahmed, H.E.; Ahmed, M.I. Optimum thermal design of triangular, trapezoidal and rectangular grooved microchannel heat sinks. Int. Commun. Heat Mass Transf. 2015, 66, 47–57. [Google Scholar] [CrossRef]
- Jing, D.; Song, S.; Pan, Y.; Wang, X. Size dependences of hydraulic resistance and heat transfer of fluid flow in elliptical microchannel heat sinks with boundary slip. Int. J. Heat Mass Transf. 2018, 119, 647–653. [Google Scholar] [CrossRef]
- Jing, D.; Song, S.; Pan, Y.; Wang, X. Optimal fractal tree-like microchannel networks with slip for laminar-flow-modified Murray’s law. Beilstein J. Nanotechnol. 2018, 9, 482–489. [Google Scholar] [CrossRef] [PubMed]
- Jing, D.; Pan, Y. Electroviscous effect and convective heat transfer of pressure driven flow through microtubes with surface charge-dependent slip. Int. J. Heat Mass Transf. 2016, 101, 648–655. [Google Scholar] [CrossRef]
- Jing, D.; Pan, Y.; Wang, X. Joule heating, viscous dissipation and convective heat transfer of pressure-driven flow in a microchannel with surface charge-dependent slip. Int. J. Heat Mass Transf. 2017, 108, 1305–1313. [Google Scholar] [CrossRef]
- Jing, D.; He, L.; Wang, X. Optimization analysis of fractal tree-like microchannel network for electroviscous flow to realize minimum hydraulic resistance. Int. J. Heat Mass Transf. 2018, 125, 749–755. [Google Scholar] [CrossRef]
- Pan, Y.; Jing, D.; Zhang, H.; Zhao, X. Effective Boundary Slip Induced by Surface Roughness and Their Coupled Effect on Convective Heat Transfer of Liquid Flow. Entropy 2018, 20, 334. [Google Scholar] [CrossRef]
- Vafai, K.; Zhu, L. Analysis of two-layered micro-channel heat sink concept in electronic cooling. Int. J. Heat Mass Transf. 1999, 31, 1176–1186. [Google Scholar] [CrossRef]
- Chong, S.H.; Ooi, K.T.; Wong, T.N. Optimization of single and double layer counter flow microchannel heat sinks. Appl. Therm. Eng. 2002, 22, 1569–1585. [Google Scholar] [CrossRef]
- Hung, T.C.; Yan, W.-M.; Li, W.-P. Analysis of heat transfer characteristics of double-layered microchannel heat sink. Int. J. Heat Mass Transf. 2012, 55, 3090–3099. [Google Scholar] [CrossRef]
- Wong, K.-C.; Nazhirin, F.; Muezzin, A. Heat transfer of a parallel flow two-layered microchannel heat sink. Int. Commun. Heat Mass Transf. 2013, 49, 136–140. [Google Scholar] [CrossRef]
- Wu, J.M.; Zhao, J.Y.; Tseng, K.J. Parametric study on the performance of double-layered microchannels heat sink. Energy Convers. Manag. 2014, 80, 550–560. [Google Scholar] [CrossRef]
- Wei, X.; Joshi, Y.; Patterson, M.K. Experimental and numerical study of a stacked microchannel heat sink for liquid cooling of microelectronic devices. J. Heat Transf. 2007, 129, 1432–1444. [Google Scholar] [CrossRef]
- Hung, T.C.; Yan, W.M.; Li, W.P.; Huang, Y.X. Optimal design of geometric parameters of double-layered microchannel heat sinks. Int. J. Heat Mass Transf. 2012, 55, 3262–3272. [Google Scholar] [CrossRef]
- Lin, L.; Chen, Y.Y.; Zhang, X.X.; Wang, X.D. Optimization of geometry and flow rate distribution for double-layer microchannel heat sink. Int. J. Therm. Sci. 2014, 78, 158–168. [Google Scholar] [CrossRef]
- Leng, C.; Wang, X.D.; Wang, T.H.; Yan, W.M. Optimization of thermal resistance and bottom wall temperature uniformity for double-layered microchannel heat sink. Energy Convers. Manag. 2015, 93, 141–150. [Google Scholar] [CrossRef]
- Leng, C.; Wang, X.D.; Wang, T.H.; Yan, W.M. Multi-parameter optimization of flow and heat transfer for a novel double-layered microchannel heat sink. Int. J. Heat Mass Transf. 2015, 84, 359–369. [Google Scholar] [CrossRef]

| Test Number i | Number of Tetrahedral Mesh | Tmax [°C] | (Tmaxi+1 − Tmaxi)/Tmaxi |
|---|---|---|---|
| 0 | 5.7 × 104 | 35.296 | - |
| 1 | 1.4 × 105 | 32.862 | 6.9 × 10−2 |
| 2 | 2.7 × 105 | 32.458 | 1.2 × 10−2 |
| 3 | 3.2 × 105 | 32.411 | 1.5 × 10−3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, D.; He, L. Thermal Characteristics of Staggered Double-Layer Microchannel Heat Sink. Entropy 2018, 20, 537. https://doi.org/10.3390/e20070537
Jing D, He L. Thermal Characteristics of Staggered Double-Layer Microchannel Heat Sink. Entropy. 2018; 20(7):537. https://doi.org/10.3390/e20070537
Chicago/Turabian StyleJing, Dalei, and Lei He. 2018. "Thermal Characteristics of Staggered Double-Layer Microchannel Heat Sink" Entropy 20, no. 7: 537. https://doi.org/10.3390/e20070537
APA StyleJing, D., & He, L. (2018). Thermal Characteristics of Staggered Double-Layer Microchannel Heat Sink. Entropy, 20(7), 537. https://doi.org/10.3390/e20070537




