A Quantum Ruler for Magnetic Deflectometry
Abstract
1. Quantum Interference of Organic Molecules
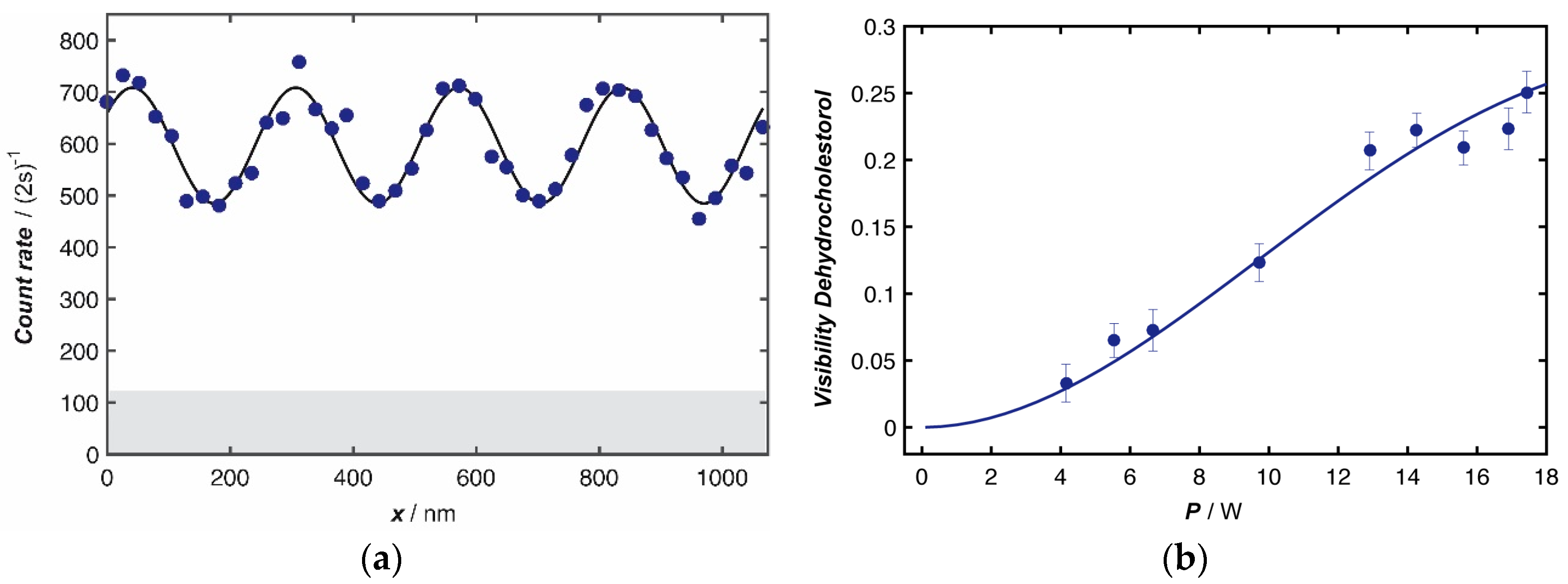
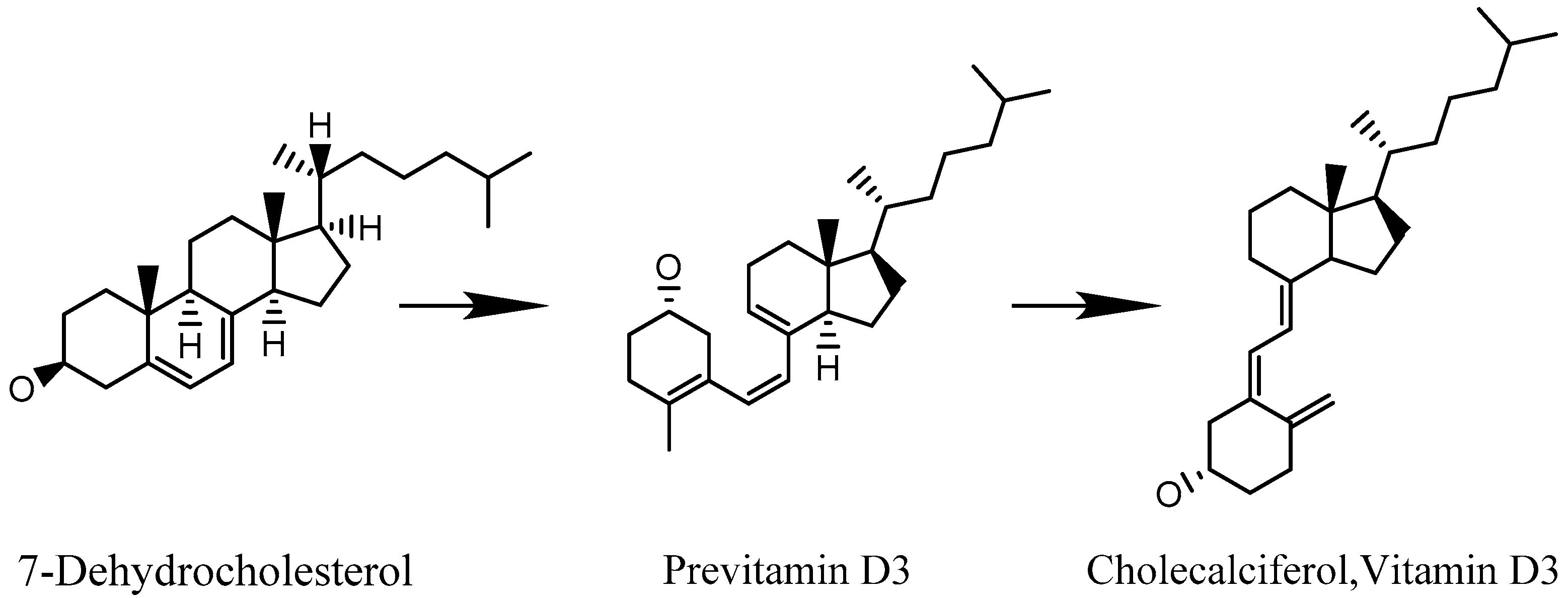
2. The Quantum Wave Nature of 7-Dehydrocholesterol
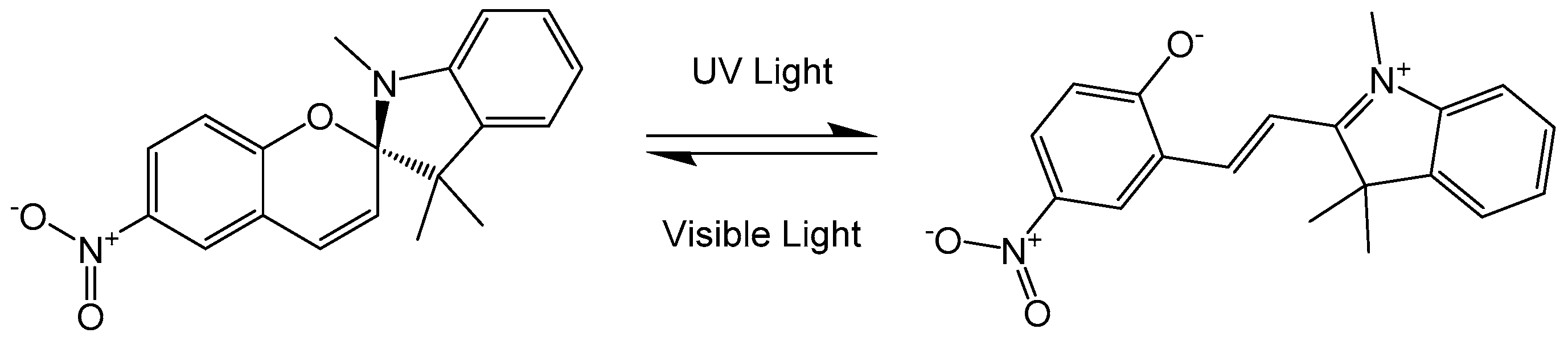
3. Photo-Switching
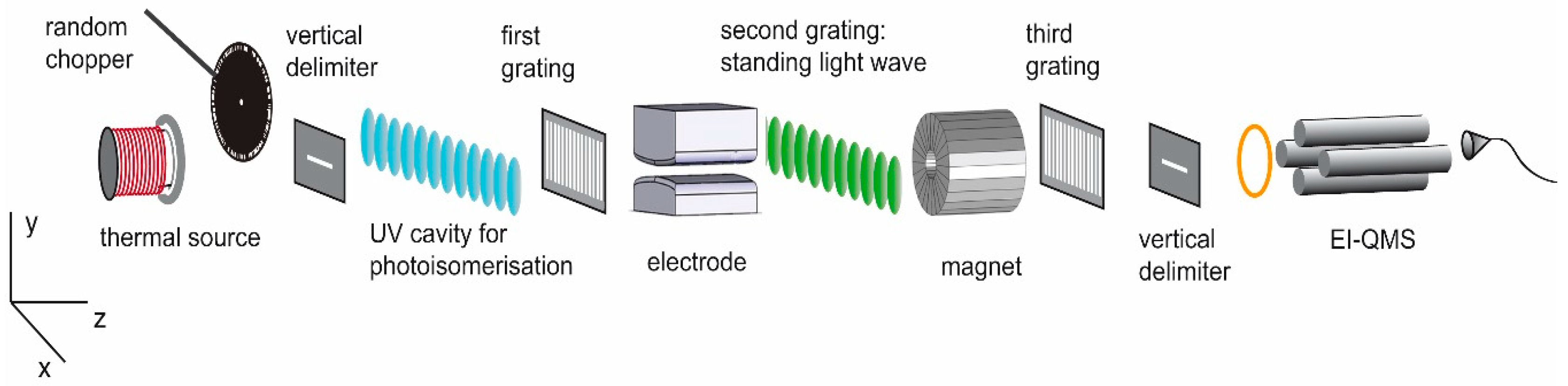
4. Magnetic Manifestations of Molecular Photoisomerization in the Gas Phase
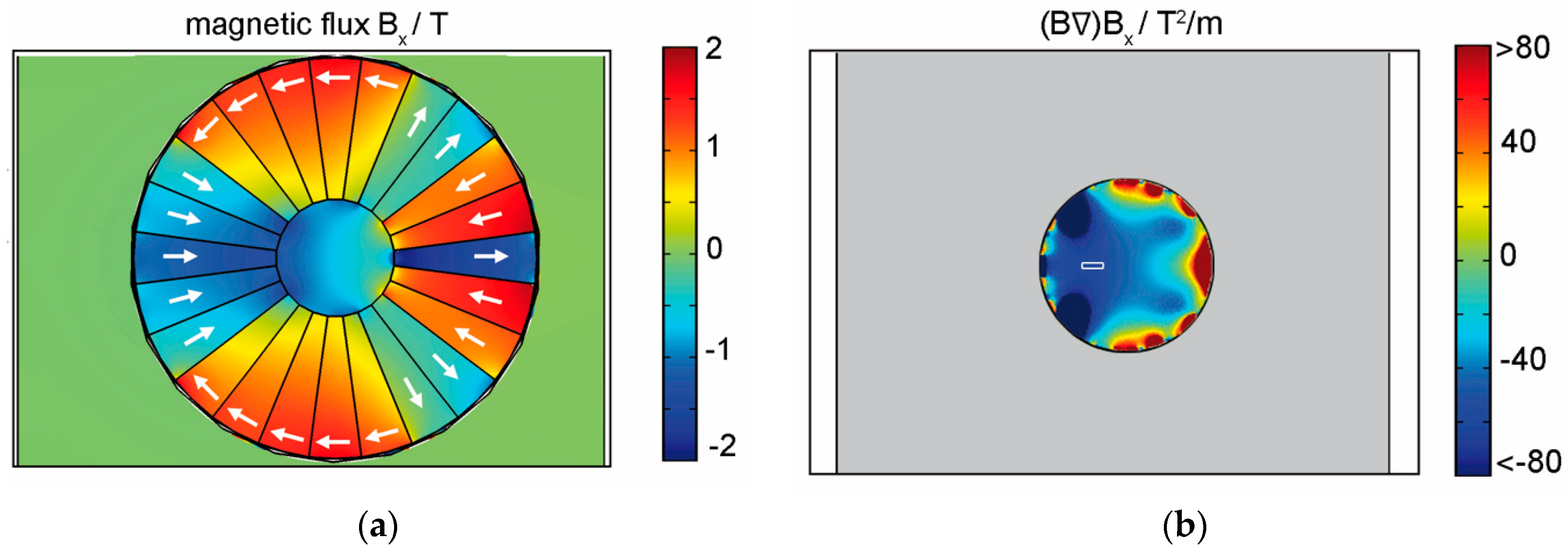
5. Design of the Required Magnetic Structures
6. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- De Broglie, L. Waves and Quanta. Nature 1923, 112, 540. [Google Scholar] [CrossRef]
- Juffmann, T.; Milic, A.; Müllneritsch, M.; Asenbaum, P.; Tsukernik, A.; Tüxen, J.; Mayor, M.; Cheshnovsky, O.; Arndt, M. Real-time single-molecule imaging of quantum interference. Nat. Nanotechnol. 2012, 7, 297–300. [Google Scholar] [CrossRef] [PubMed]
- Arndt, M.; Nairz, O.; Voss-Andreae, J.; Keller, C.; van der Zouw, G.; Zeilinger, A. Wave-particle duality of C60 molecules. Nature 1999, 401, 680–682. [Google Scholar] [CrossRef] [PubMed]
- Antoine, R.; Dugourd, P.; Rayane, D.; Benichou, E.; Broyer, M.; Chandezon, F.; Guet, C. Direct measurement of the electric polarizability of isolated C60 molecules. J. Chem. Phys. 1999, 110, 9771–9772. [Google Scholar] [CrossRef]
- Antoine, R.; Compagnon, I.; Rayane, D.; Broyer, M.; Dugourd, P.; Sommerer, N.; Rossignol, M.; Pippen, D.; Hagemeister, F.C.; Jarrold, M.F. Application of Molecular Beam Deflection Time-of-Flight Mass Spectrometry to Peptide Analysis. Anal. Chem. 2003, 75, 5512–5516. [Google Scholar] [CrossRef] [PubMed]
- Berninger, M.; Stefanov, A.; Deachapunya, S.; Arndt, M. Polarizability measurements of a molecule via a near-field matter-wave interferometer. Phys. Rev. A 2007, 76, 013607. [Google Scholar] [CrossRef]
- Gring, M.; Gerlich, S.; Eibenberger, S.; Nimmrichter, S.; Berrada, T.; Arndt, M.; Ulbricht, H.; Hornberger, K.; Müri, M.; Mayor, M.; et al. Influence of conformational molecular dynamics on matter wave interferometry. Phys. Rev. A 2010, 81, 031604. [Google Scholar] [CrossRef]
- Eibenberger, S.; Gerlich, S.; Arndt, M.; Tüxen, J.; Mayor, M. Electric moments in molecule interferometry. New J. Phys. 2011, 13, 043033. [Google Scholar] [CrossRef]
- Hornberger, K.; Gerlich, S.; Haslinger, P.; Nimmrichter, S.; Arndt, M. Colloquium: Quantum interference of clusters and molecules. Rev. Mod. Phys. 2012, 84, 157–173. [Google Scholar] [CrossRef]
- Gerlich, S.; Hackermüller, L.; Hornberger, K.; Stibor, A.; Ulbricht, H.; Gring, M.; Goldfarb, F.; Savas, T.; Müri, M.; Mayor, M.; et al. A Kapitza-Dirac-Talbot-Lau interferometer for highly polarizable molecules. Nat. Phys. 2007, 3, 711–715. [Google Scholar] [CrossRef]
- Brezger, B.; Hackermüller, L.; Uttenthaler, S.; Petschinka, J.; Arndt, M.; Zeilinger, A. Matter-Wave Interferometer for Large Molecules. Phys. Rev. Lett. 2002, 88, 100404. [Google Scholar] [CrossRef] [PubMed]
- Haslinger, P.; Dörre, N.; Geyer, P.; Rodewald, J.; Nimmrichter, S.; Arndt, M. A universal matter-wave interferometer with optical ionization gratings in the time domain. Nat. Phys. 2013, 9, 144–148. [Google Scholar] [CrossRef] [PubMed]
- Gerlich, S.; Eibenberger, S.; Tomandl, M.; Nimmrichter, S.; Hornberger, K.; Fagan, P.; Tüxen, J.; Mayor, M.; Arndt, M. Quantum interference of large organic molecules. Nat. Commun. 2011, 2, 263. [Google Scholar] [CrossRef] [PubMed]
- Eibenberger, S.; Gerlich, S.; Arndt, M.; Mayor, M.; Tüxen, J. Matter-wave interference of particles selected from a molecular library with masses exceeding 10,000 amu. Phys. Chem. Chem. Phys. 2013, 15, 14696–14700. [Google Scholar] [CrossRef] [PubMed]
- Mairhofer, L.; Eibenberger, S.; Cotter, J.P.; Romirer, M.; Shayeghi, A.; Arndt, M. Quantum-Assisted Metrology of Neutral Vitamins in the Gas Phase. Angew. Chem. Int. Ed. 2017, 56, 10947–10951. [Google Scholar] [CrossRef] [PubMed]
- Gerlich, S.; Gring, M.; Ulbricht, H.; Hornberger, K.; Tüxen, J.; Mayor, M.; Arndt, M. Matter-wave metrology as a complementary tool for mass spectrometry. Angew. Chem. Int. Ed. Engl. 2008, 47, 6195–6198. [Google Scholar] [CrossRef] [PubMed]
- Cotter, J.P.; Eibenberger, S.; Mairhofer, L.; Cheng, X.; Asenbaum, P.; Arndt, M.; Walter, K.; Nimmrichter, S.; Hornberger, K. Coherence in the presence of absorption and heating in a molecule interferometer. Nat. Commun. 2015, 6, 7336. [Google Scholar] [CrossRef] [PubMed]
- Hornberger, K.; Gerlich, S.; Ulbricht, H.; Hackermüller, L.; Nimmrichter, S.; Goldt, I.; Boltalina, O.; Arndt, M. Theory and experimental verification of Kapitza-Dirac-Talbot-Lau interferometry. New J. Phys. 2009, 11, 043032. [Google Scholar] [CrossRef]
- Nairz, O.; Brezger, B.; Arndt, M.; Zeilinger, A. Diffraction of Complex Molecules by Structures Made of Light. Phys. Rev. Lett. 2001, 87, 160401. [Google Scholar] [CrossRef] [PubMed]
- Juffmann, T.; Truppe, S.; Geyer, P.; Major, A.G.; Deachapunya, S.; Ulbricht, H.; Arndt, M. Wave and Particle in Molecular Interference Lithography. Phys. Rev. Lett. 2009, 103. [Google Scholar] [CrossRef] [PubMed]
- Oberthaler, M.K.; Bernet, S.; Rasel, E.M.; Schmiedmayer, J.; Zeilinger, A. Inertial Sensing with Classical Atomic Beams. Phys. Rev. A 1996, 54, 3165–3176. [Google Scholar] [CrossRef] [PubMed]
- Aghion, S.; Ahlen, O.; Amsler, C.; Ariga, A.; Ariga, T.; Belov, A.S.; Berggren, K.; Bonomi, G.; Braunig, P.; Bremer, J.; et al. A moire deflectometer for antimatter. Nat. Commun. 2014, 5, 4538. [Google Scholar] [CrossRef] [PubMed]
- Browne, W.R.; Feringa, B.L. Making molecular machines work. Nat. Nanotechnol. 2006, 1, 25–35. [Google Scholar] [CrossRef] [PubMed]
- Irie, M. Diarylethenes for Memories and Switches. Chem. Rev. 2000, 100, 1685–1716. [Google Scholar] [CrossRef] [PubMed]
- Yokoyama, Y. Fulgides for Memories and Switches. Chem. Rev. 2000, 100, 1717–1740. [Google Scholar] [CrossRef] [PubMed]
- Berkovic, G.; Krongauz, V.; Weiss, V. Spiropyrans and Spirooxazines for Memories and Switches. Chem. Rev. 2000, 100, 1741–1754. [Google Scholar] [CrossRef] [PubMed]
- Yang, I.; Kim, E.; Kang, J.; Han, H.; Sul, S.; Park, S.B.; Kim, S.K. Photochemical generation of a new, highly fluorescent compound from non-fluorescent resveratrol. Chem. Commun. 2012, 48, 3839–3841. [Google Scholar] [CrossRef] [PubMed]
- Fuss, W.; Höfer, T.; Hering, P.; Kompa, K.L.; Lochbrunner, S.; Schikarski, T.; Schmid, W.E. Ring Opening in the Dehydrocholesterol−Previtamin D System Studied by Ultrafast Spectroscopy. J. Phys. Chem. 1996, 100, 921–927. [Google Scholar] [CrossRef]
- Gahlmann, A.; Lee, I.R.; Zewail, A.H. Direct structural determination of conformations of photoswitchable molecules by laser desorption-electron diffraction. Angew. Chem. Int. Ed. Engl. 2010, 49, 6524–6527. [Google Scholar] [CrossRef] [PubMed]
- Tang, K.C.; Rury, A.; Orozco, M.B.; Egendorf, J.; Spears, K.G.; Sension, R.J. Ultrafast electrocyclic ring opening of 7-dehydrocholesterol in solution: The influence of solvent on excited state dynamics. J. Chem. Phys. 2011, 134, 104503. [Google Scholar] [CrossRef] [PubMed]
- Debiossac, M.; Schätti, J.; Kriegleder, M.; Geyer, P.; Shayeghi, A.; Mayor, M.; Arndt, M.; Köhler, V. Tailored photocleavable peptides: Fragmentation and neutralization pathways in high vacuum. Phys. Chem. Chem. Phys. 2018, 20, 11412–11417. [Google Scholar] [CrossRef] [PubMed]
- Gangloff, D.; Shi, M.; Wu, T.; Bylinskii, A.; Braverman, B.; Gutierrez, M.; Nichols, R.; Li, J.; Aichholz, K.; Cetina, M.; et al. Preventing and reversing vacuum-induced optical losses in high-finesse tantalum(V) oxide mirror coatings. Opt. Express 2015, 23, 18014–18028. [Google Scholar] [CrossRef] [PubMed]
- Gerlach, W.; Stern, O. Der experimentelle Nachweis des magnetischen Moments des Silberatoms. Z. Phys. 1922, 8, 110–111. [Google Scholar] [CrossRef]
- Rabi, I.I.; Millman, S.; Kusch, P.; Zacharias, J.R. The Molecular Beam Resonance Method for Measuring Nuclear Magnetic Moments. The Magnetic Moments of 3Li6, 3Li7and 9F19. Phys. Rev. 1939, 55, 526–535. [Google Scholar] [CrossRef]
- Ramsey, N.F. A Molecular Beam Resonance Method with Separated Oscillating Fields. Phys. Rev. 1950, 78, 695–699. [Google Scholar] [CrossRef]
- Moro, R.; Xu, X.; Yin, S.; de Heer, W.A. Ferroelectricity in free niobium clusters. Science 2003, 300, 1265–1269. [Google Scholar] [CrossRef] [PubMed]
- Rohrmann, U.; Schafer, R. Stern-Gerlach experiments on Mn@Sn12: Identification of a paramagnetic superatom and vibrationally induced spin orientation. Phys. Rev. Lett. 2013, 111, 133401. [Google Scholar] [CrossRef] [PubMed]
- Narevicius, E.; Parthey, C.G.; Libson, A.; Riedel, M.F.; Even, U.; Raizen, M.G. Towards magnetic slowing of atoms and molecules. New J. Phys. 2007, 9. [Google Scholar] [CrossRef]
- Akerman, N.; Karpov, M.; David, L.; Lavert-Ofir, E.; Narevicius, J.; Narevicius, E. Simultaneous deceleration of atoms and molecules in a supersonic beam. New J. Phys. 2015, 17. [Google Scholar] [CrossRef]
- Vleck, J.H.V. The Theory of Electric and Magnetic Susceptibilities; Oxford University Press: London, UK, 1965. [Google Scholar]
- Atkins, P.W.; Friedman, R. Molecular Quantum Mechanics, 4nd ed.; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- De Heer, W.A.; Kresin, V.V. Electric and magnetic dipole moments of free nanoclusters. In Handbook of Nanophysics; Sattler, K.D., Ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Heiles, S.; Schäfer, R. Dielectric Properties of Isolated Clusters Beam Deflection Studies; Springer: Heidelberg, Germany, 2014. [Google Scholar]
- Elser, V.; Haddon, R.C. Icosahedral C60: An aromatic molecule with a vanishingly small ring current magnetic susceptibility. Nature 1987, 325, 792. [Google Scholar] [CrossRef]
- Lin, J.-S.; Chiu, H.-T. Photochromic Behavior of Spiropyran and Fulgide in Thin Films of Blends of PMMA and SBS. J. Polym. Res. 2003, 10, 105–110. [Google Scholar] [CrossRef]
- Weinberger, C.R.; Tucker, G.J. Multiscale Materials Modeling for Nanomechanics; Springer: New York, NY, USA, 2016. [Google Scholar]
- Geyer, P.; Sezer, U.; Rodewald, J.; Mairhofer, L.; Dörre, N.; Haslinger, P.; Eibenberger, S.; Brand, C.; Arndt, M. Perspectives for quantum interference with biomolecules and biomolecular clusters. Phys. Scr. 2016, 91. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mairhofer, L.; Eibenberger, S.; Shayeghi, A.; Arndt, M. A Quantum Ruler for Magnetic Deflectometry. Entropy 2018, 20, 516. https://doi.org/10.3390/e20070516
Mairhofer L, Eibenberger S, Shayeghi A, Arndt M. A Quantum Ruler for Magnetic Deflectometry. Entropy. 2018; 20(7):516. https://doi.org/10.3390/e20070516
Chicago/Turabian StyleMairhofer, Lukas, Sandra Eibenberger, Armin Shayeghi, and Markus Arndt. 2018. "A Quantum Ruler for Magnetic Deflectometry" Entropy 20, no. 7: 516. https://doi.org/10.3390/e20070516
APA StyleMairhofer, L., Eibenberger, S., Shayeghi, A., & Arndt, M. (2018). A Quantum Ruler for Magnetic Deflectometry. Entropy, 20(7), 516. https://doi.org/10.3390/e20070516




