Abstract
The present work is concerned with the study of a generalized Langevin equation and its link to the physical theories of statistical mechanics and scale relativity. It is demonstrated that the form of the coefficients of the Langevin equation depends critically on the assumption of continuity of the reconstructed trajectory. This in turn demands for the fluctuations of the diffusion term to be discontinuous in time. This paper further investigates the connection between the scale-relativistic and stochastic mechanics approaches, respectively, with the study of the Burgers equation, which in this case appears as a stochastic geodesic equation for the drift. By further demanding time reversibility of the drift, the Langevin equation can also describe equivalent quantum-mechanical systems in a path-wise manner. The resulting statistical description obeys the Fokker–Planck equation of the probability density of the differential system, which can be readily estimated from simulations of the random paths. Based on the Fokker–Planck formalism, a new derivation of the transient probability densities is presented. Finally, stochastic simulations are compared to the theoretical results.
Keywords:
stochastic differential equations; Monte Carlo simulations; Burgers equation; Langevin equation; fractional velocity PACS:
02.30.Jr; 02.30.Uu; 02.50.Ga; 02.70.Uu
MSC:
60J65; 76R50; 65R20
1. Introduction
The Langevin equation was introduced in order to describe the motion of a test particle subjected to a fluctuating force and a viscous drag [1]. Its formulation was later generalized to encompass also other types of systems. The Langevin equation is also fundamental for the stochastic interpretation of Quantum Mechanics (QM) [2] and it also appears, in the form of a geodesic equation, in the scale relativity theory (SR) developed by Nottale [3]. The equation represents a substantial theoretical innovation because it was in fact the first stochastic differential equation. The formal theory of stochastic differential equations was developed much later by the works of Itô and Stratonovich (see, for example, [4] for introduction).
In contrast to the picture of diffusion as an uncorrelated random walk, the theory of dynamical systems makes it possible to treat diffusion as a deterministic dynamical process. There the Langevin dynamics can be also driven by chaotic but deterministic processes [5,6,7]. Emergence of diffusive behavior and Markovian evolution was also addressed by Gillespie [8]. The recent study of Tyran-Kaminska demonstrates that simple diffusion processes can emerge as weak limits of piecewise continuous processes constructed within a totally deterministic framework [7]. This is a finding which lends credence to the widely used techniques of Monte Carlo simulations using pseudo-random number generators.
A different way of looking at the Langevin equation is to specify a fractal driving process instead of the stochastic Wiener process. Examples can be given by the studies of deterministic diffusion, where generalized Takagi functions appear [9,10]. Using this approach, both fractal and linear behaviours of the diffusion coefficients can be demonstrated. Together, the studies mentioned so far demonstrate a fundamental interplay between emergent stochasticity, chaotic dynamics and fractality, which governs transport phenomena.
The term generalized Langevin equation is typically used in the physics literature to describe the system’s memory effects conveyed by non-Markovian color noises [11]. The present paper will generalize the Langevin equation in a different way. The Markovian character of the driving signal will be preserved, but the signal will be assumed to have some properties, leading to fractal behaviour—notably a suitably dense set of points where its Hölder exponent is fractional. Furthermore, the linearity restriction of drift term will be relaxed and instead the drift will be assumed to be a smooth function of position and time.
Interpretations of quantum mechanics are drawing a reemerging attention in the light of the centennial anniversary of David Bohm. Part of the present work was presented as a poster at the Emergent Quantum Mechanics 2017 conference in London. Results of the present work have been derived using the machinery of stochastic mechanics. On the other hand, the paper does not make strong foundational claims; instead, it is concerned with some questions about the mathematical foundations of the scale relativity theory, its link to stochastic mechanics and the theory of the Burgers equation. To the author’s knowledge, such a link to the Burgers equation was not recognized before.
The Burgers equation was initially formulated by Bateman while modeling the weakly viscous liquid motion [12]. It can be derived from the full Navier–Stokes equations under some simplifying assumptions. It was later studied extensively by Burgers as a cartoon model of turbulence [13]. Presently, the number of applications of the Burgers equation is very diverse. It has been used to model physical systems, such as surface perturbations, acoustic waves, electromagnetic waves, density waves, or traffic (see, for example, [14]). The stochastic representation of the Burgers equation can be traced back to the seminal works of Busnello et al. [15,16]. Later, Constantin and Iyer derived a probabilistic representation of the deterministic three-dimensional Navier–Stokes equations [17,18]. The result presented here complements the findings of these authors as incompressibility, and hence the harmonicity of the drift, in the Burgers equation is not required.
The paper starts by briefly presenting stochastic mechanics and scale relativity. Section 2 demonstrates a general result about stochastic representations of Hölder-continuous signals leading to the Langevin equation. Section 3 introduces Nelson’s characterization of a stochastic process. Section 4 introduces the complex representation of the drift in stochastic mechanics and scale relativity. Section 5 establishes the connection with the Burgers equation. Based on the Fokker–Planck formalism, a new derivation of the transient probability densities is presented. Section 6 discusses the Burgers equation as a geodesic-type of equation. The Cole–Hopf transformations are discussed as solution techniques for the Burgers equation in Section 7. Moreover, it is demonstrated how complex Cole–Hopf transformations map the complex Burgers equation, derived in a variational setting, to the free Schroedinger equation. Finally, in Section 8, numerical simulations are compared with the theoretical results.
1.1. Stochastic Mechanics (SM)
In the 1930s, certain similarities between the equations of classical statistical mechanics and the Schrödinger equation were discovered. These findings led to the stochastic interpretation of quantum mechanics. In stochastic mechanics, quantum phenomena are described in terms of diffusions instead of wave functions. The main equation of motion is in fact the Langevin equation. The formal equations of stochastic mechanics were formulated at first by Fényes [19] and Weizel [20] and later taken up by Nelson [2]. Following this interpretation, the trajectories of the configuration, described by a Markov stochastic process, are regarded as physically real. Nelson’s original formulation employed a stochastic version of the Newton’s law and time reversibility of the process. Interestingly, the form of the stochastic acceleration had to be postulated.
A Lagrangian formulation of stochastic mechanics was achieved by Pavon in complex form [21]. However, the given presentation is far from intuitive. In his treatment, the stochastic Lagrangian is the classical Lagrangian evaluated on a complex-valued velocity field in place of the real-valued classical velocity, while the dynamics is given by a complex-valued stochastic differential equation, similar to the treatment of Nottale. The Lagrangian problem was formulated as a constrained optimization problem, where the dynamics acted as the constraint.
1.2. Scale Relativity Theory (SR)
The scale relativity theory extends the principle of relativity also to resolution scales [3,22,23]. The main tenet of the theory is that there is no preferred scale of description of the physical reality. Therefore, a physical phenomenon must be described simultaneously at all admissible scales. While this is consistent with calculus for differentiable signals, the situation changes if non-differentiable models, such as Brownian motion or Mandelbrot’s multiplicative cascades [24], are addressed. For these cases, the scale of observation (or resolution) is present irreducibly in the local description of a phenomenon. This led Nottale to postulate the fractality of the underlying mathematical variety (i.e., a pseudo-manifold) describing the observables. It should be noted that, in Nottale’s approach, only finite differences are admissible. The scale relativistic approach results in corrections of Hamiltonian mechanics that arise due to the non-differentiability of trajectories, which are treated as virtual paths. Nottale introduces a complex operator that he calls the scale derivative, which acts as a pseudo-derivative (see Section 4 for details).Using this tool, Nottale gives an informal derivation of the Schrödinger equation from the classical Newtonian equation of dynamics, via a quantization procedure that follows from an extension of Einstein’s relativity principle called the scale relativity principle.
2. Stochastic Representation of Trajectories
If one considers the Brownian particle as a subsystem and the surrounding particles as an infinite dimensional thermal reservoir, the Langevin equation precisely models the situation where the subsystem suitably interacts with the thermal reservoir. The type of the effective random force can be identified with a Wiener process, which has continuous but non-differentiable paths almost everywhere. Mathematical descriptions of strongly nonlinear phenomena necessitate the relaxation of the global assumption of differentiability. In contrast, classical physics assumes global smoothness of the signals and continuity of their first two derivatives. Therefore, non-smooth phenomena, such as fractals slip through its conceptual net. This argument can be further elaborated as follows. Consider the measurement of a trajectory in time . Non-differentiability can occur in three scenarios:
- divergence of the velocity, that is divergence of the difference quotient,
- oscillatory singularity or
- difference between forward and backward velocities.
While for scenarios (1) and (2) the velocities (i.e., derivatives) can not be defined mathematically, scenario (3) requires dropping only the assumption of continuity of the resulting velocity. That is, at the point of non-differentiability t. A simple example of such behavior is the signal around the origin . While scenario (2) is excluded by the scale relativity theory, scenario (1) leads to scale dependence of the difference quotient. Examples of fractal functions, such as the mathematical Brownian motion paths, are typically of divergent length. This at best can be viewed as a mathematical idealization since in this case the work for moving a particle along its trajectory must be infinite. On the other hand, non-differentiability does not need to occur “everywhere” (i.e., with full Lebesgue measure) on a trajectory. In this case, the trajectory can be almost everywhere differentiable except on a certain dense set of points. Examples of these are the singular functions, such as the Salem-de Rham’s functions [25] or the well known Cantor’s function. Singular functions have finite lengths, therefore the exerted displacement work is also finite. This makes them promising candidates for conceptualization of non-smooth phenomena in physics.
The relationship between Nelson’s and Nottale’s approaches can be established in a formal way. For clarity of the argument, we focus on the one-dimensional case. First, let’s establish the concept of stochastic embedding of a signal. In the following, we assume that the deterministic signal (i.e., trajectory) will be represented by an equivalence class of stochastic paths having the same expectation as the given deterministic signal. Mathematical notation and preliminaries for the subsequent treatment are presented in Appendix A. A possibly non-differentiable continuous trajectory is represented by a continuous Markov stochastic process evaluated in the virtual space of paths as follows:
Definition 1 (Markov Stochastic Embedding).
Consider a bounded deterministic signal on the compact interval representing time. Define the stochastic embedding in the probability space (), where ρ is the probability density, as the isomorphism
under the constraint
where the random variables sampled at different times t are independent and identically distributed (i. i. d.) and is a σ-algebra.
Note: the -index will be skipped from the notation wherever convenient for clarity. In addition, and will be used interchangeably. Deterministic signals are denoted by the lower case, while the stochastic by upper case letters.
The above definition implicitly assumes that and .
The name of the embedding is justified by the following Lemma:
Lemma 1.
The stochastic process under the above definition has the Markov property.
Proof.
By construction for fixed
The conditional expectation is
where is used for notational convenience. However, by independence of the variables . Therefore, . Since can be either positive or negative, the claim follows. ☐
Consider the nonlinear problem, where the phase-space trajectory of a system is represented by a Hölder function (see Appendix A, Definition A2) and t is a real-valued parameter, for example time or curve length. Let us suppose that the continuous temporal evolution of a differential system can be represented by a generalization of the Langevin equation of the form
where and B are bounded and measurable functions of the co-ordinates and furthermore is continuous in both x and t. That is, for all , such that
This can be recognized as the Hölder growth condition of order , since is an term. The fractional exponent is treated as a free parameter with value to be determined later.
The type of admissible functions coupled to the fractional exponent depends critically on the assumption of continuity of the reconstructed trajectory. This in turn demands for the fluctuations of the fractional term to be discontinuous. The proof technique is introduced in [26], while the argument is similar to the one presented by Gillespie [8].
Without loss of generality, set . Let and . Fix the interval and choose a partition of points
Therefore, by induction
If we suppose that B is continuous in x, implying also continuity in t, after taking supremum limit on both sides
Therefore, either (which is forbidden by hypothesis) or else so that must oscillate from point to point if . Then, let’s denote the set .
The argument demonstrates that so-defined set is totally disconnected in the topology of the real line [26]. This allows for the choice of the algebra , since we can demand that has for elements the semi-open intervals . Furthermore, the initial system in Equation (1) is equivalent to the finite existence of the fractional velocity , since the differential system can be recognized as fractional Taylor series [26]. In other words, the events in the probability space are the observations of non-vanishing values of the fractional velocity of the signal.
From now on, let . Without loss of generality, suppose that . The stochastic representation is such that
Therefore, we demand that is -measurable and as a technical condition.
By the Hölder condition, for some set of constants . Then, by transfer,
Therefore, exists and is bounded. By the same argument,
Then, we proceed by induction. Let from the above partition:
Therefore, for the embedded variable,
Since are independent by Lemma 1, . Therefore, .
The argument can be specialized to where . Therefore, the variance exists and the Central Limit Theorem holds. Since by Lemma 1 the process is Markovian, it must follow that in limit the random process is Wiener.
Now suppose that . Then, since is continuous of bounded variation (BVC, see Appendix A), then a.e.,
and
with existing by the previous argument. Therefore, by the same argument as in the previous case. Therefore, for , the limit of the random process is Wiener.
Let us denote the limit Wiener process by . Using the stationarity and self-similarity of the increments where is a standard Gaussian random variable. Therefore, for the velocity can be regularized to a finite value if we take the expectation. That is,
since . However,
The estimate holds a.s. since , where denotes probability.
Finally, there is a function , such that , . This follows directly from the axiom of choice, since we can always choose . Therefore, the last equation can be treated as a definition of .
In summary, the following theorem can be formulated:
Theorem 1 (Gaussian stochastic embedding).
Suppose that is β-differentiable of order in the interval and
for , where is continuous in both x and t and is bounded but discontinuous. Furthermore, let be the set of change (Definition A6) of .
Then, can be embedded in a probability space (), such that
- 1.
- ,
- 2.
- has i. i. d. Gaussian increments,
- 3.
- and
- 4.
- hold almost sure.
Furthermore, the stochastic differential equation
holds a.s. In the last equation, is a standard Wiener process and
Such embedding can be also called a consistent stochastic embedding. This theorem allows for Nelson’s characterization of the Langevin diffusion process.
3. Nelson’s Characterization
The Langevin equation can describe equivalent quantum-mechanical systems in a path-wise manner. These are the so-called conservative diffusions of Carlen [27]. The existence of so-conceived QM particle paths was proven under certain reasonable conditions [27]. Starting from the generalized Langevin equation, the argument can be specialized to a Wiener driving process, which can be handled using the apparatus of Itô calculus. Consider the stochastic differential equation with continuous drift and diffusion coefficients
where and are smooth functions of the co-ordinates and are the increments of a Wiener process adapted to the past filtration – i.e., starting from the initial state.
Let . Following Nelson [2], the forward and backward and drift, respectively diffusion coefficients, can be identified as the averaged velocities [28]:
The evolution of the density of the process can be computed from the forward Fokker–Planck equation
which can be recognized as a conservation law for the probability current j:
Under the finite energy technical condition, there is a backwards process with the same transition density
which is adapted to the future filtration – i.e., starting from the final state. This leads to the anticipative (i.e., anti-Itô or anticipative) stochastic integrals. This process has Fokker–Planck equation
Then, it follows that the Nelson’s osmotic velocity can be defined from
where is an arbitrary function of time as and the current velocity as
so that a continuity equation holds for the density
Furthermore, Pavon [21] has established that the entropy production over the whole space is
Thus, for a Markov diffusion process,
for a constant b.
4. The Complex Velocity Operator in SR and SM Theories
Scale relativity treats velocity only as a difference quotient. This is a necessity due to the assumed non-differentiability of the trajectories. Non-differentiability leads to introduction of two velocity fields—forward and backward, depending on the direction of differentiation in time. These fields are assumed to be finite for small values of the time step dt but they diverge to infinity in the limit in a standard analysis setting. Therefore, such velocity fields can be defined only up to a finite resolution underlying the physical phenomenon under study. The velocity fields are assumed to admit representation of the form of a sum of a “classical part” plus a correction of a resolution-dependent and diverging fractal part. The classical part corresponds to the absolutely continuous part of the trajectory, while the fractal part corresponds to the singular and possibly oscillatory parts. Since, at the level of physical description, there is no way to favor the forward rather than the backward velocity, the description should incorporate them on equal grounds, i.e., forming a bivariate vector field
This bivariate vector field is represented by a complex-valued vector field [29] as with components given by where V is interpreted as the “classical” velocity and U is a new quasi-velocity quantity (i.e., the osmotic velocity in the terminology of Nelson). Under these assumptions, Nottale introduces a complexified material derivative, which is a pseudo-differential operator acting on scalar functions as
where is a constant, quantifying the effect of changing the resolution scale.
Stochastic mechanics allows for a similar treatment of the complex of forward and backward diffusions. The drift, resp. diffusion coefficients can be further embedded in a complex space as proposed by Pavon [21]:
so that the diffusion process becomes complex. It follows that
In the case when
Therefore, we can designate a new complex stochastic variable
Because of its double adaptation, retains its local martingale properties: that is, . In this case, notably , but , so that finally,
Therefore, a formal Itô differential can be introduced in exactly the same way
with quadratic variation . Therefore, in components,
which generalize to
in three dimensions [28]. It is apparent that both theories share an identical algebraical structure, while SM can be considered as a stochastic representation of SR.
Remark 1.
Conceptually, the forward process can be interpreted as a prediction, while the backward process can be interpreted as a retrodiction.
Note that, in the complex formulation of Pavon, the real part of the driving process corresponds to the forward (i.e., adapted to the past) process, while the imaginary part corresponds to the backward (i.e., adapted to the future) process. This is of course one of infinitely many choices, since the complex factor in the diffusion coefficient is a root of unity and hence represents a rotation in the complex plane.
The martingale property of the complex Wiener process conceptually means that the knowledge of the past and future of the process do not bias the outcome at the present time (i.e., at measurement). Note that the mapping is invertible since
From these formulas, it is apparent that the real part, or respectively the imaginary part of the resulting process do not have separate meanings, as they mix the predictive process with the retrodictive process. To illustrate the point, suppose that and and the original process is transformed as . Then, a straightforward calculation gives
5. The Real Stochastic Geodesic Equations
The appearance of the Wiener process entails the application of the fundamental Itô Lemma for the forward (i.e., adapted to the past, plus sign) or the backward processes (i.e., adapted to the future, minus sign), respectively. In differential notation, it reads
where is the quadratic variation of the process. It can be seen that in this case the (forward) differential operator d acts as a material derivative.
The term geodesic will be interpreted as a solution of a variational problem [30,31]. A brief treatment is given in Appendix B. By application of Itô’s Lemma, the forward geodesic equation can be obtained as:
This can be recognized as a Burgers equation with negative kinematic viscosity for the drift field [13].
The backward geodesic equation follows from the application of the Itô’s lemma for the anticipative process
This can be recognized as a Burgers equation with positive kinematic viscosity for the drift field.
The solution of the Burgers equation is well known and can be given by the convolution integrals (Equation (44)) for the case of positive viscosity [13]. The case about the negative viscosity can not be easily solved using Fourier transform. Therefore, a different solution technique will be pursued. Time-varying solutions will be constructed from topological deformations of the stationary solutions.
In QM applications, . Normalization will be assumed further in most cases to simplify calculations.
5.1. Path-Wise Separable Solutions
In the first instance, one can solve the geodesic equation by supposing separability. By making the ansatz we arrive at the equation:
This has the unique solution
The resulting Itô equation can be formulated as
The stochastic differential equation for the drift is therefore
which can be integrated exactly in Itô’s sense as
Therefore,
where T is the stopping time. Therefore, an exact numerical quadrature can be performed (Figure 1)
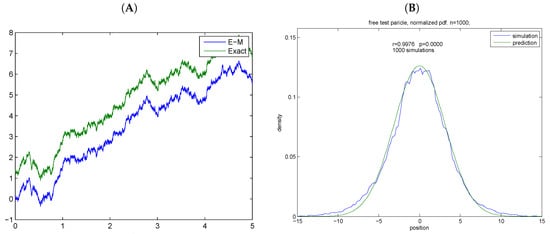
Figure 1.
Virtual trajectories of the separable process. (A) virtual trajectories; (B) empirical vs. theoretical density. (A) exact simulation of separable process is compared with the Euler–Maruyama algorithm. E—Exact simulation, E–M—Euler–Maruyama simulation; An offset is added to the exact solution for appreciation. Time is given in arbitrary units; (B) the empirical transition density is estimated from bins. Pearson’s correlation is given as an inset—r = 0.9976.
The corresponding density can be obtained from the Fokker–Planck equation
with solution
It should be noted that, under time reversion, we arrive at the same solution, which however leads to a different Fokker–Planck equation
with solution
which can be recognized as a Brownian bridge. The entropy of this density can be calculated as
5.2. Stationary Drift Fields
For time-homogeneous diffusion, the geodesic equation can be brought into the form
which can be integrated once to give
The integration constant E can be identified with the energy. The resulting first order ordinary differential equation (ODE) can be solved as
The solution for was identified by Herman [32]. By translation, invariance of the coordinates, is admissible. This observation will be used further for the transient solution. The link between the two solutions can be established as follows. Note that
is also a solution. Then,
which is the second solution.
The expectation of the trajectory can be obtained by solving the ODE
so that
In accordance with so-developed theory for
Furthermore, for
so that in the same way
The backward geodesic equation
by the same method leads to
5.3. Stationary Density Solutions
The stationary density is a solution of the Fokker–Planck (i.e., forward Kolmogorov) equations parametrized by E:
The case leads to
with stationary solution
which can be valid on a bounded domain. The entropy of this solution in the domain can be calculated as
The case leads to
with a stationary solution
which can be valid on a bounded domain.
5.4. Transient Drift Fields
The solution of the Burgers equation is well known and can be given by the convolution integrals (Equation (44)) for the case of positive viscosity [13]. The case of negative viscosity emerging here is more challenging and it will be solved by a deformation of the stationary solution, so that in limit the stationary solution is recovered:
The solution is sought in the form (neglecting scale factors)
which results in a linear ODE for the unknown function :
By variation of the parameters, the solution for is given as
where the constant E represents an energy scale and k is an arbitrary constant. We can assume normalization, for example , such that . Plots are presented in Figure 2.
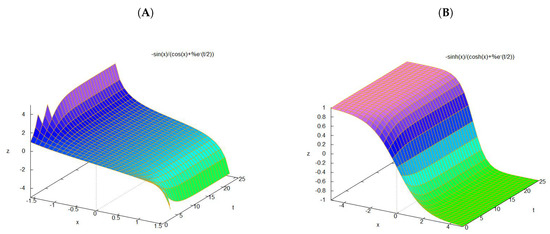
Figure 2.
Time-varying drift fields for , . (A) forward drift; (B) backward drift.
The transformed Itô drift equation for reads
It can be further noticed that rescaling in a pair of new variables leaves the ratio
invariant so that z becomes a similarity variable.
Furthermore, a formal forward Kolmogorov equation can be written in the variable with as
however its solution is challenging due to its mixed nonlinearity and will not be attempted here. Nevertheless, the analysis presented so far assures that asymptotically can be obtained as a solution of the stationary equation.
The backward geodesic equation leads to the following solution :
5.5. Asymptotic Density Solutions
The forward drift itself (symbol changed) obeys the transformed stochastic differential equations
The density is a solution of the forward Kolmogorov equations parametrized by E:
The solutions can be obtained using the Laplace transform . In this way, the partial differential equation can be transformed into an ODE for the Laplace variable:
To obtain the Green’s function, we take homogeneous initial conditions a.e. The solutions in the time domain can be obtained by the inverse Laplace transformation:
In the position space, the solution can be obtained using Grisanov’s theorem [4]:
The second equation is not acceptable from a physical point of view since diverges.
In the same way for the backward drift,
with solutions
in the drift space and in position space
respectively. This is acceptable from a physical point of view since , which is a correct asymptotic behavior.
6. The Complex Stochastic Geodesic Equations
The complexification removes the restriction of positive definiteness of the E parameter so that the substitution becomes admissible by an appropriate cut along the complex plane.
In a similar way, for the complex case, we have
which, under substitution, leads to
By the same methods as used above, the asymptotic density for the drift variable can be obtained as
For the resulting density in the position space, it can be calculated that
In a similar way, for the other solution,
which under substitution leads to the drift equation
The drift density can be readily obtained as
In the position space, the density is of the form
In either case, the densities asymptotically approach zero.
7. Real-Valued and Complex Cole–Hopf Transformations
The Burgers equation can be linearized by the Cole–Hopf transformation [33,34]. This mapping transforms the nonlinear Burgers equation into the linear heat conduction equation in the following way. Let
Substitution into Equation (11) leads to
This can be recognized as
which is equivalent to a solution of the equation
It should be noted that if instead of the forward development (i.e., prediction) one takes the backward development (i.e., retrodiction), the usual form of the Burgers equation is recovered. This corresponds to the anticipative Wiener process, which is subject to the anticipative Itô calculus [17,35]:
In this case, the usual general solution can be revealed
where is the viscosity coefficient.
In the complex case, starting from the generalized Itô differential, the complex velocity field becomes
The geodesic equation reads
Therefore, by the martingale property, this is equivalent to
which can be recognized as a generalized Burgers equation with imaginary kinematic viscosity coefficient. Applying the complex Cole–Hopf transformation as [36]
and specializing to leads to
which can be recognized as a gradient
The last equation is equivalent to the solution of the free Schrödinger equation. On the other hand, the diffusion part is simply
since .
This corresponds with the arguments given in [37] that the coefficient of the stochastic noise should be purely imaginary. Calculations can be reproduced in the computer algebra system Maxima [38].
8. Numerical Results
The different types of solutions of the stochastic geodesic equation were simulated using the Euler–Maruyama algorithm. Simulations were performed in Matlab. An example of a simulation script is given in Appendix C.
8.1. Exact Simulations
The exact simulations of the separable process were compared to simulations computed by the Euler–Maruyama algorithm. Achieved correlation was 1.0 while the mean squared error was on the order of .The comparison is presented in Figure 1. The empirical transition density was computed from simulations and correlated to the graph of Equation (16). The theoretical density was computed from Equation (16) for stopping time . Achieved correlation was 0.9976.
8.2. Free Diffusion
The normalized asymptotic transient density of the free particle distribution can be recognized as the Rayleigh’s distribution (Figure 3)
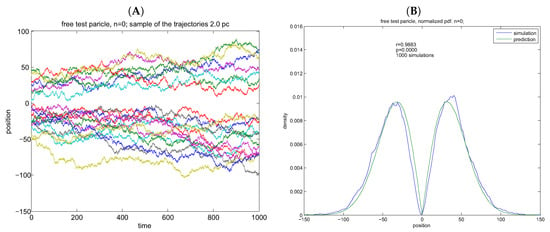
Figure 3.
Simulations of free particles virtual trajectories. (A) virtual trajectories: free particles; (B) empirical vs. theoretical density. Simulations are based on points in simulations. (A,B) width of potential well is units. The empirical pdf is estimated from bins. Pearson’s correlations are given as inset—r = 0.9883. Norming of the free particle transient results in Rayleigh density.
8.3. Particle in a Box
The third simulated case comprised a freely diffusing particle in a square potential well of size . The approach was based on Hermann [32]. Individual trajectories were simulated according to the fundamental equation using the scheme of Euler–Maruyama:
where .
Restarting boundary conditions were used for the simulations to avoid distortions of the distribution. That is, if a simulated particle crossed the boundaries its position was reset to its original position.
The initial particle positions were sampled from a uniform distribution between and L. The theoretical density for the particle in a box case is given by
Results are based on points in simulations.
The empirical pdf is estimated from bins. Pearson’s correlations are given as insets: B – r = 0.9939, D – r = 0.9871. For both cases, the numerical precision correlates excellently with the analytical solutions (Figure 4).
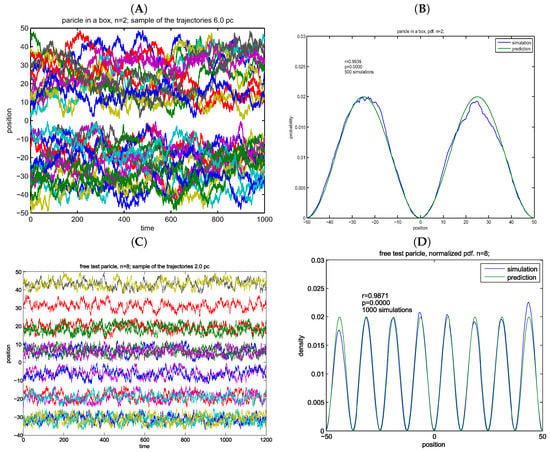
Figure 4.
Simulations of particles in a box for two quantum numbers. (A) virtual trajectories: particle in a box, n = 2; (B) empirical vs. theoretical density; (C) test particles in a box, n = 8; (D) empirical vs. theoretical density. (A,B) width of potential well is units.
9. Discussion
This work was motivated in part by the premise that inherently nonlinear phenomena need development of novel mathematical tools for their description. The relaxation of the differentiability assumption opens new avenues in describing physical phenomena, as demonstrated by SM and SR, but also challenges existing mathematical methods, which are developed for smooth signals [2,3]. While this description can be achieved also by fractional differ–integrals, or by multi-scale approaches [39], the present work focused on a local description. The reason for this choice is that locality provides a direct way of physical interpretation of the obtained results. In this regard, Hölderian functions can be used as building blocks of such strongly nonlinear models, which give rise to singular [24,40] or non-differentiable models.
The second motivation of the present work was to investigate the potential of stochastic methods for simulations of quantum-mechanical and convection-diffusive systems. While the usual presentation of the stochastic mechanics typically used the Schrödinger equation as a solution device and paths were constructed from solutions of the Schrödinger equation, this is not necessary. McClendon and Rabitz simulated several quantum systems using the differential equations of Nelson’s stochastic quantization as a starting point [41]. In the framework of scale relativity, Herman [32] and later Al Rashid et al. [42] simulated QM particle in a box using the Langevin equations. Later, Al-Rashid et al. [43] simulated the quantum harmonic oscillator extending Herman’s approach. The approach presented here can be used as an alternative to numerical solutions of the Schrödinger equation. In this scenario, the density of the solution can be sampled from Monte Carlo simulations as demonstrated. Presented numerical approaches can be used, for example, for simulations of nanoparticles or quantum dots, which are mesoscopic objects and are expected to have properties intermediate between macroscopic and quantum systems [44]. This can be of interest, for example in sedimentation studies, where Langevin dynamics was proposed [45]. In principle, presented results can be extended towards asynchronous simulations using the Gillespie’s algorithm [8]. This can be achieved using time steps distributed exponentially.
Obtained results can be also discussed in view of the fluctuation-dissipation relationships. The fluctuation-dissipation theorem relates the linear response relaxation of a system from a non-equilibrium state to the properties of fluctuations in equilibrium. This is an exact result in the case of the Ornstein–Uhlembeck process, where the drift term is linear. The geodesic treatment in the present work provides a different relationship between the drift and and diffusivity . In the small perturbation regime around the equilibrium the geodesic process can be approximated by an Ornstein–Uhlembeck process for the fluctuation term (), therefore an appropriate fluctuation-dissipation theorem can be formulated assuming that equipartition also holds.
A fact that is not fully addressed by both stochastic mechanics and scale relativity is why do the theories work only for (box) fractal dimension 2 of the paths. While Nottale gives an heuristic argument and claims that the prescription of a Wiener process may be generalized, he does not proceed to rigorously develop the argument. On the other hand, the stochastic mechanics fixes from the start the Wiener process as a driving noise. While this may look plausible in view of the traditions in the treatment of Brownian motion, it is a choice that should be justified as nowadays anomalous types of diffusion dynamics are also recognized and systematically investigated (overview in [46]). The answer to this question can be given more easily by an approach inspired by Nottale and is partially given by the argument given by Gillepsie [8]. The original argument in [8] contains an explicit assumption of existence of the second moment of the distribution, which amounts to assuming Hölder continuity of order as demonstrated here in Theorem 1. The theorem also corresponds to the result established for fractal interpolation computed via a chaos game where the limit random distribution has been identified with the Gaussian distribution [47,48].
While in SR particle ’trajectories’ are considered to be only virtual, SM and the original formulation of Bohm’s quantum mechanics treat them as physically real. It is noteworthy that recently Flack and Hiley [49] demonstrated that that a Bohm ’trajectory’ is the average of an ensemble of actual individual stochastic Feynman paths. This is in line with the treatment of the problem by the stochastic mechanics and scale relativity and promotes the view that Bohm’s quantum mechanics is a mean field theory of the stochastic mechanics.
Funding
The work has been supported in part by grants from Research Fund—Flanders (FWO), contract number VS.097.16N, Fetzer Franklin Memorial Trust and the NanoStreeM H2020 project, contract number 688194.
Acknowledgments
All calculations were assisted by the computer algebra system Maxima. The author would like to acknowledge Stephan LeBohec for critical reading and Laurent Nottale for inspirational discussions.
Conflicts of Interest
The funding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Appendix A. Notations, General Definitions and Properties of Fractional Velocity
Definition A1 (Asymptotic O notation)
The notation is interpreted as the convention that
for . The notation will be interpreted to indicate a Cauchy-null sequence with no particular power dependence of x.
Definition A2.
We say that f is of (point-wise) Hölder class if for a given x there exist two positive constants that for an arbitrary and given fulfill the inequality , where denotes the norm of the argument.
Definition A3.
Define the parametrized difference operators acting on a function as
The first one we refer to as forward difference operator, the second one we refer to as backward difference operator.
Definition A4.
Define Fractional Variation operators of order as
This section follows the presentation given recently in [50].
Definition A5 (Fractional order velocity)
Define the fractional velocity of fractional order β as the limit
where are real parameters and is real-valued function. A function for which at least one of exists finitely will be called β-differentiable at the point x.
In the above definition, we do not require upfront equality of left and right -velocities. This amounts to not demanding continuity of the -velocities in advance. Instead, continuity is a property, which is fulfilled under certain conditions.
Definition A6.
The set of points where the fractional velocity exists finitely and will be denoted as the set of change .
Since the set of change is totally disconnected [26], some of the useful properties of ordinary derivatives, notably the continuity and the semi-group composition property, are lost.
Definition A7.
β-Regularized derivative of a function is defined as:
We will require as usual that the forward and backward regularized derivatives be equal for a uniformly continuous function.
In this section, we assume that the functions are BVC in the neighborhood of the point of interest. Under this assumption, we have
- Product rule
- Quotient rule
where
wherever .
For compositions of functions,
- and
- and
Basic evaluation formula [51]:
Derivative regularization [52]:
Let be composition with , a -differentiable function at x, then
where
is the fractal q-adic (co-)variation.
Appendix B. The Stochastic Variation Problem
The study of stochastic Lagrangian variational principles has been motivated initially by quantum mechanics and optimal control problems. This section gives only a sketch for the treatment of the problem. The reader is directed to [21,30,31] for more details. In the simplest form, this is the minimization of the regularized functional assuming a constant diffusion coefficient b
for the partition and .
Thus, suppose that . Then, the increments can be interpreted as Itô integrals so that by the Itô isometry since finite summation and integration commute
Therefore, is minimal if the drift vanishes on . Suppose that is varied by a small smooth function , where the smallness is controlled by , then the Itô lemma should be applied so that on the difference process . Therefore,
should hold. The same calculation can be performed for if the Itô integral is replaced by the anticipative Itô integral. In this case, and the integration is reversed
In this case, the backward Itô formula also applies as
Remark A1.
The treatment of Pavon [21] uses the symmetrized functional together with a constraint on anti-symmetrized functional in the present notation.
Appendix C. Matlab Simulation Code
Listing 1: Exact simulation Matlab code.


References
- Langevin, P. Sur la theórie du mouvement Brownien. C. R. Acad. Sci. 1908, 146, 530–533. (in French). [Google Scholar]
- Nelson, E. Derivation of the Schrödinger equation from Newtonian mechanics. Phys. Rev. 1966, 150, 1079. [Google Scholar] [CrossRef]
- Nottale, L. Fractals in the Quantum Theory of Spacetime. Int. J. Mod. Phys. A 1989, 4, 5047–5117. [Google Scholar] [CrossRef]
- ksendal, B. Stochastic Differential Equations, 6th ed.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Beck, C. Dynamical systems of Langevin type. Phys. A Stat. Mech. Appl. 1996, 233, 419–440. [Google Scholar] [CrossRef]
- Mackey, M.; Tyran-Kaminska, M. Deterministic Brownian motion: The effects of perturbing a dynamical system by a chaotic semi-dynamical system. Phys. Rep. 2006, 422, 167–222. [Google Scholar] [CrossRef]
- Tyran-Kamińska, M. Diffusion and Deterministic Systems. Math. Model. Nat. Phenom. 2014, 9, 139–150. [Google Scholar] [CrossRef]
- Gillespie, D.T. The mathematics of Brownian motion and Johnson noise. Am. J. Phys. 1996, 64, 225–240. [Google Scholar] [CrossRef]
- Klages, R. Deterministic Diffusion in One-Dimensional Chaotic Dynamical Systems; Wissenschaft und Technik Verlag: Berlin, Germany, 1996. [Google Scholar]
- Knight, G.; Klages, R. Linear and fractal diffusion coefficients in a family of one-dimensional chaotic maps. Nonlinearity 2010, 24, 227–241. [Google Scholar] [CrossRef]
- Zwanzig, R. Nonequilibrium Statistical Mechanics; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Bateman, H. Some recent researches in the motion of fluids. Mon. Weather Rev. 1915, 43, 163–167. [Google Scholar] [CrossRef]
- Burgers, J.M. The Nonlinear Diffusion Equation; Springer: Dordrecht, The Netherlands, 1974. [Google Scholar]
- Gurbatov, S.; Malakhov, A.; Saichev, A.; Saichev, A.I.; Malakhov, A.N.; Gurbatov, S.N. Nonlinear Random Waves and Turbulence in Nondispersive Media: Waves, Rays, Particles (Nonlinear Science: Theory & Applications); John Wiley & Sons Ltd.: Hoboken, NJ, USA, 1992. [Google Scholar]
- Busnello, B. A Probabilistic Approach to the Two-Dimensional Navier-Stokes Equations. Ann. Probab. 1999, 27, 1750–1780. [Google Scholar] [CrossRef]
- Busnello, B.; Flandoli, F.; Romito, M. A probabilistic representation for the vorticity of a three-dimensional viscous fluid and for general systems of parabolic equations. Proc. Edinb. Math. Soc. 2005, 48, 295–336. [Google Scholar] [CrossRef]
- Constantin, P.; Iyer, G. A stochastic Lagrangian representation of the three-dimensional incompressible Navier-Stokes equations. Commun. Pure Appl. Math. 2007, 61, 330–345. [Google Scholar] [CrossRef]
- Constantin, P.; Iyer, G. A stochastic-Lagrangian approach to the Navier-Stokes equations in domains with boundary. Ann. Appl. Probab. 2011, 21, 1466–1492. [Google Scholar] [CrossRef]
- Fényes, I. Eine wahrscheinlichkeitstheoretische Begründung und Interpretation der Quantenmechanik. Z. Phys. 1952, 132, 81–106. [Google Scholar] [CrossRef]
- Weizel, W. Ableitung der Quantentheorie aus einem klassischen, kausal determinierten Modell. Z. Phys. 1953, 134, 264–285. [Google Scholar] [CrossRef]
- Pavon, M. Hamilton’s principle in stochastic mechanics. J. Math. Phys. 1995, 36, 6774–6800. [Google Scholar] [CrossRef]
- Nottale, L. Scale Relativity and Schrödinger’s equation. Chaos Solitons Fractals 1998, 9, 1051–1061. [Google Scholar] [CrossRef]
- Nottale, L. Macroscopic Quantum-Type Potentials in Theoretical Systems Biology. Cells 2013, 3, 1–35. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, B.B. Intermittent turbulence in self-similar cascades: divergence of high moments and dimension of the carrier. In Multifractals and 1/f Noise: Wild Self-Affinity in Physics (1963–1976); Springer: New York, NY, USA, 1999; pp. 317–357. [Google Scholar]
- Salem, R. On some singular monotonic functions which are strictly increasing. Trans. Am. Math. Soc. 1943, 53, 427–439. [Google Scholar] [CrossRef]
- Prodanov, D. Conditions for continuity of fractional velocity and existence of fractional Taylor expansions. Chaos Solitons Fractals 2017, 102, 236–244. [Google Scholar] [CrossRef]
- Carlen, E.A. Conservative diffusions. Commun. Math. Phys. 1984, 94, 293–315. [Google Scholar] [CrossRef]
- Guerra, F. The Foundations of Quantum Mechanics—Historical Analysis and Open Questions. In The Foundations of Quantum Mechanics—Historical Analysis and Open Questions: Lecce, 1993; Garola, C., Rossi, A., Eds.; Springer: Dordrecht, The Netherlands, 1995; pp. 339–355. [Google Scholar]
- Nottale, L. Fractal Space-Time And Microphysics: Towards A Theory Of Scale Relativity; World Scientific: Singapore, 1993. [Google Scholar]
- Zambrini, J.C. Variational processes and stochastic versions of mechanics. J. Math. Phys. 1986, 27, 2307–2330. [Google Scholar] [CrossRef]
- Yasue, K. Stochastic calculus of variations. J. Funct. Anal. 1981, 41, 327–340. [Google Scholar] [CrossRef]
- Hermann, R. Numerical simulation of a quantum particle in a box. J. Phys. A Math. Gen. 1997, 30, 3967. [Google Scholar] [CrossRef]
- Hopf, E. The partial differential equation ut+uux=μuxx. Commun. Pure Appl. Math. 1950, 3, 201–230. [Google Scholar] [CrossRef]
- Cole, J.D. On a quasi-linear parabolic equation occurring in aerodynamics. Quart. Appl. Math. 1951, 9, 225–236. [Google Scholar] [CrossRef]
- Dunkel, J. Relativistic Brownian Motion and Diffusion Processes. Ph.D. Thesis, Augsburg University, Augsburg, Germany, 2008. [Google Scholar]
- Lage, J.L.; Kulish, V.V. On the Relationship between Fluid Velocity and de Broglie’s Wave Function and the Implications to the Navier–Stokes Equation. Int. J. Fluid Mech. Res. 2002, 29, 13. [Google Scholar] [CrossRef]
- Tsekov, R. On the Stochastic Origin of Quantum Mechanics. Rep. Adv. Phys. Sci. 2017, 1, 1750008. [Google Scholar] [CrossRef]
- Cole Hopf Transformations in Maxima; MDPI: Switzerland, 2018. [CrossRef]
- Cresson, J. Scale calculus and the Schrödinger equation. J. Math. Phys. 2003, 44, 4907–4938. [Google Scholar] [CrossRef]
- Sornette, D. Brownian representation of fractal quantum paths. Eur. J. Phys. 1990, 11, 334. [Google Scholar] [CrossRef]
- McClendon, M.; Rabitz, H. Numerical simulations in stochastic mechanics. Phys. Rev. A 1988, 37, 3479–3492. [Google Scholar] [CrossRef]
- Al-Rashid, S.N.T.; Habeeb, M.A.Z.; Ahmad, K.A. Application of Scale Relativity (ScR) Theory to the Problem of a Particle in a Finite One-Dimensional Square Well (FODSW) Potential. J. Quantum Inf. Sci. 2011, 1, 7–17. [Google Scholar] [CrossRef]
- Al-Rashid, S.N.T.; Habeeb, M.A.Z.; Ahmed, K.A. Application of Scale Relativity to the Problem of a Particle in a Simple Harmonic Oscillator Potential. J. Quantum Inf. Sci. 2017, 7, 77–88. [Google Scholar] [CrossRef]
- Botez, I.C.; Agop, M. Order-Disorder Transition in Nanostructures via Non-Differentiability. J. Comp. Theor. Nanosci. 2015, 12, 1746–1755. [Google Scholar] [CrossRef]
- Ganguly, S.; Chakraborty, S. Sedimentation of nanoparticles in nanoscale colloidal suspensions. Phys. Lett. A 2011, 375, 2394–2399. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A Math. Gen. 2004, 37, R161. [Google Scholar] [CrossRef]
- Puente, C.; López, M.; Pinzón, J.; Angulo, J. The Gaussian Distribution Revisited. Adv. Appl. Probab. 1996, 28, 500. [Google Scholar] [CrossRef]
- Puente, C. The exquisite geometric structure of a Central Limit Theorem. Fractals 2003, 11, 39–52. [Google Scholar] [CrossRef]
- Flack, R.; Hiley, B. Feynman Paths and Weak Values. Entropy 2018, 20, 367. [Google Scholar] [CrossRef]
- Prodanov, D. Fractional Velocity as a Tool for the Study of Non-Linear Problems. Fractal Fract. 2018, 2, 4. [Google Scholar] [CrossRef]
- Prodanov, D. Characterization of strongly nonlinear and singular functions by scale space analysis. Chaos Solitons Fractals 2016, 93, 14–19. [Google Scholar] [CrossRef]
- Prodanov, D. Regularization of derivatives on non-differentiable points. J. Phys. Conf. Ser. 2016, 701, 012031. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).