Impact of Multi-Causal Transport Mechanisms in an Electrolyte Supported Planar SOFC with (ZrO2)x−1(Y2O3)x Electrolyte
Abstract
1. Introduction
- We expand the gas diffusion layers’ (GDLs’) NET models of S. Kjelstrup and D. Bedeaux [20] accounting for diffusion.
- We give a detailed description of the transport mechanisms in YSZ electrolytes based on NET using the phenomenological coefficients calculated with MD.
- Our NET model is validated with our own experimental data.
- We discuss in detail the influence of the coupled mechanisms and calculate each contribution to the entropy production rate in each layer.
2. Materials and Methods
2.1. Materials and Experimental Methods
2.2. Theoretical Methods
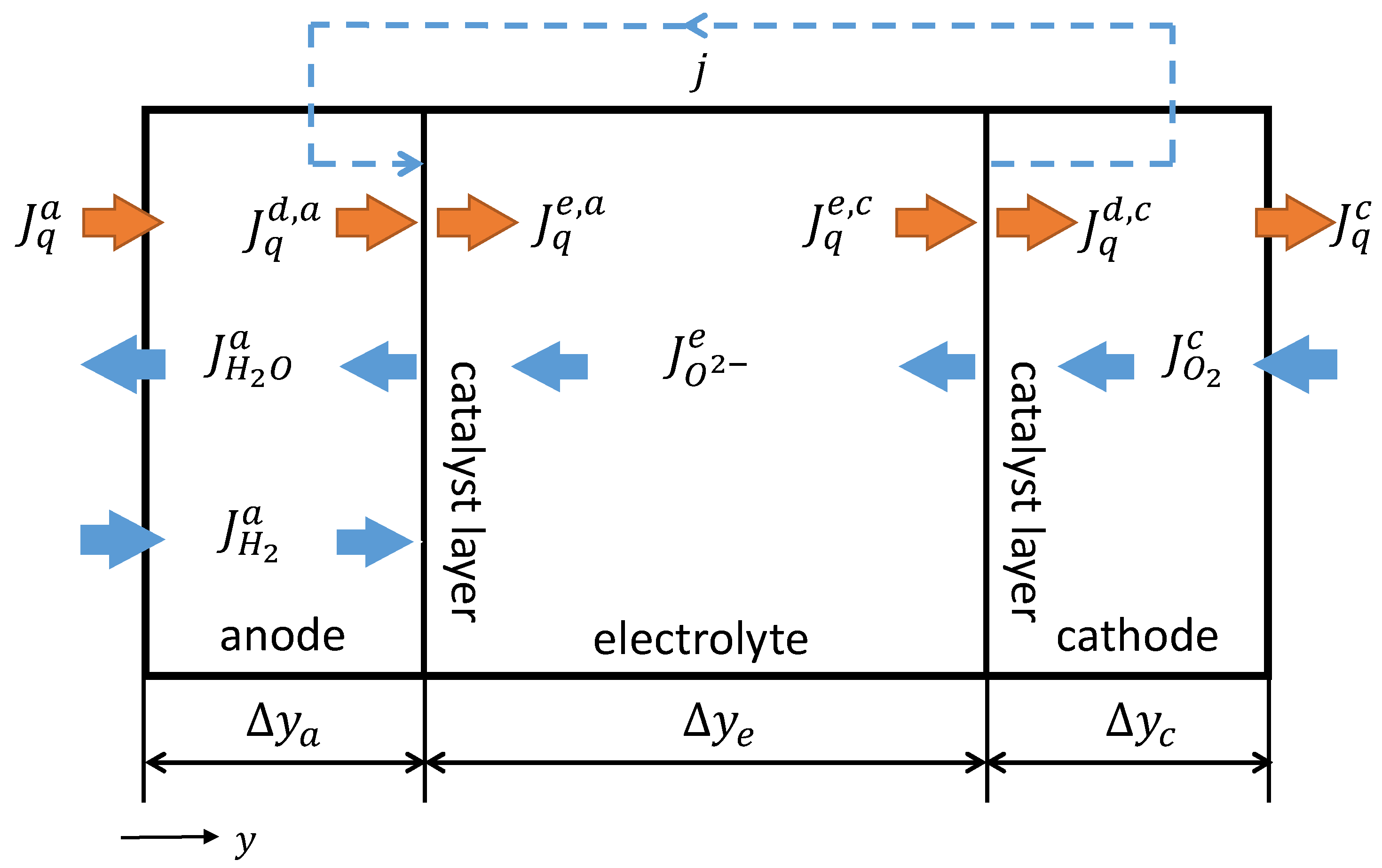
2.2.1. SOFC-System
2.2.2. Mathematical Description of the GDLs
2.2.3. Mathematical Description of the CLs
2.2.4. Mathematical Description of the Solid Oxide Electrolyte
2.2.5. Computational Details
3. Results and Discussion
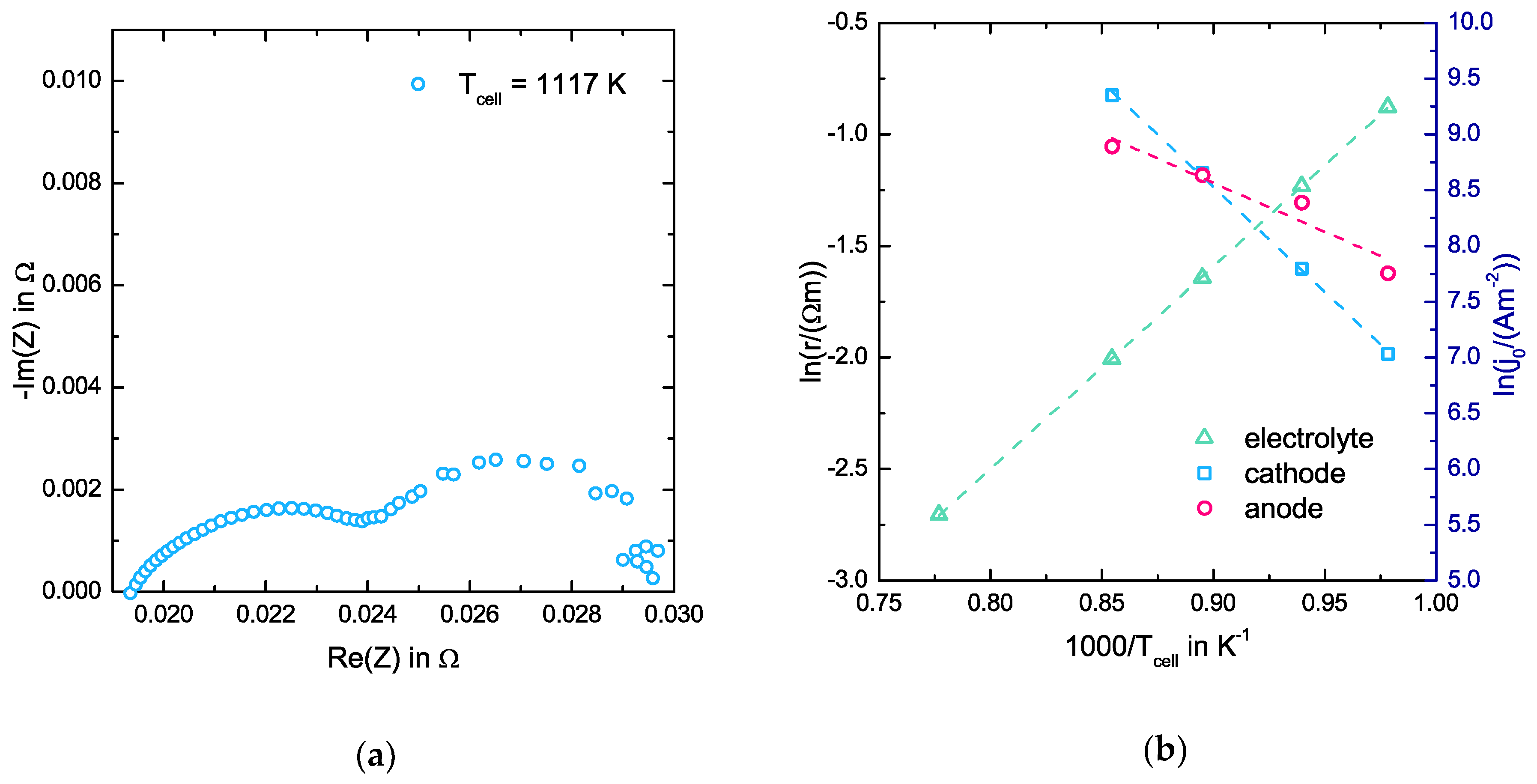
3.1. EIS Measurements
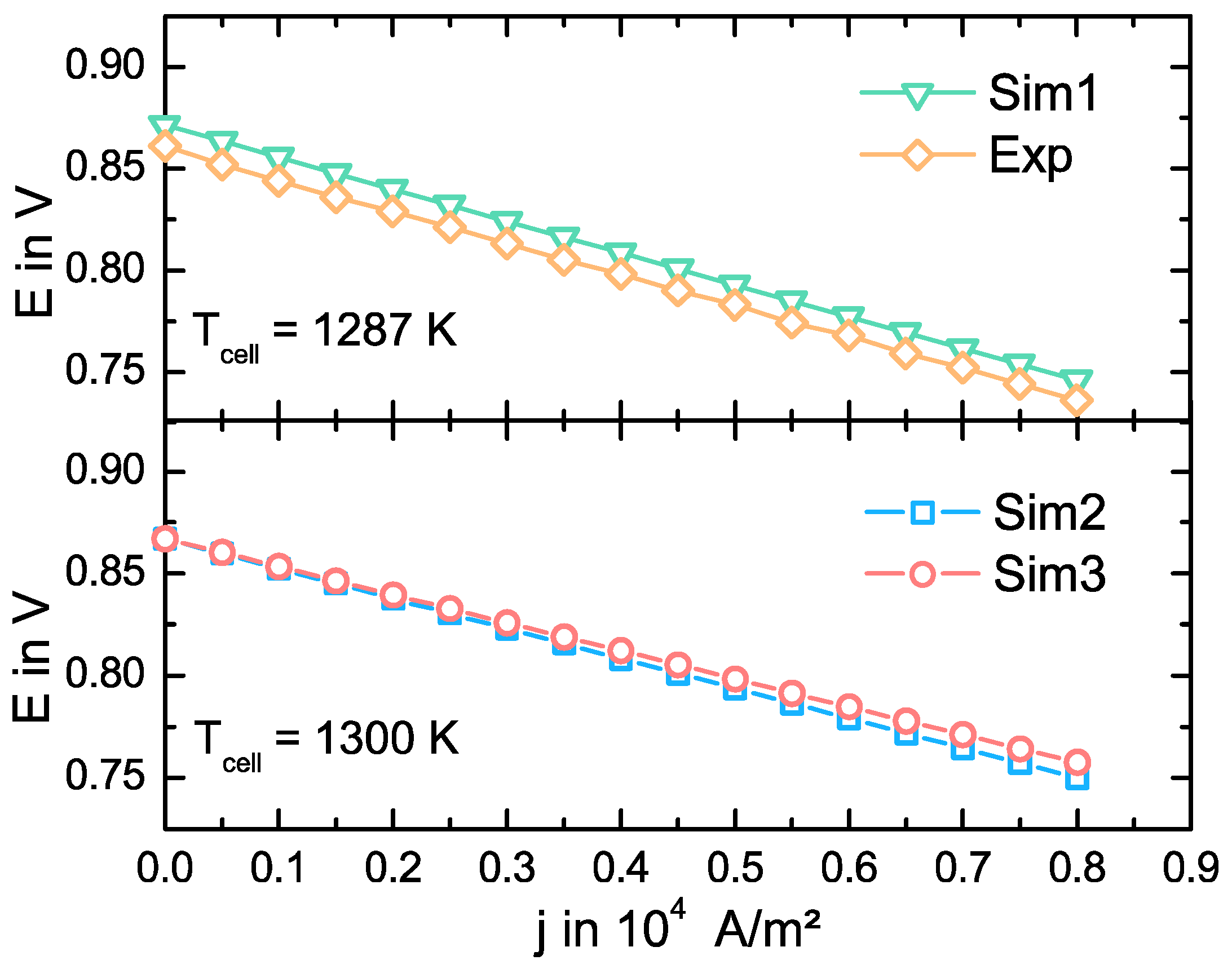
3.2. Model Validation
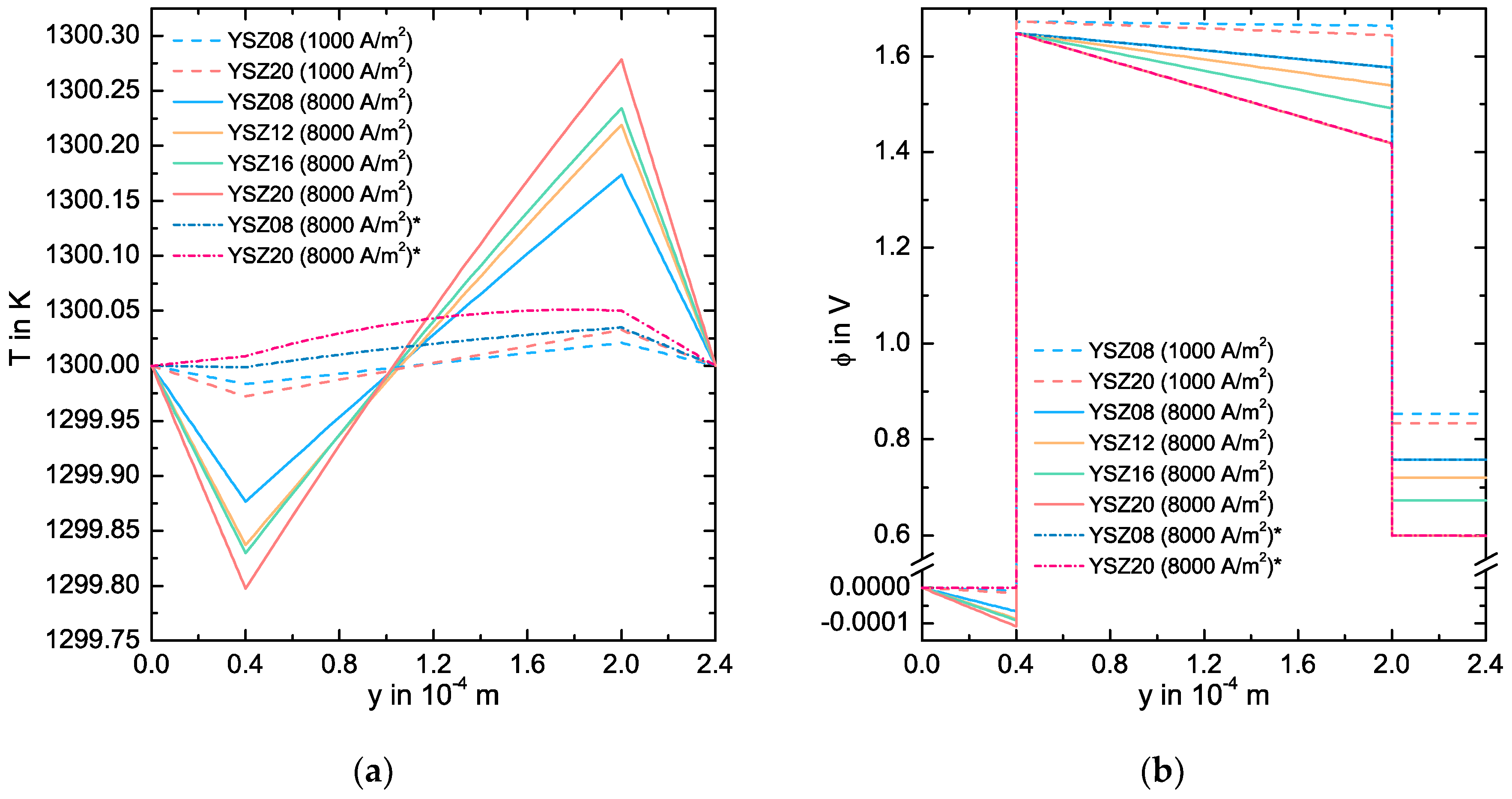
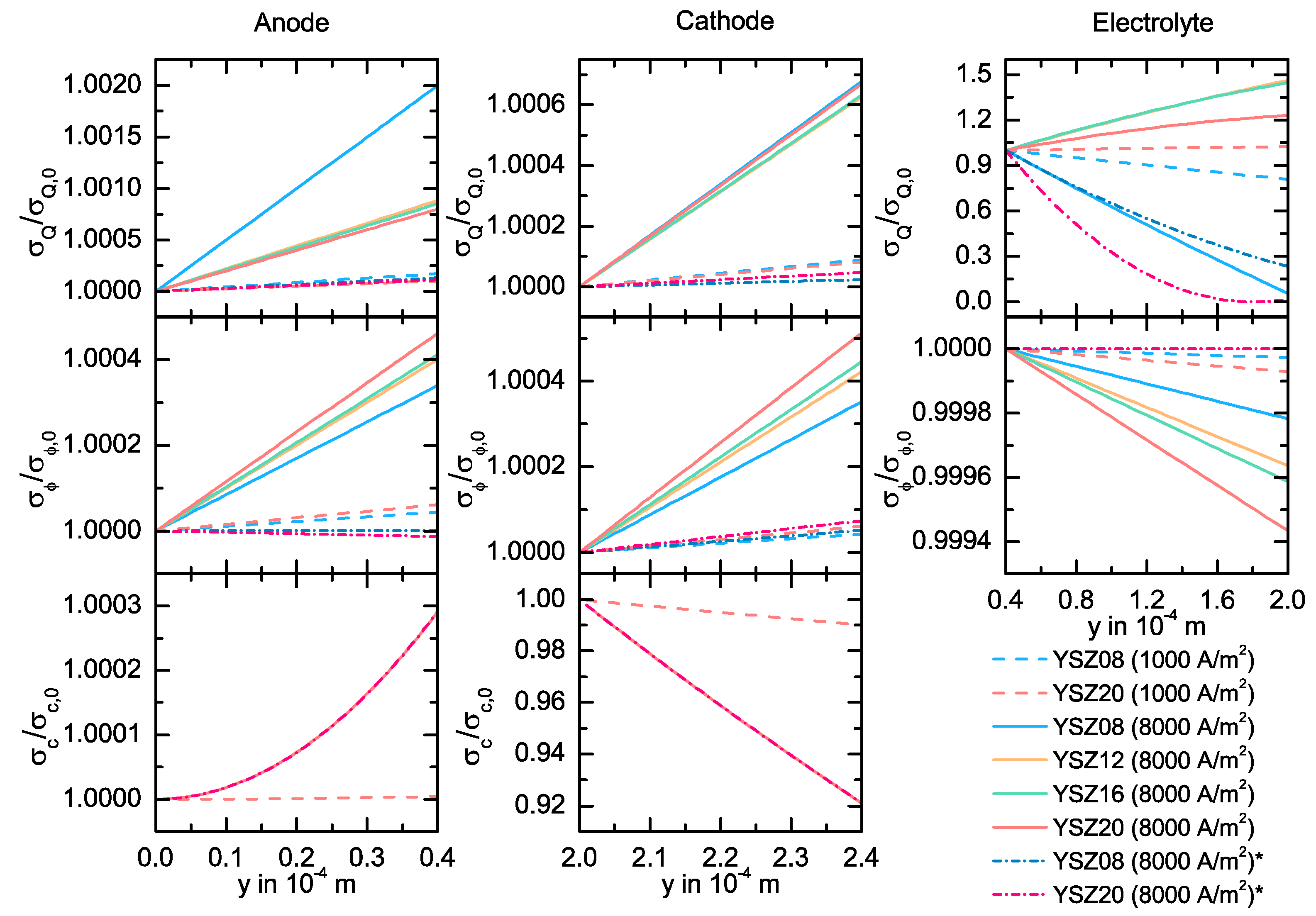
3.3. Simulation Results
4. Summary and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Das, V.; Padmanaban, S.; Venkitusamy, K.; Selvamuthukumaran, R.; Blaabjerg, F.; Siano, P. Recent advances and challenges of fuel cell based power system architectures and control—A review. Renew. Sustain. Energy Rev. 2017, 73, 10–18. [Google Scholar] [CrossRef]
- Boudghene Stambouli, A.; Traversa, E. Solid oxide fuel cells (SOFCs): A review of an environmentally clean and efficient source of energy. Renew. Sustain. Energy Rev. 2002, 6, 433–455. [Google Scholar] [CrossRef]
- Ostergaard Gadsboll, R.; Thomsen, J.; Bang-Moller, C.; Ahrenfeldt, J.; Henriksen, U.B. Solid oxide fuel cells powered by biomass gasification for high efficiency power generation. Energy 2017, 131, 198–206. [Google Scholar] [CrossRef]
- Wang, S.; Jiang, S.P. Prospects of fuel cell technologies. Natl. Sci. Rev. 2017, 4, 761–780. [Google Scholar] [CrossRef]
- Litzelman, S.J.; Lemmon, J.P. The Promise and Challenges of Intermediate Temperature Fuel Cells. ECS Trans. 2015, 68, 39–47. [Google Scholar] [CrossRef]
- Sengodan, S.; Lan, R.; Humphreys, J.; Dongwei, D.; Xu, W.; Wang, H.; Tao, S. Advances in reforming and partial oxidation of hydrocarbons for hydrogen production and fuel cell applications. Renew. Sustain. Energy Rev. 2018, 82, 761–780. [Google Scholar] [CrossRef]
- Valadez Huerta, G.; Álvarez Jordán, J.; Dragon, M.; Leites, K.; Kabelac, S. Exergy analysis of the diesel pre-reforming solid oxide fuel cell system with anode off-gas recycling in the SchIBZ project. Part I: Modeling and validation. Int. J. Hydrogen Energy 2018. [Google Scholar] [CrossRef]
- Nehter, P.; Wildrath, B.; Bauschulte, A.; Leites, K. Diesel Based SOFC Demonstrator for Maritime Applications. ECS Trans. 2017, 78, 171–180. [Google Scholar] [CrossRef]
- Santos, T.H.; Grilo, J.P.F.; Loureiro, F.J.A.; Fagg, D.P.; Fonseca, F.C.; Macedo, D.A. Structure, densification and electrical properties of Gd3+ and Cu2+ co-doped ceria solid electrolytes for SOFC applications: Effects of Gd2O3. Ceram. Int. 2018, 44, 2745–2751. [Google Scholar] [CrossRef]
- Irshad, M.; Siraj, K.; Raza, R.; Ali, A.; Tiwari, P.; Zhu, B.; Rafique, A.; Ali, A.; Ullah, M.K.; Usman, A. A Brief Description of High Temperature Solid Oxide Fuel Cell’s Operation, Materials, Design, Fabrication Technologies and Performance. Appl. Sci. 2016, 6, 75. [Google Scholar] [CrossRef]
- Steele, B.C.H.; Heinzel, A. Materials for fuel-cell technologies. Nature 2001, 414, 345–352. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.H.; Strand, R.K. SOFC cogeneration system for building applications, part 1: Development of SOFC system-level model and the parametric study. Renew. Energy 2009, 34, 2831–2838. [Google Scholar] [CrossRef]
- Peksen, M. Safe heating-up of a full scale SOFC system using 3D multiphysics modelling optimization. Int. J. Hydrogen Energy 2018, 43, 354–362. [Google Scholar] [CrossRef]
- Peksen, M.; Al-Masri, A.; Peter, R.; Blum, L.; Stolten, D. Recent Developments in 3D Multiphysics Modelling of Whole Fuel Cell Systems for Assisting Commercialization and Improved Reliability. ECS Trans. 2017, 75, 15–22. [Google Scholar] [CrossRef]
- Dokmaingam, P.; Areesinpitak, S.; Laosiripojana, N. Transient Modeling of Tubular-Designed IIR-SOFC Fueled by Methane, Methanol, and Ethanol. Eng. J. 2017, 21, 235–249. [Google Scholar] [CrossRef]
- Hering, M.; Brouwer, J.; Winkler, W. Dynamic model of a micro-tubular solid oxide fuel cell stack including an integrated cooling system. J. Power Sources 2017, 342, 504–514. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, T.; Kang, J.; Zhao, L.; Guo, L.; Feng, P.; Zhou, F.; Ling, Y. Numerical modeling of ceria-based SOFCs with bi-layer electrolyte free from internal short circuit: Comparison of two cell configurations. Electrochim. Acta 2017, 138, 728–738. [Google Scholar] [CrossRef]
- Song, T.W.; Sohn, J.L.; Kim, J.H.; Kim, T.S.; Ro, S.T.; Suzuki, K. Performance analysis of a tubular solid oxide fuel cell/micro gas turbine hybrid power system based on a quasi-two dimensional model. J. Power Sources 2005, 142, 30–42. [Google Scholar] [CrossRef]
- Bove, R.; Lunghi, P.; Sammes, N.M. SOFC mathematic model for systems simulations—Part 2: Definition of an analytical model. Int. J. Hydrogen Energy 2005, 30, 189–200. [Google Scholar] [CrossRef]
- Kjelstrup, S.; Bedeaux, D. Jumps in electric potential and in temperature at the electrode surfaces of the solid oxide fuel cell. Physica A 1997, 244, 213–226. [Google Scholar] [CrossRef]
- Kjelstrup, S.; Bedeaux, D. Non-Equilibrium Thermodynamics of Heterogeneous Systems; World Scientific: Singapore, 2017; pp. 1–6. ISBN 13 978-981-277-913-7. [Google Scholar]
- Onsager, L. Reciprocal Relations in Irreversible Processes. I. Phys. Rev. 1931, 37, 405–426. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal Relations in Irreversible Processes. II. Phys. Rev. 1931, 38, 2265–2279. [Google Scholar] [CrossRef]
- Costamagna, P.; Selimovic, A.; Del Borghi, M.; Agnew, G. Electrochemical model of the integrated planar solid oxide fuel cell (IP-SOFC). Chem. Eng. J. 2004, 102, 61–69. [Google Scholar] [CrossRef]
- Hajimolana, S.A.; Hussain, M.A.; Ashri Wan Daud, W.M.; Soroush, M.; Shamiri, A. Mathematical modeling of solid oxide fuel cell: A review. Renew. Sustain. Energy Rev. 2011, 15, 1893–1917. [Google Scholar] [CrossRef]
- Nazari, A.; Farhad, S. Heat generation in lithium-ion batteries with different nominal capacities and chemistries. Appl. Therm. Eng. 2017, 125, 1501–1517. [Google Scholar] [CrossRef]
- Suwanwarangkul, R.; Croiset, E.; Fowler, M.W.; Douglas, P.L.; Entchev, E.; Douglas, M.A. Performance comparison of Fick’s, dusty gas and Stefan-Maxwell models to predict the concentration overpotential of a SOFC anode. J. Power Sources 2003, 122, 9–18. [Google Scholar] [CrossRef]
- Taylor, R.; Krishna, R. Multicomponent Mass Transfer; John Wiley & Sons, Inc.: New York, NY, USA, 1993; pp. 124–138. ISBN 978-047-157-417-0. [Google Scholar]
- Benfenati, F.; Beretta, G.P. Ergodicity, Maximum Entropy Production, and Steepest Entropy Ascent in the Proofs of Onsager’s Reciprocal Relations. J. Non-Equilib. Thermodyn. 2018, 43, 101–110. [Google Scholar] [CrossRef]
- Alahverdyan, A.E.; Nieuwenhuizen, T.M. Steady adiabatic state: Its thermodynamic, entropy production, energy dissipation, and violation of Onsager relations. Phys. Rev. E 2000, 62, 845–850. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Verda, V. Entropy generation analysis in a monolithic-type solid oxide fuel cell (SOFC). Energy 2009, 34, 850–865. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Verda, V. Entropy Generation Minimization in a Tubular Solid Oxide Fuel Cell. J. Energy Resour. Technol. 2010, 132, 012601. [Google Scholar] [CrossRef]
- Ramírez-Minguela, J.J.; Rangel-Hernández, V.H.; Alfaro-Ayala, J.A.; Uribe-Ramírez, A.R.; Mendoza-Miranda, J.M.; Belman-Flores, J.M.; Ruiz-Camacho, B. Energy and entropy study of a SOFC using biogas from different sources considering internal reforming of methane. Int. J. Heat Mass Transf. 2018, 120, 1044–1054. [Google Scholar] [CrossRef]
- Ramírez-Minguela, J.J.; Mendoza-Miranda, J.M.; Rodríguez-Muñoz, J.L.; Perez-García, V.; Alfaro-Ayala, J.A.; Uribe-Ramírez, A.R. Entropy Generation Analysis of a Solid Oxide Fuel Cell by Computational Fluid Dynamics. Influence of Electrochemical Model and Its Parameters. Therm. Sci. 2018, 22, 577–589. [Google Scholar]
- Choudhary, S.; Sanja, S. Thermodynamic assessment of SOFC-ICGT hybrid cycle: Energy analysis and entropy generation minimization. Energy 2017, 134, 1013–1028. [Google Scholar] [CrossRef]
- Timurkutluk, B.; Mat, M.D. A review on micro-level modeling of solid oxide fuel cells. Int. J. Hydrogen Energy 2016, 41, 9968–9981. [Google Scholar] [CrossRef]
- Peksen, M. Numerical thermomechanical modelling of solid oxide fuel cells. Prog. Energy Combust. Sci. 2015, 48, 1–20. [Google Scholar] [CrossRef]
- Siemer, M.; Marquardt, T.; Valadez Huerta, G.; Kabelac, S. Local Entropy Production Rates in a Polymer Electrolyte Membrane Fuel Cell. J. Non-Equilib. Thermodyn. 2017, 42, 1–30. [Google Scholar] [CrossRef]
- Kjelstrup, S.; Seip Forland, K. The Transported Entropy of Oxygen Ion in Yttria-Stabilized Zirconia. J. Electrochem. Soc. 1991, 138, 2374–2376. [Google Scholar] [CrossRef]
- Valadez Huerta, G.; Kelle, A.; Kabelac, S. A phenomenological study of yttria stabilized zirconia at 1300 K with the Green-Kubo formulation and equilibrium molecular dynamics. Chem. Phys. 2017, 485, 108–117. [Google Scholar] [CrossRef]
- Ahamer, C.; Opitz, A.K.; Rupp, G.M.; Feig, J. Revisiting the Temperature Dependent Ionic Conductivity of Yttria Stabilized Zirconia (YSZ). J. Electrochem. Soc. 2017, 164, F790–F803. [Google Scholar] [CrossRef]
- Grosso, R.L.; Muccillo, E.N.S. Sintering, phase composition and ionic conductivity of zirconia-scandia-ceria. J. Power Sources 2013, 233, 6–13. [Google Scholar] [CrossRef]
- Liu, X.; Martín-Calvo, A.; McGarrity, E.; Schnell, S.K.; Calero, S.; Simon, J.M.; Bedeaux, D.; Kjelstrup, S.; Bardow, A.; Vlugt, T.J.H. Fick Diffusion Coefficients in Ternary Liquid Systems from Equilibrium Molecular Dynamics Simulations. Ind. Eng. Chem. Res. 2012, 51, 10247–10258. [Google Scholar] [CrossRef]
- Gao, C.Y.; Limmer, D.T. Transport Coefficients from Large Deviation Functions. Entropy 2017, 19, 571. [Google Scholar] [CrossRef]
- Dufty, J.; Wrighton, J.; Luo, K.; Trickey, S.B. On the Kubo-Greenwood model for electron conductivity. Contrib. Plasma Phys. 2018, 58, 150–154. [Google Scholar] [CrossRef]
- Valadez Huerta, G.; Siemen, M.; Kabelac, S. Approach to the Coulomb Contribution of Thermodynamic Properties from the Mean Electrostatic Potential of the Ions in (ZrO2)1-x(Y2O3)x. J. Phys. Chem. C 2018, 122, 62–70. [Google Scholar] [CrossRef]
- Kabelac, S.; Siemer, M.; Ahrendts, J. Thermodynamische Stoffdaten für Biogase. Forschung im Ingenieurwesen 2005, 70, 46–55. [Google Scholar] [CrossRef]
- Valadez Huerta, G.; Reus, L.; Kabelac, S. A Diffusivity Study of (Sc2O3)0.1(CeO2)0.01(ZrO2)0.89 between 1100 and 1500 K at Zero Pressure with Molecular Dynamics. J. Chem. Eng. Data 2018, 63, 1955–1960. [Google Scholar] [CrossRef]
- Preis, W.; Egger, A.; Waldhäusl, J.; Sitte, W.; de Carvalho, E.; Irvine, J.T.S. Bulk and Grain Boundary Conductivities as Function of Temperature and Oxygen Partial Pressure of Scandia-Stabilized Zirconia Co-Doped with Yttria and Ceria. ECS Trans. 2009, 25, 1635–1642. [Google Scholar] [CrossRef]
- Atkins, P.; de Paula, J. Physical Chemistry; Oxford University Press: Oxford, UK, 2006; pp. 935–938. ISBN 0-7167-8759-8. [Google Scholar]
- Yonekura, T.; Tachikawa, Y.; Yoshizumi, T.; Shiratori, Y.; Ito, K.; Sasaki, K. Exchange Current Density of Solid Oxide Fuel Cell Electrode. ECS Trans. 2011, 35, 1007–1014. [Google Scholar] [CrossRef]
- Kilo, M.; Taylor, M.A.; Argirusis, C.; Borchardt, G.; Jackson, R.A.; Schulz, O.; Martin, M.; Weller, M. Modeling of cation diffusion in oxygen ion conductors using molecular dynamics. Solid State Ion. 2004, 175, 823–827. [Google Scholar] [CrossRef]
- Shampine, L.F.; Reichelt, M.W. The MATLAB ODE Suite. SIAM. J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- Eveloy, V.; Karunkeyoon, W.; Rodgers, P.; Al Alili, A. Validation of Solid Oxide Fuel Cell Thermodynamic Models for System-level Integration. Int. J. Therm. Environ. Eng. 2016, 11, 25–32. [Google Scholar] [CrossRef]
- Fischer, K.; Seume, J.R. Impact of the Temperature Profile on Thermal Stress in a Tubular Solid Oxide Fuel Cell. J. Fuel Cell Sci. Technol. 2009, 6, 011017. [Google Scholar] [CrossRef]


| Parameter | Anode GDL | Anode CL | Cathode CL | Cathode GDL | Reference |
|---|---|---|---|---|---|
| in | - | - | - | ||
| in | - | - | [25] | ||
| - | - | [25] | |||
| in | - | - | [20] | ||
| in | - | - | [20] | ||
| in | - | - | [24] | ||
| in | - | - | [24] | ||
| - | - | [24] | |||
| YSZ | |||
|---|---|---|---|
| YSZ08 | |||
| YSZ12 | |||
| YSZ16 | |||
| YSZ20 |
| YSZ| | Anode GDL || | Electrolyte | | Cathode GDL || |
|---|---|---|---|
| YSZ08| | || | | | || |
| YSZ20| | || | | | || |
| YSZ08| | || | | | || |
| YSZ12| | || | | | || |
| YSZ16| | || | | | || |
| YSZ20| | || | | | || |
| YSZ08*| | || | | | || |
| YSZ20*| | || | | | || |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valadez Huerta, G.; Flasbart, V.; Marquardt, T.; Radici, P.; Kabelac, S. Impact of Multi-Causal Transport Mechanisms in an Electrolyte Supported Planar SOFC with (ZrO2)x−1(Y2O3)x Electrolyte. Entropy 2018, 20, 469. https://doi.org/10.3390/e20060469
Valadez Huerta G, Flasbart V, Marquardt T, Radici P, Kabelac S. Impact of Multi-Causal Transport Mechanisms in an Electrolyte Supported Planar SOFC with (ZrO2)x−1(Y2O3)x Electrolyte. Entropy. 2018; 20(6):469. https://doi.org/10.3390/e20060469
Chicago/Turabian StyleValadez Huerta, Gerardo, Vincent Flasbart, Tobias Marquardt, Pablo Radici, and Stephan Kabelac. 2018. "Impact of Multi-Causal Transport Mechanisms in an Electrolyte Supported Planar SOFC with (ZrO2)x−1(Y2O3)x Electrolyte" Entropy 20, no. 6: 469. https://doi.org/10.3390/e20060469
APA StyleValadez Huerta, G., Flasbart, V., Marquardt, T., Radici, P., & Kabelac, S. (2018). Impact of Multi-Causal Transport Mechanisms in an Electrolyte Supported Planar SOFC with (ZrO2)x−1(Y2O3)x Electrolyte. Entropy, 20(6), 469. https://doi.org/10.3390/e20060469







