Hierarchical Scaling in Systems of Natural Cities
Abstract
1. Introduction
2. Theoretical Models
2.1. Hierarchical Exponential Laws
2.2. Hierarchical Power Laws
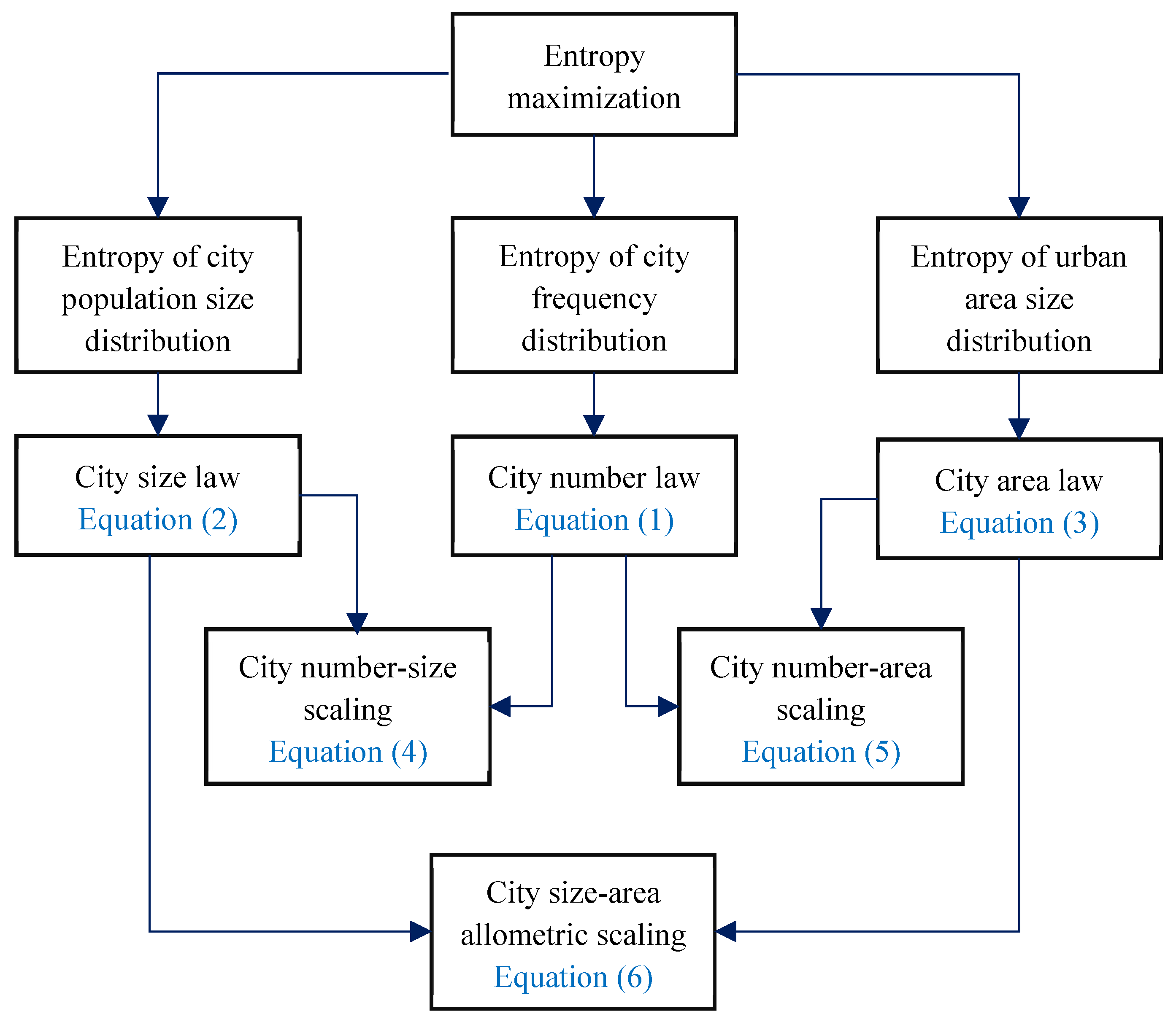
2.3. Entropy Maximization and Power Laws
3. Empirical Analysis
3.1. Study Area, Data, and Methods
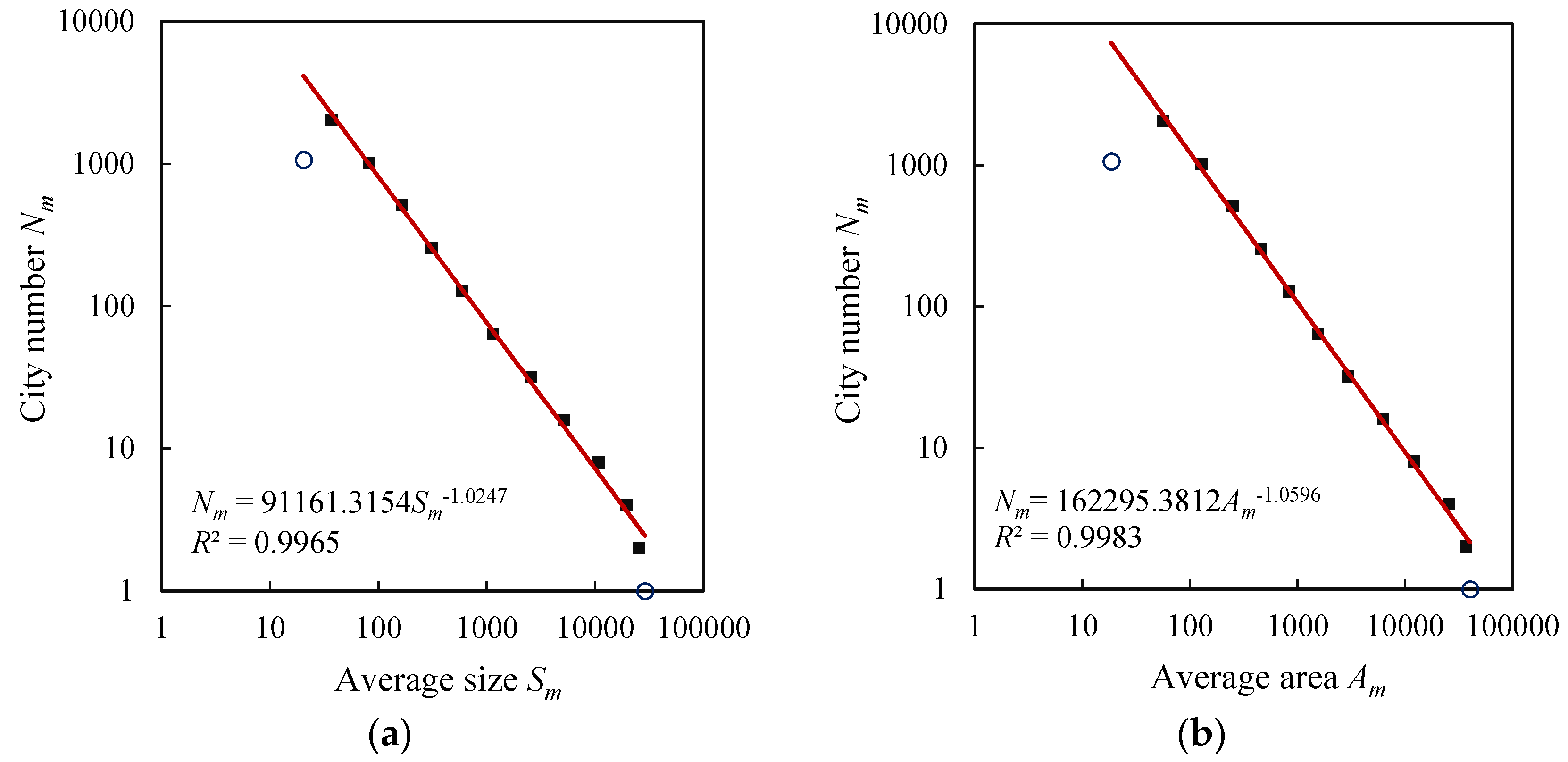
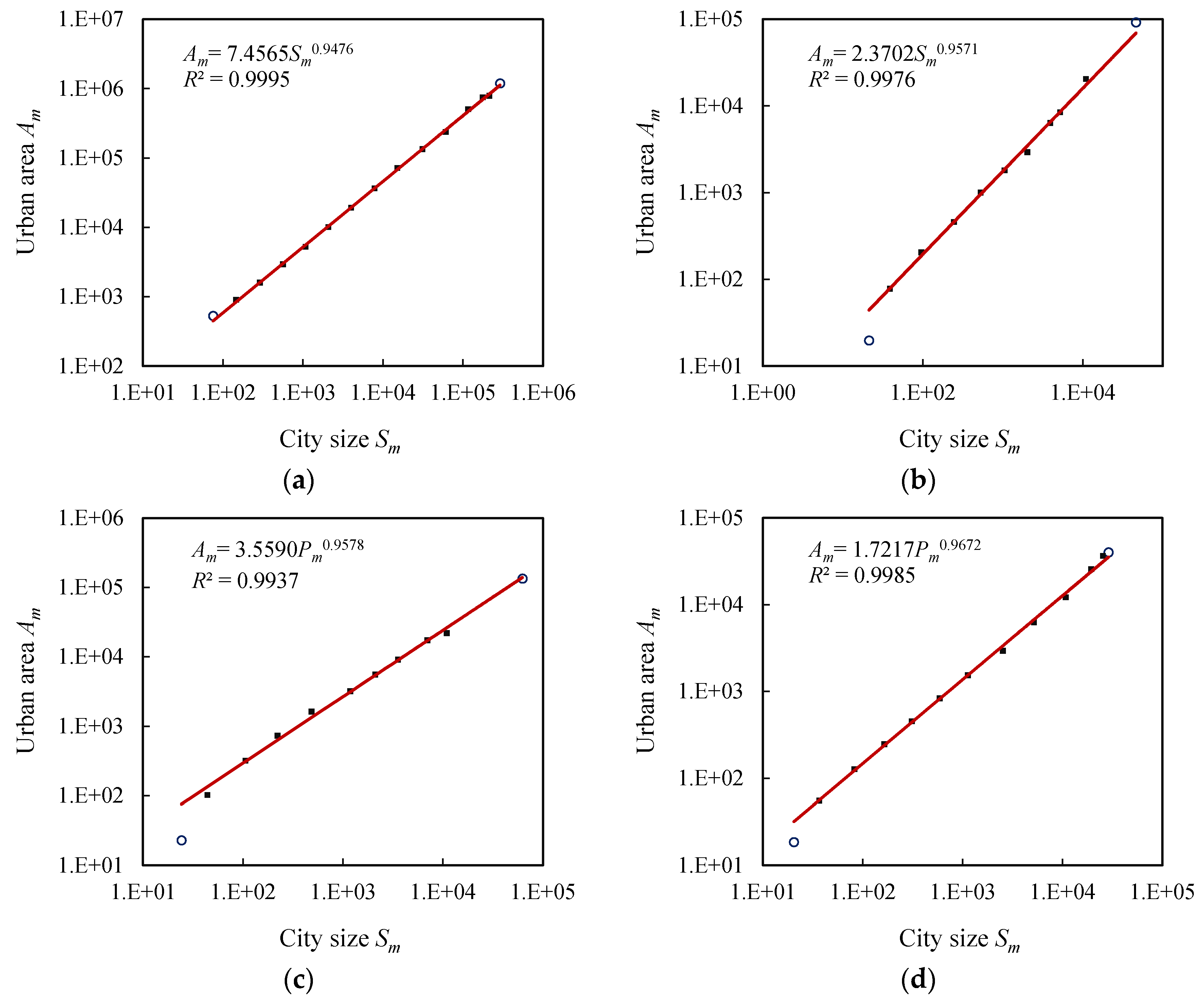
3.2. Results and Findings
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Pumain, D. (Ed.) Hierarchy in Natural and Social Sciences; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Frankhauser, P. The fractal approach: A new tool for the spatial analysis of urban agglomerations. Popul. Engl. Sel. 1998, 10, 205–240. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman and Company: New York, NY, USA, 1982. [Google Scholar]
- Batty, M.; Longley, P.A. Fractal Cities: A Geometry of Form and Function; Academic Press: London, UK, 1994. [Google Scholar]
- Frankhauser, P. La Fractalité des Structures Urbaines (The Fractal Aspects of Urban Structures); Economica: Paris, France, 1994. (In French) [Google Scholar]
- Chen, Y.-G. Fractal Urban Systems: Scaling, Symmetry, and Spatial Complexity; Science Press: Beijing, China, 2008. (In Chinese) [Google Scholar]
- Chen, Y.-G. The rank-size scaling law and entropy-maximizing principle. Physica A 2012, 391, 767–778. [Google Scholar] [CrossRef]
- Williams, G.P. Chaos Theory Tamed; Joseph Henry Press: Washington, DC, USA, 1997. [Google Scholar]
- Batty, M. The size, scale, and shape of cities. Science 2008, 319, 769–771. [Google Scholar] [CrossRef] [PubMed]
- Bettencourt, L.M.A. The origins of scaling in cities. Science 2013, 340, 1438–1441. [Google Scholar] [CrossRef] [PubMed]
- Bettencourt, L.M.A.; Lobo, J.; Helbing, D.; Kühnert, C.; West, G.B. Growth, innovation, scaling, and the pace of life in cities. Proc. Natl. Acad. Sci. USA 2007, 104, 7301–7306. [Google Scholar] [CrossRef] [PubMed]
- Jiang, B. The image of the city out of the underlying scaling of city artifacts or locations. Ann. Assoc. Am. Geogr. 2013, 103, 1552–1566. [Google Scholar] [CrossRef]
- Lobo, J.; Bettencourt, L.M.A.; Strumsky, D.; West, G.B. Urban scaling and the production function for cities. PLoS ONE 2013, 8, e58407. [Google Scholar] [CrossRef] [PubMed]
- Rybski, D.; Buldyrev, S.V.; Havlin, S.; Liljeros, F.; Hernán, A.; Makse, H.A. Scaling laws of human interaction activity. Proc. Natl. Acad. Sci. USA 2009, 106, 12640–12645. [Google Scholar] [CrossRef] [PubMed]
- Arcaute, E.; Hatna, E.; Ferguson, P.; Youn, H.; Johansson, A.; Batty, M. Constructing cities, deconstructing scaling laws. J. R. Soc. Interface 2015, 12, 20140745. [Google Scholar] [CrossRef] [PubMed]
- Louf, R.; Barthelemy, M. Scaling: Lost in the smog. Environ. Plan. B Plan. Des. 2014, 41, 767–769. [Google Scholar] [CrossRef]
- West, G.B.; Woodruff, W.H.; Brown, J.H. Allometric scaling of metabolic rate from molecules and mitochondria to cells and mammals. Proc. Natl. Acad. Sci. USA 2002, 99, 2473–2478. [Google Scholar] [CrossRef] [PubMed]
- Zipf, G.K. Human Behavior and the Principle of Least Effort; Addison–Wesley: Reading, MA, USA, 1949. [Google Scholar]
- Christaller, W. Central Places in Southern Germany; (Translated by C. W. Baskin, 1966); Prentice Hall: Englewood Cliffs, NJ, USA, 1933. [Google Scholar]
- Beckmann, M.J. City hierarchies and distribution of city sizes. Econ. Dev. Cult. Chang. 1958, 6, 243–248. [Google Scholar] [CrossRef]
- Davis, K. World urbanization: 1950–1970. In Systems of Cities; Bourne, I.S., Simons, J.W., Eds.; Oxford University Press: New York, NY, USA, 1978; pp. 92–100. [Google Scholar]
- Woldenberg, M.J.; Berry, B.J.L. Rivers and central places: Analogous systems? J. Reg. Sci. 1967, 7, 129–139. [Google Scholar] [CrossRef]
- Chen, Y.-G.; Feng, J. A hierarchical allometric scaling analysis of Chinese cities: 1991–2014. Discret. Dyn. Nat. Soc. 2017, 2017, 5243287. [Google Scholar] [CrossRef]
- Jiang, B.; Yao, X. (Eds.) Geospatial Analysis and Modeling of Urban Structure and Dynamics; Springer: Berlin, Germany, 2010. [Google Scholar]
- Waldrop, M. Complexity: The Emerging of Science at the Edge of Order and Chaos; Simon and Schuster: New York, NY, USA, 1992. [Google Scholar]
- Chen, Y.-G. The evolution of Zipf’s law indicative of city development. Physica A 2016, 443, 555–567. [Google Scholar] [CrossRef]
- Gabaix, X. Zipf’s law and the growth of cities. Am. Econ. Rev. 1999, 89, 129–132. [Google Scholar] [CrossRef]
- Gabaix, X. Zipf’s law for cities: An explanation. Q. J. Econ. 1999, 114, 739–767. [Google Scholar] [CrossRef]
- Batty, M. Hierarchy in cities and city systems. In Hierarchy in Natural and Social Sciences; Pumain, D., Ed.; Springer: Dordrecht, The Netherlands, 2006; pp. 143–168. [Google Scholar]
- Chen, Y.-G. The mathematical relationship between Zipf’s law and the hierarchical scaling law. Physica A 2012, 391, 3285–3299. [Google Scholar] [CrossRef]
- Chen, Y.-G. Characterizing growth and form of fractal cities with allometric scaling exponents. Discret. Dyn. Nat. Soc. 2000, 2010, 194715. [Google Scholar]
- Goodchild, M.F.; Mark, D.M. The fractal nature of geographical phenomena. Ann. Assoc. Am. Geogr. 1987, 77, 265–278. [Google Scholar] [CrossRef]
- Curry, L. The random spatial economy: An exploration in settlement theory. Ann. Assoc. Am. Geogr. 1964, 54, 138–146. [Google Scholar] [CrossRef]
- Wilson, A.G. Modelling and systems analysis in urban planning. Nature 1968, 220, 963–966. [Google Scholar] [CrossRef] [PubMed]
- Wilson, A.G. Entropy in urban and regional modelling: Retrospect and prospect. Geogr. Anal. 2010, 42, 364–394. [Google Scholar] [CrossRef]
- Bussière, R.; Snickers, F. Derivation of the negative exponential model by an entropy maximizing method. Environ. Plan. A 1970, 2, 295–301. [Google Scholar] [CrossRef]
- Chen, Y.-G. The distance-decay function of geographical gravity model: Power law or exponential law? Chaos Solitons Fractals 2015, 77, 174–189. [Google Scholar] [CrossRef]
- Jiang, B.; Jia, T. Zipf’s law for all the natural cities in the United States: A geospatial perspective. Int. J. Geogr. Inf. Sci. 2011, 25, 1269–1281. [Google Scholar] [CrossRef]
- Jiang, B.; Liu, X.T. Scaling of geographic space from the perspective of city and field blocks and using volunteered geographic information. Int. J. Geogr. Inf. Sci. 2012, 26, 215–229. [Google Scholar] [CrossRef]
- Longley, P.A.; Batty, M.; Shepherd, J. The size, shape and dimension of urban settlements. Trans. Inst. Br. Geogr. (New Ser.) 1991, 16, 75–94. [Google Scholar] [CrossRef]
- Rozenfeld, H.D.; Rybski, D.; Andrade, D.S., Jr.; Batty, M.; Stanley, H.E.; Makse, H.A. Laws of population growth. Proc. Natl. Acad. Sci. USA 2008, 105, 18702–18707. [Google Scholar] [CrossRef] [PubMed]
- Rozenfeld, H.D.; Rybski, D.; Gabaix, X.; Makse, H.A. The area and population of cities: New insights from a different perspective on cities. Am. Econ. Rev. 2011, 101, 2205–2225. [Google Scholar] [CrossRef]
- Tannier, C.; Thomas, I.; Vuidel, G.; Frankhauser, P. A fractal approach to identifying urban boundaries. Geogr. Anal. 2011, 43, 211–227. [Google Scholar] [CrossRef]
- Jiang, B.; Miao, Y.F. The evolution of natural cities from the perspective of location-based social media. Prof. Geogr. 2014, 67, 295–306. [Google Scholar] [CrossRef]
- Jiang, B.; Yin, J. Ht-index for quantifying the fractal or scaling structure of geographic features. Ann. Assoc. Am. Geogr. 2014, 104, 530–541. [Google Scholar] [CrossRef]
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-law distributions in empirical data. Siam Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Newman, M.E.J. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005, 46, 323–351. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, T.K. Allometric scaling of countries. Physica A 2010, 389, 4887–4896. [Google Scholar] [CrossRef]
- Charnes, A.; Frome, E.L.; Yu, P.L. The equivalence of generalized least squares and maximum likelihood estimates in the exponential family. J. Am. Stat. Assoc. 1976, 71, 169–171. [Google Scholar] [CrossRef]
- Bak, P. How Nature Works: The Science of Self-Organized Criticality; Springer: New York, NY, USA, 1996. [Google Scholar]
- Auerbach, F. Das gesetz der bevölkerungskonzentration (The law of population concentration). Petermann’s Geogr. Mitt. (Petermann’s Geogr. Inf.) 1913, 59, 74–76. (In German) [Google Scholar]
- Lee, T.D. Symmetries, Asymmetries, and the World of Particles; University of Washington Press: Seattle, WA, USA; London, UK, 1988. [Google Scholar]
- Louf, R.; Barthelemy, M. How congestion shapes cities: From mobility patterns to scaling. Sci. Rep. 2014, 4, 5561. [Google Scholar] [CrossRef] [PubMed]
- Von Bertalanffy, L. General System Theory: Foundations, Development, and Applications; George Breziller: New York, NY, USA, 1968. [Google Scholar]
- Chen, Y.-G. Modeling fractal structure of city-size distributions using correlation functions. PLoS ONE 2011, 6, e24791. [Google Scholar] [CrossRef] [PubMed]
- Pumain, D.; Moriconi-Ebrard, F. City size distributions and metropolisation. GeoJournal 1997, 43, 307–314. [Google Scholar] [CrossRef]
- Chen, Y.-G. An allometric scaling relation based on logistic growth of cities. Chaos Solitons Fractals 2014, 65, 65–77. [Google Scholar] [CrossRef]
- Chen, Y.-G. The spatial meaning of Pareto’s scaling exponent of city-size distributions. Fractals 2014, 22, 1450001. [Google Scholar] [CrossRef]
- Arbesman, S. The Half-Life of Facts: Why Everything We Know Has An Expiration Date; Penguin Group: New York, NY, USA, 2012. [Google Scholar]
- Dendrinos, D.S. The Dynamics of Cities: Ecological Determinism, Dualism and Chaos; Routledge: New York, NY, USA, 1992. [Google Scholar]
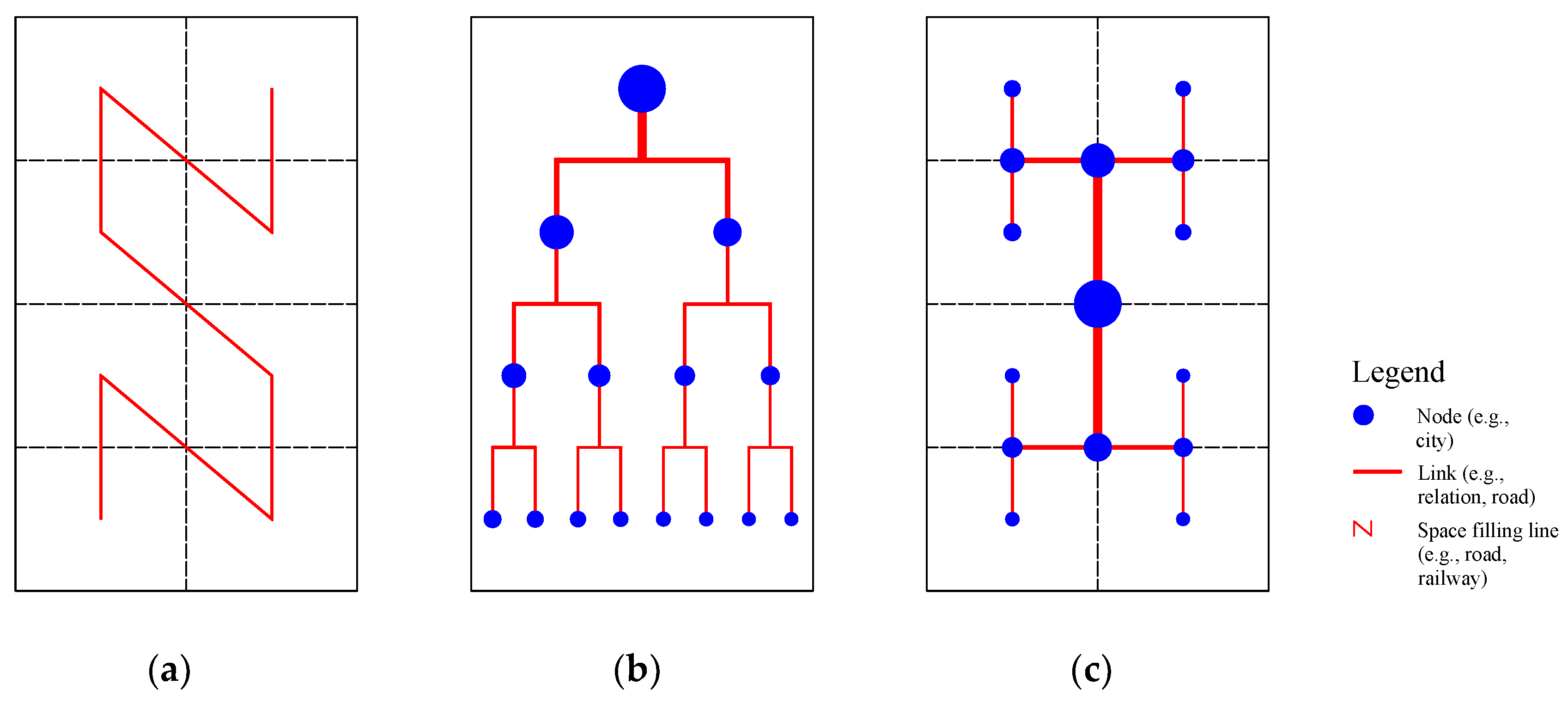

| Entropy Process | Law | Formula | Equation | Complexity |
|---|---|---|---|---|
| Entropy maximization of frequency distribution | City number law | (1) | External complexity | |
| Entropy maximization of size distribution | Population size law | (2) | Internal complexity | |
| Area size law | (3) | Internal complexity |
| Level m | Number Nm | Total Tm | Hierarchical Reconstruction of the Rank-Size Distribution (Sm = ln2/2m−1) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | P1 = 1 | |||||||
| 2 | 2 | 0.833 | P2 = 1/2 | P3 = 1/3 | ||||||
| 3 | 4 | 0.760 | P4 = 1/4 | P5 = 1/5 | P6 = 1/6 | P7 = 1/7 | ||||
| 4 | 8 | 0.725 | P8 = 1/8 | P9 = 1/9 | P10 = 1/10 | P11 = 1/11 | P12 = 1/12 | P13 = 1/13 | P14 = 1/14 | P15 = 1/15 |
| … | … | … | … | … | … | … | … | … | … | … |
| M | 2M−1 | ln(2) | 1/2M−1 | … | … | … | … | … | … | 1/(2M−1) |
| Class | America | Britain | France | Germany | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m | Nm | Sm | Am | Nm | Sm | Am | Nm | Sm | Am | Nm | Sm | Am |
| 1 | 1 | 290,503.000 | 1,194,500.000 | 1 | 46,299.000 | 91,938.879 | 1 | 62,242.000 | 133,817.492 | 1 | 28,866.000 | 40,265.780 |
| 2 | 2 | 213,517.000 | 783,975.000 | 2 | 10,993.500 | 20,368.164 | 2 | 10,877.000 | 21,812.770 | 2 | 25,354.500 | 36,563.584 |
| 3 | 4 | 176,132.500 | 746,975.000 | 4 | 5230.250 | 8434.331 | 4 | 6972.250 | 17,203.731 | 4 | 19,394.000 | 25,766.545 |
| 4 | 8 | 115,663.500 | 501,678.125 | 8 | 3946.375 | 6340.649 | 8 | 3541.875 | 9044.170 | 8 | 10,758.875 | 12,169.475 |
| 5 | 16 | 60,697.125 | 236,468.750 | 16 | 2034.188 | 2925.685 | 16 | 2097.688 | 5529.493 | 16 | 5168.750 | 6245.420 |
| 6 | 32 | 31,127.938 | 134,110.156 | 32 | 1059.219 | 1802.168 | 32 | 1179.563 | 3175.526 | 32 | 2528.500 | 2940.365 |
| 7 | 64 | 15,077.375 | 71,724.609 | 64 | 530.453 | 1000.051 | 64 | 483.063 | 1622.074 | 64 | 1131.203 | 1541.896 |
| 8 | 128 | 7804.250 | 3,6437.695 | 128 | 246.094 | 457.709 | 128 | 220.945 | 728.457 | 128 | 588.867 | 836.570 |
| 9 | 256 | 3992.852 | 19,124.316 | 256 | 96.258 | 204.449 | 256 | 105.547 | 319.176 | 256 | 309.762 | 455.393 |
| 10 | 512 | 2068.379 | 10,039.502 | 512 | 38.986 | 77.708 | 512 | 44.010 | 102.194 | 512 | 164.701 | 248.410 |
| 11 | 1024 | 1072.855 | 5235.742 | 228 | 21.311 | 19.792 | 217 | 24.249 | 22.879 | 1024 | 82.616 | 128.013 |
| 12 | 2048 | 560.370 | 2922.583 | 2048 | 36.726 | 55.571 | ||||||
| 13 | 4096 | 288.579 | 1593.188 | 1065 | 20.488 | 18.542 | ||||||
| 14 | 8192 | 145.798 | 903.534 | |||||||||
| 15 | 14,922 | 75.202 | 530.333 | |||||||||
| Type | Parameter and Statistic | U.S.A. | Britain | France | Germany |
|---|---|---|---|---|---|
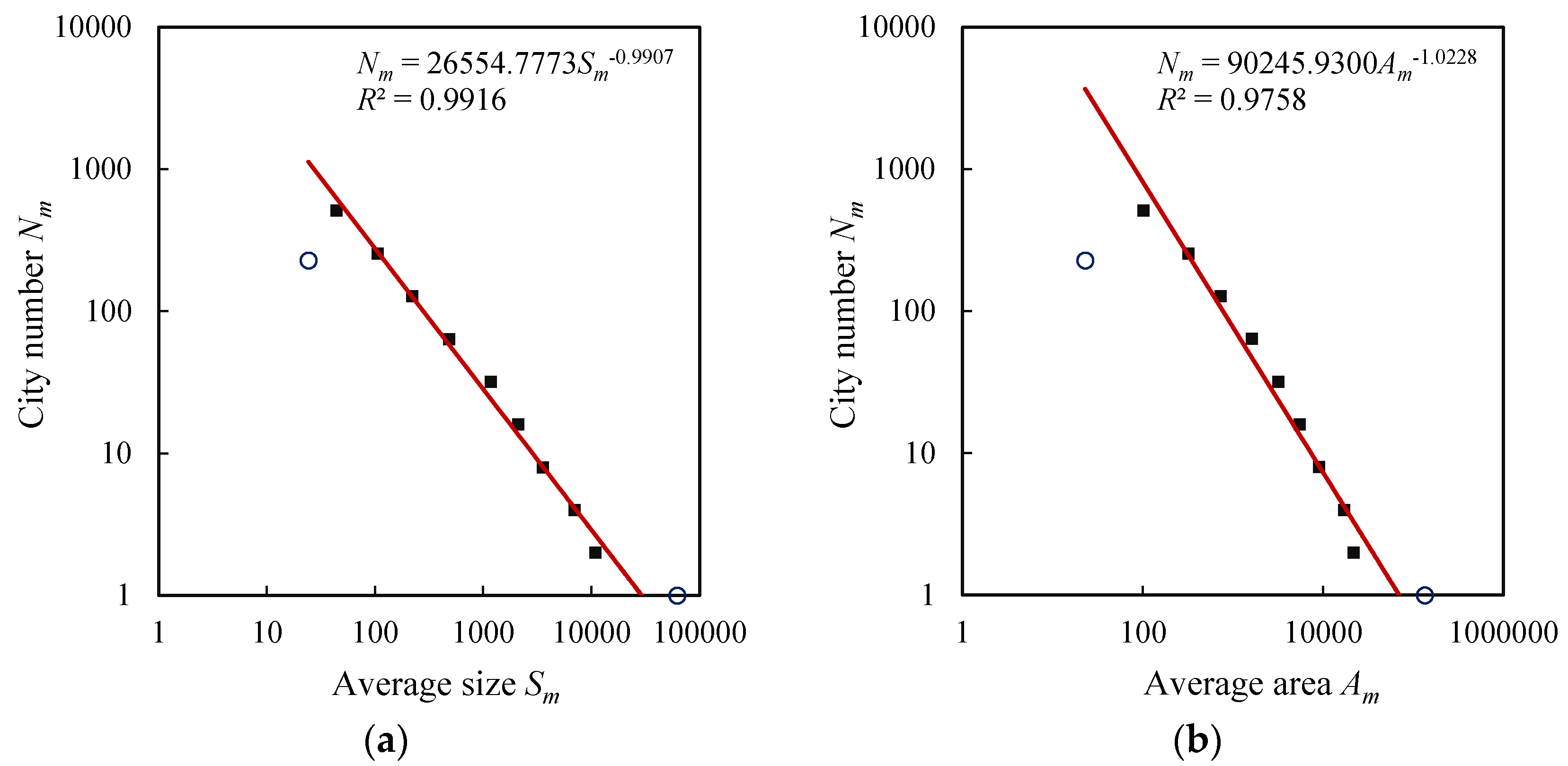
| Size distribution | Fractal dimension (D) | 1.0827 | 0.9899 | 0.9907 | 1.0247 |
| Standard error (σ) | 0.0222 | 0.0438 | 0.0344 | 0.0203 | |
| Goodness of fit (R2) | 0.9954 | 0.9865 | 0.9916 | 0.9965 | |
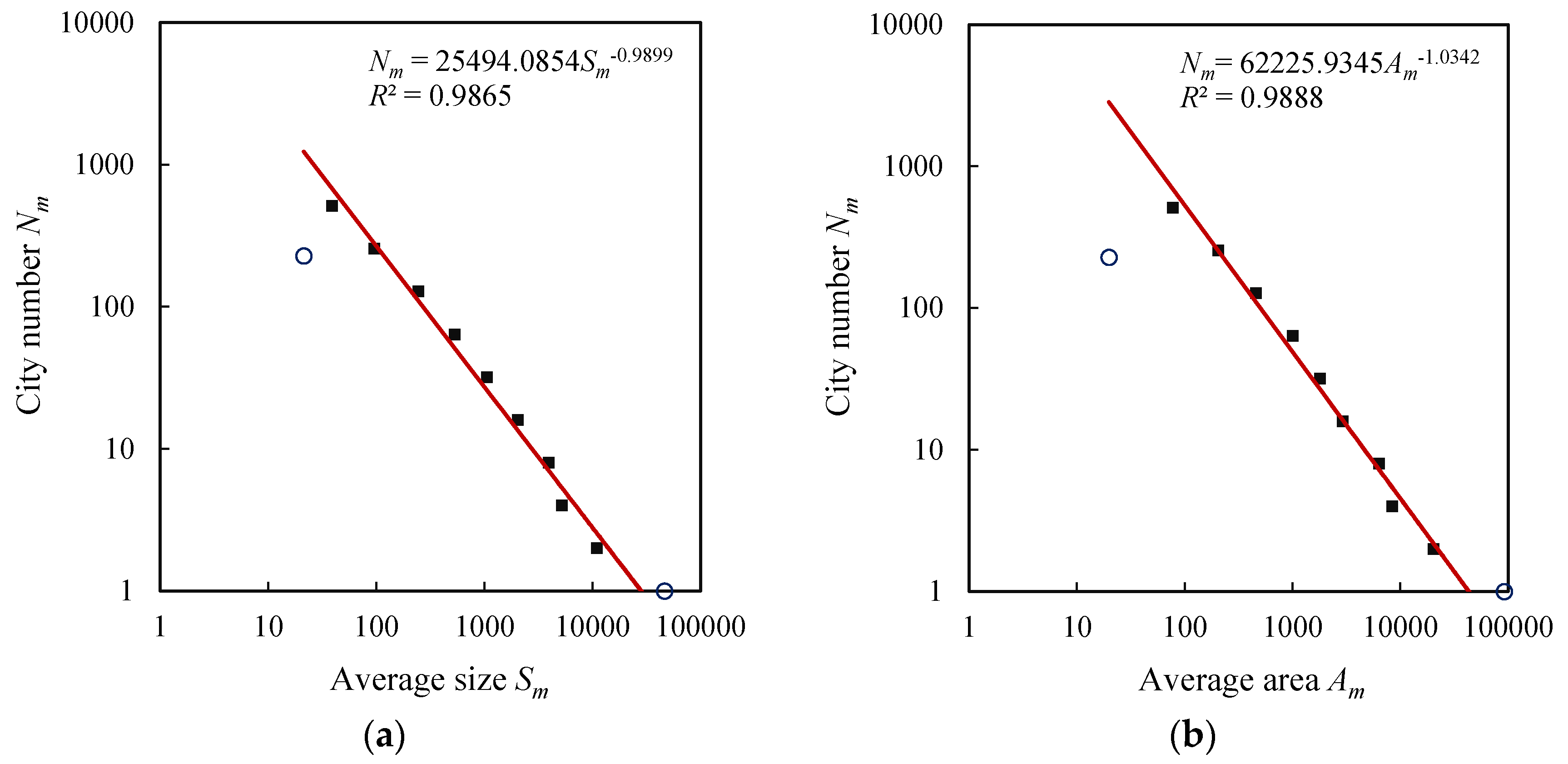
| Area distribution | Fractal dimension (d) | 1.1416 | 1.0342 | 1.0228 | 1.0596 |
| Standard error (σ) | 0.0263 | 0.0415 | 0.0609 | 0.0147 | |
| Goodness of fit (R2) | 0.9942 | 0.9888 | 0.9758 | 0.9983 | |
| Size-area allometry | Allometric exponent (b) | 0.9476 | 0.9571 | 0.9578 | 0.9672 |
| Standard error (σ) | 0.0063 | 0.0179 | 0.0289 | 0.0124 | |
| Goodness of fit (R2) | 0.9995 | 0.9976 | 0.9937 | 0.9985 | |
| Fractal dimension quotient | D/d | 0.9484 | 0.9571 | 0.9686 | 0.9671 |
| Related quantity | City number (n) | 31,305 | 1251 | 1240 | 5160 |
| Level number (M) | 15 | 11 | 11 | 13 | |
| Scaling range | 2~14 | 2~10 | 2~10 | 2~12 | |
| Degree of freedom | 11 | 7 | 7 | 9 |
| Type | Sub-Type | Basic Models | Main Model | Parameters |
|---|---|---|---|---|
| Longitudinal allometry | Exponential allometry | |||
| Logistic allometry | ||||
| Crosssectional allometry | Power allometry | |||
| Hierarchical allometry | Exponential allometry | |||
| Power allometry |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Jiang, B. Hierarchical Scaling in Systems of Natural Cities. Entropy 2018, 20, 432. https://doi.org/10.3390/e20060432
Chen Y, Jiang B. Hierarchical Scaling in Systems of Natural Cities. Entropy. 2018; 20(6):432. https://doi.org/10.3390/e20060432
Chicago/Turabian StyleChen, Yanguang, and Bin Jiang. 2018. "Hierarchical Scaling in Systems of Natural Cities" Entropy 20, no. 6: 432. https://doi.org/10.3390/e20060432
APA StyleChen, Y., & Jiang, B. (2018). Hierarchical Scaling in Systems of Natural Cities. Entropy, 20(6), 432. https://doi.org/10.3390/e20060432






