Refrigeration Performance and Entropy Generation Analysis for Reciprocating Magnetic Refrigerator with Gd Plates
Abstract
1. Introduction
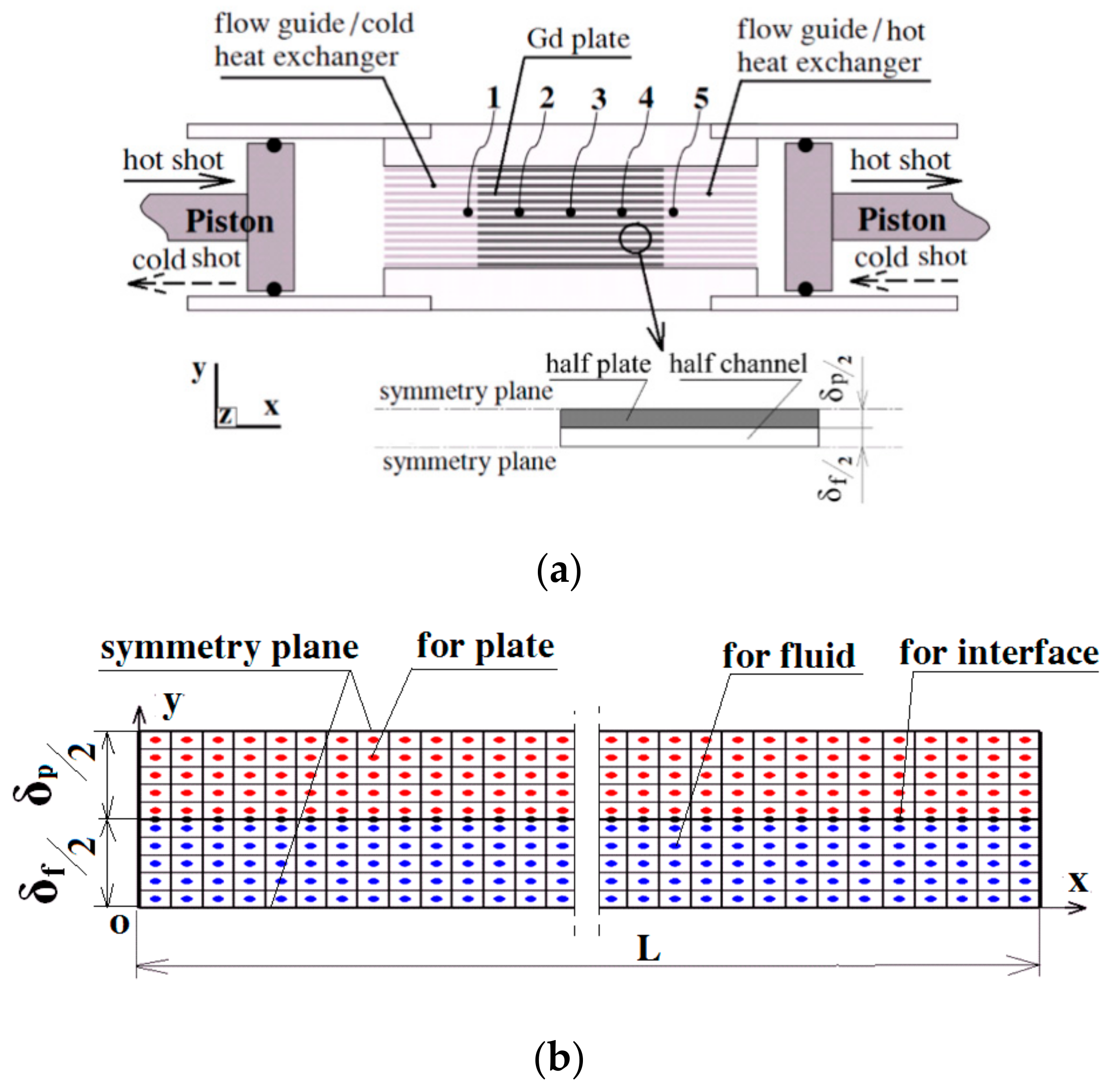
2. Physical Model
3. Numerical Model and Computation Scheme
3.1. Governing Equations
3.2. Computation Domain, Mesh Generation, and Solution Scheme
3.3. Model Validation
4. Numerical Results and Discussions
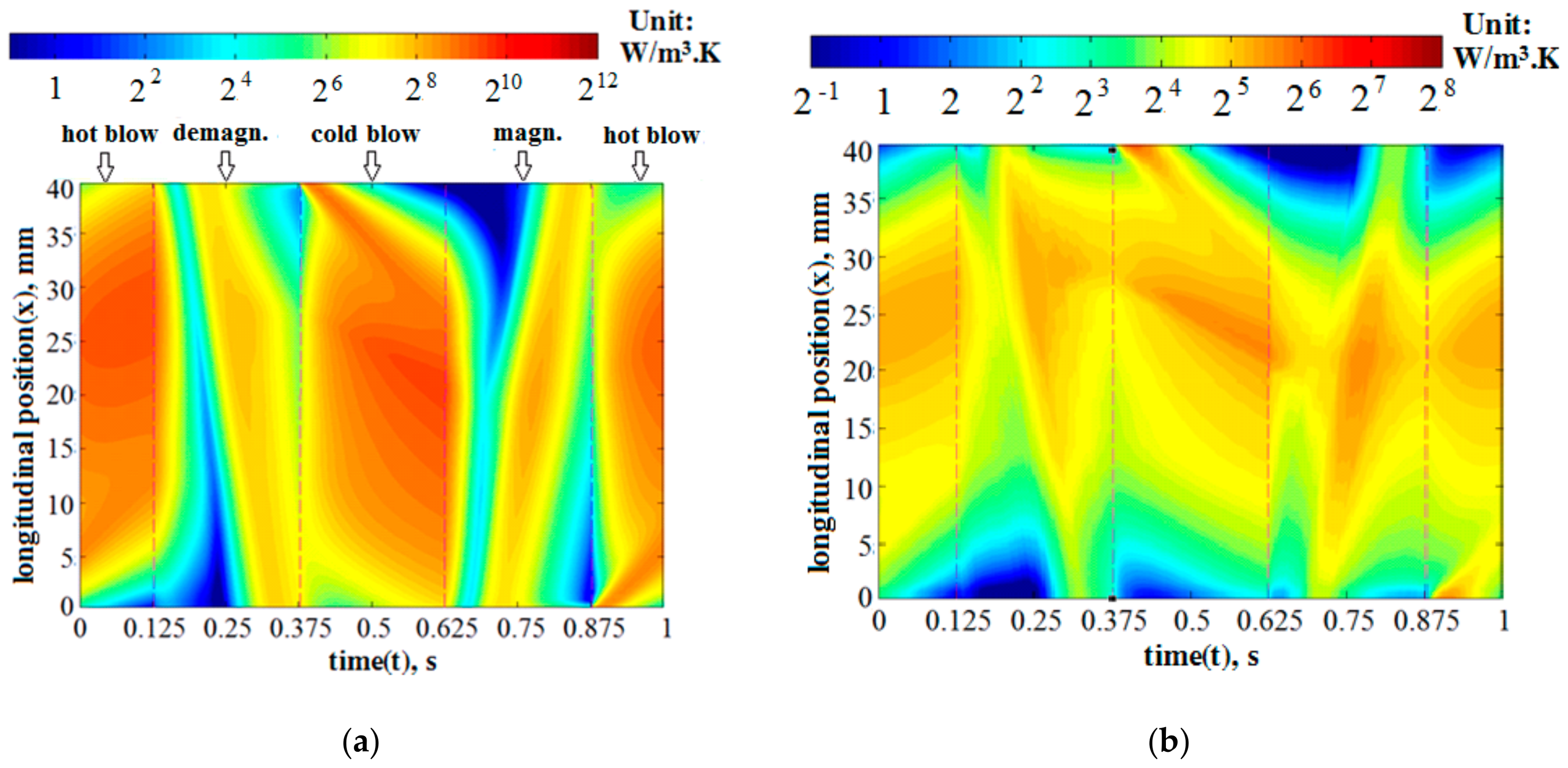
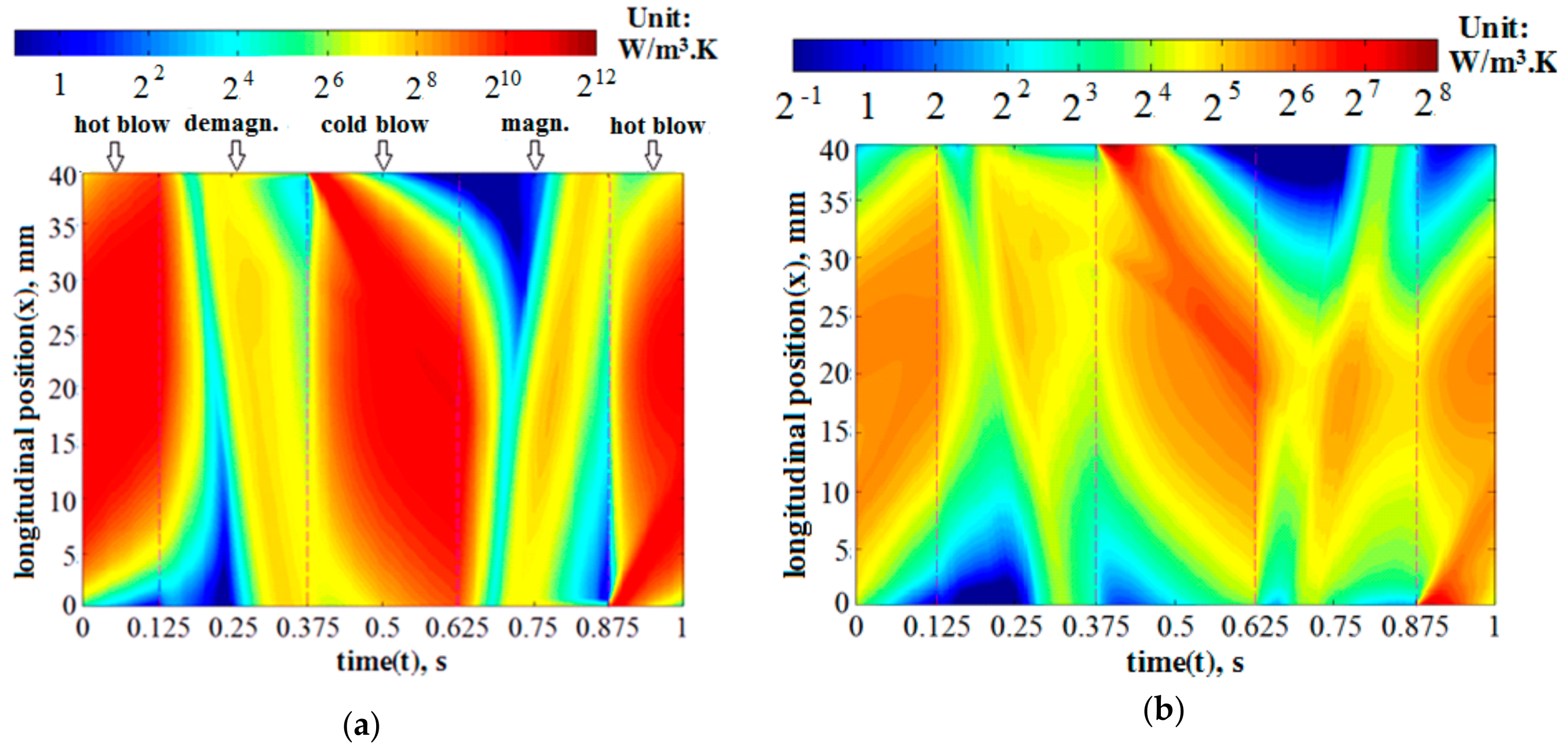
4.1. Calculations of Refrigeration Performance and Entropy Generation
4.1.1. Refrigeration Capacity and Coefficient of Performance
4.1.2. Specific Entropy Generation Rate and Entropy Generation Number
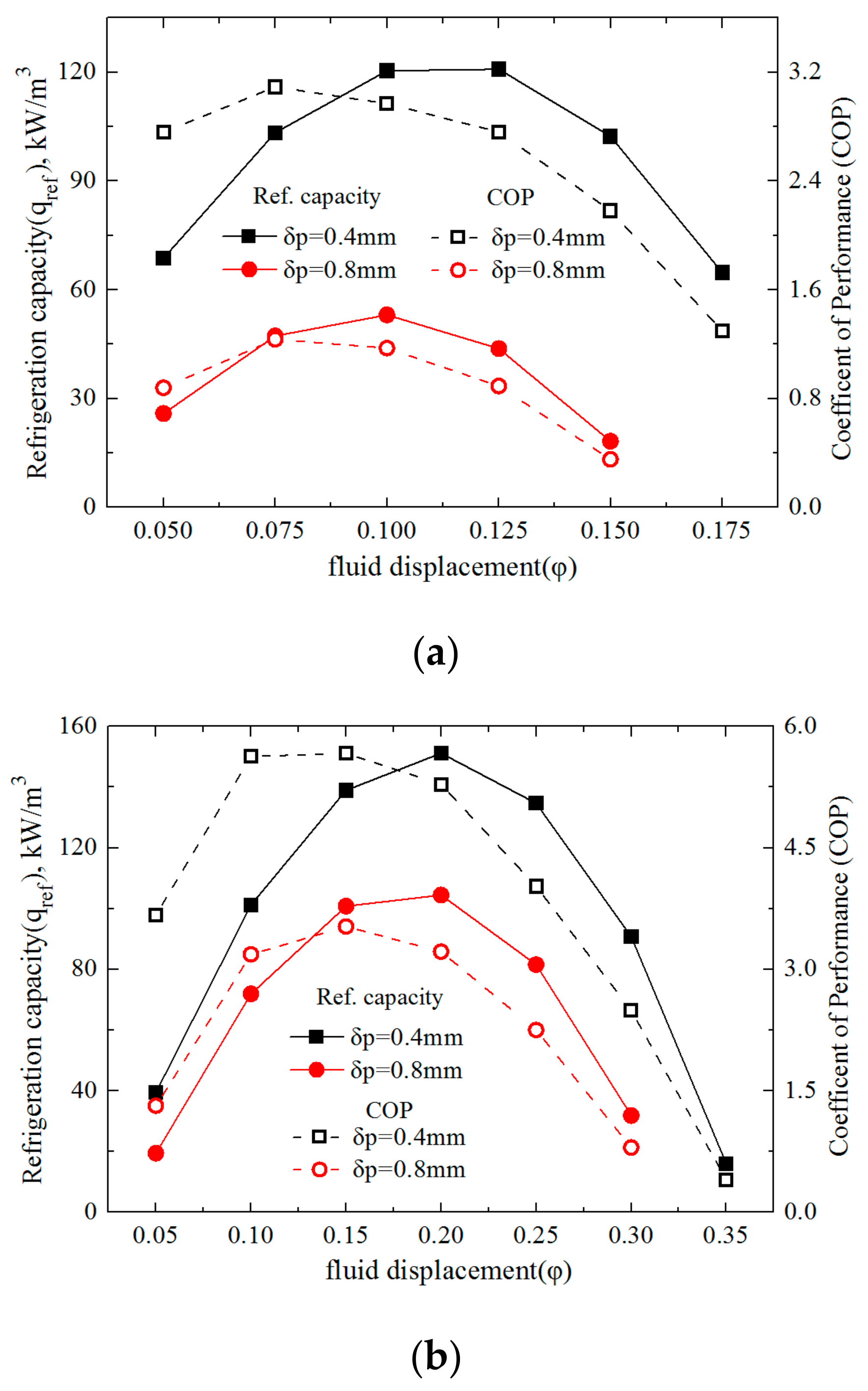
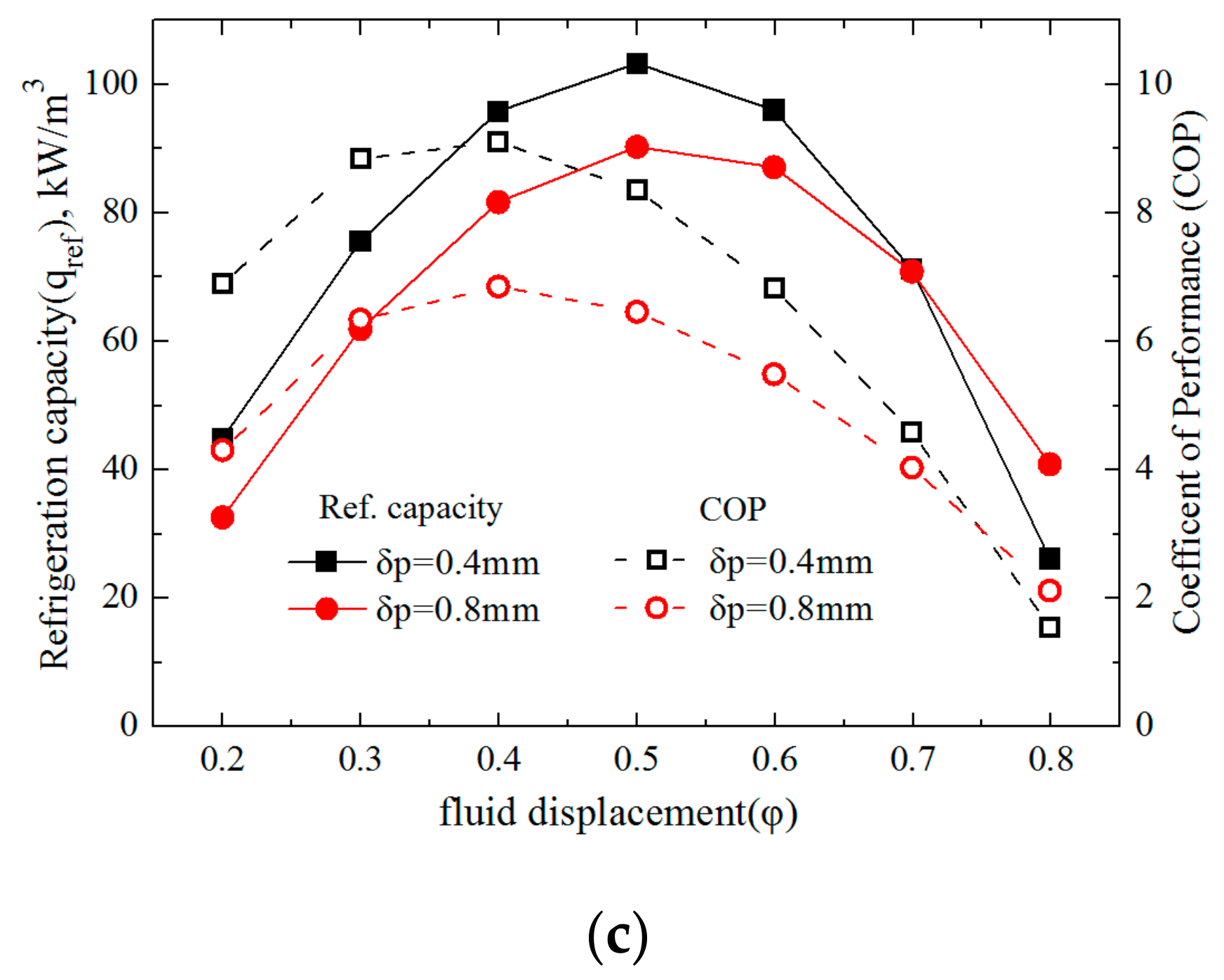
4.2. Variations of Refrigeration Performance with Relative Fluid Displacement
4.2.1. Variations of Specific Refrigeration Capacity
4.2.2. Variations of the Coefficient of Performance
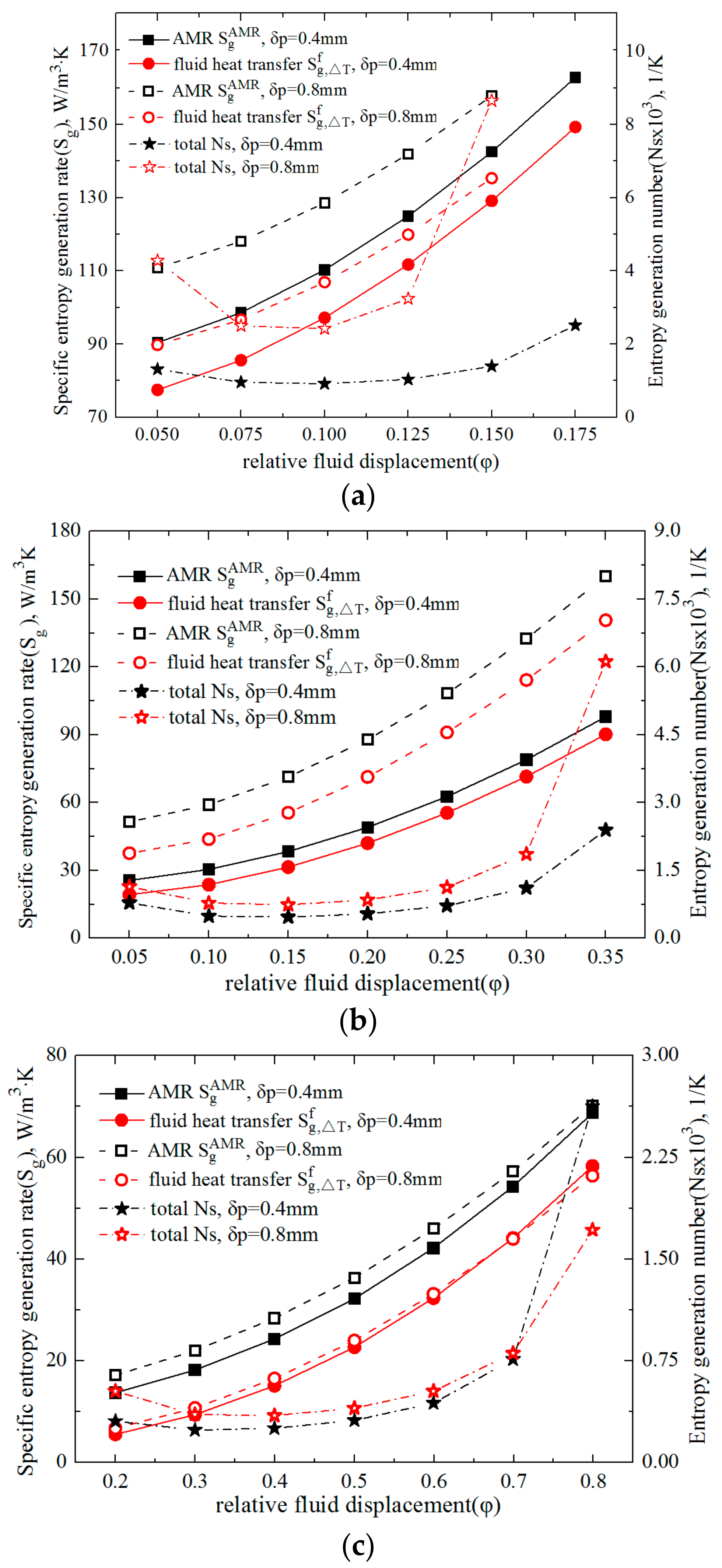
4.3. Variations of Entropy Generation with Relative Fluid Displacement
4.3.1. Variations of Specific Entropy Generation Rates
4.3.2. Variation of the Entropy Generation Number
5. Conclusions
- (1)
- The qref and COP of the magnetic refrigerator followed the convex variation trend with increasing φ, and a smaller plate thickness (δp) facilitated a larger peak of the qref and COP. Furthermore, the largest τ produced the largest COP (=9.11), while the greatest qref (=151.2 kW/m3) was generated at a moderate τ.
- (2)
- With increments of φ, the Sg in the AMR rose monotonically, while the Ns varied concavely. Moreover, a larger τ, or a smaller δp, resulted in a smaller pit Ns, and the lowest Ns was 2.4 × 10−4 K−1.
- (3)
- The optimal φ for the largest qref and COP and the lowest Ns was inconsistent, and were 0.2, 0.4 and 0.3, respectively, in the current work. Thus, some compromises need be made in the optimization of AMR.
Author Contributions
Funding
Conflicts of Interest
References
- Russek, S.L.; Zimm, C.B. Potential for cost effective magnetocaloric air conditioning systems. Int. J. Refrig. 2006, 29, 1366–1373. [Google Scholar] [CrossRef]
- Kitanovski, A.; Tušek, J.; Tomc, U.; Plaznik, U.; Ozbolt, M.; Poredoš, A. Magnetocaloric Energy Conversion: From Theory to Applications; Springer: London, UK, 2015. [Google Scholar]
- Aprea, C.; Greco, A.; Maiorino, A. GeoThermag: A geothermal magnetic refrigerator. Int. J. Refrig. 2015, 59, 75–83. [Google Scholar] [CrossRef]
- Tegus, O.; Bruck, E.; Buschow, K.H.; de Boer, F.R. Transition metal-based magnetic refrigerants for room temperature applications. Nature 2002, 415, 150–152. [Google Scholar] [CrossRef] [PubMed]
- Gschneidner, K.A., Jr.; Pecharsky, V.K.; Tsokol, A.O. Recent developments in magnetocaloric materials. Rep. Prog. Phys. 2005, 68, 1479–1539. [Google Scholar] [CrossRef]
- Bjørk, R.; Bahl, C.R.H.; Smith, A.; Pryds, N. Review and comparison of magnet designs for magnetic refrigeration. Int. J. Refrig. 2010, 33, 437–448. [Google Scholar] [CrossRef]
- You, Y.H.; Guo, Y.; Xiao, S.F.; Yu, S.; Ji, H.; Luo, X. Numerical simulation and performance improvement of a multi-polar concentric Halbach cylindrical magnet for magnetic refrigeration. J. Magn. Magn. Mater. 2016, 405, 231–237. [Google Scholar] [CrossRef]
- Eriksen, D.; Engelbrecht, K.; Bahl, C.R.H.; Bjørk, R.; Nielsen, K.K.; Insinga, A.R.; Pryds, N. Design and experimental tests of a rotary active magnetic regenerator prototype. Int. J. Refrig. 2015, 58, 14–21. [Google Scholar] [CrossRef]
- Gomez, J.R.; Garcia, R.F.; Catoira, A.D.M.; Gómez, R.M. Magnetocaloric effect: A review of the thermodynamic cycles in magnetic refrigeration. Renew. Sustain. Energy Rev. 2013, 17, 74–82. [Google Scholar] [CrossRef]
- Plaznik, U.; Tusek, J.; Kitanovski, A.; Poredoš, A. Numerical and experimental analyses of different magnetic thermodynamic cycles with an active magnetic regenerator. Appl. Therm. Eng. 2013, 59, 52–59. [Google Scholar] [CrossRef]
- You, Y.H.; Yu, S.; Tian, Y.Q.; Luo, X.; Huang, S. A numerical study on the unsteady heat transfer in active regenerator with multi-layer refrigerants of rotary magnetic refrigerator near room temperature. Int. J. Refrig. 2016, 65, 238–249. [Google Scholar] [CrossRef]
- You, Y.H.; Wu, Z.D.; Xiao, S.F.; Li, H.; Xu, X. A comprehensive two-dimensional numerical study on unsteady conjugate heat transfer in magnetic refrigerator with Gd plates. Int. J. Refrig. 2017, 79, 217–225. [Google Scholar] [CrossRef]
- You, Y.H.; Wu, Z.D.; Chen, P.A.; Ji, H.; Zeng, X.; Xu, X.; Dai, F. Improving magnetic refrigerator performances by enhancing convection heat transfer with staggered twin-wedged elements. Appl. Therm. Eng. 2018, 132, 423–431. [Google Scholar] [CrossRef]
- Vuarnoz, D.; Kawanami, T. Numerical analysis of a reciprocating active magnetic regenerator made of gadolinium wires. Appl. Therm. Eng. 2012, 37, 388–395. [Google Scholar] [CrossRef]
- Chen, Z.H.; Utaka, Y.; Tasaki, Y. Measurement and numerical simulation on the heat transfer characteristics of reciprocating flow in microchannels for the application in magnetic refrigeration. Appl. Therm. Eng. 2014, 65, 150–157. [Google Scholar] [CrossRef]
- Arnold, D.S.; Tura, A.; Ruebsaat-Trott, A.; Rowe, A. Design improvements of a permanent magnet active magnetic refrigerator. Int. J. Refrig. 2014, 37, 99–105. [Google Scholar] [CrossRef]
- Zimm, C.; Boeder, A.; Chell, J.; Sternberg, A.; Fujita, A.; Fujieda, S.; Fukamichi, K. Design and performance of a permanent magnet rotary refrigerator. Int. J. Refrig. 2006, 29, 1302–1306. [Google Scholar] [CrossRef]
- Lozano, J.A.; Engelbrecht, K.; Bahl, C.R.H.; Nielsen, K.K.; Barbosa, J.R., Jr.; Prata, A.T.; Pryds, N. Experimental and numerical results of a high frequency rotating active magnetic refrigerator. Int. J. Refrig. 2014, 37, 92–98. [Google Scholar] [CrossRef]
- Bahl, C.R.H.; Petersen, T.F.; Pryds, N.; Smith, A. A versatile magnetic refrigeration test device. Rev. Sci. Instrum. 2008, 79, 093906. [Google Scholar] [CrossRef] [PubMed]
- Tomc, U.; Tušek, J.; Kitanovski, A.; Poredoš, A. A numerical comparison of a parallel-plate AMR and a magnetocaloric device with embodied micro thermoelectric thermal diodes. Int. J. Refrig. 2014, 37, 185–193. [Google Scholar] [CrossRef]
- Qian, S.X.; Yuan, L.F.; Yu, J.L.; Yan, G. Variable load control strategy for room-temperature magnetocaloric cooling applications. Energy 2018, 153, 763–775. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A. An application of the artificial neural network to optimize the energy performances of a magnetic refrigerator. Int. J. Refrig. 2017, 82, 238–251. [Google Scholar] [CrossRef]
- Gschneidner, K.A., Jr.; Pecharsky, V.K. Review: Thirty years of near room temperature magnetic cooling: Where we are today and future prospects. Int. J. Refrig. 2008, 31, 945–961. [Google Scholar] [CrossRef]
- Yu, B.; Liu, M.; Egolf, P.W.; Kitanovski, A. A review of magnetic refrigerator and heat pump prototypes built before the year 2010. Int. J. Refrig. 2010, 33, 1029–1060. [Google Scholar] [CrossRef]
- Aprea, C.; Maiorino, A. A flexible numerical model to study an active magnetic refrigerator for near room temperature applications. Appl. Energy 2010, 87, 2690–2698. [Google Scholar] [CrossRef]
- Nielsen, K.K.; Bahl, C.R.H.; Smith, A.; Bjørk, R.; Pryds, N.; Hattel, J. Detailed numerical modeling of a linear parallel-plate Active Magnetic Regenerator. Int. J. Refrig. 2009, 32, 1478–1486. [Google Scholar] [CrossRef]
- Nielsen, K.K.; Tušek, J.; Engelbrecht, K.; Schopfer, S.; Kitanovski, A.; Bahl, C.R.H.; Smith, A.; Pryds, N.; Poredos, A. Review on numerical modeling of active magnetic regenerators for room temperature applications. Int. J. Refrig. 2011, 34, 603–616. [Google Scholar] [CrossRef]
- Tušek, J.; Kitanovski, A.; Poredoš, A. Geometrical optimization of packed-bed and parallel-plate active magnetic regenerators. Int. J. Refrig. 2013, 36, 1456–1464. [Google Scholar] [CrossRef]
- Kamran, M.S.; Ali, H.; Farhan, M.; Tang, Y.B.; Chen, Y.G.; Wang, H.S. Performance optimization of room temperature magnetic refrigerator with layered/multi-material microchannel regenerators. Int. J. Refrig. 2016, 68, 94–106. [Google Scholar] [CrossRef]
- Monfared, B. Design and optimization of regenerators of a rotary magnetic refrigeration device using a detailed simulation model. Int. J. Refrig. 2018, 88, 260–274. [Google Scholar] [CrossRef]
- Teyber, R.; Trevizoli, P.V.; Christiaanse, T.V.; Govindappa, P.; Niknia, I.; Rowe, A. Semi-analytic AMR element model. Appl. Therm. Eng. 2018, 128, 1022–1029. [Google Scholar] [CrossRef]
- Bejan, A. Method of entropy generation minimization, or modeling and optimization based on combined heat transfer and thermodynamics. Rev. Gen. Therm. 1996, 35, 637–646. [Google Scholar] [CrossRef]
- Cheng, X.T.; Liang, X.G. Discussion on the applicability of entropy generation minimization to the analyses and optimizations of thermodynamic processes. Energy Convers. Manag. 2013, 73, 121–127. [Google Scholar] [CrossRef]
- Turkakar, G.; Ozyurt, T.O. Entropy generation analysis and dimensional optimization of an evaporator for use in a microscale refrigeration cycle. Int. J. Refrig. 2015, 56, 140–153. [Google Scholar] [CrossRef]
- You, Y.H.; Fan, A.W.; Liang, Y.M.; Jin, S.; Liu, W.; Daia, F. Entropy generation analysis for laminar thermal augmentation with conical strip inserts in horizontal circular tubes. Int. J. Therm. Sci. 2015, 88, 201–214. [Google Scholar] [CrossRef]
- Rowe, A.M.; Barclay, J.A. Ideal magnetocaloric effect for active magnetic regenerators. J. Appl. Phys. 2003, 93, 1672–1676. [Google Scholar] [CrossRef]
- Li, P.; Gong, M.; Wu, J. Geometric optimization of an active magnetic regenerative refrigerator via second-law analysis. J. Appl. Phys. 2008, 104, 103536. [Google Scholar] [CrossRef]
- Lei, T.; Engelbrecht, K.; Nielsen, K.K.; Veje, C.T. Study of geometries of active magnetic regenerators for room temperature magnetocaloric refrigeration. Appl. Therm. Eng. 2017, 111, 1232–1243. [Google Scholar] [CrossRef]
- Trevizoli, P.V.; Alcalde, D.P.; Barbosa, J.R., Jr. Second law optimization of regenerative geometries for magnetic cooling applications. In Proceedings of the 6th International Conference on Magnetic Refrigeration, Victoria, BC, Canada, 7–10 September 2014. [Google Scholar]
- Morrish, A.H. The Physical Principles of Magnetism; Wiley Inc.: New York, NY, USA, 1965. [Google Scholar]
- Petersen, T.F.; Pryds, N.; Smith, A.; Hattel, J.; Schmidt, H.; Knudsen, H.H. Two-dimensional mathematical model of a reciprocating room-temperature Active Magnetic Regenerator. Int. J. Refrig. 2008, 31, 432–443. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, Y.; Wu, Z.; Yang, Y.; Yu, J.; Zhang, D.; Zhang, Z. Refrigeration Performance and Entropy Generation Analysis for Reciprocating Magnetic Refrigerator with Gd Plates. Entropy 2018, 20, 427. https://doi.org/10.3390/e20060427
You Y, Wu Z, Yang Y, Yu J, Zhang D, Zhang Z. Refrigeration Performance and Entropy Generation Analysis for Reciprocating Magnetic Refrigerator with Gd Plates. Entropy. 2018; 20(6):427. https://doi.org/10.3390/e20060427
Chicago/Turabian StyleYou, Yonghua, Zhongda Wu, Yong Yang, Jie Yu, Dong Zhang, and Zhuang Zhang. 2018. "Refrigeration Performance and Entropy Generation Analysis for Reciprocating Magnetic Refrigerator with Gd Plates" Entropy 20, no. 6: 427. https://doi.org/10.3390/e20060427
APA StyleYou, Y., Wu, Z., Yang, Y., Yu, J., Zhang, D., & Zhang, Z. (2018). Refrigeration Performance and Entropy Generation Analysis for Reciprocating Magnetic Refrigerator with Gd Plates. Entropy, 20(6), 427. https://doi.org/10.3390/e20060427




