A Forward-Reverse Brascamp-Lieb Inequality: Entropic Duality and Gaussian Optimality
Abstract
:1. Introduction
- For all nonnegative functions g and such that:we have:
- For all nonnegative measurable functions and f such that:we have:
- (i)
- m and l are positive integers; , is a compact metric space;
- (ii)
- , is a finite Borel measure on a Polish space , and is a random transformation from to , for each ;
- (iii)
- , is a finite Borel measure on a Polish space , and is a random transformation from to , for each ;
- (iv)
- For any such that , there exists such that , and , where , .
- 1.
- If the nonnegative continuous functions , are bounded away from zero and satisfy:then:
- 2.
- For any such that (of course, this assumption is not essential (if we adopt the convention that the infimum in (14) is when it runs over an empty set)), ,where , , and the infimum is over such that , .
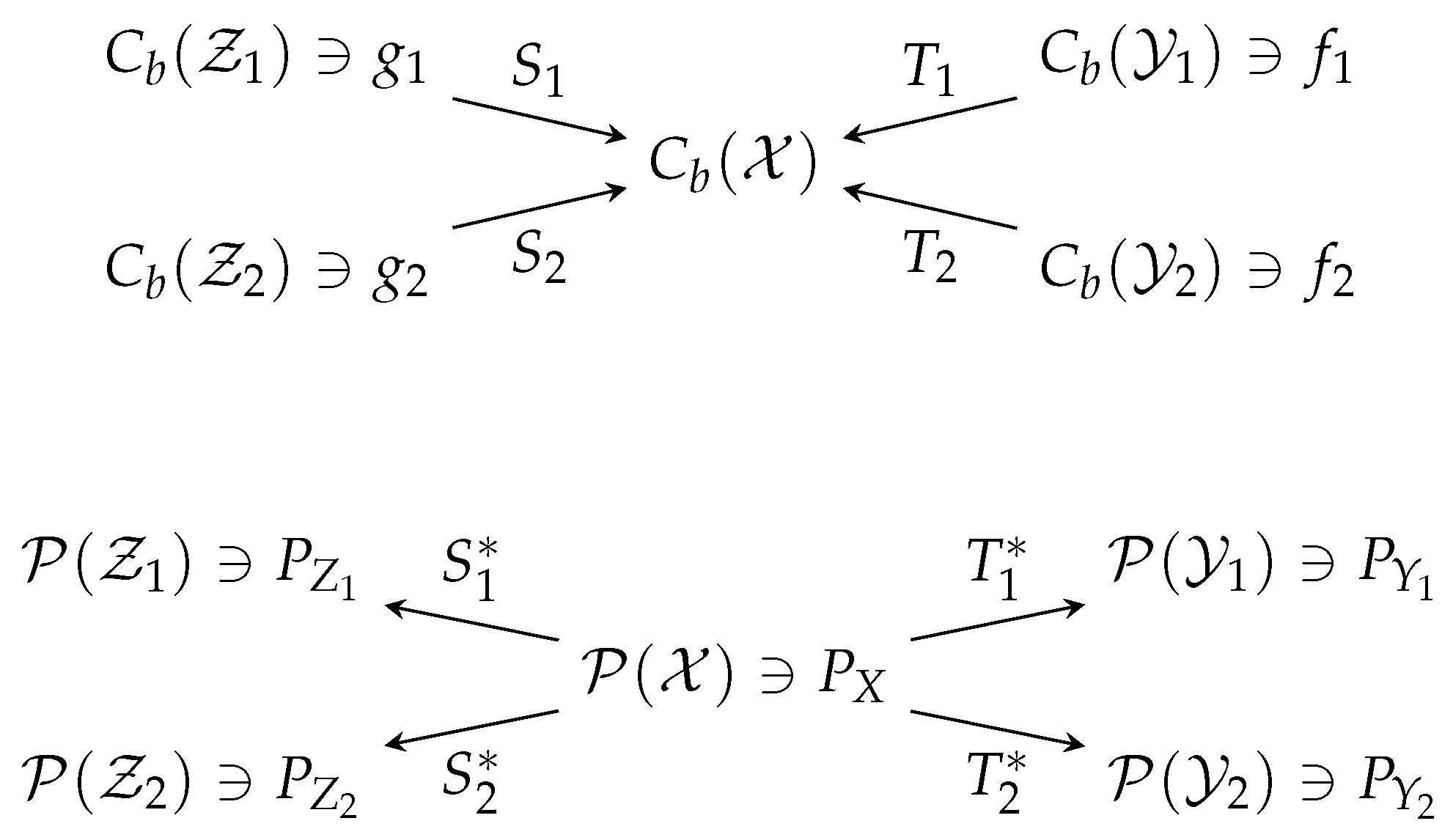
2. Review of the Legendre-Fenchel Duality Theory
- denotes the space of continuous functions on with a compact support;
- denotes the space of all continuous functions f on that vanish at infinity (i.e., for any , there exists a compact set such that for );
- denotes the space of bounded continuous functions on ;
- denotes the space of finite signed Borel measures on ;
- denotes the space of probability measures on .
- is called a canonical map, whose action is almost trivial: it sends a function of to itself, but viewed as a function of .
- is called marginalization, which simply takes a joint distribution to a marginal distribution.
- 1.
- If the interior of C is non-empty, then there exists , such that:
- 2.
- If A is locally convex, B is compact and C is closed, then there exists such that:
3. The Entropic-Functional Duality
3.1. Compact
- 1)⇒2)
- This is the nontrivial direction, which relies on certain (strong) min-max type results. In Theorem 4, put (in (36), means that u is pointwise non-positive):Then,For each , set:where the infimum is over such that ; if there is no such v, then as a convention. Observe that:
- is convex: indeed, given arbitrary and , suppose that and respectively achieve the infimum in (38) for and (if the infimum is not achievable, the argument still goes through by the approximation and limit argument). Then, for any , satisfies where . Thus, the convexity of follows from the convexity of the functional in (23);
- for any . Otherwise, for any and , we have:which contradicts the assumption that in the theorem;
- From Steps (39)–(41), we see for any , where the definition of is extended using the Donsker-Varadhan formula (that is, it is infinite when the argument is not a probability measure).
Finally, for the given , choose:Notice that:- is convex;
- is well defined (that is, the choice of in (43) is inconsequential). Indeed, if is such that , then:where is such that , , whose existence is guaranteed by the assumption of the theorem. This also shows that .
Invoking Theorem 4 (where the in Theorem 4 can be chosen as the constant function , ):where denotes the collection of the functions , and similarly for . Note that the left side of (46) is exactly the right side of (14). For any , choose , and , such that and:Now, invoking (13) with , and , , we upper bound the left side of (47) by:where the last step follows by the Donsker-Varadhan formula. Therefore, (14) is established since is arbitrary. - 2)⇒1)
- Since is finite and is bounded by assumption, we have , . Moreover, (13) is trivially true when for some i, so we will assume below that for each i. Define by:Then, for any ,where:
- (51) uses the Donsker-Varadhan formula, and we have chosen , , such that:
- (52) also follows from the Donsker-Varadhan formula.
The result follows since can be arbitrary.☐
- For any such that , , there exists such that for each i and for each j.
- 1.
- For any nonnegative continuous functions , bounded away from zero and such that:we have:
- 2.
- For any such that , ,
- To see (67), we note that the sup in (66) can be restricted to , which is a probability measure, since otherwise, the relative entropy terms in (66) are by its definition via the Donsker-Varadhan formula. Then, we select such that (67) holds.
- In (68), we have chosen such that:and then applied the assumption (54). The result follows since can be arbitrary.☐
3.2. Noncompact
- The assumption that is a compact metric space is relaxed to the assumption that it is a locally compact and σ-compact Polish space;
- and , are canonical maps (see Definition 2).
4. Gaussian Optimality
4.1. Non-Degenerate Forward Channels
- Fix Lebesgue measures and Gaussian measures on ;
- non-degenerate (Definition 3 below) linear Gaussian random transformation (where ) associated with conditional expectation operators ;
- are induced by coordinate projections;
- positive and .
- 1.
- For any , the infimum in (75) is attained by some Borel .
- 2.
- If are non-degenerate (Definition 3), then the supremum in (76) is achieved by some Borel .
- Assume that and are maximizers of (possibly equal). Let . Define:Define and analogously. Then, is independent of , and is independent of .
- Next, we perform the same algebraic expansion as in the proof of tensorization:where:
- (84) uses Lemma 1.
- (86) is because of the Markov chain (for any coupling).
- In (87), we selected a particular instance of coupling , constructed as follows: first, we select an optimal coupling for given marginals . Then, for any , let be an optimal coupling of (for a justification that we can select optimal coupling in a way that is indeed a regular conditional probability distribution, see [7]). With this construction, it is apparent that , and hence:
- (88) is because in the above, we have constructed the coupling optimally.
- (89) is because maximizes , .
- Thus, in the expansions above, equalities are attained throughout. Using the differentiation technique as in the case of forward inequality, for almost all , , we have:where (92) is because by symmetry, we can perform the algebraic expansions in a different way to show that is also a maximizer of . Then, , which, combined with , shows that and are Gaussian with the same covariance. Lastly, using Lemma 1 and the doubling trick, one can show that the optimal coupling is also Gaussian.☐
4.2. Analysis of Example 1 Using Gaussian Optimality
- There exists such that for every ,which follows by continuity and the fact that when is uniform, the sup (97) is achieved at the strictly positive definite .
- When is the uniform probability vector, (96) equals one, which is uniquely achieved by . To see the uniqueness, take to be diagonal in the denominator and observe that the denominator is strictly bigger than the numerator when the diagonals of are not a permutation of . Then, since the extreme value of a continuous functions is achieved on a compact set, we can find such that:for any .
- Finally, by continuity, we can choose small enough such that for any ,
5. Relation to Hypercontractivity and Its Reverses
5.1. Hypercontractivity
5.2. Reverse Hypercontractivity (Positive Parameters)
5.3. Reverse Hypercontractivity (One Negative Parameter)
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Recovering Theorem 1 from Theorem 6 as a Special Case
Appendix B. Existence of Weakly-Convergent Couplings
Appendix C. Upper Semicontinuity of the Infimum
Appendix D. Weak Semicontinuity of Differential Entropy under a Moment Constraint
Appendix E. Proof of Proposition 2
- For any , by the continuity of measure, there exists such that:By the union bound,wherever is a coupling of . Now, let , be such that:where , . The sequence is tight by (A23). Thus, invoking the Prokhorov theorem and by passing to a subsequence, we may assume that converges weakly to some . Therefore, converges to weakly, and by the semicontinuity property in Lemma A2, we have:establishing that is an infimizer.
- Suppose is such that , , where is as in Proposition 1 and:The regularization on the covariance implies that for each i, is a tight sequence. Thus, upon the extraction of subsequences, we may assume that for each i, converges to some . We have the moment bound:where and . Then, by Lemma A2,Under the covariance regularization and the nondegenerateness assumption, we showed in Proposition 1 that the value of (76) cannot be or . This implies that we can assume (by passing to a subsequence) that , , since otherwise . Moreover, since is bounded above under the nondegenerateness assumption, the sequence must also be bounded from above, which implies, using (A30), that:In particular, we have for each i. Now, Corollary A1 shows that:Thus, (A30) and (A32) show that is in fact a maximizer.
Appendix F. Gaussian Optimality in Degenerate Cases: A Limiting Argument
Appendix F.1. Proof of the Claim in Example 1
Appendix F.2. Proof of Theorem 2
References
- Brascamp, H.J.; Lieb, E.H. Best constants in Young’s inequality, its converse, and its generalization to more than three functions. Adv. Math. 1976, 20, 151–173. [Google Scholar] [CrossRef]
- Brascamp, H.J.; Lieb, E.H. On extensions of the Brunn-Minkowski and Prékopa-Leindler theorems, including inequalities for log concave functions, and with an application to the diffusion equation. J. Funct. Anal. 1976, 22, 366–389. [Google Scholar] [CrossRef]
- Bobkov, S.G.; Ledoux, M. From Brunn-Minkowski to Brascamp-Lieb and to logarithmic Sobolev inequalities. Geom. Funct. Anal. 2000, 10, 1028–1052. [Google Scholar] [CrossRef]
- Cordero-Erausquin, D. Transport inequalities for log-concave measures, quantitative forms and applications. arXiv, 2015; arXiv:1504.06147. [Google Scholar]
- Barthe, F. On a reverse form of the Brascamp-Lieb inequality. Invent. Math. 1998, 134, 335–361. [Google Scholar] [CrossRef]
- Bennett, J.; Carbery, A.; Christ, M.; Tao, T. The Brascamp-Lieb inequalities: finiteness, structure and extremals. Geom. Funct. Anal. 2008, 17, 1343–1415. [Google Scholar] [CrossRef]
- Liu, J.; Courtade, T.A.; Cuff, P.; Verdú, S. Information theoretic perspectives on Brascamp-Lieb inequality and its reverse. arXiv, 2017; arXiv:1702.06260. [Google Scholar]
- Gardner, R. The Brunn-Minkowski inequality. Bull. Am. Math. Soc. 2002, 39, 355–405. [Google Scholar] [CrossRef]
- Gross, L. Logarithmic Sobolev inequalities. Am. J. Math. 1975, 97, 1061–1083. [Google Scholar] [CrossRef]
- Erkip, E.; Cover, T.M. The efficiency of investment information. IEEE Trans. Inf. Theory Mar. 1998, 44, 1026–1040. [Google Scholar] [CrossRef]
- Courtade, T. Outer bounds for multiterminal source coding via a strong data processing inequality. In Proceedings of the IEEE International Symposium on Information Theory, Istanbul, Turkey, 7–12 July 2013; pp. 559–563. [Google Scholar]
- Polyanskiy, Y.; Wu, Y. Dissipation of information in channels with input constraints. IEEE Trans. Inf. Theory 2016, 62, 35–55. [Google Scholar] [CrossRef]
- Polyanskiy, Y.; Wu, Y. A Note on the Strong Data-Processing Inequalities in Bayesian Networks. Available online: http://arxiv.org/pdf/1508.06025v1.pdf (accessed on 25 August 2015).
- Liu, J.; Cuff, P.; Verdú, S. Key capacity for product sources with application to stationary Gaussian processes. IEEE Trans. Inf. Theory 2016, 62, 984–1005. [Google Scholar]
- Liu, J.; Cuff, P.; Verdú, S. Secret key generation with one communicator and a one-shot converse via hypercontractivity. In Proceedings of the IEEE International Symposium on Information Theory, Hong Kong, China, 14–19 June 2015; pp. 710–714. [Google Scholar]
- Xu, A.; Raginsky, M. Converses for distributed estimation via strong data processing inequalities. In Proceedings of the IEEE International Symposium on Information Theory, Hong Kong, China, 14–19 June 2015; pp. 2376–2380. [Google Scholar]
- Kamath, S.; Anantharam, V. On non-interactive simulation of joint distributions. arXiv, 2015; arXiv:1505.00769. [Google Scholar]
- Kahn, J.; Kalai, G.; Linial, N. The influence of variables on Boolean functions. In Proceedings of the 29th Annual Symposium on Foundations of Computer Science, White Plains, NY, USA, 24–26 October 1988; pp. 68–80. [Google Scholar]
- Ganor, A.; Kol, G.; Raz, R. Exponential separation of information and communication. In Proceedings of the 2014 IEEE 55th Annual Symposium on Foundations of Computer Science (FOCS), Philadelphia, PA, USA, 18–21 Otctober 2014; pp. 176–185. [Google Scholar]
- Dvir, Z.; Hu, G. Sylvester-Gallai for arrangements of subspaces. arXiv, 2014; arXiv:1412.0795. [Google Scholar]
- Braverman, M.; Garg, A.; Ma, T.; Nguyen, H.L.; Woodruff, D.P. Communication lower bounds for statistical estimation problems via a distributed data processing inequality. arXiv, 2015; arXiv:1506.07216. [Google Scholar]
- Garg, A.; Gurvits, L.; Oliveira, R.; Wigderson, A. Algorithmic aspects of Brascamp-Lieb inequalities. arXiv, 2016; arXiv:1607.06711. [Google Scholar]
- Talagrand, M. On Russo’s approximate zero-one law. Ann. Probab. 1994, 22, 1576–1587. [Google Scholar] [CrossRef]
- Friedgut, E.; Kalai, G.; Naor, A. Boolean functions whose Fourier transform is concentrated on the first two levels. Adv. Appl. Math. 2002, 29, 427–437. [Google Scholar] [CrossRef]
- Bourgain, J. On the distribution of the Fourier spectrum of Boolean functions. Isr. J. Math. 2002, 131, 269–276. [Google Scholar] [CrossRef]
- Mossel, E.; O’Donnell, R.; Oleszkiewicz, K. Noise stability of functions with low influences: Invariance and optimality. Ann. Math. 2010, 171, 295–341. [Google Scholar] [CrossRef]
- Garban, C.; Pete, G.; Schramm, O. The Fourier spectrum of critical percolation. Acta Math. 2010, 205, 19–104. [Google Scholar] [CrossRef]
- Duchi, J.C.; Jordan, M.; Wainwright, M.J. Local privacy and statistical minimax rates. In Proceedings of the IEEE 54th Annual Symposium on Foundations of Computer Science (FOCS), Berkeley, CA, USA, 26–29 October 2013; pp. 429–438. [Google Scholar]
- Lieb, E.H. Gaussian kernels have only Gaussian maximizers. Invent. Math. 1990, 102, 179–208. [Google Scholar] [CrossRef]
- Barthe, F. Optimal Young’s inequality and its converse: A simple proof. Geom. Funct. Anal. 1998, 8, 234–242. [Google Scholar] [CrossRef]
- Barthe, F.; Cordero-Erausquin, D. Inverse Brascamp-Lieb inequalities along the Heat equation. In Geometric Aspects of Functional Analysis; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 2004; Volume 1850, pp. 65–71. [Google Scholar]
- Carlen, E.A.; Cordero-Erausquin, D. Subadditivity of the entropy and its relation to Brascamp-Lieb type inequalities. Geom. Funct. Anal. 2009, 19, 373–405. [Google Scholar] [CrossRef]
- Barthe, F.; Cordero-Erausquin, D.; Ledoux, M.; Maurey, B. Correlation and Brascamp-Lieb inequalities for Markov semigroups. Int. Math. Res. Notices 2011, 2011, 2177–2216. [Google Scholar] [CrossRef]
- Lehec, J. Short probabilistic proof of the Brascamp-Lieb and Barthe theorems. Can. Math. Bull. 2014, 57, 585–587. [Google Scholar] [CrossRef]
- Ball, K. Volumes of sections of cubes and related problems. In Geometric Aspects of Functional Analysis; Springer: Berlin/Heidelberg, Germany, 1989; pp. 251–260. [Google Scholar]
- Ahlswede, R.; Gács, P. Spreading of sets in product spaces and hypercontraction of the Markov operator. Ann. Probab. 1976, 4, 925–939. [Google Scholar] [CrossRef]
- Csiszár, I.; Körner, J. Information Theory: Coding Theorems for Discrete Memoryless Systems, 2nd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Liu, J.; van Handel, R.; Verdú, S. Beyond the Blowing-Up Lemma: Sharp Converses via Reverse Hypercontractivity. In Proceedings of the IEEE International Symposium on Information Theory, Aachen, Germany, 25–30 June 2017; pp. 943–947. [Google Scholar]
- Ahlswede, R.; Gács, P.; Körner, J. Bounds on conditional probabilities with applications in multi-user communication. Probab. Theory Relat. Fields 1976, 34, 157–177. [Google Scholar] [CrossRef]
- Villani, C. Topics in Optimal Transportation; American Mathematical Soc.: Providence, RI, USA, 2003; Volume 58. [Google Scholar]
- Atar, R.; Merhav, N. Information-theoretic applications of the logarithmic probability comparison bound. IEEE Trans. Inf. Theory 2015, 61, 5366–5386. [Google Scholar] [CrossRef]
- Radhakrishnan, J. Entropy and counting. In Kharagpur Golden Jubilee Volume; Narosa: New Delhi, India, 2001. [Google Scholar]
- Madiman, M.M.; Tetali, P. Information inequalities for joint distributions, with interpretations and applications. IEEE Trans. Inf. Theory 2010, 56, 2699–2713. [Google Scholar] [CrossRef]
- Nair, C. Equivalent Formulations of Hypercontractivity Using Information Measures; International Zurich Seminar: Zurich, Switzerland, 2014. [Google Scholar]
- Beigi, S.; Nair, C. Equivalent characterization of reverse Brascamp-Lieb type inequalities using information measures. In Proceedings of the IEEE International Symposium on Information Theory, Barcelona, Spain, 10–15 July 2016. [Google Scholar]
- Bobkov, S.G.; Götze, F. Exponential integrability and transportation cost related to Logarithmic Sobolev inequalities. J. Funct. Anal. 1999, 163, 1–28. [Google Scholar] [CrossRef]
- Carlen, E.A.; Lieb, E.H.; Loss, M. A sharp analog of Young’s inequality on SN and related entropy inequalities. J. Geom. Anal. 2004, 14, 487–520. [Google Scholar] [CrossRef]
- Geng, Y.; Nair, C. The capacity region of the two-receiver Gaussian vector broadcast channel with private and common messages. IEEE Trans. Inf. Theory 2014, 60, 2087–2104. [Google Scholar] [CrossRef]
- Liu, J.; Courtade, T.A.; Cuff, P.; Verdú, S. Brascamp-Lieb inequality and its reverse: An information theoretic view. In Proceedings of the IEEE International Symposium on Information Theory, Barcelona, Spain, 10–15 July 2016; pp. 1048–1052. [Google Scholar]
- Lax, P.D. Functional Analysis; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Tao, T. 245B, Notes 12: Continuous Functions on Locally Compact Hausdorff Spaces. Available online: https://terrytao.wordpress.com/2009/03/02/245b-notes-12-continuous-functions-on-locally-compact-hausdorff-spaces/ (accessed on 2 March 2009).
- Bourbaki, N. Intégration; (Chaps. I-IV, Actualités Scientifiques et Industrielles, no. 1175); Hermann: Paris, France, 1952. [Google Scholar]
- Dembo, A.; Zeitouni, O. Large Deviations Techniques and Applications; Springer: Berlin, Germany, 2009; Volume 38. [Google Scholar]
- Lane, S.M. Categories for the Working Mathematician; Springer: New York, NY, USA, 1978. [Google Scholar]
- Hatcher, A. Algebraic Topology; Tsinghua University Press: Beijing, China, 2002. [Google Scholar]
- Rockafellar, R.T. Convex Analysis; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Prokhorov, Y.V. Convergence of random processes and limit theorems in probability theory. Theory Probab. Its Appl. 1956, 1, 157–214. [Google Scholar] [CrossRef]
- Verdú, S. Information Theory; In preparation; 2018. [Google Scholar]
- Kamath, S. Reverse hypercontractivity using information measures. In Proceedings of the 53rd Annual Allerton Conference on Communications, Control and Computing, Champaign, IL, USA, 30 September–2 October 2015; pp. 627–633. [Google Scholar]
- Wu, Y.; Verdú, S. Functional properties of minimum mean-square error and mutual information. IEEE Trans. Inf. Theory 2012, 58, 1289–1301. [Google Scholar] [CrossRef]
- Godavarti, M.; Hero, A. Convergence of differential entropies. IEEE Trans. Inf. Theory 2004, 50, 171–176. [Google Scholar] [CrossRef]

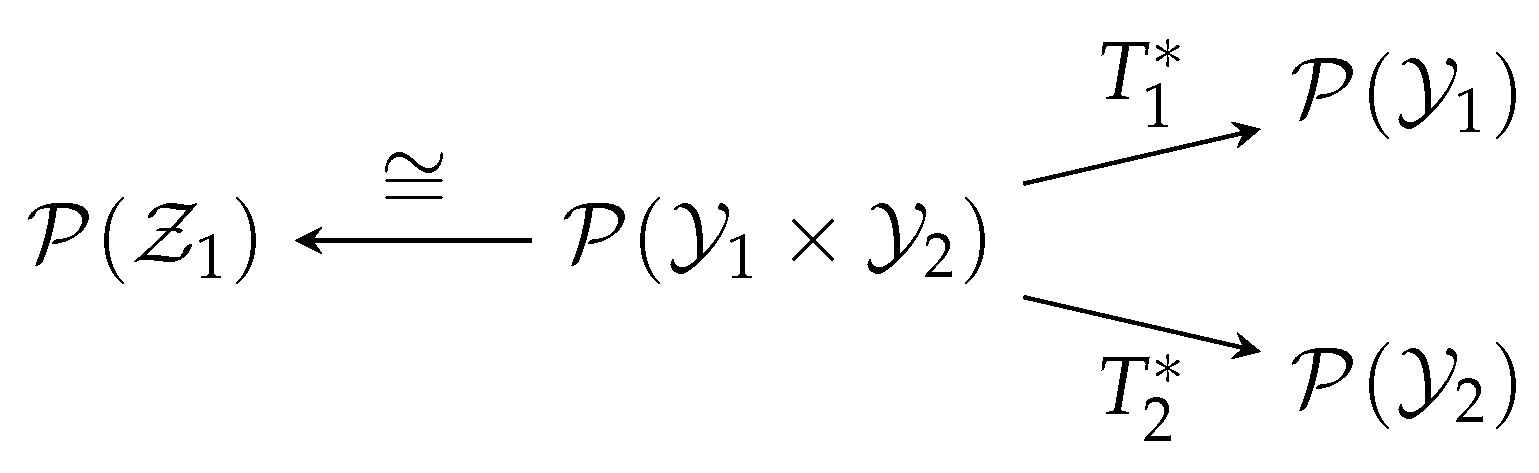
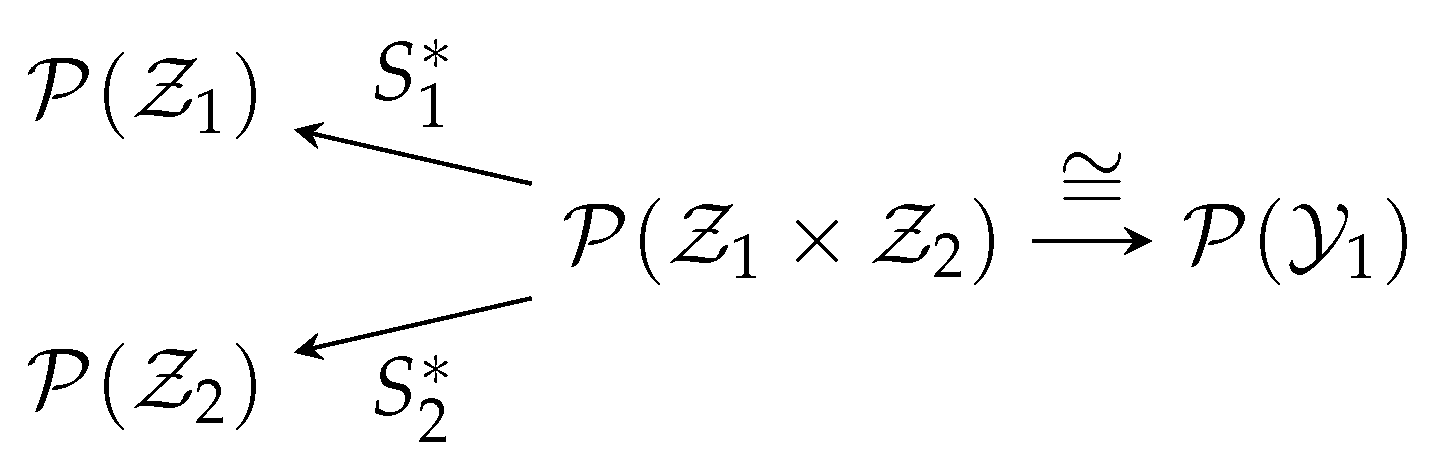
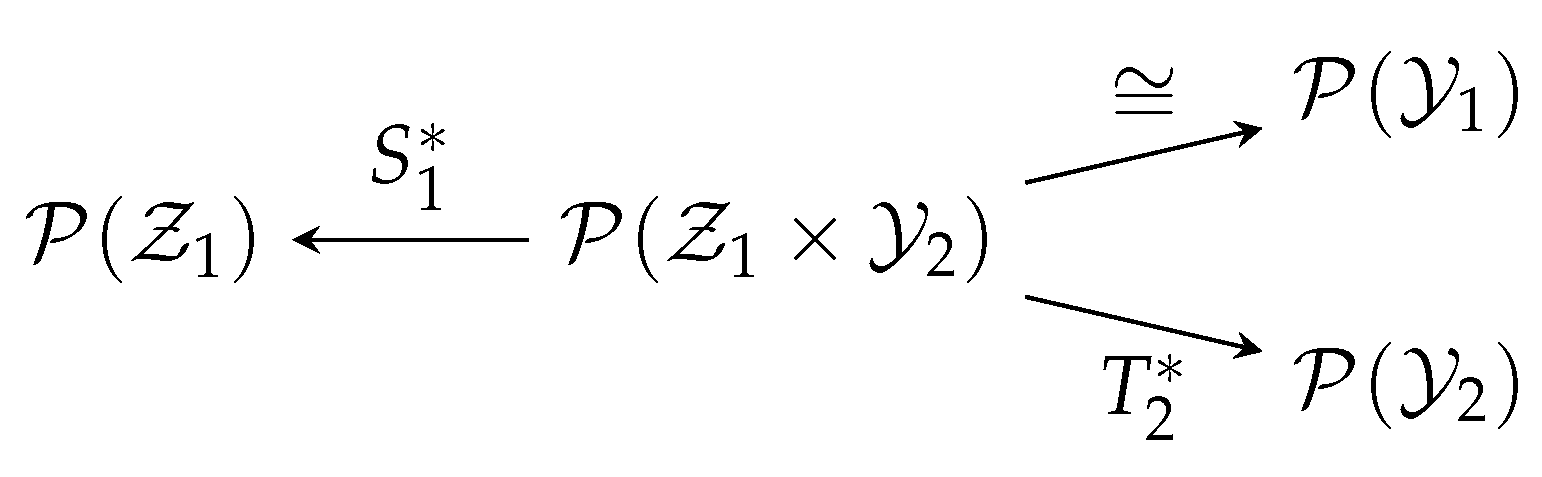
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Courtade, T.A.; Cuff, P.W.; Verdú, S. A Forward-Reverse Brascamp-Lieb Inequality: Entropic Duality and Gaussian Optimality. Entropy 2018, 20, 418. https://doi.org/10.3390/e20060418
Liu J, Courtade TA, Cuff PW, Verdú S. A Forward-Reverse Brascamp-Lieb Inequality: Entropic Duality and Gaussian Optimality. Entropy. 2018; 20(6):418. https://doi.org/10.3390/e20060418
Chicago/Turabian StyleLiu, Jingbo, Thomas A. Courtade, Paul W. Cuff, and Sergio Verdú. 2018. "A Forward-Reverse Brascamp-Lieb Inequality: Entropic Duality and Gaussian Optimality" Entropy 20, no. 6: 418. https://doi.org/10.3390/e20060418
APA StyleLiu, J., Courtade, T. A., Cuff, P. W., & Verdú, S. (2018). A Forward-Reverse Brascamp-Lieb Inequality: Entropic Duality and Gaussian Optimality. Entropy, 20(6), 418. https://doi.org/10.3390/e20060418



