A New Class of Retrocausal Models
Abstract
:1. Introduction
2. Conceptual Framework
3. Constrained Classical Fields
3.1. Classical Photons
3.2. Simple Model Example
- The a priori probability distribution on each unknown field intensity is given by Equation (1)—to be updated for any given experiment.
- The unknown field values are further constrained to be equal as pairs, .
- is non-negligible because it accompanies a known “photon”.
- The probability of each diagram is given by , or equivalently, .
3.3. Discussion
4. Averaged Fields and Weak Values
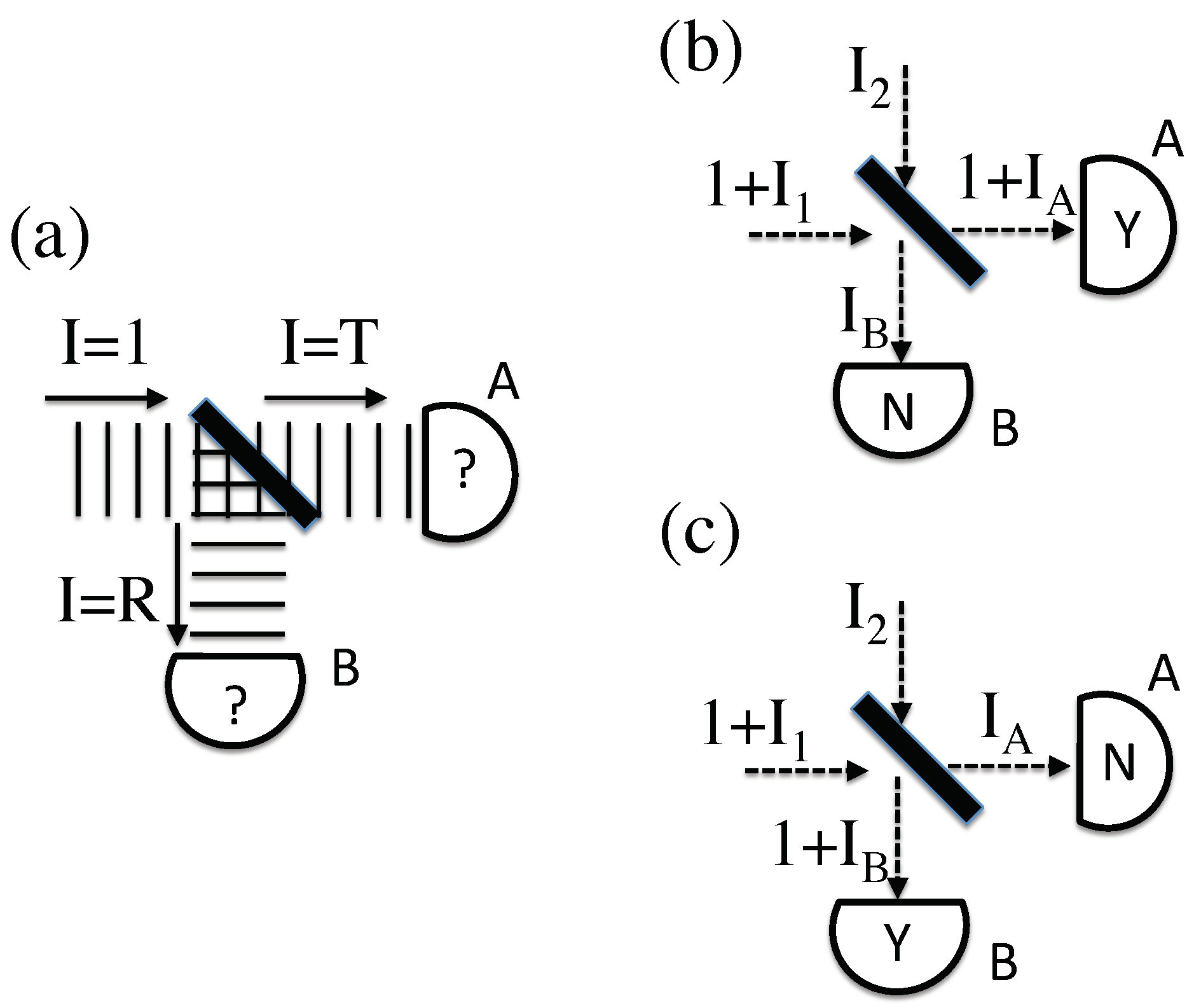
4.1. Beamsplitter Analysis
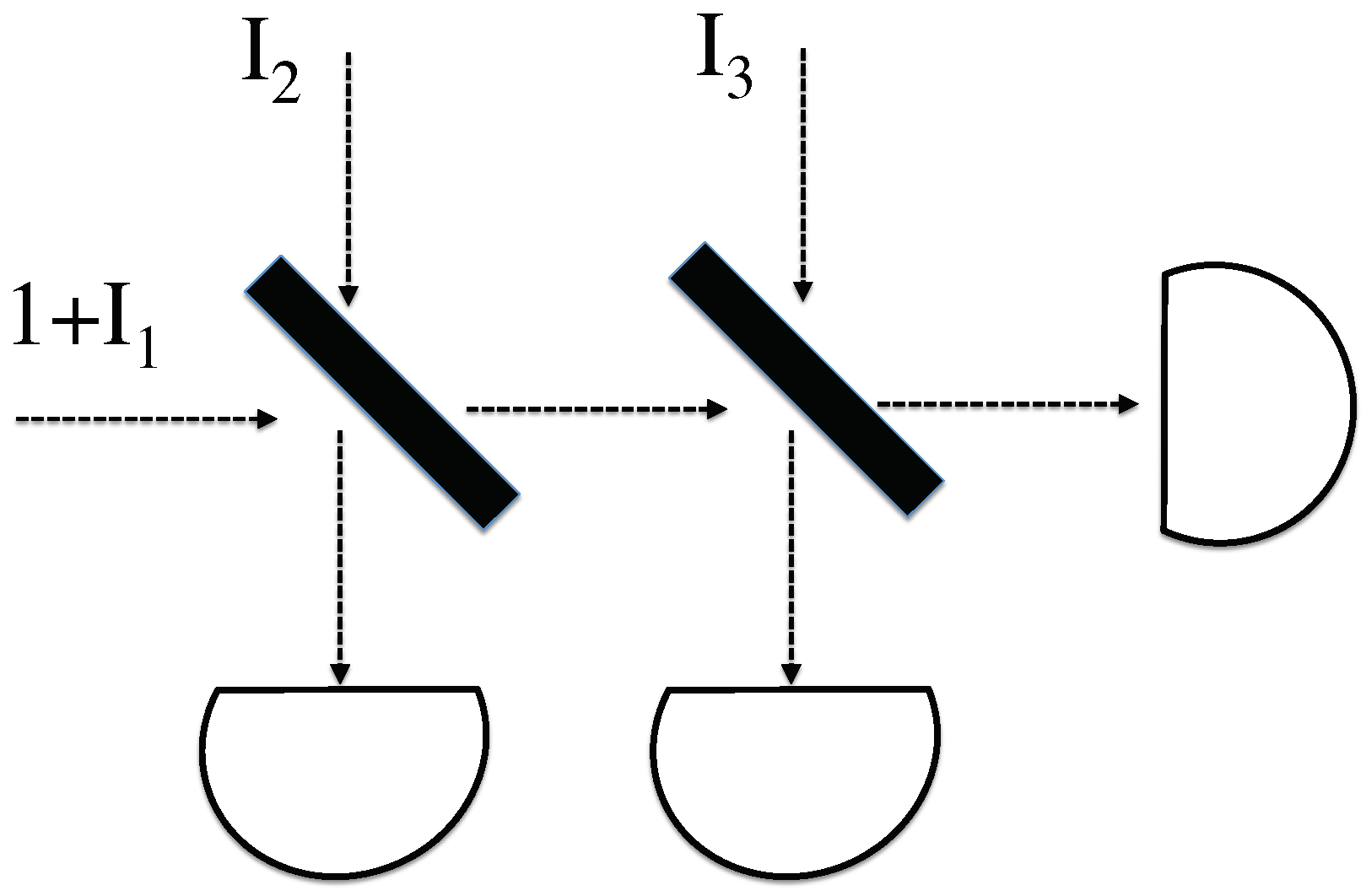
4.2. Interferometer Analysis
4.3. Weak Values
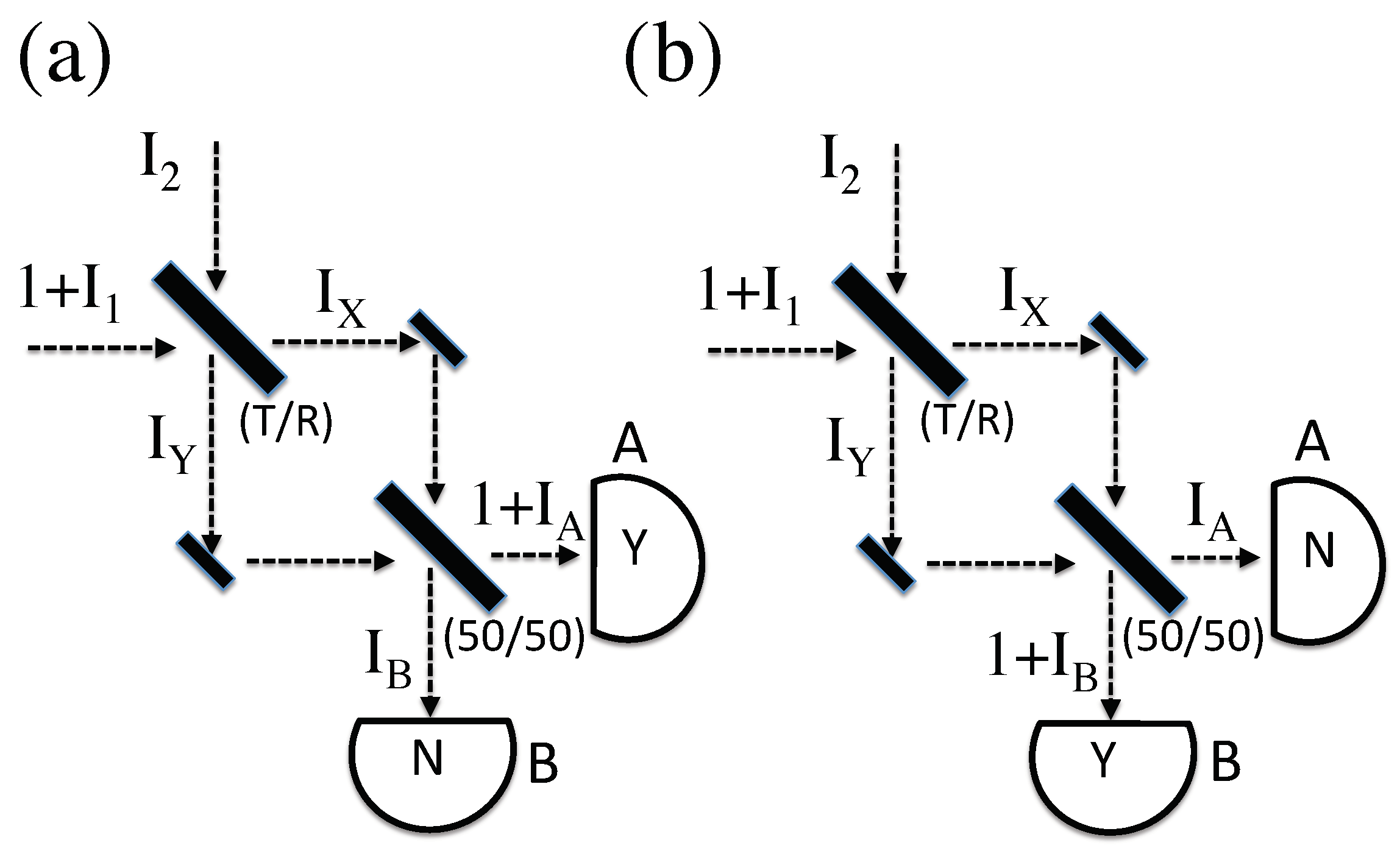
5. An Improved Model
- The unknown field values are constrained to all be equal: .
- The probability distribution on each unknown field intensity is given by Equation (22)—but must be updated for any given experiment.
- The relative phase between the incoming fields is a priori completely unknown—but must be updated for any given experiment.
6. Summary and Future Directions
- Distributed classical fields can be consistent with particle-like detection events.
- There exist simple constraints and a priori field intensity distributions that yield the correct probabilities for basic experimental geometries.
- Most unobserved field modes are expected to have zero intensity (unlike in SED).
- The usual retrocausal account for maximally entangled photons still seems to be available.
- The average intermediate field values, minus the unobserved background, is precisely equal to the “weak value” predicted by quantum theory (in the cases considered so far).
- Negative weak values can have a classical interpretation, provided the unobserved background is sufficiently large.
Acknowledgments
Conflicts of Interest
References
- Sutherland, R.I. Bell’s theorem and backwards-in-time causality. Int. J. Theor. Phys. 1983, 22, 377–384. [Google Scholar] [CrossRef]
- Price, H. Time’s Arrow & Archimedes’ Point: New Directions for the Physics of Time; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Wharton, K. Quantum states as ordinary information. Information 2014, 5, 190–208. [Google Scholar] [CrossRef]
- Price, H.; Wharton, K. Disentangling the quantum world. Entropy 2015, 17, 7752–7767. [Google Scholar] [CrossRef]
- Leifer, M.S.; Pusey, M.F. Is a time symmetric interpretation of quantum theory possible without retrocausality? Proc. R. Soc. A 2017, 473, 20160607. [Google Scholar] [CrossRef] [PubMed]
- Adlam, E. Spooky Action at a Temporal Distance. Entropy 2018, 20, 41. [Google Scholar] [CrossRef]
- Argaman, N. Bell’s theorem and the causal arrow of time. Am. J. Phys. 2010, 78, 1007–1013. [Google Scholar] [CrossRef]
- Almada, D.; Ch’ng, K.; Kintner, S.; Morrison, B.; Wharton, K. Are Retrocausal Accounts of Entanglement Unnaturally Fine-Tuned? Int. J. Quantum Found. 2016, 2, 1–14. [Google Scholar]
- Weinstein, S. Learning the Einstein-Podolsky-Rosen correlations on a Restricted Boltzmann Machine. arXiv, 2017; arXiv:1707.03114. [Google Scholar]
- Sen, I. A local ψ-epistemic retrocasual hidden-variable model of Bell correlations with wavefunctions in physical space. arXiv, 2018; arXiv:1803.06458. [Google Scholar]
- Sutherland, R.I. Lagrangian Description for Particle Interpretations of Quantum Mechanics: Entangled Many-Particle Case. Found. Phys. 2017, 47, 174–207. [Google Scholar] [CrossRef]
- Bohm, D.; Hiley, B.J.; Kaloyerou, P.N. An ontological basis for the quantum theory. Phys. Rep. 1987, 144, 321–375. [Google Scholar] [CrossRef]
- Kaloyerou, P. The GRA beam-splitter experiments and particle-wave duality of light. J. Phys. A 2006, 39, 11541. [Google Scholar] [CrossRef]
- Aharonov, Y.; Albert, D.Z.; Vaidman, L. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett. 1988, 60, 1351. [Google Scholar] [CrossRef] [PubMed]
- Dressel, J.; Malik, M.; Miatto, F.M.; Jordan, A.N.; Boyd, R.W. Colloquium: Understanding quantum weak values: Basics and applications. Rev. Mod. Phys. 2014, 86, 307. [Google Scholar] [CrossRef]
- Boyer, T.H. A brief survey of stochastic electrodynamics. In Foundations of Radiation Theory and Quantum Electrodynamics; Springer: Berlin/Heidelberg, Germany, 1980; pp. 49–63. [Google Scholar]
- De La Pena, L.; Cetto, A.M. The qUantum Dice: An Introduction to Stochastic Electrodynamics; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Woodward, J. Making Things Happen: A Theory of Causal Explanation; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Price, H. Agency and probabilistic causality. Br. J. Philos. Sci. 1991, 42, 157–176. [Google Scholar] [CrossRef]
- Pearl, J. Causality; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Menzies, P.; Price, H. Causation as a secondary quality. Br. J. Philos. Sci. 1993, 44, 187–203. [Google Scholar] [CrossRef]
- Price, H. Toy models for retrocausality. Stud. Hist. Philos. Sci. Part B 2008, 39, 752–761. [Google Scholar] [CrossRef]
- Leifer, M.S. Is the Quantum State Real? An Extended Review of ψ-ontology Theorems. Quanta 2014, 3, 67–155. [Google Scholar] [CrossRef]
- Dressel, J.; Bliokh, K.Y.; Nori, F. Classical field approach to quantum weak measurements. Phys. Rev. Lett. 2014, 112, 110407. [Google Scholar] [CrossRef] [PubMed]
- Dressel, J. Weak values as interference phenomena. Phys. Rev. A 2015, 91, 032116. [Google Scholar] [CrossRef]
- Ritchie, N.; Story, J.G.; Hulet, R.G. Realization of a measurement of a “weak value”. Phys. Rev. Lett. 1991, 66, 1107. [Google Scholar] [CrossRef] [PubMed]
- Bliokh, K.Y.; Bekshaev, A.Y.; Kofman, A.G.; Nori, F. Photon trajectories, anomalous velocities and weak measurements: A classical interpretation. New J. Phys. 2013, 15, 073022. [Google Scholar] [CrossRef]
- Howell, J.C.; Starling, D.J.; Dixon, P.B.; Vudyasetu, P.K.; Jordan, A.N. Interferometric weak value deflections: Quantum and classical treatments. Phys. Rev. A 2010, 81, 033813. [Google Scholar] [CrossRef]
- Aharonov, Y.; Vaidman, L. The two-state vector formalism: An updated review. In Time in Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 2008; pp. 399–447. [Google Scholar]
- Sinclair, J.; Spierings, D.; Brodutch, A.; Steinberg, A. Weak values and neoclassical realism. 2018; in press. [Google Scholar]
- De Beauregard, O.C. Une réponse à l’argument dirigé par Einstein, Podolsky et Rosen contre l’interprétation bohrienne des phénomènes quantiques. C. R. Acad. Sci. 1953, 236, 1632–1634. (In French) [Google Scholar]
- Wharton, K. A novel interpretation of the Klein-Gordon equation. Found. Phys. 2010, 40, 313–332. [Google Scholar] [CrossRef]
- Wharton, K.B.; Miller, D.J.; Price, H. Action duality: A constructive principle for quantum foundations. Symmetry 2011, 3, 524–540. [Google Scholar] [CrossRef]
- Evans, P.W.; Price, H.; Wharton, K.B. New slant on the EPR-Bell experiment. Br. J. Philos. Sci. 2012, 64, 297–324. [Google Scholar] [CrossRef]
- Harrison, A.K. Wavefunction collapse via a nonlocal relativistic variational principle. arXiv, 2012; arXiv:1204.3969. [Google Scholar]
- Schulman, L.S. Experimental test of the “Special State” theory of quantum measurement. Entropy 2012, 14, 665–686. [Google Scholar] [CrossRef] [Green Version]
- Heaney, M.B. A symmetrical interpretation of the Klein-Gordon equation. Found. Phys. 2013, 43, 733–746. [Google Scholar] [CrossRef]
- Corry, R. Retrocausal models for EPR. Stud. Hist. Philos. Sci. Part B 2015, 49, 1–9. [Google Scholar] [CrossRef]
- Lazarovici, D. A relativistic retrocausal model violating Bell’s inequality. Proc. R. Soc. A 2015, 471, 20140454. [Google Scholar] [CrossRef]
- Silberstein, M.; Stuckey, W.M.; McDevitt, T. Beyond the Dynamical Universe: Unifying Block Universe Physics and Time as Experienced; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Wharton, K. Time-symmetric boundary conditions and quantum foundations. Symmetry 2010, 2, 272–283. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wharton, K. A New Class of Retrocausal Models. Entropy 2018, 20, 410. https://doi.org/10.3390/e20060410
Wharton K. A New Class of Retrocausal Models. Entropy. 2018; 20(6):410. https://doi.org/10.3390/e20060410
Chicago/Turabian StyleWharton, Ken. 2018. "A New Class of Retrocausal Models" Entropy 20, no. 6: 410. https://doi.org/10.3390/e20060410
APA StyleWharton, K. (2018). A New Class of Retrocausal Models. Entropy, 20(6), 410. https://doi.org/10.3390/e20060410



