Entropy Change of Biological Dynamics in Asthmatic Patients and Its Diagnostic Value in Individualized Treatment: A Systematic Review
Abstract
:1. Introduction
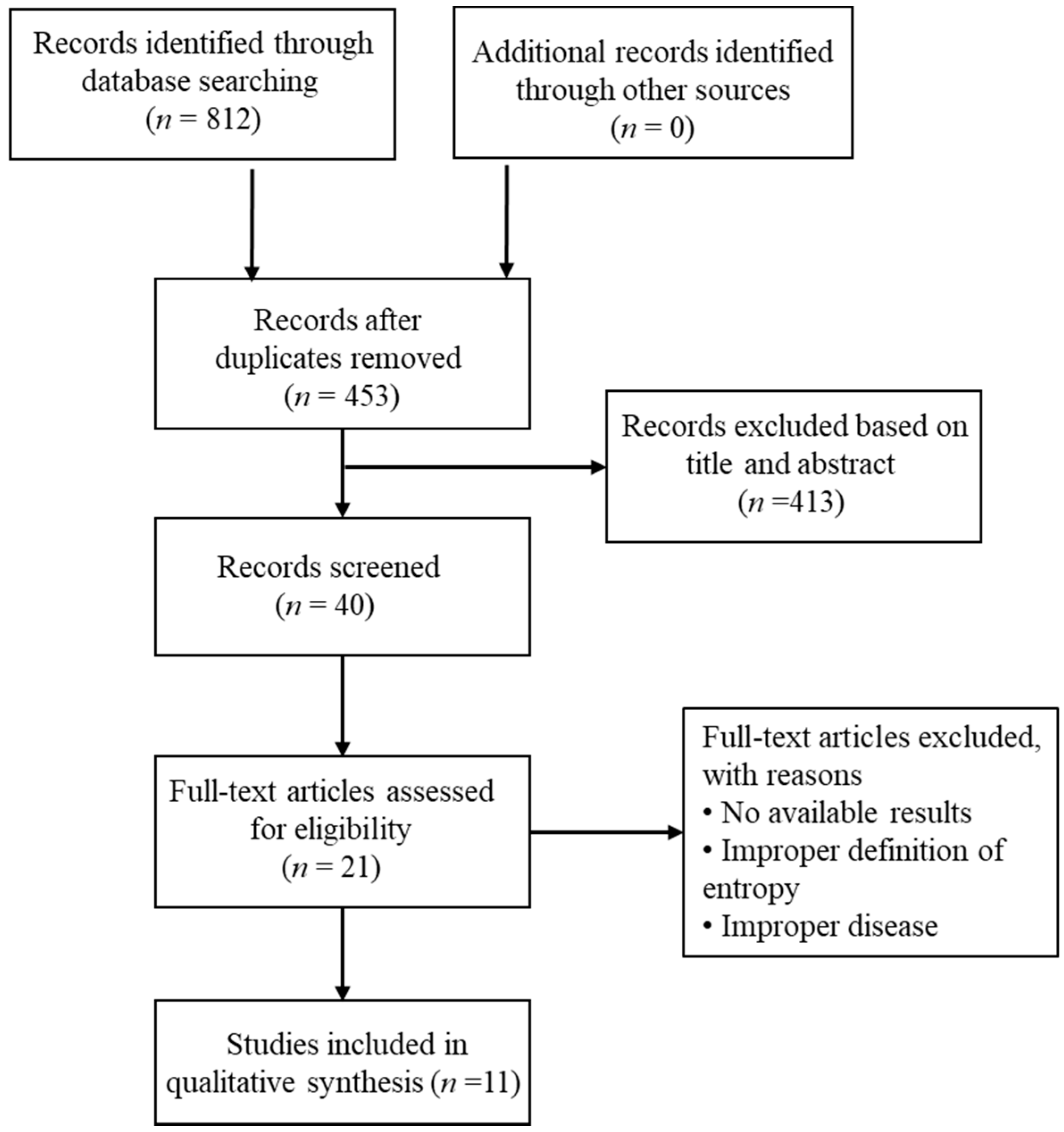
2. Materials and Methods
2.1. Search Strategy and Inclusion Criteria
2.2. Information Extraction and Quality Evaluation
2.3. Brief Introduction of Entropies
3. Results
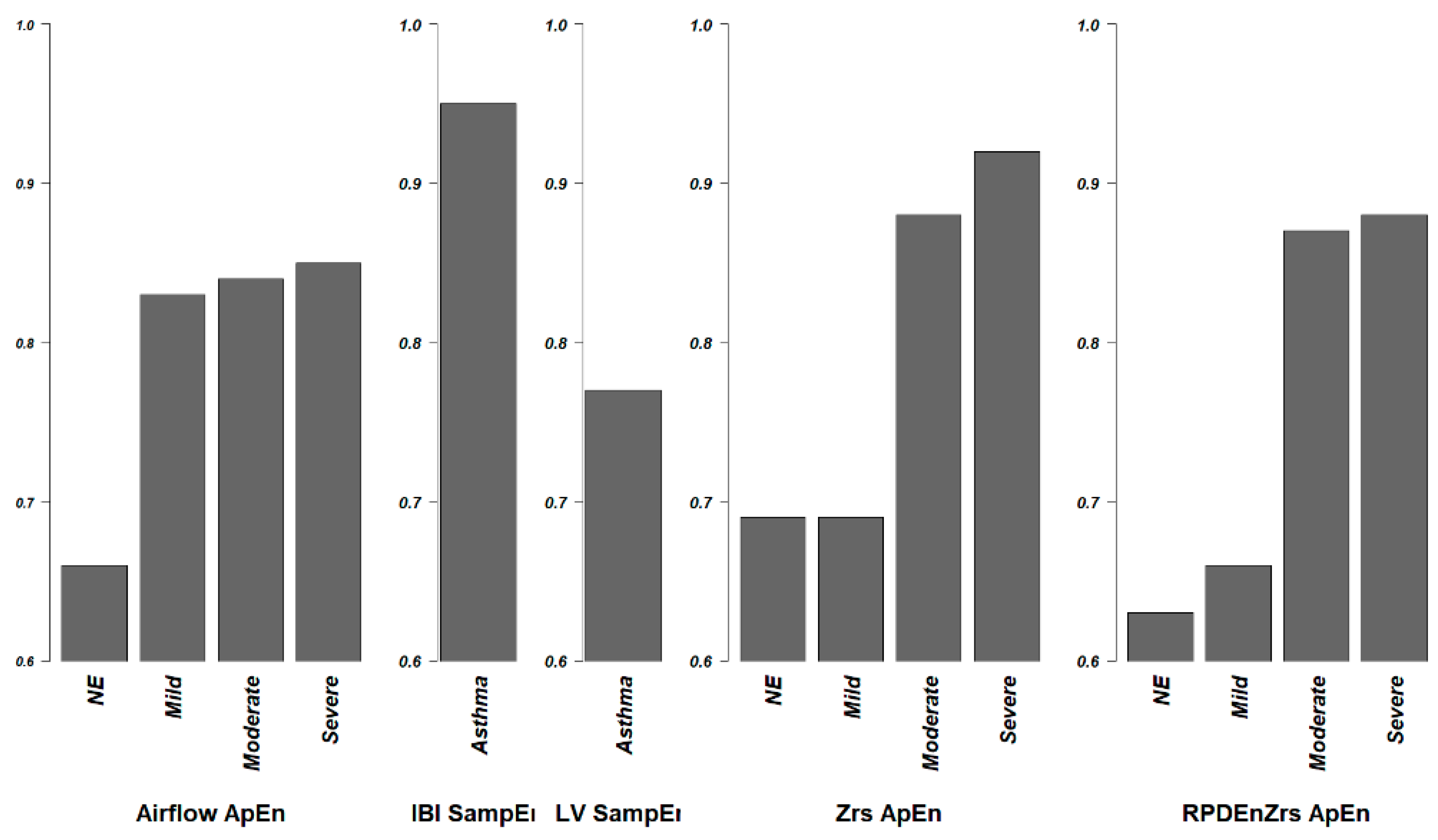
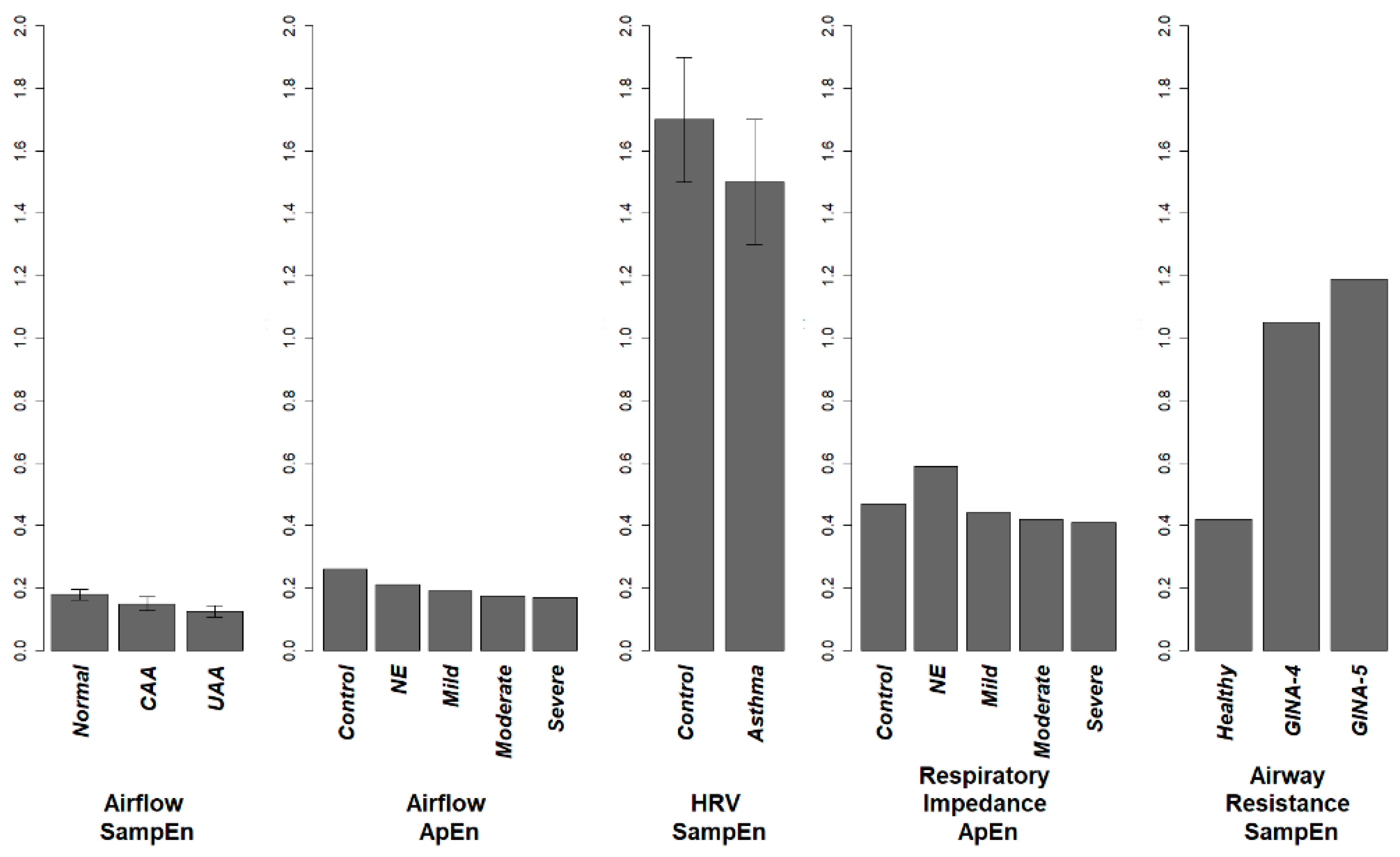
3.1. Airflow
3.2. Heart Rate Variability
3.3. Center of Pressure
3.4. Respiratory Sound
3.5. Respiratory Impedance and Airway Resistance
3.6. Summary
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Pocket Guide for Asthma Management and Prevention. Available online: http://ginasthma.org/wp-content/uploads/2016/01/GINA_Pocket_2015.pdf (accessed on 12 March 2017).
- World Health Organization. Asthma. Available online: http://www.who.int/mediacentre/factsheets/fs307/en/ (accessed on 12 March 2017).
- Pijnenburg, M.W.; Baraldi, E.; Brand, P.L.; Carlsen, K.H.; Eber, E.; Frischer, T.; Hedlin, G.; Kulkarni, N.; Lex, C.; Makela, M.J.; et al. Monitoring asthma in children. Eur. Respir. J. 2015, 45, 906–925. [Google Scholar] [CrossRef] [PubMed]
- Que, C.L.; Kenyon, C.M.; Olivenstein, R.; Macklem, P.T.; Maksym, G.N. Homeokinesis and short-term variability of human airway caliber. J. Appl. Physiol. 2001, 91, 1131–1141. [Google Scholar] [CrossRef] [PubMed]
- Frey, U.; Brodbeck, T.; Majumdar, A.; Taylor, D.R.; Town, G.I.; Silverman, M.; Suki, B. Risk of severe asthma episodes predicted from fluctuation analysis of airway function. Nature 2005, 438, 667–670. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S.; Singer, B.H. Randomness and degrees of irregularity. Proc. Natl. Acad. Sci. USA 1996, 93, 2083–2088. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.D.; Goldberger, A.L. Generalized multiscale entropy analysis: Application to quantifying the complex volatility of human heartbeat time series. Entropy 2015, 17, 1197–1203. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.; Chen, C.; Cao, Z.; Sun, B.; Lo, I.L.; Liu, T.-M.; Zheng, J.; Sun, S.; Shi, Y.; Zhang, X.D. Entropy change of biological dynamics in COPD. Int. J. Chron. Obstr. Pulm. Dis. 2017, 12, 2997–3005. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.D.; Zhang, Z.; Wang, D. CGManalyzer: An R package for analyzing continuous glucose monitoring studies. Bioinformatics 2018, 1, 3. [Google Scholar] [CrossRef]
- Sharma, R.; Pachori, R.; Acharya, U. An integrated index for the identification of focal electroencephalogram signals using discrete wavelet transform and entropy measures. Entropy 2015, 17, 5218–5240. [Google Scholar] [CrossRef]
- Volterrani, M.; Scalvini, S.; Mazzuero, G.; Lanfranchi, P.; Colombo, R.; Clark, A.L.; Levi, G. Decreased heart rate variability in patients with chronic obstructive pulmonary disease. Chest 1994, 106, 1432–1437. [Google Scholar] [CrossRef] [PubMed]
- Corbo, G.M.; Inchingolo, R.; Sgueglia, G.A.; Lanza, G.; Valente, S. C-reactive protein, lung hyperinflation and heart rate variability in chronic obstructive pulmonary disease—A pilot study. COPD J. Chron. Obstr. Pulm. Dis. 2013, 10, 200–207. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Jin, Y.; Lo, I.L.; Zhao, H.; Sun, B.; Zhao, Q.; Zheng, J.; Zhang, X.D. Complexity change in cardiovascular disease. Int. J. Biol. Sci. 2017, 13, 1320–1328. [Google Scholar] [CrossRef] [PubMed]
- Da Luz Goulart, C.; Simon, J.C.; De Borba Schneiders, P.; San Martin, E.A.; Cabiddu, R.; Borghi-Silva, A.; Trimer, R.; Da Silva, A.L.G. Respiratory muscle strength effect on linear and nonlinear heart rate variability parameters in COPD patients. Int. J. Chron. Obstr. Pulm. Dis. 2016, 11, 1671–1677. [Google Scholar] [CrossRef] [PubMed]
- Dames, K.K.; Lopes, A.J.; de Melo, P.L. Airflow pattern complexity during resting breathing in patients with COPD: Effect of airway obstruction. Respir. Physiol. Neurobiol. 2014, 192, 39–47. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Araujo, A.S.; Pires Di Lorenzo, V.A.; Labadessa, I.G.; Jurgensen, S.P.; Di Thommazo-Luporini, L.; Garbim, C.L.; Borghi-Silva, A. Increased sympathetic modulation and decreased response of the heart rate variability in controlled asthma. J. Asthma 2015, 52, 246–253. [Google Scholar] [CrossRef] [PubMed]
- Gonem, S.; Umar, I.; Burke, D.; Desai, D.; Corkill, S.; Owers-Bradley, J.; Brightling, C.E.; Siddiqui, S. Airway impedance entropy and exacerbations in severe asthma. Eur. Respir. J. 2012, 40, 1156–1163. [Google Scholar] [CrossRef] [PubMed]
- Veiga, J.; Faria, R.C.; Esteves, G.P.; Lopes, A.J.; Jansen, J.M.; Melo, P.L. Approximate entropy as a measure of the airflow pattern complexity in asthma. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Buenos Aires, Argentina, 31 August–4 September 2010; Volume 2010, pp. 2463–2466. [Google Scholar]
- Veiga, J.; Lopes, A.J.; Jansen, J.M.; Melo, P.L. Fluctuation analysis of respiratory impedance waveform in asthmatic patients: Effect of airway obstruction. Med. Biol. Eng. Comput. 2012, 50, 1249–1259. [Google Scholar] [CrossRef] [PubMed]
- Veremchuk, L.V.; Yankova, V.I.; Vitkina, T.I.; Nazarenko, A.V.; Golokhvast, K.S. Urban air pollution, climate and its impact on asthma morbidity. Asian Pac. J Trop. Biomed. 2016, 6, 76–79. [Google Scholar] [CrossRef]
- Aydore, S.; Sen, I.; Kahya, Y.P.; Mihcak, M.K. Classification of respiratory signals by linear analysis. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBC 2009, Minneapolis, MN, USA, 3–6 Septtember 2009; pp. 2617–2620. [Google Scholar]
- Jadad, A.R.; Moore, R.A.; Carroll, D.; Jenkinson, C.; Reynolds, D.J.M.; Gavaghan, D.J.; McQuay, H.J. Assessing the quality of reports of randomized clinical trials: Is blinding necessary? Control. Clin. Trials 1996, 17, 1–12. [Google Scholar] [CrossRef]
- Chakrabarti, C.G.; De, K. Boltzmann entropy: Generalization and applications. J. Biol. Phys. 1997, 23, 163–170. [Google Scholar] [CrossRef] [PubMed]
- Shannon, C.E. Communication theory of secrecy systems. Bell Labs Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Estimation of the kolmogorov entropy from a chaotic signal. Phys. Rev. A 1983, 28, 2591. [Google Scholar] [CrossRef]
- Gonzalez Andino, S.L.; Grave de Peralta Menendez, R.; Thut, G.; Spinelli, L.; Blanke, O.; Michel, C.M.; Seeck, M.; Landis, T. Measuring the complexity of time series: An application to neurophysiological signals. Hum. Brain Mapp. 2000, 11, 46–57. [Google Scholar] [CrossRef]
- Slomczynski, W.; Kwapien, J.; Zyczkowski, K. Entropy computing via integration over fractal measures. Chaos 2000, 10, 180–188. [Google Scholar] [CrossRef] [PubMed]
- Shannon, C.E.; Weaver, W. The mathematical theory information. Math. Gazette 1949, 97, 170–180. [Google Scholar]
- El-Khatib, M.F. A diagnostic software tool for determination of complexity in respiratory pattern parameters. Comput. Biol. Med. 2007, 37, 1522–1527. [Google Scholar] [CrossRef] [PubMed]
- Bates, J.H.; Davis, G.S.; Majumdar, A.; Butnor, K.J.; Suki, B. Linking parenchymal disease progression to changes in lung mechanical function by percolation. Am. J. Respir. Crit. Care Med. 2007, 176, 617–623. [Google Scholar] [CrossRef] [PubMed]
- Venegas, J.G.; Winkler, T.; Musch, G.; Melo, M.F.V.; Layfield, D.; Tgavalekos, N.; Fischman, A.J.; Callahan, R.J.; Bellani, G.; Harris, R.S. Self-organized patchiness in asthma as a prelude to catastrophic shifts. Nature 2005, 434, 777–782. [Google Scholar] [CrossRef] [PubMed]
- Veiga, J.; Lopes, A.J.; Jansen, J.M.; Melo, P.L. Airflow pattern complexity and airway obstruction in asthma. J. Appl. Physiol. 2011, 111, 412–419. [Google Scholar] [CrossRef] [PubMed]
- Raoufy, M.R.; Ghafari, T.; Darooei, R.; Nazari, M.; Mahdaviani, S.A.; Eslaminejad, A.R.; Almasnia, M.; Gharibzadeh, S.; Mani, A.R.; Hajizadeh, S. Classification of asthma based on nonlinear analysis of breathing pattern. PLoS ONE 2016, 11, e0147976. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, N.A.; Luberto, C.M.; Avallone, K.; Kraemer, K.; McLeish, A.C.; Riley, M.A. Characteristics of postural control among young adults with asthma. J. Asthma 2015, 52, 191–197. [Google Scholar] [CrossRef] [PubMed]
- Jin, F.; Sattar, F.; Goh, D.Y. Automatic wheeze detection using histograms of sample entropy. In Proceedings of the 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS 2008, Vancouver, BC, Canada, 20–25 August 2008; Volume 2008, pp. 1890–1893. [Google Scholar]
- Mondal, A.; Bhattacharya, P.; Saha, G. Detection of lungs status using morphological complexities of respiratory sounds. Sci. World J. 2014, 2014, 182938. [Google Scholar] [CrossRef] [PubMed]
- Oostveen, E.; MacLeod, D.; Lorino, H.; Farré, R.; Hantos, Z.; Desager, K.; Marchal, F. The forced oscillation technique in clinical practice: Methodology, recommendations and future developments. Eur. Respir. J. 2003, 22, 1026–1041. [Google Scholar] [CrossRef] [PubMed]
- Umar, I.; Desai, D.; Corkill, S.; Shelley, M.; Singapuri, A.; Brightling, C.; Siddiqui, S. The use of impulse oscillometry (IOS) to study fractal scaling and sample entropy in airway resistance time series in severe asthma. Thorax 2010, 65, A129. [Google Scholar] [CrossRef]
- Kvedar, J.C.; Fogel, A.L.; Elenko, E.; Zohar, D. Digital medicine’s march on chronic disease. Nat. Biotechnol. 2016, 34, 239–246. [Google Scholar] [CrossRef] [PubMed]
- Elenko, E.; Underwood, L.; Zohar, D. Defining digital medicine. Nat. Biotechnol. 2015, 33, 456–461. [Google Scholar] [CrossRef] [PubMed]
- Goldberger, A.L. Fractal variability versus pathologic periodicity: Complexity loss and stereotypy in disease. Perspect. Biol. Med. 1997, 40, 543–561. [Google Scholar] [CrossRef] [PubMed]
- Kaguara, A.; Myoung Nam, K.; Reddy, S. A Deep Neural Network Classifier for Diagnosing Sleep Apnea from ECG Data on Smartphones and Small Embedded Systems. Available online:https://www.researchgate.net/publication/273633242_A_deep_neural_network_classifier_for_diagnosing_sleep_apnea_from_ECG_data_on_smartphones_and_small_embedded_systems (accessed on 11 April 2018).
- Acharya, U.R.; Fujita, H.; Lih, O.S.; Hagiwara, Y.; Tan, J.H.; Adam, M. Automated detection of arrhythmias using different intervals of tachycardia ECG segments with convolutional neural network. Inf. Sci. 2017, 405, 81–90. [Google Scholar] [CrossRef]
- Niu, J.; Shi, Y.; Cai, M.; Cao, Z.; Wang, D.; Zhang, Z.; Zhang, X.D. Detection of sputum by interpreting the time-frequency distribution of respiratory sound signal using image processing techniques. Bioinformatics 2018, 34, 820–827. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Wang, G.; Niu, J.; Zhang, Q.; Cai, M.; Sun, B.; Wang, D.; Xue, M.; Zhang, X.D. Classification of sputum sounds using artificial neural network and wavelet transform. Int. J. Biol. Sci. in press. [CrossRef]
- Li, K.; Pan, W.; Li, Y.; Jiang, Q.; Liu, G. A method to detect sleep apnea based on deep neural network and hidden markov model using single-lead ECG signal. Neurocomputing 2018, 294, 94–101. [Google Scholar] [CrossRef]
| OutcomeMeasure | N (Arms) | Risk of Bias | Limitation of Study | Inconsistency | Indirectness | Imprecision | Effect Size | Quality of Evidence |
|---|---|---|---|---|---|---|---|---|
| Airflow | 128(3) | No | No obvious limitations | No | No indirectness | No | Significant | High |
| HRV | 24(1) | No | No obvious limitations | No | No indirectness | No | Significant | High |
| entre of Pressure | 39(1) | No | No obvious limitations | No | No serious indirectness | No | Significant | Moderate |
| Respiratory sound | 51(3) | No | Limitation in study design and data collection | No | No serious indirectness | No | Significant | Low |
| Respiratory impedance | 74(1) | No | No obvious limitations | No | No indirectness | No | Significant | High |
| Airway resistance | 186(2) | No | Limitation in study design and data collection | No | No indirectness | No | Significant | Moderate |
| Physiologic Signals | Study (Year) | Study Type | Entropy Method | Location | Number of Subjects | Age in Years as Mean ± SD or Range | Gender Ratio (M/F) | Pulmonary Function | Entropy Result | AUC |
|---|---|---|---|---|---|---|---|---|---|---|
| Airflow | Veiga et al., 2010 | Observational | ApEn | Brazil | Control 5 NE 5 Mild 5 Moderate 6 Severe 5 | Control 47.6 ± 19.7 NE 33.2 ± 8.5 Mild 49.2 ± 14.7 Moderate 54.3 ± 7.8 Severe 61.4 ± 6.7 | N/A | FVC, FEV1, FEF25–75%, FEV1/FVC, FEF/FVC | lower in asthmatic patients | No |
| Veiga et al., 2011 | Observational | ApEn | Brazil | Control 11 NE 11 Mild 14 Moderate 14 Severe 12 | Control 54.4 ± 15.1 NE 34.9 ± 10.3 Mild 51.1 ± 13.5 Moderate 54.2 ± 10.7 Severe 60.5 ± 12.5 | N/A | FVC, FEV1, FEF25–75%, FEV1/FVC, FEF/FVC | lower in asthmatic patients | Yes | |
| Raoufy et al., 2016 | Observational | SampEn | Iran | Control 10 CAA 10 UAA 10 UNAA 10 | Control 27.6 ± 5.3 CAA 30.8 ± 9.8 UAA 31.1 ± 7.2 UNAA 32.7 ± 8.1 | N/A | N/A | lower in asthmatic subjects | Yes | |
| HRV | Garcia-Araujo et al., 2014 | Observational | ApEn SampEn Shannon | Brazil | Healthy 10 Asthma 14 | Healthy 31 ± 8.7 Asthma 28 ± 8.5 | Healthy: 10/0 Asthma: 11/3 | FEV1, FVC, FEV1/FVC, VO2 | lower in asthmatic patients during respiratory sinus arrhythmia maneuver | No |
| Center of pressure | Kuznetsov et al., 2014 | Observational | SampEn | USA | Healthy 18 Asthma 21 | Healthy 9.87 ± 2.77 Asthma 20.04 ± 1.85 | Healthy: 3/15 Asthma: 6/15 | N/A | lower in asthmatic patients | No |
| Respiratory Sound | Jin et al. 2008 | Observational | SampEn | Singapore | Control 7 Asthma 7 | N/A | N/A | N/A | SampEn is effective for wheeze detection. | No |
| Aydore et al., 2009 | Retrospective | Renyi | USA | 7 (COPD & asthma) | 50 ± 17 | 4/3 | N/A | The Renyi entropy of wheeze signal has a uniform distribution | No | |
| Mondal et al., 2014 | Retrospective | SampEn | India | Normal 10 Abnormal 20 | N/A | N/A | N/A | higher in asthmatic subjects | No | |
| Respiratory Impedance | Veiga et al., 2012 | Observational | ApEn | Brazil | Control 12 NE 12 Mild 20 Moderate 18 Severe 12 | Control 52.7 ± 16.4 NE 35.2 ± 9.9 Mild 51.8 ± 13.8 Moderate 53.2 ± 14.2 Severe 60.5 ± 12.5 | N/A | FVC, FEV1, FEF25–75%, FEV1/FVC, FEF/FVC | higher in asthmatic patients | Yes |
| Airway Resistance | Gonem et al., 2012 | Observational | SampEn | UK | Control: 30 GINA4: 33 GINA5: 33 | Control: 47.0 ± 2.2 GINA4: 51.0 ± 2.3 GINA5: 56.5 ± 1.9 | Control: 12/18 GINA4: 16/17 GINA5: 15/18 | FEV1, FEV1/FVC | higher in asthmatic patients | No |
| Umar et al., 2010 | Observational | SampEn | UK | Control: 27 Asthma: 66 | Control: 54.1 ± 1.4 Asthma: 48.4 ± 2.2 | Control: 9/18 Asthma: 31/35 | FEV1 | higher in asthmatic patients | No |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, S.; Jin, Y.; Chen, C.; Sun, B.; Cao, Z.; Lo, I.L.; Zhao, Q.; Zheng, J.; Shi, Y.; Zhang, X.D. Entropy Change of Biological Dynamics in Asthmatic Patients and Its Diagnostic Value in Individualized Treatment: A Systematic Review. Entropy 2018, 20, 402. https://doi.org/10.3390/e20060402
Sun S, Jin Y, Chen C, Sun B, Cao Z, Lo IL, Zhao Q, Zheng J, Shi Y, Zhang XD. Entropy Change of Biological Dynamics in Asthmatic Patients and Its Diagnostic Value in Individualized Treatment: A Systematic Review. Entropy. 2018; 20(6):402. https://doi.org/10.3390/e20060402
Chicago/Turabian StyleSun, Shixue, Yu Jin, Chang Chen, Baoqing Sun, Zhixin Cao, Iek Long Lo, Qi Zhao, Jun Zheng, Yan Shi, and Xiaohua Douglas Zhang. 2018. "Entropy Change of Biological Dynamics in Asthmatic Patients and Its Diagnostic Value in Individualized Treatment: A Systematic Review" Entropy 20, no. 6: 402. https://doi.org/10.3390/e20060402
APA StyleSun, S., Jin, Y., Chen, C., Sun, B., Cao, Z., Lo, I. L., Zhao, Q., Zheng, J., Shi, Y., & Zhang, X. D. (2018). Entropy Change of Biological Dynamics in Asthmatic Patients and Its Diagnostic Value in Individualized Treatment: A Systematic Review. Entropy, 20(6), 402. https://doi.org/10.3390/e20060402