Finite Difference Method for Time-Space Fractional Advection–Diffusion Equations with Riesz Derivative
Abstract
1. Introduction
2. Preliminaries
- 1.
- 2.
- 3.
- there exists a positive constant such that
- 1.
- are monotonically decreasing when n increases.
- 2.
- are monotonically decreasing when n increases.
- 3.
- are monotonically decreasing when n increases.
3. Finite Difference Approximation
Fractional Trapezoid Formula
4. Stability and Convergence Analysis
4.1. Stability
4.2. Convergence
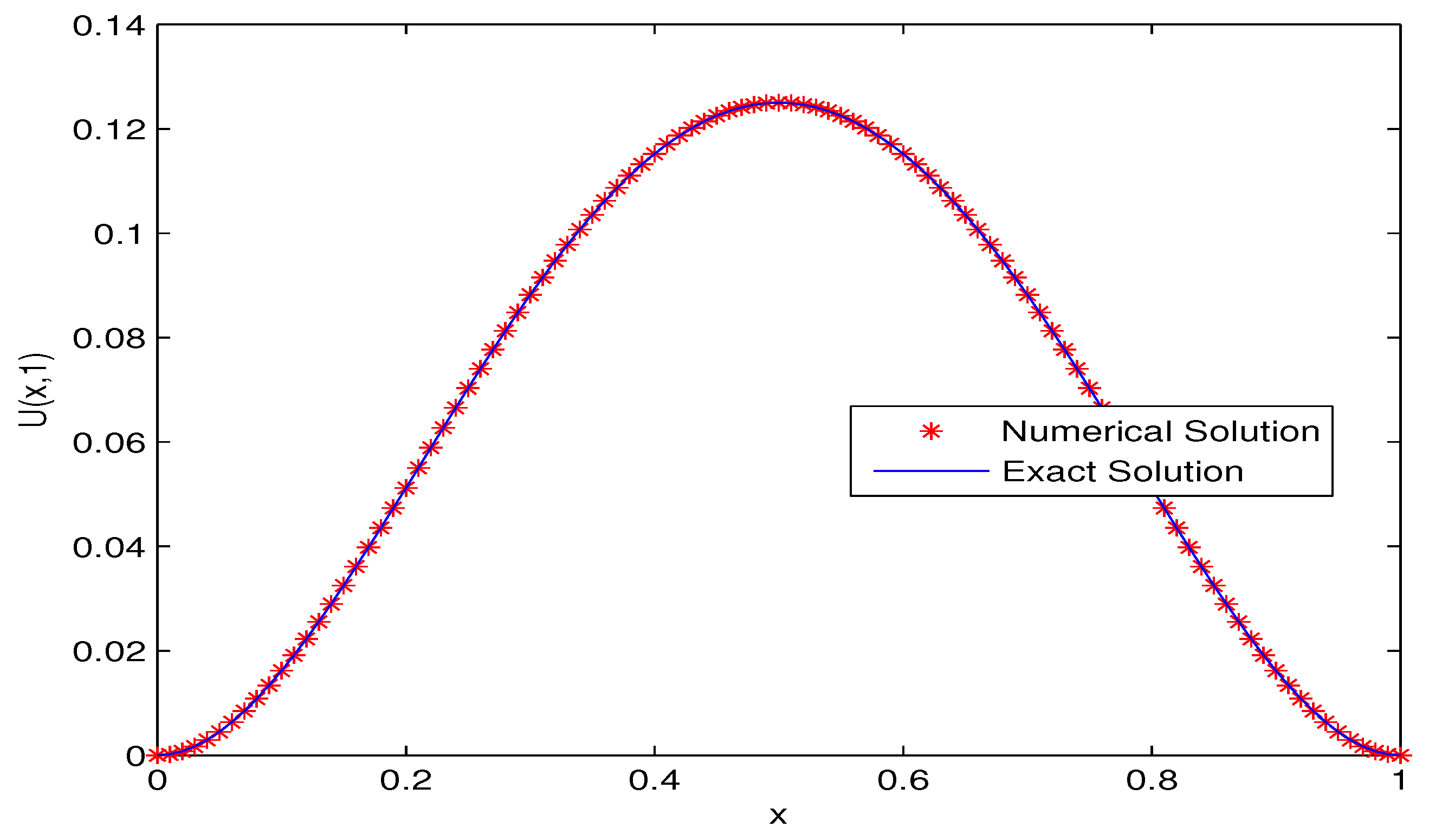
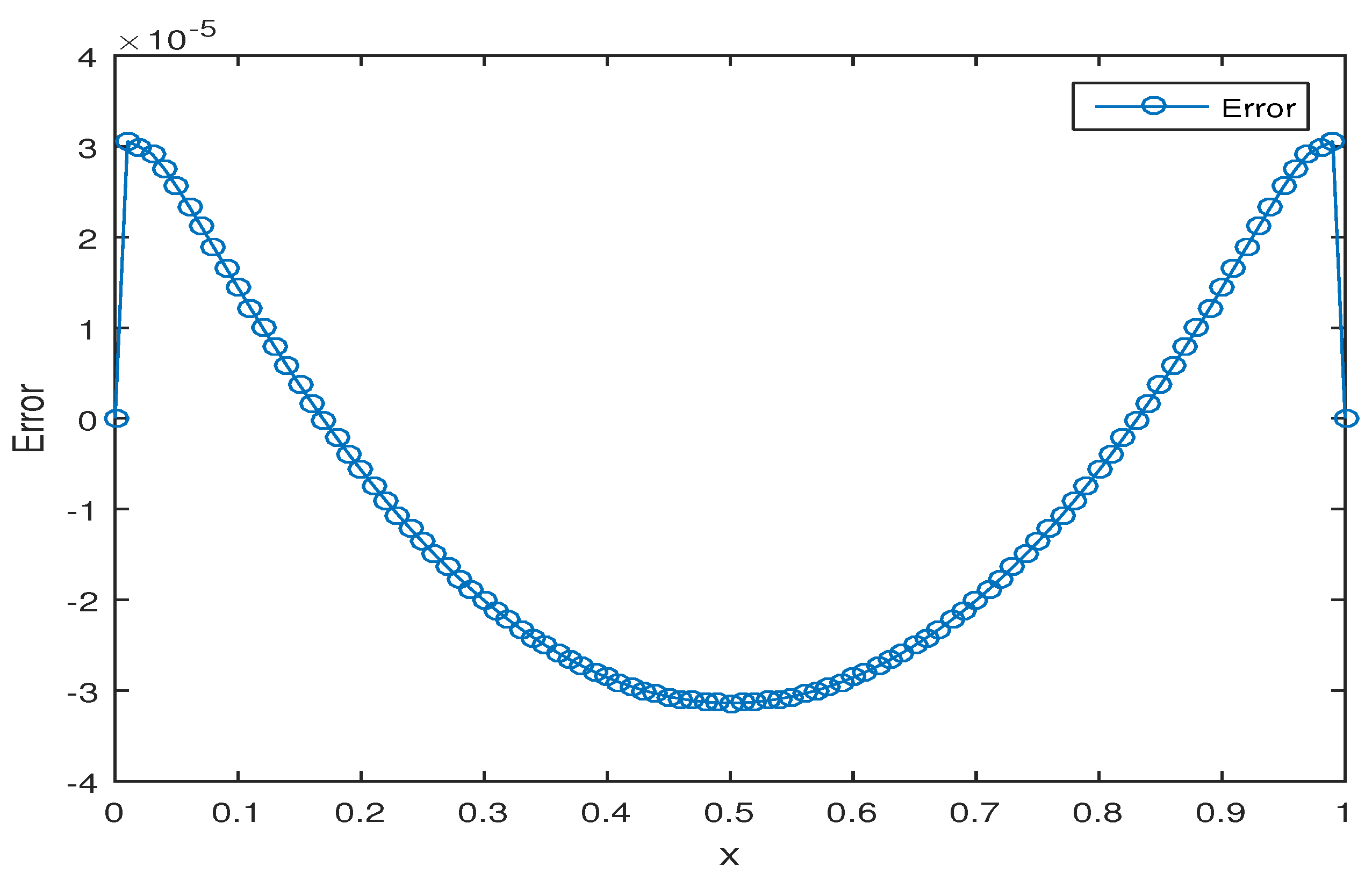
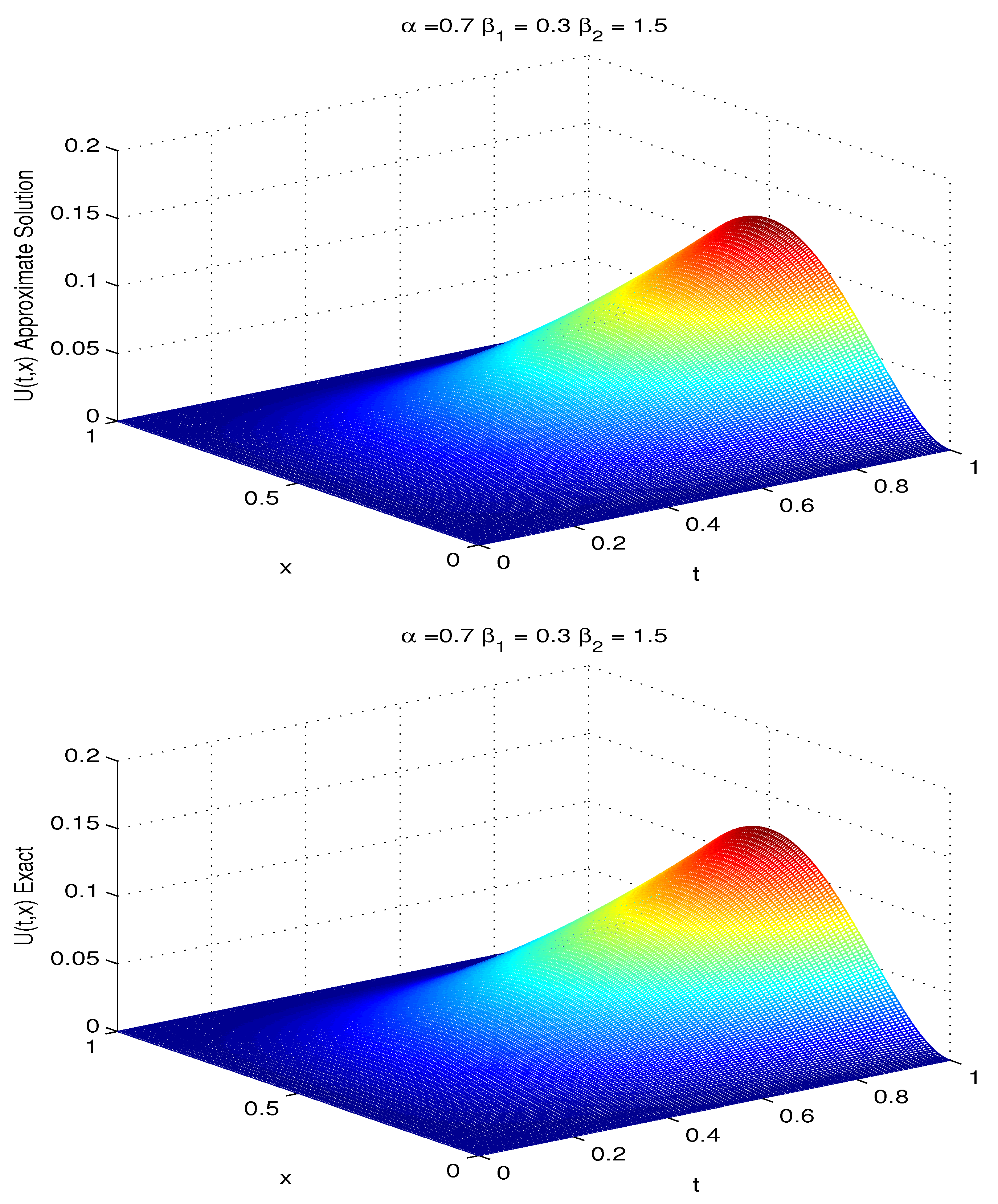
5. Numerical Experiments
Example
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Machado, J.A.T. Entropy analysis of integer and fractional dynamical systems. Nonlinear Dyn. 2010, 62, 371–378. [Google Scholar]
- Hoffmann, K.H.; Essex, C.; Schulzky, C. Fractional diffusion and entropy production. J. Non-Equilib. Thermodyn. 1998, 23, 166–175. [Google Scholar] [CrossRef]
- Magin, R.L.; Ingo, C. Entropy and information in a fractional order model of anomalous diffusion. IFAC Proc. 2012, 45, 428–433. [Google Scholar] [CrossRef]
- Bueno-Orovio, A.; Kay, D.; Grau, V.; Rodriguez, B.; Burrage, K. Fractional Diffusion Models of Cardiac Electrical Propagation: Role of Structural Heterogeneity in Dispersion of Repolarization; Technical Report OCCAM 13/35; Oxford Centre for Collaborative Applied Mathematics: Oxford, UK, 2013. [Google Scholar]
- Cafagna, D.; Grassi, G. Observer-based projective synchronization of fractional systems via a scalar signal: Application to hyperchaotic Rösslersystems. Nonlinear Dyn. 2012, 68, 117–128. [Google Scholar] [CrossRef]
- Caponetto, R.; Maione, G.; Pisano, A.; Rapaic, M.M.R.; Usai, E. Analysis and shaping of the self-sustained oscillations in relay controlled fractional-order systems. Fract. Calculus Appl. Anal. 2013, 16, 93–108. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations, vol. 204 of North-Holland Mathematics Studies; Elsevier: New York, NY, USA, 2006. [Google Scholar]
- Machado, J.T.; Stefanescu, P.; Tintareanu, O.; Baleanu, D. Fractional calculus analysis of the cosmic microwave background. Romanian Rep. Phys. 2013, 65, 316–323. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications, Gordon and Breach; Science Publishers: Hauppauge, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Acdemic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algor. 2004, 36, 31–52. [Google Scholar] [CrossRef]
- Zhuang, P.; Liu, F.; Anh, V.; Turner, I. New solution and analytical techniques of the implicit numerical method for the anomalous subdiffusion equation. SIAM J. Numer. Anal. 2008, 46, 1079–1095. [Google Scholar] [CrossRef]
- Tang, T. A finite difference scheme for partial integro-differential equations with weakly singular kernel. Appl. Numer. Math. 1993, 11, 309–319. [Google Scholar] [CrossRef]
- Chen, H.; Xu, D.; Peng, Y. An alternating direction implicit fractional trapezoidal rule type difference scheme for the two-dimensional fractional evolution equation. Int. J. Comput. Math. 2015, 92, 2178–2197. [Google Scholar] [CrossRef]
- Chen, H.; Gan, S.; Xu, D. A fractional trapezoidal rule type difference scheme for fractional order integro–differential equation. J. Frac. Calcul. Appl. 2016, 7, 133–146. [Google Scholar]
- Arshad, S.; Huang, J.; Khaliq, A.Q.M.; Tang, Y. Trapezoidal scheme for time-space fractional diffusion equation with Riesz derivative. J. Comput. Phys. 2017, 350, 1–15. [Google Scholar] [CrossRef]
- Arshad, S.; Bu, W.; Huang, J.; Tang, Y.; Zhao, Y. Finite difference method for time-space linear and nonlinear fractional diffusion equations. Int. J. Comp. Math. 2018, 95, 202–217. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Tadjeran, C. Finite difference approximations for fractional advection–dispersion flow equations. J. Comput. Appl. Math. 2004, 172, 65–77. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, F.; Turner, I. Numerical methods for fractional partial differential equations with Riesz space fractional derivatives. Appl. Math. Model. 2010, 34, 200–218. [Google Scholar] [CrossRef]
- Sousa, E. A second order explicit finite difference method for the fractional advection diffusion equation. Comput. Math. Appl. 2012, 64, 3141–3152. [Google Scholar] [CrossRef]
- Tian, W.Y.; Zhou, H.; Deng, W.H. A class of second order difference approximation for solving space fractional diffusion equations. Math. Comput. 2015, 84, 1703–1727. [Google Scholar] [CrossRef]
- Ding, H.F.; Li, C.P.; Chen, Y.Q. High-order algorithms for Riesz derivative and their applications (I). Abstr. Appl. Anal. 2014, 2014, 653797. [Google Scholar] [CrossRef]
- Lubich, C. Discretized fractional calculus. SIAM J. Math. Anal. 1986, 17, 704–719. [Google Scholar] [CrossRef]
- Ding, H.F.; Li, C.P.; Chen, Y.Q. High-order algorithms for Riesz derivative and their applications (II). J. Comput. Phys. 2015, 293, 218–237. [Google Scholar] [CrossRef]
- Ding, H.F.; Li, C.P. High-order algorithms for Riesz derivative and their applications (III). Fract. Calc. Appl. Anal. 2016, 19, 19–55. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Benson, D.A.; Wheatcraft, S.W.; Meerschaert, M.M. Application of a fractional advection–dispersion equation. Water Resour. Res. 2000, 36, 1403–1412. [Google Scholar] [CrossRef]
- Povstenko, Y.; Kyrylych, T.; Ryga, G. Fractional diffusion in a solid with mass absorption. Entropy 2017, 19, 203. [Google Scholar] [CrossRef]
- Liu, F.; Anh, V.; Turner, I.; Zhuang, P. Time fractional advection dispersion equation. J. Appl. Math. Comput. 2003, 13, 233–245. [Google Scholar] [CrossRef]
- Povstenko, Y.; Kyrylych, T. Two approaches to obtaining the space-time fractional advection–diffusion equation. Entropy 2017, 19, 297. [Google Scholar] [CrossRef]
- Huang, F.; Liu, F. The fundamental solution of the space–time fractional advection–dispersion equation. J. Appl. Math. Comput. 2005, 19, 233–245. [Google Scholar] [CrossRef]
- Tripathi, N.K.; Das, S.; Ong, S.H.; Jafari, H.; Qurashi, M.A. Solution of higher order nonlinear time-fractional reaction diffusion equation. Entropy 2016, 18, 329. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Numerical solutions of the space–time fractional advection–dispersion equation. Numer. Meth. Part. Differ. Equat. 2008, 24, 1416–1429. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, F.; Turner, I.; Anh, V. Approximation of the Lëvy–Feller advection–dispersion process by random walk and finite difference method. J. Comput. Phys. 2007, 222, 57–70. [Google Scholar] [CrossRef]
- Liu, F.; Zhuang, P.; Anh, V.; Turner, I.; Burra, K. Stability and convergence of the difference methods for the space-time fractional advection–diffusion equation. Appl. Math. Comput. 2007, 191, 12–20. [Google Scholar] [CrossRef]
- Ervin, V.J.; Roop, J.P. Variational formulation for the stationary fractional advection–dispersion equation. Numer. Meth. Part. Diff. Equ. 2006, 22, 558–576. [Google Scholar] [CrossRef]
- Hejazi, H.; Moroney, T.; Liu, F. Stability and convergence of a finite volume method for the space fractional advection–dispersion equation. J. Comput. Appl. Math. 2014, 255, 684–697. [Google Scholar] [CrossRef]
- Golbabai, A.; Sayevand, K. Analytical modelling of fractional advection–dispersion equation defined in a bounded space domain. Math. Comput. Model. 2011, 53, 1708–1718. [Google Scholar] [CrossRef]
- Carella, A.R.; Dorao, C.A. Least-squares spectral method for the solution of a fractional advection–dispersion equation. J. Comput. Phys. 2013, 232, 33–45. [Google Scholar] [CrossRef]
- Zheng, G.H.; Wei, T. Spectral regularization method for a Cauchy problem of the time fractional advection–dispersion equation. J. Comput. Appl. Math. 2010, 233, 2631–2640. [Google Scholar] [CrossRef]
- Donatelli, M.; Mazza, M.; Serra-Capizzano, S. Spectral analysis and structure preserving preconditioners for fractional diffusion equations. J. Comput. Phys. 2016, 307, 262–279. [Google Scholar] [CrossRef]
- Lei, S.L.; Sun, H.W. A circulant preconditioner for fractional diffusion equations. J. Comput. Phys. 2013, 242, 715–725. [Google Scholar] [CrossRef]
- Lin, X.L.; Ng, M.K.; Sun, H.W. A splitting preconditioner for Toeplitz-like linear systems arising from fractional diffusion equations. SIAM J. Matrix Anal. Appl. 2017, 38, 1580–1614. [Google Scholar] [CrossRef]
- Pan, J.; Ng, K.M.; Wang, H. Hong Fast iterative solvers for linear systems arising from time-dependent space-fractional diffusion equations. SIAM J. Sci. Comput. 2016, 38, A2806–A2826. [Google Scholar] [CrossRef]
- Feng, L.B.; Zhuang, P.; Liu, F.; Turner, I.; Li, J. High-order numerical methods for the Riesz space fractional advection–dispersion equations. Comput. Math. Appl. 2016. [Google Scholar] [CrossRef]
- Yu, B.; Jiang, X.; Xu, H. A novel compact numerical method for solving the two-dimensional non-linear fractional reaction-subdiffusion equation. Numer. Algor. 2015, 68, 923–950. [Google Scholar] [CrossRef]
- Zhuang, P.; Liu, F.; Anh, V.; Turner, I. Stability and convergence of an implicit numerical method for the non-linear fractional reaction–subdiffusion process. IMA J. Appl. Math. 2009, 74, 645–667. [Google Scholar] [CrossRef]
| order | order | order | order | |||||
| 2.3743 | - | 2.4068 | - | 2.4513 | - | 2.5127 | - | |
| 5.7815 | 2.0380 | 5.8594 | 2.0382 | 5.9700 | 2.0377 | 6.1222 | 2.0371 | |
| 1.4044 | 2.0414 | 1.4235 | 2.0413 | 1.4512 | 2.0404 | 1.4893 | 2.0393 | |
| 3.3971 | 2.0475 | 3.4438 | 2.0473 | 3.5130 | 2.0464 | 3.6083 | 2.0452 | |
| 7.9725 | 2.0912 | 8.0845 | 2.0907 | 8.2539 | 2.0895 | 8.4892 | 2.0876 | |
| order | order | order | order | |||||
| 2.1509 | - | 2.4462 | - | 2.7484 | - | 2.9426 | - | |
| 5.4062 | 1.9923 | 5.9481 | 2.0400 | 6.6725 | 2.0422 | 7.3624 | 1.9988 | |
| 1.3605 | 1.9904 | 1.4434 | 2.0429 | 1.6095 | 2.0516 | 1.8368 | 2.0029 | |
| 3.4175 | 1.9931 | 3.4894 | 2.0484 | 3.8429 | 2.0663 | 4.5457 | 2.0146 | |
| 8.3926 | 2.0257 | 8.1970 | 2.0898 | 8.8282 | 2.1220 | 1.0893 | 2.0609 | |
| order | order | order | order | |||||
| 1.4377 | - | 2.0772 | - | 2.3616 | - | 2.5162 | - | |
| 3.8544 | 1.8992 | 5.3402 | 1.9596 | 5.9403 | 1.9911 | 6.2750 | 2.0035 | |
| 1.0120 | 1.9293 | 1.3551 | 1.9784 | 1.4831 | 2.0018 | 1.5587 | 2.0092 | |
| 2.5497 | 1.9888 | 3.3379 | 2.0214 | 3.6155 | 2.0363 | 3.7925 | 2.0391 | |
| 5.7769 | 2.1419 | 7.5305 | 2.1481 | 8.1450 | 2.1502 | 8.5804 | 2.1440 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arshad, S.; Baleanu, D.; Huang, J.; Al Qurashi, M.M.; Tang, Y.; Zhao, Y. Finite Difference Method for Time-Space Fractional Advection–Diffusion Equations with Riesz Derivative. Entropy 2018, 20, 321. https://doi.org/10.3390/e20050321
Arshad S, Baleanu D, Huang J, Al Qurashi MM, Tang Y, Zhao Y. Finite Difference Method for Time-Space Fractional Advection–Diffusion Equations with Riesz Derivative. Entropy. 2018; 20(5):321. https://doi.org/10.3390/e20050321
Chicago/Turabian StyleArshad, Sadia, Dumitru Baleanu, Jianfei Huang, Maysaa Mohamed Al Qurashi, Yifa Tang, and Yue Zhao. 2018. "Finite Difference Method for Time-Space Fractional Advection–Diffusion Equations with Riesz Derivative" Entropy 20, no. 5: 321. https://doi.org/10.3390/e20050321
APA StyleArshad, S., Baleanu, D., Huang, J., Al Qurashi, M. M., Tang, Y., & Zhao, Y. (2018). Finite Difference Method for Time-Space Fractional Advection–Diffusion Equations with Riesz Derivative. Entropy, 20(5), 321. https://doi.org/10.3390/e20050321






