Abstract
In this article, a numerical scheme is formulated and analysed to solve the time-space fractional advection–diffusion equation, where the Riesz derivative and the Caputo derivative are considered in spatial and temporal directions, respectively. The Riesz space derivative is approximated by the second-order fractional weighted and shifted Grünwald–Letnikov formula. Based on the equivalence between the fractional differential equation and the integral equation, we have transformed the fractional differential equation into an equivalent integral equation. Then, the integral is approximated by the trapezoidal formula. Further, the stability and convergence analysis are discussed rigorously. The resulting scheme is formally proved with the second order accuracy both in space and time. Numerical experiments are also presented to verify the theoretical analysis.
1. Introduction
The concepts of fractional calculus and entropy are becoming more popular for analyzing the dynamics of complex systems. The idea of entropy was introduced in the field of thermodynamics by Clausius (1862) and Boltzmann (1896) and was later applied by Shannon (1948) and Jaynes (1957) in information theory. Recently, more general entropy measures have being proposed for application in several types of complex systems due to the relaxation of the additivity axiom. The concept of entropy for analyzing the dynamics of multi-particle systems with integer and fractional order behavior was proposed in [1]. The entropy production rate for the fractional diffusion process was calculated in [2]. In [3] it has been shown that the total spectral entropy can be used as a measure of the information content in a fractional order model of anomalous diffusion.
Fractional calculus has been applied to almost every field of science, engineering, and mathematics during the last decades [4,5,6,7,8]. Particularly fractional calculus has significant impact in the fields of viscoelasticity and rheology, physics, electrical engineering, electrochemistry, signal and image processing, biology, biophysics and bioengineering, mechanics, mechatronics, and control theory. Fractional calculus is indeed a worthwhile mathematical tool that can undertake more than integer calculus. The monographs authored by Samko, Kilbas, Marichev [9], Podlubny [10] and Kilbas, Srivastava, Trujillo [7] have been helpful in understanding the theory and applications of fractional differential equations.
Numerous numerical methods have been proposed for solving the time-fractional differential equations. In this paper, we convert the fractional differential equation into the equivalent integral equation. Then, fractional trapezoidal formula is used to approximate fractional integral which has second-order accuracy [11,12]. Early in 1993, Tang [13] presented a finite difference method for the numerical solution of the partial integro-differential equations with a weakly singular kernel based on the product trapezoidal formula. Chen et al. [14] proposed fractional trapezoidal rule (FTR) type difference scheme by combining the second order difference quotient for spatial discretization and the FTR alternating direction implicit method in the time stepping for a two-dimensional fractional evolution equation. Chen et al. [15] derived a fractional trapezoidal rule type difference scheme for fractional order integro-differential equation with second order accuracy both in temporal and spatial directions. Recently, a finite difference scheme has been proposed in [16] to solve time-space fractional diffusion equation of second-order accuracy in both time and space by employing trapezoidal rule. Numerical schemes for linear and nonlinear time-space fractional diffusion equations were constructed in [17] using the trapezoidal formula for temporal approximation and the centred difference approximation for the spatial Riesz fractional derivative. Several numerical schemes have been proposed to approximate Riesz fractional derivative based on numerical methods to approximate Riemann–Liouville derivative such as standard Grünwald–Letnikov formula (first-order accuracy), shifted Grünwald–Letnikov formula (first-order accuracy) [18], L-2 approximation method [19] (first-order accuracy), spline interpolation method [20] (second-order accuracy), weighted and shifted Grünwald–Letnikov formulas [21] (second and third-order accuracy), fractional average central difference formula [22] (second and fourth-order accuracy). It is worth mentioning that high-order algorithms for Riemann–Liouville derivatives were first proposed by Lubich [23], however, the high order algorithms for Riesz derivatives were constructed by Ding and Li [22,24,25].
Many researchers studied the fractional advection–dispersion equation (ADE) recently. Fractional ADE is used for the description of transport dynamics in the complex systems which are controlled by the anomalous diffusion and the non-exponential relaxation patterns [26]. The fractional ADE is also used in groundwater hydrology research to model the transport of passive tracers carried by the fluid flow in a porous medium [27]. Our aim is to investigate the time-space fractional ADE. Time nonlocality deals with memory effects, whereas space nonlocality describes the long-range interaction. The fundamental idea is that fractional order models convey more information about the underlying structure and dynamics of complex systems. Total Shannon spectral entropy for the case of anomalous diffusion governed by a fractional order diffusion equation generalized in space and in time is calculated in [3] as it can be used as a measure of the information content in a fractional order model of anomalous diffusion. This fractional order representation of the continuous time, random walk model of diffusion gives a spectral entropy minimum for normal (i.e., Gaussian) diffusion with surrounding values leading to greater values of spectral entropy. Povstenko et al. [28] examined the fundamental solutions to space-time fractional diffusion equation with mass absorption (mass release) in the case of axial symmetry. Liu et al. [29] considered time fractional ADE and the solution was obtained using variable transformation, Mellin and Laplace transforms, and H-functions. Povstenko and Kyrylych [30] discussed two different generalizations of the space-time fractional advection–diffusion equation. They studied the fundamental solutions to the corresponding Cauchy and source problems for one spatial variable using Laplace transform and Fourier transform with respect to time and spatial coordinate, respectively. Huang and Liu [31] also considered time-space fractional ADE and obtained the solution in terms of Green functions. Meerschaert et al. [18] proposed numerical methods to solve the one-dimensional space fractional ADE with variable coefficients on a finite domain. Tripathi et al. [32] investigated the approximate analytical solution of fractional order nonlinear diffusion equations by using the homotopy analysis method. Momani et al. [33] developed a reliable algorithm using the Adomian decomposition method to construct a numerical solution for the time-space fractional ADE. Liu et al. [34] proposed an approximation of the Lëvy–Feller advection–dispersion process by employing a random walk and finite difference methods. Finite difference methods [35], finite element methods [36], finite volume methods [37], homotopy perturbation methods [38] and spectral methods [39,40] are also employed to approximate the fractional ADE. Furthermore, recent advances in numerical linear algebra had a substantial impact on designing efficient methods for the solution of the resulting linear systems which are dense but whose computational cost can be essentially reduced to where N is the size of the underlying coefficient matrix (see [41,42,43,44] and references therein). In this article, we construct a numerical scheme for the time-space fractional ADE by transforming the fractional differential equations into equivalent Volterra integral equations. As it is known that numerical methods for an integral equation have better numerical stability over the schemes designed for equivalent differential equation. Also the numerical methods for an integral equation can be constructed based on the weaker smoothness requirement than that for the differential equation. To the best of our knowledge, all of the other higher order methods are proposed based on the discretizations for fractional derivative directly.
This paper is organized as follows. In Section 2, some useful notations and auxiliary lemmas are introduced. In Section 3, the fractional trapezoidal scheme is derived combined with the second-order fractional weighted and shifted Grünwald–Letnikov formula for the approximation of the Riesz derivative. Section 4 is devoted to the study of the stability and convergence of the proposed scheme. Some numerical experiments are presented to verify the efficiency of our theoretical results in Section 5. The last section concludes our work.
2. Preliminaries
Definition 1.
The order left and right Riemann–Liouville fractional derivatives of the function f on are given by:
Left Riemann–Liouville fractional derivative:
Right Riemann–Liouville fractional derivative:
Definition 2.
The Caputo fractional derivative of order of the function f on is defined by:
Definition 3.
The Riemann–Louville fractional integral of order of the function f on is defined by:
In this paper, we will consider the following time-space fractional ADE
with the initial conditions
and the Dirichlet boundary conditions
where and is the Caputo fractional derivative. In addition, and are the Riesz fractional derivatives of order and respectively, defined on the domain as follows [19]
where
and
In the interval , let be mesh points in space, where is the uniform spatial step size. Meerschaert and Tadjeran [18] showed that the standard Grünwald–Letnikov difference formula was often unstable for time dependent problems and they proposed the shifted Grünwald difference operators to approximate the left and right Riemann–Liouville fractional derivatives
that have the first order accuracy given by,
where are integers, and . In fact, the coefficients are the coefficients of the power series of the function ,
for all and they can be evaluated recursively by using the following relation
Lemma 1 ([35]).
Suppose that then the coefficients satisfy
Lemma 2 ([35]).
Suppose that then the coefficients satisfy
Tian et al. in [21] derived the following weighted shifted Grünwald difference operators based on the multi-step method
Lemma 3 ([21]).
Suppose that let and their Fourier transforms belong to , then the weighted and shifted Grünwald difference operators satisfy
uniformly for where are integers and
Consider a function under the same assumptions as in Lemma 3 on the bounded interval , if or , the function can be zero extended for or . In addition, then, the order left and right Riemann–Liouville fractional derivatives of at each point x can be approximated with the second order accuracy as follows
where and
Lemma 4.
When the discrete approximations for the Riemann–Liouville fractional derivatives on the domain are
where
Lemma 5 ([45]).
Suppose that , then the coefficients satisfy
Lemma 6 ([21]).
Suppose that , then the coefficients satisfy
Lemma 7 ([46]).
Suppose for there exists a positive constant such that
Lemma 8 ([47]).
Let
then satisfy the following properties
- 1.
- 2.
- 3.
- there exists a positive constant such that
Lemma 9 ([46]).
Suppose then we have
for where
and depends on τ with
Here, we assume that is,
Lemma 10 ([46]).
Suppose that are defined by Lemma 9, then we can conclude that:
- 1.
- are monotonically decreasing when n increases.
- 2.
- are monotonically decreasing when n increases.
- 3.
- are monotonically decreasing when n increases.
3. Finite Difference Approximation
We define and where and are the time and space step sizes, respectively. Considering system (1)–(3) at the point , we have
Assume that denotes the numerical approximation of . We can discretize the Riesz fractional derivatives and in truncated bounded domain as follows:
Let and . Noting that and since for and for . Using the approximation to the Riesz fractional derivative given in (15) and (16) into (14), we obtain
where with initial and boundary conditions discretized as follows:
Fractional Trapezoid Formula
In this subsection and in the sequel, the symbol C denotes a generic constant, whose value may be different from one line to another. Integrating both sides of (17) with respect to the time t from to and using Lemmas 4, 7 and 9, we obtain
where depends on h and by using Lemma 4, we have
and
Here depends on and h as by Lemma 7, we get
Letting , we obtain
Hence, the solution for system (1)–(3) can be approximated by the following scheme:
where . We can write this system into the following matrix form:
where
with I is an identity matrix, and are matrices that satisfy
Let
then we obtain the following numerical scheme based on fractional trapezoid formula
with initial and boundary conditions
4. Stability and Convergence Analysis
4.1. Stability
In this section, we analyze the stability and convergence for the scheme (26).
Remark 1.
For If
then we obtain
Remark 2.
Let be as defined in Lemma 8, then where Using , we have
Lemma 11.
if
Proof.
Since is equivalent to
that is
☐
Let numerical solution of the numerical scheme (21) with a different initial value , and
According to (21), we have
For convenience, we suppose that
Put , and assume that
4.2. Convergence
Put , and assume that
Theorem 2.
5. Numerical Experiments
In this section, some numerical experiments are given to demonstrate the effectiveness and accuracy of the proposed numerical scheme. Consider the following time-space fractional advection–diffusion equation .
Example
We solve this fractional advection–dispersion equation with the proposed numerical scheme with . The comparison of the numerical solution with the exact solution for , at is given in Figure 1. To compare the numerical and the exact solutions, error plot is given in Figure 2. For fixed the exact solution and the approximate solution with temporal and spatial steps are shown in Figure 3.
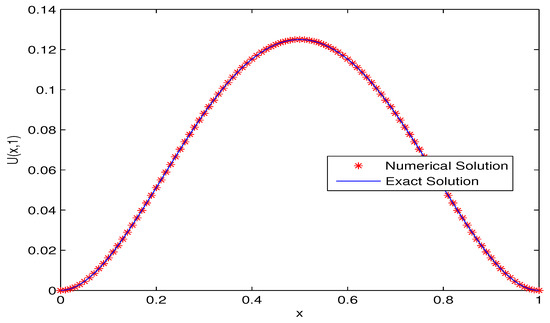
Figure 1.
Comparison between numerical solution and exact solution for .

Figure 2.
Error plot for .
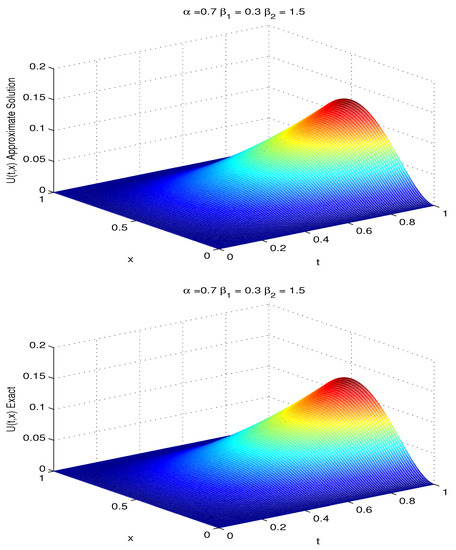
Figure 3.
Approximate solution (Upper) and exact solution (Lower) for .
The spatial errors and convergence orders of the proposed scheme for solving (35) are shown in Table 1 and Table 2 for different values of and , respectively. Fixing . The –norm is used to compute the error of the numerical solution at the last time step by

Table 1.
The errors and convergence order when .

Table 2.
The errors and convergence order when , .
Next, we fix the spatial step size and vary the time step. Table 3 presents the errors and convergence order for various values of at time . The numerical convergence order in the spatial and temporal direction is , as in Theorem 2.

Table 3.
The errors and convergence order when , .
6. Conclusions
In this article, we have proposed a finite difference method for solving a class of time-space fractional advection–dispersion equation. We combined the trapezoidal formula, which is well known for the numerical integration of Riemann–Liouville integral, with the Grünwald–Letnikov discretization of the Riesz fractional derivative in space to obtain a numerical scheme. We proved that our proposed scheme is stable and convergent with the accuracy of under the sufficient conditions and However, our numerical experiments given in Table 2 and Table 3 depict that when and the presented numerical method is still stable and convergent for various temporal and spatial time steps. Finally, some numerical experiments for the fractional finite difference method are given that agree very well with our theoretical results.
Author Contributions
Sadia Arshad designed this manuscript. Sadia arshad and Jianfei Huang performed the numerical experiments. Dumitru Baleanu, Maysaa Mohamed Al Qurashi, Yifa Tang and Zhao Yue prepared the final version of the paper and analyzed. All the authors have equally contributed in the discussion and overall preparation of the manuscript, as well as read and improved the final version of the manuscript.
Acknowledgments
This research is supported by the National Natural Science Foundation of China under grant 11771438 and 11701502, the Scientific and Technological Research Council of Turkey (TÜBİTAK) under grant TBAG-117F473, Higher Education Commission of Pakistan (HEC) under NRPU project 2017 and the “Research Center of the Center for Female Scientific and Medical Colleges”, Deanship of Scientific Research, King Saud University. The authors are extending their heartfelt thanks to the reviewers for their constructive suggestions towards the improvement of the revised article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Machado, J.A.T. Entropy analysis of integer and fractional dynamical systems. Nonlinear Dyn. 2010, 62, 371–378. [Google Scholar]
- Hoffmann, K.H.; Essex, C.; Schulzky, C. Fractional diffusion and entropy production. J. Non-Equilib. Thermodyn. 1998, 23, 166–175. [Google Scholar] [CrossRef]
- Magin, R.L.; Ingo, C. Entropy and information in a fractional order model of anomalous diffusion. IFAC Proc. 2012, 45, 428–433. [Google Scholar] [CrossRef]
- Bueno-Orovio, A.; Kay, D.; Grau, V.; Rodriguez, B.; Burrage, K. Fractional Diffusion Models of Cardiac Electrical Propagation: Role of Structural Heterogeneity in Dispersion of Repolarization; Technical Report OCCAM 13/35; Oxford Centre for Collaborative Applied Mathematics: Oxford, UK, 2013. [Google Scholar]
- Cafagna, D.; Grassi, G. Observer-based projective synchronization of fractional systems via a scalar signal: Application to hyperchaotic Rösslersystems. Nonlinear Dyn. 2012, 68, 117–128. [Google Scholar] [CrossRef]
- Caponetto, R.; Maione, G.; Pisano, A.; Rapaic, M.M.R.; Usai, E. Analysis and shaping of the self-sustained oscillations in relay controlled fractional-order systems. Fract. Calculus Appl. Anal. 2013, 16, 93–108. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations, vol. 204 of North-Holland Mathematics Studies; Elsevier: New York, NY, USA, 2006. [Google Scholar]
- Machado, J.T.; Stefanescu, P.; Tintareanu, O.; Baleanu, D. Fractional calculus analysis of the cosmic microwave background. Romanian Rep. Phys. 2013, 65, 316–323. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications, Gordon and Breach; Science Publishers: Hauppauge, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Acdemic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algor. 2004, 36, 31–52. [Google Scholar] [CrossRef]
- Zhuang, P.; Liu, F.; Anh, V.; Turner, I. New solution and analytical techniques of the implicit numerical method for the anomalous subdiffusion equation. SIAM J. Numer. Anal. 2008, 46, 1079–1095. [Google Scholar] [CrossRef]
- Tang, T. A finite difference scheme for partial integro-differential equations with weakly singular kernel. Appl. Numer. Math. 1993, 11, 309–319. [Google Scholar] [CrossRef]
- Chen, H.; Xu, D.; Peng, Y. An alternating direction implicit fractional trapezoidal rule type difference scheme for the two-dimensional fractional evolution equation. Int. J. Comput. Math. 2015, 92, 2178–2197. [Google Scholar] [CrossRef]
- Chen, H.; Gan, S.; Xu, D. A fractional trapezoidal rule type difference scheme for fractional order integro–differential equation. J. Frac. Calcul. Appl. 2016, 7, 133–146. [Google Scholar]
- Arshad, S.; Huang, J.; Khaliq, A.Q.M.; Tang, Y. Trapezoidal scheme for time-space fractional diffusion equation with Riesz derivative. J. Comput. Phys. 2017, 350, 1–15. [Google Scholar] [CrossRef]
- Arshad, S.; Bu, W.; Huang, J.; Tang, Y.; Zhao, Y. Finite difference method for time-space linear and nonlinear fractional diffusion equations. Int. J. Comp. Math. 2018, 95, 202–217. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Tadjeran, C. Finite difference approximations for fractional advection–dispersion flow equations. J. Comput. Appl. Math. 2004, 172, 65–77. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, F.; Turner, I. Numerical methods for fractional partial differential equations with Riesz space fractional derivatives. Appl. Math. Model. 2010, 34, 200–218. [Google Scholar] [CrossRef]
- Sousa, E. A second order explicit finite difference method for the fractional advection diffusion equation. Comput. Math. Appl. 2012, 64, 3141–3152. [Google Scholar] [CrossRef]
- Tian, W.Y.; Zhou, H.; Deng, W.H. A class of second order difference approximation for solving space fractional diffusion equations. Math. Comput. 2015, 84, 1703–1727. [Google Scholar] [CrossRef]
- Ding, H.F.; Li, C.P.; Chen, Y.Q. High-order algorithms for Riesz derivative and their applications (I). Abstr. Appl. Anal. 2014, 2014, 653797. [Google Scholar] [CrossRef]
- Lubich, C. Discretized fractional calculus. SIAM J. Math. Anal. 1986, 17, 704–719. [Google Scholar] [CrossRef]
- Ding, H.F.; Li, C.P.; Chen, Y.Q. High-order algorithms for Riesz derivative and their applications (II). J. Comput. Phys. 2015, 293, 218–237. [Google Scholar] [CrossRef]
- Ding, H.F.; Li, C.P. High-order algorithms for Riesz derivative and their applications (III). Fract. Calc. Appl. Anal. 2016, 19, 19–55. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Benson, D.A.; Wheatcraft, S.W.; Meerschaert, M.M. Application of a fractional advection–dispersion equation. Water Resour. Res. 2000, 36, 1403–1412. [Google Scholar] [CrossRef]
- Povstenko, Y.; Kyrylych, T.; Ryga, G. Fractional diffusion in a solid with mass absorption. Entropy 2017, 19, 203. [Google Scholar] [CrossRef]
- Liu, F.; Anh, V.; Turner, I.; Zhuang, P. Time fractional advection dispersion equation. J. Appl. Math. Comput. 2003, 13, 233–245. [Google Scholar] [CrossRef]
- Povstenko, Y.; Kyrylych, T. Two approaches to obtaining the space-time fractional advection–diffusion equation. Entropy 2017, 19, 297. [Google Scholar] [CrossRef]
- Huang, F.; Liu, F. The fundamental solution of the space–time fractional advection–dispersion equation. J. Appl. Math. Comput. 2005, 19, 233–245. [Google Scholar] [CrossRef]
- Tripathi, N.K.; Das, S.; Ong, S.H.; Jafari, H.; Qurashi, M.A. Solution of higher order nonlinear time-fractional reaction diffusion equation. Entropy 2016, 18, 329. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Numerical solutions of the space–time fractional advection–dispersion equation. Numer. Meth. Part. Differ. Equat. 2008, 24, 1416–1429. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, F.; Turner, I.; Anh, V. Approximation of the Lëvy–Feller advection–dispersion process by random walk and finite difference method. J. Comput. Phys. 2007, 222, 57–70. [Google Scholar] [CrossRef]
- Liu, F.; Zhuang, P.; Anh, V.; Turner, I.; Burra, K. Stability and convergence of the difference methods for the space-time fractional advection–diffusion equation. Appl. Math. Comput. 2007, 191, 12–20. [Google Scholar] [CrossRef]
- Ervin, V.J.; Roop, J.P. Variational formulation for the stationary fractional advection–dispersion equation. Numer. Meth. Part. Diff. Equ. 2006, 22, 558–576. [Google Scholar] [CrossRef]
- Hejazi, H.; Moroney, T.; Liu, F. Stability and convergence of a finite volume method for the space fractional advection–dispersion equation. J. Comput. Appl. Math. 2014, 255, 684–697. [Google Scholar] [CrossRef]
- Golbabai, A.; Sayevand, K. Analytical modelling of fractional advection–dispersion equation defined in a bounded space domain. Math. Comput. Model. 2011, 53, 1708–1718. [Google Scholar] [CrossRef]
- Carella, A.R.; Dorao, C.A. Least-squares spectral method for the solution of a fractional advection–dispersion equation. J. Comput. Phys. 2013, 232, 33–45. [Google Scholar] [CrossRef]
- Zheng, G.H.; Wei, T. Spectral regularization method for a Cauchy problem of the time fractional advection–dispersion equation. J. Comput. Appl. Math. 2010, 233, 2631–2640. [Google Scholar] [CrossRef]
- Donatelli, M.; Mazza, M.; Serra-Capizzano, S. Spectral analysis and structure preserving preconditioners for fractional diffusion equations. J. Comput. Phys. 2016, 307, 262–279. [Google Scholar] [CrossRef]
- Lei, S.L.; Sun, H.W. A circulant preconditioner for fractional diffusion equations. J. Comput. Phys. 2013, 242, 715–725. [Google Scholar] [CrossRef]
- Lin, X.L.; Ng, M.K.; Sun, H.W. A splitting preconditioner for Toeplitz-like linear systems arising from fractional diffusion equations. SIAM J. Matrix Anal. Appl. 2017, 38, 1580–1614. [Google Scholar] [CrossRef]
- Pan, J.; Ng, K.M.; Wang, H. Hong Fast iterative solvers for linear systems arising from time-dependent space-fractional diffusion equations. SIAM J. Sci. Comput. 2016, 38, A2806–A2826. [Google Scholar] [CrossRef]
- Feng, L.B.; Zhuang, P.; Liu, F.; Turner, I.; Li, J. High-order numerical methods for the Riesz space fractional advection–dispersion equations. Comput. Math. Appl. 2016. [Google Scholar] [CrossRef]
- Yu, B.; Jiang, X.; Xu, H. A novel compact numerical method for solving the two-dimensional non-linear fractional reaction-subdiffusion equation. Numer. Algor. 2015, 68, 923–950. [Google Scholar] [CrossRef]
- Zhuang, P.; Liu, F.; Anh, V.; Turner, I. Stability and convergence of an implicit numerical method for the non-linear fractional reaction–subdiffusion process. IMA J. Appl. Math. 2009, 74, 645–667. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
