1. Introduction
The presence of correlations in bipartite quantum systems is one of the main features of quantum mechanics. The most important one among such correlations is entanglement [
1]. However, recently much attention has been devoted to the study and the characterization of quantum correlations that go beyond the paradigm of entanglement, being necessary but not sufficient for its presence. Non-entangled quantum correlations also play important roles in various quantum communications and quantum computing tasks [
2,
3,
4,
5].
For the last two decades, various methods have been proposed to quantify quantum correlations, such as quantum discord (QD) [
6,
7], geometric quantum discord [
8,
9], measurement-induced nonlocality (MIN) [
10] and measurement-induced disturbance (MID) [
11] for discrete-variable systems. It is also important to develop new simple criteria for witnessing correlations beyond entanglement for continuous-variable systems. In this direction, Giorda, Paris [
12] and Adesso, Datta [
13] independently introduced the definition of Gaussian QD for Gaussian states and discussed its properties. Adesso and Girolami in [
14] proposed the concept of Gaussian geometric discord (GD) for Gaussian states. Measurement-induced disturbance of Gaussian states was studied in [
15], while MIN for Gaussian states was discussed in [
16]. For other related results, see [
17,
18] and the references therein. Note that not every quantum correlation defined for discrete-variable systems has a Gaussian analogy for continuous-variable systems [
16]. On the other hand, the values of Gaussian QD and Gaussian GD are very difficult to be computed and the known formulas are only for some
-mode Gaussian states. Little information is revealed by Gaussian QD and GD. The purpose of this paper is to introduce a new measure of nonclassicality for
-mode quantum states in continuous-variable systems, which is simpler to be computed and can be used with any
-mode Gaussian states.
Given a bipartite quantum state
acting on Hilbert space
, denote by
the reduced density operator in subsystem A. For the case of finite dimensional systems, the author of [
19] proposed a quantity
defined by
where
denotes the Frobenius norm and
is any unitary operator satisfying
. This quantity demands that the reduced density matrix of the subsystem A is invariant under this unitary transformation. However, the global density matrix may be changed after such local unitary operation, and therefore
may be non-zero for some
. Then, Datta, Gharibian, et al. discussed respectively in [
20,
21] the properties of
and revealed that
can be used to investigate the nonclassical effect.
Motivated by the works in [
19,
20,
21], we can consider an analogy for continuous-varable systems. In the present paper, we introduce a quantity
in terms of local Gaussian unitary operations for
-mode quantum states in Gaussian systems. Different from the finite dimensional case, besides the local Gaussian unitary invariance property for quantum states, we also show that
if and only if
is a Gaussian product state. This reveals that the quantity
is a kind of faithful measure of the nonclassicality for Gaussian states that a state has this nonclassicality if and only if it is not a product state. In addition, we show that
for each
-mode Gaussian state
and the upper bound 1 is sharp. An estimate of
for any
-mode Gaussian states is provided and an explicit formula of
for any
-mode Gaussian states is obtained. As an application, a criterion of entanglement for
-mode Gaussian states is established in terms of
by numerical approaches. Finally, we compare
with Gaussian QD and Gaussian GD to illustrate that it is a better measure of the nonclassicality.
2. Gaussian States and Gaussian Unitary Operations
Recall that, for arbitrary state
in an
n-mode continuous-variable system, its characteristic function
is defined as
where
with
the field of real numbers and
the transposition, and
is the Weyl operator. Let
. As usual,
and
stand respectively for the position and momentum operators for each
. They satisfy the Canonical Commutation Relation (CCR) in natural units (
)
Gaussian states: is called a Gaussian state if
is of the form
where
is called the mean or the displacement vector of
and
is the covariance matrix (CM) of
defined by
with
([
22,
23,
24]). Here,
stands for the set of all
l-by-
k real matrices and, when
, we write
as
. Note that the CM
of a state is symmetric and must satisfy the uncertainty principle
, where
with
for each
i. From the diagonal terms of the above inequality, one can easily derive the usual Heisenberg uncertainty relation for position and momentum
with
[
25].
Now assume that
is any
-mode Gaussian state. Then, the CM
of
can be written as
where
,
and
. Particularly, if
, by means of local Gaussian unitary (symplectic at the CM level) operations,
has a standard form:
where
,
,
,
,
and
([
26,
27,
28,
29]).
Gaussian unitary operations. Let us consider an
n-mode continuous-variable system with
. For a unitary operator
U, the unitary operation
is said to be Gaussian if its output is a Gaussian state whenever its input is a Gaussian state, and such
U is called a Gaussian unitary operator. It is known that a unitary operator
U is Gaussian if and only if
for some vector
in
and some
, the symplectic group of all
real matrices
that satisfy
Thus, every Gaussian unitary operator
U is determined by some affine symplectic map
acting on the phase space, and can be denoted by
([
23,
24]).
The following well-known facts for Gaussian states and Gaussian unitary operations are useful for our purpose.
Lemma 1 ([
23])
. For any -mode Gaussian state , write its CM Γ
as in Equation (1). Then, the CMs of the reduced states and are matrices A and B, respectively. Denote by the set of all quantum states of , where and are respectively the state space for n-mode and m-mode continuous-variable systems.
Lemma 2 ([
30])
. If is an -mode Gaussian state, then is a product state, that is, for some and , if and only if , where Γ
, and are the CMs of , and , respectively. Lemma 3 ([
23,
24])
. Assume that ρ is any n-mode Gaussian state with CM Γ
and displacement vector , and is a Gaussian unitary operator. Then, the characteristic function of the Gaussian state is of the form , where and . 3. Quantum Correlation Introduced by Gaussian Unitary Operations
Now, we introduce a quantum correlation by local Gaussian unitary operations in the continuous-variable system.
Definition 1. For any -mode quantum state , the quantum correlation of by Gaussian unitary operations is defined by where the supremum is taken over all Gaussian unitary operators satisfying , and is the reduced state. Here, is the set of all bounded linear operators acting on . Observe that holds for every product state. Thus, the product state contains no such correlation.
Remark 1. For any Gaussian state , there exist many Gaussian unitary U so that . This ensures that the definition of the quantity makes sense for each Gaussian state .
To see this, we need Williamson Theorem ([
31]), which states that, for any
n-mode Gaussian state
with CM
, there exists a
symplectic matrix
such that
with
. The diagonal matrix
and
s are called respectively the Williamson form and the symplectic eigenvalues of
. By the Williamson Theorem, there exists a Gaussian unitary operator
such that
, where
are thermal states. Let
with
. Then,
is a symplectic matrix, and the corresponding Gaussian unitary operator
has the form
. It is easily checked that
, and so
. Now, write
. Obviously,
W is Gaussian unitary and satisfies
.
We first prove that is local Gaussian unitary invariant for all quantum states.
Proposition 1 (Local Gaussian unitary invariance)
. If is an -mode quantum state, then holds for any Gaussian unitary operators and .
Proof of Proposition 1. Let
be an
-mode Gaussian state. For any Gaussian unitary operators
and
, denote
. Then,
. For any Gaussian unitary operator
satisfying
, we have
. Let
. Then,
is also a Gaussian unitary operator and satisfies
. It is clear that
runs over all Gaussian unitary operators that commutes with
when
W runs over all Gaussian unitary operators commuting with
. Hence, by Equation (
3), we have
as desired. ☐
The next theorem shows that is a faithful nonclassicality measure for Gaussian states.
Theorem 1. For any -mode Gaussian state , if and only if is a product state.
Proof of Theorem 1. By Definition 1, the “if” part is apparent. Let us check the “only if” part. Since the mean of any Gaussian state can be transformed to zero under some local Gaussian unitary operation, it is sufficient to consider those Gaussian states whose means are zero by Proposition 1. In the sequel, assume that
is an
-mode Gaussian state with zero mean vector and CM
as in Equation (
1), so that
.
By Lemma 1, the CM of
is
B. According to the Williamson Theorem, there exists a symplectic matrix
such that
and
, where
and
are of the thermal states. Write
. It follows from Proposition 1 that
. Obviously,
has the CM of form:
and the mean
.
For any
for
, let
be the symplectic matrix as in Remark 1. Then,
and
. As
, by Equation (
3),
, and hence they must have the same CMs, that is,
Note that
is an invertible matrix if we take
for each
i. Then, it follows from
that we must have
Thus,
is a product state by Lemma 2, and, consequently,
is also a product state. ☐
We can give an analytic formula of for (1+1)-mode Gaussian state . Since is locally Gaussian unitary invariant, it is enough to assume that the mean vector of is zero and the CM is standard.
Theorem 2. For any -mode Gaussian state with CM Γ whose standard form is as in Equation (2), we have Particularly, whenever is pure. Proof of Theorem 2. By Proposition 1, we may assume that the mean vector of
is zero. Let
be a Gaussian unitary operator such that
. Then,
and
meet the conditions
and
. It follows that
. Thus, we can denote
by
. As
, there exists some
such that
. Thus, the CM of Gaussian state
is
and the mean of
is
as
. Hence, by Equations (
3) and (
4), one gets
Hence, Equation (
4) is true.
Particularly, if
is a pure state, then, by [
29], we have
This entails that
. ☐
For the general -mode case, it is difficult to give an analytic formula of for all -mode Gaussian states . However, we are able to give an estimate of .
Theorem 3. For any -mode Gaussian state with CM as in Equation (1), we have Particularly, when is pure, Moreover, the upper bound 1 in the inequality (5) is sharp, that is, we have Proof of Theorem 3. By Proposition 1, without loss of generality, we may assume that the mean of
is
. Let
be a Gaussian unitary operator such that
. Then, the CM and the mean of the Gaussian state
are
and
, respectively. Note that, for any
n-mode Gaussian states
with CMs
and means
, respectively, it is shown in [
32] that
Hence,
Since
,
and
, by Fischer’s inequality (p. 506, [
33]), we have
. Thus, we get
. If
is a pure state, then
, which gives
Notice that, by Equation (
6), we have
. This implies that
since
and
, that is, the inequality (
5) is true.
To see that the upper bound 1 is sharp, consider the two-mode squeezed vacuum state
, where
is the two-mode squeezing operator with squeezed number
and
is the vacuum state ([
24]). The CM of
is
, where
and
. By Theorem 2, it is easily calculated that
Clearly,
as
, thus
completeing the proof. ☐
4. Comparison with Other Quantum Correlations
Entanglement is one of the most important quantum correlations, being central in most quantum information protocols [
1]. However, it is an extremely difficult task to verify whether a given quantum state is entangled or not. Recall that a quantum state
is said to be separable if it belongs to the closed convex hull of the set of all product states
. Note that a state
is separable if and only if it admits a representation
, where
is a Borel probability measure and
is a Borel
-valued function on some complete, separable metric space
[
34]. One of the most useful separability criteria is the positive partial transpose (PPT) criterion, which can be found in [
35,
36]. The PPT criterion states that if a state is separable, then its partial transposition is positive. For discrete systems, the positivity of the partial transposition of a state is necessary and sufficient for its separability in the
and
cases. However, it is not true for higher dimensional systems [
36]. For continuous systems, in [
27,
37], the authors extended the PPT criterion to
-mode continuous systems. It is remarkable that, for any
-mode Gaussian state, it has PPT if and only if it is separable. Furthermore, for the
-mode case, it is shown that a
-mode Gaussian state
is separable if and only if
, where
is the smallest symplectic eigenvalue of the CM of the partial transpose
[
24,
29].
Comparing
with the entanglement, we conjecture that there exists some positive number
such that
for any
-mode separable Gaussian state
, that is,
If this is true, then
is entangled when
. This will give a criterion of entanglement for
-mode Gaussian states in terms of correlation
. Though we can not give a mathematical proof, we show that this is true for
-mode separable Gaussian states with
by a numerical approach (Firstly, we randomly generated one million, five million, ten million, fifty million, one hundred million, five hundred million separable Gaussian states with
ranging from 1 to 2, respectively. We found that the maximum of
is smaller than
. Secondly, we used the same method and extended the range to 5. Then, the maximum of
is smaller than
. Thirdly, using the same method and extending the range to
, respectively, we found that the maximum of
is still smaller than
. We repeated the above computations ten times, and the result is just the same).
Proposition 2. for any -mode separable Gaussian state .
It is followed from Theorem 1 that the quantum correlation exists in all entangled Gaussian states and almost all separable Gaussian states except product states. In addition, Proposition 2 can be viewed as a sufficient condition for the entanglement of two-mode Gaussian states: if , then is entangled.
To have an insight into the behavior of this quantum correlation by
and to compare it with the entanglement and the discords, we consider a class of physically relevant states–squeezed thermal state (STS). This kind of Gaussian state is used by many authors to illustrate the behavior of several interesting quantum correlations [
12,
13]. Recall that a two-mode Gaussian state
is an STS if
where
is the thermal state with thermal photon number
(
) and
is the two-mode squeezing operator. Particularly, when
,
is a pure two-mode squeezed vacuum state, also known as an Einstein–Podolski–Rosen (EPR) state [
24]. When
or
,
is a mixed Gaussian state. For fixed
r,
is separable (not in product form) for large enough
. Notice that if
is a STS with the CM
in the standard form in Equation (
2), then
. In this case, by Theorem 2, we have
Using this parametrization, one can get
,
and
, where
([
12]). Especially, if
, then
is called a symmetric squeezed thermal state (SSTS). Now assume that
is a SSTS. Then,
is a mixed state if and only if
. The global purity of
is
and the smallest symplectic eigenvalue
of CM of
is
. Moreover,
is entangled if and only if
.
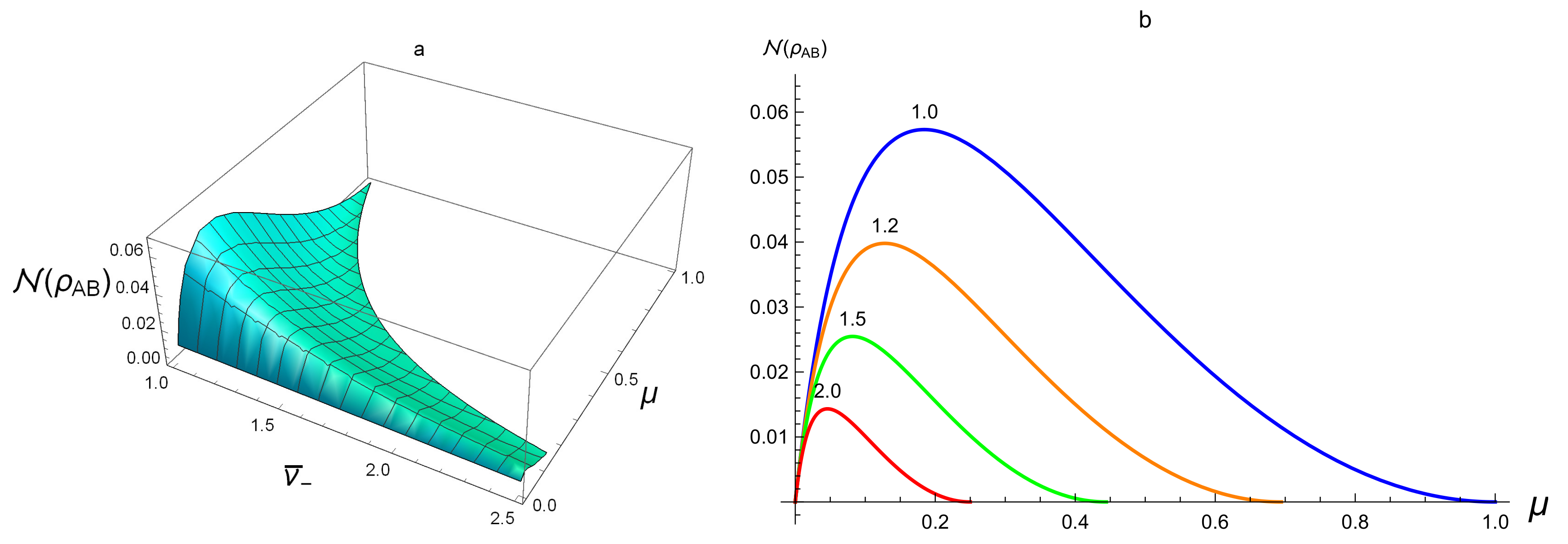
We first discuss the relation between
and the entanglement by considering SSTS. Regard
as a function of
and
. From
Figure 1a, for separable states, we see that the value
at the separable SSTS is always smaller than 0.06, which supports positively Proposition 2. From
Figure 1b, for fixed purity
,
turns out to be a decreasing function of
. However, for fixed
,
tends to 0 when
increases.
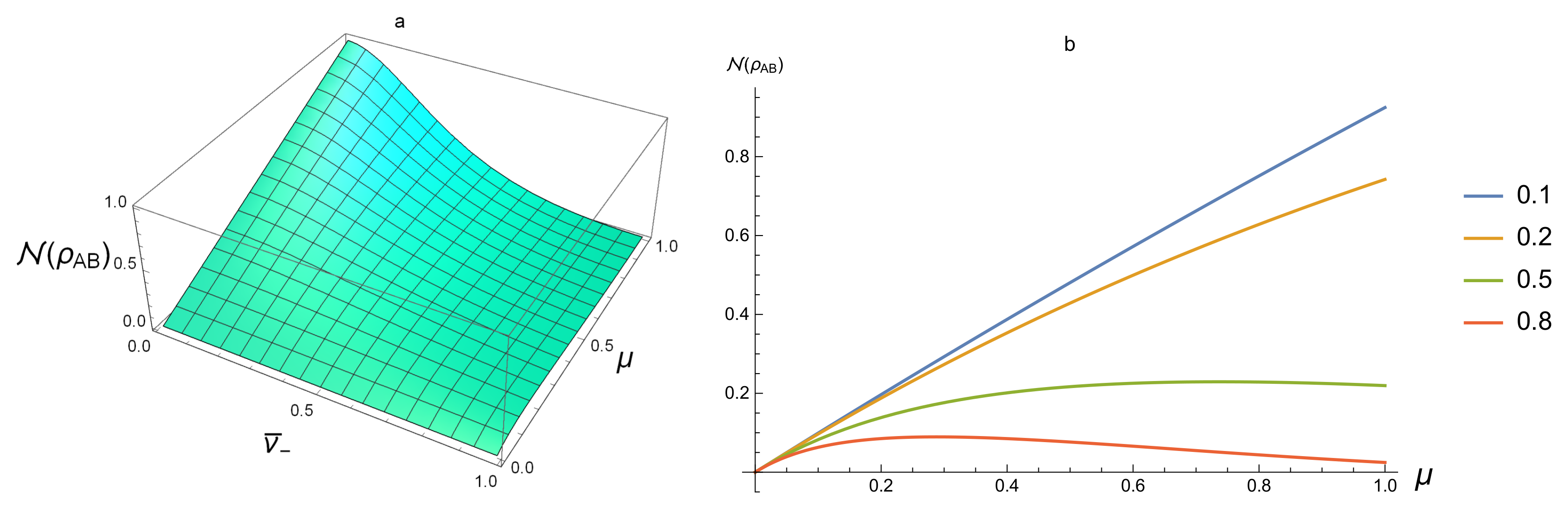
For the entangled SSTS, one sees from
Figure 2a,b that the value of
is from 0 to 1. This reveals that, for some entangled SSTSs,
can be smaller than
. Thus, Proposition 2 is only a necessary condition for a Gaussian state to be separable. For fixed purity
, from
Figure 1b and
Figure 2b,
increases when entanglement increases (that is,
) and
. However, for fixed
, the behavior of
on
is more complex.
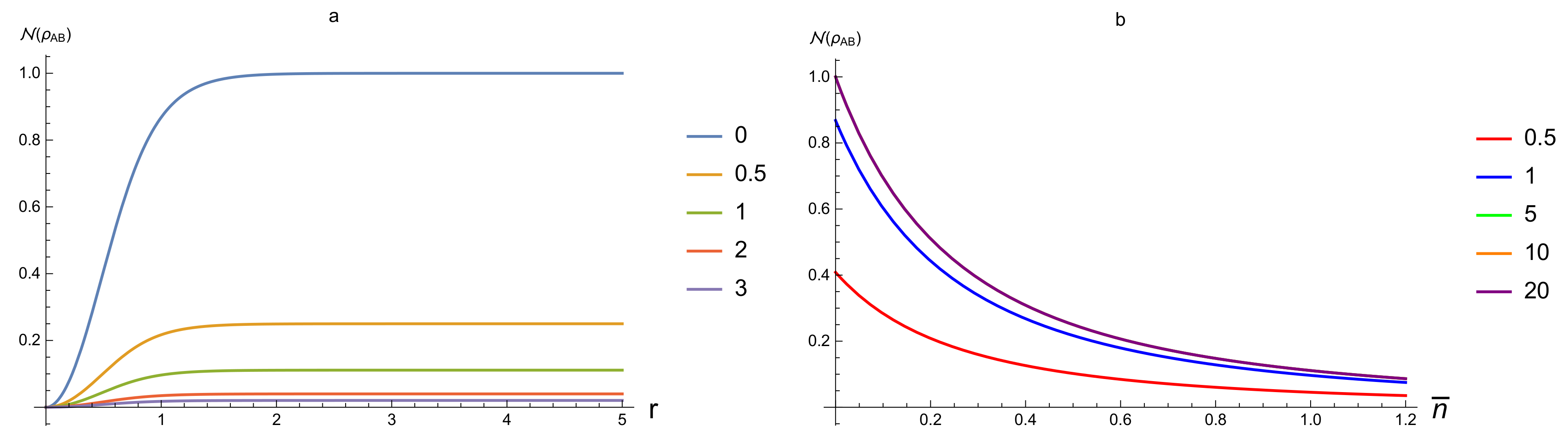
Regarding
as a function of
r and
,
Figure 3 shows that
is an increasing function of
r and a decreasing function of
, respectively. The value of
always gains the maximum at
, that is, at pure states.
Figure 3b also shows that
almost depends only on
when
r is large enough because the curves for
are almost the same.
Recall that an
n-mode Gaussian positive operator-valued measure (GPOVM) is a collection of positive operators
satisfying
, where
with
the Weyl operators and
an
n-mode Gaussian state, which is called the seed of the GPOVM
[
38,
39]. Let
be a
-mode Gaussian state and
be a GPOVM of the subsystem B. Denote by
the reduced state of the system A after the GPOVM
performed on the system B, where
. Write the von Neumann entropy of a state
as
, that is,
. Then, the Gaussian QD of
is defined as
[
12,
13], where the infimum takes over all GPOVMs
performed on the system B. It is known that a
-mode Gaussian state has zero Gaussian QD if and only if it is a product state; in addition, for all separable
-mode Gaussian states,
; if the standard form of the CM of a
-mode Gaussian state
is as in Equation (
2), then
where the infimum takes over all one-mode Gaussian states
,
,
and
are the symplectic eigenvalues of the CM of
,
with
the CM of
. Let
, then we have [
13]
In [
14], the quantum GD
is proposed. Consider an
-mode Gaussian state
, its Gaussian GD is defined by
, where the infimum takes over all GPOVM
performed on system
B,
stands for the Hilbert–Schmidt norm and
. If
is a
-mode Gaussian state with the CM
as in Equation (
1) and
is an one-mode Gaussian POVM performed on mode B with seed
, then
, where
is a Gaussian state of which the CM
with
the CM of
. It is known from [
14] that
Now it is clear that, for
-mode Gaussian state
,
if and only if
is a product state.
By Theorem 1 and the results mentioned above,
and
describe the same quantum correlation for
-mode Gaussian states. However, from the definitions,
use all GPOVMs, while
only employs Gaussian unitary operations, which is simpler and may consume less physical resources. Moreover, though an analytical formula of
D is given for two-mode Gaussian states, the expression is more complex and more difficult to calculate (Equations (
8) and (
9)).
is not handled in general and there is no analytical formula for all
-mode Gaussian states (Equation (
10)). As far as we know, there are no results obtained on
for general
-mode case.
To have a better insight into the behavior of
and
, we compare them in scale with the help of two-mode STS. Note that
of any two-mode STS
is given by [
14]
Clearly, our formula (
7) for
is simpler then formula (
11) for
.
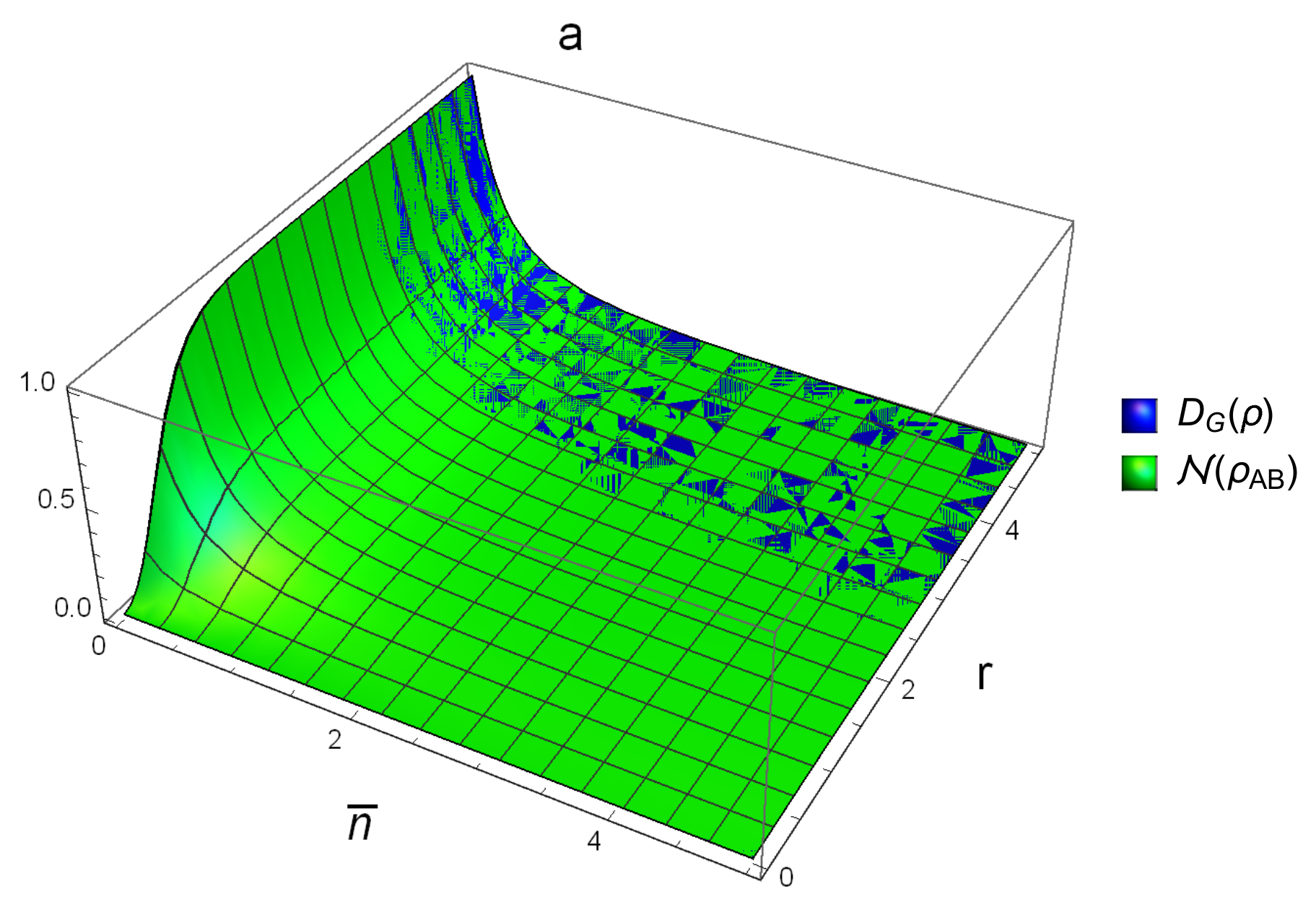
Figure 4 and
Figure 5 are plotted in terms of photo number
and squeezing parameter
r.
Figure 4 shows that, for the case of SSTS and for
, we have
. This means that
is better than
when they are used to detect the correlation that they describe in the SSTS with
.
Figure 5a reveals that, for the case of nonsymmetric STS and for
, we have
; that is,
is better in this situation too. However, for
,
and
can not be compared with each other globally, which suggests that one may use
to detect the correlation.