1. Introduction
Network science [
1,
2,
3,
4] is one of the most rapidly advancing scientific fields of investigation. The success of this field is deeply rooted in its interdisciplinarity. In fact, network science characterizes the underlying structure and dynamics of complex systems ranging from on-line social networks to molecular networks and the brain. Additionally, the theoretical tools and techniques used by network science are coming from different disciplines including statistical mechanics, statistics, machine learning and computer science.
In the last twenty years significant attention has been addressed to modelling framework of complex networks. Since most real networks, from the Internet to molecular networks, are sparse, i.e., they have an average degree that does not depend on the network size, statistical mechanics models focus on modelling sparse networks. These statistical mechanics models can be divided between non-equilibrium growing network models [
5,
6,
7,
8,
9,
10,
11,
12,
13] such as the famous Barabási–Albert model [
5] and equilibrium models such as maximum entropy network ensembles [
14,
15,
16,
17,
18,
19] including Exponential Random Networks [
16,
17,
20,
21,
22] and block models [
23,
24]. The non-equilibrium growing network models have the power to explain the fundamental mechanisms giving rise to emergent properties such as scale-free distributions [
5,
6,
7,
8], degree correlations [
6], communities [
9,
10,
11] and network geometry [
11,
12,
13]. On the contrary, maximum network ensembles constitute the least biased models satisfying a given set of constraints. These models are not explanatory but constitute the ideal null hypothesis to which real networks can be compared.
Recently the need to formulate reliable statistical models is receiving significant attention [
25]. A reliable statistical model will include projectivity and exchangeability [
26,
27,
28,
29,
30]. The projectivity of the statistical network model guarantees that the conclusions reached by considering a subsample of the data are consistent with the ones that can be drawn starting from a larger sample of the data. The exchangeability of the nodes implies that the probability of a network does not depend on the specific labels of the nodes. However, how to reconcile these statistical requirements with the sparseness of the networks, i.e., a average degree that is independent of the network size, constitutes a major impasse of network modelling. For instance it has been shown that random uncorrelated networks are only projective if the average degree
of the network increases linearly with the network size
N, i.e., if the network is maximally dense and
[
27,
30,
31].
In physical terms, the desired projective and exchangeable network process mimicking the subsequent sampling of an increasing portion of the network is a modelling framework that goes beyond the traditional statistical mechanics division between equilibrium and non-equilibrium network modelling approaches. This observation reinforces the belief that actually combining these two properties might be not an easy task.
Already several works have addressed this problem [
32,
33,
34,
35,
36,
37,
38], using different approaches such as relaxing the condition
but always characterizing models with average degree diverging with the network size
N, considering edge exchangeable models or alternatively using an embedding space as a basic mechanism to combine sparsity with projectivity and exchangeability [
31,
39].
Here we propose a network process describing a network evolution mimicking the sampling of a network by subsequently expanding the nodes set. Each node is assigned an hidden variable from a hidden variable distribution. This distribution is the key quantity determining the properties of the network process. If the hidden variable is power-law distributed and the network is sufficiently sparse, the degree distribution displays a power-law tail with the same power-law exponent as the hidden variable distribution.
This model is a projective network process but it is not exchangeable. Nevertheless, this non-equilibrium network model can be directly related to an equilibrium uncorrelated network ensemble in the sparse regime. In fact, by permuting the order in which nodes are sampled it is possible to calculate the probability that two nodes are connected given their corresponding hidden variables. This connection probability is equal to the connection probability in an uncorrelated exchangeable network ensemble in which the hidden variable of each node is identified with half of its expected degree. The “proximity” between the network process and the uncorrelated network ensemble is here quantified by using information theory tools and comparing the entropy of the two models. In particular, we use the entropy of the two network models [
14,
15,
16,
17,
40] to evaluate the difference in the information content of the two models, finding that the two models have small relative entropy difference.
Finally we study how well the proposed model can be used as a null model for real power-law network datasets. To this end we identify the hidden variable of each node with half of its observed degree and we run the model by adding the nodes in the network according to a random permutation of the nodes’ labels. The degree distribution of the real dataset and the degree distribution of the simulation results are in good agreement when starting from power-law networks, and the agreement remains good if the network is grown by only considering a subsample of the nodes of the real data. We also compare the correlations of the real dataset with the correlations of the simulation results to show that the simulations are able to generate only weak correlations of the degrees. Therefore a more refined model should be formulated to capture this additional network property.
The paper is structured as described in the following. In
Section 2 we introduce the definition of the desired statistical properties of network models:
projectivity and
exchangeability. In
Section 3 we discuss major examples of sparse network models (the Barabási–Albert model and the uncorrelated network ensembles) and characterize them with respect to the properties of projectivity and exchangeability. In
Section 4 we present an account of the difficulties in combining projectivity and exchangeability with the sparseness of networks and we give a brief review of the approaches investigated in the recent literature on the subject. In
Section 5 we present a network process mimicking a network sampling process. We characterize its structural and dynamical properties relating this non-equilibrum model to equilibrium uncorrelated network ensembles, and we characterize its statistical properties. In
Section 6 we show the possible use of the proposed network process as a null model for modelling real power-law network datasets. Finally in
Section 7 we give the conclusions.
2. Statistical Terms
Projectivity and exchangeability are two very basic and very natural statistical requirements for reliable statistical network models. In physical terms, projectivity is directly related to the principle of locality, while exchangeability is related to symmetry. In this section, we first discuss projectivity and exchangebility to make clear that they really are “must-haves” in any statistically useful network model, while in the next two sections we will comment on difficulties in combining them both in models of sparse networks, i.e., having average degree independent of the network size
N [
41]. While projectivity and exchangeability are desired properties of statistically reliable network models, the relevance and of these requirements for any realistic network model is a subject of scientific debate (see for instance contribution of Karthik Bharath in the discussion of the F. Caron and E. Fox paper [
33]). In fact it is often observed that most real networks can hardly be exchangeable. Indeed, in a vast majority of real networks nodes are labelled with labels related to some rich metadata and a random permutation of the nodes labels would result in a different network whose probability to be produced by the same stochastic process that produces the real network is certainly not expected to be equal to the probability with which it generates the real network.
In order to investigate the properties of reliable statistical models we consider a network process mimicking the subsequent sampling a network by expanding the set of sampled nodes and detecting all the interactions among this set of nodes.
To this end we consider a set of networks
with
and increasing network size
. The sequence of networks defines a network process, i.e.,
is an induced subgraph of the network
for all
with node set
if
. We label the nodes in order of their appearance in the network such that
and assign a probability
to each network
.
2.1. Projectivity
Given the set of networks projectivity implies that the statistical properties of the network are directly related to the statistical properties of the network with by a proper marginalization of the probability of the network over its subgraph .
By definition [
26,
27], a projective network model is a model that attributes a given probability
to each network
of the sequence, such that
where the projective map
maps networks
of a larger size
to their subgraph
of a smaller size
t.
In other words this means that one can first generate a larger graph using the model, then reduce its size to t by throwing out some nodes according to the projective map specification, and the probability with which the resulting graph is generated using this two-step procedure will be the same as if graph was generated by the model directly.
2.2. Exchangeability
Exchangeability implies that the order in which two nodes are observed or labelled is not important. Specifically, a network model is exchangeable if, by definition [
29,
30], the probability
of a network
is independent on the nodes labels, i.e.,
where
is any network isomorphic to the network
, i.e., it is any network obtained from the network
by permuting the nodes labels
according to the permutation
. If a network model is exchangeable it follows that the marginal the probability
of the generic link between node
i and node
j is unchanged if the node labels are permuted, implying that they are sampled in a different order, i.e.,
Therefore exchangeability enforces the symmetry of the model with respect to the group of graph isomorphisms.
3. Characterization of Relevant Sparse Network Models from the Statistical Perspective
In this section we investigate major examples of non-equilibrium (growing) network models and equilibrium (static) network models widely used to model sparse complex networks. In particular we discuss the Barabási–Albert model [
5] and the uncorrelated network ensembles from the statistical perspective. This discussion will reveal that neither of these two very popular frameworks for modelling sparse complex networks display both projectivity and exchangeability, indicating the difficulties in combining these properties with the sparseness of the networks.
3.1. Barabási–Albert Model
The Barabási–Albert model begins with an initial finite network and at each time
t a new node enters in the network and is connected to the network by establishing
m new links. Each of these links connect the new node to a node
i with degree
chosen with probability
This probability enforces preferential attachment, i.e., allows nodes with higher degree to more rapidly acquire new links.
The Barabási–Albert model describes a model that is projective, because as the network grows the network
obtained at time
t is an induced subgraph of the network
obtained at a later time
. However the Barabási–Albert model is not exchangeable. The fact that the network is not exchangeable is revealed for instance by the expression for the average number of links
of a node
i arrived in the network at time
,
This expression explicitly indicates that the older nodes are statistically different from the younger nodes, and their degree is much larger than that of younger nodes. Additionally it is possible to observe that the model is not exchangeable because the order of the addition of the nodes, i.e., their time of arrival in the network, is the key property that determines the connection probability [
42], i.e.,
Nevertheless we observe the interesting property that for this model the connection probability
between node
i and node
j can be also expressed as
indicating that actually, although the network process has different statistical properties than the uncorrelated network with the same degree distribution, the expected degree correlations are weak. The relation between the Barabási–Albert (BA) model and the uncorrelated network ensemble with the same degree distribution is investigated in detail using information theoretic tools in Ref. [
43].
3.2. Uncorrelated Network Ensembles
The Barabási–Albert model is projective but not exchangeable. On the contrary the widely used uncorrelated network ensembles are exchangeable models but they are not projective in the sparse regime. In order to show this let us consider an uncorrelated network model in which each node
i has an expected degree
, where the expected degrees of the nodes are consistent with a structural cutoff, i.e.,
In this case the probability
of a link between node
i and node
j is given by
and therefore it only depends on the expected degrees
and
of the nodes
i and
j and not on the order in which node
i and node
j have been sampled. The model is therefore exchangeable as long as we consider the simultaneous permutation of the node labels and the expected degrees of the nodes. However if we consider a large sample of the network with
nodes, we see that the model is projective if and only if it is also dense, with the number of links scaling as
. In fact if we assume that in the larger sample the expected degrees of nodes
i and
j are given by
and
, the probability that node
i and node
j are connected in the larger network models including
nodes is
If we impose projectivity, i.e.,
for
, and we assume that the number of nodes
can be written as
it is easy to see that we should also have
Therefore to guarantee projectivity the expected degree of each node should grow linearly with the network size, resulting in a dense network with the total number of links L scaling with the network size N as . This implies that the random network with p independent of N is an exchangeable model whereas the Poisson random network with and z independent of N is not exchangeable. In fact one cannot throw out nodes from a network of size produced by , and hope that the resulting network will have the same probability as in , simply because the links in the and ensembles exist with different probabilities and that depend on the graph size N. Alternatively, if one attempts to formulate as a growing model, then since the edge existence probability depends on N, the addition of a new node affects the probability of existence of edges in the existing network. Since this probability is a decreasing function of N (), upon the addition of a new node all the existing edges must be removed with some probability (). In other words, in such a growing model new node additions must necessarily affect the existing network structure.
4. Impasse with Sparsity
Surprisingly, combining projectivity and exchangeability with the additional constraint of sparsity, i.e., the requirement that the average degree of the sampled networks is independent of the network size, has been a major impasse. If we exclude spatially embedded networks [
31], to the best of our knowledge there exists no model of sparse networks that would be both projective and exchangeable at the same time. This situation is in stark contrast with the case of dense graphs. Dense graphs are known to have well-defined thermodynamic limits known as graphons, and any graphon-based network model is both exchangeable and projective [
30].
The thermodynamic limits of sparse graphs are at present quite poorly understood, which appears to be one of the reasons behind the mentioned impasse. Several attempts have been made to understand the limits of sparse graphs, including, for example, sparse
graphons [
32], which are not projective, or stretched graphons a.k.a. graphexes [
33,
34,
35]. In the latter case, graphs are sparse, exchangeable and projective, but with two major caveats:
- (1)
the average degree cannot be constant, it must diverge with N (but possibly slower than linearly),
- (2)
exchangeability is completely redefined: it is not with respect to node labels , but with respect to artificial labels which are positive real numbers.
Another class of attempts suggests to completely give up on the node label exchangeability requirement, and to consider edge exchangeability instead, e.g., using variations of Pitman–Yor processes [
36,
37,
38]. It remains unclear at present whether these developments imply that too many network models that were found to be quite useful in practice and that do use node labels
, are statistically hopeless. It seems more likely that further research is needed to understand and resolve this projectivity vs. exchangeability impasse in sparse network models.
Proposed Solution of the Impasse Based on Network Geometry
In [
31] it was shown that a generic network model is projective if the probability of edge existence, i.e., the connection probability, does not depend on the network size
N. In fact if the connection probability does depend on
N, then, the addition of new nodes to the existing network in the growing formulation of the model necessarily affects the existing network structure and the network cannot be projective.
In order to formulate network models in which the connection probability does not depend on the network size
N, embedding networks in space can turn out to be very useful. In fact spatially embedded networks can combine projectivity with a constant average degree [
31] as their spatial embedding ensures projectivity when the connection probability is
local and nodes connect typically to nodes that are spatially close. For instance if the nodes are uniformly distributed in
and each node connects only to the nodes with a constant radius
, by sampling the network by progressively expanding the spatial region of interest we can build a projective model with constant average degree. This is clearly a realistic scenario in most real networks as it unlikely that a local event in a spatial network causes a global change in the network. For instance in the Internet, the appearance of a new customer of a local Internet provider in Bolivia cannot lead to immediate severance of customers by a local Internet provider in Bhutan.
It turns out that models that are not explicitly constructed from spatial embeddings can also be analysed using geometrical arguments, hence shedding light on their statistical properties. In this vein, it was recently shown that the hypersoft configuration model, which defines maximum-entropy random graphs with a given degree distribution, is sparse and
either exchangeable
or projective [
39]. Both sparsity and exchangeability definitions are traditional in the model, i.e., the average degree is constant and exchangeability is with respect to labels
, so that the only caveats are in “either-or” and also in that this “either-or” is achieved only for specific degree distributions (power law with exponent
in [
39]).
In the
exchangeable equilibrium formulation of the model, nodes are points sprinkled at random onto an interval
of an
N-dependent length
, where
is a growing function of
N, according to a non-uniform point density (if this point density is exponential, then the resulting degree distribution is a power law), and then all pairs of points/nodes
i and
j,
, at sprinkled coordinates
and
are connected by an edge with the entropy-maximizing Fermi–Dirac connection probability
that does not depend on the network size
N.
In the projective growing formulation of the same model, the interval grows with N, its length growing according to , new node appears in the interval increment of length , and then connects to existing nodes with the same connection probability as in the exchangeable formulation.
The difficulty of combining projectivity and exchangeability is evident in this example: in the exchangeable formulation, node labels i are random and uncorrelated with their coordinates , while in the projective formulation, nodes are labelled in the increasing order of their coordinates: . If nodes are labelled this way, then the projective map trivially throws out nodes with labels , and the resulting graph satisfies the projectivity requirement since the connection probability does not depend on N, and since the remaining N nodes lie in . If the node labels are random, however, as they are in the exchangeable formulation, then it remains unclear if even an asymptotically correct projective map can be constructed.
5. Statistical Mechanics Model with Hidden Variables
Our goal is here to reconcile sparseness with a reliable statistical modelling framework without assuming the existence of an embedding geometrical space. In this endeavour we will define a projective network process yielding a sequence of networks growing by the subsequent addition of nodes and links. To each node i we associate a hidden variable that is a proxy for the degree that the node will acquire in the model. The statistical properties of the network model when we average over all the possible sequences determining the subsequent addition of the links obey scaling laws and reduce to the uncorrelated network model of any size N in the sparse regime.
Although this model does not ultimately reconcile sparseness with both exchageability and projectivity, we will see in
Section 6 that it provides a very reliable null model for power-law networks also if only a subsample of the original network is considered.
5.1. The Model
The model can be interpreted as a weighted growing network model where we allow multiedges. In the model every node i is assigned a hidden variable from a hidden variable distribution .
Starting at
from a single isolated node, at each time
a new node
i is added to the network and draws
links to the existing nodes of the network, where
is chosen according to the Poisson distribution with average
, i.e.,
Each new link is attached to a node
j already present in the network with probability
Note that not all the new links will yield new connections because the nodes i and j might be already connected. Additionally note that this model does not implement preferential attachment as the linking probability is only dependent on the externally attributed hidden variable and not to the dynamically acquired degree . Whenever a new link connects node i to an already connected node j the multi-edge between node i and node j is reinforced, i.e., the weight of the links between node i and node j increases by one.
Here and in the following we will indicate by the adjacency matrix of the network, with the time at which node i has been added to the network, with the node degree and with the node strength, i.e., the sum of the weights of the links incident to node i.
5.2. The Strength of a Node and Its Dependence on the Hidden Variable
The hidden variable
modulates the temporal evolution of the strength of the node
i. In fact in the mean-field approach [
1,
5,
44], since at each time an average of
links are added and reinforced, the average strength
of node
i given the time
of its arrival in the network, its hidden variable
and its initial strength
obeys the equation
with initial condition
. The solution of this equation is
Therefore in this model the strength depends both on the time of arrival of the node in the network and on its hidden variable. If we average the strength over the nodes with the same hidden variable however, we see that the average strength
of nodes with hidden variable
is given in the large network limit
by
This implies that if we attribute to a node a hidden variable and we consider a set of models in which the time of arrival of node i is taken randomly, the strength of node i is (on average over the different network models) determined only by its hidden variable.
5.3. Strength Distribution
The strength distribution of the model is a convolution of exponentials. To find the strength distribution we use the master equation approach [
44] under the assumption that the hidden variable distribution has a well defined average value
. To this end we write the equation for
, the average number of nodes with hidden variable
that have strength
at time
t, as
where
indicates the Kronecker delta and where we denote by
the probability that a node with hidden variable
is attached to the new node arrived in the network at time
t by one of its connections, i.e.,
Given the continuous growth of the network asymptotically in time, for
it is possible to assume that
where
is the probability that a random node has strength
s and hidden variable
.
By inserting this asymptotic expression in the master Equation (21) and solving for
we get
Therefore given the value of the hidden variable
and the initial number of links
the strength distribution is exponential. The overall strength distribution
of the model determining the probability that a random node has strength
s is given by the integral of
over all possible value of the hidden variable
, i.e.,
This result reveals that the strength distribution can be different from the distribution of hidden variables. For instance if all the hidden variables are the same, the strength distribution will still allow for fluctuations of the strengths. However for power-law hidden variable distributions
the strength distribution has a power-law tail with the same exponent
for
. In fact, by inserting the explicit expression of
and of
in Equation (25) we get
For
we can approximate the sum over
with the infinite sum getting
where the last expression is valid if
. Therefore, although in general it is not true that the hidden variable distribution is the same as the strength distribution, in the case of power-law distributed hidden variables the strength distribution displays a power-law tail with the same exponent. Note that this is valid for power-law exponents in the range
but also in the range
. Therefore in this case the hidden variables can be used to directly tune the strength distribution.
5.4. Connection Probability
In this section we derive the expression for the connection probability between any two nodes. Let us consider the probability
that node
i is connected to node
j, i.e.,
given the hidden variables of node
i and node
j, their time of arrival with
and the initial strength
of node
j. This probability is one minus the probability that all of the initial links of node
j do not connect to node
i, i.e.,
If we now average over the probability
we get the closed form expression
where we have assumed that the average of the hidden variables
is well defined. Therefore we have found that the connection probability between two nodes depends both on the hidden variables and on their time of arrival in the network. It follows that the model is not expected to be exchangeable, as this would require a connection probability independent of the time of arrival of the two nodes. However the fact that this connection probability does not
only depend on the time of arrival of the nodes in the network (or the order in which they are sampled) can be a useful characteristic of a reliable statistical model.
5.5. Degree Distribution in the Sparse Regime
Here we derive the degree distribution of the model in the sparse regime, when we can assume that . We will show that in this regime, each node has a Poisson degree distribution with an expected average degree depending both on the value of its hidden variable and on the time of its arrival in the network.
The probability
that a node
i arrived in the network at time
and, having hidden variable
, has degree
can be calculated starting from the connection probabilities
given by Equation (31). Let us indicate with
the elements of the adjacency matrix in the
i-th row indicating the connections of node
i. Since node
i is connected with each node
j with probability
given by Equation (31), the probability
is given by
Using this result we can express the probability
that node
i has degree
as
where we have used the integral representation of the Kronecker delta
. By performing the sum over all the elements of
we get
where
For
we can approximate
with
where
is the expected degree of node
i given by
Note here that since the connection probability
depends both on the hidden variables of the nodes
i and
j and on their arrival time in the network, it follows that also the expected degree
of node
i will be both a function of the node’s hidden variable and its time of arrival in the network. Using Equations (
34) and (
36) we can derive the explicit expression for
. In fact we have
and by identifying the last integral with the Kronecker delta
we get the Poisson distribution
Therefore the probability that node
i, which arrived in the network at time
with hidden variable
, has degree
is given by the Poisson distribution with average
given by Equation (
37). It follows that the degree distribution
of the network at time
t is given by
Note that for sufficiently sparse networks where each two connected nodes are typically connected by a link of weight one, the degree of a node can be identified with its strength
It follows that in this case the degree distribution can be approximated by the strength distribution and we have that if the hidden variables are power-law distributed with power-law
(as described in Equation (26)) then also the degree distribution has a power-law tail with the same exponent
, i.e.,
for
.
5.6. Random Permutation of the Node Sequence
Here we investigate whether the described network process can be related to the generation of uncorrelated networks. In this way we aim at reconciling the non-equilibrium growing nature of the network model, displaying projectivity, with the properties of exchangeable but not projective uncorrelated network models.
We observe that this expression depends both on the hidden variable and on the time of arrival of the nodes
i and
j in the network. However if we consider several realizations of the model in which the times of arrival of node
i and node
j are random, but the hidden variables are preserved, we observe that the probability that node
i and node
j are connected satisfies
Therefore if the network is sufficiently sparse, i.e.,
we have that the expected degree
of a random node
i of hidden variable
is given by
and the probability that a node with hidden variable
is connected with a node with hidden variable
independently of their time of arrival in the network, is given by the uncorrelated network marginal corresponding to the number of nodes in the sample, i.e.,
Note that in this case if the sample increases in size and includes
nodes, the probability that node
i and node
j are connected will satisfy
In this case the network process induces a probability that depends on the network size N and at the same time enforces the sparseness of the network. In fact the expected degrees of the nodes are only determined the the hidden variable and are independent on the network size.
5.7. Entropy of the Network Model
In order to compare our model with hidden variable distribution
to an uncorrelated network ensemble in which the expected degrees are
, in this section we use information theory tools. Specifically we will compare the entropy of the two ensembles. The entropy of a network model or of a network ensemble [
14,
15,
16,
17,
40] is a fundamental tool to evaluate the information content in the network model. It indicates the logarithm of the typical number of networks generated by the ensemble and as such evaluates the complexity of the model and can be used in inference problems [
40]. Since for our network model the connection probability
of any two pair of nodes is
i and
j is given by Equation (31), the entropy of the model is given by
where in the sparse regime we can approximate
with
as
Similarly for the uncorrelated network ensemble with connection probability
the entropy is given by
In order to compare these two entropies we use the explicit expression for the connection probability
when we put
which reads
By performing a straightforward calculation we find that
S is given, up to the linear terms in
N, by
and that the entropy
S of our model is smaller than the entropy of the uncorrelated network ensemble. In fact,
S differs from
only by
The entropy difference quantifies the information loss when the proposed network process is approximated with its corresponding uncorrelated network model. We observe here that the uncorrelated network model is obtained when the causal construction of the original network model is disregarded and the only retained information is the probability that two nodes of hidden variables and are connected regardless of their time of arrival in the network. Therefore captures the loss of information when the causal nature of the original model is disregarded. Interestingly in the large network limit , is low when compared to S revealing the proximity between the two models. Additionally is only dependent on indicating that the information loss from one model to the other is independent of the particular distribution of the hidden variables as long as is kept constant.
6. Statistical Testing of the Model
In order to study the utility of the proposed model as a null model for sampled data we consider three power-law networks: the arxiv hep-ph (high energy physics phenomenology) citation network [
45,
46], the Berkeley–Stanford web network [
47] and the Notre Dame web network [
48] of network sizes
34,546,
685,230,
325,000 respectively. All data are freely available on the Stanford Network Analysis Project webpage. To each node of the network we assign a different label
according to a random permutation of the indices from 1 up to
N. We then assign to each node
i of the network a hidden variable
where
is the observed degree of node
i in the dataset. Given our random node labelling and the hidden variables
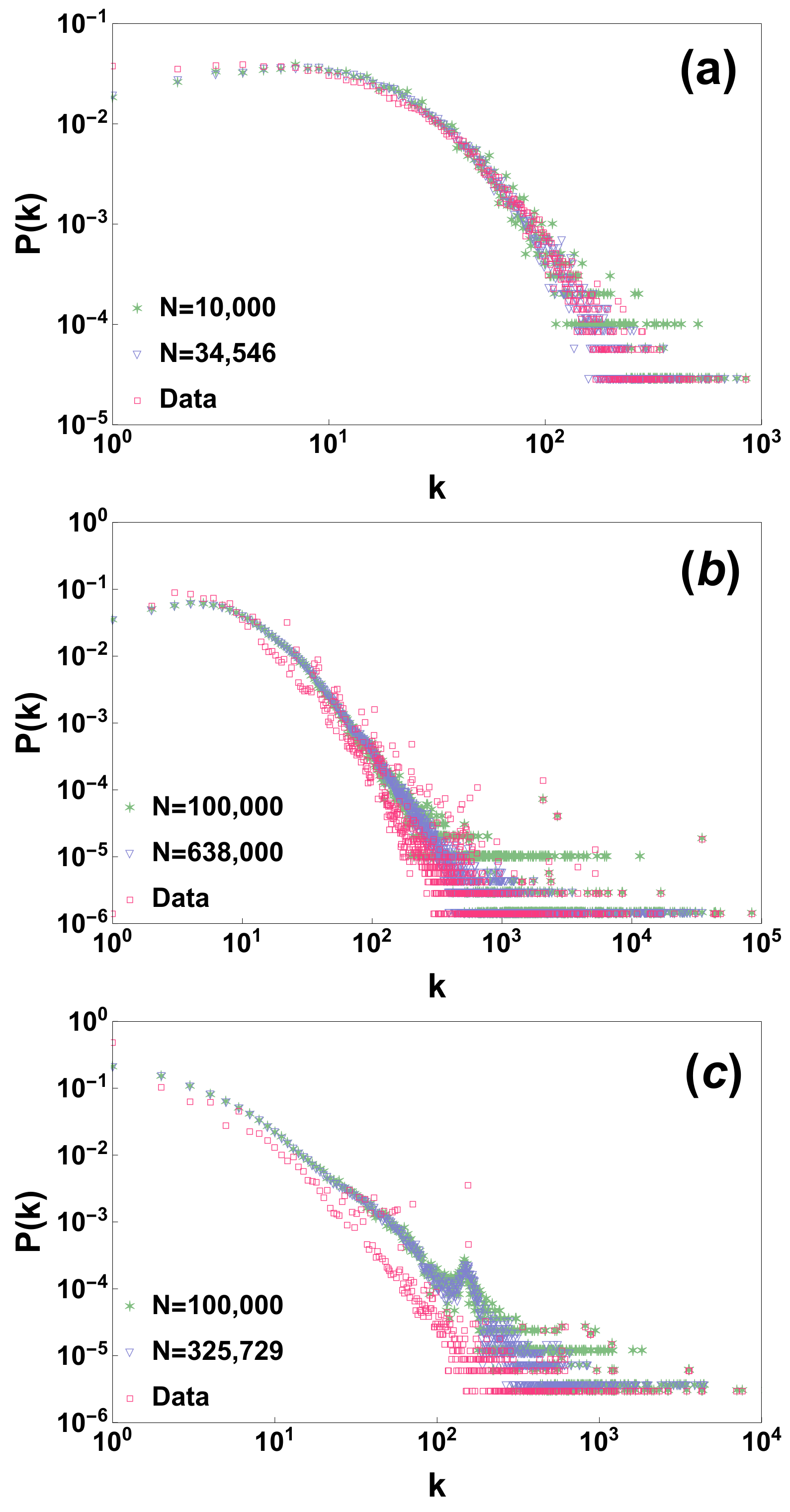
we have generated a random network according to the proposed network process. Interestingly the proposed model preserves to a large extent the degree distribution (see comparison of the real degree distribution with the one generated by the model in
Figure 1). Additionally these results are quite stable if we consider a model generated only by adding a subsample of randomly chosen nodes, showing that the model preserves the degree distribution under random sub-sampling of the nodes (see
Figure 1).
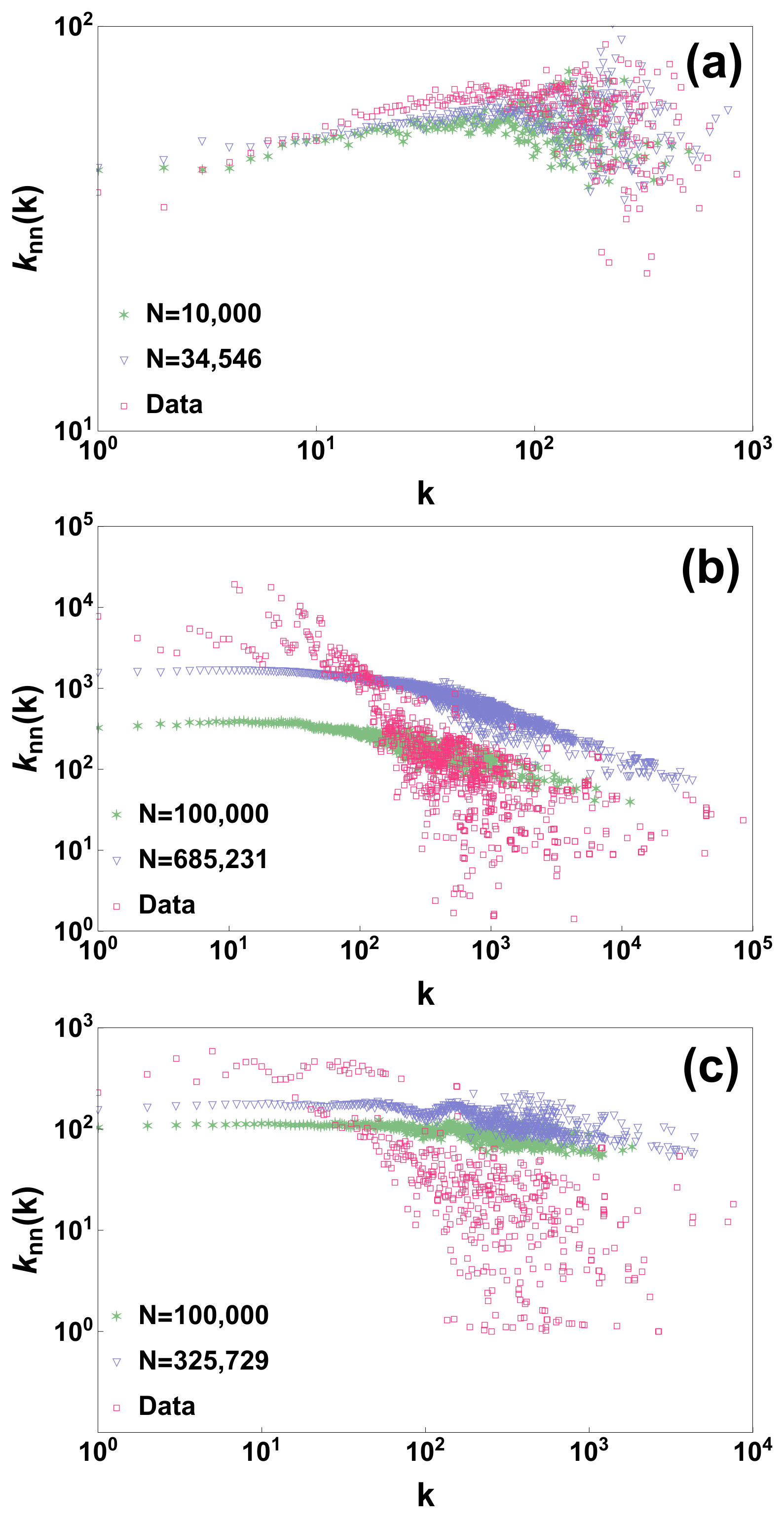
The generated model however is to be considered mostly as uncorrelated. In fact if we compare the degree correlations of the real datasets with the degree correlations of the network generated by the model we observe that the model deviates from the real data and displays very weak/marginal degree correlations (see
Figure 2). In fact from the results obtained for the three studied network datasets it seems that the model is able to better reproduce weakly assortative behaviour than strongly disassortative behaviour. In future, modifications of the proposed model could be envisaged to capture also the degree correlations of real datasets.