Modeling of the Atomic Diffusion Coefficient in Nanostructured Materials
Abstract
:1. Introduction
2. Model
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gleiter, H. Nanostructured materials: Basic concepts and microstructure. Acta Mater. 2000, 48, 1–29. [Google Scholar] [CrossRef]
- Sun, C.Q. Thermo-mechanical behavior of low-dimensional systems: The local bond average approach. Prog. Mater. Sci. 2009, 54, 179–307. [Google Scholar] [CrossRef]
- Tjong, S.C.; Chen, H. Nanocrystalline materials and coatings. Mater. Sci. Eng. R 2004, 45, 1–88. [Google Scholar] [CrossRef]
- Höfler, H.J.; Averback, R.S.; Gleiter, H. Diffusion of boron in nanocrystalline iron A new type of diffusion kinetics: Type C’. Philos. Mag. Lett. 1993, 68, 99–105. [Google Scholar] [CrossRef]
- Dobruskin, V.K. Correlation between saturation pressures and dimensions of nanoparticles. Are the fundamental equations really fair? Langmuir 2003, 19, 4004–4013. [Google Scholar] [CrossRef]
- Di, W.H.; Willinger, M.G.; Ferreira, R.A.S.; Ren, X.; Lu, S.Z.; Pinna, N. Citric acid-assisted hydrothermal synthesis of luminescent TbPO4: Eu nanocrystals: Controlled morphology and tunable emission. J. Phys. Chem. C 2008, 112, 18815–18820. [Google Scholar] [CrossRef]
- Xiao, S.; Hu, W.; Yang, J. Melting behaviors of nanocrystalline Ag. J. Phys. Chem. B 2005, 109, 20339–20342. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.F.; Zheng, W.T.; Jiang, Q. Distinct young’s modulus of nanostructured materials in comparison with nanocrystals. Phys. Chem. Chem. Phys. 2011, 13, 21328–21332. [Google Scholar] [CrossRef] [PubMed]
- Boukai, A.; Xu, K.; Heath, J.R. Size-dependent transport and thermoelectric properties of individual polycrystalline bismuth nanowires. Adv. Mater. 2006, 18, 864–869. [Google Scholar] [CrossRef]
- Sun, T.; Yao, B.; Warren, A.P.; Barmak, K.; Toney, M.F.; Peale, R.E.; Coffey, K.R. Dominant role of grain boundary scattering in the resistivity of nanometric Cu films. Phys. Rev. B 2009, 79, 041402. [Google Scholar] [CrossRef]
- Zhu, Y.F.; Lian, J.S.; Jiang, Q. Modeling of the melting point, debye temperature, thermal expansion coefficient, and the specific heat of nanostructured materials. J. Phys. Chem. C 2009, 113, 16896–16900. [Google Scholar] [CrossRef]
- Laughlin, D.E.; Hono, K. Physical Metallurgy, 5th ed.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 389–559. [Google Scholar]
- Guisbiers, G.; Buchaillot, L. Size and shape effects on creep and diffusion at the nanoscale. Nanotechnology 2008, 19, 435701. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Q.; Zhang, S.H.; Li, J.C. Grain size-dependent diffusion activation energy in nanomaterials. Solid State Commun. 2004, 130, 581–584. [Google Scholar] [CrossRef]
- Hofler, H.J.; Averback, R.S.; Hahn, H.; Gleiter, H. Diffusion of bismuth and gold in nanocrystalline copper. J. Appl. Phys. 1993, 74, 3832–3839. [Google Scholar] [CrossRef]
- Sundaram, D.S.; Puri, P.; Yang, V. Thermochemical behavior of nano-sized aluminum-coated nickel particles. J. Nanopart. Res. 2014, 16, 2392. [Google Scholar] [CrossRef]
- Masiha, H.R. Effect of surface nanostructuring of aluminum alloy on post plasma electrolytic oxidation. Appl. Surf. Sci. 2014, 317, 962–969. [Google Scholar] [CrossRef]
- Belmonte, T.; Gouné, M.; Michel, H. Numerical modeling of interstitial diffusion in binary systems. Application to iron nitriding. Mater. Sci. Eng. A 2001, 302, 246–257. [Google Scholar] [CrossRef]
- Tao, Q.; Wang, J.; Fu, L. Ultrahigh hardness of carbon steel surface realized by novel solid carburizing with rapid diffusion of carbon nanostructures. J. Mater. Sci. Technol. 2017, 33, 1210–1218. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, G.X.; Ye, C. A numerical model coupling diffusion and grain growth in nanocrystalline materials. Comp. Mater. Sci. 2017, 136, 243–252. [Google Scholar] [CrossRef]
- Moriarty, P. Nanostructured materials. Rep. Prog. Phys. 2001, 64, 297–381. [Google Scholar] [CrossRef]
- Dick, K.; Dhanasekaran, T.; Zhang, Z.; Meisel, D. Size-dependent melting of silica-encapsulated gold nanoparticles. J. Am. Chem. Soc. 2002, 124, 2312–2317. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Q.; Zhang, S.; Zhao, M. Size-dependent melting point of noble metals. Mater. Chem. Phys. 2003, 82, 225–227. [Google Scholar] [CrossRef]
- Jiang, Q.; Lu, H.M. Size dependent interface energy and its applications. Surf. Sci. Rep. 2008, 63, 427–464. [Google Scholar] [CrossRef]
- Shibata, T.; Bunker, B.A.; Zhang, Z.; Meisel, D.; Vardeman, C.F., II; Gezelter, J.D. Size-dependent spontaneous alloying of Au-Ag nanoparticles. J. Am. Chem. Soc. 2002, 124, 11989–11996. [Google Scholar] [CrossRef] [PubMed]
- Liang, L.H.; Shen, C.M.; Chen, X.P.; Liu, W.M.; Gao, H.J. The size-dependent phonon frequency of semiconductor nanocrystals. J. Phys. Condens. Matter 2004, 16, 267–272. [Google Scholar] [CrossRef]
- Horvath, J.; Birringer, R.; Gleiter, H. Diffusion in nanocrystalline material. Solid State Commun. 1987, 62, 319–322. [Google Scholar] [CrossRef]
- Cai, B.; Kong, Q.P.; Lu, L.; Lu, K. Low temperature creep of nanocrystalline pure copper. Mater. Sci. Eng. A 2000, 286, 188–192. [Google Scholar] [CrossRef]
- Lu, H.M.; Wen, Z.; Jiang, Q. Nucleus-liquid interfacial energy of elements. Colloids Surf. A 2006, 278, 160–165. [Google Scholar] [CrossRef]
- WebElements. Available online: https://www.webelements.com/ (accessed on 17 March 2018).
- Gorur, O.; Ozturk, Y.; Yildirim, G. Sn diffusion coefficient and activation energy determined by way of XRD measurement and evaluation of micromechanical properties of Sn diffused YBa2Cu3O7−x superconducting ceramics. J. Mater. Sci. Mater. Electron. 2013, 24, 3063–3072. [Google Scholar] [CrossRef]
- Luo, W.H.; Hu, W.Y.; Xiao, A. Size effect on the thermodynamic properties of silver nanoparticles. J. Phys. Chem. C 2008, 112, 2359–2369. [Google Scholar] [CrossRef]
- Safaei, A.; Shandiz, M.A.; Sanjabi, S.; Barber, Z.H. Modeling the melting temperature of nanoparticles by an analytical approach. J. Phys. Chem. C 2008, 112, 99–105. [Google Scholar] [CrossRef]
- Wronski, C.R. The size dependence of the melting point of small particles of tin. J. Appl. Phys. 1967, 18, 1731–1737. [Google Scholar] [CrossRef]
- Peters, K.F.; Chung, Y.W.; Cohen, J.B. Surface melting on small particles. Appl. Phys. Lett. 1997, 71, 2391–2393. [Google Scholar] [CrossRef]
- Zhu, Y.F.; Lang, X.Y.; Zheng, W.T.; Jiang, Q. Electron scattering and electrical conductance in polycrystalline metallic films and wires: Impact of grain boundary scattering related to melting point. ACS Nano 2010, 4, 3781–3788. [Google Scholar] [CrossRef] [PubMed]
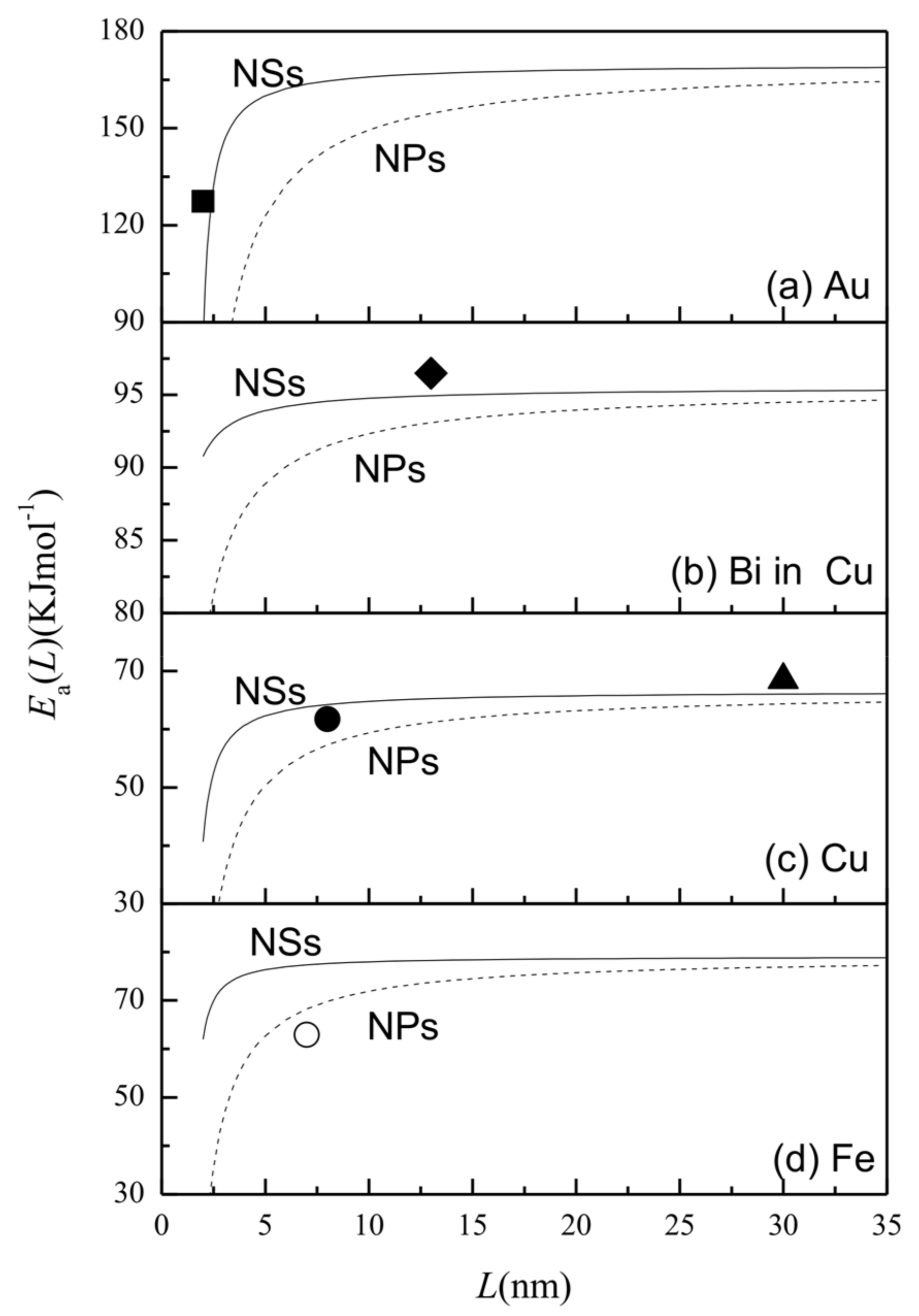
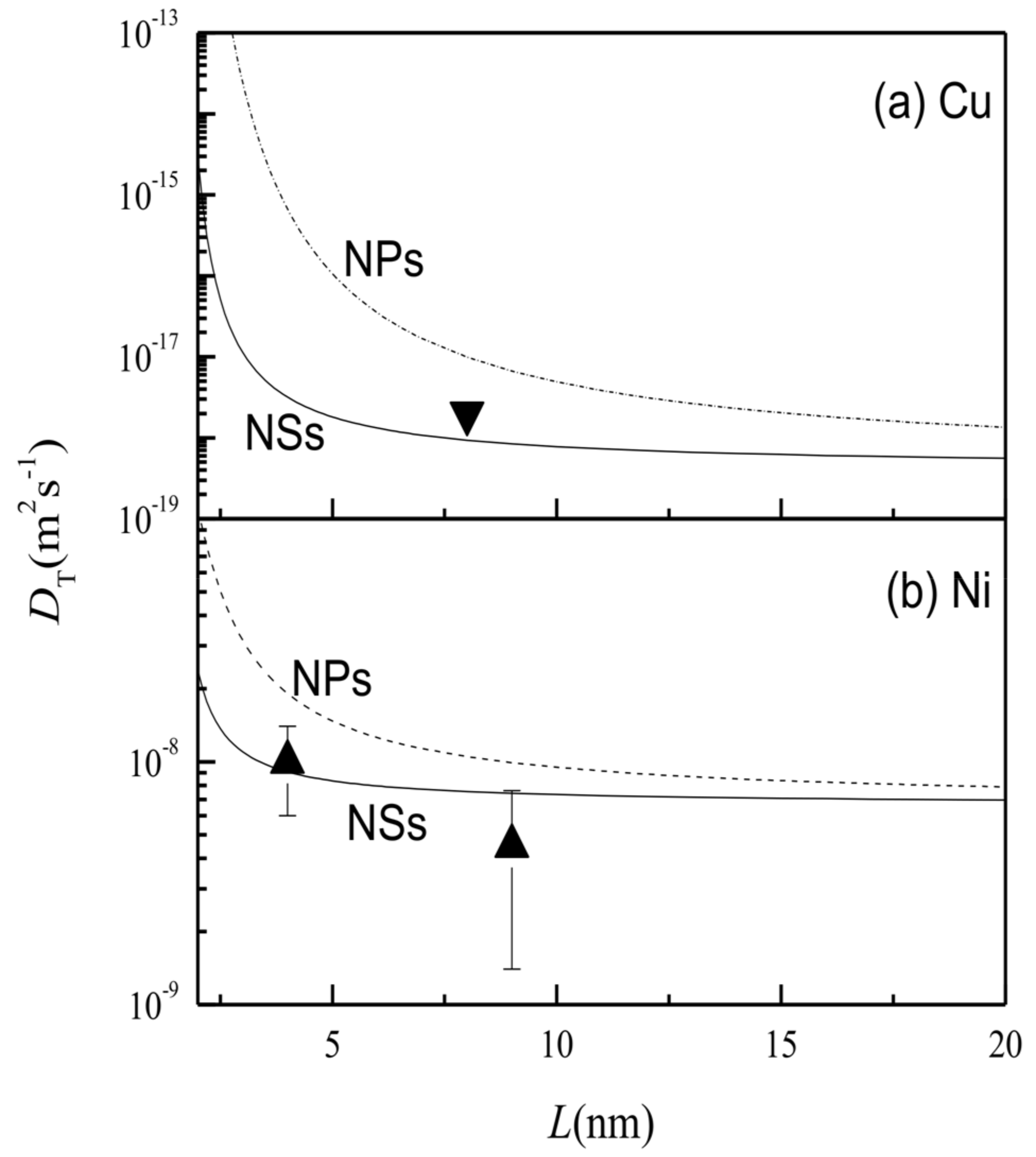
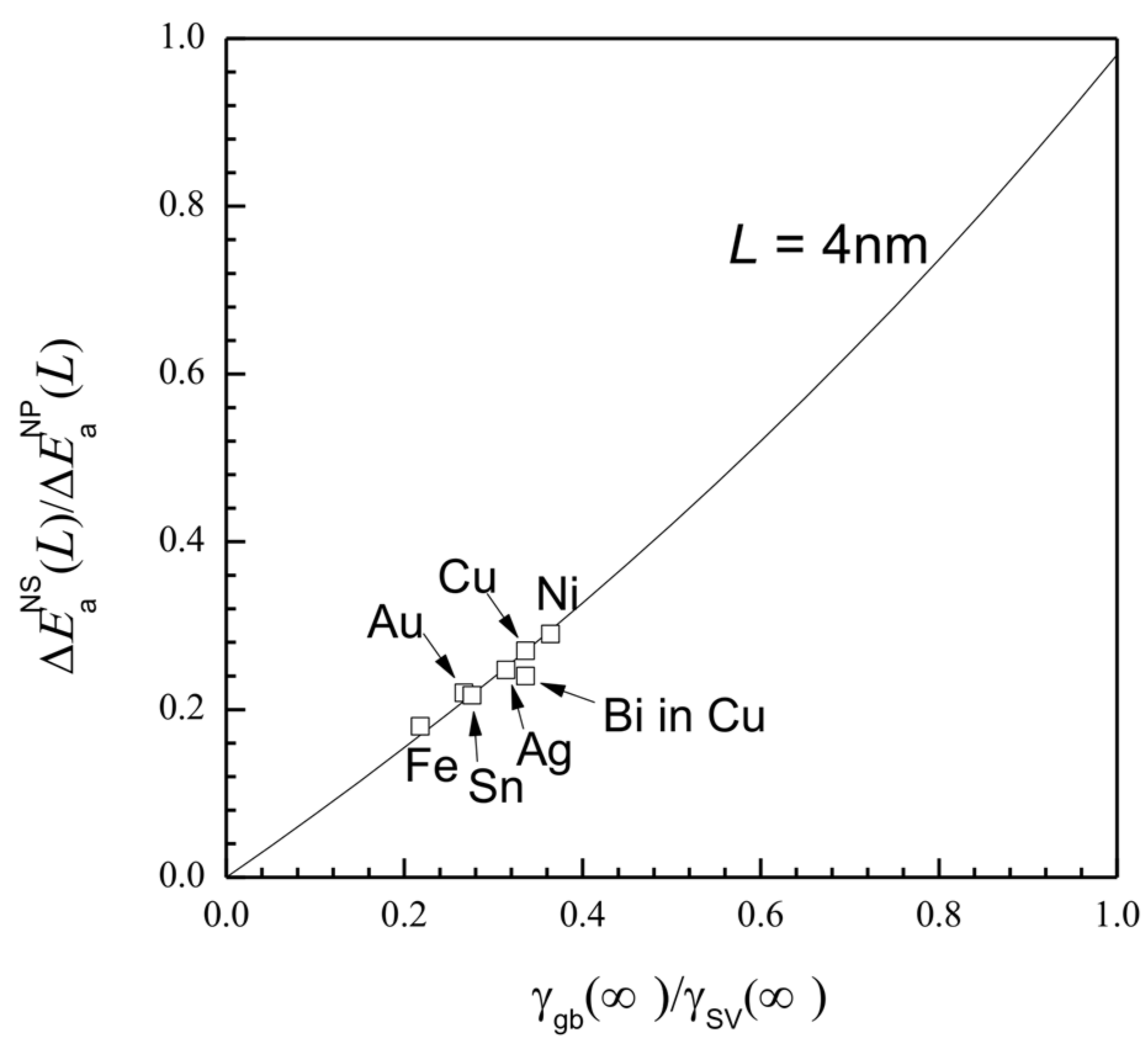
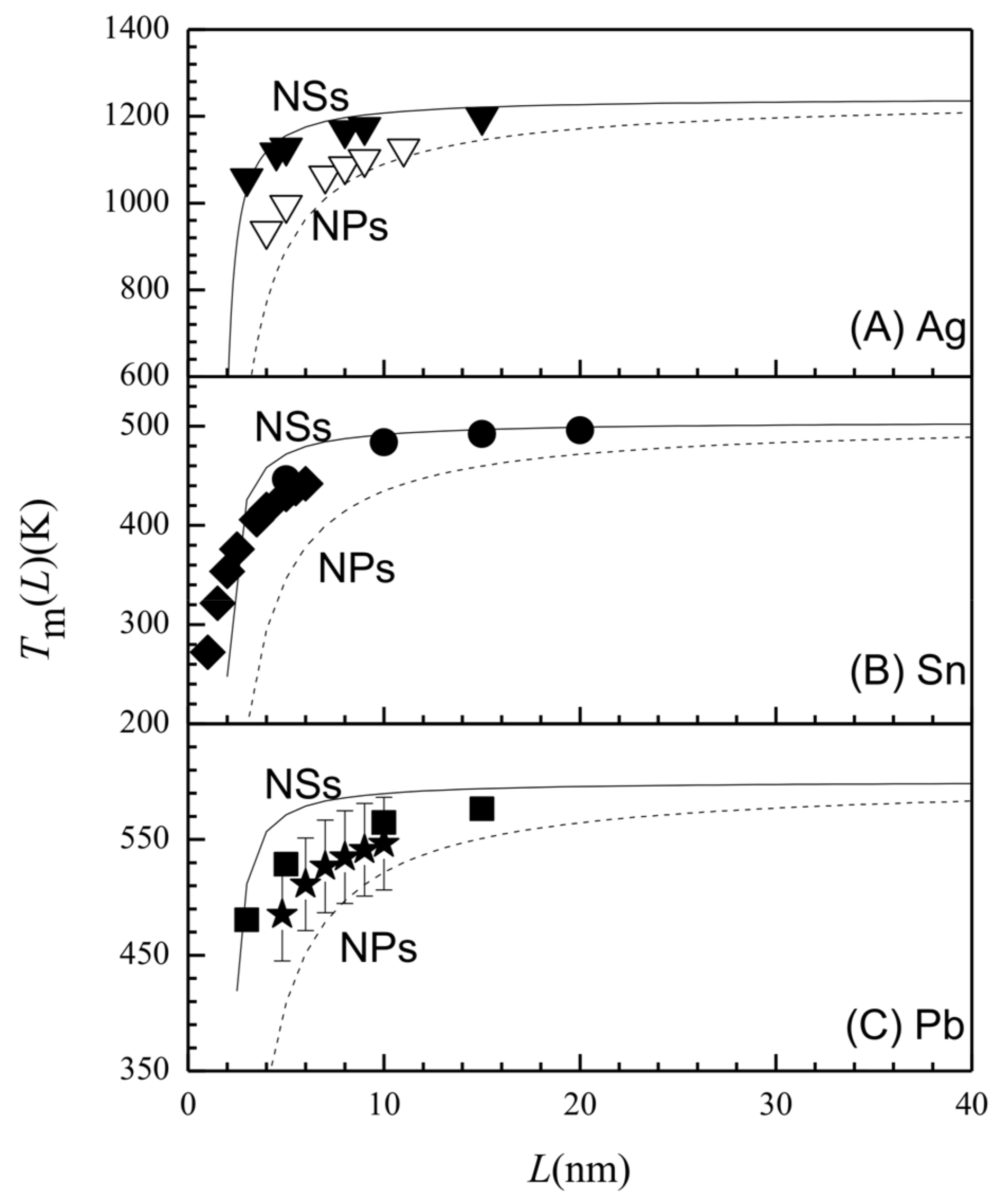
| h [29] (nm) | Tm (∞) [30] (k) | Svib (∞) [29] (Jmol−1·k−1) | γsv (∞) [24] (Jm−2) | γgb (∞) [24] (Jm−2) | Ea (∞) (kJ·mol−1) | ||
|---|---|---|---|---|---|---|---|
| Ag | 0.289 | 1234 | 7.82 | 1.250 | 0.392 | - | - |
| Pb | 0.350 | 600.61 | 6.65 | 0.600 | 0.111 | - | - |
| Sn | 0.281 | 505.08 | 9.22 | 0.649 | 0.179 | - | 56.93 [31] |
| Fe | 0.248 | 6.82 | 2.420 | 0.528 | - | 79.11 [4] | |
| Au | 0.288 | 7.62 | 1.500 | 0.400 | - | 169.81 [22] | |
| Cu | 0.256 | 7.85 | 1.790 | 0.601 | - | 95.52 [15] | |
| 2 × 10−18 [27] | 66.57 [27] | ||||||
| Ni | 0.249 | 8.11 | 2.380 | 0.866 | 1.77 × 10−7 [16] | 43.65 [16] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Li, Z.; Tang, K.; Wen, Z.; Zhu, Y. Modeling of the Atomic Diffusion Coefficient in Nanostructured Materials. Entropy 2018, 20, 252. https://doi.org/10.3390/e20040252
Hu Z, Li Z, Tang K, Wen Z, Zhu Y. Modeling of the Atomic Diffusion Coefficient in Nanostructured Materials. Entropy. 2018; 20(4):252. https://doi.org/10.3390/e20040252
Chicago/Turabian StyleHu, Zhiqing, Zhuo Li, Kai Tang, Zi Wen, and Yongfu Zhu. 2018. "Modeling of the Atomic Diffusion Coefficient in Nanostructured Materials" Entropy 20, no. 4: 252. https://doi.org/10.3390/e20040252
APA StyleHu, Z., Li, Z., Tang, K., Wen, Z., & Zhu, Y. (2018). Modeling of the Atomic Diffusion Coefficient in Nanostructured Materials. Entropy, 20(4), 252. https://doi.org/10.3390/e20040252





