Strong- and Weak-Universal Critical Behaviour of a Mixed-Spin Ising Model with Triplet Interactions on the Union Jack (Centered Square) Lattice
Abstract
:1. Introduction
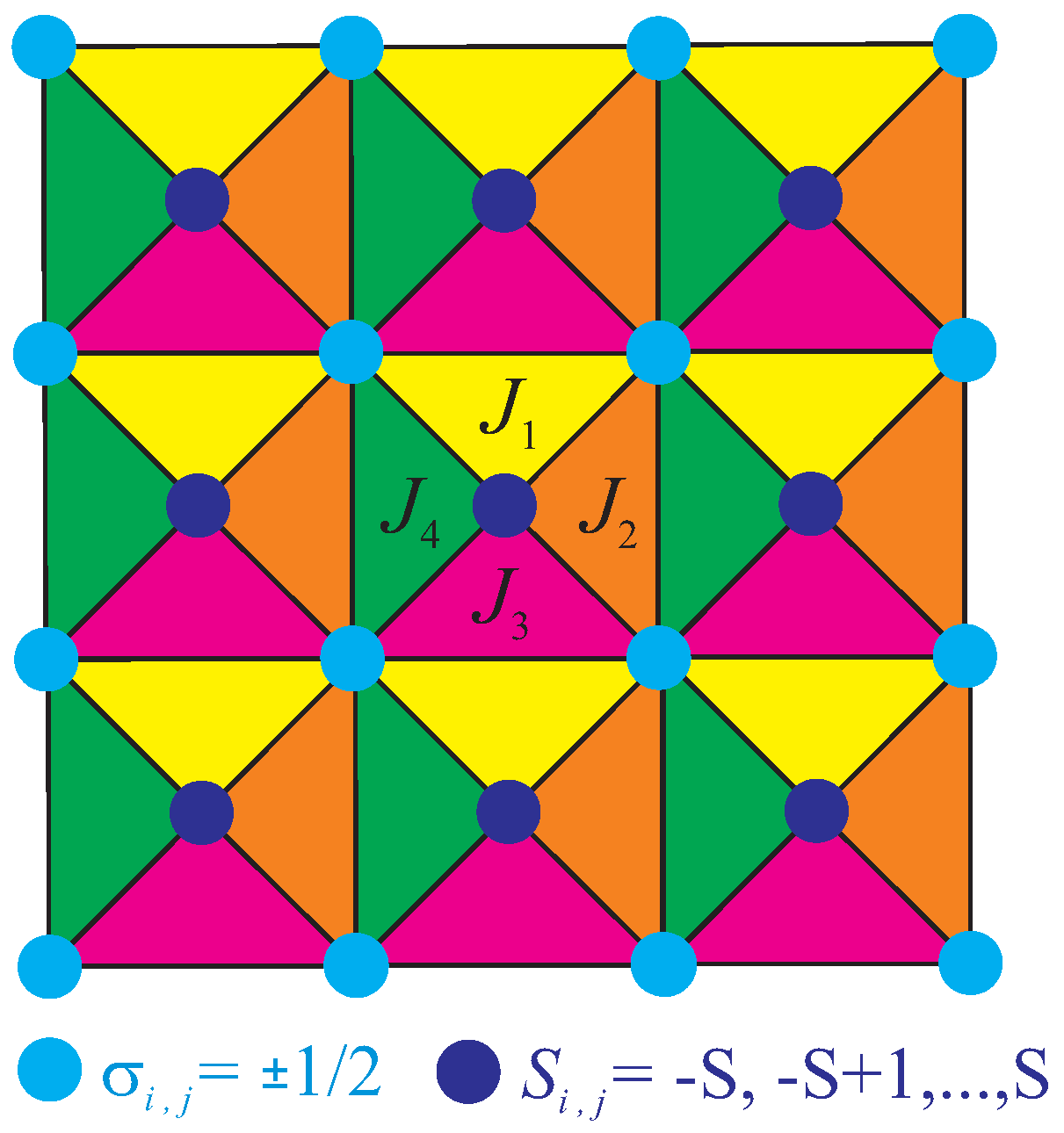
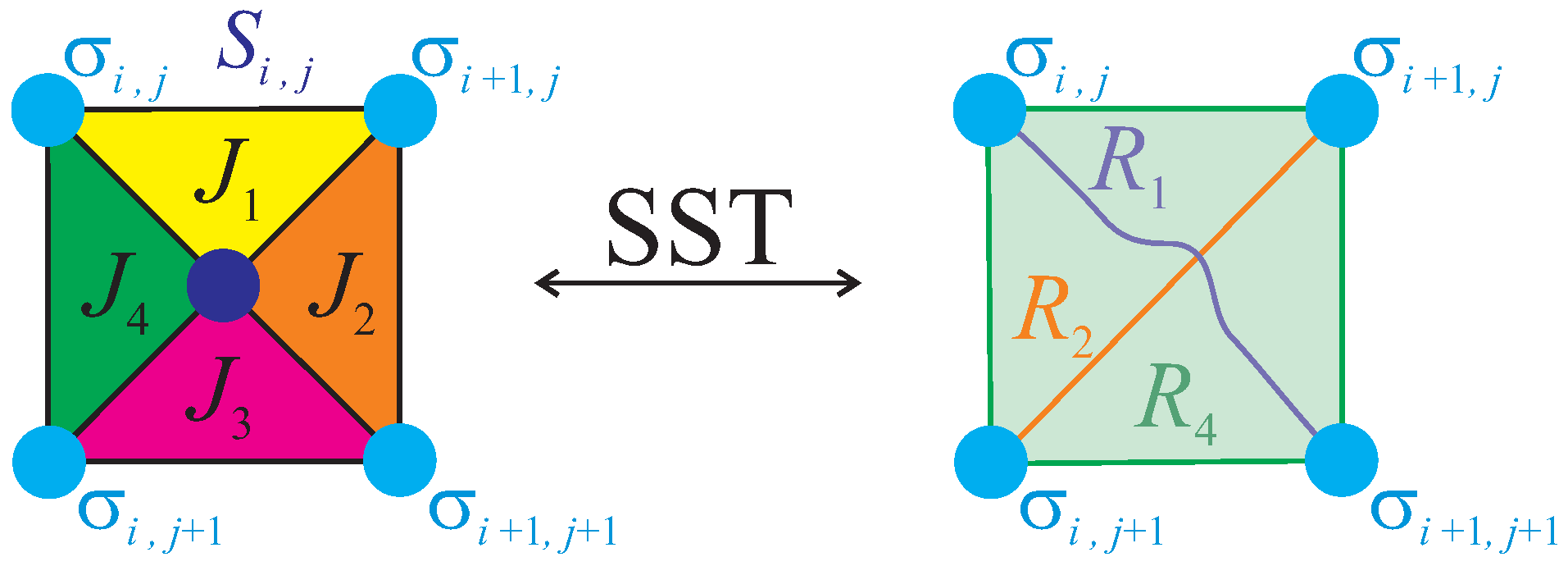
2. Model and Exact Solution
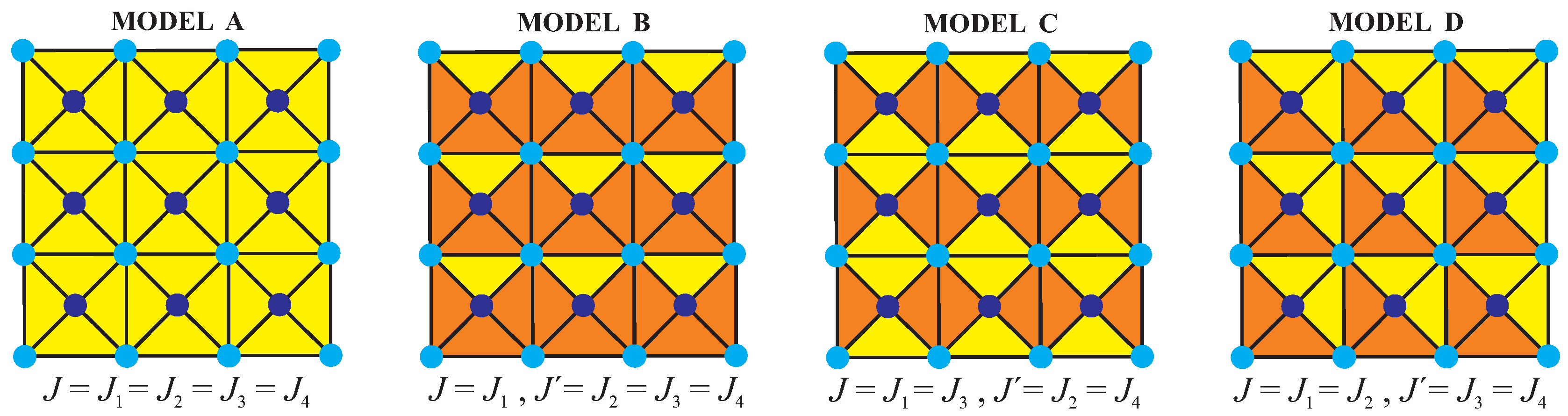
3. Results and Discussion
- Model A: ,
- Model B: ,
- Model C: ,
- Model D: ,
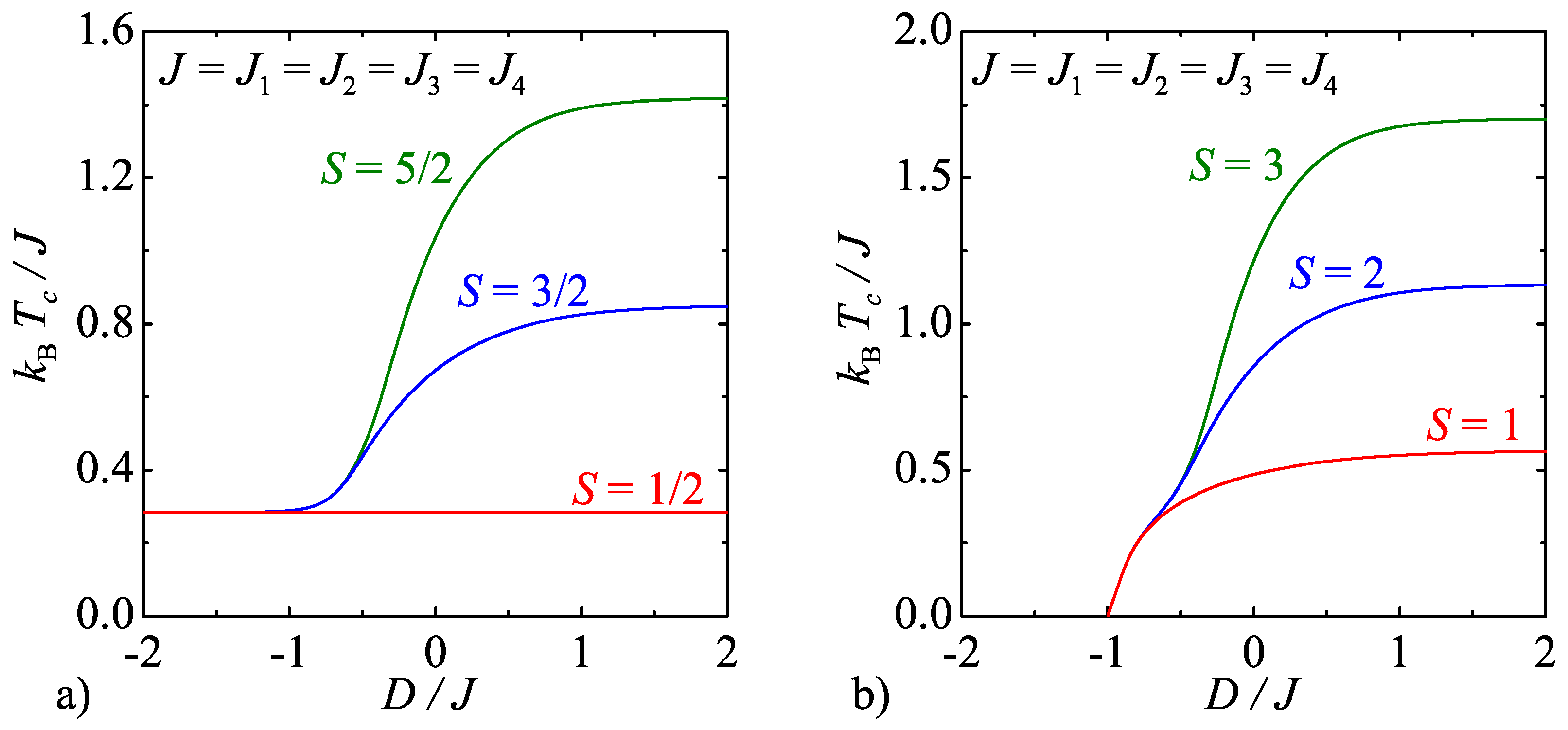
3.1. Model A
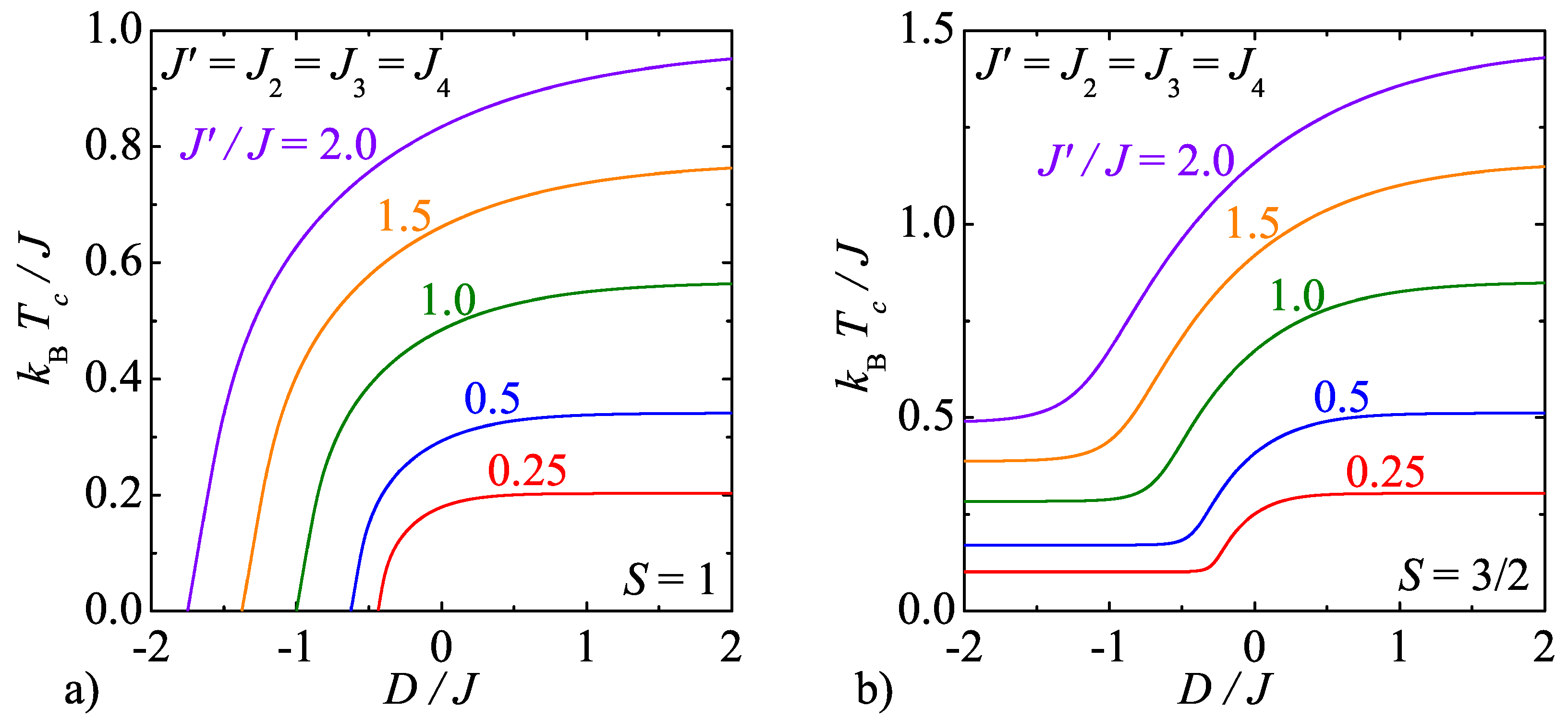
3.2. Model B
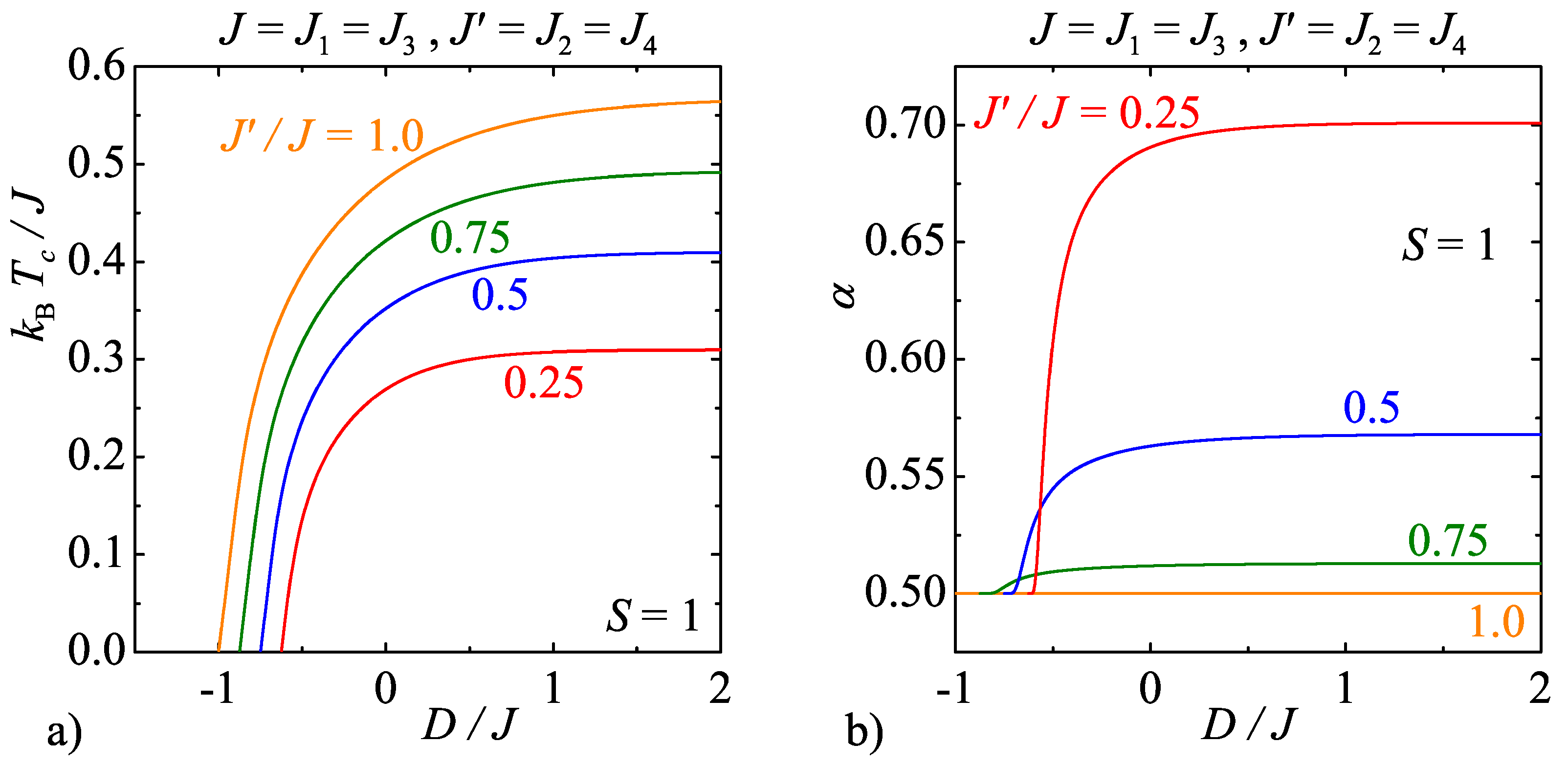
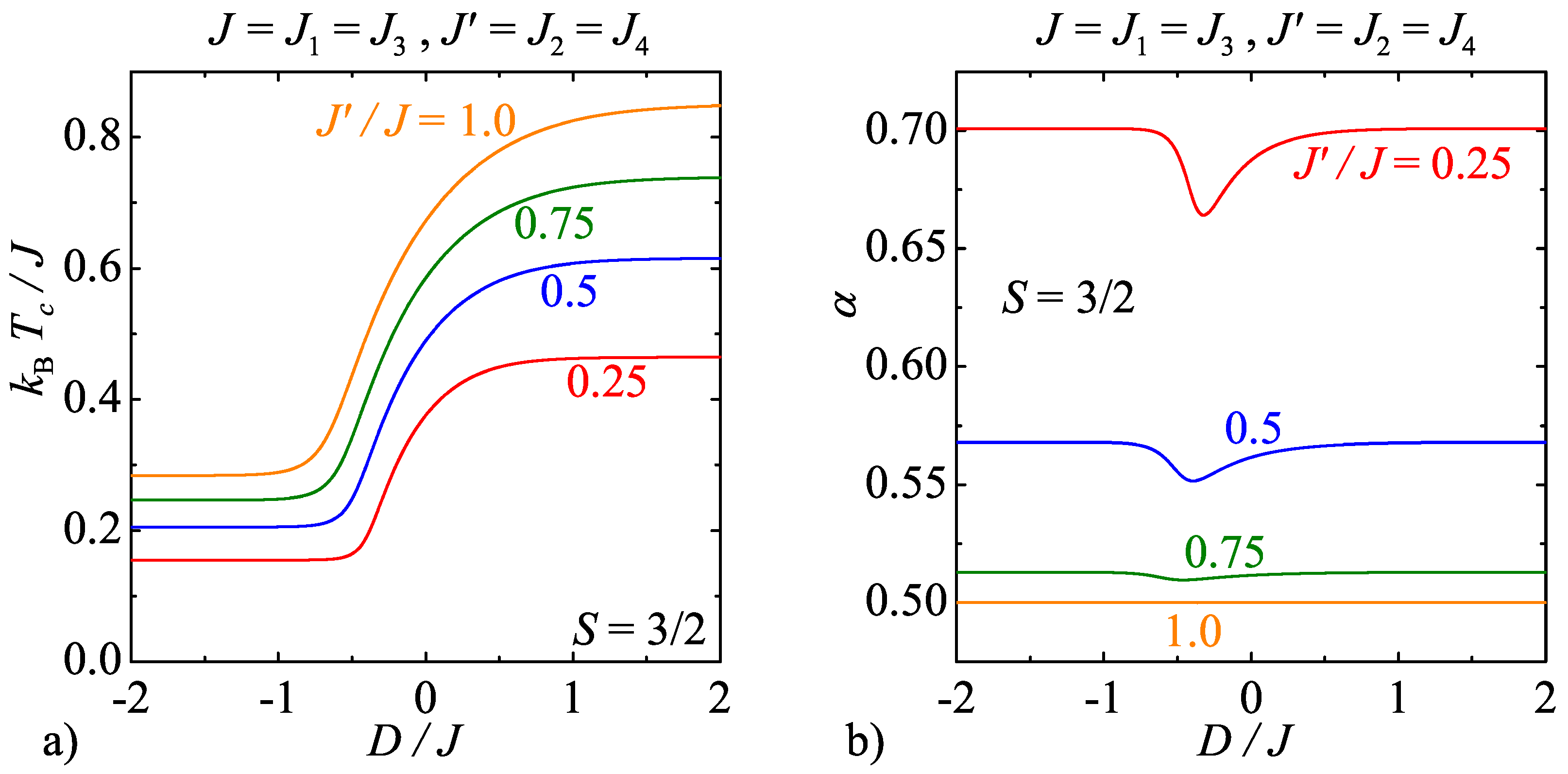
3.3. Model C ()
3.4. Model D
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Baxter, R.J. Exactly Solved Models in Statistical Mechanics; Academic: New York, NY, USA, 1982. [Google Scholar]
- Hintermann, A.; Merlini, D. Exact solution of a two dimensional Ising model with pure 3 spin interactions. Phys. Lett. 1972, 41, 208–210. [Google Scholar] [CrossRef]
- Baxter, R.J.; Wu, F.Y. Exact Solution of an Ising Model with Three-Spin Interactions on a Triangular Lattice. Phys. Rev. Lett. 1973, 31, 1294–1297. [Google Scholar] [CrossRef]
- Baxter, R.J.; Wu, F.Y. Ising Model on a Triangular Lattice with Three-spin Interactions. I. The Eigenvalue Equation. Aust. J. Phys. 1974, 27, 357–368. [Google Scholar] [CrossRef]
- Baxter, R.J. Ising Model on a Triangular Lattice with Three-spin Interactions. II. Free Energy and Correlation Length. Aust. J. Phys. 1974, 27, 369–382. [Google Scholar] [CrossRef]
- Wood, D.W. A free-fermion model, and the solution of an Ising model with pure triplet interactions. J. Phys. C Solid State Phys. 1973, 6, L135–L138. [Google Scholar] [CrossRef]
- Liu, L.L.; Stanley, H.E. Exact solution in an external magnetic field of Ising models with three-spin interactions. Phys. Rev. B 1974, 10, 2958–2961. [Google Scholar] [CrossRef]
- Barry, J.H.; Wu, F.Y. Exact Solutions for a 4-Spin-interaction Ising Model on the d = 3 Pyrochlore Lattice. Int. J. Mod. Phys. 1989, 3, 1247–1275. [Google Scholar] [CrossRef]
- Urumov, V. Examples of Spin and External Field Dependent Critical Exponents. In Ordering in Two Dimensions; Sinha, S.K., Ed.; Elsevier: New York, NY, USA, 1980; pp. 361–364. [Google Scholar]
- Baxter, R.J. Eight-Vertex Model in Lattice Statistics. Phys. Rev. Lett. 1971, 26, 832–833. [Google Scholar] [CrossRef]
- Baxter, R.J. Partition function of the Eight-Vertex lattice model. Ann. Phys. 1972, 70, 193–228. [Google Scholar] [CrossRef]
- Suzuki, M. New Universality of Critical Exponents. Prog. Theor. Phys. 1974, 51, 1992–1993. [Google Scholar] [CrossRef]
- Fisher, M.E. Transformations of Ising Models. Phys. Rev. 1959, 113, 969–981. [Google Scholar] [CrossRef]
- Rojas, O.; Valverde, J.S.; de Souza, S.M. Generalized transformation for decorated spin models. Physica A 2009, 388, 1419–1430. [Google Scholar] [CrossRef]
- Strečka, J. Generalized algebraic transformations and exactly solvable classical-quantum models. Phys. Lett. A 2010, 374, 3718–3722. [Google Scholar] [CrossRef]
- Wu, F.Y. Ising Model with Four-Spin Interactions. Phys. Rev. B 1971, 4, 2312–2314. [Google Scholar] [CrossRef]
- Kadanoff, L.P.; Wegner, R.J. Some Critical Properties of the Eight-Vertex Model. Phys. Rev. B 1971, 4, 3989–3993. [Google Scholar] [CrossRef]
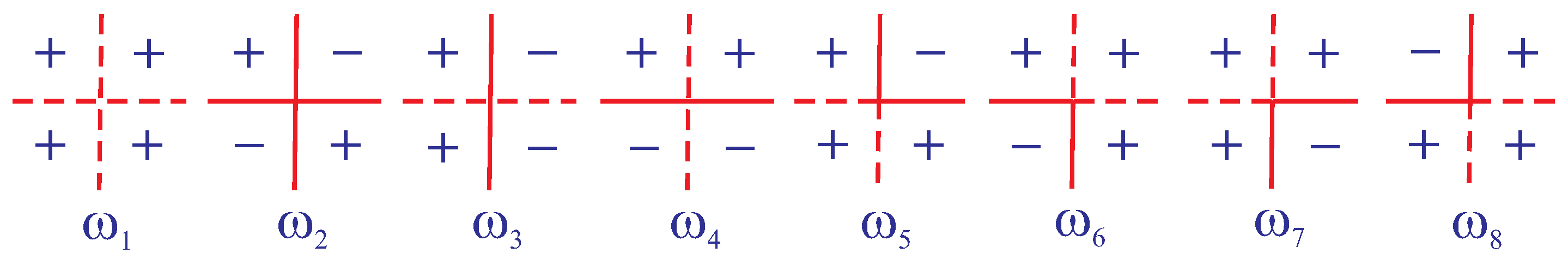


© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strečka, J. Strong- and Weak-Universal Critical Behaviour of a Mixed-Spin Ising Model with Triplet Interactions on the Union Jack (Centered Square) Lattice. Entropy 2018, 20, 91. https://doi.org/10.3390/e20020091
Strečka J. Strong- and Weak-Universal Critical Behaviour of a Mixed-Spin Ising Model with Triplet Interactions on the Union Jack (Centered Square) Lattice. Entropy. 2018; 20(2):91. https://doi.org/10.3390/e20020091
Chicago/Turabian StyleStrečka, Jozef. 2018. "Strong- and Weak-Universal Critical Behaviour of a Mixed-Spin Ising Model with Triplet Interactions on the Union Jack (Centered Square) Lattice" Entropy 20, no. 2: 91. https://doi.org/10.3390/e20020091
APA StyleStrečka, J. (2018). Strong- and Weak-Universal Critical Behaviour of a Mixed-Spin Ising Model with Triplet Interactions on the Union Jack (Centered Square) Lattice. Entropy, 20(2), 91. https://doi.org/10.3390/e20020091




