Minimising the Kullback–Leibler Divergence for Model Selection in Distributed Nonlinear Systems
Abstract
:1. Introduction
2. Related Work
3. Background
3.1. Notation
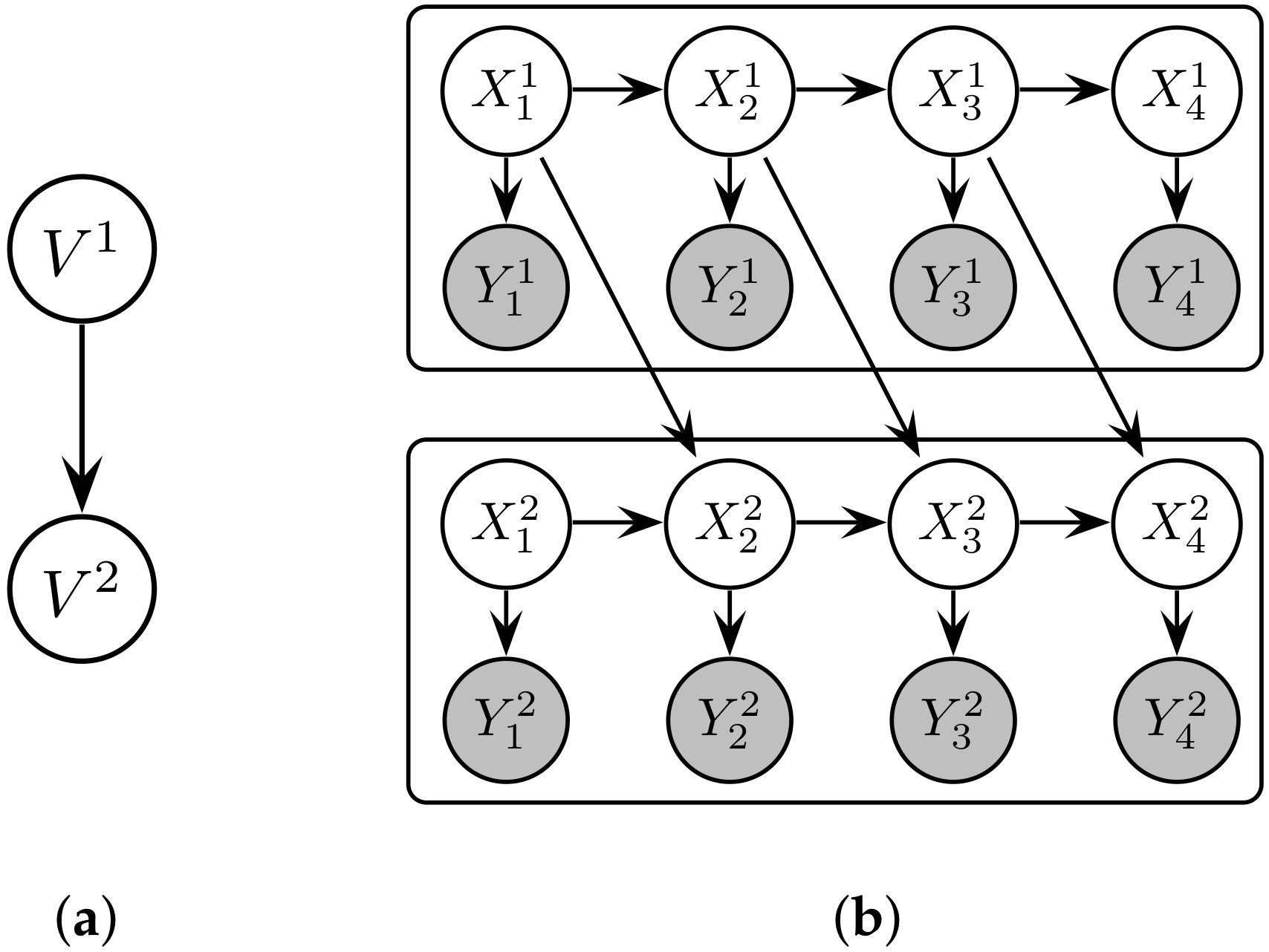
3.2. Representing Distributed Dynamical Systems as Probabilistic Graphical Models
3.3. Network Scoring Functions
4. Computing Conditional KL Divergence
4.1. A Tractable Expression via Embedding Theory
4.2. Information-Theoretic Interpretation
5. Application to Structure Learning
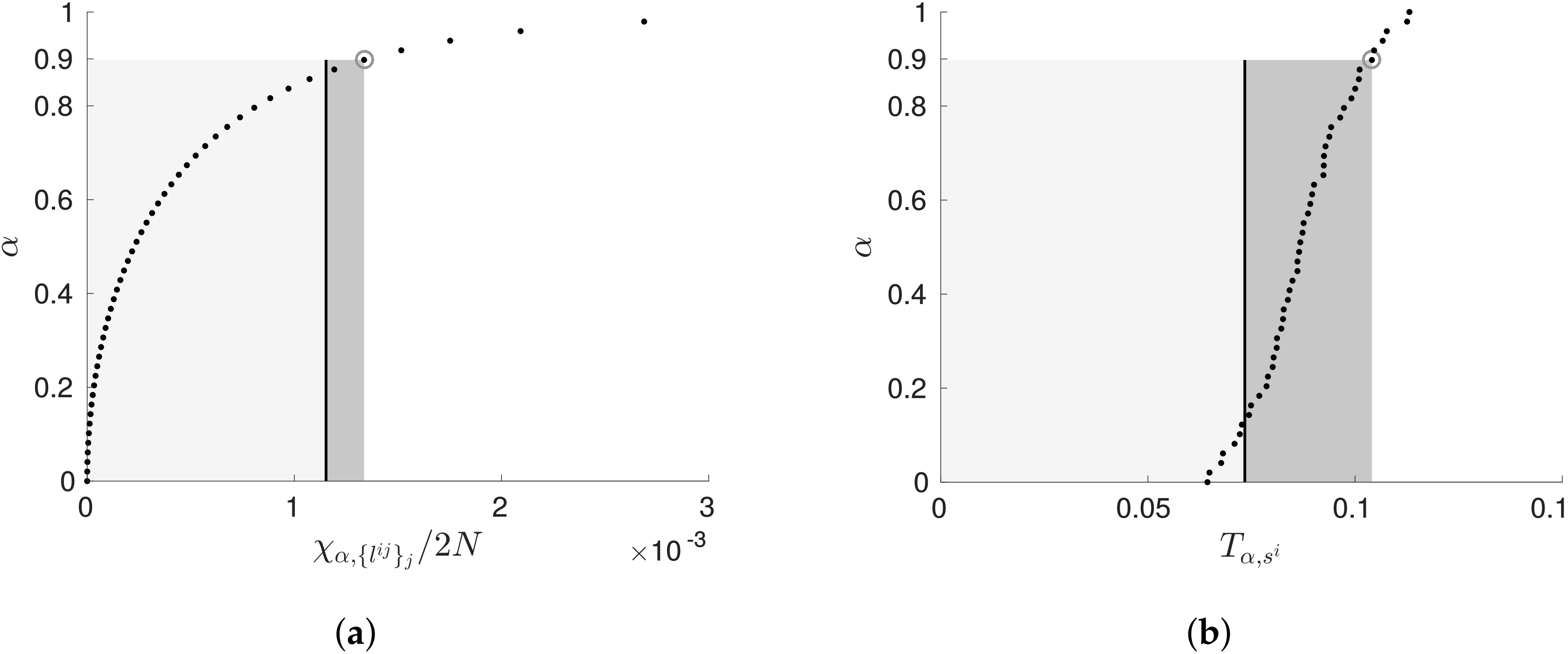
5.1. Penalising Transfer Entropy by Independence Tests
5.2. Implementation Details and Algorithm Analysis
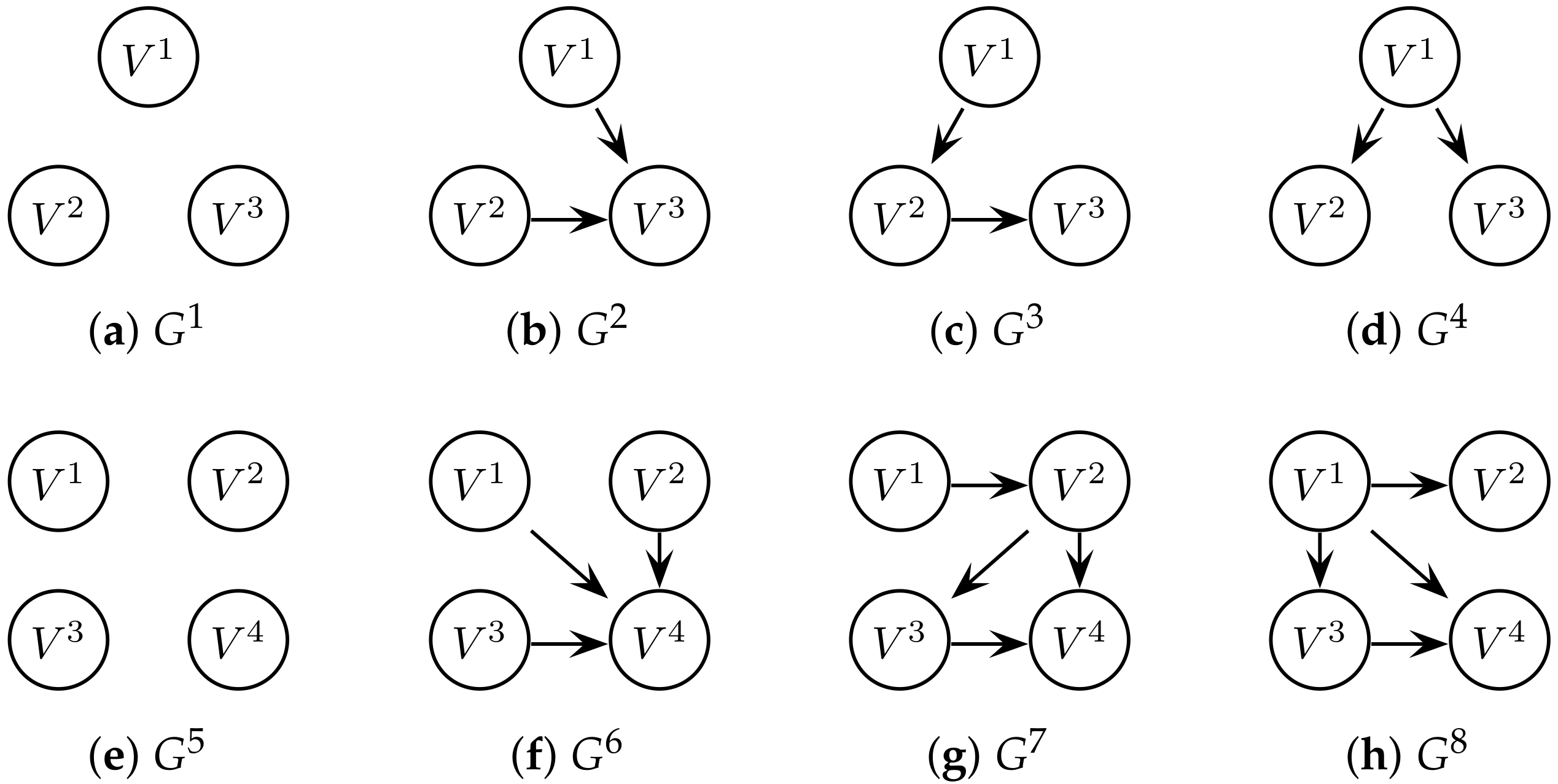
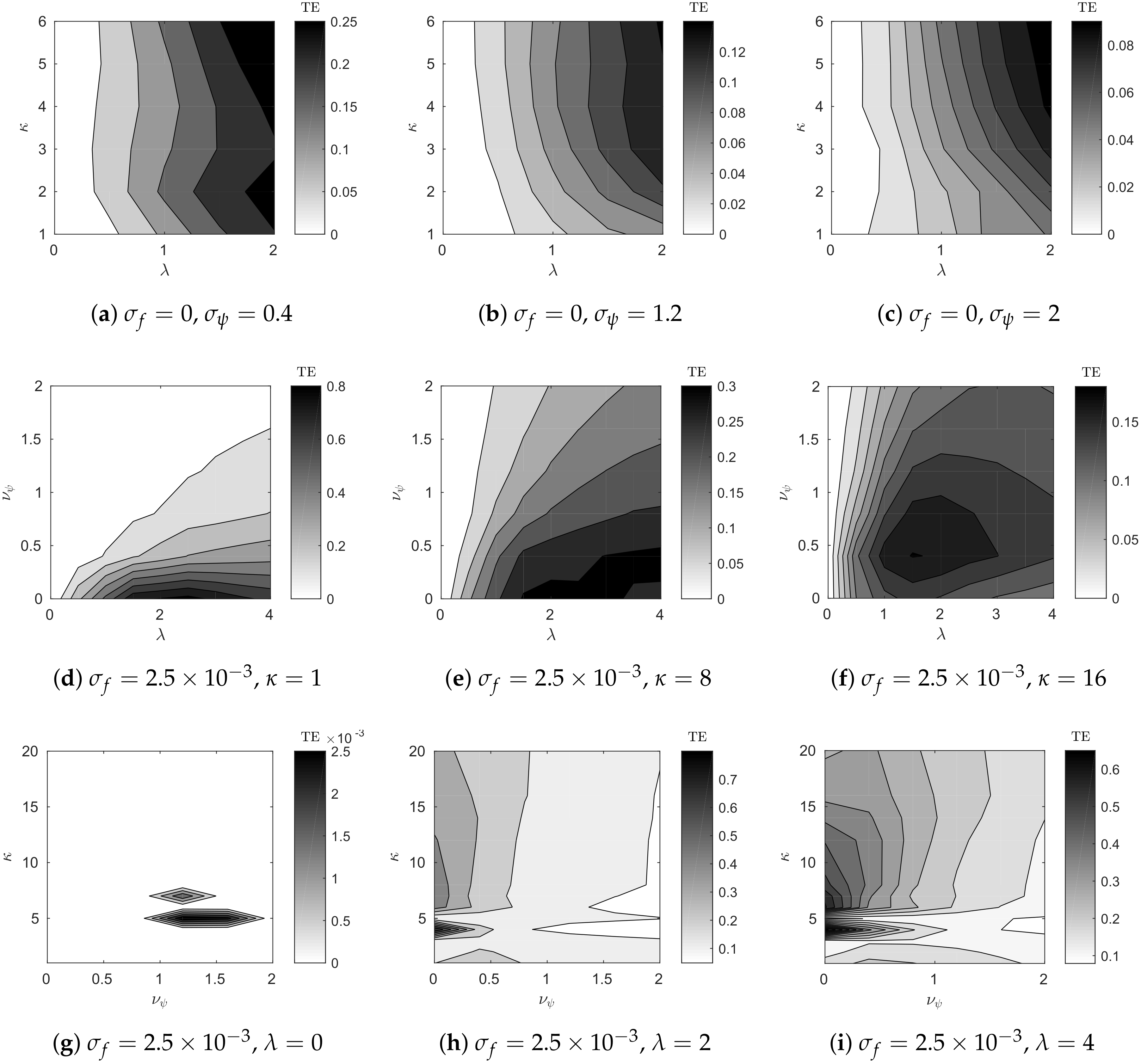
6. Experimental Validation
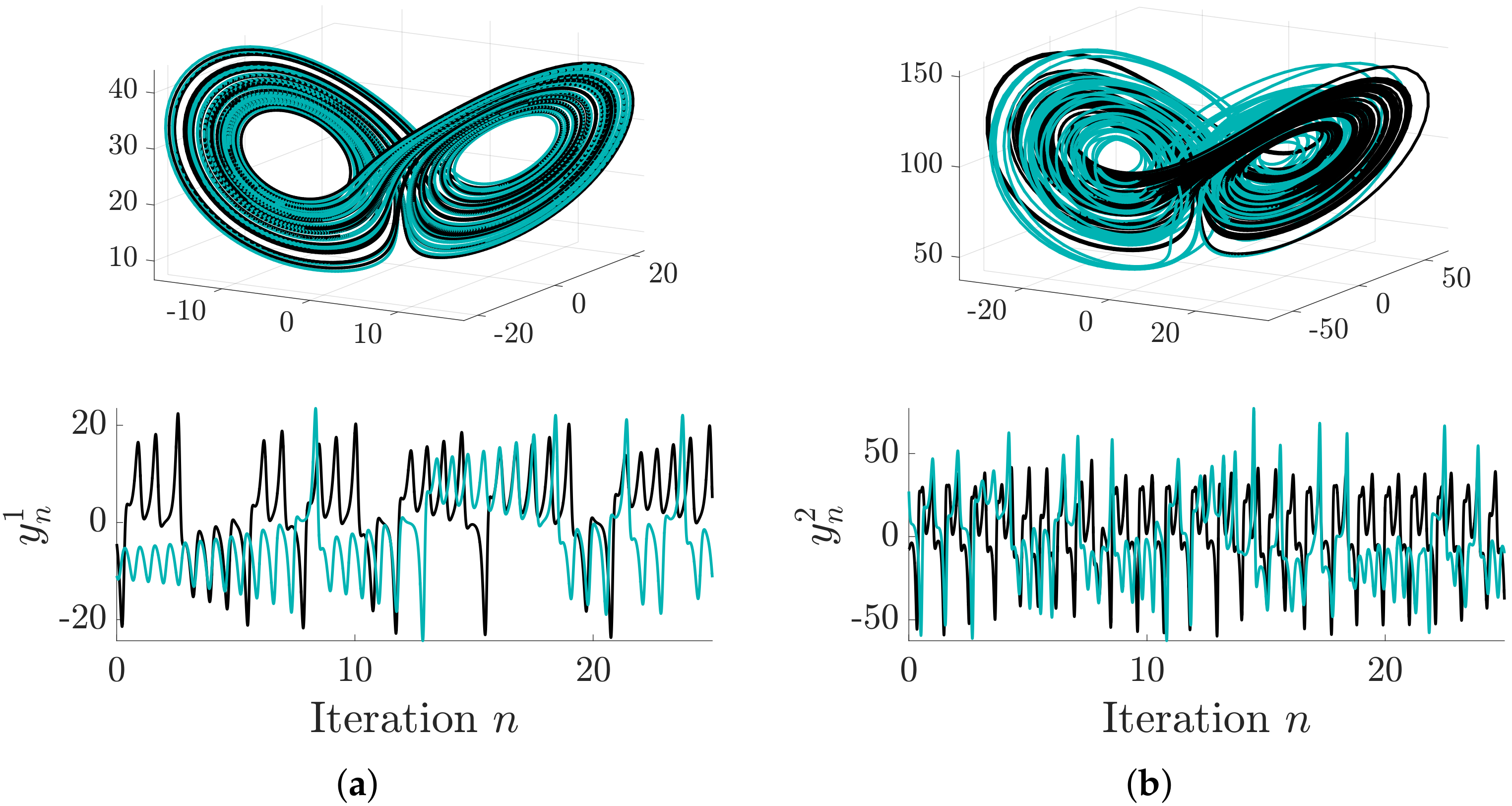
6.1. Distributed Lorenz and Rössler Attractors
6.2. Case Study: Coupled Lorenz–Rössler System
6.3. Case Study: Network of Lorenz Attractors
7. Discussion and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Embedding Theory
Appendix B. Information Theory
Appendix C. Extended Results
| Graph | p-Value | ∞ | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 10 | 1 | 10 | 1 | 10 | ||
| R | - | - | - | - | - | - | - | - | |
| F | 0.33 | 0.22 | 0.33 | 0.22 | 0.22 | 0.33 | 0.33 | 0.22 | |
| P | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| - | - | - | - | - | - | - | - | ||
| R | 1 | 0.5 | 1 | 0.5 | 1 | 0.5 | 1 | 0.5 | |
| F | 0.14 | 0.14 | 0.14 | 0.14 | 0.14 | 0.14 | 0.14 | 0.14 | |
| P | 0.67 | 0.5 | 0.67 | 0.5 | 0.67 | 0.5 | 0.67 | 0.5 | |
| 0.8 | 0.5 | 0.8 | 0.5 | 0.8 | 0.5 | 0.8 | 0.5 | ||
| R | 1 | 0.5 | 1 | 1 | 1 | 1 | 1 | 0.5 | |
| F | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| P | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 0.67 | 1 | 1 | 1 | 1 | 1 | 0.67 | ||
| R | 1 | 0 | 1 | 1 | 1 | 0.5 | 1 | 0 | |
| F | 0.14 | 0.43 | 0.14 | 0.14 | 0.14 | 0.14 | 0.14 | 0.43 | |
| P | 0.67 | 0 | 0.67 | 0.67 | 0.67 | 0.5 | 0.67 | 0 | |
| 0.8 | - | 0.8 | 0.8 | 0.8 | 0.5 | 0.8 | - | ||
| Graph | p-Value | ∞ | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 10 | 1 | 10 | 1 | 10 | ||
| R | - | - | - | - | - | - | - | - | |
| F | 0.31 | 0.25 | 0.31 | 0.19 | 0.31 | 0.25 | 0.31 | 0.19 | |
| P | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| - | - | - | - | - | - | - | - | ||
| R | 0.67 | 0.67 | 0.67 | 0.33 | 0.67 | 0.33 | 0.67 | 0 | |
| F | 0.15 | 0.23 | 0.15 | 0.23 | 0.15 | 0.23 | 0.15 | 0.31 | |
| P | 0.5 | 0.4 | 0.5 | 0.25 | 0.5 | 0.25 | 0.5 | 0 | |
| 0.57 | 0.5 | 0.57 | 0.29 | 0.57 | 0.29 | 0.57 | - | ||
| R | 1 | 0.25 | 1 | 0.25 | 0.75 | 0.25 | 0.75 | 0.5 | |
| F | 0 | 0.25 | 0 | 0.17 | 0.083 | 0.25 | 0.083 | 0.083 | |
| P | 1 | 0.25 | 1 | 0.33 | 0.75 | 0.25 | 0.75 | 0.67 | |
| 1 | 0.25 | 1 | 0.29 | 0.75 | 0.25 | 0.75 | 0.57 | ||
| R | 1 | 0.25 | 1 | 0.5 | 1 | 0.75 | 1 | 0.25 | |
| F | 0 | 0.25 | 0 | 0.083 | 0 | 0.083 | 0 | 0.25 | |
| P | 1 | 0.25 | 1 | 0.67 | 1 | 0.75 | 1 | 0.25 | |
| 1 | 0.25 | 1 | 0.57 | 1 | 0.75 | 1 | 0.25 | ||
| Graph | p-Value | ∞ | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 10 | 1 | 10 | 1 | 10 | ||
| R | - | - | - | - | - | - | - | - | |
| F | 0.22 | 0.11 | 0.22 | 0.11 | 0.22 | 0.22 | 0.22 | 0.11 | |
| P | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| - | - | - | - | - | - | - | - | ||
| R | 1 | 0.5 | 1 | 0.5 | 1 | 0.5 | 1 | 0.5 | |
| F | 0 | 0.14 | 0 | 0.14 | 0 | 0.14 | 0 | 0.14 | |
| P | 1 | 0.5 | 1 | 0.5 | 1 | 0.5 | 1 | 0.5 | |
| 1 | 0.5 | 1 | 0.5 | 1 | 0.5 | 1 | 0.5 | ||
| R | 1 | 0.5 | 1 | 1 | 1 | 0 | 1 | 0.5 | |
| F | 0 | 0.14 | 0 | 0 | 0 | 0.29 | 0 | 0.14 | |
| P | 1 | 0.5 | 1 | 1 | 1 | 0 | 1 | 0.5 | |
| 1 | 0.5 | 1 | 1 | 1 | - | 1 | 0.5 | ||
| R | 1 | 1 | 1 | 0.5 | 1 | 0.5 | 1 | 1 | |
| F | 0.14 | 0.14 | 0 | 0 | 0.14 | 0.14 | 0.14 | 0.14 | |
| P | 0.67 | 0.67 | 1 | 1 | 0.67 | 0.5 | 0.67 | 0.67 | |
| 0.8 | 0.8 | 1 | 0.67 | 0.8 | 0.5 | 0.8 | 0.8 | ||
| Graph | p-Value | ∞ | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 10 | 1 | 10 | 1 | 10 | ||
| R | - | - | - | - | - | - | - | - | |
| F | 0.31 | 0.25 | 0.31 | 0.19 | 0.31 | 0.19 | 0.31 | 0.25 | |
| P | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| - | - | - | - | - | - | - | - | ||
| R | 0.67 | 0.33 | 0.67 | 0 | 1 | 1 | 0.67 | 0.33 | |
| F | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | |
| P | 0.5 | 0.33 | 0.5 | 0 | 0.6 | 0.6 | 0.5 | 0.33 | |
| 0.57 | 0.33 | 0.57 | - | 0.75 | 0.75 | 0.57 | 0.33 | ||
| R | 0.75 | 0.5 | 1 | 0.5 | 1 | 0.25 | 0.75 | 0.5 | |
| F | 0.083 | 0.083 | 0 | 0.083 | 0 | 0.17 | 0.083 | 0.083 | |
| P | 0.75 | 0.67 | 1 | 0.67 | 1 | 0.33 | 0.75 | 0.67 | |
| 0.75 | 0.57 | 1 | 0.57 | 1 | 0.29 | 0.75 | 0.57 | ||
| R | 1 | 0.25 | 1 | 0.25 | 1 | 0 | 1 | 0.25 | |
| F | 0 | 0.17 | 0 | 0.17 | 0 | 0.25 | 0 | 0.17 | |
| P | 1 | 0.33 | 1 | 0.33 | 1 | 0 | 1 | 0.33 | |
| 1 | 0.29 | 1 | 0.29 | 1 | - | 1 | 0.29 | ||
| Graph | p-Value | ∞ | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 10 | 1 | 10 | 1 | 10 | ||
| R | - | - | - | - | - | - | - | - | |
| F | 0.22 | 0.11 | 0.22 | 0.11 | 0.22 | 0.22 | 0.22 | 0.11 | |
| P | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| - | - | - | - | - | - | - | - | ||
| R | 1 | 1 | 1 | 0.5 | 1 | 0.5 | 1 | 1 | |
| F | 0 | 0.14 | 0 | 0.14 | 0 | 0.14 | 0 | 0.14 | |
| P | 1 | 0.67 | 1 | 0.5 | 1 | 0.5 | 1 | 0.67 | |
| 1 | 0.8 | 1 | 0.5 | 1 | 0.5 | 1 | 0.8 | ||
| R | 1 | 1 | 1 | 0.5 | 1 | 1 | 1 | 1 | |
| F | 0 | 0 | 0 | 0.14 | 0 | 0 | 0 | 0 | |
| P | 1 | 1 | 1 | 0.5 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 0.5 | 1 | 1 | 1 | 1 | ||
| R | 1 | 1 | 1 | 1 | 1 | 0.5 | 1 | 1 | |
| F | 0 | 0 | 0 | 0 | 0 | 0.14 | 0 | 0 | |
| P | 1 | 1 | 1 | 1 | 1 | 0.5 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 0.5 | 1 | 1 | ||
| Graph | p-Value | ∞ | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 10 | 1 | 10 | 1 | 10 | ||
| R | - | - | - | - | - | - | - | - | |
| F | 0.31 | 0.19 | 0.31 | 0.19 | 0.31 | 0.19 | 0.31 | 0.19 | |
| P | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| - | - | - | - | - | - | - | - | ||
| R | 1 | 0.33 | 1 | 0.33 | 1 | 0.33 | 1 | 0.33 | |
| F | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.23 | 0.15 | 0.15 | |
| P | 0.6 | 0.33 | 0.6 | 0.33 | 0.6 | 0.25 | 0.6 | 0.33 | |
| 0.75 | 0.33 | 0.75 | 0.33 | 0.75 | 0.29 | 0.75 | 0.33 | ||
| R | 1 | 0.5 | 1 | 0.75 | 1 | 0.75 | 1 | 0.5 | |
| F | 0 | 0.17 | 0 | 0 | 0 | 0 | 0 | 0.17 | |
| P | 1 | 0.5 | 1 | 1 | 1 | 1 | 1 | 0.5 | |
| 1 | 0.5 | 1 | 0.86 | 1 | 0.86 | 1 | 0.5 | ||
| R | 1 | 0.75 | 1 | 0.75 | 1 | 0.75 | 1 | 0.75 | |
| F | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| P | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 0.86 | 1 | 0.86 | 1 | 0.86 | 1 | 0.86 | ||
| Graph | p-Value | ∞ | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 10 | 1 | 10 | 1 | 10 | ||
| R | - | - | - | - | - | - | - | - | |
| F | 0 | 0.11 | 0 | 0 | 0 | 0.11 | 0 | 0.22 | |
| P | - | 0 | - | - | - | 0 | - | 0 | |
| - | - | - | - | - | - | - | - | ||
| R | 1 | 0.5 | 1 | 0.5 | 1 | 0.5 | 1 | 0.5 | |
| F | 0 | 0.14 | 0 | 0.14 | 0 | 0.14 | 0 | 0.14 | |
| P | 1 | 0.5 | 1 | 0.5 | 1 | 0.5 | 1 | 0.5 | |
| 1 | 0.5 | 1 | 0.5 | 1 | 0.5 | 1 | 0.5 | ||
| R | 1 | 1 | 1 | 0.5 | 1 | 1 | 1 | 1 | |
| F | 0 | 0.14 | 0 | 0.14 | 0 | 0.14 | 0 | 0 | |
| P | 1 | 0.67 | 1 | 0.5 | 1 | 0.67 | 1 | 1 | |
| 1 | 0.8 | 1 | 0.5 | 1 | 0.8 | 1 | 1 | ||
| R | 1 | 0.5 | 1 | 1 | 1 | 0.5 | 1 | 1 | |
| F | 0 | 0.14 | 0 | 0 | 0 | 0.14 | 0 | 0 | |
| P | 1 | 0.5 | 1 | 1 | 1 | 0.5 | 1 | 1 | |
| 1 | 0.5 | 1 | 1 | 1 | 0.5 | 1 | 1 | ||
| Graph | p-Value | ∞ | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 10 | 1 | 10 | 1 | 10 | ||
| R | - | - | - | - | - | - | - | - | |
| F | 0.19 | 0.062 | 0.19 | 0.19 | 0.19 | 0.12 | 0.19 | 0.12 | |
| P | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| - | - | - | - | - | - | - | - | ||
| R | 1 | 0.33 | 1 | 0 | 1 | 0.33 | 1 | 0.33 | |
| F | 0 | 0.15 | 0 | 0 | 0 | 0.23 | 0.15 | 0.15 | |
| P | 1 | 0.33 | 1 | - | 1 | 0.25 | 0.6 | 0.33 | |
| 1 | 0.33 | 1 | - | 1 | 0.29 | 0.75 | 0.33 | ||
| R | 1 | 0.75 | 1 | 0.5 | 1 | 0.5 | 1 | 0.75 | |
| F | 0 | 0 | 0 | 0.17 | 0 | 0.083 | 0 | 0 | |
| P | 1 | 1 | 1 | 0.5 | 1 | 0.67 | 1 | 1 | |
| 1 | 0.86 | 1 | 0.5 | 1 | 0.57 | 1 | 0.86 | ||
| R | 1 | 0.75 | 1 | 0.75 | 1 | 0.75 | 1 | 0.75 | |
| F | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| P | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 0.86 | 1 | 0.86 | 1 | 0.86 | 1 | 0.86 | ||
| Graph | p-Value | ∞ | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 10 | 1 | 10 | 1 | 10 | ||
| R | - | - | - | - | - | - | - | - | |
| F | 0 | 0.22 | 0 | 0.11 | 0 | 0.22 | 0 | 0.11 | |
| P | - | 0 | - | 0 | - | 0 | - | 0 | |
| - | - | - | - | - | - | - | - | ||
| R | 1 | 0.5 | 1 | 1 | 1 | 1 | 1 | 1 | |
| F | 0 | 0.14 | 0 | 0 | 0 | 0 | 0 | 0.14 | |
| P | 1 | 0.5 | 1 | 1 | 1 | 1 | 1 | 0.67 | |
| 1 | 0.5 | 1 | 1 | 1 | 1 | 1 | 0.8 | ||
| R | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| F | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| P | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| R | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| F | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| P | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| Graph | p-Value | ∞ | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 1 | 10 | 1 | 10 | 1 | 10 | ||
| R | - | - | - | - | - | - | - | - | |
| F | 0.19 | 0.062 | 0.19 | 0.062 | 0.19 | 0.19 | 0.19 | 0.12 | |
| P | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| - | - | - | - | - | - | - | - | ||
| R | 1 | 0.33 | 1 | 0.67 | 1 | 0.33 | 1 | 0.33 | |
| F | 0 | 0.15 | 0 | 0.15 | 0 | 0.077 | 0 | 0.15 | |
| P | 1 | 0.33 | 1 | 0.5 | 1 | 0.5 | 1 | 0.33 | |
| 1 | 0.33 | 1 | 0.57 | 1 | 0.4 | 1 | 0.33 | ||
| R | 1 | - | 1 | - | 1 | - | 1 | - | |
| F | 0 | - | 0 | - | 0 | - | 0 | - | |
| P | 1 | - | 1 | - | 1 | - | 1 | - | |
| 1 | - | 1 | - | 1 | - | 1 | - | ||
| R | 1 | 0.75 | 1 | 0.75 | 1 | 0.5 | 1 | 0.75 | |
| F | 0 | 0 | 0 | 0 | 0 | 0.083 | 0 | 0 | |
| P | 1 | 1 | 1 | 1 | 1 | 0.67 | 1 | 1 | |
| 1 | 0.86 | 1 | 0.86 | 1 | 0.57 | 1 | 0.86 | ||
References
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Proceedings of the Second International Symposium on Information Theory, Tsahkadsor, Armenia, USSR, 2–8 September 1971; pp. 267–281. [Google Scholar]
- Lam, W.; Bacchus, F. Learning Bayesian belief networks: An approach based on the MDL principle. Comput. Intell. 1994, 10, 269–293. [Google Scholar] [CrossRef]
- de Campos, L.M. A Scoring Function for Learning Bayesian Networks Based on Mutual Information and Conditional Independence Tests. J. Mach. Learn. Res. 2006, 7, 2149–2187. [Google Scholar]
- Sugihara, G.; May, R.; Ye, H.; Hsieh, C.H.; Deyle, E.; Fogarty, M.; Munch, S. Detecting causality in complex ecosystems. Science 2012, 338, 496–500. [Google Scholar] [CrossRef] [PubMed]
- Vicente, R.; Wibral, M.; Lindner, M.; Pipa, G. Transfer entropy—A model-free measure of effective connectivity for the neurosciences. J. Comput. Neurosci. 2011, 30, 45–67. [Google Scholar] [CrossRef] [PubMed]
- Schumacher, J.; Wunderle, T.; Fries, P.; Jäkel, F.; Pipa, G. A statistical framework to infer delay and direction of information flow from measurements of complex systems. Neural Comput. 2015, 27, 1555–1608. [Google Scholar] [CrossRef] [PubMed]
- Best, G.; Cliff, O.M.; Patten, T.; Mettu, R.R.; Fitch, R. Decentralised Monte Carlo Tree Search for Active Perception. In Proceedings of the International Workshop on the Algorithmic Foundations of Robotics (WAFR), San Francisco, CA, USA, 18–20 December 2016. [Google Scholar]
- Cliff, O.M.; Lizier, J.T.; Wang, X.R.; Wang, P.; Obst, O.; Prokopenko, M. Delayed Spatio-Temporal Interactions and Coherent Structure in Multi-Agent Team Dynamics. Art. Life 2017, 23, 34–57. [Google Scholar] [CrossRef] [PubMed]
- Best, G.; Forrai, M.; Mettu, R.R.; Fitch, R. Planning-aware communication for decentralised multi-robot coordination. In Proceedings of the International Conference on Robotics and Automation, Brisbane, Australia, 21 May 2018. [Google Scholar]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Mortveit, H.; Reidys, C. An Introduction to Sequential Dynamical Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Cliff, O.M.; Prokopenko, M.; Fitch, R. An Information Criterion for Inferring Coupling in Distributed Dynamical Systems. Front. Robot. AI 2016, 3. [Google Scholar] [CrossRef]
- Daly, R.; Shen, Q.; Aitken, J.S. Learning Bayesian networks: Approaches and issues. Knowl. Eng. Rev. 2011, 26, 99–157. [Google Scholar] [CrossRef]
- Chickering, D.M. Learning equivalence classes of Bayesian-network structures. J. Mach. Learn. Res. 2002, 2, 445–498. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Rissanen, J. Modeling by shortest data description. Automatica 1978, 14, 465–471. [Google Scholar] [CrossRef]
- Ay, N.; Wennekers, T. Temporal infomax leads to almost deterministic dynamical systems. Neurocomputing 2003, 52, 461–466. [Google Scholar] [CrossRef]
- Ay, N. Information geometry on complexity and stochastic interaction. Entropy 2015, 17, 2432–2458. [Google Scholar] [CrossRef]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Information modification and particle collisions in distributed computation. Chaos 2010, 20, 037109. [Google Scholar] [CrossRef] [PubMed]
- Murphy, K. Dynamic Bayesian Networks: Representation, Inference and Learning. Ph.D. Thesis, UC Berkeley, Berkeley, CA, USA, 2002. [Google Scholar]
- Kocarev, L.; Parlitz, U. Generalized synchronization, predictability, and equivalence of unidirectionally coupled dynamical systems. Phys. Rev. Lett. 1996, 76, 1816–1819. [Google Scholar] [CrossRef] [PubMed]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann: Burlington, MA, USA, 2014. [Google Scholar]
- Granger, C.W.J. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Granger Causality and Transfer Entropy Are Equivalent for Gaussian Variables. Phys. Rev. Lett. 2009, 103, e238701. [Google Scholar] [CrossRef] [PubMed]
- Lizier, J.T.; Prokopenko, M. Differentiating information transfer and causal effect. Eur. Phys. J. B 2010, 73, 605–615. [Google Scholar] [CrossRef]
- Smirnov, D.A. Spurious causalities with transfer entropy. Phys. Rev. E 2013, 87, 042917. [Google Scholar] [CrossRef] [PubMed]
- James, R.G.; Barnett, N.; Crutchfield, J.P. Information flows? A critique of transfer entropies. Phys. Rev. Lett. 2016, 116, 238701. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.S. Information flow and causality as rigorous notions ab initio. Phys. Rev. E 2016, 94, 052201. [Google Scholar] [CrossRef] [PubMed]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence; Lecture Notes in Math; Springer: Berlin/Heidelberg, Germany, 1981; Volume 898, pp. 366–381. [Google Scholar]
- Stark, J. Delay embeddings for forced systems. I. Deterministic forcing. J. Nonlinear Sci. 1999, 9, 255–332. [Google Scholar] [CrossRef]
- Stark, J.; Broomhead, D.S.; Davies, M.E.; Huke, J. Delay embeddings for forced systems. II. Stochastic forcing. J. Nonlinear Sci. 2003, 13, 519–577. [Google Scholar] [CrossRef]
- Valdes-Sosa, P.A.; Roebroeck, A.; Daunizeau, J.; Friston, K. Effective connectivity: influence, causality and biophysical modeling. Neuroimage 2011, 58, 339–361. [Google Scholar] [CrossRef] [PubMed]
- Sporns, O.; Chialvo, D.R.; Kaiser, M.; Hilgetag, C.C. Organization, development and function of complex brain networks. Trends Cogn. Sci. 2004, 8, 418–425. [Google Scholar] [CrossRef] [PubMed]
- Park, H.J.; Friston, K. Structural and functional brain networks: From connections to cognition. Science 2013, 342, 1238411. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.; Moran, R.; Seth, A.K. Analysing connectivity with Granger causality and dynamic causal modelling. Curr. Opin. Neurobiol. 2013, 23, 172–178. [Google Scholar] [CrossRef] [PubMed]
- Lizier, J.T.; Rubinov, M. Multivariate Construction of Effective Computational Networks from Observational Data; Preprint 25/2012; Max Planck Institute for Mathematics in the Sciences: Leipzig, Germany, 2012. [Google Scholar]
- Sandoval, L. Structure of a global network of financial companies based on transfer entropy. Entropy 2014, 16, 4443–4482. [Google Scholar] [CrossRef]
- Rodewald, J.; Colombi, J.; Oyama, K.; Johnson, A. Using Information-theoretic Principles to Analyze and Evaluate Complex Adaptive Supply Network Architectures. Procedia Comput. Sci. 2015, 61, 147–152. [Google Scholar] [CrossRef]
- Crosato, E.; Jiang, L.; Lecheval, V.; Lizier, J.T.; Wang, X.R.; Tichit, P.; Theraulaz, G.; Prokopenko, M. Informative and misinformative interactions in a school of fish. arXiv, 2017; arXiv:1705.01213. [Google Scholar]
- Kozachenko, L.; Friston, L.F.; Leonenko, N.N. Sample estimate of the entropy of a random vector. Probl. Peredachi Inf. 1987, 23, 9–16. [Google Scholar]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed]
- Stark, J.; Broomhead, D.S.; Davies, M.E.; Huke, J. Takens embedding theorems for forced and stochastic systems. Nonlinear Anal. Theory Methods Appl. 1997, 30, 5303–5314. [Google Scholar] [CrossRef]
- Friedman, N.; Murphy, K.; Russell, S. Learning the structure of dynamic probabilistic networks. In Proceedings of the Fourteenth Conference on Uncertainty in Artificial Intelligence, Madison, WI, USA, 24–26 July 1998; pp. 139–147. [Google Scholar]
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Wilks, S.S. The large-sample distribution of the likelihood ratio for testing composite hypotheses. Ann. Math. Stat. 1938, 9, 60–62. [Google Scholar] [CrossRef]
- Barnett, L.; Bossomaier, T. Transfer entropy as a log-likelihood ratio. Phys. Rev. Lett. 2012, 109, 138105. [Google Scholar] [CrossRef] [PubMed]
- Vinh, N.X.; Chetty, M.; Coppel, R.; Wangikar, P.P. GlobalMIT: Learning globally optimal dynamic Bayesian network with the mutual information test criterion. Bioinformatics 2011, 27, 2765–2766. [Google Scholar] [CrossRef] [PubMed]
- Deyle, E.R.; Sugihara, G. Generalized theorems for nonlinear state space reconstruction. PLoS ONE 2011, 6, e18295. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, A.L. The coupled logistic map: a simple model for the effects of spatial heterogeneity on population dynamics. J. Theor. Biol. 1995, 173, 217–230. [Google Scholar] [CrossRef]
- Lizier, J.T. JIDT: An information-theoretic toolkit for studying the dynamics of complex systems. Front. Robot. AI 2014, 1. [Google Scholar] [CrossRef]
- Silander, T.; Myllymaki, P. A simple approach for finding the globally optimal Bayesian network structure. In Proceedings of the Twenty-Second Conference on Uncertainty in Artificial Intelligence, Cambridge, MA, USA, 13–16 July 2006; pp. 445–452. [Google Scholar]
- Ragwitz, M.; Kantz, H. Markov models from data by simple nonlinear time series predictors in delay embedding spaces. Phys. Rev. E 2002, 65, 056201. [Google Scholar] [CrossRef] [PubMed]
- Small, M.; Tse, C.K. Optimal embedding parameters: A modelling paradigm. Physica 2004, 194, 283–296. [Google Scholar]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Rössler, O.E. An equation for continuous chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Haken, H. Analogy between higher instabilities in fluids and lasers. Phys. Lett. A 1975, 53, 77–78. [Google Scholar] [CrossRef]
- Cuomo, K.M.; Oppenheim, A.V. Circuit implementation of synchronized chaos with applications to communications. Phys. Rev. Lett. 1993, 71, 65–68. [Google Scholar] [CrossRef] [PubMed]
- He, R.; Vaidya, P.G. Analysis and synthesis of synchronous periodic and chaotic systems. Phys. Rev. A 1992, 46, 7387–7392. [Google Scholar] [CrossRef] [PubMed]
- Fujisaka, H.; Yamada, T. Stability theory of synchronized motion in coupled-oscillator systems. Prog. Theor. Phys. 1983, 69, 32–47. [Google Scholar] [CrossRef]
- Rulkov, N.F.; Sushchik, M.M.; Tsimring, L.S.; Abarbanel, H.D. Generalized synchronization of chaos in directionally coupled chaotic systems. Phys. Rev. E 1995, 51, 980–994. [Google Scholar] [CrossRef]
- Acid, S.; de Campos, L.M. Searching for Bayesian network structures in the space of restricted acyclic partially directed graphs. J. Artif. Intell. Res. 2003, 18, 445–490. [Google Scholar]
- Friston, K.; Kilner, J.; Harrison, L. A free energy principle for the brain. J. Physiol. Paris 2006, 100, 70–87. [Google Scholar] [CrossRef] [PubMed]
- Williams, P.L.; Beer, R.D. Generalized measures of information transfer. arXiv, 2011; arXiv:1102.1507. [Google Scholar]
- Vakorin, V.A.; Krakovska, O.A.; McIntosh, A.R. Confounding effects of indirect connections on causality estimation. J. Neurosci. Methods 2009, 184, 152–160. [Google Scholar] [CrossRef] [PubMed]
- Spinney, R.E.; Prokopenko, M.; Lizier, J.T. Transfer entropy in continuous time, with applications to jump and neural spiking processes. Phys. Rev. E 2017, 95, 032319. [Google Scholar] [CrossRef] [PubMed]
- Hefferan, B.; Cliff, O.M.; Fitch, R. Adversarial Patrolling with Reactive Point Processes. In Proceedings of the Australasian Conference on Robotics and Automation (ACRA), Brisbane, Australia, 5–7 December 2016. [Google Scholar]
- Prokopenko, M.; Einav, I. Information thermodynamics of near-equilibrium computation. Phys. Rev. E 2015, 91, 062143. [Google Scholar] [CrossRef] [PubMed]
- Spinney, R.E.; Lizier, J.T.; Prokopenko, M. Transfer entropy in physical systems and the arrow of time. Phys. Rev. E 2016, 94, 022135. [Google Scholar] [CrossRef] [PubMed]
- Takens, F. The reconstruction theorem for endomorphisms. Bull. Braz. Math. Soc. 2002, 33, 231–262. [Google Scholar] [CrossRef]
- Ay, N.; Wennekers, T. Dynamical properties of strongly interacting Markov chains. Neural Netw. 2003, 16, 1483–1497. [Google Scholar] [CrossRef]
- Edlund, J.A.; Chaumont, N.; Hintze, A.; Koch, C.; Tononi, G.; Adami, C. Integrated information increases with fitness in the evolution of animats. PLoS Comput. Biol. 2011, 7, e1002236. [Google Scholar] [CrossRef] [PubMed]
| Graph | N | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 5 K | 0.8 | 0.5 | 0.8 | 0.5 | 0.8 | 0.5 | 0.8 | 0.5 | |
| 25 K | 1 | 0.8 | 1 | 0.5 | 1 | 0.5 | 1 | 0.8 | |
| 100 K | 1 | 0.5 | 1 | 1 | 1 | 1 | 1 | 0.8 | |
| 5 K | 1 | 0.67 | 1 | 1 | 1 | 1 | 1 | 0.67 | |
| 25 K | 1 | 1 | 1 | 0.5 | 1 | 1 | 1 | 1 | |
| 100 K | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 5 K | 0.8 | - | 0.8 | 0.8 | 0.8 | 0.5 | 0.8 | - | |
| 25 K | 1 | 1 | 1 | 1 | 1 | 0.5 | 1 | 1 | |
| 100 K | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| Graph | N | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 5 K | 0.57 | 0.5 | 0.57 | 0.29 | 0.57 | 0.29 | 0.57 | - | |
| 25 K | 0.75 | 0.33 | 0.75 | 0.33 | 0.75 | 0.29 | 0.75 | 0.33 | |
| 100 K | 1 | 0.33 | 1 | 0.57 | 1 | 0.4 | 1 | 0.33 | |
| 5 K | 1 | 0.25 | 1 | 0.29 | 0.75 | 0.25 | 0.75 | 0.57 | |
| 25 K | 1 | 0.5 | 1 | 0.86 | 1 | 0.86 | 1 | 0.5 | |
| 100 K | 1 | 0.86 | 1 | 0.86 | 1 | 0.86 | 1 | 0.86 | |
| 5 K | 1 | 0.25 | 1 | 0.57 | 1 | 0.75 | 1 | 0.25 | |
| 25 K | 1 | 0.86 | 1 | 0.86 | 1 | 0.86 | 1 | 0.86 | |
| 100 K | 1 | 0.86 | 1 | 0.86 | 1 | 0.57 | 1 | 0.86 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cliff, O.M.; Prokopenko, M.; Fitch, R. Minimising the Kullback–Leibler Divergence for Model Selection in Distributed Nonlinear Systems. Entropy 2018, 20, 51. https://doi.org/10.3390/e20020051
Cliff OM, Prokopenko M, Fitch R. Minimising the Kullback–Leibler Divergence for Model Selection in Distributed Nonlinear Systems. Entropy. 2018; 20(2):51. https://doi.org/10.3390/e20020051
Chicago/Turabian StyleCliff, Oliver M., Mikhail Prokopenko, and Robert Fitch. 2018. "Minimising the Kullback–Leibler Divergence for Model Selection in Distributed Nonlinear Systems" Entropy 20, no. 2: 51. https://doi.org/10.3390/e20020051
APA StyleCliff, O. M., Prokopenko, M., & Fitch, R. (2018). Minimising the Kullback–Leibler Divergence for Model Selection in Distributed Nonlinear Systems. Entropy, 20(2), 51. https://doi.org/10.3390/e20020051






