Uncertainty Relation Based on Wigner–Yanase–Dyson Skew Information with Quantum Memory
Abstract
:1. Introduction
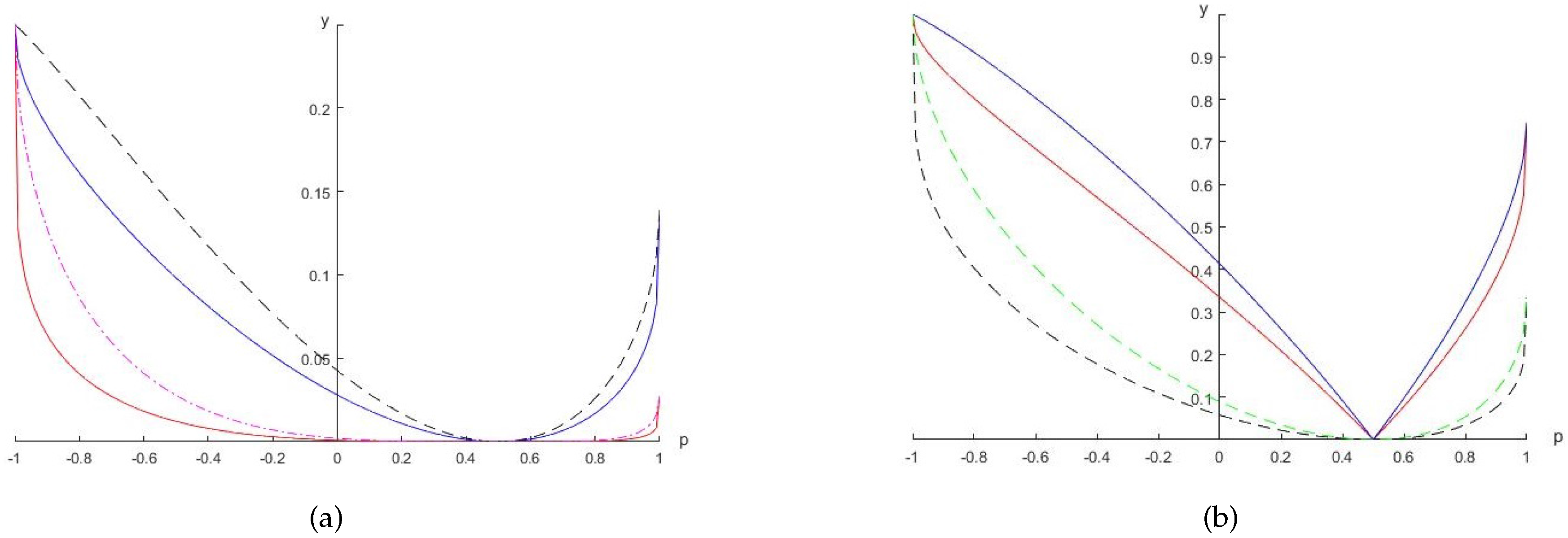
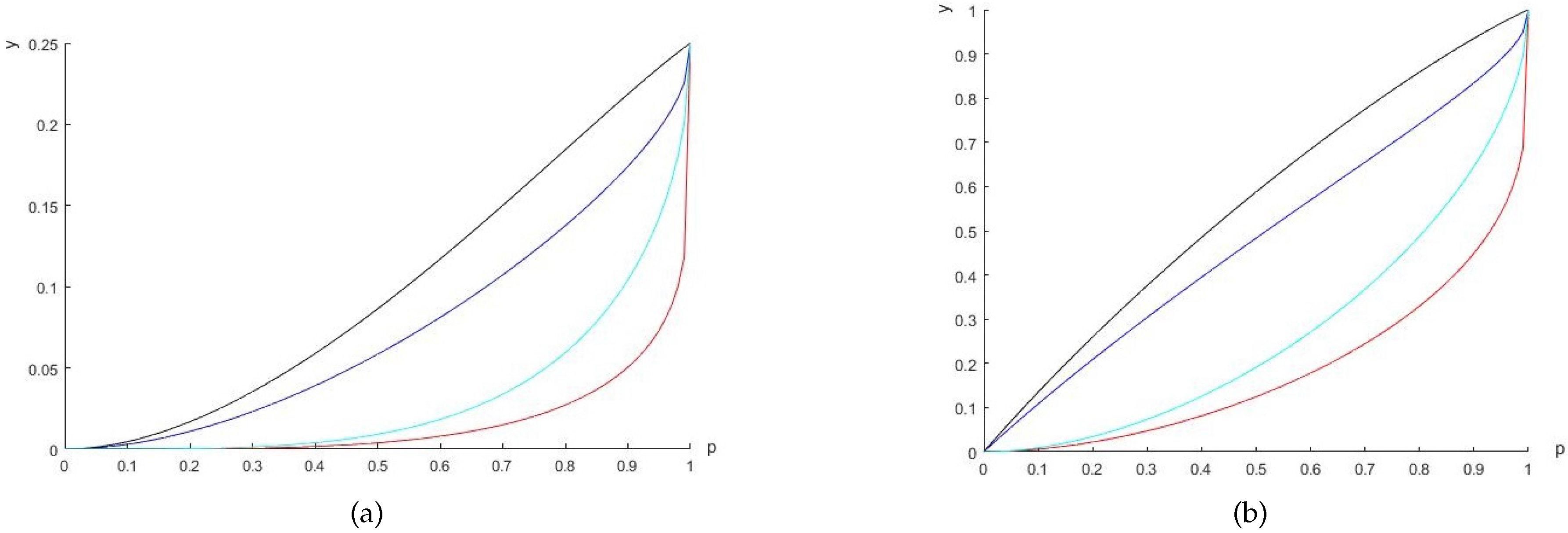
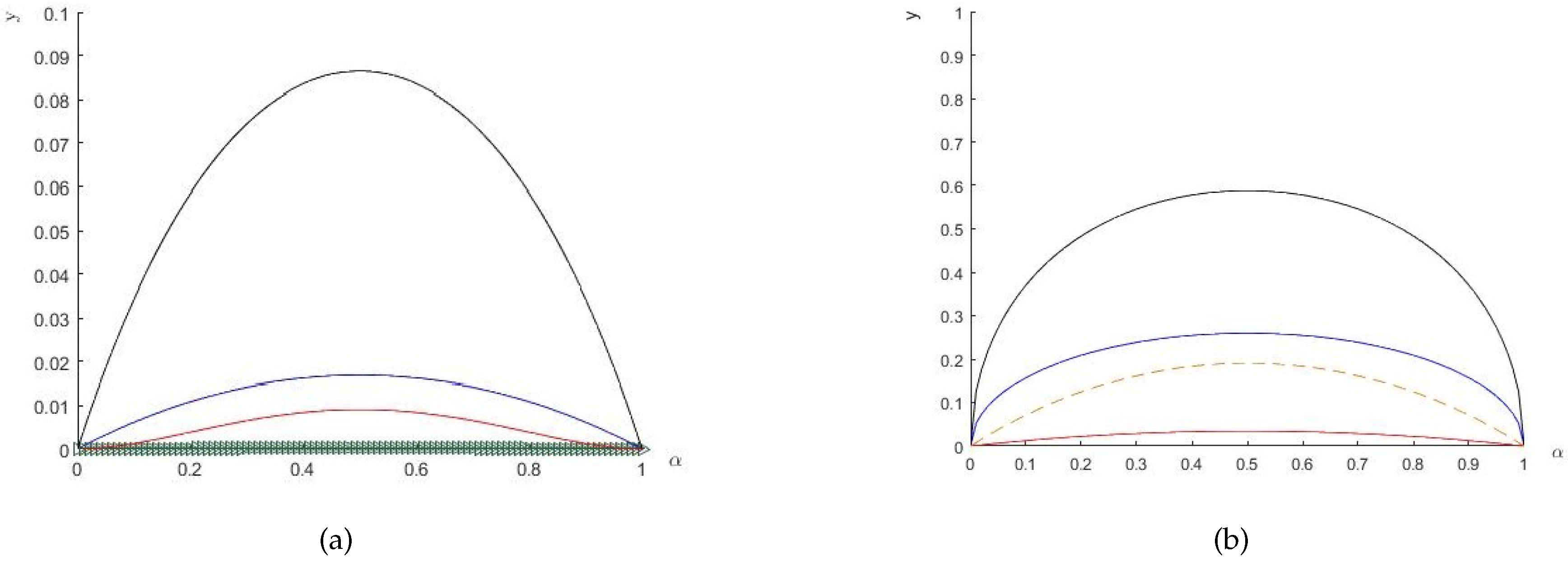
2. Results
3. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 1927, 43, 172–198. (In German) [Google Scholar] [CrossRef]
- Robertson, H.P. The Uncertainty Principle. Science 1929, 73, 653. [Google Scholar] [CrossRef]
- Schrödinger, E. Zum Heisenbergschen Unschärfeprinzip. Sitzungsberichte Akad. Berl. 1930, 19, 296–303. (In German) [Google Scholar]
- Busch, P.; Lahti, P.; Werner, R.F. Proof of Heisenberg’s Error-Disturbance Relation. Phys. Rev. Lett. 2013, 111, 160405. [Google Scholar] [CrossRef] [PubMed]
- Busch, P.; Lahti, P.; Werner, R.F. Heisenberg uncertainty for qubit measurements. Phys. Rev. A 2014, 89, 012129. [Google Scholar] [CrossRef]
- Sulyok, G.; Sponar, S.; Demirel, B.; Buscemi, F.; Hall, M.J.W.; Ozawa, M.; Hasegawa, Y. Experimental test of entropic noise-disturbance uncertainty relations for spin-1/2 measurements. Phys. Rev. Lett. 2015, 115, 030401. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.; Ma, Z.; Wang, H.; Liu, Y.; Chen, Z.; Kong, F.; Li, Z.; Shi, M.; Shi, F.; Fei, S.-M.; et al. Experimental demonstration of Heisenberg’s measurement uncertainty relation based on statistical distances. Phys. Rev. Lett. 2016, 116, 160405. [Google Scholar] [CrossRef] [PubMed]
- Puchała, Z.; Rudnicki, Ł.; Zyczkowski, K.J. Majorization entropic uncertainty relations. Phys. A Math. Theor. 2013, 46, 272002. [Google Scholar] [CrossRef]
- Friedland, S.; Gheorghiu, V.; Gour, G. Universal Uncertainty Relations. Phys. Rev. Lett. 2013, 111, 230401. [Google Scholar] [CrossRef] [PubMed]
- Maccone, L.; Pati, A.K. Stronger Uncertainty Relations for All Incompatible Observables. Phys. Rev. Lett. 2014, 113, 260401. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.C.; Chen, B.; Liu, Y.; Wang, M.Q.; Ye, X.Y.; Kong, F.; Shi, F.Z.; Fei, S.M.; Du, J.F. Experimental Demonstration of Uncertainty Relations for the Triple Components of Angular Momentum. Phys. Rev. Lett. 2014, 118, 180402. [Google Scholar] [CrossRef] [PubMed]
- Coles, P.J.; Berta, M.; Tomamichel, M.; Wehner, S. Entropic uncertainty relations and their applications. Rev. Mod. Phys. 2017, 89, 015002. [Google Scholar] [CrossRef]
- Deutsch, D. Uncertainty in Quantum Measurements. Phys. Rev. Lett. 1983, 50, 631. [Google Scholar] [CrossRef]
- Maassen, H.; Uffink, J.B.M. Generalized entropic uncertainty relations. Phys. Rev. Lett. 1988, 60, 1103. [Google Scholar] [CrossRef] [PubMed]
- Berta, M.; Christandl, M.; Colbeck, R.; Renes, J.; Renner, R. The uncertainty principle in the presence of quantum memory. Nat. Phys. 2010, 6, 659–662. [Google Scholar] [CrossRef]
- Coles, P.J.; Piani, M. Improved entropic uncertainty relations and information exclusion relations. Phys. Rev. A 2014, 89, 022112. [Google Scholar] [CrossRef]
- Rudnicki, Ł.; Puchała, Z.; Życzkowski, K. Strong majorization entropic uncertainty relations. Phys. Rev. A 2014, 89, 052115. [Google Scholar] [CrossRef]
- Xiao, Y.; Jing, N.; Fei, S.M.; Li-Jost, X.J. Improved uncertainty relation in the presence of quantum memory. Phys. A Math. Theor. 2016, 49, 49LT01. [Google Scholar] [CrossRef]
- Romera, E.; de los Santos, F. Fractional revivals through Rényi uncertainty relations. Phys. Rev. A 2008, 78, 013837. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I. Formulation of uncertainty relations in terms of the Rényi entropies. Phys. Rev. A 2012, 74, 052101. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Yu, C.S. Rényi entropy uncertainty relation for successive projective measurements. Quantum Inf. Process. 2015, 14, 2239–2253. [Google Scholar] [CrossRef]
- Rastegin, A.E. Uncertainty and certainty relations for complementary qubit observables in terms of Tsallis’ entropies. Quantum Inf. Process. 2013, 12, 2947–2963. [Google Scholar] [CrossRef]
- Rastegin, A.E. Uncertainty and Certainty Relations for Successive Projective Measurements of a Qubit in Terms of Tsallis’ Entropies. Commun. Theor. Phys. 2015, 63, 687–694. [Google Scholar] [CrossRef]
- Kurzyk, D.; Pawela, L.; Puchała, Z. Conditional entropic uncertainty relations for Tsallis entropies. arXiv, 2017; arXiv:1707.09278. [Google Scholar]
- Zozor, S.; Bosyk, G.M.; Portesi, M. General entropy-like uncertainty relations in finite dimensions. J. Phys. A Math. Theor. 2014, 47, 495302. [Google Scholar] [CrossRef]
- Prevedel, R.; Hamel, D.R.; Colbeck, R.; Fisher, K.; Resch, K.J. Experimental investigation of the uncertainty principle in the presence of quantum memory and its application to witnessing entanglement. Nat. Phys. 2011, 7, 757–761. [Google Scholar] [CrossRef]
- Hofmann, H.F.; Takeuchi, S. Violation of local uncertainty relations as a signature of entanglement. Phys. Rev. A 2003, 68, 032103. [Google Scholar] [CrossRef]
- Walls, D.F.; Zoller, P. Reduced Quantum Fluctuations in Resonance Fluorescence. Phys. Rev. Lett. 1981, 47, 709–711. [Google Scholar] [CrossRef]
- Ma, J.; Wang, X.; Sun, C.P.; Nori, F. Quantum spin squeezing. Phys. Rep. 2011, 509, 89–165. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-Enhanced Measurements: Beating the Standard Quantum Limit. Science 2004, 306, 1330–1336. [Google Scholar] [CrossRef] [PubMed]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in quantum metrology. Nat. Photonics 2011, 5, 222–229. [Google Scholar] [CrossRef]
- Ma, Z.H.; Chen, Z.H.; Fei, S.M. Uncertainty relations based on skew information with quantum memory. Sci. China Phys. Mech. Astron. 2017, 60, 010321. [Google Scholar] [CrossRef]
- Wigner, E.P.; Yanase, M.M. Information contents of distributions. Proc. Natl. Acad. Sci. USA 1963, 49, 910–918. [Google Scholar] [CrossRef] [PubMed]
- Lieb, E.H. Convex trace functions and the Wigner-Yanase-Dyson conjecture. Adv. Math. 1973, 11, 267–288. [Google Scholar] [CrossRef]
- Yanagi, K. Uncertainty relation on Wigner–Yanase–Dyson skew information. J. Math. Anal. Appl. 2010, 365, 12–18. [Google Scholar] [CrossRef]
- Luo, S. Heisenberg uncertainty relation for mixed states. Phys. Rev. A 2005, 72, 042110. [Google Scholar] [CrossRef]
- Luo, S. Notes on Superadditivity of Wigner–Yanase–Dyson Information. J. Stat. Phys. 2007, 128, 1177–1188. [Google Scholar] [CrossRef]
- Luo, S.; Fu, S.; Oh, C.H. Quantifying correlations via the Wigner-Yanase skew information. Phys. Rev. A 2012, 85, 32117. [Google Scholar] [CrossRef]
- Chen, B.; Fei, S.M. Sum uncertainty relations for arbitrary N incompatible observables. Sci. Rep. 2015, 5, 14238. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Fei, S.-M. Uncertainty Relation Based on Wigner–Yanase–Dyson Skew Information with Quantum Memory. Entropy 2018, 20, 132. https://doi.org/10.3390/e20020132
Li J, Fei S-M. Uncertainty Relation Based on Wigner–Yanase–Dyson Skew Information with Quantum Memory. Entropy. 2018; 20(2):132. https://doi.org/10.3390/e20020132
Chicago/Turabian StyleLi, Jun, and Shao-Ming Fei. 2018. "Uncertainty Relation Based on Wigner–Yanase–Dyson Skew Information with Quantum Memory" Entropy 20, no. 2: 132. https://doi.org/10.3390/e20020132
APA StyleLi, J., & Fei, S.-M. (2018). Uncertainty Relation Based on Wigner–Yanase–Dyson Skew Information with Quantum Memory. Entropy, 20(2), 132. https://doi.org/10.3390/e20020132



