On a Dynamical Approach to Some Prime Number Sequences
Abstract
:1. Introduction
2. Tools from Nonlinear and Symbolic Dynamics
2.1. Enumerating Blocks: Spectrum of Renyi Entropies
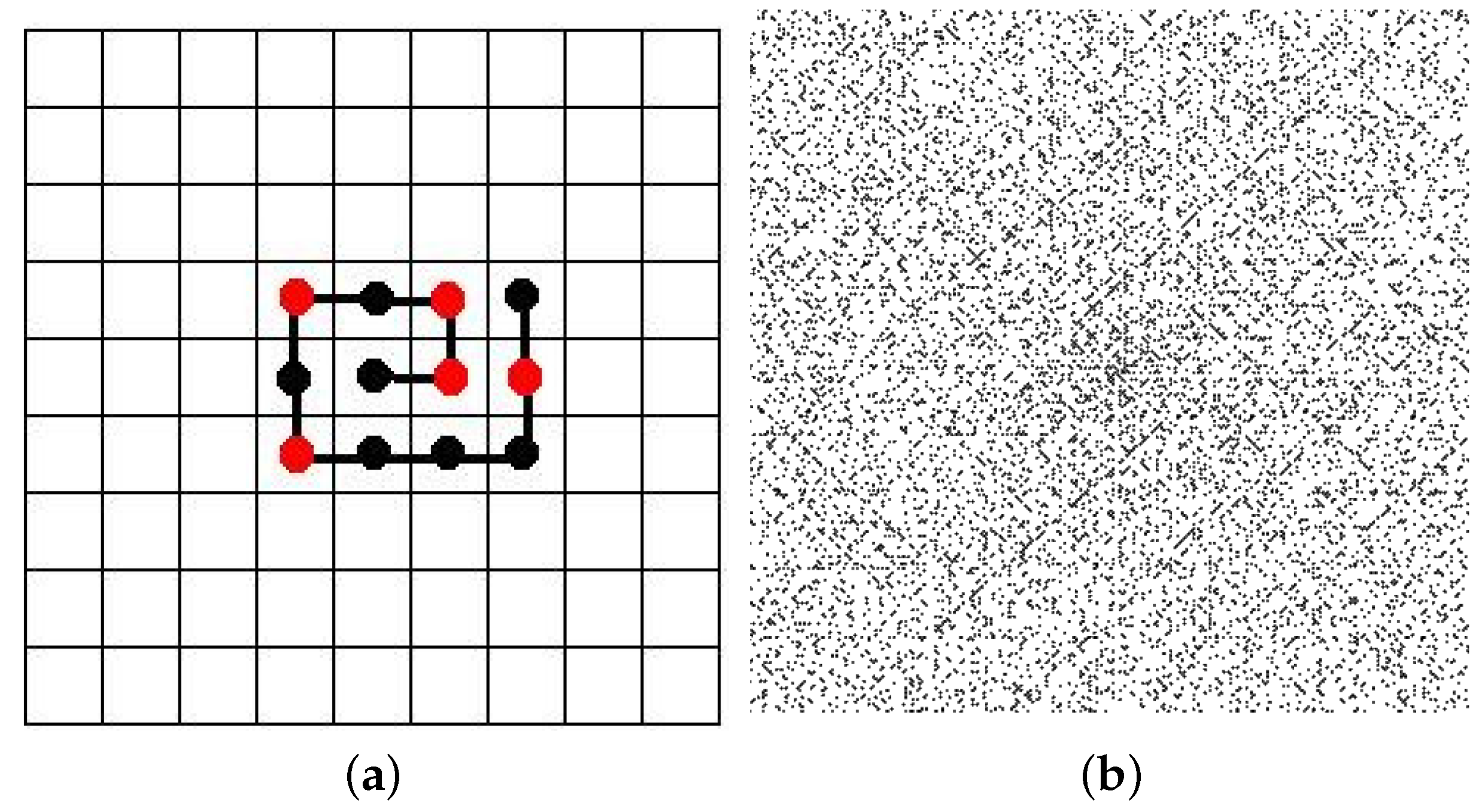
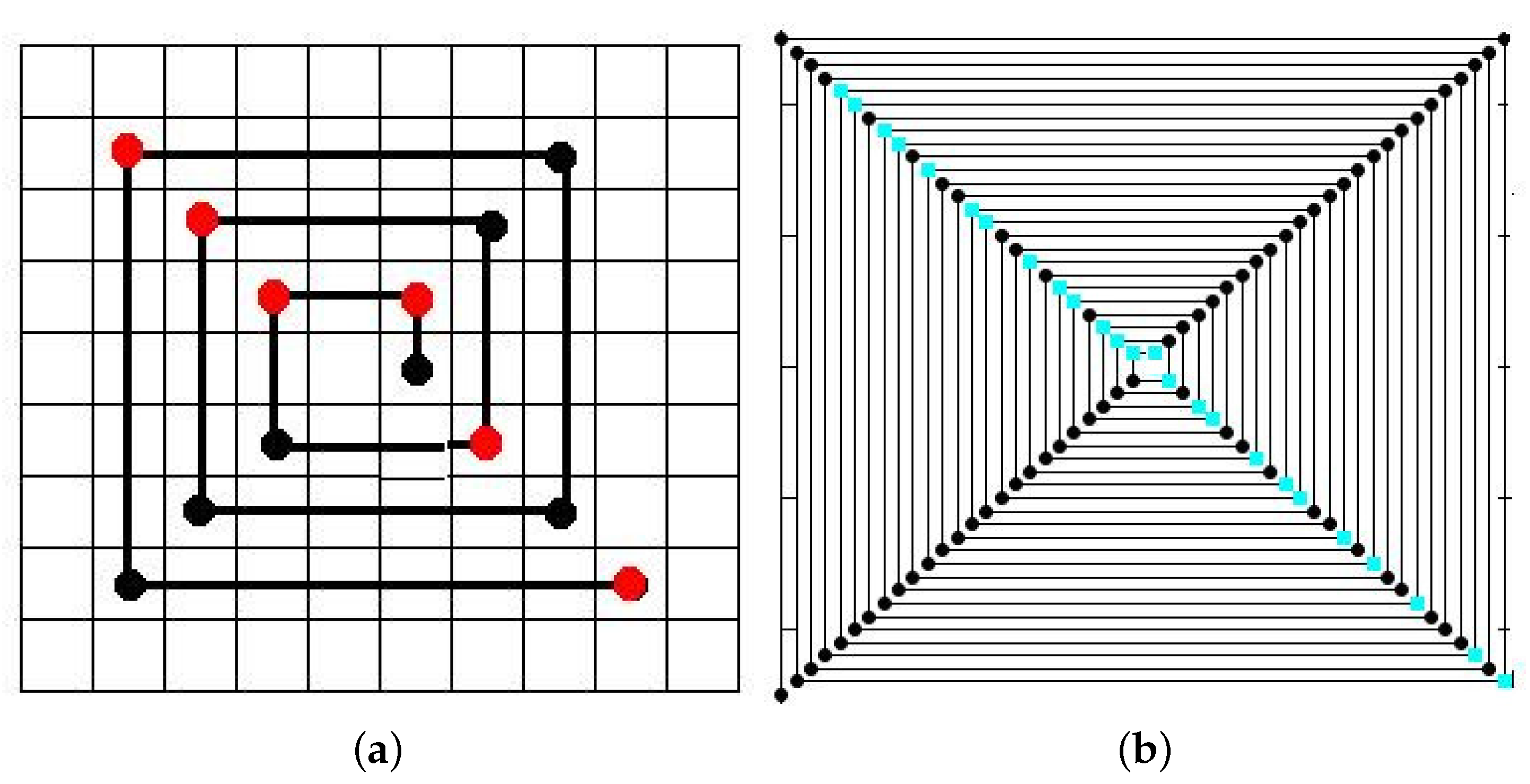
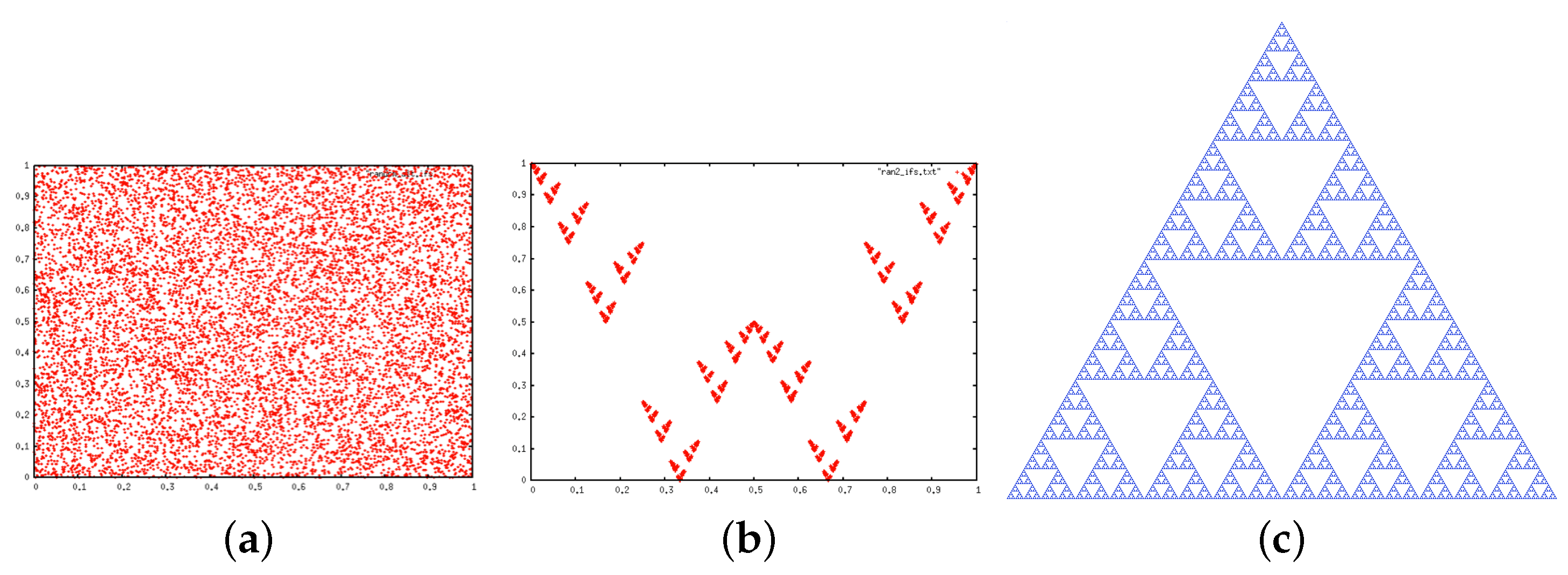
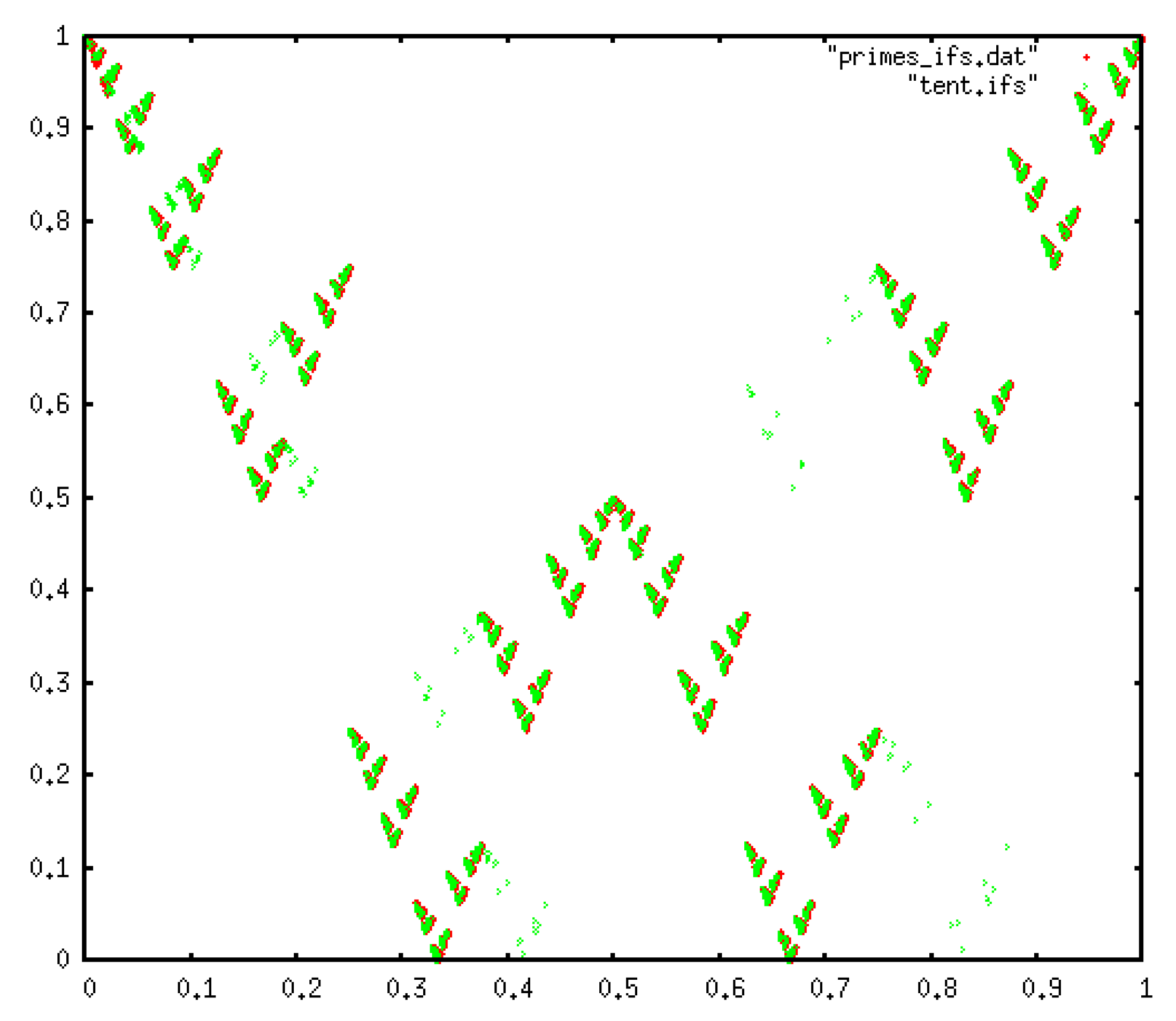
2.2. Iterated Function Systems (IFS) and the Chaos Game
3. Results
3.1. Null Models: What to Expect if Primes Lack Structure?
3.1.1. Type I: Symbols i.i.d. with Uniform and Non-Uniform Probability Densities
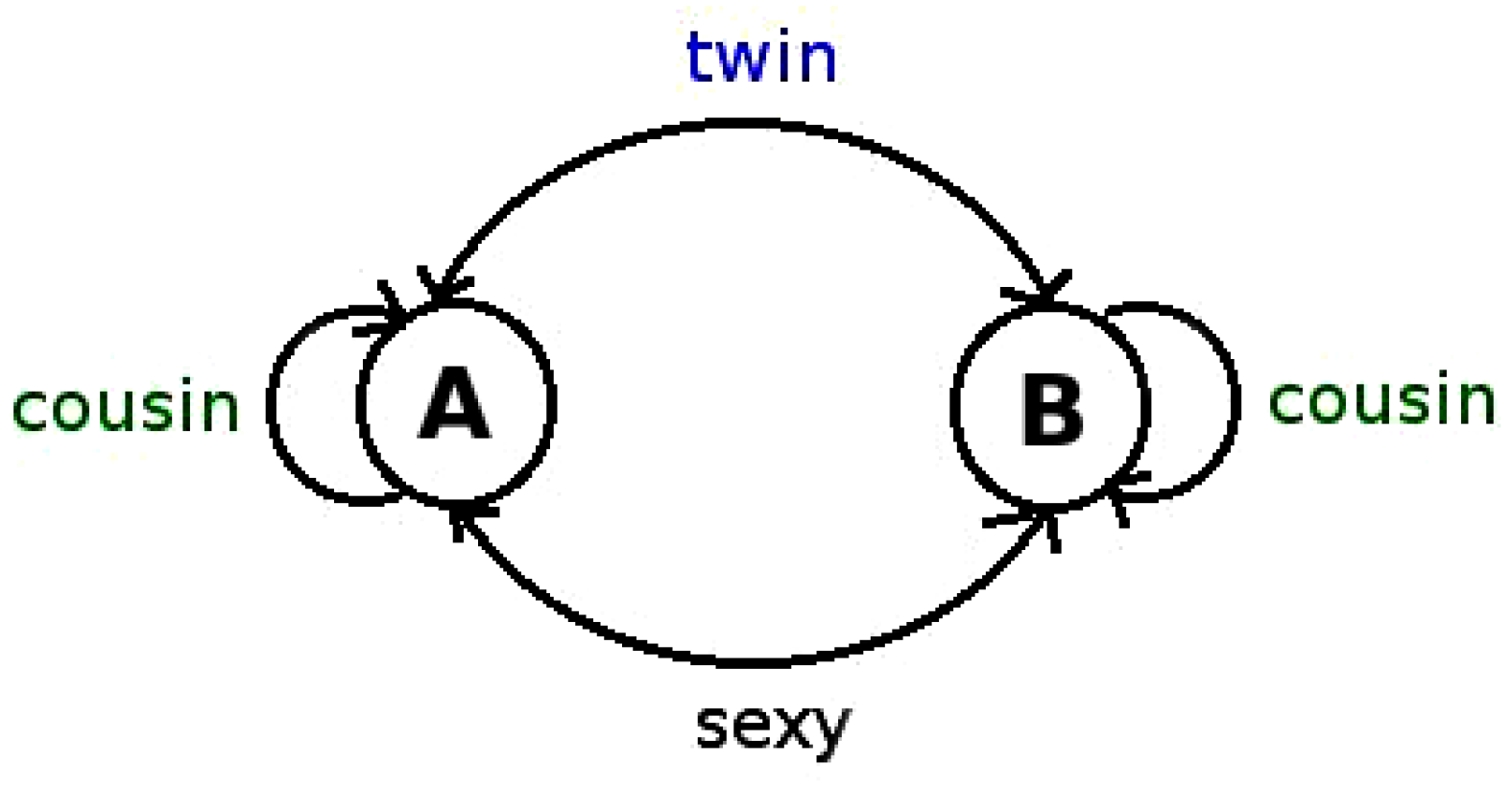
3.1.2. Type II: Transitions
- Generate a random sequence via a type I null model with two symbols A and B (where asymptotically , however for finite size series one should account for Tchebytchev bias),
- Then construct the resulting sequence with symbols .
3.1.3. Type III: Cramer Null Model
3.1.4. Some Fully Chaotic Maps
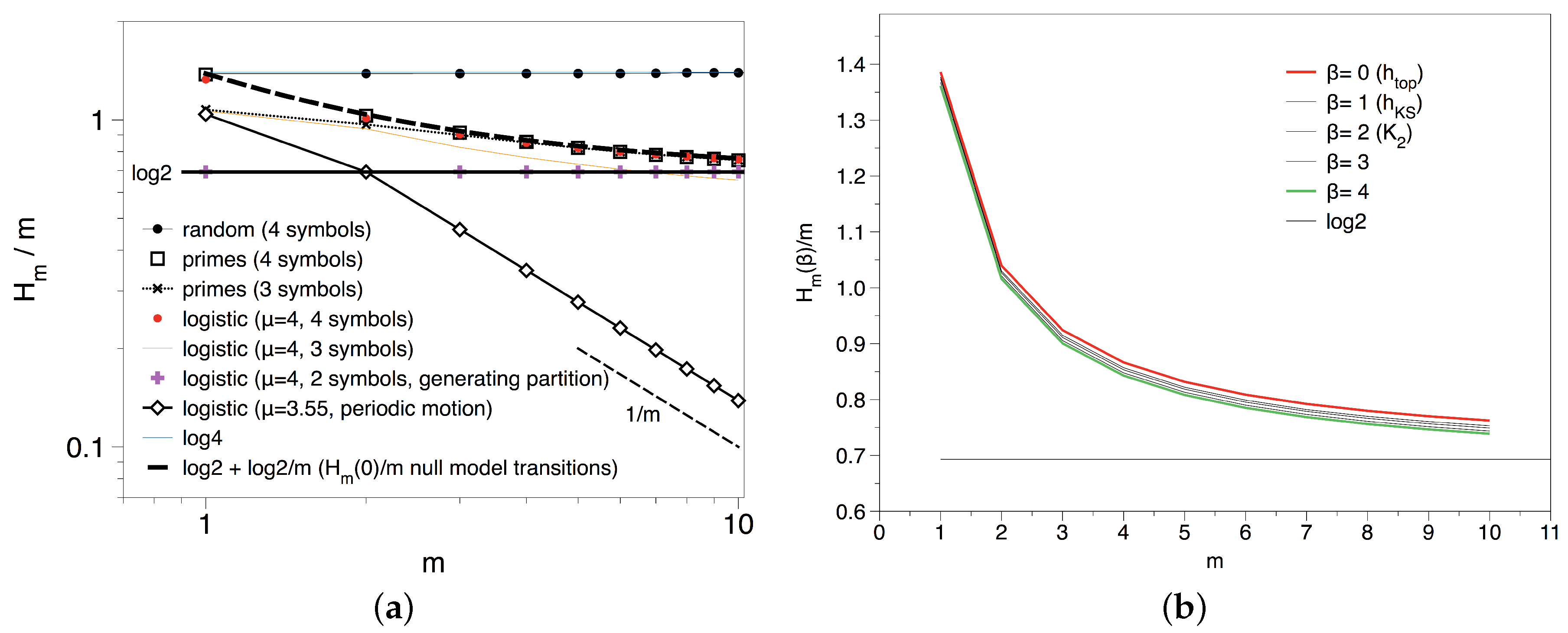
3.2. Results and Interpretation for the Transition Sequence
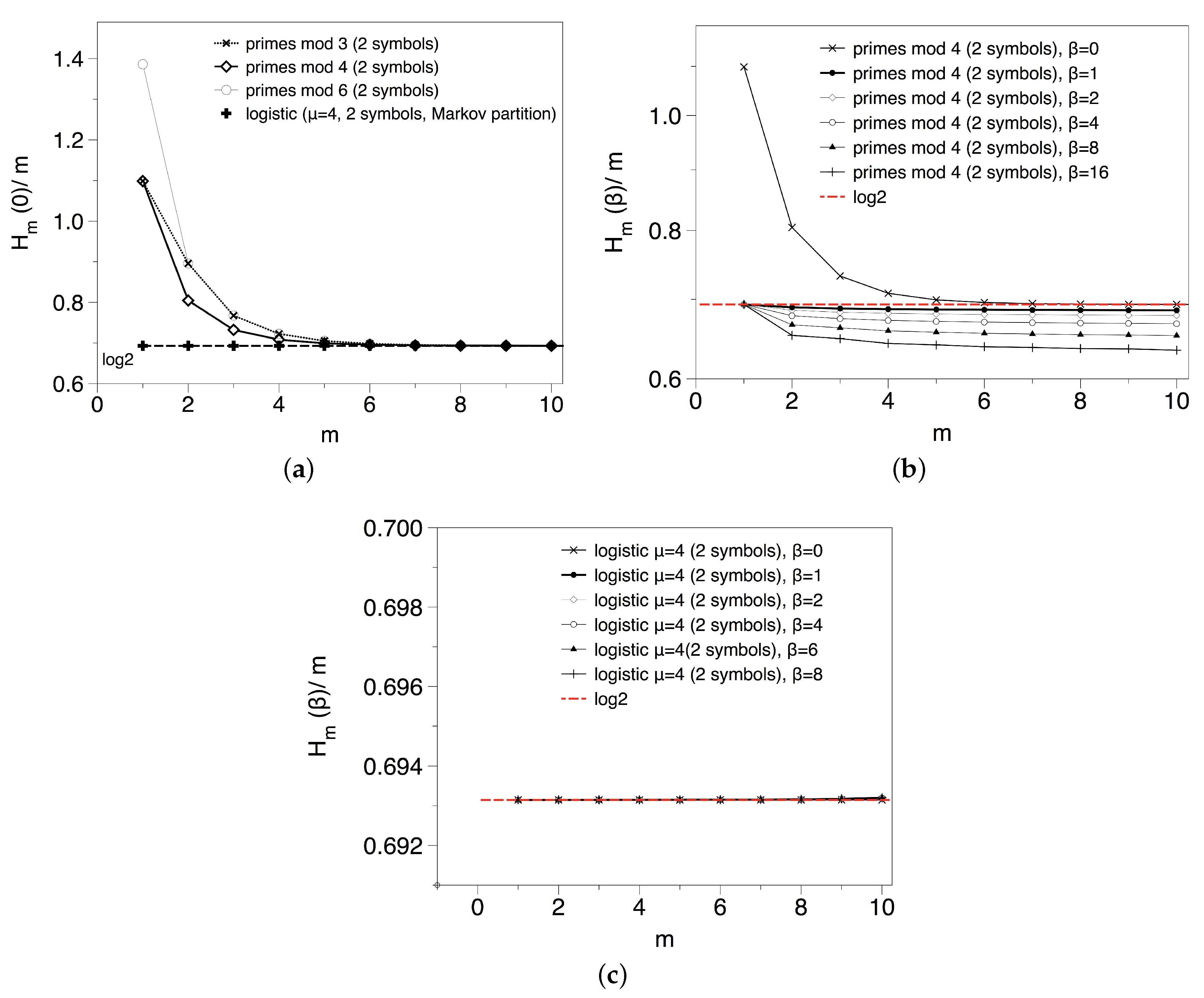
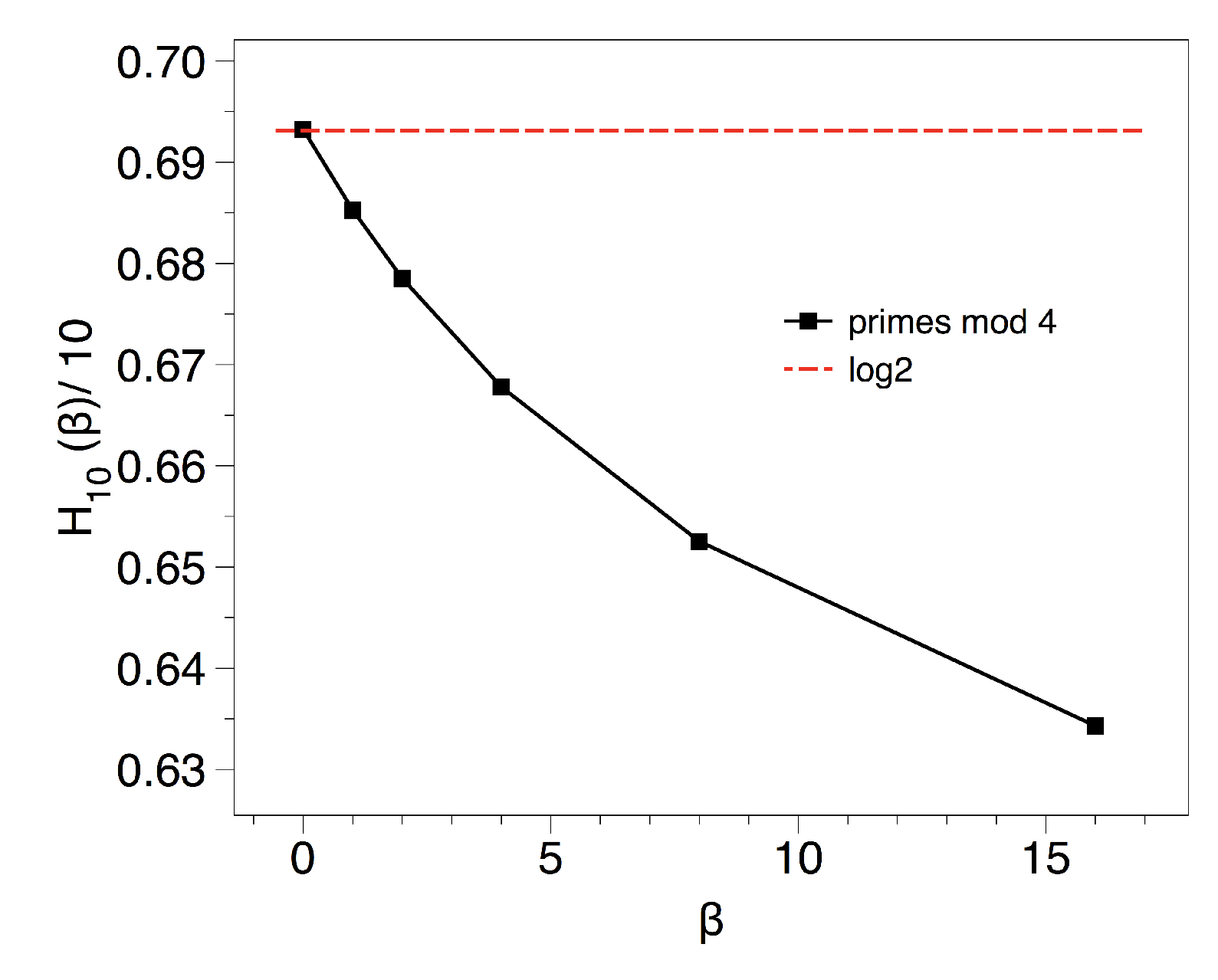
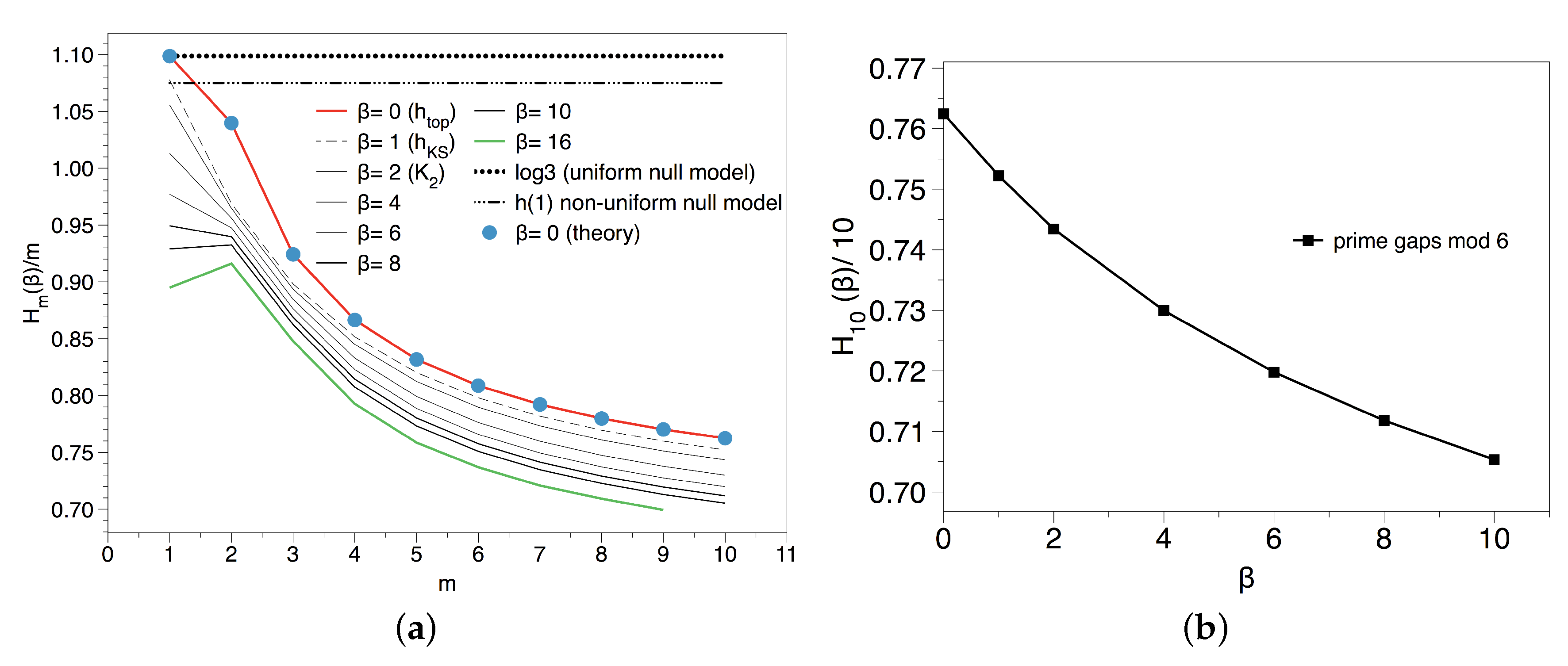
3.3. Results and Interpretation for the Primes Mod k
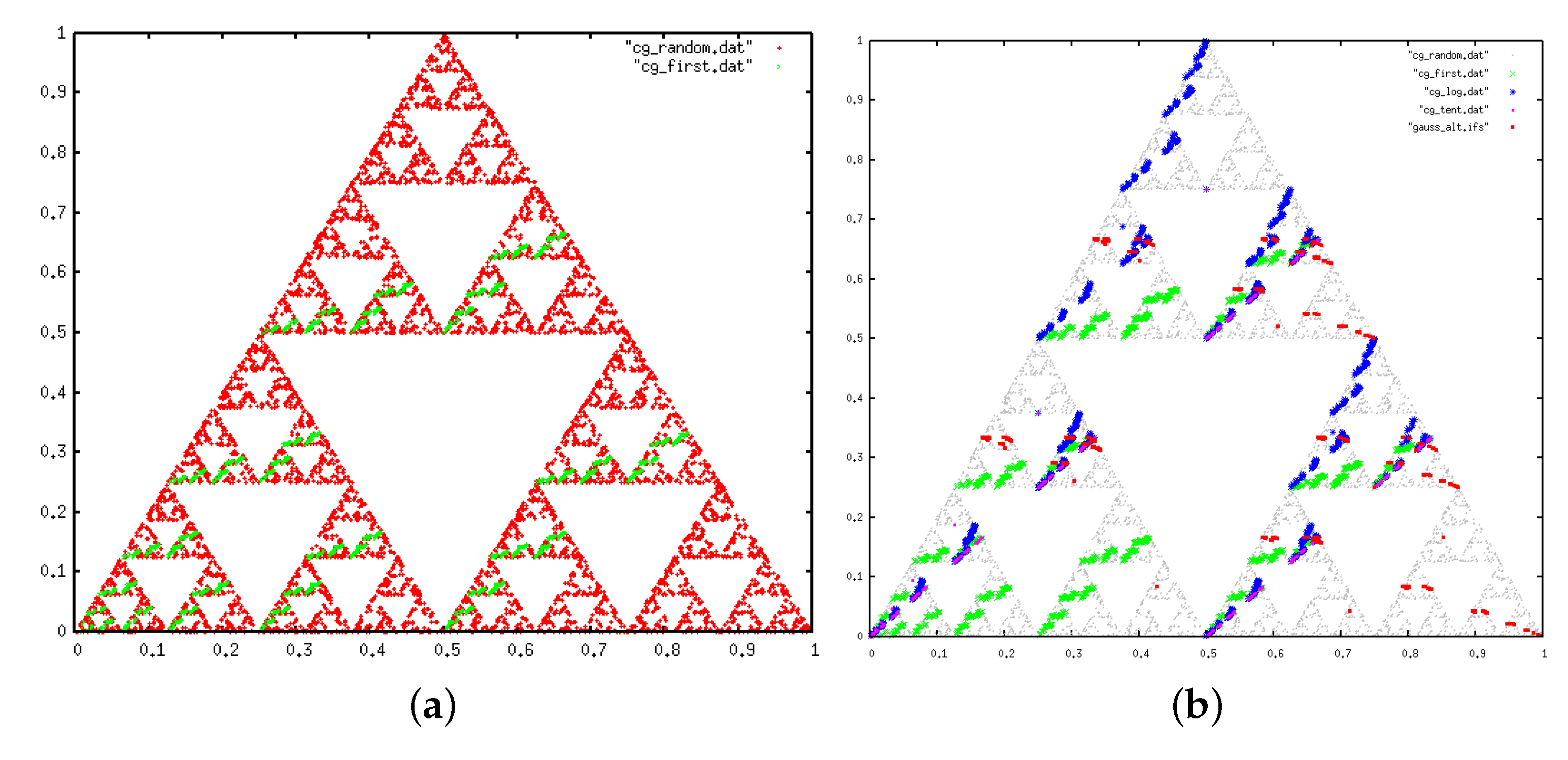
3.4. Results and Interpretation for the Gaps Residue Sequence
3.4.1. Entropic Analysis
3.4.2. IFS
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Silverman, J.H. The Arithmetic of Dynamical Systems. In Graduate Texts in Mathematics; Springer: New York, NY, USA, 2007. [Google Scholar]
- Schroeder, M. Number Theory in Science and Communication, 5th ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- France, M.; Van der Poorten, A.J. Arithmetic and analytic properties of paper folding sequences. Bull. Aust. Math. Soc. 1981, 24, 123–131. [Google Scholar] [CrossRef]
- Ostafe, A.; Shparlinski, I.E. On the degree growth in some polynomial dynamical systems and nonlinear pseudorandom number generators. Math. Comp. 2010, 79, 501–511. [Google Scholar] [CrossRef]
- Number Theory and Physics Archive. Available online: http://empslocal.ex.ac.uk/people/staff/mrwatkin/zeta/physics.htm (accessed on 19 February 2018).
- Dyson, F.J. A Brownian Motion Model for the Eigenvalues of a Random Matrix. J. Math. Phys. 1962, 3, 1191–1198. [Google Scholar] [CrossRef]
- Montgomery, H.L. The pair correlation of zeros of the zeta function. Proc. Symp. Pure 1973, 41, 181–193. [Google Scholar]
- Odlyzko, A.M. On the distribution of spacings between zeros of the zeta function. Math. Comput. 1999, 48, 273–308. [Google Scholar] [CrossRef]
- Julia, B.L. Statistical theory of Numbers, Number Theory and Physics; Springer: Berlin, Germany, 1990. [Google Scholar]
- Berry, M.V.; Keating, J.P. The Riemann zeros and eigenvalue asymptotics. Siam Rev. 1999, 41, 236–266. [Google Scholar] [CrossRef]
- Wolf, M. Multifractality of prime numbers. Physica A 1989, 160, 24–42. [Google Scholar] [CrossRef]
- Mertens, S. Phase transition in the number partitioning problem. Phys. Rev. Lett. 1998, 81, 4281–4284. [Google Scholar] [CrossRef]
- Luque, B.; Lacasa, L.; Miramontes, O. Phase transition in a stochastic prime number generator. Phys. Rev. E 2007, 76, 010103R. [Google Scholar] [CrossRef] [PubMed]
- Luque, B.; Miramontes, O.; Lacasa, L. Number theoretic example of scale-free topology inducing self-organized criticality. Phys. Rev. Lett. 2008, 101, 158702. [Google Scholar] [CrossRef] [PubMed]
- Lacasa, L.; Luque, B. Phase transition in the Countdown problem. Phys. Rev. E 2012, 86, 010105R. [Google Scholar] [CrossRef] [PubMed]
- Luque, B.; Torre, I.G.; Lacasa, L. Phase transitions in Number Theory: from the Birthday Problem to Sidon Sets. Phys. Rev. E 2013, 88, 052119. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Perez, G.; Serrano, M.A.; Boguna, M. Complex architecture of primes and natural numbers. Phys. Rev. E 2014, 90, 022806. [Google Scholar] [CrossRef] [PubMed]
- Stein, M.L.; Ulam, S.; Wells, M.B. A Visual Display of Some Properties of the Distribution of Primes. Am. Math. Mon. 1964, 71, 516–520. [Google Scholar] [CrossRef]
- Hao, B.L.; Zheng, W.M. Applied Symbolic Dynamics and Chaos; World Scientific Publishing: Singapore, 1998. [Google Scholar]
- Ares, S.; Castro, M. Hidden structure in the randomness of the prime number sequence? Physica A 2006, 360, 285–296. [Google Scholar] [CrossRef]
- Lemke Oliver, R.J.; Soundararajan, K. Unexpected biases in the distribution of consecutive primes. Proc. Natl. Acad. Sci. USA 2016, 113, E4446–E4454. [Google Scholar] [CrossRef] [PubMed]
- Shiu, D.K.L. Strings of congruent primes. J. Lond. Math. Soc. 2000, 61, 359–373. [Google Scholar] [CrossRef]
- Maynard, J. Dense clusters of primes in subsets. Compos. Math. 2016, 152, 1517–1554. [Google Scholar] [CrossRef]
- Ash, A.; Beltis, L.; Gross, R.; Sinnott, W. Frequencies of successive pairs of prime residues. Exp. Math. 2011, 20, 400–411. [Google Scholar] [CrossRef]
- Hardy, G.H.; Littlewood, J.E. Some Problems of ‘Partitio Numerorum’; III. On the Expression of a Number as a Sum of Primes. Acta Math. 1923, 44, 1–70. [Google Scholar] [CrossRef]
- Beck, C.; Schlogl, F. Thermodynamics of Chaotic Systems; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Barnsley, M. Fractals Everywhere; Academic Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Peitgen, H.O.; JŸrgens, H.; Saupe, D. The chaos Game: How Randomness Creates Deterministic Shapes. In Chaos and Fractals; Springer: New York, NY, USA, 1992; pp. 297–352. [Google Scholar]
- Jeffrey, H.J. Chaos game visualization of sequences. Comput. Gr. 1992, 16, 25–33. [Google Scholar] [CrossRef]
- Rubinstein, M.; Sarnak, P. Chebyshev’s bias. Exp. Math. 1994, 3, 173–197. [Google Scholar] [CrossRef]
- Cramér, H. On the order of magnitude of the difference between consecutive prime numbers. Acta Arith. 1936, 2, 23–46. [Google Scholar] [CrossRef]
- Jost, J. Dynamical Systems: Examples of Complex Behavior; Springer: Berlin, Germany, 2005. [Google Scholar]

| m | ||
| ine 1 | ∅ | 0 |
| 2 | {(4,4)} | 1 |
| 3 | 11 | |
| 4 | 49 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lacasa, L.; Luque, B.; Gómez, I.; Miramontes, O. On a Dynamical Approach to Some Prime Number Sequences. Entropy 2018, 20, 131. https://doi.org/10.3390/e20020131
Lacasa L, Luque B, Gómez I, Miramontes O. On a Dynamical Approach to Some Prime Number Sequences. Entropy. 2018; 20(2):131. https://doi.org/10.3390/e20020131
Chicago/Turabian StyleLacasa, Lucas, Bartolome Luque, Ignacio Gómez, and Octavio Miramontes. 2018. "On a Dynamical Approach to Some Prime Number Sequences" Entropy 20, no. 2: 131. https://doi.org/10.3390/e20020131
APA StyleLacasa, L., Luque, B., Gómez, I., & Miramontes, O. (2018). On a Dynamical Approach to Some Prime Number Sequences. Entropy, 20(2), 131. https://doi.org/10.3390/e20020131




