A Simple Thermodynamic Model of the Internal Convective Zone of the Earth
Abstract
:1. Introduction
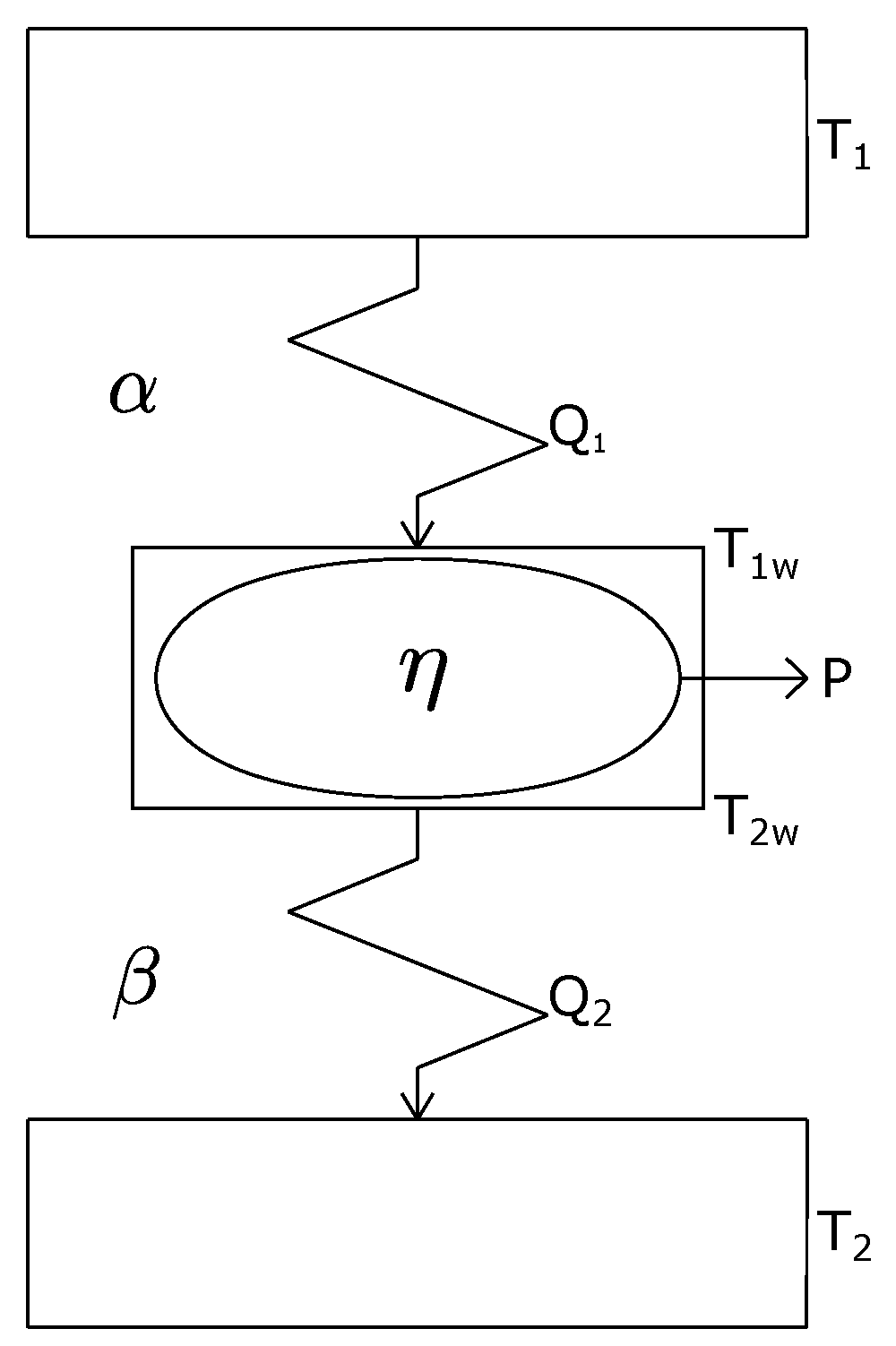
2. Finite-Time Thermodynamics and the Gordon-Zarmi Convective Model
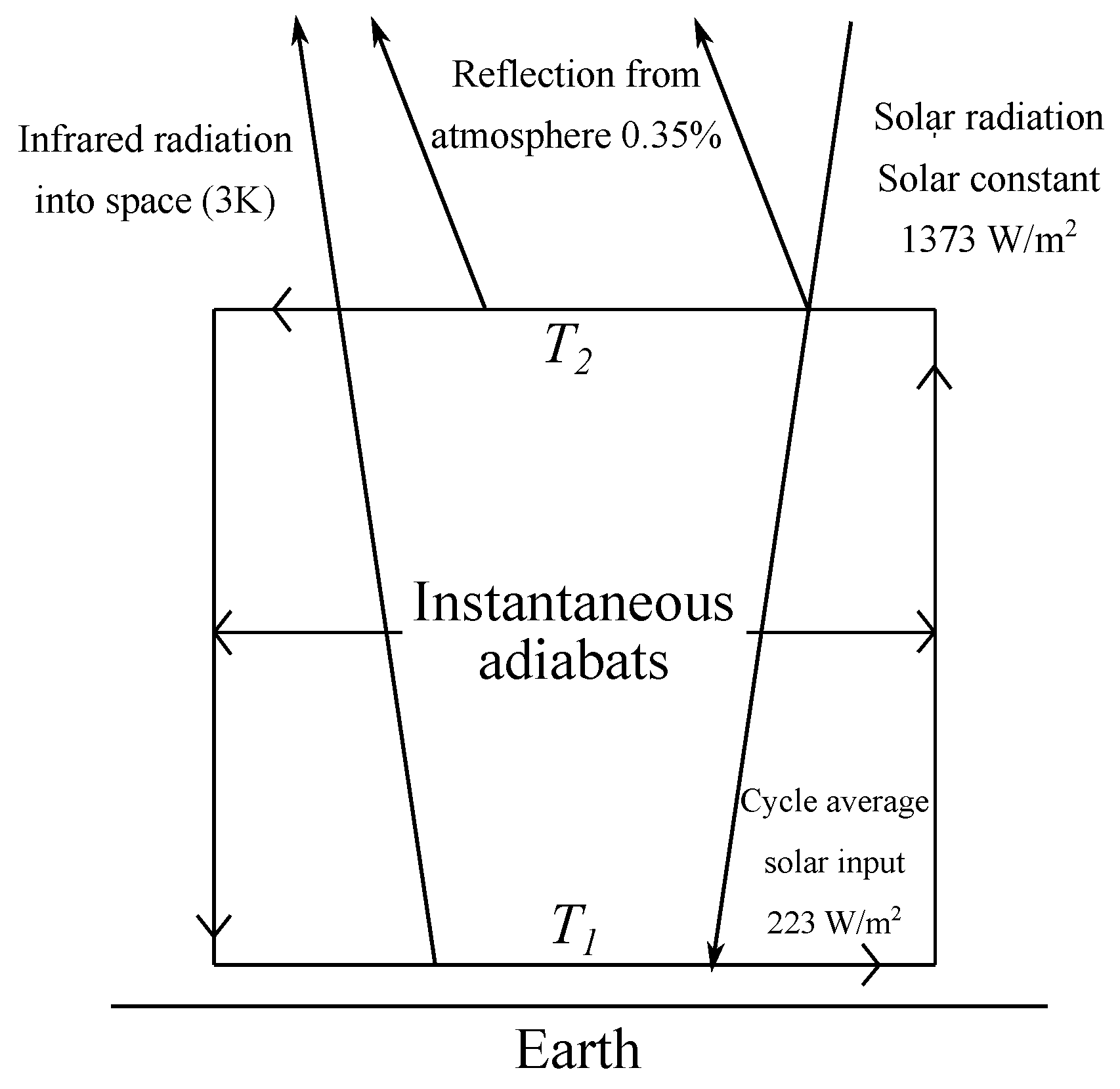
Atmospheric Convection
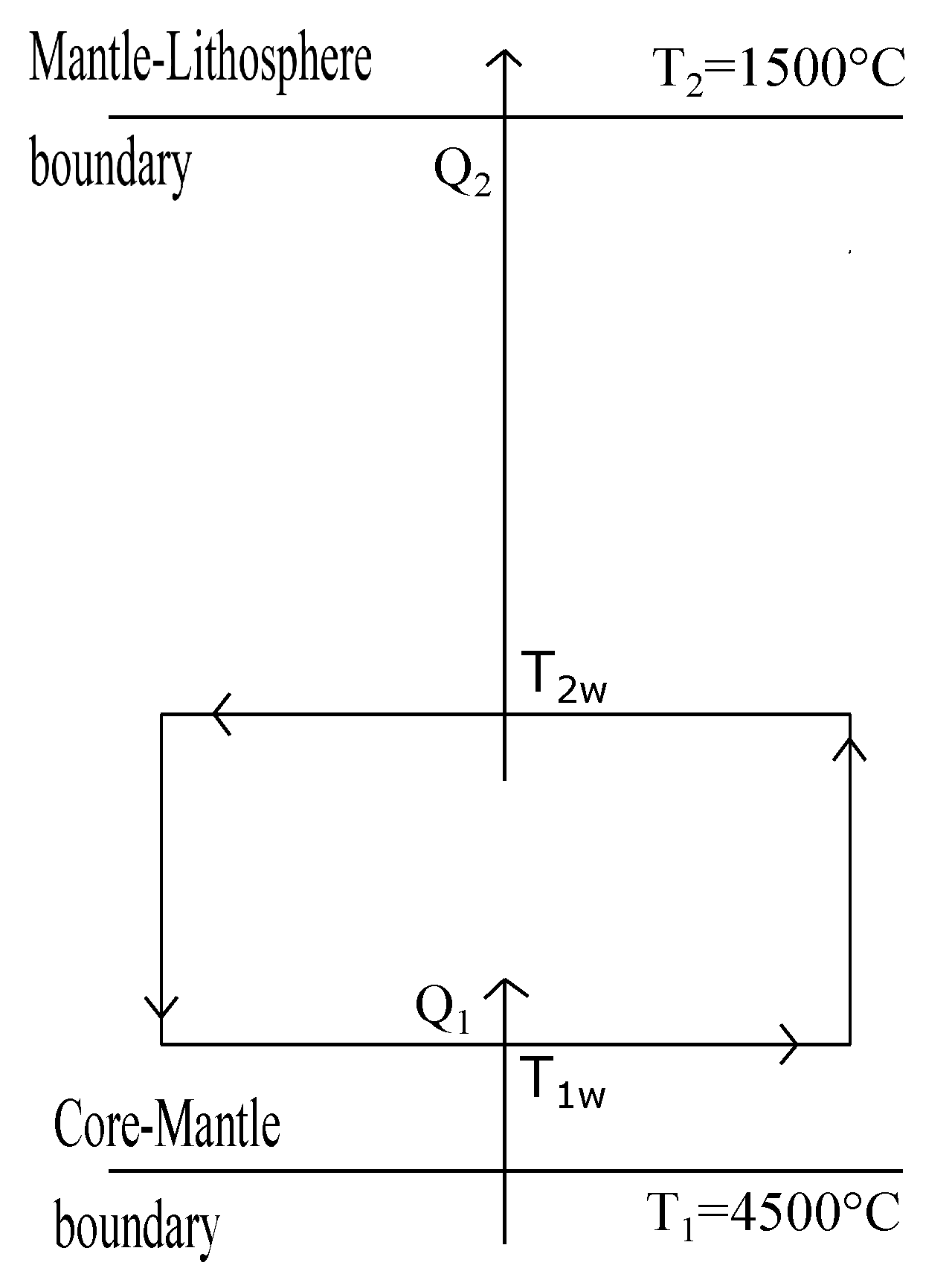
3. GZ Model Applied to the Convective Zone of the Earth
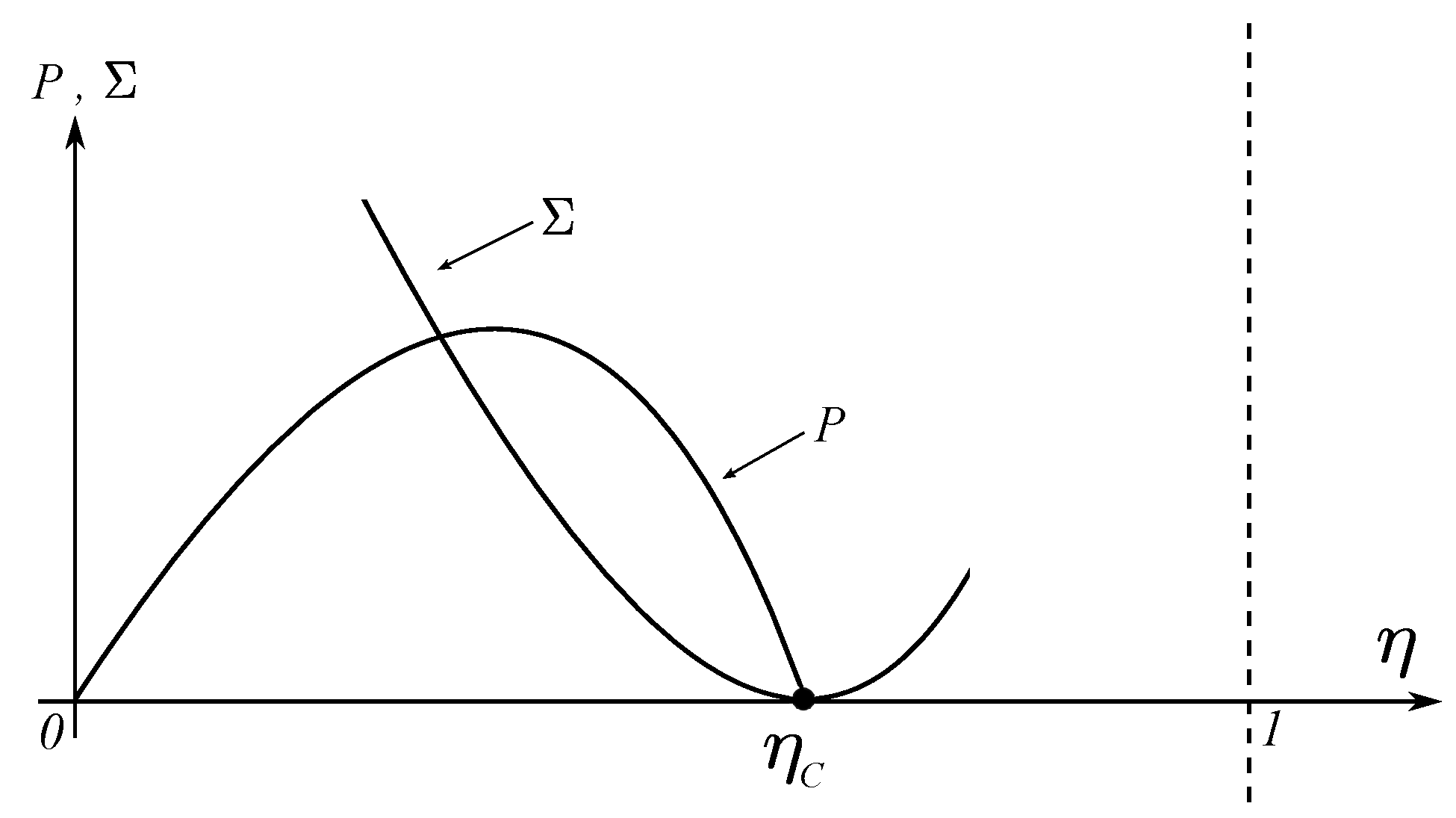
3.1. Maximum Power Regime
3.2. Ecological Function Regime
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tarbuck, E.J.; Lutgens, F.K. Earth Science; Prentice Hall/Pearson: Upper Saddle River, NJ, USA, 2012. [Google Scholar]
- Jackson, I. The Earth’s Mantle: Composition, Structure and Evolution; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Shubert, G.; Turcotte, D.L.; Olson, P. Mantle Convection in the Earth and Planets; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Karato, S. The Dynamic Structure of the Deep Earth: An Interdisciplinary Approach; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Bunge, H.P.; Richards, M.A.; Baumgardner, J.R. A sensitivity study of three-dimensional spherical mantle convection at 108 Rayleigh number: Effects of depth-dependent viscosity, heating mode, and an endothermic phase change. J. Geophys. Res. 1997, 102, 11991–12007. [Google Scholar] [CrossRef]
- Ttackley, P.J.; Stevenson, D.J.; Glatzmaier, G.A.; Schubert, G. Effects of an endothermic phase transition at 670 km depth in a spherical model of convection in the Earth’s mantle. Lett. Nat. 1993, 361, 699–704. [Google Scholar] [CrossRef]
- Gordon, J.M.; Zarmi, Y. Wind energy as a solar-driven heat engine: A thermodynamic approach. Am. J. Phys. 1989, 57, 995–999. [Google Scholar] [CrossRef]
- De Vos, A.; Flatter, G. The maximum efficiency of the conversion of solar-energy into wind energy. Am. J. Phys. 1991, 59, 751–754. [Google Scholar] [CrossRef]
- De Vos, A.; Van der Wel, P. Endoreversible Models for the Conversion of Solar Energy into Wind Energy. J. Non-Equilib. Thermodyn. 1992, 17, 77–89. [Google Scholar] [CrossRef]
- De Vos, A.; Van der Wel, P. The efficiency of the conversion of solar energy into wind energy by means of Hadley cells. Theor. Appl. Climatol. 1993, 46, 193–202. [Google Scholar] [CrossRef]
- Barranco-Jiménez, M.A.; Angulo-Brown, F. A nonendoreversible model for wind energy as a solar-driven heat engine. J. Appl. Phys. 1996, 80, 4872–4876. [Google Scholar] [CrossRef]
- Barranco-Jiménez, M.A.; Angulo-Brown, F. A simple model on the influence of the greenhouse effect on the effi-ciency of solar-to-wind energy conversion. IL Nuovo Cimento C 2003, 26, 235–246. [Google Scholar]
- Barranco-Jiménez, M.A.; Chimal-Eguıa, J.C.; Angulo-Brown, F. The Gordon and Zarmi model for convective atmospheric cells under the ecological criterion applied to the planets of the solar system. Rev. Mex. Fís. 2006, 52, 205–212. [Google Scholar]
- Reis, A.H.; Bejan, A. Constructal theory of global circulation and climate. Int. J. Heat Mass Transf. 2006, 49, 1857–1873. [Google Scholar] [CrossRef]
- Bejan, A. Shape and Structure, from Engineering to Nature; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Lucia, U. Exergy flows at bases of Constructal law. Physica A 2013, 392, 6284–6287. [Google Scholar] [CrossRef]
- Pollarolo, G.; Sertorio, L. Energy and entropy balance for a black piecewise homogeneous planet. IL Nuovo Cimento C 1979, 2, 335–351. [Google Scholar] [CrossRef]
- Peixoto, J.; Oort, A. Physics of Climate; American Institute of Physics: New York, NY, USA, 1992. [Google Scholar]
- Andresen, B.; Salamon, P.; Berry, S. Thermodynamics in finite time. Phys. Today 1984, 37, 62–70. [Google Scholar] [CrossRef]
- De Vos, A. Endoreversible Thermodynamics of Solar Energy Conversion; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Bejan, A. Entropy generation, minimization: The new thermodynamic of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef]
- Wu, C.; Chen, L.; Chen, J. Recent Advances in Finite-Time Thermodynamics; Nova Science Publishers, Inc.: Commack, NY, USA, 1999. [Google Scholar]
- Durmayaz, A.; Sogut, O.S.; Sahin, B.; Yavuz, H. Optimization of thermal systems based on finite-time thermodynamics and thermoeconomics. Prog. Energy Combust. Sci. 2004, 30, 175–217. [Google Scholar] [CrossRef]
- Sieniutycz, S.; Salamon, P. Finite Time Thermodynamics and Thermoeconomics; Taylor and Francis: New York, NY, USA, 1990. [Google Scholar]
- Feidt, M.; Costea, M.; Petre, C.; Petrescu, S. Optimisation of the direct carnot cycle. Appl. Therm. Eng. 2007, 27, 829–839. [Google Scholar] [CrossRef]
- Ortuño-Araujo, J.; Barranco-Jiménez, M.A.; Zsargo, J.; Angulo-Brown, F. An Endoreversible Thermodynamic Model Applied to the Convective Zone of the Sun. ISRN Astron. Astrophys. 2012, 2012, 894056. [Google Scholar] [CrossRef]
- Stacey, F.D. Thermodynamics of the Earth. Rep. Prog. Phys. 2010, 73, 046801. [Google Scholar] [CrossRef]
- Curzon, F.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Hoffmann, K.H.; Burzler, J.M.; Schubert, S. Endoreversible thermodynamics. J. Non-Equilib. Thermodyn. 1997, 22, 311–355. [Google Scholar]
- Rubin, M.H. Optimal configuration of a class of irreversible heat engines-I. Phys. Rev. A 1979, 19, 1272–1276. [Google Scholar] [CrossRef]
- Fisher, M.; Hoffmann, K.H. Can a quantitative simulation of an Otto engine be accurately rendered by a simple Novikov model with heat leak? J. Non-Equilib. Thermodyn. 2004, 29, 9–28. [Google Scholar] [CrossRef]
- Curto-Risso, P.L.; Medina, A.; Calvo-Hernández, A. Theoretical and simulated models for an irreversible Otto cycle. J. Appl. Phys. 2008, 104, 094911. [Google Scholar] [CrossRef]
- Gülder, O.L. Correlations of laminar combustion data for alternative S. I. engine fuels. SAE Tech. Rep. 1984, 841000. [Google Scholar] [CrossRef]
- Chambadal, P. Les Centrales Nucléaires; Armand Colin: Paris, France, 1957. [Google Scholar]
- Novikov, I.I. The efficiency of atomic power stations (a review). J. Nucl. Energy 1958, 7, 125–128. [Google Scholar] [CrossRef]
- Angulo-Brown, F. An ecological optimization criterion for finite-time heat engines. J. Appl. Phys. 1991, 69, 7465–7469. [Google Scholar] [CrossRef]
- Chen, L.; Sun, F. Advances in Finite Time Thermodynamics, Analysis and Optimization; Nova Science Publishers: New York, NY, USA, 2004. [Google Scholar]
- Angulo-Brown, F.; Santillán, M.; Calleja-Quevedo, E. Thermodynamic optimality in some biochemical reactions. IL Nuovo Cimento D 1995, 17, 87–90. [Google Scholar] [CrossRef]
- Santillán, M.; Árias-Hernández, L.A.; Angulo-Brown, A. Some optimization criteria for biological systems in linear irreversible thermodynamics. IL Nuovo Cimento D 1997, 19, 99–112. [Google Scholar]
- Árias-Hernández, L.A.; Angulo-Brown, A. Thermodynamic optimization of endoreversible engines. Rev. Mex. Fis. 1994, 40, 866–877. [Google Scholar]
- Árias-Hernández, L.A.; Angulo-Brown, F. A general property of endoreversible thermal engines. J. Appl. Phys. 1997, 81, 2973–2979. [Google Scholar] [CrossRef]
- Gordon, J.M.; Orlov, V.N. Performance characteristics of endoreversible chemical engines. J. Appl. Phys. 1993, 74, 5303–5309. [Google Scholar] [CrossRef]
- Ocampo-García, A.; Barranco-Jiménez, M.A.; Angulo-Brown, F. Thermodynamic and themoeconomic optimization of isothermal endoreversible chemical engine models. Physica A 2017, 488, 149–161. [Google Scholar] [CrossRef]
- Ocampo-García, A.; Barranco-Jiménez, M.A.; Angulo-Brown, F. Thermodynamic and thermoeconomic optimization of coupled thermal and chemical engines by means of an equivalent array of uncoupled endoreversible engines. EPJ-P 2018, 133, 342. [Google Scholar] [CrossRef]
- Angulo-Brown, F.; Páez-Hernández, R.T. Endoreversible thermal cycle with a nonlinear heat transfer law. J. Appl. Phys. 1993, 74, 2216–2219. [Google Scholar] [CrossRef]
- Barranco-Jiménez, M.A.; Angulo-Brown, F. Thermoeconomic optimisation of Novikov power plant model under maximum ecological conditions. J. Energy Inst. 2007, 80, 96–104. [Google Scholar] [CrossRef]
- Barranco-Jiménez, M.A.; Angulo-Brown, F. Thermoeconomic optimisation of endoreversible heat engine under maximum modified ecological criterion. J. Energy Inst. 2007, 80, 232–238. [Google Scholar] [CrossRef]
- Gustavson, M. Limits to Wind Power Utilization. Science 1979, 204, 13–17. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, D.C.; Gordon, J.M.; Huleihil, M. Endoreversible engines with finite-time adiabats. Indian J. Eng. Mater. Sci. 1994, 1, 195–198. [Google Scholar]
- Turcotte, D.L.; Oxburgh, E.R. Finite amplitude convective cells and continental drift. J. Fluid Mech. 1967, 28, 29–42. [Google Scholar] [CrossRef]
- O’Sullivan, W. Newton’s law of cooling—A critical assessment. Am. J. Phys. 1990, 58, 956–960. [Google Scholar] [CrossRef]
- Condie, K.C. Plate Tectonics and Crustal Evolution, 4th ed.; Butterworth Heinemann: Oxford, UK, 1997. [Google Scholar]
- Sertorio, L. Thermodynamics of Complex Systems (An Introduction to Ecophysics); World Scientific: Singapore, 1991. [Google Scholar]
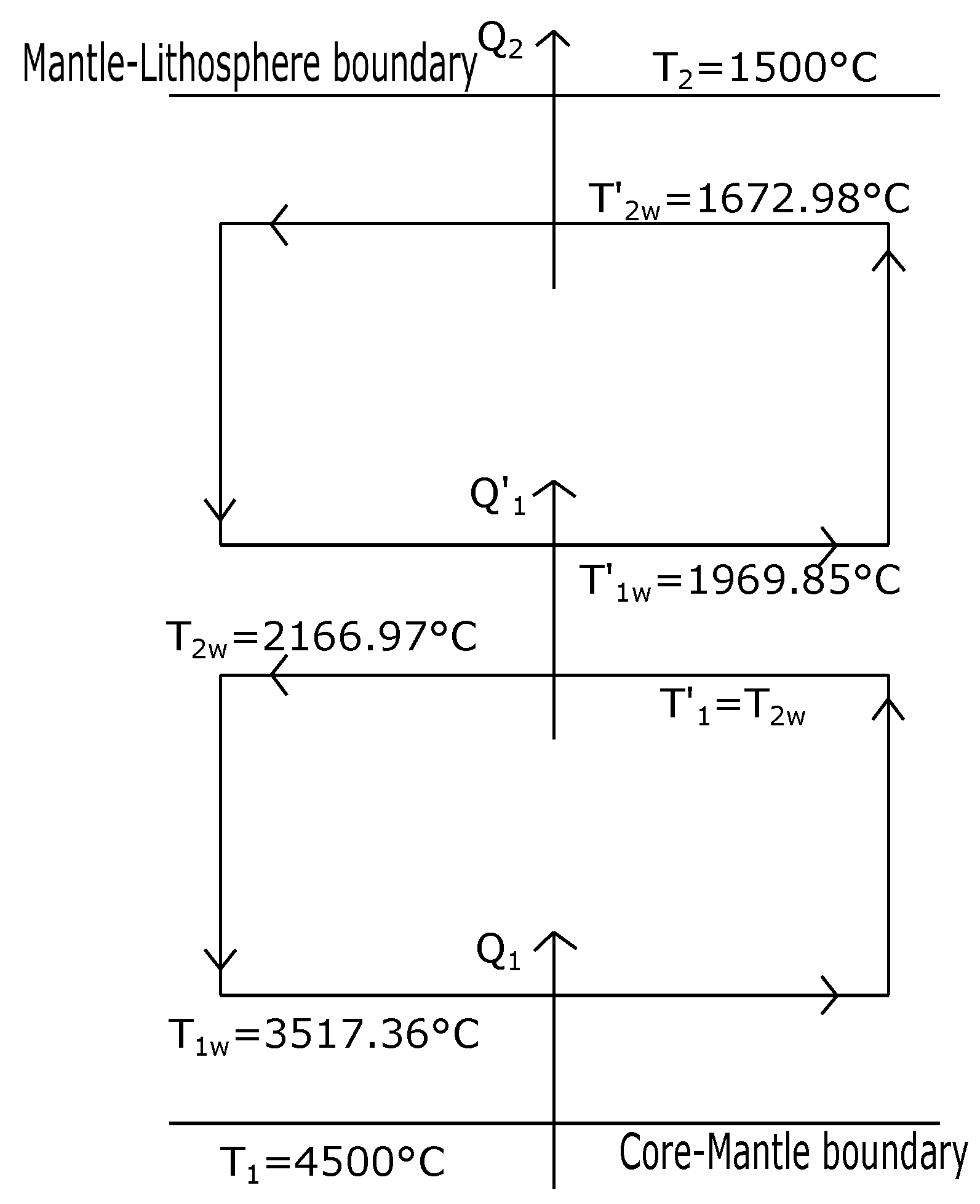
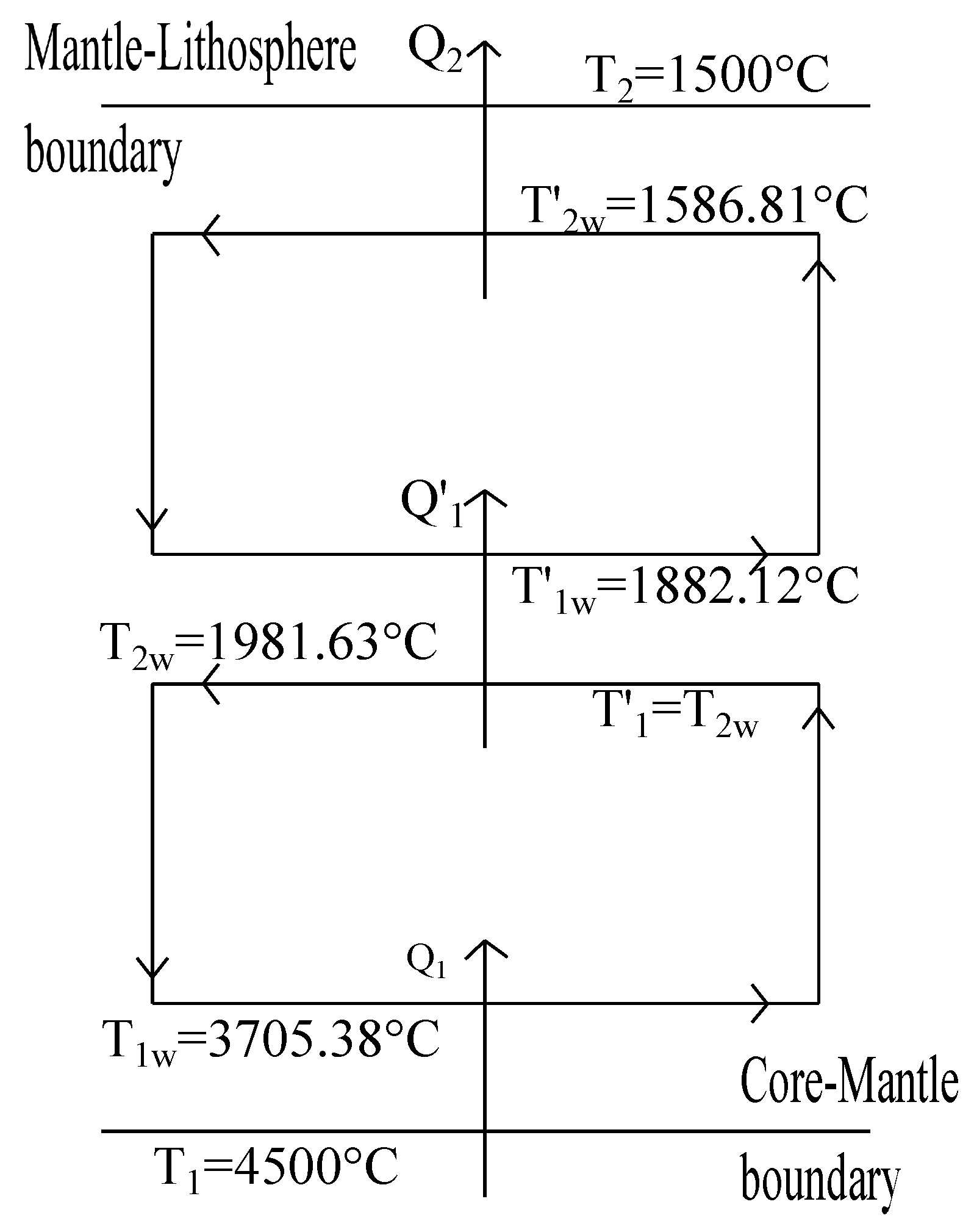
| n | (C) | (C) | (C) | (C) |
|---|---|---|---|---|
| (1st It) | (1st It) | (2nd It) | (2nd It) | |
| 1 | 3249.04 | 2049.04 | 1901.1 | 1626.58 |
| 1.2 | 3524.01 | 2145.41 | 1957.67 | 1663.95 |
| 1.25 | 3517.36 | 2166.97 | 1969.85 | 1672.98 |
| 1.5 | 3483.91 | 2261.83 | 2021.24 | 1715.69 |
| n | (C) | (C) | (C) | (C) |
|---|---|---|---|---|
| (1st It) | (1st It) | (2nd It) | (2nd It) | |
| 1 | 3256.23 | 2427.05 | 2025.06 | 1871.51 |
| 1.2 | 3709.21 | 1965.91 | 1871.34 | 1582.23 |
| 1.25 | 3705.38 | 1981.63 | 1882.12 | 1586.81 |
| 1.5 | 3685.58 | 2051.01 | 1933.14 | 1602.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arango-Reyes, K.; Barranco-Jiménez, M.A.; Ares de Parga-Álvarez, G.; Angulo-Brown, F. A Simple Thermodynamic Model of the Internal Convective Zone of the Earth. Entropy 2018, 20, 985. https://doi.org/10.3390/e20120985
Arango-Reyes K, Barranco-Jiménez MA, Ares de Parga-Álvarez G, Angulo-Brown F. A Simple Thermodynamic Model of the Internal Convective Zone of the Earth. Entropy. 2018; 20(12):985. https://doi.org/10.3390/e20120985
Chicago/Turabian StyleArango-Reyes, Karen, Marco Antonio Barranco-Jiménez, Gonzalo Ares de Parga-Álvarez, and Fernando Angulo-Brown. 2018. "A Simple Thermodynamic Model of the Internal Convective Zone of the Earth" Entropy 20, no. 12: 985. https://doi.org/10.3390/e20120985
APA StyleArango-Reyes, K., Barranco-Jiménez, M. A., Ares de Parga-Álvarez, G., & Angulo-Brown, F. (2018). A Simple Thermodynamic Model of the Internal Convective Zone of the Earth. Entropy, 20(12), 985. https://doi.org/10.3390/e20120985






