Bulk-Surface Electrothermodynamics and Applications to Electrochemistry
Abstract
:1. Introduction
Outline
2. General Setting and Basic Quantities
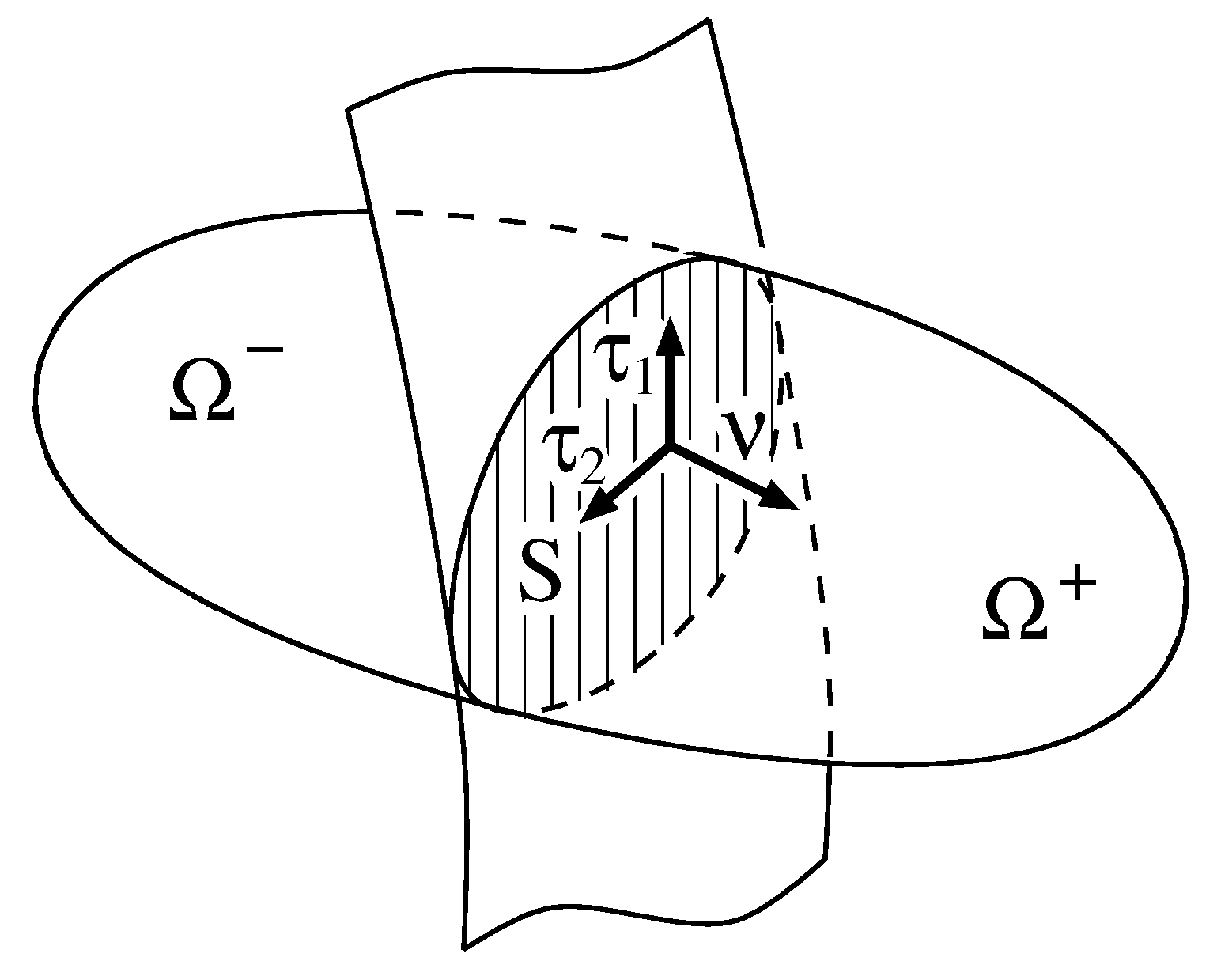
2.1. Geometrical Setup
Covariant Derivatives
Traces, Jumps and Mean Values on Surfaces
2.2. Description of Reacting Mixtures
Constituents and Chemical Reactions
Electro- and Thermodynamic State
Deformation Gradient
3. Universal Balance Equations of Electrothermodynamics
3.1. Balance Equations of Matter
Balance of Mass
Balance of Momentum
Balance of Energy
3.2. Electromagnetic Fields
Conservation of Electric Charge
Conservation of Magnetic Flux
Maxwell–Lorentz Aether Relations
3.3. Coupling of Equations for Matter and Electrodynamics
3.3.1. Polarization and Magnetization
3.3.2. Lorentz Force and Joule Heat
Balance of Electromagnetic Energy
Balance of Electromagnetic Momentum
Identification of Lorentz Force and Joule Heat
3.3.3. Balances of Total Momentum and Internal Energy
4. Symmetry Principles for Observer Transformations
Symmetry Principles
Galilean Symmetry Principle
Classification of the Involved Fields
5. The Entropy Principle
5.1. Formulation of the Entropy Principle
The Entropy Principle
- I.
- The entropy densities , entropy fluxes and entropy productions satisfy the balance equations:
- II.
- and are absolute scalars and are absolute vectors with respect to Galilean transformations.
- III.
- The entropy productions satisfy
- (i)
- the entropy productions are non-negative for each solution of the balance equations and Maxwell’s equations.
- (ii)
- the entropy productions have representations as sums of binary productsThe factors of each product are either scalars, vectors or tensors with respect to Galilean transformations. Each product resp. can be associated with exactly one dissipation mechanism.
- (iii)
- The entropy productions vanish in equilibrium.
- IV.
- The entropy densities have representations as concave functions , of the independent variables. For elastic, viscous, magnetizable, polarizable, heat conducting and reactive mixtures, the independent variables are in the bulk and on the surface
- V.
- The (absolute) temperature and the chemical potentials are defined as
Remarks
5.2. Exploitation of the Entropy Principle—General Approach
Linear Relations
Nonlinear Relations
Galilean Symmetry Principle
Remark on Cross Effects and Symmetry of the Phenomenological Coefficient Matrix
6. Constitutive Equations for Magnetizable, Polarizable, Viscous and Reactive Mixtures
6.1. Constitutive Relations for the Bulk
Thermodiffusion
Reactions
Viscosity
Polarization and Magnetization
6.2. Constitutive Relations for the Surface
Thermodiffusion
Surface Reactions
Surface Viscosity
Mass Flux and Stress Normal to the Surface
6.3. Remarks on the Constitutive Relations
Comparison of Bulk and Surface Equations
Free Energy Density
Pressure, Surface Tension and Gibbs–Duhem Equation
Adsorption
6.4. Discussion on Polarization and Debye Equation for Dielectric Relaxation
Relaxation
Debye Equation
7. Application to Electrochemical Systems
7.1. Dimensional Analysis of Maxwell’s Equations
Magnetostatics:
Electrostatics:
Application to Electrochemical Systems
7.2. Free Energy Models for Liquid Electrolytes and Metal–Electrolyte Interfaces
Bulk Free Energy Density
Surface Free Energy Density
The Incompressible Limit
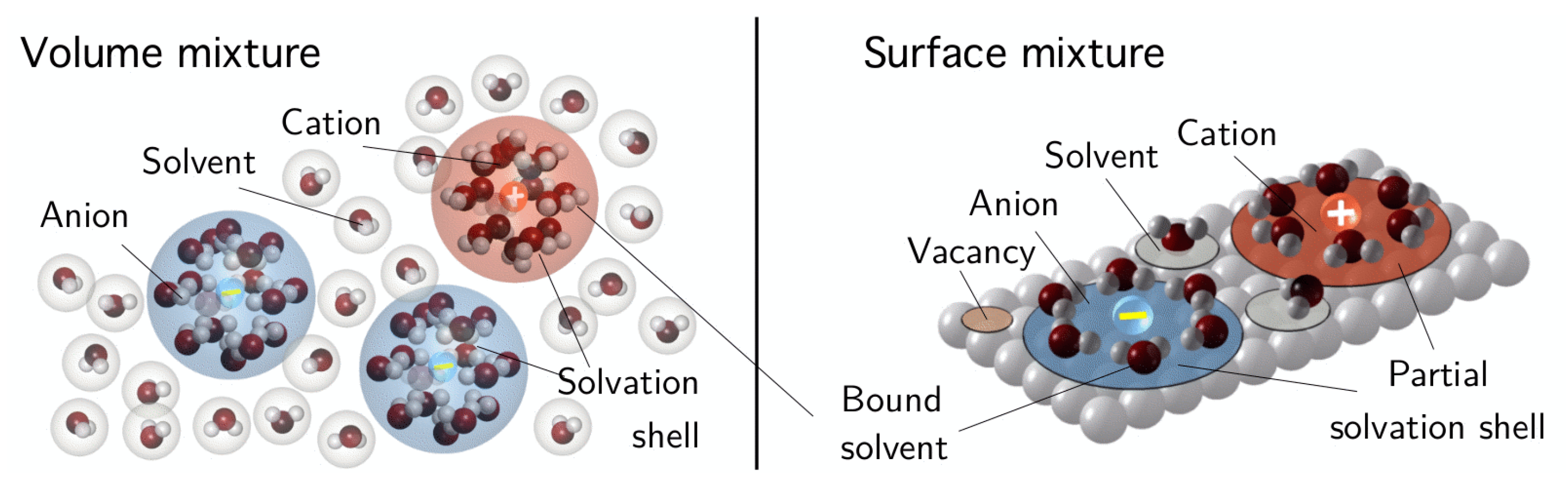
Solvation
7.3. The Electrochemical Double Layer in Equilibrium
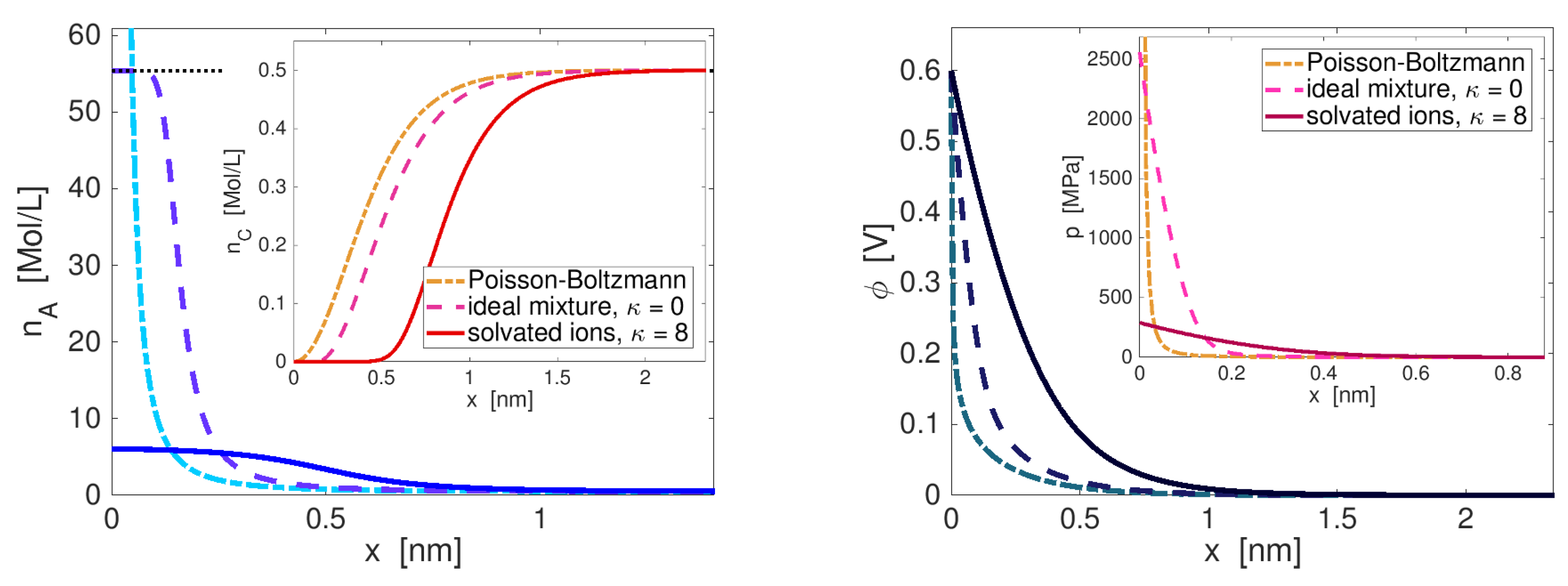
Boundary Layer Structure
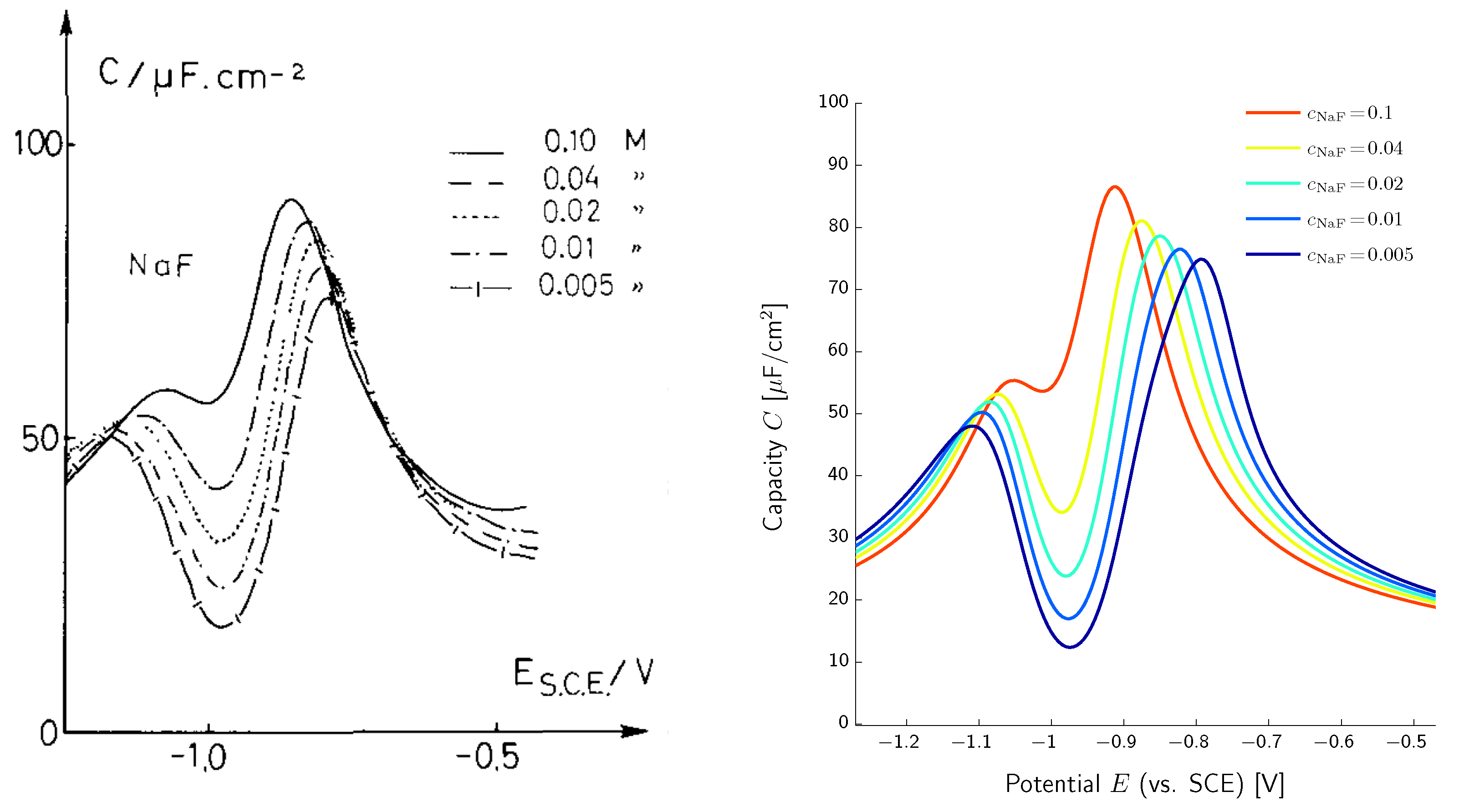
Double Layer Capacity
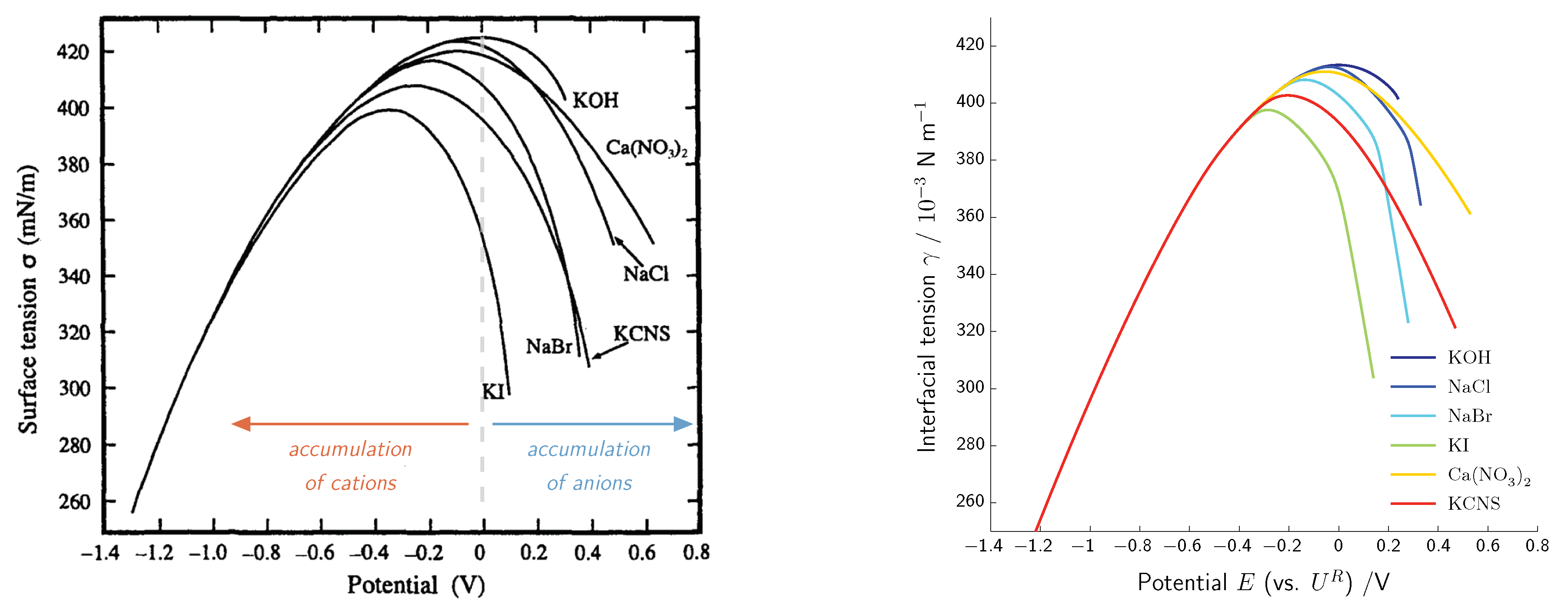
Electrocapillarity—Lippmann Equation
7.4. Electrochemical Systems in Non-Equilibrium
Generalized Nernst–Planck Flux
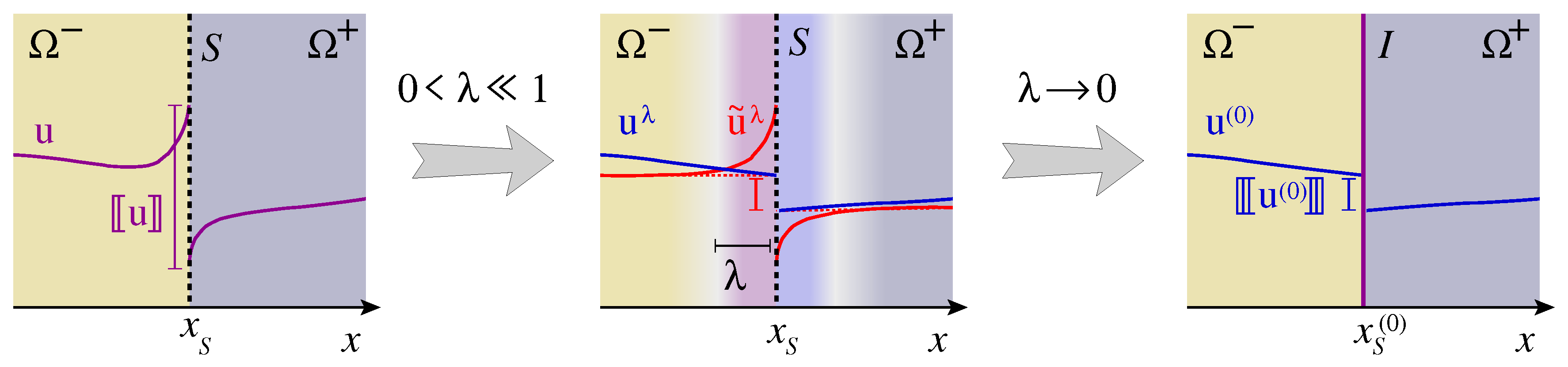
Asymptotic Analysis and Reduced Models
- In leading order, the bulk domain is locally electroneutral and pressure is constant in the bulk.
- The double layer is globally electroneutral and is in quasi-equilibrium. Thus, the results of the preceding section can be applied.
- Boundary layer charge and surface charge are both quantities of first higher order in .
- Analysis of the inner equations allows the formulation of new boundary conditions in terms of the outer variables.
Surface Reactions—Butler–Volmer Equation
8. Conclusions
Outlook
Author Contributions
Funding
Conflicts of Interest
Appendix A. Formal Solution of Surface Balances
Appendix B. Symmetry Properties of the Entropy Density
Bulk
Surface
References
- Yang, Z.; Zhang, J.; Kintner-Meyer, M.C.W.; Lu, X.; Choi, D.; Lemmon, J.P.; Liu, J. Electrochemical Energy Storage for Green Grid. Chem. Rev. 2011, 111, 3577–3613. [Google Scholar] [CrossRef] [PubMed]
- Janek, J.; Zeier, W.G. A solid future for battery development. Nat. Energy 2016, 1, 1–4. [Google Scholar] [CrossRef]
- Yue, L.; Ma, J.; Zhang, J.; Zhao, J.; Dong, S.; Liu, Z.; Cui, G.; Chen, L. All solid-state polymer electrolytes for high-performance lithium ion batteries. Energy Storage Mater. 2016, 5, 139–164. [Google Scholar] [CrossRef]
- Lotsch, B.V.; Maier, J. Relevance of solid electrolytes for lithium-based batteries: A realistic view. J. Electroceram. 2017, 38, 128–141. [Google Scholar] [CrossRef] [Green Version]
- Placke, T.; Kloepsch, R.; Dühnen, S.; Winter, M. Lithium ion, lithium metal, and alternative rechargeable battery technologies: the odyssey for high energy density. J. Solid State Electr. 2017, 21, 1939–1964. [Google Scholar] [CrossRef]
- Strathmann, H. Electrodialysis, a mature technology with a multitude of new applications. Desalination 2010, 264, 268–288. [Google Scholar] [CrossRef]
- Anderson, M.; Cudero, A.; Palma, J. Capacitive deionization as an electrochemical means of saving energy and delivering clean water. Comparison to present desalination practices: Will it compete? Electrochim. Acta 2010, 55, 3845–3856. [Google Scholar] [CrossRef]
- Suss, M.E.; Porada, S.; Sun, X.; Biesheuvel, P.M.; Yoon, J.; Presser, V. Water desalination via capacitive deionization: what is it and what can we expect from it? Energy Environ. Sci. 2015, 8, 2296–2319. [Google Scholar] [CrossRef] [Green Version]
- Bard, A.; Faulkner, L. Electrochemical Methods: Fundamentals and Applications; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Newman, J.; Thomas-Alyea, K. Electrochemical Systems; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Borukhov, I.; Andelman, D.; Orland, H. Steric Effects in Electrolytes: A Modified Poisson–Boltzmann Equation. Phys. Rev. Lett. 1997, 79, 435–438. [Google Scholar] [CrossRef]
- Kilic, M.S.; Bazant, M.Z.; Ajdari, A. Steric effects in the dynamics of electrolytes at large applied voltages. I. Double-layer charging. Phys. Rev. E 2007, 75, 021502. [Google Scholar] [CrossRef]
- Guhlke, C. Theorie der Elektrochemischen Grenzfläche. Ph.D. Thesis, TU-Berlin, Berlin, Germany, 2015. [Google Scholar]
- Dreyer, W.; Guhlke, C.; Müller, R. Overcoming the shortcomings of the Nernst–Planck model. Phys. Chem. Chem. Phys. 2013, 15, 7075–7086. [Google Scholar] [CrossRef] [PubMed]
- Dreyer, W.; Guhlke, C.; Landstorfer, M. A mixture theory of electrolytes containing solvation effects. Electrochem. Commun. 2014, 43, 75–78. [Google Scholar] [CrossRef]
- Dreyer, W.; Guhlke, C.; Müller, R. Modeling of electrochemical double layers in thermodynamic non-equilibrium. Phys. Chem. Chem. Phys. 2015, 17, 27176–27194. [Google Scholar] [CrossRef] [PubMed]
- Dreyer, W.; Guhlke, C.; Müller, R. A new perspective on the electron transfer: Recovering the Butler-Volmer equation in non-equilibrium thermodynamics. Phys. Chem. Chem. Phys. 2016, 18, 24966–24983. [Google Scholar] [CrossRef] [PubMed]
- Landstorfer, M.; Guhlke, C.; Dreyer, W. Theory and structure of the metal–electrolyte interface incorporating adsorption and solvation effects. Electrochim. Acta 2016, 201, 187–219. [Google Scholar] [CrossRef]
- Dreyer, W.; Guhlke, C.; Landstorfer, M.; Müller, R. New insights on the interfacial tension of electrochemical interfaces and the Lippmann equation. Eur. J. Appl. Math. 2017, 29, 708–753. [Google Scholar] [CrossRef]
- deGroot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; Dover Publications: New York, NY, USA, 1984. [Google Scholar]
- Müller, I. Thermodynamics; Pitman Publishing: London, UK, 1985. [Google Scholar]
- Albano, A.; Bedeaux, D. Non-Equilibrium Electro-Thermodynamics of Polarizable Mulitcomponent Fluids with an Interface. Physica A 1987, 147, 407–435. [Google Scholar] [CrossRef]
- Alts, T.; Hutter, K. Continuum Description of the Dynamics and Thermodynamics of Phase Boundaries Between Ice and Water, Part II. J. Non-Equilib. Thermodyn. 1988, 13, 259–280. [Google Scholar] [CrossRef]
- Bothe, D.; Dreyer, W. Continuum thermodynamics of chemically reacting fluid mixtures. Acta Mech. 2015, 226, 1757–1805. [Google Scholar] [CrossRef]
- Truesdell, C.; Toupin, R. The Classical Field Theories; Handbuch der Physik; Springer: Berlin/Göttingen/Heidelberg, Germany, 1960; Volume III/1. [Google Scholar]
- Costen, R.C.; Adamson, D. Three-dimensional derivation of the electrodynamic jump conditions and momentum-energy laws at a moving boundary. Proc. IEEE 1965, 53, 1181–1196. [Google Scholar] [CrossRef]
- Kovetz, A. Electromagn. Theory; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Landau, L.; Lifschitz, E. Elektrodynamik der Kontinua; Lehrbuch der Theoretischen Physik; Akademie-Verlag: Berlin, Germany, 1985; Volume VIII. [Google Scholar]
- Becker, R.; Sauter, F. Theorie der Elektrizität; Teubner: Stuttgart, Germany, 1973; Volume 1. [Google Scholar]
- Hutter, K.; Pao, Y.H. A dynamic theory for magnetizable elastic solids with thermal and electrical conduction. J. Elast. 1974, 4, 89–114. [Google Scholar] [CrossRef]
- Hutter, K.; von de Ven, A.; Ursescu, A. Electromagnetic Field Matter Interactions in Thermoelasic Solids and Viscous Fluids; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Albano, A.; Bedeaux, D.; Vlieger, J. On the description of interfacial electromagnetic properties using singular fields, charge density and currents at a diving surface. Physica A 1980, 102, 105–119. [Google Scholar] [CrossRef]
- Meixner, J.; Reik, H. Thermodynamik der Irreversiblen Prozesse; Handbuch der Physik; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1959; Volume III/2. [Google Scholar]
- Müller, I. A thermodynamic theory of mixtures of fluids. Arch. Ration. Mech. Anal. 1968, 28, 1–39. [Google Scholar] [CrossRef]
- Dreyer, W.; Guhlke, C.; Müller, R. The impact of solvation and dissociation on the transport parameters of liquid electrolytes: Continuum modeling and numerical study. WIAS-Preprint 2018, 2526. [Google Scholar]
- Klika, V.; Pavelka, M.; Benziger, J.B. Functional constraints on phenomenological coefficients. Phys. Rev. E 2017, 95, 022125. [Google Scholar] [CrossRef] [PubMed]
- Thomson, W. Mathematical and Physical Papers; Cambridge University Press: Cambridge, UK, 1882; Volume 1. [Google Scholar]
- Onsager, L. Reciprocal Relations in Irreversible Processes. I. Phys. Rev. 1931, 37, 405–426. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal Relations in Irreversible Processes. II. Phys. Rev. 1931, 38, 2265–2279. [Google Scholar] [CrossRef]
- Casimir, H.B.G. On Onsager’s Principle of Microscopic Reversibility. Rev. Mod. Phys. 1945, 17, 343–350. [Google Scholar] [CrossRef]
- Dreyer, W.; Guhlke, C. Sharp limit of the viscous Cahn–Hilliard equation and thermodynamic consistency. Contin. Mech. Thermodyn. 2017, 29, 913–934. [Google Scholar] [CrossRef]
- Bedeaux, D. Nonequilibrium Thermodynamics and Statistical Physics of Surfaces. In Advances in Chemical Physics; Wiley: Hoboken, NJ, USA, 1986; Volume 64, pp. 47–109. [Google Scholar]
- Kjelstrup, S.; Bedeaux, D. Non-Equilibrium Thermodynamics of Heterogeneous Systems; World Scientific: Singapore, 2008. [Google Scholar]
- Müller, I.; Wilmanski, K. Extended thermodynamics of a non-Newtonian fluid. Rheol. Acta 1986, 25, 335–349. [Google Scholar] [CrossRef]
- Müller, I.; Ruggeri, T. Rational Extended Thermodynamics, 2nd ed.; Springer: New York, NY, USA, 1998. [Google Scholar]
- Barsoukov, E.; Macdonald, J. Impedance Spectroscopy: Theory, Experiment, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Sommerfeld, A. Zur Elektronentheorie der Metalle auf Grund der Fermischen Statistik. Z. Phys. 1928, 47, 1–32. [Google Scholar] [CrossRef]
- Dreyer, W.; Gaberšček, M.; Guhlke, C.; Huth, R.; Jamnik, J. Phase transition in a rechargeable lithium battery. Eur. J. Appl. Math. 2010, 22, 267–290. [Google Scholar] [CrossRef]
- Bockris, J.; Reddy, A.; Gamboa-Aldeco, M. Modern Electrochemistry 2A: Fundamentals of Electrodics; Kluwer: New York, NY, USA, 2000. [Google Scholar]
- Valette, G. Double layer on silver single-crystal electrodes in contact with electrolytes having anions which present a slight specific adsorption: Part I. The (110) face. J. Electroanal. Chem. 1981, 122, 285–297. [Google Scholar] [CrossRef]
- Valette, G. Double layer on silver single crystal electrodes in contact with electrolytes having anions which are slightly specifically adsorbed: Part II. The (100) face. J. Electroanal. Chem. 1982, 138, 37–54. [Google Scholar] [CrossRef]
- Valette, G. Double layer on silver single crystal electrodes in contact with electrolytes having anions which are slightly specifically adsorbed: Part III. The (111) face. J. Electroanal. Chem. 1989, 269, 191–203. [Google Scholar] [CrossRef]
- Grahame, D. The Electrical Double Layer and the Theory of Electrocapillarity. Chem. Rev. 1947, 41, 441–501. [Google Scholar] [CrossRef]
- Bothe, D.; Fischer, A.; Saal, J. Global Well-Posedness and Stability of Electrokinetic Flows. SIAM J. Math. Anal. 2014, 46, 1263–1316. [Google Scholar] [CrossRef] [Green Version]
- Taylor, R.; Krishna, R. Multicomponent Mass Transfer; John Wiley & Sons: New York, NY, USA, 1993; Volume 2. [Google Scholar]
- Bazant, M.Z.; Thornton, K.; Ajdari, A. Diffuse-charge dynamics in electrochemical systems. Phys. Rev. E 2004, 70, 021506. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dreyer, W.; Guhlke, C.; Müller, R. Bulk-Surface Electrothermodynamics and Applications to Electrochemistry. Entropy 2018, 20, 939. https://doi.org/10.3390/e20120939
Dreyer W, Guhlke C, Müller R. Bulk-Surface Electrothermodynamics and Applications to Electrochemistry. Entropy. 2018; 20(12):939. https://doi.org/10.3390/e20120939
Chicago/Turabian StyleDreyer, Wolfgang, Clemens Guhlke, and Rüdiger Müller. 2018. "Bulk-Surface Electrothermodynamics and Applications to Electrochemistry" Entropy 20, no. 12: 939. https://doi.org/10.3390/e20120939
APA StyleDreyer, W., Guhlke, C., & Müller, R. (2018). Bulk-Surface Electrothermodynamics and Applications to Electrochemistry. Entropy, 20(12), 939. https://doi.org/10.3390/e20120939



