Vector Generation of Quantum Contextual Sets in Even Dimensional Hilbert Spaces
Abstract
1. Introduction
2. Results
- (α)
- No two vertices within any of its edges are both assigned the value 1;
- (β)
- In any of its edges, not all of the vertices are assigned the value 0.
2.1. Formalism
2.2. KS Vector Lists vs. Vector Component MMP Hypergraphs
2.3. Vector-Component-Generated Hypergraph Masters
- (i)
- the input set of components for generating two-qubit KS hypergraphs (4D) should contain number pairs of opposite signs, e.g., , and zero (0); we conjecture that the same holds for 3, 4, ...qubits; with 6D it does not hold literally; e.g., generate a KS master; however, the following combination of ’s gives the opposite sign to 1: ;
- (ii)
- mixing real and complex components gives a denser distribution of smaller KS hypergraphs;
- (iii)
- reducing the number of components shortens the time needed to generate smaller hypergraphs and apparently does not affect their distribution.
- As for the features (ii) and (iii) above, components generate the master 180-203 which has the following smallest criticals 18-9, 20...22-11, 22...26-13, 24...30-15, 30...31-16, 28...35-17, 33...37-18, etc. This distribution is much denser than that of, e.g., the list-master 24-24 with real vectors which in the same span of edges consists only of 18-9, 20-11, 22-13, and 24-15 criticals or of the list-master 60-75 which starts with the 26-13 critical. In Appendix A, we give a detailed description of a 21-11 critical with a complex coordinatization and give a blueprint for its experimental implementation;
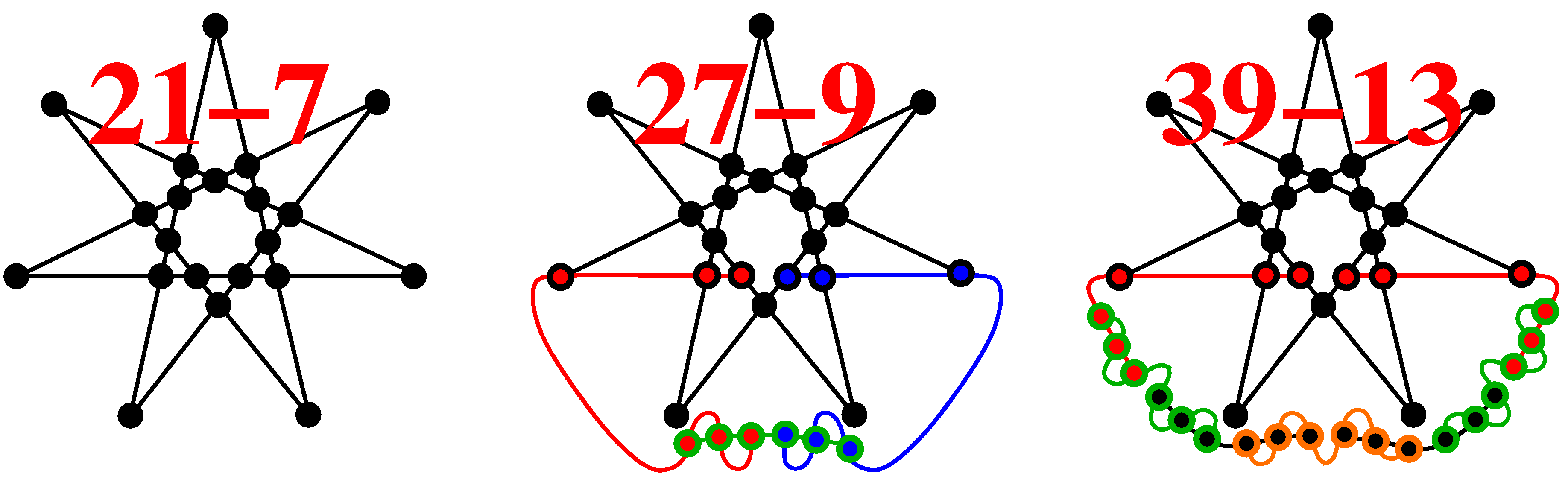
- In [19], the reader is challenged to find a master set which would contain the "seven context star" 21-7 KS critical (shown in Table 1 and Table 2). We find that generate the 216-153 6D master which contains just three criticals 21-7, 27-9, and 33-11, generate 834-1609 master from which we obtained criticals, and generate 11808-314446 master from which we obtained criticals, all of them containing the seven context star. Some of the obtained criticals are given in Appendix B;
- The 60-75 list-master contains criticals with up to 41 edges and 60 vertices, while the 2316-3052 component-master generated from the same vector components contains criticals with up to close to 200 edges and 300 vertices;
- The 60-105 list-master contains criticals with up to 40 edges and 60 vertices, while the 156-249 component-master generated from the same vector components contains criticals with up to at least 58 edges and 88 vertices;
- Components generate 332-1408 6D master which contains the 236-1216 list-master while originally components were used;
- In [37], we generated 6D criticals with up to 177 vertices and 87 edges from the list-master 236-1216, while, now, from the component-master 11808-314446, we obtain criticals with up to 201 vertices and 107 edges;
3. Methods
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| KS | Kochen–Specker; defined in Section 1 |
| MMP | McKay-Megill-Pavičić; defined in Section 2.1 |
Appendix A. 21-11 KS Critical with Complex States from
Appendix B. 6D Criticals from the Masters Containing the Seven Context Star.
References
- Cabello, A.; D’Ambrosio, V.; Nagali, E.; Sciarrino, F. Hybrid Ququart-Encoded Quantum Cryptography Protected by Kochen-Specker Contextuality. Phys. Rev. A 2011, 84, 030302(R). [Google Scholar] [CrossRef]
- Nagata, K. Kochen-Specker Theorem as a Precondition for Secure Quantum Key Distribution. Phys. Rev. A 2005, 72, 012325. [Google Scholar] [CrossRef]
- Howard, M.; Wallman, J.; Veitech, V.; Emerson, J. Contextuality Supplies the ‘Magic’ for Quantum Computation. Nature 2014, 510, 351–355. [Google Scholar] [CrossRef] [PubMed]
- Bartlett, S.D. Powered by Magic. Nature 2014, 510, 345–346. [Google Scholar] [CrossRef] [PubMed]
- Pavičić, M.; McKay, B.D.; Megill, N.D.; Fresl, K. Graph Approach to Quantum Systems. J. Math. Phys. 2010, 51, 102103. [Google Scholar] [CrossRef]
- Megill, N.D.; Pavičić, M. Kochen-Specker Sets and Generalized Orthoarguesian Equations. Ann. Henri Poincare 2011, 12, 1417–1429. [Google Scholar] [CrossRef]
- Simon, C.; Żukowski, M.; Weinfurter, H.; Zeilinger, A. Feasible Kochen-Specker Experiment with Single Particles. Phys. Rev. Lett. 2000, 85, 1783–1786. [Google Scholar] [CrossRef] [PubMed]
- Michler, M.; Weinfurter, H.; Żukowski, M. Experiments towards Falsification of Noncontextual Hidden Variables. Phys. Rev. Lett. 2000, 84, 5457–5461. [Google Scholar] [CrossRef]
- Amselem, E.; Rådmark, M.; Bourennane, M.; Cabello, A. State-Independent Quantum Contextuality with Single Photons. Phys. Rev. Lett. 2009, 103, 160405. [Google Scholar] [CrossRef]
- Liu, B.H.; Huang, Y.F.; Gong, Y.X.; Sun, F.W.; Zhang, Y.S.; Li, C.F.; Guo, G.C. Experimental Demonstration of Quantum Contextuality with Nonentangled Photons. Phys. Rev. A 2009, 80, 044101. [Google Scholar] [CrossRef]
- D’Ambrosio, V.; Herbauts, I.; Amselem, E.; Nagali, E.; Bourennane, M.; Sciarrino, F.; Cabello, A. Experimental Implementation of a Kochen-Specker Set of Quantum Tests. Phys. Rev. X 2013, 3, 011012. [Google Scholar] [CrossRef]
- Huang, Y.F.; Li, C.F.; Zhang, Y.S.; Pan, J.W.; Guo, G.C. Experimental Test of the Kochen-Specker Theorem with Single Photons. Phys. Rev. Lett. 2003, 90, 250401. [Google Scholar] [CrossRef] [PubMed]
- Cañas, G.; Etcheverry, S.; Gómez, E.S.; Saavedra, C.; Xavier, G.B.; Lima, G.; Cabello, A. Experimental Implementation of an Eight-Dimensional Kochen-Specker Set and Observation of Its Connection with the Greenberger-Horne-Zeilinger Theorem. Phys. Rev. A 2014, 90, 012119. [Google Scholar] [CrossRef]
- Hasegawa, Y.; Loidl, R.; Badurek, G.; Baron, M.; Rauch, H. Quantum Contextuality in a Single-Neutron Optical Experiment. Phys. Rev. Lett. 2006, 97, 230401. [Google Scholar] [CrossRef] [PubMed]
- Cabello, A.; Filipp, S.; Rauch, H.; Hasegawa, Y. Proposed Experiment for Testing Quantum Contextuality with Neutrons. Phys. Rev. Lett. 2008, 100, 130404. [Google Scholar] [CrossRef] [PubMed]
- Bartosik, H.; Klepp, J.; Schmitzer, C.; Sponar, S.; Cabello, A.; Rauch, H.; Hasegawa, Y. Experimental Test of Quantum Contextuality in Neutron Interferometry. Phys. Rev. Lett. 2009, 103, 040403. [Google Scholar] [CrossRef] [PubMed]
- Kirchmair, G.; Zähringer, F.; Gerritsma, R.; Kleinmann, M.; Gühne, O.; Cabello, A.; Blatt, R.; Roos, C.F. State-Independent Experimental Test of Quantum Contextuality. Nature 2009, 460, 494–497. [Google Scholar] [CrossRef]
- Moussa, O.; Ryan, C.A.; Cory, D.G.; Laflamme, R. Testing Contextuality on Quantum Ensembles with One Clean Qubit. Phys. Rev. Lett. 2010, 104, 160501. [Google Scholar] [CrossRef]
- Lisoněk, P.; Badziag, P.; Portillo, J.R.; Cabello, A. Kochen-Specker Set with Seven Contexts. Phys. Rev. A 2014, 89, 042101. [Google Scholar] [CrossRef]
- Cañas, G.; Arias, M.; Etcheverry, S.; Gómez, E.S.; Cabello, A.; Saavedra, C.; Xavier, G.B.; Lima, G. Applying the Simplest Kochen-Specker Set for Quantum Information Processing. Phys. Rev. Lett. 2014, 113, 090404. [Google Scholar] [CrossRef]
- Barrett, J.; Kent, A. Noncontextuality, Finite Precision Measurement and the Kochen-Specker. Stud. Hist. Philos. Mod. Phys. 2004, 35, 151–176. [Google Scholar] [CrossRef]
- Spekkens, R.W. Contextuality for Preparations, Transformations, and Unsharp Measurements. Phys. Rev. A 2005, 71, 052108. [Google Scholar] [CrossRef]
- Kunjwal, R.; Spekkens, R.W. From the Kochen-Specker Theorem to Noncontextuality Inequalities without Assuming Determinism. Phys. Rev. Lett. 2015, 115, 110403. [Google Scholar] [CrossRef] [PubMed]
- Kunjwal, R. Hypergraph Framework for Irreducible Noncontextuality Inequalities from Logical Proofs of the Kochen-Specker Theorem. arXiv, 2018; arXiv:1805.02083. [Google Scholar]
- Cabello, A.; Estebaranz, J.M.; García-Alcaine, G. Bell-Kochen-Specker Theorem: A Proof with 18 Vectors. Phys. Lett. A 1996, 212, 183–187. [Google Scholar] [CrossRef]
- Pavičić, M.; Merlet, J.P.; McKay, B.D.; Megill, N.D. Kochen-Specker Vectors. arXiv, 2005; arXiv:quant-ph/0409014. [Google Scholar]
- Waegell, M.; Aravind, P.K. Critical Noncolorings of the 600-Cell Proving the Bell-Kochen-Specker Theorem. J. Phys. A 2010, 43, 105304. [Google Scholar] [CrossRef]
- Waegell, M.; Aravind, P.K. Parity Proofs of the Kochen-Specker Theorem Based on 60 Complex Rays in Four Dimensions. J. Phys. A 2011, 44, 505303. [Google Scholar] [CrossRef]
- Megill, N.D.; Fresl, K.; Waegell, M.; Aravind, P.K.; Pavičić, M. Probabilistic Generation of Quantum Contextual Sets. Phys. Lett. A 2011, 375, 3419–3424. [Google Scholar] [CrossRef]
- Pavičić, M.; Megill, N.D.; Aravind, P.K.; Waegell, M. New Class of 4-Dim Kochen-Specker Sets. J. Math. Phys. 2011, 52, 022104. [Google Scholar] [CrossRef]
- Waegell, M.; Aravind, P.K.; Megill, N.D.; Pavičić, M. Parity Proofs of the Bell-Kochen-Specker Theorem Based on the 600-cell. Found. Phys. 2011, 41, 883–904. [Google Scholar] [CrossRef]
- Waegell, M.; Aravind, P.K. Proofs of Kochen-Specker Theorem Based on a System of Three Qubits. J. Phys. A 2012, 45, 405301. [Google Scholar] [CrossRef]
- Waegell, M.; Aravind, P.K. Proofs of the Kochen-Specker Theorem Based on the N-Qubit Pauli Group. Phys. Rev. A 2013, 88, 012102. [Google Scholar] [CrossRef]
- Waegell, M.; Aravind, P.K. Parity Proofs of the Kochen-Specker Theorem Based on 120-Cell. Found. Phys. 2014, 44, 1085–1095. [Google Scholar] [CrossRef]
- Waegell, M.; Aravind, P.K. Parity Proofs of the Kochen-Specker Theorem Based on the Lie Algebra E8. J. Phys. A 2015, 48, 225301. [Google Scholar] [CrossRef]
- Waegell, M.; Aravind, P.K. The Penrose Dodecahedron and the Witting Polytope Are Identical in ℂℙ3. Phys. Lett. A 2017, 381, 1853–1857. [Google Scholar] [CrossRef]
- Pavičić, M. Arbitrarily Exhaustive Hypergraph Generation of 4-, 6-, 8-, 16-, and 32-Dimensional Quantum Contextual Sets. Phys. Rev. A 2017, 95, 062121. [Google Scholar] [CrossRef]
- Pavičić, M.; Merlet, J.P.; McKay, B.D.; Megill, N.D. Kochen-Specker Vectors. J. Phys. A 2005, 38, 1577–1592. [Google Scholar] [CrossRef]
- McKay, B.D.; Megill, N.D.; Pavičić, M. Algorithms for Greechie Diagrams. Int. J. Theor. Phys. 2000, 39, 2381–2406. [Google Scholar] [CrossRef]
- Pavičić, M.; Megill, N.D.; Merlet, J.P. New Kochen-Specker Sets in Four Dimensions. Phys. Lett. A 2010, 374, 2122–2128. [Google Scholar] [CrossRef]
- Megill, N.D.; Fresl, K.; Waegell, M.; Aravind, P.K.; Pavičić, M. Probabilistic Generation of Quantum Contextual Sets. arXiv, 2011; arXiv:1105.1840. [Google Scholar] [CrossRef]
- Peres, A. Two Simple Proofs of the Bell-Kochen-Specker Theorem. J. Phys. A 1991, 24, L175–L178. [Google Scholar] [CrossRef]
- Kernaghan, M. Bell-Kochen-Specker Theorem for 20 Vectors. J. Phys. A 1994, 27, L829–L830. [Google Scholar] [CrossRef]
- Harvey, C.; Chryssanthacopoulos, J. BKS Theorem and Bell’s Theorem in 16 Dimensions; Technical Report PH-PKA-JC08; Worcester Polytechnic Institute: Worcester, MA, USA, 2012; Available online: https://web.wpi.edu/Pubs/E-project/Available/E-project-042108-171725/unrestricted/MQPReport.pdf (accessed on 26 November 2018).
- Planat, M. On Small Proofs of the Bell-Kochen-Specker Theorem for Two, Three and Four Qubits. Eur. Phys. J. Plus 2012, 127, 86. [Google Scholar] [CrossRef]
- Planat, M.; Saniga, M. Five-Qubit Contextuality, Noise-Like Distribution of Distances Between Maximal Bases and Finite Geometry. Phys. Lett. A 2012, 376, 3485–3490. [Google Scholar] [CrossRef]
- Pavičić, M.; Megill, N.D. Quantum Logic and Quantum Computation. In Handbook of Quantum Logic and Quantum Structures; Engesser, K., Gabbay, D., Lehmann, D., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 751–787. [Google Scholar]
- Megill, N.D.; Pavičić, M. New Classes of Kochen-Specker Contextual Sets (Invited Talk). In Proceedings of the 2017 40th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO 2017), Opatija, Croatia, 22–26 May 2017; Biljanović, P., Ed.; Institute of Electrical and Electronics Engineers (IEEE), Curran Associates, Inc.: Red Hook, NY, USA, 2017; pp. 195–200, ISBN 9781509049691. [Google Scholar]


| dim | Master Size | Vector List | List Origin | Smallest Hypergraph | Vector Components |
|---|---|---|---|---|---|
| 4D | 24-24 | [25,42,43] | symmetry, geometry |  | {0,} |
| 4D | 60-105 | [28,37] | Pauli operators |  | {0,} |
| 4D | 60-75 | [27,30,37,41] | regular polytope 600-cell |  | |
| 4D | 148-265 | [36,37] | Witting polytope |  | |
| 6D | 21-7 | [19] | symmetry | 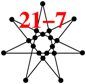 | |
| 6D | 236-1216 | Aravind & Waegell 2016, [37] | hypercube→hexaract Schäfli | 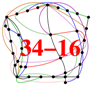 | |
| 8D | 36-9 | [37] | symmetry | 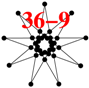 | |
| 8D | 120-2025 | [35,37] | Lie algebra E8 |  | as given in [35] |
| 16D | 80-265 | [37,44,45] | Qubit states |  | |
| 32D | 160-661 | [37,46] | Qubit states |  |
| dim | Vector Components | Component-Master Size | No of KS Criticals in Master | Smallest Hypergraph | Contains List-Masters |
|---|---|---|---|---|---|
| 4D | {0,} or {0,} or or ... | 40-32 | 6 | 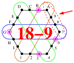 | 24-24 |
| 4D | {0,} | 156-249 | 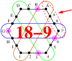 | 24-24, 60-105 | |
| 4D | 2316-3052 | 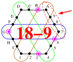 | 24-24, 60-75 | ||
| 4D | 400-1012 | 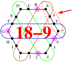 | 24-24, 60-105 148-265 | ||
| 6D | 11808-314446 |  | 21-7, 236-1216 | ||
| 8D | 3280-1361376 |  | 36-9, 120-2025 | ||
| 16D | computationally too demanding |  [33]. | 80-265 | ||
| 32D | computationally too demanding |  [33]. | 160-661 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavičić, M.; Megill, N.D. Vector Generation of Quantum Contextual Sets in Even Dimensional Hilbert Spaces. Entropy 2018, 20, 928. https://doi.org/10.3390/e20120928
Pavičić M, Megill ND. Vector Generation of Quantum Contextual Sets in Even Dimensional Hilbert Spaces. Entropy. 2018; 20(12):928. https://doi.org/10.3390/e20120928
Chicago/Turabian StylePavičić, Mladen, and Norman D. Megill. 2018. "Vector Generation of Quantum Contextual Sets in Even Dimensional Hilbert Spaces" Entropy 20, no. 12: 928. https://doi.org/10.3390/e20120928
APA StylePavičić, M., & Megill, N. D. (2018). Vector Generation of Quantum Contextual Sets in Even Dimensional Hilbert Spaces. Entropy, 20(12), 928. https://doi.org/10.3390/e20120928





