Rolling Element Bearing Fault Diagnosis by Combining Adaptive Local Iterative Filtering, Modified Fuzzy Entropy and Support Vector Machine
Abstract
1. Introduction
2. Adaptive Local Iterative Filtering
3. Modified Fuzzy Entropy
3.1. Fuzzy Entropy
- (1)
- For a sequence with length N , construct the vectors of m-dimension :where stands for a new time series, being generalized by subtracting the mean of the m consecutive u values:
- (2)
- The distance between and is denoted as
- (3)
- The similarity degree can be computed by
- (4)
- Denote as
- (5)
- The function is defined as
- (6)
- Similarly, the is obtained by repeating the above steps
- (7)
- Then define FuzzyEn of the sequence
- (8)
- Lastly, for a N with finite length, FuzzyEn could be calculated by
3.2. Modified Fuzzy Entropy
3.3. Parameter Selection
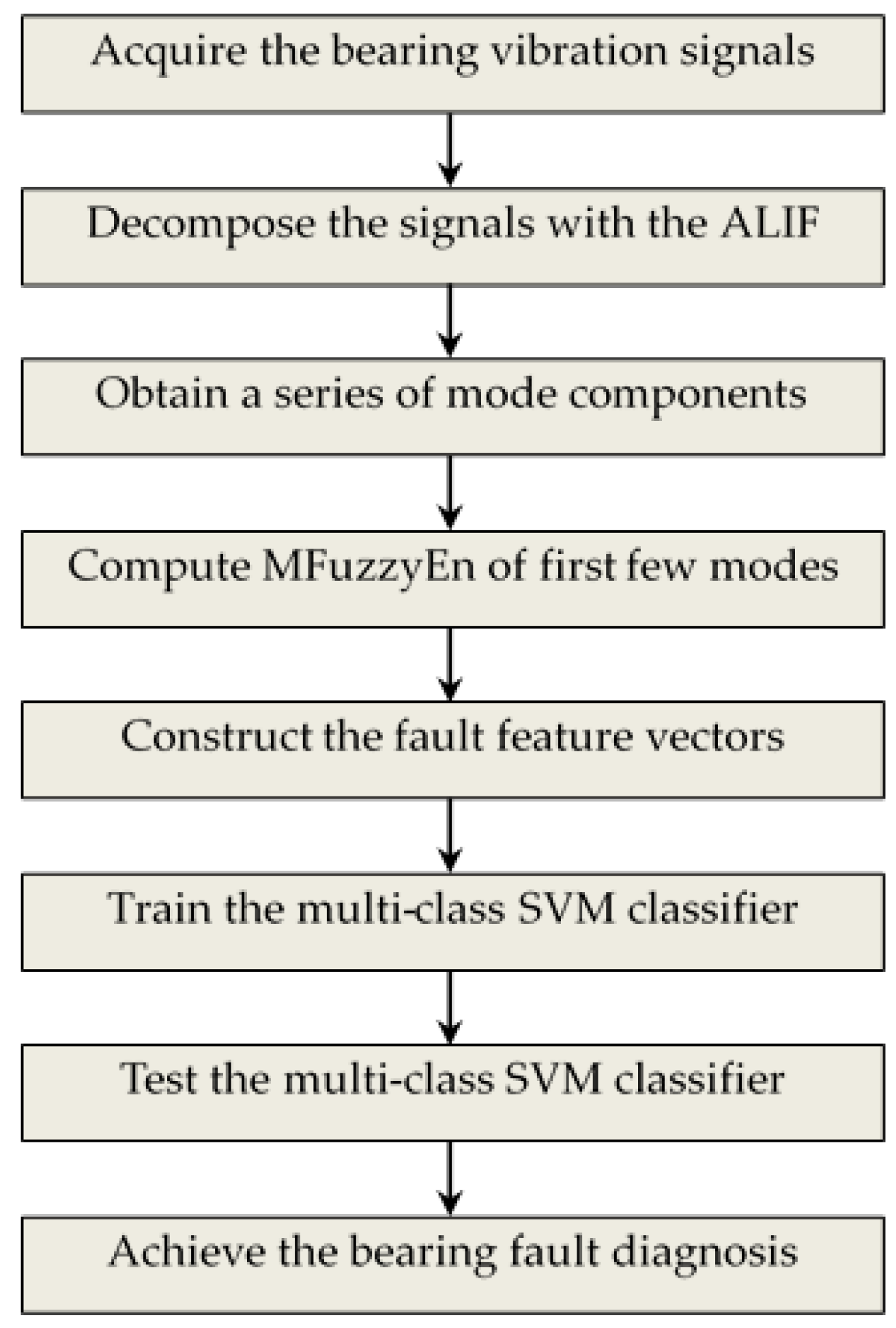
4. The Proposed Bearing Fault Diagnosis Method
- (1)
- Vibration signals of rolling element bearing under different conditions are acquired by using an accelerometer.
- (2)
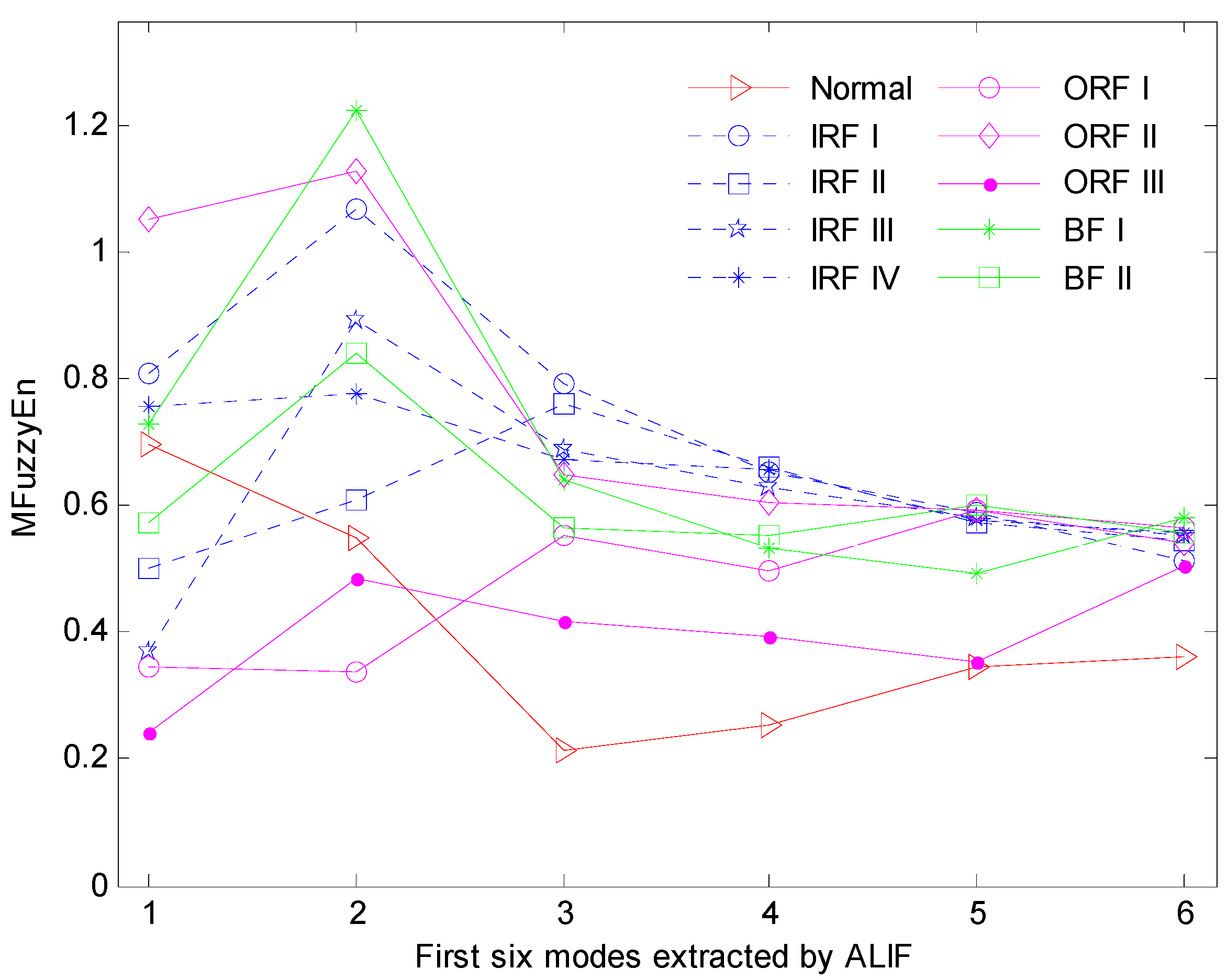
- The ALIF algorithm is utilized to decompose the acquired bearing vibration signals and a series of mode components are obtained. The first several modes containing rich fault information are chosen for research.
- (3)
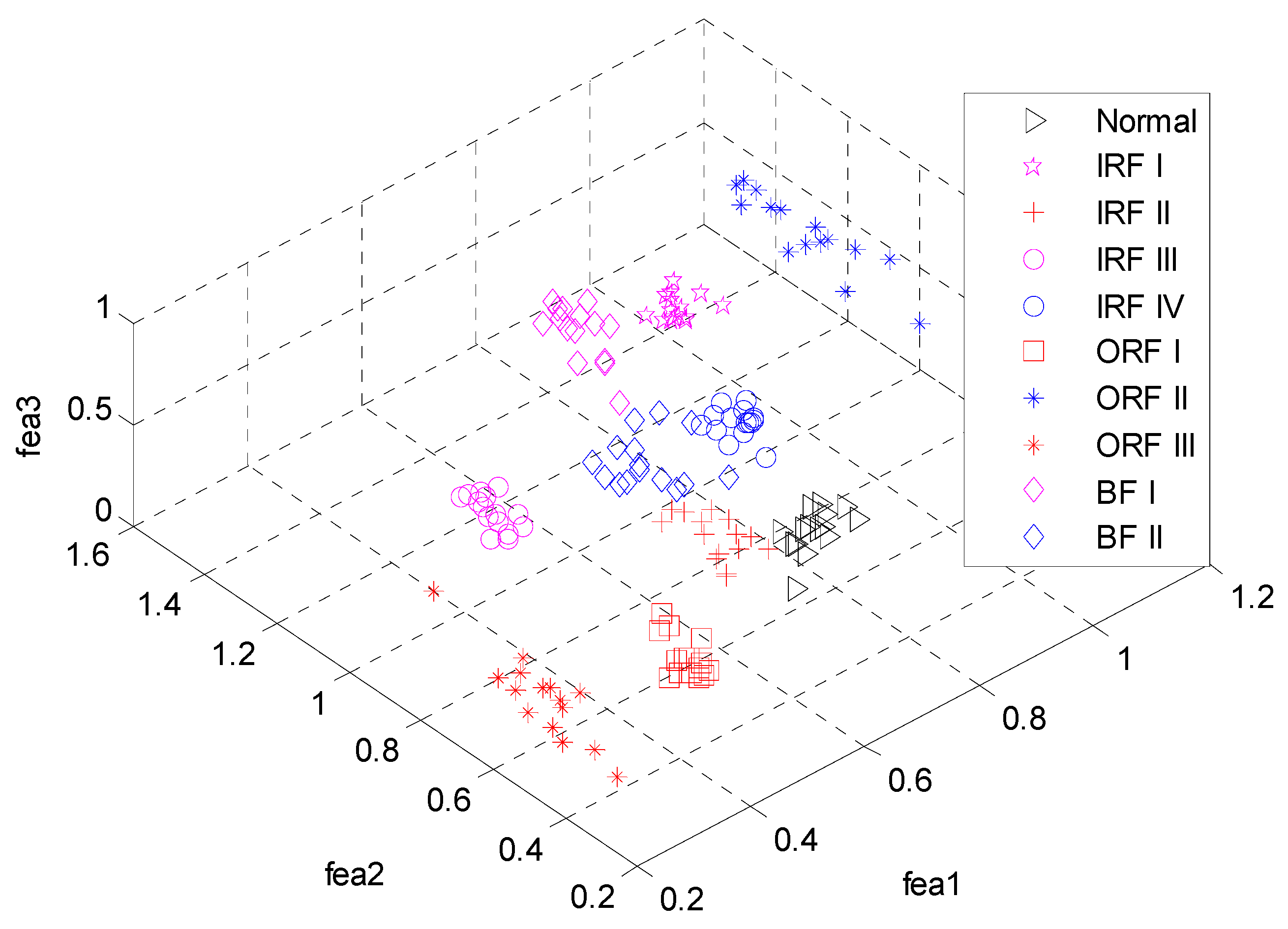
- Calculate the MFuzzyEn of chosen components, and then the corresponding entropy value is treated as fault feature for reflecting working conditions of rolling element bearing.
- (4)
- The obtained fault feature set is used for the training and testing of multi-class SVM classifier and fault recognition for rolling element bearing is completed automatically.
5. Application
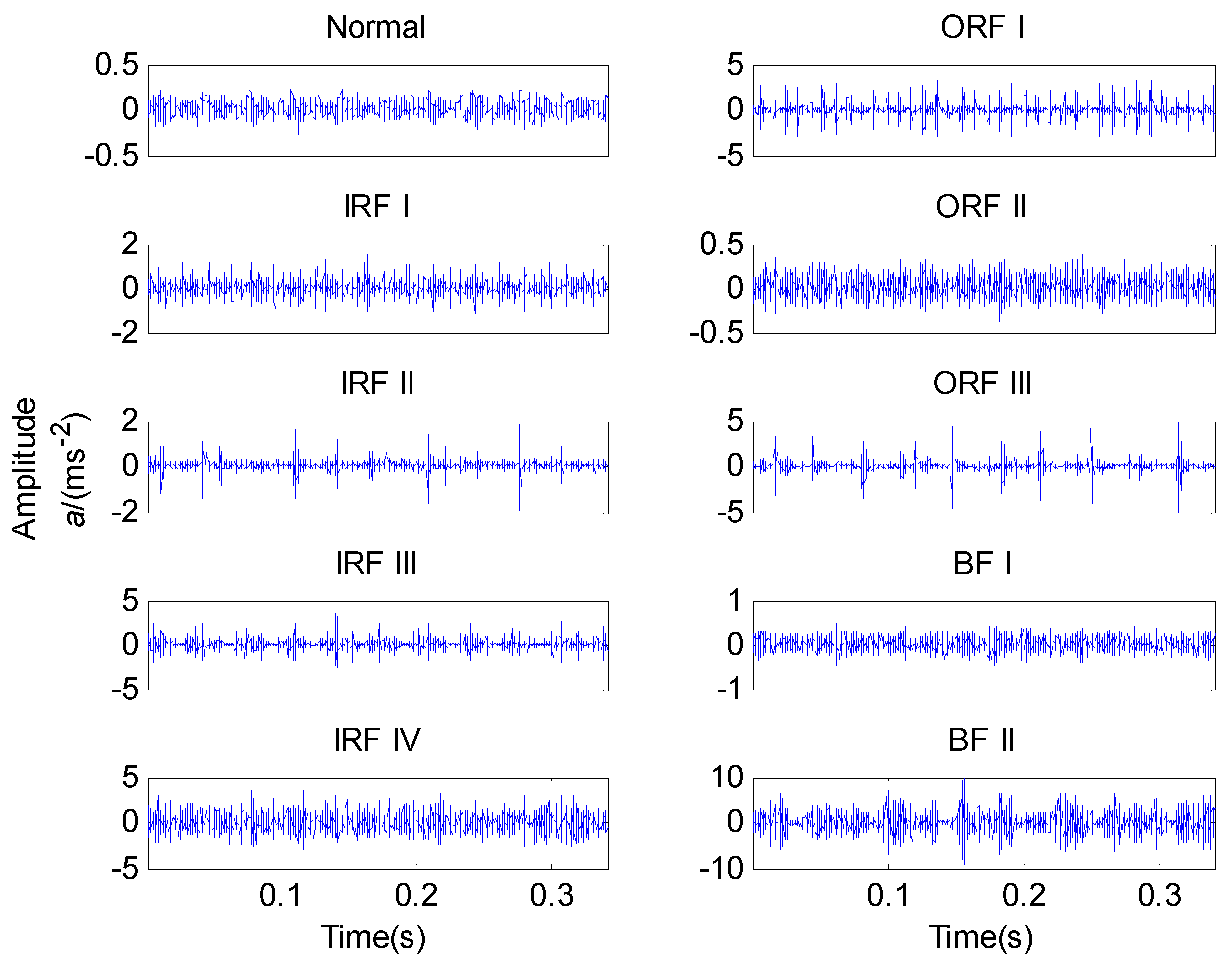
5.1. Experimental Data
5.2. Experimental Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhu, X.L.; Zheng, J.D.; Pan, H.Y.; Bao, J.H.; Zhang, Y.F. Time-shit multiscale fuzzy entropy and Laplacian support vector machine based rolling bearing fault diagnosis. Entropy 2018, 20, 602. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K.; Nembhard, A.D. A novel fault diagnosis technique for enhancing maintenance and reliability of rotating machines. Struct. Health Monit. 2015, 14, 604–621. [Google Scholar] [CrossRef]
- Pan, J.; Chen, J.L.; Zi, Y.Y.; Li, Y.M.; He, Z.J. Mono-component feature extraction for mechanical fault diagnosis using modified empirical wavelet transform via data-driven adaptive Fourier spectrum segment. Mech. Syst. Signal Process. 2016, 72–73, 160–183. [Google Scholar] [CrossRef]
- Zhang, N.N.; Wu, L.F.; Yang, J.; Guan, Y. Naïve Bayes bearing fault diagnosis based on enhanced independence of data. Sensors 2018, 18, 463. [Google Scholar] [CrossRef] [PubMed]
- Yunusa-Kaltungo, A.; Sinha, J.K. Generic vibration-based faults identification approach for identical rotating machines installed on different foundations, VIRM 11-Vibrations in Rotating. Machinery 2016, 499–510. [Google Scholar]
- Dong, G.M.; Chen, J. Study on cyclic energy indicator for degradation assessment of rolling element bearings. J. Vib. Control 2010, 17, 1805–1816. [Google Scholar] [CrossRef]
- Nembhard, A.D.; Sinha, J.K.; Yunusa-Kaltungo, A. Development of a generic rotating machinery fault diagnosis approach insensitive to machine speed and support type. J. Sound Vib. 2015, 337, 321–341. [Google Scholar] [CrossRef]
- Yang, Y.; Yu, D.J.; Cheng, J.S. A roller bearing fault diagnosis method based on EMD energy entropy and ANN. J. Sound Vib. 2006, 294, 269–277. [Google Scholar]
- Rodriguez, N.; Cabrera, G.; Lagos, C.; Cabrera, E. Stationary wavelet singular entropy and kernel extreme learning for bearing multi-fault diagnosis. Entropy 2017, 19, 541. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A Math. Phys. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Mohanty, S.; Gupta, K.K.; Raju, K.S. Adaptive fault identification of bearing using empirical mode decomposition–principal component analysis-based average kurtosis technique. IET Sci. Meas. Technol. 2017, 11, 30–40. [Google Scholar] [CrossRef]
- Wang, F.T.; Deng, G.; Liu, C.X.; Su, W.S.; Han, Q.K.; Li, H.K. A deep feature extraction method for bearing fault diagnosis based on empirical mode decomposition and kernel function. Adv. Mech. Eng. 2018, 10, 1–12. [Google Scholar] [CrossRef]
- Feng, Z.P.; Zhang, D.; Zuo, M.J. Adaptive mode decomposition methods and their applications in signal analysis for machinery fault diagnosis: A review with examples. IEEE Access 2017, 5, 24301–24331. [Google Scholar] [CrossRef]
- Smith, J.S. The local mean decomposition and its application to EEG perception data. J. Roy. Soc. Interf. 2005, 2, 443–454. [Google Scholar] [CrossRef] [PubMed]
- Gilles, J. Empirical wavelet transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Liu, H.H.; Han, M.H. A fault diagnosis method based on local mean decomposition and muti-scale entropy for roller bearings. Mech. Mach. Theory 2014, 75, 67–78. [Google Scholar] [CrossRef]
- Chen, J.L.; Pan, J.; Li, Z.P.; Zi, Y.Y.; Chen, X.F. Generator bearing fault diagnosis for wind turbine via empirical wavelet transform using measured vibration signals. Renew. Energy 2016, 89, 80–92. [Google Scholar] [CrossRef]
- Cao, H.R.; Fan, F.; Zhou, K.; He, Z.J. Wheel-bearing fault diagnosis of trains using empirical wavelet transform. Measurement 2016, 82, 439–449. [Google Scholar] [CrossRef]
- Abdoos, A.A.; Mianaei, P.K.; Ghadikolaei, M.R. Combined VMD-SVM based feature selection method for classification of power quality events. Appl. Soft Comput. 2016, 38, 637–646. [Google Scholar] [CrossRef]
- Cicone, A.; Liu, J.; Zhou, H. Adaptive local iterativefiltering for signal decomposition and instantaneous frequency analysis. Appl. Comput. Harmonic Anal. 2016, 41, 384–411. [Google Scholar] [CrossRef]
- An, X.; Zeng, H.; Yang, W.; An, X. Fault diagnosis of a wind turbine rolling bearing using adaptive local iterative filtering and singular value decomposition. Trans. Inst. Meas. Control 2017, 39, 1643–1648. [Google Scholar] [CrossRef]
- An, X.; Zeng, H.; Li, C. Demodulation analysis based on adaptive local iterative filtering for bearing fault diagnosis. Measurement 2016, 94, 554–560. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X. Approximate entropy as a diagnostic tool for machine health monitoring. Mech. Syst. Signal Process. 2007, 21, 241–250. [Google Scholar] [CrossRef]
- Zhang, L.; Xiong, G.L.; Liu, H.S.; Zou, H.J.; Guo, W.Z. Bearing fault diagnosis using multi-scale entropy and adaptive neuro-fuzzy inference. Expert Syst. Appl. 2010, 37, 6017–6085. [Google Scholar] [CrossRef]
- Zhu, K.H.; Song, X.G.; Xue, D.X. A roller bearing fault diagnosis method based on hierarchical entropy and support vector machine with particle swarm optimization algorithm. Measurement 2014, 47, 669–675. [Google Scholar] [CrossRef]
- Chen, W.T.; Wang, Z.Z.; Xie, H.B.; Yu, W.X. Characterization of surface EMG signal based on fuzzy entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef]
- Zheng, J.D.; Cheng, J.S.; Yang, Y.; Luo, S.R. A rolling bearing fault diagnosis method based on multi-scale fuzzy entropy and variable predictive model-based class discrimination. Mech. Mach. Theory 2014, 78, 187–200. [Google Scholar] [CrossRef]
- Li, Y.B.; Xu, M.Q.; Wang, R.X.; Huang, W.H. A fault diagnosis scheme for rolling bearing based on local mean decomposition and improved multiscale fuzzy entropy. J. Sound Vib. 2016, 360, 277–299. [Google Scholar] [CrossRef]
- Liu, C.Y.; Li, K.; Zhao, L.N.; Liu, F.; Zheng, D.C.; Liu, C.C.; Liu, S.T. Analysis of heart variability using fuzzy measure entropy. Comput. Biol. Med. 2013, 43, 100–108. [Google Scholar] [CrossRef]
- Zhou, S.H.; Qian, S.L.; Chang, W.B.; Xiao, Y.Y.; Cheng, Y. A novel bearing multi-fault diagnosis approach based on weighted permutation entropy and an improved SVM ensemble classifier. Sensors 2018, 18, 1934. [Google Scholar] [CrossRef] [PubMed]
- Abbasion, S.; Rafsanjani, A.; Farshidianfar, A.; Irani, N. Rolling element bearings multi-fault classification based on the wavelet denoising and support vector machine. Mech. Syst. Signal Process. 2007, 21, 2933–2945. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Lin, L.; Wang, Y.; Zhou, H. Iterative filtering as an alternative algorithm for empirical mode decomposition. Adv. Adapt. Data Anal. 2009, 1, 543–560. [Google Scholar] [CrossRef]
- Zhu, K.H.; Li, H.L. A rolling element bearing fault diagnosis approach based on hierarchical fuzzy entropy and support vector machine. J. Mech. Eng. Sci. 2016, 230, 2314–2322. [Google Scholar] [CrossRef]
- The Case Western Reserve University bearing data center. Available online: http://csegroups.case.edu/bearingdatacenter/pages/download-data-file (accessed on 17 October 2012).
- Widodo, A.; Yang, B.S. Support vector machine in machine condition monitoring and fault diagnosis. Mech. Syst. Signal Process. 2007, 21, 2560–2574. [Google Scholar] [CrossRef]

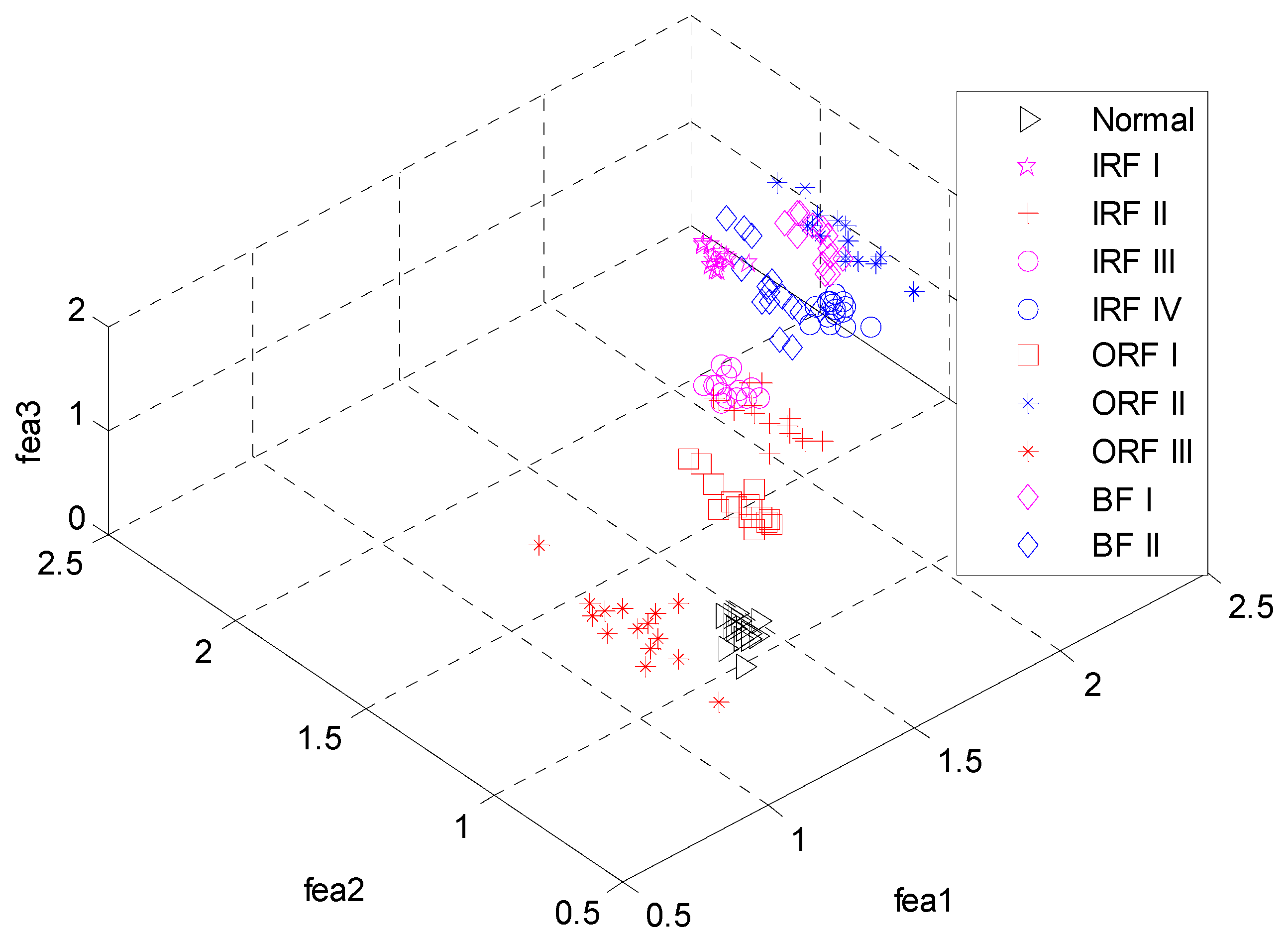

| Bearing State | Fault Diameter (mm) | Label of Classification | Bearing State | Fault Diameter (mm) | Label of Classification |
|---|---|---|---|---|---|
| Normal | 0 | 1 | ORF I | 0.1778 | 6 |
| IRF I | 0.1778 | 2 | ORF II | 0.3556 | 7 |
| IRF II | 0.3556 | 3 | ORF III | 0.5334 | 8 |
| IRF III | 0.5334 | 4 | BF I | 0.1778 | 9 |
| IRF IV | 0.7112 | 5 | BF II | 0.7112 | 10 |
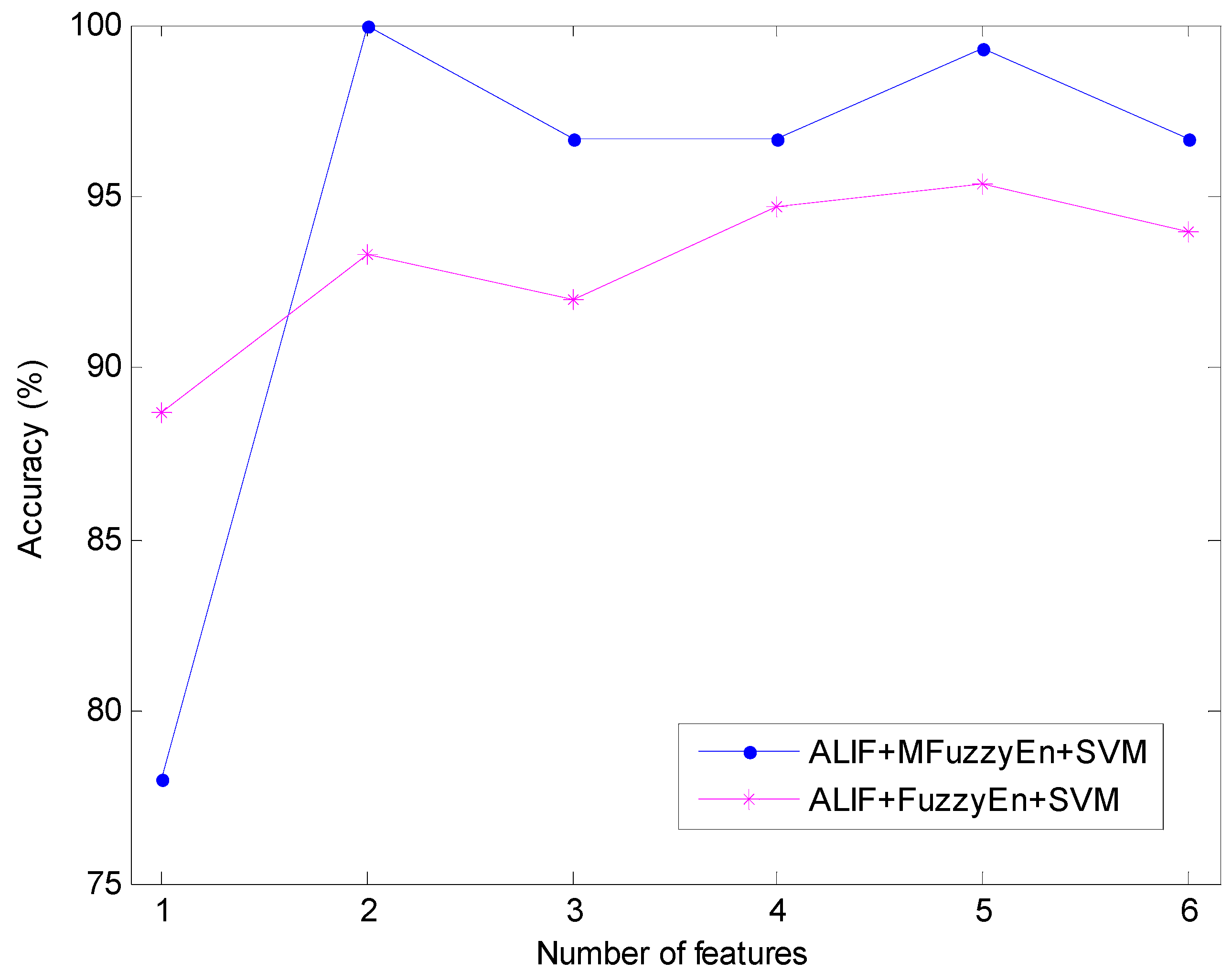
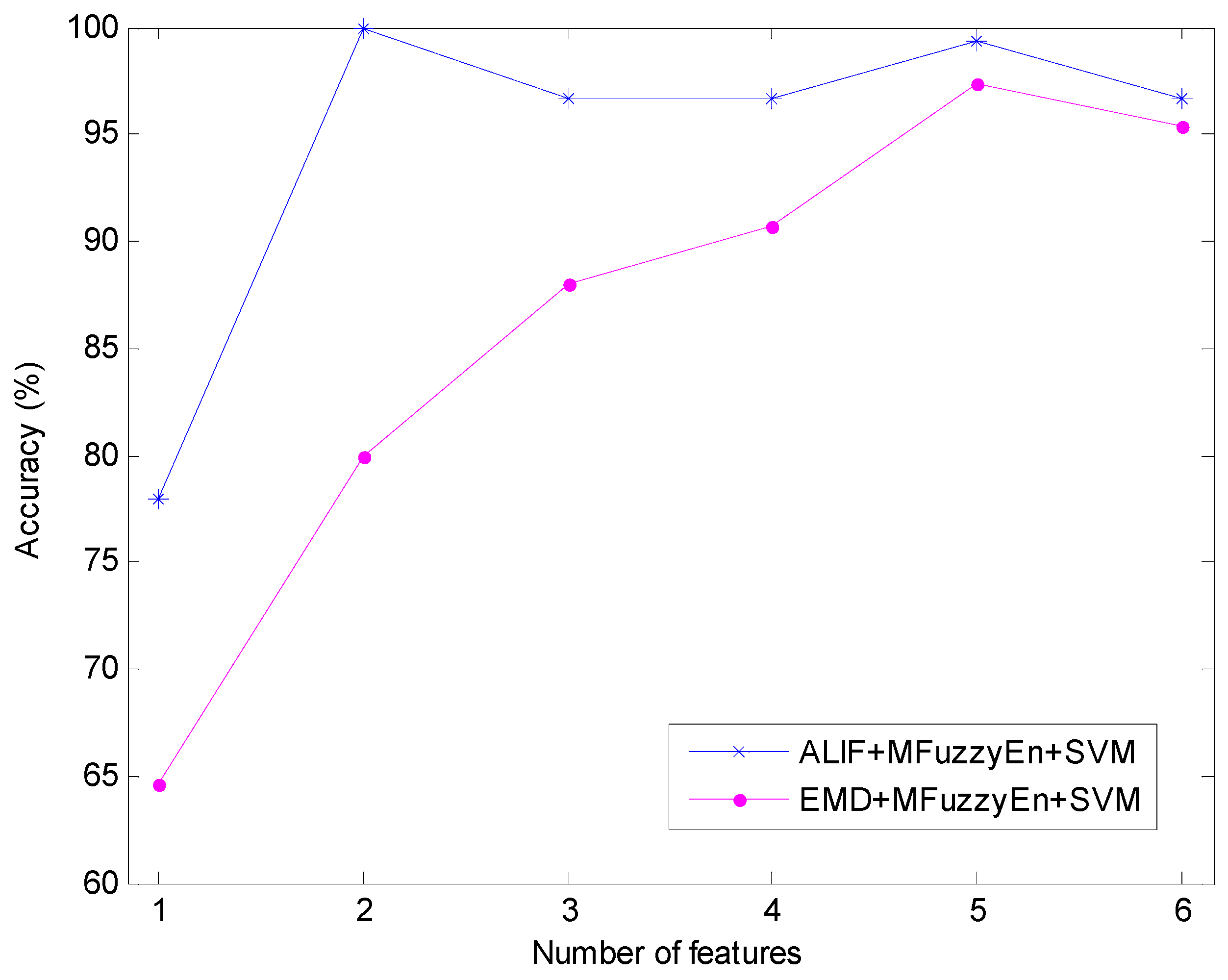
| Used Features | ALIF + MFuzzyEn + SVM | ALIF + FuzzyEn + SVM | ||
|---|---|---|---|---|
| The Number of Misclassified Data | Accuracy (%) | The Number of Misclassified Data | Accuracy (%) | |
| First 1 | 33 | 78 | 17 | 88.67 |
| First 2 | 0 | 100 | 10 | 93.33 |
| First 3 | 5 | 96.67 | 12 | 92 |
| First 4 | 5 | 96.67 | 8 | 94.67 |
| First 5 | 1 | 99.33 | 7 | 95.33 |
| First 6 | 5 | 96.67 | 9 | 94 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, K.; Chen, L.; Hu, X. Rolling Element Bearing Fault Diagnosis by Combining Adaptive Local Iterative Filtering, Modified Fuzzy Entropy and Support Vector Machine. Entropy 2018, 20, 926. https://doi.org/10.3390/e20120926
Zhu K, Chen L, Hu X. Rolling Element Bearing Fault Diagnosis by Combining Adaptive Local Iterative Filtering, Modified Fuzzy Entropy and Support Vector Machine. Entropy. 2018; 20(12):926. https://doi.org/10.3390/e20120926
Chicago/Turabian StyleZhu, Keheng, Liang Chen, and Xiong Hu. 2018. "Rolling Element Bearing Fault Diagnosis by Combining Adaptive Local Iterative Filtering, Modified Fuzzy Entropy and Support Vector Machine" Entropy 20, no. 12: 926. https://doi.org/10.3390/e20120926
APA StyleZhu, K., Chen, L., & Hu, X. (2018). Rolling Element Bearing Fault Diagnosis by Combining Adaptive Local Iterative Filtering, Modified Fuzzy Entropy and Support Vector Machine. Entropy, 20(12), 926. https://doi.org/10.3390/e20120926





