Perspectives on Thermoelectric Energy Conversion in Ion-Exchange Membranes
Abstract
1. Introduction
2. The Cell
3. The Electromotive Force of the Ag|AgCl-Cell
3.1. Connecting Leads
3.2. The Electrochemical Reaction at the Interface
3.3. The Membrane
3.4. The Seebeck Coefficient of the Complete Cell
4. The emf of the Cell with Calomel Electrodes
Theory of Tasaka and Coworkers
5. Review of Experimental Results
5.1. Experimental Issues: Temperature Polarization
5.2. Properties Derived From Experimental Results
5.2.1. Electrode Contributions
5.2.2. Electrolyte Property Variations
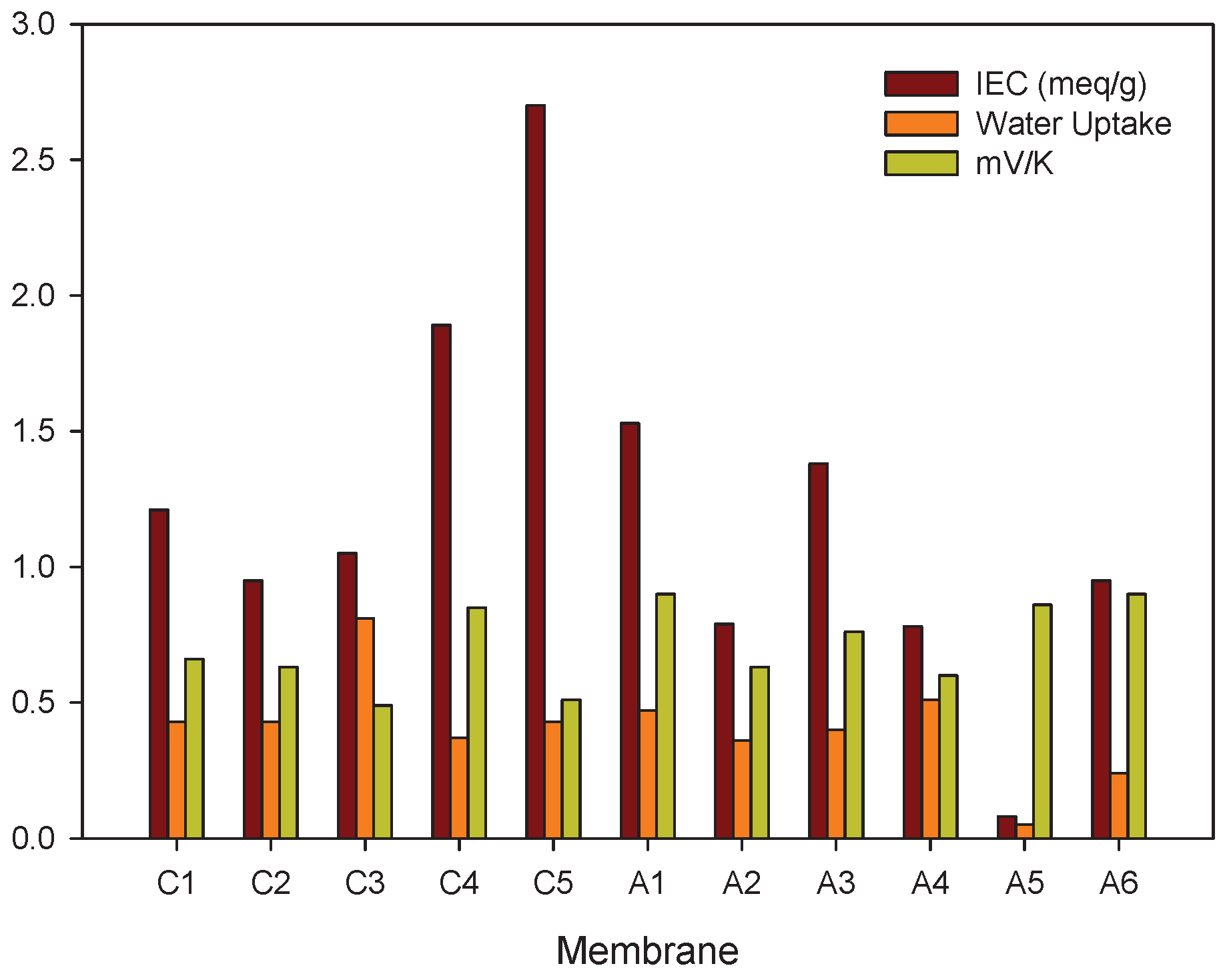
5.2.3. Membrane Structure, Counter Ion, and Water Content
- Membrane structureHeterogeneous ion-exchange membranes contain more than one charged polymer. It was found that heterogeneous ion-exchange membranes have in general larger thermoelectric potentials than homogeneous ion-exchange membranes, both cationic and anionic membranes [31,37]. Laksminarayanayah [26] and Huda et al. [52] studied the effect of crosslinking of membrane polymers. The degree of crosslinking of the polymethacrylic acid membrane did not have much impact [26] on the Seebeck coefficient. But membranes made of poly(4-vinylpyridineco-styrene) [45] gave thermoelectric potentials that increased with an increase in weight fraction of hydrophobic hydrocarbon matrix, or in the molality of fixed charges. Poly(styrene)-based copolymer anion-exchange membranes with divinylbenzene were investigated in the presence of various electrolyte solutions [52]. Positive contributions were found with KIO solutions, and negative for more hydrophobic Cl-form membranes. The water term seemed predominant for IO-form membranes with high water contents. The value of the thermoelectric potential was always negative, which seems to show that the contribution from water on the thermal membrane potential is significant. More systematic studies of the degree of cross-linking as well as membrane hydrophobicity may help obtain better membranes for thermoelectric energy conversion.
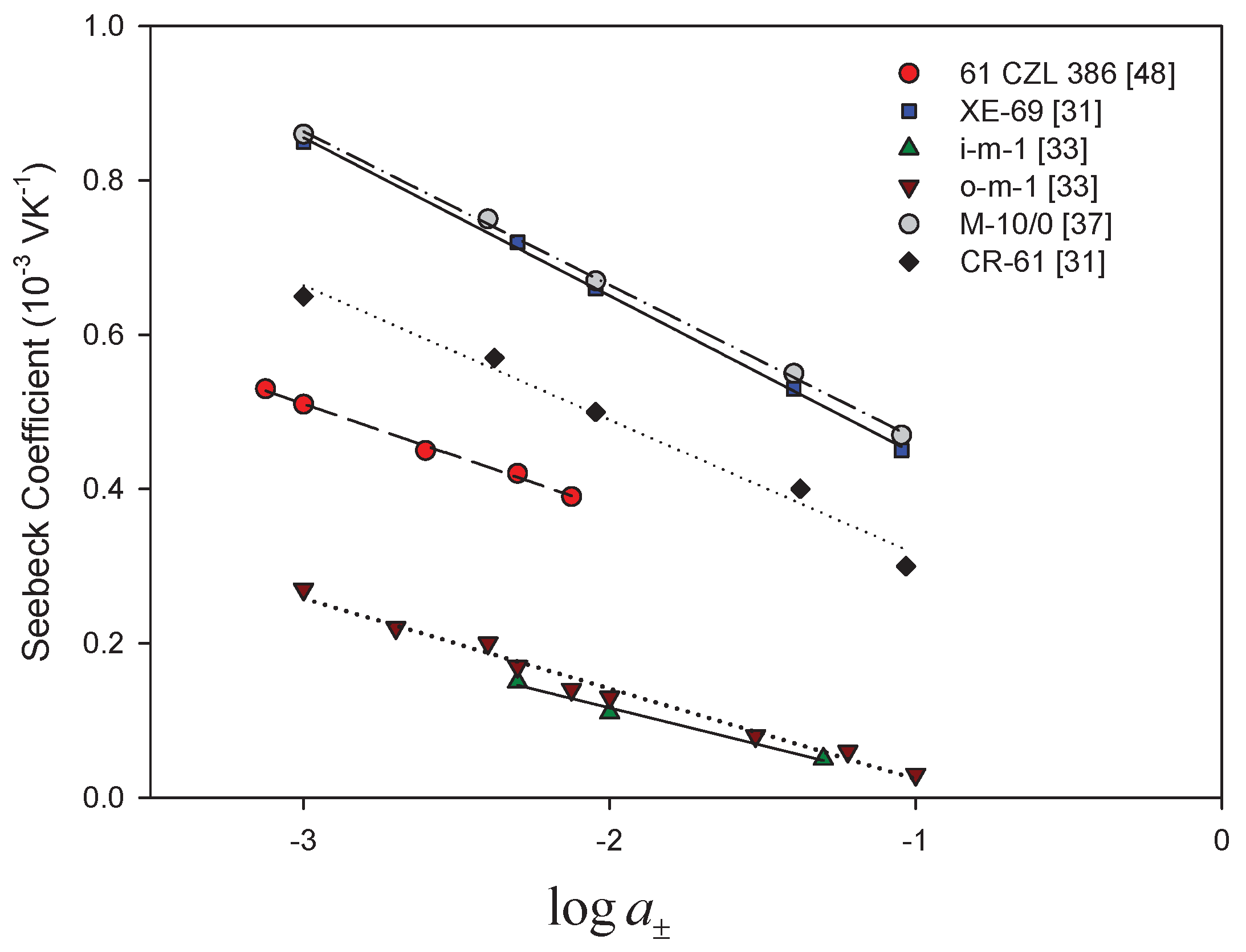
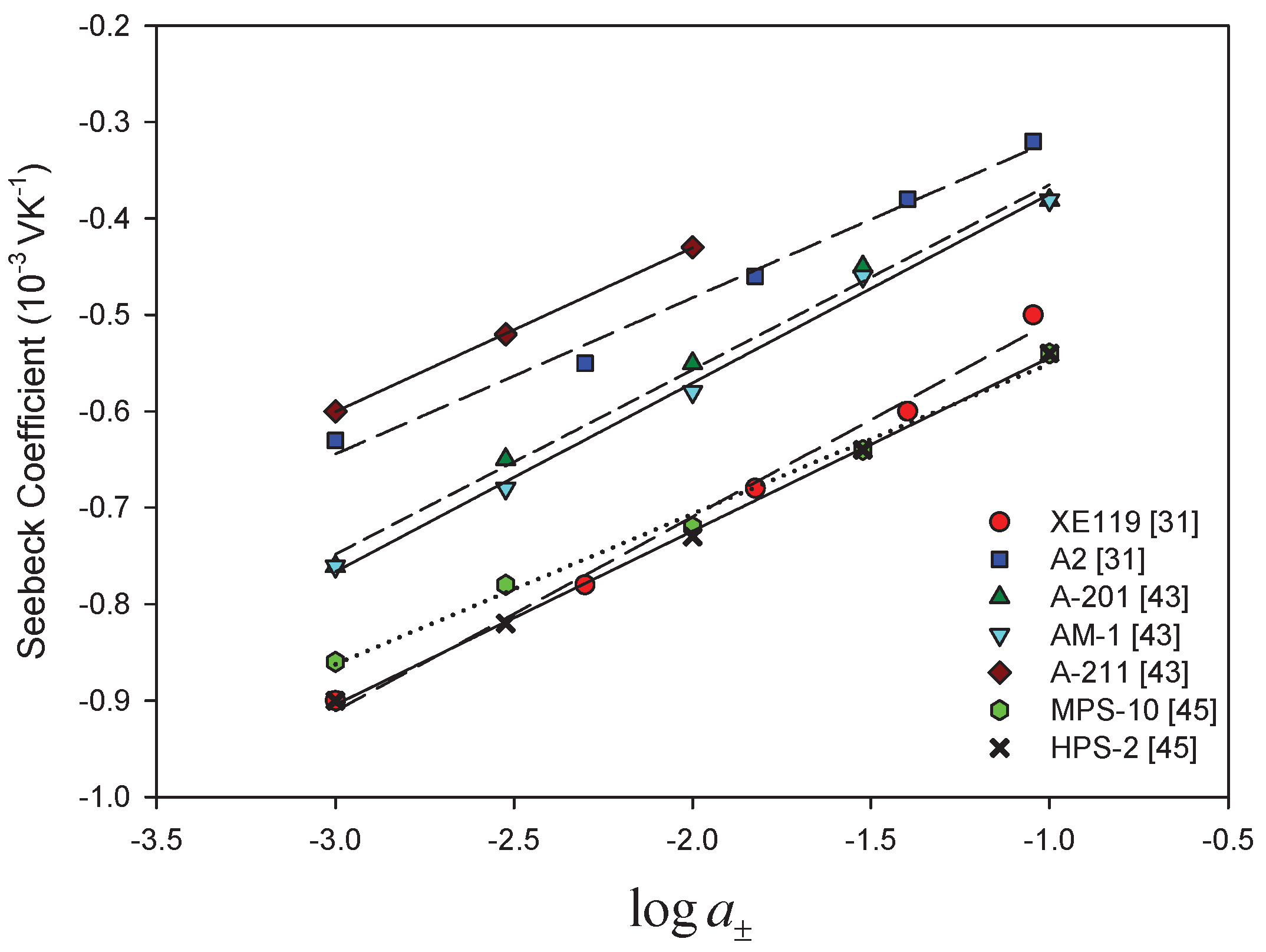
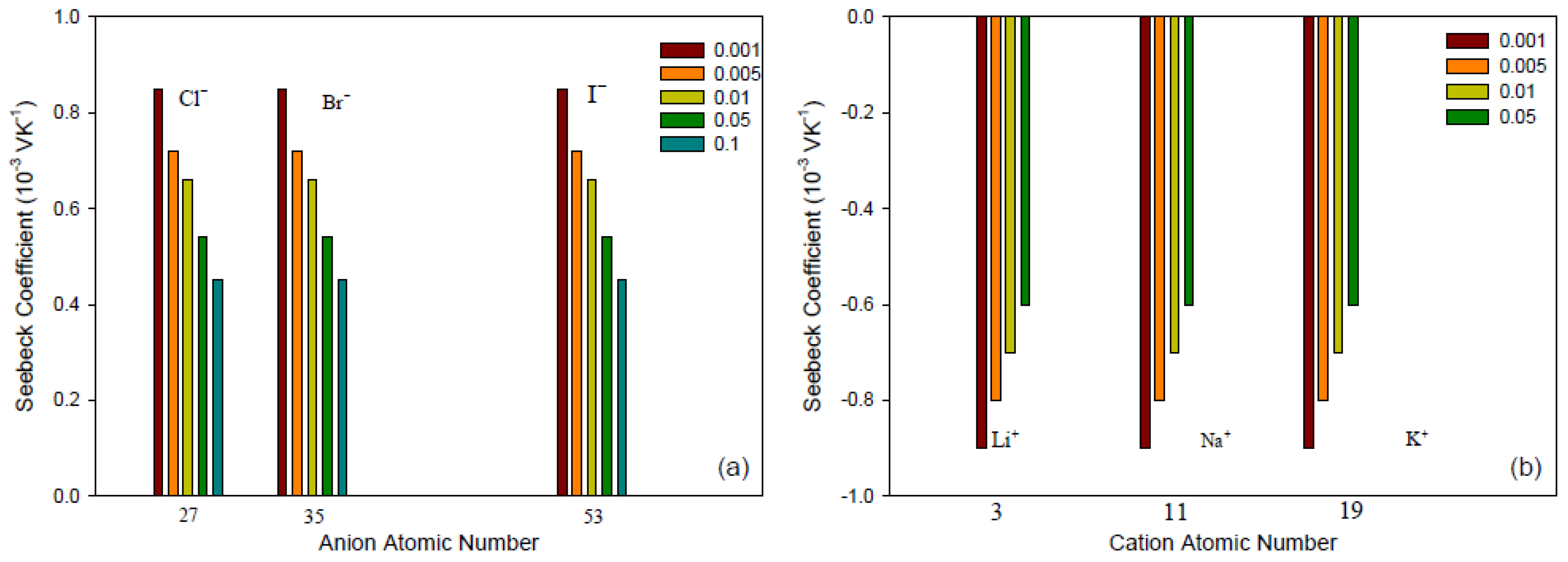
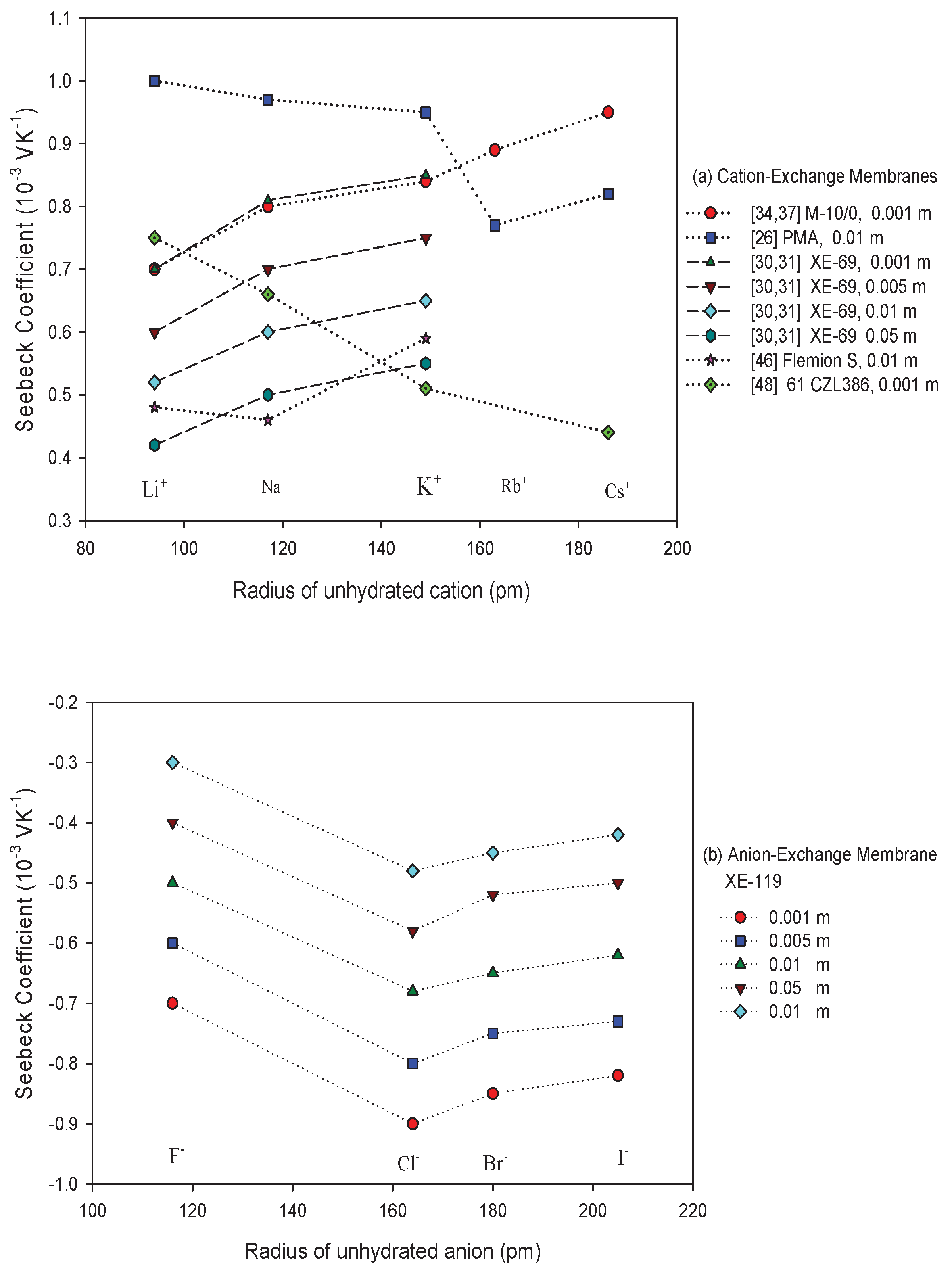
- Membrane counter-ionThe type of ion in the membrane has a clear impact. Figure 5a,b show Seebeck coefficients for different ion-exchange membranes as a function of the radius of unhydrated counter-ion. We see that, in general, the Seebeck coefficient for cationic membranes increases with the atomic number of the cation involved. With HCl and alkali metal chloride solutions, the thermoelectric potential varies roughly with the inverse of the radius of the ions. However, the opposite trend was also observed for some membrane systems [26,46,48]. With anion-exchange membrane Amberlite X-119, the magnitude of Seebeck coefficient increased with increasing molecular weight of halogen ions except for F ion. Similar results were found by Huda et al. [52] with poly(styrene)-based copolymer anion-exchange membranes. This property may have some bearing on the transported entropy which enter the expression for .Kiyono et al. [44] reported that the size of the Seebeck coefficient depended on the ion-exchange capacity and the membrane water content. They found larger Seebeck coefficients for KCl-solutions than for NaCl, but this was at variance with results of Laksminarayanaiah [28]. It is difficult to see that ion-exchange capacity per se should have an impact on . Indirectly it may play a role, through its impact on the transported entropies, however. No systematic study has been made of the transported entropy and its dependencies.At constant selectivity, cation oxidized collodion and anion cellophane membranes gave an absolute value of the thermoelectric potential higher for anion-exchange membranes than for cation-exchange membranes using calomel electrodes [61]. Tasaka et al. [31] measured thermoelectric potentials between 0.85 mV/K and mV/K, respectively, with Amberlite XE-69 cation-exchange membranes and Amberlite XE-119 anion-exchange membranes and a 10 M aqueous KCl solutions.
- Water contentIt is difficult to separate the effects of water content from that of, say, the ion exchange capacity. The properties are interrelated and the first of them is strongly dependent on the membrane structure. Both properties have only an indirect effect through their impact on the transport numbers and transported entropies appearing in Equation (34). Nevertheless, the larger Seebeck coefficients have been found for membranes with low water content [36,43,45]. Kiyono et al. [45] atributed this behavior to the restricted movement of ions in the membrane with small water content and high weight fraction of hydrophobic backbone. A hydrophobic membrane matrix affects the state of the counter-ion, and therefore also the transported entropy in membrane. Huda et al. [52] altered the hydrophobicity of anion-exchange membranes by changing the length of the alkyl chain of benziltrialkilammonium groups. They observed that the thermoelectric potential decreased roughly with hydrophobicity of the ion-exchange groups.In general, the absolute value of thermoelectric potential decreases with the membrane water content (Figure 6). Tasaka et al. [37] also related the decrease in the absolute value of the thermoelectric potential to the water content, leading to a much smaller value of the transported entropy of counter-ion. As can be seen in Figure 6, anion-exchange membranes on the whole have relatively low water content (high apparent transport numbers). It may be explained by the smaller deviation from the theoretical slope of the Seebeck coefficient with the logarithm of the electrolyte concentration observed for anion-exchange membranes (Figure 3). The relatively small ion-exchange capacity does not have much of an impact. The cation-exchange membrane Ionics 61CZL386, with a high ion-exchange capacity, shows a Seebeck coefficient similar to those of other membranes with lower IEC value. In Equation (34), a high water content may mean a high water transport number, positive for cation-exchange membranes [60]. The membrane structure may have an impact on the transported entropy of the counter-ion in the membrane phase.When we compare the anion-exchange membranes Nepton AR-111 (homogeneous) and Nepton XE-119 (heterogeneous), we find a higher Seebeck coefficient for the heterogeneous XE-69 membrane with large water content. High water transport numbers are expected for membranes with high water contents. The water transport numbers are negative in anionic membranes [60], so according to Equation (34), a higher water content would increase the Seebeck coefficient. This explanation agrees with the observed experimental results.The Seebeck coefficient depends on the solvent, but aqueous solutions seem favorable for a high value [66].
5.2.4. Membrane Temperature: Other Barriers to Transport
6. Competing Thermoelectric Materials
7. The Potential for Thermoelectric Energy Conversion
8. Conclusions and Perspectives
- It typically varies between absolute values 0.4 and 1 mV/K. Major contributions to this value come from the electrode compartment (including the electrodes) and from water and ion transport in the membrane. These values are relatively large, compared to values for semiconductors. In the calomel electrode system, the sign of the coefficient is typically positive for cation-exchange membranes and negative for anion-exchange membranes. This sign change is attributed mainly to the thermoelectric potential across the salt bridges in the system, but also to water transport when the electrolyte concentration is high.
- It predicts a reduction for ideal membranes with the logarithm of the electrolyte activity. This variation is experimentally validated.
- It has a possible optimal value with respect to the mean temperature across the membrane.
- It does not depend significantly on water content in spite of its dependence on the water transference number.
- It does not depend significantly on the membrane ion exchange capacity. One explanation is that the transport number is the ratio of the ionic and the total conductivity.
- It depends on membrane heterogeneity, probably because this has an impact on the transported entropies of the ions in the membrane.
- It increases in absolute value with the radius of the un-hydrated counter-ion.
- It may have positive contributions from a membrane pressure difference.
- In order to have access to the membrane dependent terms in the Seebeck coefficients, it is advantageous to use electrodes without salt bridges, such as the Ag|AgCl-electrode.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Membrane (Reference) | Type | Electrolyte | Seebeck Coefficient () | Electrodes | |
|---|---|---|---|---|---|
| Collodion Ikeda [24] | KCl | M | 0.052 | Ag|AgCl | |
| Oxidized collodium Ikeda [61] | Apparent transport number 0.9 | KCl | M | 0.03 | Calomel |
| PMA Laksminarayanaiah [26] | Crosslinked polymetrarylic acid | LiCl | M | 1.00 | Ag|AgCl |
| NaCl | 0.97 | ||||
| KCl | 0.95 | ||||
| RbCl | 0.77 | ||||
| CsCl | 0.82 | ||||
| Amberlite XE-69-polyvinyl chloride 40% Tasaka et al. [30,31] | Heterogeneous polystyrenesulfonate | LiCl | M | 0.70 | Calomel |
| M | 0.60 | ||||
| M | 0.52 | ||||
| M | 0.42 | ||||
| NaCl | M | 0.81 | |||
| M | 0.70 | ||||
| M | 0.60 | ||||
| M | 0.50 | ||||
| KCl | M | 0.85 | |||
| M | 0.72 | ||||
| M | 0.66 | ||||
| M | 0.54 | ||||
| KBr | M | 0.83 | |||
| M | 0.75 | ||||
| M | 0.65 | ||||
| M | 0.50 | ||||
| KI | M | 0.83 | |||
| M | 0.75 | ||||
| M | 0.65 | ||||
| M | 0.55 | ||||
| o-m-1 Tasaka et al. [30,33] | Oxidized Collodion | KCl | M | 0.27 | Calomel |
| M | 0.17 | ||||
| M | 0.13 | ||||
| M | 0.07 | ||||
| i-m-1 Tasaka et al. [33] | Collodion-sulfonated Polystyrene interpolymer | KCl | M | 0.15 | Calomel |
| M | 0.11 | ||||
| M | 0.05 | ||||
| M-10/0 Tasaka [34,37] | Heterogeneous Sulfonate polystyrene+ PVC (40%) | LiCl | M | 0.70 | Calomel |
| NaCl | 0.80 | ||||
| KCl | 0.84 | ||||
| RbCl | 0.89 | ||||
| CsCl | 0.95 | ||||
| NHCl | 0.93 | ||||
| Nepton CR-61 Tasaka [37] | Homogeneous Sulfonate polystyrene | KCl | M | 0.66 | Calomel |
| Nepton CR-51 Tasaka [37] | Homogeneous Sulfonated phenol resin | KCl | M | 0.63 | Calomel |
| Interpolymer Tasaka [37] | Sulfonated polystyrene + dried collodion (95%) | KCl | M | 0.49 | Calomel |
| Flemion S Hanaoka et al. [46] | Porous perfluorosulfonic acid-type | HCl | M | 0.053 | Calomel |
| LiCl | 0.48 | ||||
| NaCl | 0.46 | ||||
| KCl | 0.59 | ||||
| NHCl | 0.62 | ||||
| Nafion 117 Kjelstrup et al. [47] | Homogeneous Sulfonated | HCl | M | 0.66 | Ag|AgCl |
| Ionics 61 CZL 386 Barragán et al. [48] | Heterogeneous sulfonated | KCl | M | 0.53 | Calomel |
| M | 0.51 | ||||
| M | 0.45 | ||||
| M | 0.42 | ||||
| M | 0.39 | ||||
| LiCl | M | 0.75 | |||
| NaCl | 0.66 | ||||
| KCl | 0.51 | ||||
| CsCl | 0.44 | ||||
| Nafion 1110 Kjelstrup et al. [14] | Homogeneous Sulfonated | HCl | 0.67 | Hydrogen | |
| Membrane (Reference) | Type | Electrolyte | Seebeck Coefficient () | Electrodes | |
|---|---|---|---|---|---|
| Celophane Ikeda [61] | Anilline-formaldehyde resin-cellophane matrix | KCl | M | calomel | |
| Amberlite XE-119 polyvinyl chloride 40% Tasaka et al. [30] | Heterogeneous polystyrene with quaternary ammonium | LiCl | M | calomel | |
| M | |||||
| M | |||||
| M | |||||
| NaCl | M | ||||
| M | |||||
| M | |||||
| M | |||||
| KCl | M | ||||
| M | |||||
| KF | M | ||||
| M | |||||
| M | |||||
| M | |||||
| KBr | M | ||||
| M | |||||
| M | |||||
| M | |||||
| KI | M | ||||
| M | |||||
| M | |||||
| Aciplex A-201 Hanaoka et al. [43] | Hydrocarbonsulfonic acid | KCl | M | calomel | |
| M | |||||
| M | |||||
| M | |||||
| M | |||||
| KIO | M | ||||
| M | |||||
| Neosepta AM-1 Hanaoka et al. [43] | Hydrocarbonsulfonic acid | KCl | M | calomel | |
| M | |||||
| M | |||||
| M | |||||
| M | |||||
| KIO | M | ||||
| M | |||||
| Aciplex A-211 Hanaoka et al. [43] | Hydrocarbonsulfonic acid | KCl | M | calomel | |
| M | |||||
| M | |||||
| MPS-10 Kiyono et al. [45] | Poly(4-vinylpyridine-co-styrene) with methyl iodide | KCl | M | calomel | |
| M | |||||
| M | |||||
| M | |||||
| M | |||||
| HPS-2 Kiyono et al. [45] | Poly(4-vinylpyridine-co-styrene) with 1.6-dibromo-n-hexane | KCl | M | calomel | |
| M | −0.82 | ||||
| M | |||||
| M | |||||
| M | |||||
| M-1(4.5) Huda et al. [52] | Polysterine-based copolymer + 4.5% divinylbencene | KCl | M | calomel | |
| KIO | |||||
| M-1(8) Huda et al. [52] | Polysterine-based copolymer + 8% divinylbencene | KCl | M | calomel | |
References
- Seebeck, T.J. Magnetische Polarisation der Metalle und erze durch Temperatur-Differenz. In Ostwald’s Klassiker der Exakten Wissenshaften; Oettingen, A.J.V., Ed.; Verlag Von Wilhem Engelman: Lemgo, Germany, 1895. [Google Scholar]
- Savani, I.; Waage, M.H.; Børset, M.; Kjelstrup, S.; Wilhelmsen, Ø. Harnessing thermoelectric power from transient heat source: Waste heat recovery from silicon production. Energy Convers. Manag. 2017, 138, 171–182. [Google Scholar] [CrossRef]
- Dresselhaus, M.; Chen, G.; Tang, M.; Yand, R.; Lee, H.; Wang, D.; Ren, Z.; Fleurial, J.P.; Gogna, P. New directions for low-dimensional thermoelectric materials. Adv. Mater. 2007, 19, 1043–1053. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Chen, G.; Ren, Z.; Dresselhaus, G.; Henry, A.; Fleurial, J.P. New composite thermoelectric materials for energy harvesting applications. JOM 2009, 61, 86–90. [Google Scholar] [CrossRef]
- Caballero-Calero, O.; D’Agosta, R. Review—Towards the next generation of thermoelectric materials: Tailoring electronic and phononic properties of nanomaterials. ECS J. Solid State Sci. Technol. 2017, 6, 3065–3079. [Google Scholar] [CrossRef]
- Hicks, L.D.; Dresselhaus, M.S. Effect of quantum-well structures on the thermoelectric figure of merit. Phys. Rev. Lett. 1993, 19, 12727–12731. [Google Scholar] [CrossRef]
- Hicks, L.D.; Dresselhaus, M.S. Thermoelectric figure of merit of a one-dimensional conductor. Phys. Rev. Lett. 1993, 24, 16631–16634. [Google Scholar] [CrossRef]
- Bentien, A.; Johnsen, S.; Madsen, G.K.H.; Iversen, B.B.; Steglich, F. Colossal Seebeck coefficient in strongly correlated semiconductor FeSb2. EPL 2007, 80, 17008. [Google Scholar] [CrossRef]
- Jiao, F.; Naderi, A.; Zhao, D.; Schlueter, J.; Shahi, M.; Sundström, J.; Granberg, H.; Edberg, J. Ionic thermoelectric paper. J. Mater. Chem. A 2017, 5, 16883–16888. [Google Scholar] [CrossRef]
- Datta, R.; Said, S.M.; Sahamir, S.; Karim, M.; Sabri, M.; Nakajo, T.; Kubouchi, M.; Hayashi, K.; Miyakazi, Y. Thermoelectric potential of polymerscaffolded ionic liquid membranes. J. Electrochem. Mater. 2014, 43, 1585–1589. [Google Scholar] [CrossRef]
- Bonetti, M.; Huang, S.N.B.; Salez, T.J.; Wiertel-Gasquet, C.; Roger, M. Thermoelectric energy recovery at ionic-liquid/electrode interface. J. Chem. Phys. 2015, 142, 244708. [Google Scholar] [CrossRef] [PubMed]
- Revil, A. Ion diffusivity, electrical conductivity, membrane and thermoelectric potentials in colloids and granular porous media: A unified model. J. Colloid Int. Sci. 1999, 70, 555–559. [Google Scholar]
- Shakouri, A.; Li, S. Thermoelectric Power Factor for Electrically conductive polymers. In Proceedings of the International Conference on Thermoelectrics, Baltimore, MD, USA, 29 August–2 September 1999. [Google Scholar]
- Kjelstrup, S.; Vie, P.J.S.; Akyalcin, L.; Zefaniya, P.; Pharoah, J.G.; Burheim, O.S. The Seebeck coefficient and the Peltier effect in a polymer electrolyte membrane cell with two hydrogen electrodes. Electrochim. Acta 2013, 99, 166–175. [Google Scholar] [CrossRef]
- Sandbakk, K.D.; Bentien, A.; Kjelstrup, S. Thermoelectric effects in ion conducting membranes and perspectives for thermoelectric energy conversion. J. Membr. Sci. 2013, 434, 10–17. [Google Scholar] [CrossRef]
- Manzanares, J.A.; Jokinen, M.; Cervera, J. On the different formalisms for the transport equations of thermoelectricity: A review. J. Non-Equilib. Thermodyn. 2015, 40, 211–227. [Google Scholar] [CrossRef]
- Jokinen, M.; Manzanares, J.A.; Kontturi, K.; Murtomäki, L. Thermal potential of ion-exchange membranes and its application to thermoelectric power generation. J. Membr. Sci. 2016, 499, 234–244. [Google Scholar] [CrossRef]
- Benneker, T.; Rijnaars, T.; Lammertink, R.G.H.; Wood, J.A. Effect of temperature gradients in (reverse) electrodialysis in the ohmic regime. J. Membr. Sci. 2018, 548, 421–428. [Google Scholar] [CrossRef]
- Hasan, S.W.; Said, S.M.; Bakar, A.S.B.A.; Sabri, M.F.M.S.; Sajid, I.H.; Hashim, N.A. Optimization of poly(vinylidene fluoride) membranes for enhanced power density of thermally driven electrochemical cells. J. Mater. Sci. 2017, 52, 10353–10363. [Google Scholar] [CrossRef]
- Kristiansen, K.; Barragán, V.M.; Kjelstrup, S. Thermoelectric power of ion exchange membrane cells revelant to reverse electrodialysis plants. 2018; submitted. [Google Scholar]
- Vermass, D.A.; Saakes, M.; Nijmeijer, K. Power generation using profiled membranes in reverse electrodialysis. J. Membr. Sci. 2011, 385–386, 234–242. [Google Scholar] [CrossRef]
- Tyrrell, H.J.V. The Seebeck effect in a purely ionic system. Nature 1956, 177, 668–669. [Google Scholar] [CrossRef] [PubMed]
- Hills, G.J.; Jacobs, N.; Lakshminarayanayah, N. Non-isothermal membrane potential. Nature 1957, 179, 96–97. [Google Scholar] [CrossRef]
- Ikeda, T. Thermal membrane potential. J. Chem. Phys. 1958, 28, 166–167. [Google Scholar] [CrossRef]
- Ikeda, T. Erratum: Thermal membrane potential. J. Chem. Phys. 1959, 31, 267–268. [Google Scholar] [CrossRef]
- Lakshminarayanayah, N. Transport phenomena in artificial membranes. Chem. Rev. 1965, 65, 451–465. [Google Scholar] [CrossRef]
- Tasaka, M.; Morita, S.; Nagasawa, M. Membrane potential in nonisothermal systems. J. Phys. Chem. 1965, 69, 451–465. [Google Scholar] [CrossRef]
- Lakshminarayanayah, N. Transport Phenomena in Membranes; Academic Press: New York, NY, USA, 1969. [Google Scholar]
- Lorimer, J.W. Nonisothermal transport in charged gels. In Charged Gels and Membranes, Part II; Sélégny, E., Ed.; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1976. [Google Scholar]
- Tasaka, M.; Nagasawa, K.M. Nonisothermal membrane phenomena through charged membranes. J. Polym. Sci. Polym. Symp. 1975, 49, 31–42. [Google Scholar] [CrossRef]
- Tasaka, M.; Hanaoka, K.; Kurosawa, Y.; Wada, C. Thermal membrane potential through charged membranes in electrolyte solutions. Biophys. Chem. 1975, 3, 331–337. [Google Scholar] [CrossRef]
- Tasaka, M.; Ichijo, N.; Kobayashi, S.; Kobayashi, H. Thermal membrane potential across charged membranes in NaCl-NH4Cl and LiCl-NH4Cl solutions. Biophys. Chem. 1976, 4, 269–274. [Google Scholar] [CrossRef]
- Tasaka, M.; Abe, S.; Sugiura, S.; Nagasawa, M. Thermoosmosis through charged membranes. Biophys. Chem. 1977, 6, 271–278. [Google Scholar] [CrossRef]
- Tasaka, M. Thermal membrane potential across mosaic membranes. J. Membr. Sci. 1978, 4, 51–59. [Google Scholar] [CrossRef]
- Tasaka, M.; Ogawa, K.; Yayazaki, T. Thermal membrane potential across charged membranes in 2-1 and 1-2 electrolyte solutions. Biophys. Chem. 1978, 7, 279–283. [Google Scholar] [CrossRef]
- Tasaka, M.; Futamura, H. The effect of temperature on thermoosmosis. J. Membr. Sci. 1986, 28, 183–190. [Google Scholar] [CrossRef]
- Tasaka, M. Thermal membrane potential and thermoosmosis across charged membranes. Pure Appl. Chem. 1986, 58, 1637–1646. [Google Scholar] [CrossRef]
- Kjelstrup, S.; Ikeshoji, T.; Siverund, K. Heat and internal energy changes at electrodes and junctions in thermocells. J. Electrochem. Soc. 1990, 137, 219–228. [Google Scholar]
- Tasaka, M.; Mizuta, T.; Sekiguchi, O. Mass transfer through polymer membranes due to a temperature gradient. J. Membr. Sci. 1990, 54, 191–204. [Google Scholar] [CrossRef]
- Scibona, G.; Botré, C.; Botré, F.; Fabiani, C. Nafion membrane potential in non-isothermal systems. Electrochim. Acta 1991, 36, 135–138. [Google Scholar] [CrossRef]
- Tasaka, M.; Urata, T.; Kiyono, R.; Aki, Y. Solvent transport across anion-exchange membranes under a temperature difference and an osmotic pressure difference. J. Membr. Sci. 1992, 67, 83–91. [Google Scholar] [CrossRef]
- Tasaka, M.; Hirai, T.; Kiyono, R.; Aki, Y. Solvent transport across cation-exchange membranes under a temperature difference and an osmotic pressure difference. J. Membr. Sci. 1992, 71, 83–91. [Google Scholar] [CrossRef]
- Hanaoka, K.; Kiyono, R.; Tasaka, M. Thermal membrane potential across anion-exchange membranes in KCl and KIO3 solutions and the transported entropy of ions. J. Membr. Sci. 1993, 82, 255–263. [Google Scholar] [CrossRef]
- Kiyono, R. Thermal membrane potential across charged membranes for various halide solutions. Colloid Polym. Sci. 1993, 271, 1183–1190. [Google Scholar] [CrossRef]
- Kiyono, R.; Kuwashita, A.; Tanaka, Y.; Sekiguchi, O.; Tasaka, M. Thermal membrane potential across poly(4-vinylpyridine-co-styrene) membranes. Bull. Soc. Water Sci. Jpn. 1994, 48, 159–164. [Google Scholar]
- Hanaoka, K.; Kiyono, R.; Tasaka, M. Nonisothermal membrane potential across perfluorosulfonic acid-type membranes, Flemion S: Part II. Thermal membrane potential and transported entropy of ions. Colloid Polym. Sci. 1994, 272, 979–985. [Google Scholar] [CrossRef]
- Kjelstrup, S.; Ottøy, M.; Halseid, R.; Strømgård, M. Thermoelectric power relevant for the solid polymer fuel cell. J. Membr. Sci. 1995, 107, 219–228. [Google Scholar]
- Barragán, V.M.; Ruiz-Bauzá, C. Effect of unstirred solution layers on the thermal membrane potential through cation-exchange membranes. J. Membr. Sci. 1997, 125, 219–229. [Google Scholar] [CrossRef]
- Barragán, V.M.; Ruiz-Bauzá, C. On the dependence of the thermal membrane potential across cation-exchange membranes on the mean temperature. J. Membr. Sci. 1997, 134, 75–84. [Google Scholar] [CrossRef]
- Tasaka, M.; Kiyono, R.; Huda, M.S. Membrane phenomena in non-isothermal systems. Part 1: Theory. Bull. Chem. Soc. Jpn. 1997, 70, 555–559. [Google Scholar] [CrossRef]
- Huda, M.S.; Kiyono, R.; Tasaka, M.; Yamaguchi, T.; Sata, T. Membrane phenomena in non-isothermal systems. Part 3: Thermal membrane potential across various hydrophobic anion-exchange membranes with 10 and 14% divinylbenzene. Bull. Chem. Soc. Jpn. 1998, 71, 555–562. [Google Scholar] [CrossRef]
- Huda, M.S.; Kiyono, R.; Tasaka, M.; Yamaguchi, T.; Sata, T. Thermal membrane potential across anion-exchange membranes with different benzyltrialkylammonium groups. Sep. Pur. Technol. 1998, 14, 95–106. [Google Scholar] [CrossRef]
- Katchalsky, A.; Curran, P.F. Nonequilibrium Thermodynamics in Biophysics; Harvard University Press: Cambridge, UK, 1965. [Google Scholar]
- Førland, K.S.; Førland, T.; Kjelstrup Ratkje, S. Irreversible Thermodynamics: Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 1988. [Google Scholar]
- Kjelstrup, S.; Bedeaux, D. Non-Equilibrium Thermodynamics of Heterogeneous Systems; World Scientific Publishing Co.: Singapore, 2008. [Google Scholar]
- Kjelstrup, S.; Bedeaux, D. Electrochemical Energy Conversion. In Experimental Thermodynamics Volume X: Non-Equilibrium Thermodynamics with Applications; Kjelstrup, S., Bedeaux, D., Sengers, J., Eds.; Royal Society of Chemistry: Cambridge, UK, 2016. [Google Scholar]
- Kjelstrup, S.; Bedeaux, D. Thermodynamics of Electrochemical Systems. In Springer Handbook of Electrochemical Energy; Breitkopf, C., Swider-Lyons, K., Eds.; Springer: New York, NY, USA, 2017; pp. 69–91. [Google Scholar]
- Haase, R. Thermodynamics of Irreversible Processes; Addison-Wesley: Reading, PA, USA, 1963. [Google Scholar]
- Goupil, C.; Seifert, W.; Zabrocki, K.; Müller, E.; Snyder, G.J. Thermodynamics of thermoelectric phenomena and applications. Entropy 2011, 13, 1481–1517. [Google Scholar] [CrossRef]
- Zlotorowicz, A.; Strand, R.V.; Burheim, O.S.; Wilhelmsen, Ø.; Kjelstrup, S. The permselectivity and water transference number of ion exchange membranes in reverse electrodialysis. J. Membr. Sci. 2017, 523, 402–408. [Google Scholar] [CrossRef]
- Ikeda, T.; Tsuchiya, M.; Nakano, M. The thermal membrane potential as a function of the apparent ionic transport number of membranes. Bull. Chem. Soc. Jpn. 1964, 37, 1482–1485. [Google Scholar] [CrossRef]
- Børset, M.T.; Kang, X.; Burheim, O.S.; Haarberg, G.M.; Xu, Q.; Kjelstrup, S. Seebeck coefficients of cell with lithium carbonate and gas electrodes. Electrochim. Acta 2015, 182, 699–706. [Google Scholar] [CrossRef]
- Kristiansen, K.; Barragán, V.M.; Kjelstrup, S. Non-isothermal saline power plant: Concept proposal for low-temperature waste heat recovery. 2018; submitted. [Google Scholar]
- Sales, B.B.; Saakes, M.; Post, J.W.; Buisman, C.J.N.; Biesheuvel, P.M.; Hamelers, H.V.M. Direct power production from a water salinity difference in a membrane-modified supercapacitor flow cell. Environ. Sci. Technol. Lett. 2010, 44, 5661–5665. [Google Scholar] [CrossRef] [PubMed]
- Hu, R.; Cola, B.A.; Haram, N.; Barisci, J.N.; Lee, S.; Stoughton, S.; Wallace, G.; Too, C.; Thomas, M.; Gestos, A.; et al. Harvesting waste thermal energy using a carbon-nanotube-based thermo-electrochemical cell. Nano Lett. 2010, 10, 838–846. [Google Scholar] [CrossRef] [PubMed]
- Abraham, T.J.; MacFarlane, D.R.; Pringle, J.M. Seebeck coefficients in ionic liquids—Prospects for thermo-electrochemical cells. Chem. Commun. 2011, 47, 6260–6262. [Google Scholar] [CrossRef] [PubMed]
- Ikeshoji, T.; Ratkje, S.K. Thermoelectric power of a cell with complex formation. J. Electrochem. Soc. 1986, 133, 1107–1113. [Google Scholar] [CrossRef]
- Volkov, A.G.; Paula, S.; Deamer, D.W. Two mechanisms of permeation of small neutral molecules and hydrated ions across phospholipid bilayers. Bioelectrochem. Bioenerget. 1997, 42, 153–160. [Google Scholar] [CrossRef]
- Leinov, E.; Vinogradow, J.; Jackson, M.D. Salinity dependence of the thermoelectric coupling coefficient in brine-saturated sandstones. Geophys. Res. Lett. 2010, 37, L23308. [Google Scholar] [CrossRef]
- Härtel, A.; Janssen, M.; Weingarth, D.; Presser, V.; van Roij, R. Heat-to-current conversion of low-grade heat from a thermocapacitive cycle by supercapacitors. Electrochim. Acta 2015, 8, 2396–2401. [Google Scholar] [CrossRef]
- Culebras, M.; Gómez, C.M.; Cantanero, A. Review on polymers for thermoelectric applications. Materials 2014, 182, 6701–6732. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Liu, L.; Lim, H.; Quao, Y.; Chen, X. Harvesting energy from low-grade heat based on nanofluids. Nano Energy 2012, 1, 805–811. [Google Scholar] [CrossRef]
- Kandhasamy, S.; Solheim, A.; Kjelstrup, S.; Haarberg, G. Electrolyte melt composition for low temperature molten carbonate thermocell. ACS Appl. Energy Mater. 2018, in press. [Google Scholar] [CrossRef]
- Ioffe, A.F. Semiconductor Thermoelements and Thermoelectric Cooling; Infosearch: London, UK, 1957. [Google Scholar]
- Kjelstrup, S.; Bedeaux, D.; Johannessen, E.; Gross, J. Non-Equilibrium Thermodynamics for Engineers, 2nd ed.; World Scientific Publishing Co.: Singapore, 2017. [Google Scholar]
- Dlugolecki, P.; Ogonowski, P.; Metz, S.J.; Saakes, M.; Nijmeijer, K.; Weeling, M. On the resistances of membrane, diffusion boundary layer and double layer in ion exchange membrane transport. J. Membr. Sci. 2010, 349, 369–379. [Google Scholar] [CrossRef]
- Catalano, J.; Bentien, A. Influence of temperature on the electrokinetic properties and power generation efficiency of Nafion 117 membranes. J. Power Sources 2014, 262, 192–200. [Google Scholar] [CrossRef]
- Fontananova, E.; Messana, D.; Tufa, R.A.; Nicotera, I.; Kosma, V.; Curcio, E.; van Baak, W.; Drioli, E.; Profio, G.D. Effect of solution concentration and composition on the electrochemical properties of ion exchange membranes for energy conversion. J. Power Sources 2017, 340, 282–293. [Google Scholar] [CrossRef]
- Zhang, B.; Hong, J.G.; Xie, S.; Xia, S.; Chen, Y. An integrative modeling and experimental study of the ionic resistance of ion-exchange membranes. J. Membr. Sci. 2017, 524, 362–369. [Google Scholar] [CrossRef]
- Zhu, S.; Kingsbury, R.S.; Call, D.F.; Coronell, O. Impact of solution composition on the resisance of ion exchange membranes. J. Membr. Sci. 2018, 554, 39–47. [Google Scholar] [CrossRef]
- Burheim, O.; Vie, P.J.S.; Pharoah, J.G.; Kjestrup, S. Ex situ measurements of through-plane thermal conductivities in a polymer electroyte fuel cell. J. Power Sources 2010, 195, 249–256. [Google Scholar] [CrossRef]
- Khandelwal, M.; Mench, M.M. Direct measurement of through-plane thermal conductivity and contact resistance in fuel cell materials. J. Power Sources 2006, 161, 1106–1115. [Google Scholar] [CrossRef]
- Alhazmi, N.; Ingham, D.B.; Ismail, M.S.; Hughes, K.; Ma, L.; Pourkashanian, M. The throungh-plane thermal conductivity and the contact resistance of the components of the membrane electrode assembly and gas diffusion layer in proton exchange membrane fuel cells. J. Power Sources 2016, 270, 59–67. [Google Scholar] [CrossRef]
- Ramousse, J.; Lottin, O.; Didierjean, S.; Maillet, D. Heat sources in proton exchange membrane (PEM) fuel cells. J. Power Sources 2009, 192, 435–441. [Google Scholar] [CrossRef]
- Weber, A.Z.; Newman, J. Coupled thermal and water management in polymer electrolyte fuel cells. J. Electrochem. Soc. 2006, 153, A2205–A2214. [Google Scholar] [CrossRef]
- Barragán, V.M.; Kjelstrup, S. Thermo-osmosis in membrane systems: A review. J. Non-Equilib. Thermodyn. 2017, 42, 117–236. [Google Scholar] [CrossRef]
- Elsheikh, M.H.; Shnawah, D.A.; Sabri, M.F.M.; Said, S.B.M.; Hassan, M.; Bashir, M.B.A. A review on thermoelectric renewable energy: Principle parameters that affect their performance. Renew. Sustain Energy Rev. 2014, 30, 337–355. [Google Scholar] [CrossRef]

| Increasing Parameter | Trend | Section | Conclusion, cf. Bullet Point No |
|---|---|---|---|
| Electrolyte concentration | decreasing, logarithmic dependence | 5.2.2 | 1, 2 |
| Counter-ion un-hydrated radius | increasing | 5.2.2 | 7 |
| Membrane hydrophobicity | decreasing | 5.2.3 | 6 |
| Mean temperature | possible optimum | 5.2.4 | 3 |
| Pressure difference | linear increase | 5.2.1 | 8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barragán, V.M.; Kristiansen, K.R.; Kjelstrup, S. Perspectives on Thermoelectric Energy Conversion in Ion-Exchange Membranes. Entropy 2018, 20, 905. https://doi.org/10.3390/e20120905
Barragán VM, Kristiansen KR, Kjelstrup S. Perspectives on Thermoelectric Energy Conversion in Ion-Exchange Membranes. Entropy. 2018; 20(12):905. https://doi.org/10.3390/e20120905
Chicago/Turabian StyleBarragán, V. María, Kim R. Kristiansen, and Signe Kjelstrup. 2018. "Perspectives on Thermoelectric Energy Conversion in Ion-Exchange Membranes" Entropy 20, no. 12: 905. https://doi.org/10.3390/e20120905
APA StyleBarragán, V. M., Kristiansen, K. R., & Kjelstrup, S. (2018). Perspectives on Thermoelectric Energy Conversion in Ion-Exchange Membranes. Entropy, 20(12), 905. https://doi.org/10.3390/e20120905






