A Novel Image Encryption Scheme Based on Collatz Conjecture
Abstract
1. Introduction
- The permutation and diffusion processes are replaced by an encoding block which uses a non-fixed length mapping.
- The encoding process is accomplished by following the Collatz conjecture.
- The encrypted content corresponds to a speech signal instead of a ciphered image.
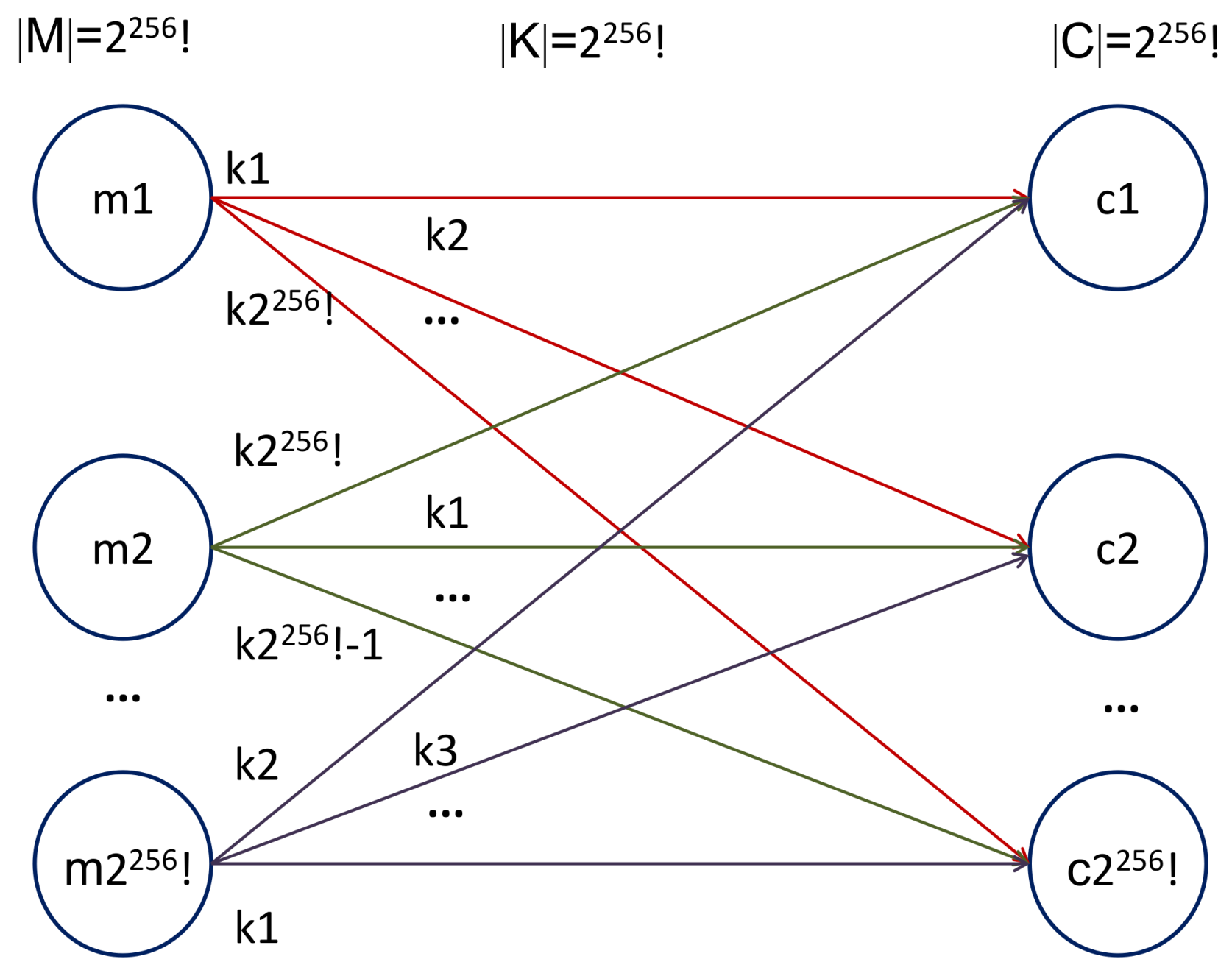
- Security of the scheme relies only on the key, with a size of the key space equal to .
- The process is completely reversible and highly sensitive to the key.
2. Background of Concepts
2.1. Collatz Conjecture
2.2. Correlation Coefficient
2.3. Entropy
2.4. Disorder Scrambling (DS)
2.5. Structural Similarity Index (SSIM)
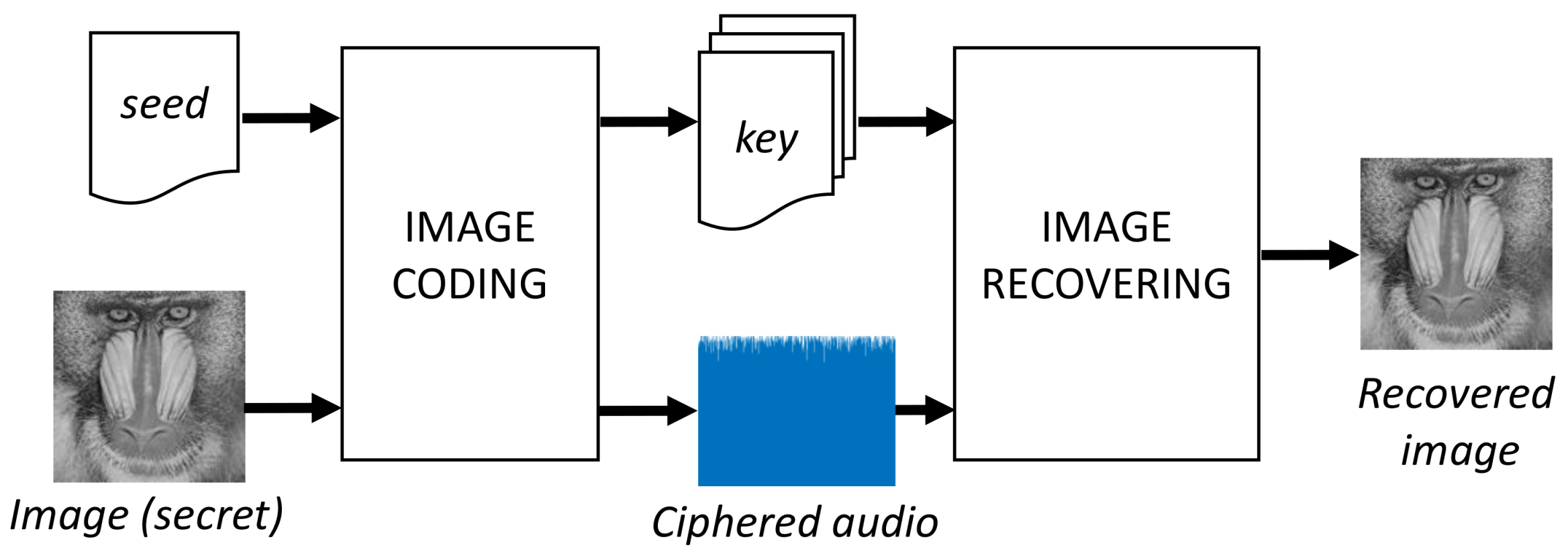
3. The Proposed Scheme
3.1. Image Coding
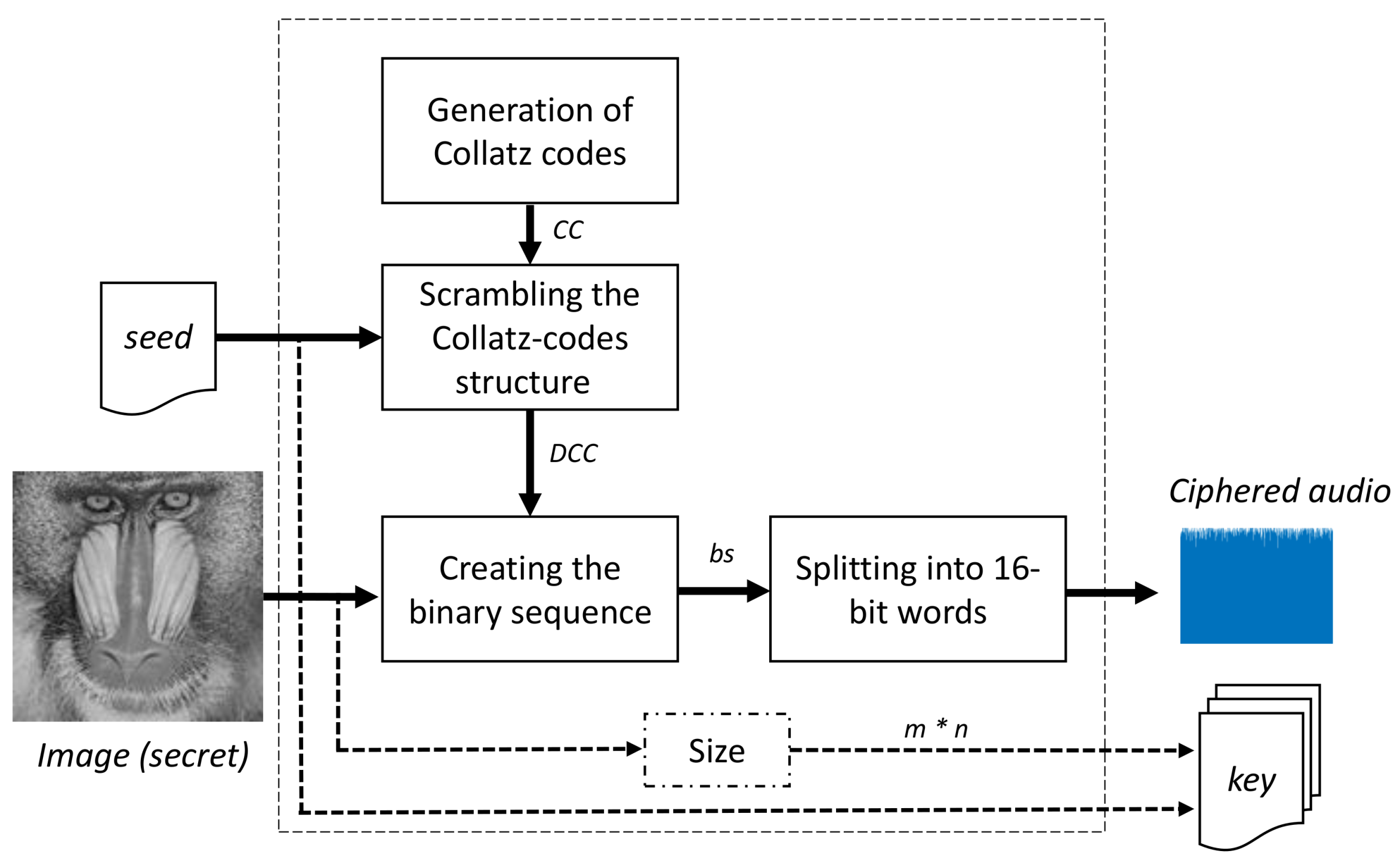
- Generation of Collatz codesAccording to the Collatz conjecture explained in Section 2, we have proposed a new method for data encoding with variable output length as follows:
- -
- First iteration: if input data x is even, x is divided by two; a value of 0 is put in the LSB place. Otherwise, the operation is carried out; a value of 1 is put in the LSB place. If the result of the mathematical operation, , is 1, the iteration process stops.
- -
- Second iteration: if is even, the operation is applied; a value of 0 is located in the position before LSB. Otherwise, the operation is carried out; a value of 1 is put before the LSB place. If the result of the mathematical operation, , is 1, the iteration process stops.
- -
- The above procedure is performed until the value of 1 is reached. Its corresponding code is 0. Then, the iteration process stops.
- -
- In the last step, a header “11” is put at the beginning of the binary code. Therefore, the Collatz code length is equal to the number of iterations needed to reach the value of 1, plus the length of the header. Figure 3 illustrates an example.
According to Figure 3, a 10-bit Collatz code is obtained for . For the case , only three iterations are required to reduce the value to 1, and its Collatz code length is then 5. On the other hand, for , the number of iterations required is 6. Then, its Collatz code length is 8. It is clear that the Collatz code does not follow a “specific rule” in terms of its length, which means larger numbers can require a higher or lower number of iterations.Consequently, our proposed encoding method for image encryption has the following characteristics:- The above coding method works for positive integer numbers.
- Since gray-scale images have their pixels in the range of 0 to 255, the value of the pixel is increased by 1 before applying the iterative process. This means our collection Collatz codes are in the range instead of .
- The length of the Collatz code is not a fixed value. There is not a specific rule in terms of its length.
- Every code begins with the header “11” because this sequence is not viable with the proposed iteration process. Therefore, if a number is odd, the following number is always even, and the code corresponding to the sequence odd – odd (i.e., “11”) thus does not exist.
At the output of this block, a cell array of 256 cells and variable number of elements in each cell is obtained. The first cell has the Collatz code of the number 1, the second cell has the Collatz code of the number 2, the last cell has the Collatz code of the number 256, and so on. - Scrambling the Collatz-code structureThe aim of this block is to provide a level of security of the encoding method, because if a non-authorized user knows the method, the image content can be revealed. Then, the cell array obtained in the above block is scrambled according to a seed. A new sequence is obtained, and every row of the structure is then located in a new position. Since the total number of sequences is , our system can work with a huge number of available scrambled matrices.The output of this block, , is a cell array with similar characteristics to the one obtained in the last block. However, in this case, the first cell does not contain the Collatz code of the number 1. With a new seed, the corresponding code to a specific row changes every time.
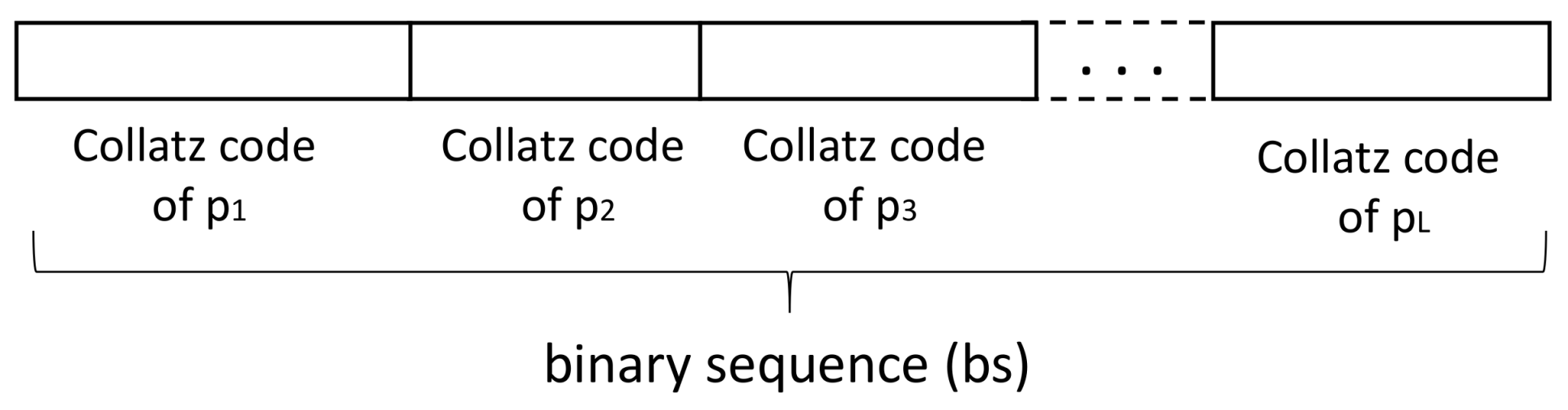
- Creating the binary sequenceOnce the scrambled structure, , is obtained, the next step consists in creating the binary sequence. This block is performed with the following steps:
- -
- The input image pixels sweep from left to right and top to bottom. The output of this step is a 1D sequence of L elements (with , m is the number of rows, and n the number of columns of the image).
- -
- The first value, , of the 1D sequence is selected. Its Collatz code corresponds to the row of the scrambled structure. For example, if is equal to zero, its Collatz code is the first row of . This code is located at the beginning of the binary sequence, .
- -
- The second value, , of the 1D sequence is selected. Its Collatz code corresponds to the row of the scrambled structure. Its code is located at the end of the binary sequence, .
- -
- The above procedure is repeated for the L elements of the 1D sequence (Figure 4).
- Splitting into words of n bitsOne important characteristic of our proposal is that the output of this module is an audio instead of a ciphered image. One of the reasons to change the format of the content is that the number of bits of the image differs from the number of bits of the encoded sequence. In addition, the relationship between secret and ciphered content is very low.Therefore, in this block, a task related to splitting the binary sequence into w blocks of 16 bits each is performed. In the case that the last block contains less than 16 bits, the rest of the sequence is set to zero. Later, every block of 16 bits is transformed to a floating point value in the range of to 1. Finally, data are saved in a wav file.
3.2. Image Recovering
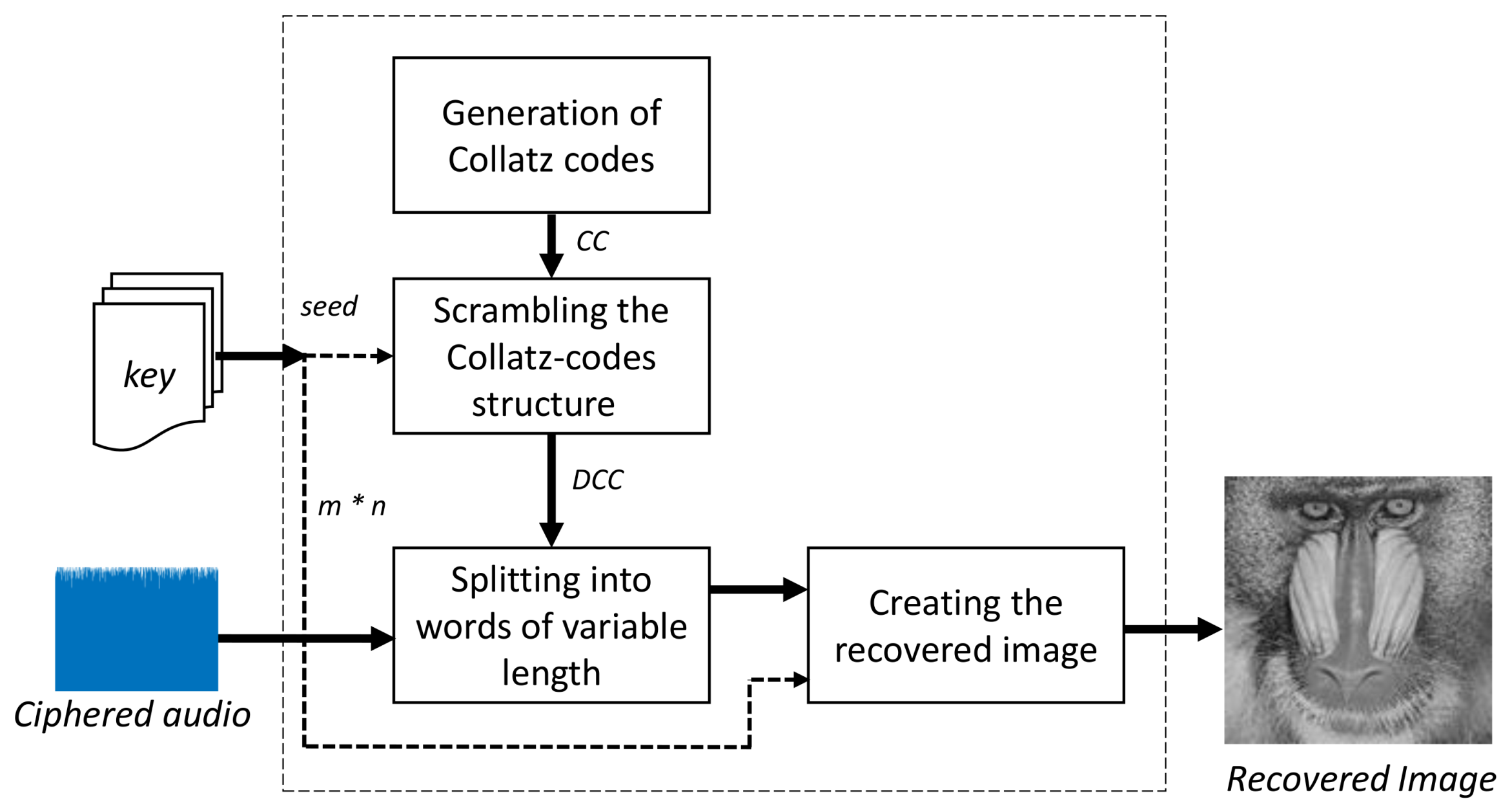
- Generation of Collatz codesThis block works equally with the corresponding image coding module. Its aim is to obtain a structure of Collatz codes for the numbers 1 to 256.
- Disordering up the Collatz codesIn a similar way to its counterpart of the image coding module, in this block, the above structure gets disordered in terms of its rows, according to the input seed.
- Splitting into words of variable lengthThe input of this block is the ciphered audio. The first step consists in transforming the floating-point value of every sample into a binary code of 16 bits. Secondly, all codes are put together into a binary sequence of length Z, where Z is the result of multiplying the total number of samples by 16. Next, each header “11” is located in the above binary sequence. Finally, the binary sequence is split into frames (i.e., Collatz codes) taking into account the position of each header. The number of obtained codes is equal to the number of pixels of the secret image.
- Creating the recovered imageIn the last block of this module, every Collatz code is transformed to a decimal value in the range 0 to 255. The first code obtained with the above block is searched into the scrambled structure. Once a match is found, the position of the code minus one corresponds to the decimal value of the pixel. For example, suppose a code “110000101” is found in the first row of the structure. The value of this corresponding pixel is then zero. This procedure is carried out for every Collatz code. Once the decimal value of all pixels has been obtained, the last step consists in rearranging the pixels from left to right and top to bottom. The number of rows and columns of the image is included in the key, together with the value of the seed. The output of this block is the recovered gray-scale image.
4. Simulation Results
5. Security Analysis
5.1. Security Key Analysis
5.1.1. Size of the Key Space
5.1.2. Key Sensitivity Analysis
5.2. Sensitivity to the Changes of Plain Image
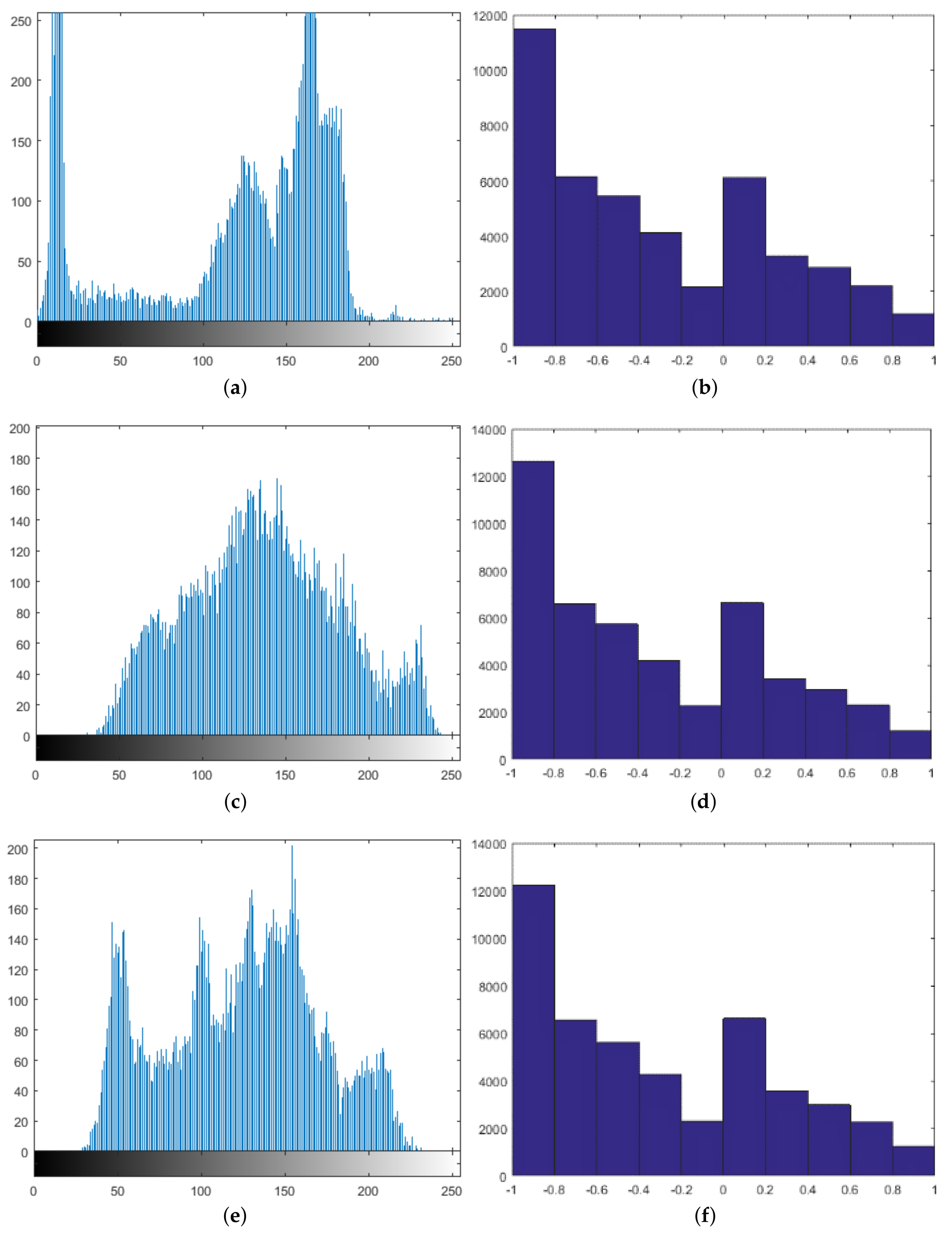
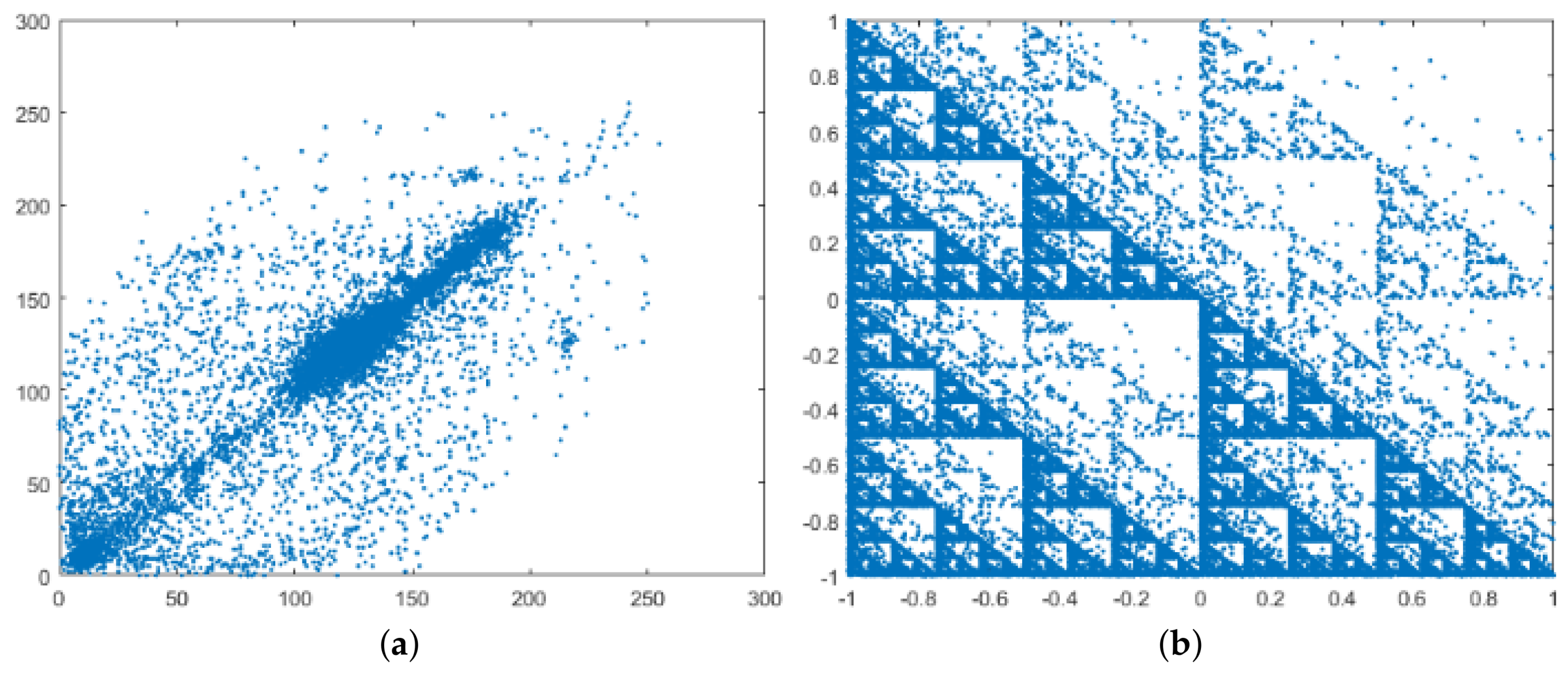
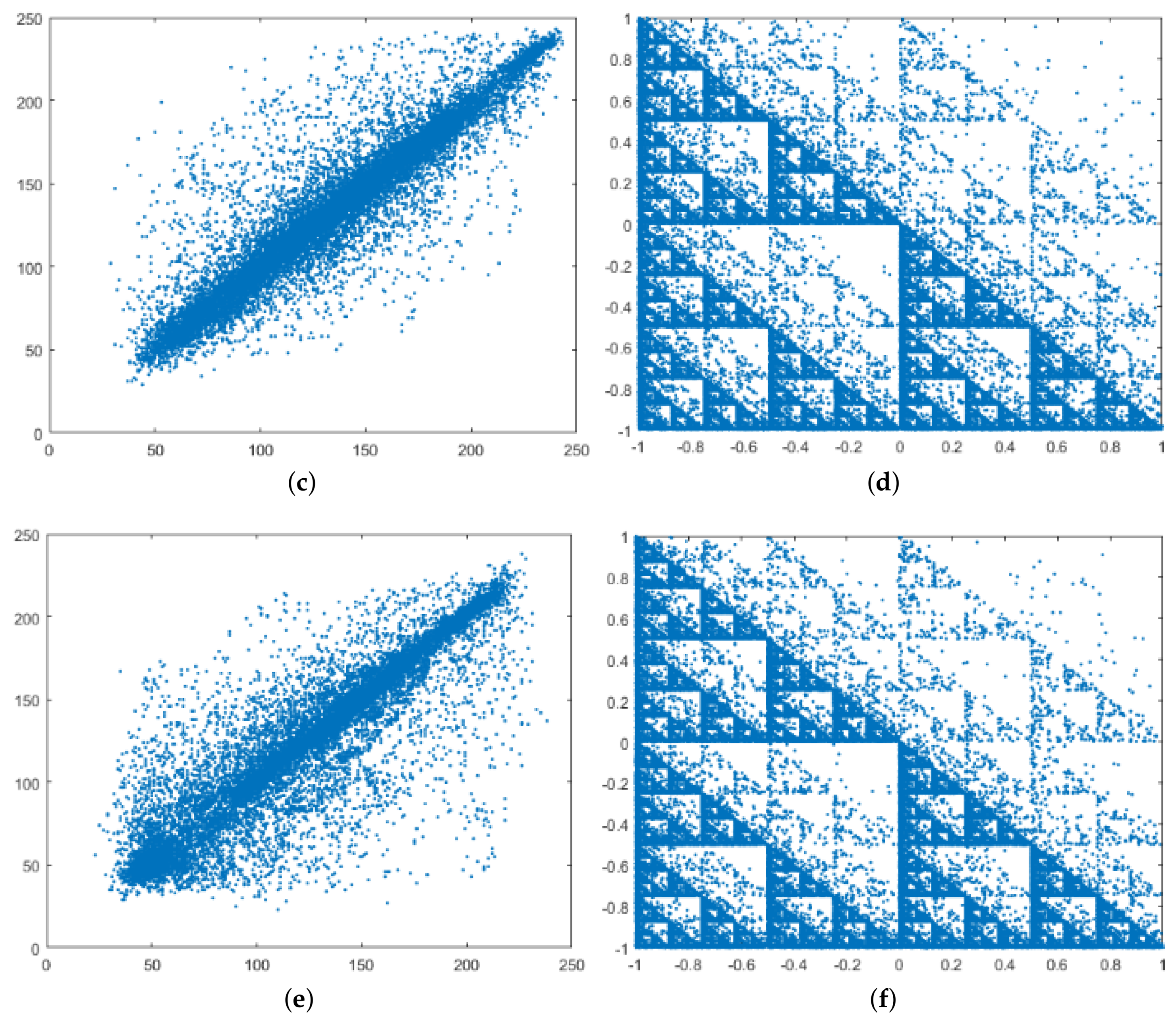
5.3. Data Correlation Analysis
5.4. Uncertainty and Disorder Analysis
6. Comparison with State-of-the Art Methods
7. Conclusion
- Identify weaknesses of our proposal in terms of the probability of the available space (theoretical it is equally likely) and what can affect the robustness against brute force attack and differential attack. This is related to the way to randomize the Collatz codes. For that purpose, three pairs of original images and encrypted data are available at https://data.mendeley.com/datasets/y8kn5mx4d2/draft?a=384e6a23-062e-401b-bdcd-621be1f952da.
- Apply bit scrambling to the binary sequence, , of Figure 2 with the purpose of increasing the entropy of the encrypted data.
- Explore other choices of image coding based on the Collatz conjecture. For example, applying the Collatz code not for the pixel value but for the pixel position. Analyze the performance of the system in terms of security.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Faragallah, O.S.; El-Samie, F.E.A.; Ahmed, H.E.H.; Elashry, I.F.; Shahieen, M.H.; El-Rabaie, E.S.M.; Alshebeili, S.A. Image Encryption: A Communication Perspective; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Pareek, N.K.; Patidar, V.; Sud, K.K. Diffusion–substitution based gray image encryption scheme. Digit. Signal Process. 2013, 23, 894–901. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X. Multiple-image encryption algorithm based on mixed image element and permutation. Opt. Lasers Eng. 2017, 92, 6–16. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, X.; Yu, H.; Zhao, C.; Zhu, Z. A Novel Image Encryption Scheme Using the Composite Discrete Chaotic System. Entropy 2016, 18, 276. [Google Scholar] [CrossRef]
- Silva-García, V.; Flores-Carapia, R.; Rentería-Márquez, C.; Luna-Benoso, B.; Aldape-Pérez, M. Substitution box generation using Chaos: An image encryption application. Appl. Math. Comput. 2018, 332, 123–135. [Google Scholar] [CrossRef]
- Wang, X.Y.; Zhang, Y.Q.; Bao, X.M. A Colour Image Encryption Scheme Using Permutation-Substitution Based on Chaos. Entropy 2015, 17, 3877–3897. [Google Scholar] [CrossRef]
- Ye, G. Image scrambling encryption algorithm of pixel bit based on chaos map. Pattern Recognit. Lett. 2010, 31, 347–354. [Google Scholar] [CrossRef]
- Huang, X. Image encryption algorithm using chaotic Chebyshev generator. Nonlinear Dynam. 2011, 67, 2411–2417. [Google Scholar] [CrossRef]
- Wang, X.; Teng, L.; Qin, X. A novel colour image encryption algorithm based on chaos. Signal Process. 2012, 92, 1101–1108. [Google Scholar] [CrossRef]
- Zhou, Y.; Bao, L.; Chen, C.P. A new 1D chaotic system for image encryption. Signal Process. 2014, 97, 172–182. [Google Scholar] [CrossRef]
- Ye, G.; Huang, X. An Image Encryption Algorithm Based on Autoblocking and Electrocardiography. IEEE MultiMedia 2016, 23, 64–71. [Google Scholar] [CrossRef]
- Pak, C.; Huang, L. A new color image encryption using combination of the 1D chaotic map. Signal Process. 2017, 138, 129–137. [Google Scholar] [CrossRef]
- Tu, G.; Liao, X.; Xiang, T. Cryptanalysis of a color image encryption algorithm based on chaos. Optik 2013, 124, 5411–5415. [Google Scholar] [CrossRef]
- Wang, X.; Luan, D.; Bao, X. Cryptanalysis of an image encryption algorithm using Chebyshev generator. Digit. Signal Process. 2014, 25, 244–247. [Google Scholar] [CrossRef]
- Dhall, S.; Pal, S.K.; Sharma, K. Cryptanalysis of image encryption scheme based on a new 1D chaotic system. Signal Process. 2018, 146, 22–32. [Google Scholar] [CrossRef]
- Wang, H.; Xiao, D.; Chen, X.; Huang, H. Cryptanalysis and enhancements of image encryption using combination of the 1D chaotic map. Signal Process. 2018, 144, 444–452. [Google Scholar] [CrossRef]
- Li, C.; Lin, D.; Lu, J. Cryptanalyzing an Image-Scrambling Encryption Algorithm of Pixel Bits. IEEE MultiMedia 2017, 24, 64–71. [Google Scholar] [CrossRef]
- Li, C.; Lin, D.; Lu, J.; Hao, F. Cryptanalyzing an image encryption algorithm based on autoblocking and electrocardiography. IEEE MultiMedia 2018. [Google Scholar] [CrossRef]
- Xie, E.Y.; Li, C.; Yu, S.; Lu, J. On the cryptanalysis of Fridrich’s chaotic image encryption scheme. Signal Process. 2017, 132, 150–154. [Google Scholar] [CrossRef]
- Chai, X.; Chen, Y.; Broyde, L. A novel chaos-based image encryption algorithm using DNA sequence operations. Opt. Lasers Eng. 2017, 88, 197–213. [Google Scholar] [CrossRef]
- Jain, A.; Rajpal, N. A robust image encryption algorithm resistant to attacks using DNA and chaotic logistic maps. Multimed. Tools Appl. 2015, 75, 5455–5472. [Google Scholar] [CrossRef]
- Dou, Y.; Liu, X.; Fan, H.; Li, M. Cryptanalysis of a DNA and chaos based image encryption algorithm. Optik 2017, 145, 456–464. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, Y.; Zhou, Q.; Lin, Z. Image encryption using partitioned cellular automata. Neurocomputing 2018, 275, 1318–1332. [Google Scholar] [CrossRef]
- Xiong, Y.; Quan, C.; Tay, C. Multiple image encryption scheme based on pixel exchange operation and vector decomposition. Multimed. Tools Appl. 2018, 101, 113–121. [Google Scholar] [CrossRef]
- Ping, P.; Xu, F.; Mao, Y.; Wang, Z. Designing permutation–substitution image encryption networks with Henon map. Neurocomputing 2018, 283, 53–63. [Google Scholar] [CrossRef]
- Bendegem, J.P.V. The Collatz conjecture. A case study in mathematical problem solving. Log. Log. Philos. 2005, 14. [Google Scholar] [CrossRef]
- Bruckman, P.S. A proof of the Collatz conjecture. Int. J. Math. Educ. Sci. Technol. 2008, 39, 403–407. [Google Scholar] [CrossRef]
- Ballesteros, D.M.; Sandoval, A.; Renza, D. Evolutionary algorithm for speech scrambling based on asexual reproduction. J. Inf. Hiding Multimed. Signal Process. 2018, 9, 796–806. [Google Scholar]
- Renza, D.; Lemus, C.; Ballesteros, D.M. Audio authenticity and tampering detection based on information hiding and collatz p-bit code. J. Inf. Hiding Multimed. Signal Process. 2017, 8, 1294–1304. [Google Scholar]
- Robinson, D. Entropy and Uncertainty. Entropy 2008, 10, 493–506. [Google Scholar] [CrossRef]
- Madain, A.; Dalhoum, A.L.A.; Hiary, H.; Ortega, A.; Alfonseca, M. Audio scrambling technique based on cellular automata. Multimed. Tools Appl. 2012, 71, 1803–1822. [Google Scholar] [CrossRef]
- Ballesteros, D.M.; Renza, D.; Camacho, S. An unconditionally secure speech scrambling scheme based on an imitation process to a gaussian noise signal. J. Inf. Hiding Multimed. Signal Process. 2016, 7, 233–242. [Google Scholar]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Lan, R.; He, J.; Wang, S.; Gu, T.; Luo, X. Integrated chaotic systems for image encryption. Signal Process. 2018, 147, 133–145. [Google Scholar] [CrossRef]
- Hua, Z.; Jin, F.; Xu, B.; Huang, H. 2D Logistic-Sine-coupling map for image encryption. Signal Process. 2018, 149, 148–161. [Google Scholar] [CrossRef]
- Song, C.; Qiao, Y. A Novel Image Encryption Algorithm Based on DNA Encoding and Spatiotemporal Chaos. Entropy 2015, 17, 6954–6968. [Google Scholar] [CrossRef]
- Karawia, A. Encryption Algorithm of Multiple-Image Using Mixed Image Elements and Two Dimensional Chaotic Economic Map. Entropy 2018, 20, 801. [Google Scholar] [CrossRef]
- Fu, X.Q.; Liu, B.C.; Xie, Y.Y.; Li, W.; Liu, Y. Image Encryption-Then-Transmission Using DNA Encryption Algorithm and The Double Chaos. IEEE Photonics J. 2018, 10, 1–15. [Google Scholar] [CrossRef]



| Ref. | Method | Size of the Key Space | Key Sensitivity | Relative Entropy | UACI |
|---|---|---|---|---|---|
| [34] | Chaotic maps | Very high | 99.8% | 0.5 (binary images) 0.33 (gray-scale image) | |
| [35] | Chaotic maps | Very high | 99.7% | 0.33 | |
| [36] | DNA encoding + chaos | Very high | 99.8% | 0.33 | |
| [37] | Chaotic maps | Very high | 99.8% | 0.33 | |
| [38] | DNA encoding + chaos | Very high | 99.9% | 0.33 | |
| ours | Collatz encoding | Very high | 87.5% | 0.44 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ballesteros, D.M.; Peña, J.; Renza, D. A Novel Image Encryption Scheme Based on Collatz Conjecture. Entropy 2018, 20, 901. https://doi.org/10.3390/e20120901
Ballesteros DM, Peña J, Renza D. A Novel Image Encryption Scheme Based on Collatz Conjecture. Entropy. 2018; 20(12):901. https://doi.org/10.3390/e20120901
Chicago/Turabian StyleBallesteros, Dora M., Jimmy Peña, and Diego Renza. 2018. "A Novel Image Encryption Scheme Based on Collatz Conjecture" Entropy 20, no. 12: 901. https://doi.org/10.3390/e20120901
APA StyleBallesteros, D. M., Peña, J., & Renza, D. (2018). A Novel Image Encryption Scheme Based on Collatz Conjecture. Entropy, 20(12), 901. https://doi.org/10.3390/e20120901





