Nonlocal Means Two Dimensional Histogram-Based Image Segmentation via Minimizing Relative Entropy
Abstract
1. Introduction
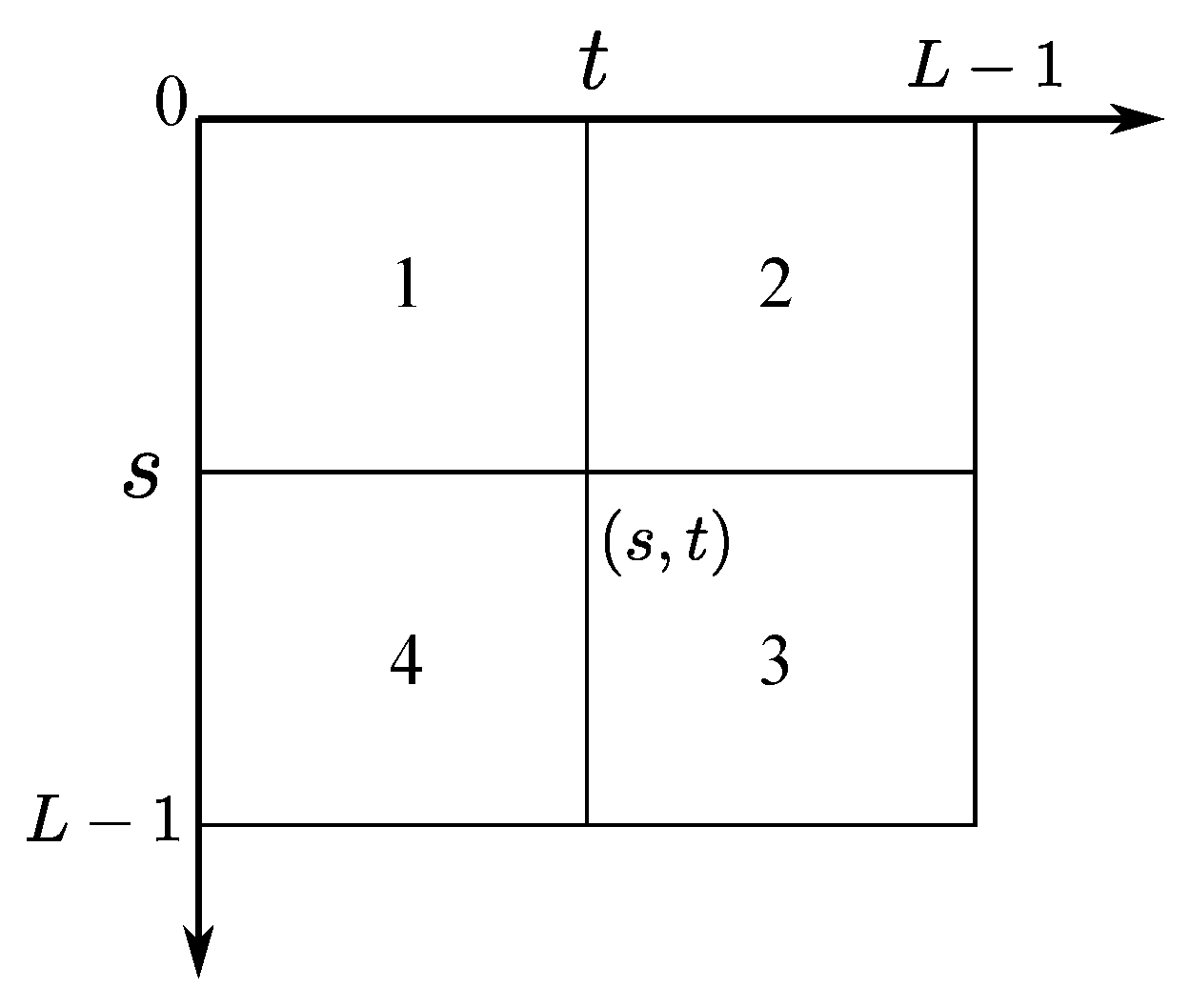
2. Non-Local Mean Two Dimensional Histogram (NLMTDH)
2.1. Non-Local Mean Filter
2.2. Construction of NLMTDH
3. Image Thresholding Based on NLMTDH Using Relative Entropy
3.1. Relative Entropy
3.2. Threshold Selection Based on NLMTDH Using Relative Entropy
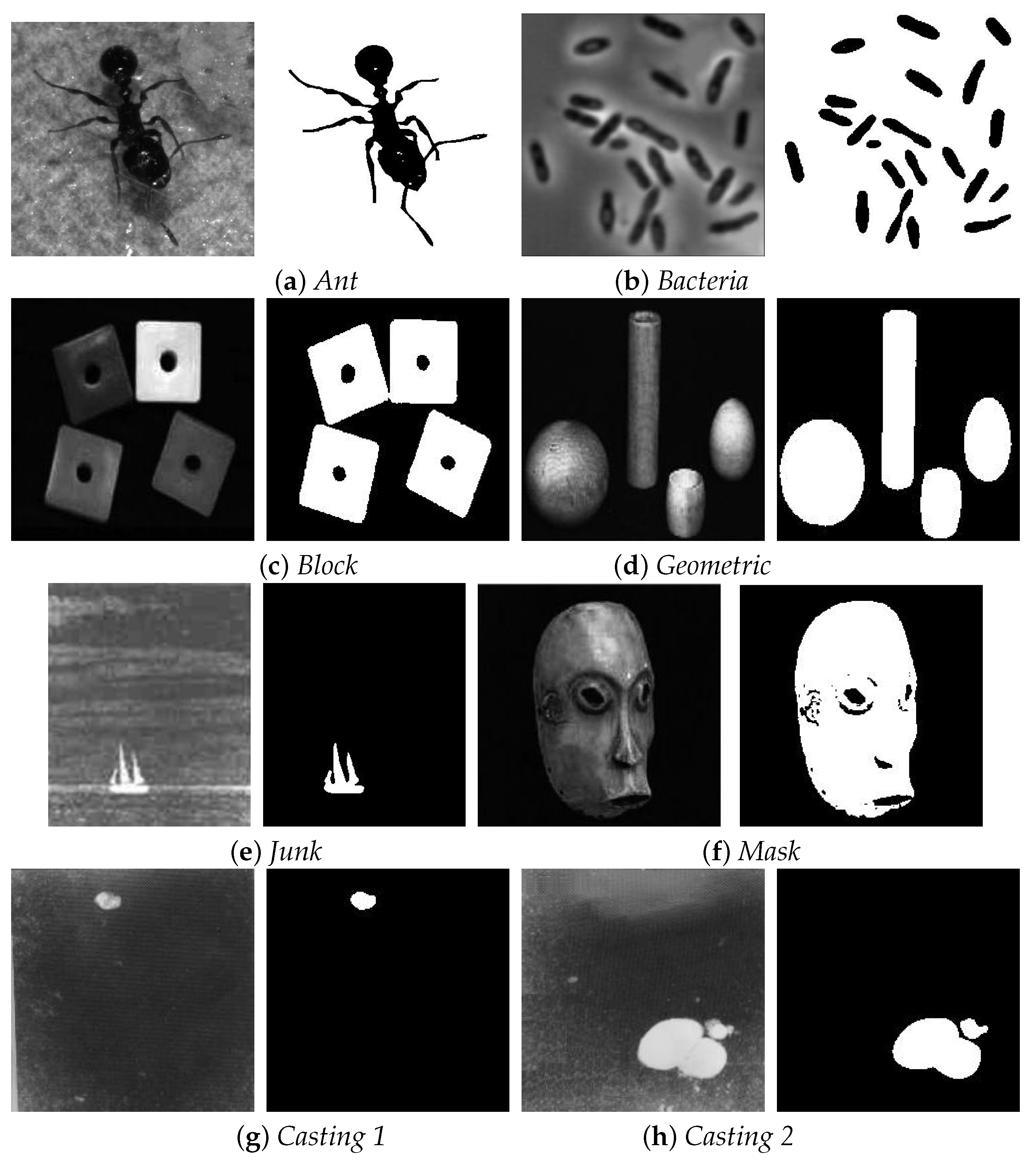
4. Experimental Results and Discussion
4.1. Results
4.2. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of Equation (10)
References
- Cao, F.; Cai, M.; Chu, J.; Zhao, J.; Zhou, Z. A novel segmentation algorithm for nucleus in white blood cells based on low-rank representation. Neural Comput. Appl. 2017, 28, 503–511. [Google Scholar] [CrossRef]
- Gao, G. A parzen-window-kernel-based CFAR algorithm for ship detection in SAR Images. IEEE Geosci. Remote Sens. Lett. 2011, 8, 557–561. [Google Scholar] [CrossRef]
- Malarvel, M.; Sethumadhavan, G.; Bhagi, P.C.R.; Kar, S.; Thangavel, S. An improved version of Otsu’s method for segmentation of weld defects on X-radiography images. Opt. Int. J. Light Electron Opt. 2017, 109, 109–118. [Google Scholar] [CrossRef]
- Yuan, X.C.; Wu, L.S.; Peng, Q. An improved Otsu method using the weighted object variance for defect detection. Appl. Surf. Sci. 2015, 349, 472–484. [Google Scholar] [CrossRef]
- Stutz, D.; Hermans, A.; Leibe, B. Superpixels: An Evaluation of the State-of-the-Art. Comput. Vis. Image Underst. 2017, 166, 1–27. [Google Scholar] [CrossRef]
- Levinshtein, A.; Stere, A.; Kutulakos, K.N.; Fleet, D.J.; Dickinson, S.J.; Siddiqi, K. TurboPixels: Fast superpixels using geometric flows. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 2290–2297. [Google Scholar] [CrossRef] [PubMed]
- Ciecholewski, M. River channel segmentation in polarimetric SAR images: Watershed transform combined with average contrast maximisation. Expert Syst. Appl. 2017, 82, 196–215. [Google Scholar] [CrossRef]
- Cousty, J.; Bertrand, G.; Najman, L.; Couprie, M. Watershed cuts: Thinnings, shortest path forests, and topological watersheds. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 925–939. [Google Scholar] [CrossRef] [PubMed]
- Ding, K.; Xiao, L.; Weng, G. Active contours driven by region-scalable fitting and optimized Laplacian of Gaussian energy for image segmentation. Signal Process. 2017, 134, 224–233. [Google Scholar] [CrossRef]
- Balla-Arabé, S.; Gao, X. Geometric active curve for selective entropy optimization. Neurocomputing 2014, 139, 65–76. [Google Scholar] [CrossRef]
- Qureshi, M.N.; Ahamad, M.V. An improved method for image segmentation using K-means clustering with neutrosophic logic. Procedia Comput. Sci. 2018, 132, 534–540. [Google Scholar] [CrossRef]
- Parida, P.; Bhoi, N. Fuzzy clustering based transition region extraction for image segmentation. Eng. Sci. Technol. Int. J. 2018, 21, 547–563. [Google Scholar] [CrossRef]
- Zhao, X.; Wu, Y.; Song, G.; Li, Z.; Zhang, Y.; Fan, Y. A deep learning model integrating FCNNs and CRFs for brain tumor segmentation. Med. Image Anal. 2018, 43, 98–111. [Google Scholar] [CrossRef] [PubMed]
- Milletari, F.; Ahmadi, S.A.; Kroll, C.; Plate, A.; Rozanski, V.; Maiostre, J.; Levin, J.; Dietrich, O.; Ertl-Wagner, B.; Bötzel, K.; et al. Hough-CNN: Deep learning for segmentation of deep brain regions in MRI and ultrasound. Comput. Vis. Image Underst. 2017, 164, 92–102. [Google Scholar] [CrossRef]
- Khairuzzaman, A.K.M.; Chaudhury, S. Multilevel thresholding using grey wolf optimizer for image segmentation. Expert Syst. Appl. 2017, 86, 64–76. [Google Scholar] [CrossRef]
- Wang, B.; Chen, L.; Cheng, J. New result on maximum entropy threshold image segmentation based on P system. Optik 2018, 163, 81–85. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histogram. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Kittler, J.; Illingworth, J. Minimum error thresholding. Pattern Recognit. 1986, 19, 41–47. [Google Scholar] [CrossRef]
- Pun, T. A new method for gray-level picture thresholding using the entropy of the histogram. Comput. Vis. Graph. Image Process. 1980, 2, 223–227. [Google Scholar]
- Wong, K.C.; Sahoo, P.K. A gray-level threshold selection method based on maximum entropy principle. IEEE Trans. Syst. Man Cybern. 1989, 19, 866–871. [Google Scholar] [CrossRef]
- Kapur, J.N.; Sahoo, P.K.; Wong, A.K.C. A new method for gray-level picture thresholding using the entropy of the histogram. Comput. Vis. Graph. Image Process. 1985, 29, 273–285. [Google Scholar] [CrossRef]
- Li, C.H.; Lee, C.K. Minimum cross entropy thresholding. Pattern Recognit. 1993, 26, 617–625. [Google Scholar] [CrossRef]
- Abutaleb, A. Automatic thresholding of gray-level pictures using two-dimensional entropy. Comput. Vis. Graph. Image Process. 1989, 47, 22–32. [Google Scholar] [CrossRef]
- Sahoo, P.K.; Arora, G. A thrsholding methd based on two-dimensional Renyi’s entropy. Pattern Recognit. 2004, 37, 1149–1161. [Google Scholar] [CrossRef]
- Liu, J.Z.; Li, W.Q. The automatic threshold of gray 2 level pictures via two 2 dimensional otsu method. Autom. Sin. 1993, 19, 101–105. (In Chinese) [Google Scholar]
- Sahoo, P.K.; Arora, G. Image thresholding using two-dimensional Tsallis-Havrda-Charvat entropy. Pattern Recognit. Lett. 2006, 27, 520–528. [Google Scholar] [CrossRef]
- Xiao, Y.; Cao, Z.; Zhang, T. Entropic thresholding based on gray-level spatial correlation histogram. In Proceedings of the 19th International Conference on Pattern Recognition, Tampa, FL, USA, 8–11 December 2008. [Google Scholar]
- Yimit, A.; Hagihara, Y.; Miyoshi, T.; Hagihara, Y. 2-D direction histogram based entropic thresholding. Neurocomputing 2013, 120, 287–297. [Google Scholar] [CrossRef]
- Xiao, Y.; Cao, Z.; Yuan, J. Entropic image thresholding based on GLGM histogram. Pattern Recognit. Lett. 2014, 40, 47–55. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.M. A non-local algorithm for image denoising. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; pp. 60–65. [Google Scholar]
- Li, Z.; Liu, C.; Liu, G.; Cheng, Y.; Yang, X.; Zhao, C. A novel statistical image thresholding method. Int. J. Electron. Commun. 2010, 64, 1137–1147. [Google Scholar] [CrossRef]

| Methods | Advantages | Disadvantages |
|---|---|---|
| superpixel [5,6] | reduce redundant information; less complexity | cannot locate the edges accurately |
| watershed [7,8] | simple and intuition | usually result in over segmention |
| active contour models [9,10] | rigorous mathematical base; | sensitive noise; high computation complexity |
| clustering [11,12] | intensive value is enough; simple | the number of cluster cannot be determined automatically; spatial information is ignored; |
| deep learning [13,14] | high segmentation accuracy | large computation burden |
| thresholding [15,16] | simple, easy to be implemented | ignore spatial information |
| Image | The Proposed | 2DMCE | MCE | OTSU | KAPUR | |
|---|---|---|---|---|---|---|
| ant | threshold | 52 52 | 44 45 | 69 | 84 | 183 |
| ME | 0.0344 | 0.0379 | 0.0481 | 0.0829 | 0.8852 | |
| bacteria | threshold | 65 65 | 44 45 | 98 | 99 | 70 |
| ME | 0.0101 | 0.0605 | 0.4266 | 0.4398 | 0.0221 | |
| block | threshold | 26 26 | 36 36 | 38 | 120 | 88 |
| ME | 0.0183 | 0.0621 | 0.0679 | 0.2861 | 0.2613 | |
| geometric | threshold | 36 36 | 36 36 | 41 | 70 | 126 |
| ME | 0.0324 | 0.0347 | 0.0381 | 0.0986 | 0.2323 | |
| junk | threshold | 187 186 | 209 206 | 129 | 134 | 158 |
| ME | 0.0072 | 0.0090 | 0.0633 | 0.0492 | 0.0166 | |
| mask | threshold | 23 24 | 28 30 | 30 | 57 | 116 |
| ME | 0.0016 | 0.0129 | 0.0136 | 0.1134 | 0.2860 | |
| casting13 | threshold | 144 144 | 134 127 | 74 | 80 | 114 |
| ME | 0.0115 | 0.0128 | 0.1046 | 0.0795 | 0.0170 | |
| casting18 | threshold | 154 153 | 158 154 | 92 | 138 | 114 |
| ME | 0.0050 | 0.0063 | 0.2200 | 0.0074 | 0.0611 |
| Image | The Propsed | 2DMCE | MCE | Otsu | Kapur |
|---|---|---|---|---|---|
| ant | 170.3123 | 21.1812 | 0.0317 | 0.0032 | 0.0067 |
| bacteria | 163.7921 | 23.9648 | 0.0097 | 0.0031 | 0.0081 |
| block | 94.4108 | 21.3898 | 0.0079 | 0.0027 | 0.0077 |
| casting13 | 56.5179 | 9.2832 | 0.0066 | 0.0023 | 0.0043 |
| casting14 | 56.6691 | 10.2639 | 0.0068 | 0.0027 | 0.0051 |
| geometric | 62.0219 | 18.1187 | 0.0073 | 0.0020 | 0.0059 |
| junk | 116.4295 | 14.0563 | 0.0061 | 0.0019 | 0.0045 |
| mask | 99.1112 | 22.3298 | 0.0088 | 0.0023 | 0.0057 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, C.; Yang, W.; Guo, Y.; Wu, F.; Tang, Y. Nonlocal Means Two Dimensional Histogram-Based Image Segmentation via Minimizing Relative Entropy. Entropy 2018, 20, 827. https://doi.org/10.3390/e20110827
Jiang C, Yang W, Guo Y, Wu F, Tang Y. Nonlocal Means Two Dimensional Histogram-Based Image Segmentation via Minimizing Relative Entropy. Entropy. 2018; 20(11):827. https://doi.org/10.3390/e20110827
Chicago/Turabian StyleJiang, Chundi, Wei Yang, Yu Guo, Fei Wu, and Yinggan Tang. 2018. "Nonlocal Means Two Dimensional Histogram-Based Image Segmentation via Minimizing Relative Entropy" Entropy 20, no. 11: 827. https://doi.org/10.3390/e20110827
APA StyleJiang, C., Yang, W., Guo, Y., Wu, F., & Tang, Y. (2018). Nonlocal Means Two Dimensional Histogram-Based Image Segmentation via Minimizing Relative Entropy. Entropy, 20(11), 827. https://doi.org/10.3390/e20110827





