1. Introduction
In information theory, there is a duality between the concepts entropy and information: entropy is a measure of uncertainty or freedom of choice, whereas information is a measure of reduction of uncertainty (increase in certainty) or restriction of choice. Interestingly, this description of information as a restriction of choice predates even Shannon [
1], originating with Hartley [
2]:
“By successive selections a sequence of symbols is brought to the listener’s attention. At each selection there are eliminated all of the other symbols which might have been chosen. As the selections proceed more and more possible symbol sequences are eliminated, and we say that the information becomes more precise.”
Indeed, this interpretation led Hartley to derive the measure of information associated with a set of equally likely choices, which Shannon later generalised to account for unequally likely choices. Nevertheless, despite being used since the foundation of information theory, there is a surprising lack of a formal characterisation of information in terms of the elimination of choice. Both Fano [
3] and Ash [
4] motivate the notion of information in this way, but go on to derive the measure without explicit reference to the restriction of choice. More specifically, their motivational examples consider a set of possible choices
modelled by a random variable
X. Then in alignment with Hartley’s description, they consider information to be something which excludes possible choices
x, with more eliminations corresponding to greater information; however, this approach does not capture the concept of information in its most general sense since it cannot account for information provided by partial eliminations which merely reduces the likelihood of a choice
x from occurring. (Of course, despite motivating the notion of information in this way, both Fano and Ash provide Shannon’s generalised measure of information which can account for unequally likely choices.) Nonetheless,
Section 2 of this paper generalises Hartley’s interpretation of information by providing a formal characterisation of information in terms of probability mass exclusions.
Our interest in providing a formal interpretation of information in terms of exclusions is driven by a desire to understand how information is distributed in complex systems [
5,
6]. In particular, we are interested in decomposing the total information provided by a set of source variables about one or more target variables into the following atoms of information: the unique information provided by each individual source variable, the shared information that could be provided by two or more source variables, and the synergistic information which is only available through simultaneous knowledge of two or more variables [
7]. This idea was originally proposed by Williams and Beer who also introduced an axiomatic framework for such a decomposition [
8]. However, flaws have been identified with a specific detail in their approach regarding “whether different random variables carry
the same information or just
the same amount of information” [
9] (see also [
10,
11]). With this problem in mind,
Section 3 discusses how probability mass exclusions may provide a principled method for determining if variables provide the same information. Based upon this,
Section 4 derives an information-theoretic expression which can distinguish between different probability mass exclusions. Finally,
Section 5 closes by discussing how this expression could be used to identify when distinct events provide the same information.
2. Information and Eliminations
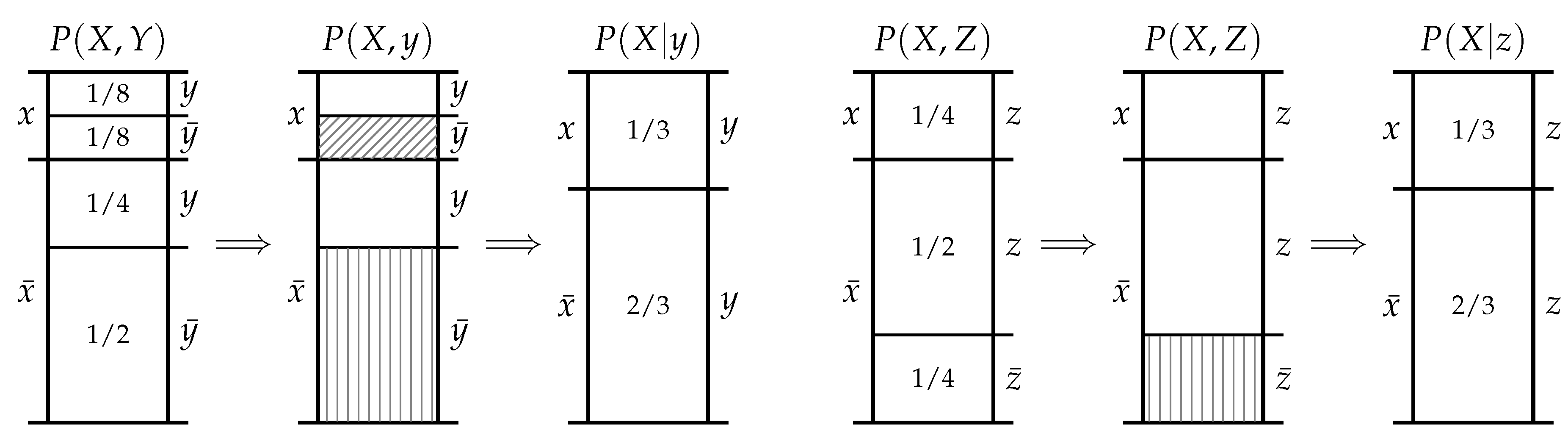
Consider two random variables X and Y with discrete sample spaces and , and say that we are trying to predict or infer the value of an event x from X using an event y from Y which has occurred jointly. Ideally, there is a one-to-one correspondence between the occurrence of events from X and Y such that an event x can be exactly predicted using an event y. However, in most complex systems, the presence of noise or some other such ambiguity means that we typically do not have this ideal correspondence. Nevertheless, when a particular event y is observed, knowledge of the distributions and can be utilised to improve the prediction on average by using the posterior in place of the prior . Our goal now is to understand how Hartley’s description relates to the notion of conditional probability.
When a particular event
y is observed, we know that the complementary event
did not occur. Thus we can consider the joint distribution
and eliminate the probability mass which is associated with this complementary event
. In other words, we exclude the probability mass
which leaves only the probability mass
remaining. The surviving probability mass can then be normalised by dividing by
, which, by definition, yields the conditional distribution
. Hence, with this elimination process in mind, consider the following definition:
Definition 1 (Probability Mass Exclusion). A probability mass exclusion induced by the event y from the random variable Y is the probability mass associated with the complementary event , i.e., .
Echoing Hartley’s description, it is perhaps tempting to think that the greater the probability mass exclusion
, the greater the information that
y provides about
x; however, this is not true in general. To see this, consider the joint event
x from the random variable
X. Knowing the event
x occurred enables us to categorise the probability mass exclusions induced by
y into two distinct types: the first is the portion of the probability mass exclusion associated with the complementary event
, i.e.,
; while the second is the portion of the exclusion associated with the event
x, i.e.,
. Before discussing these distinct types of exclusion, consider the conditional probability of
x given
y written in terms of these two categories,
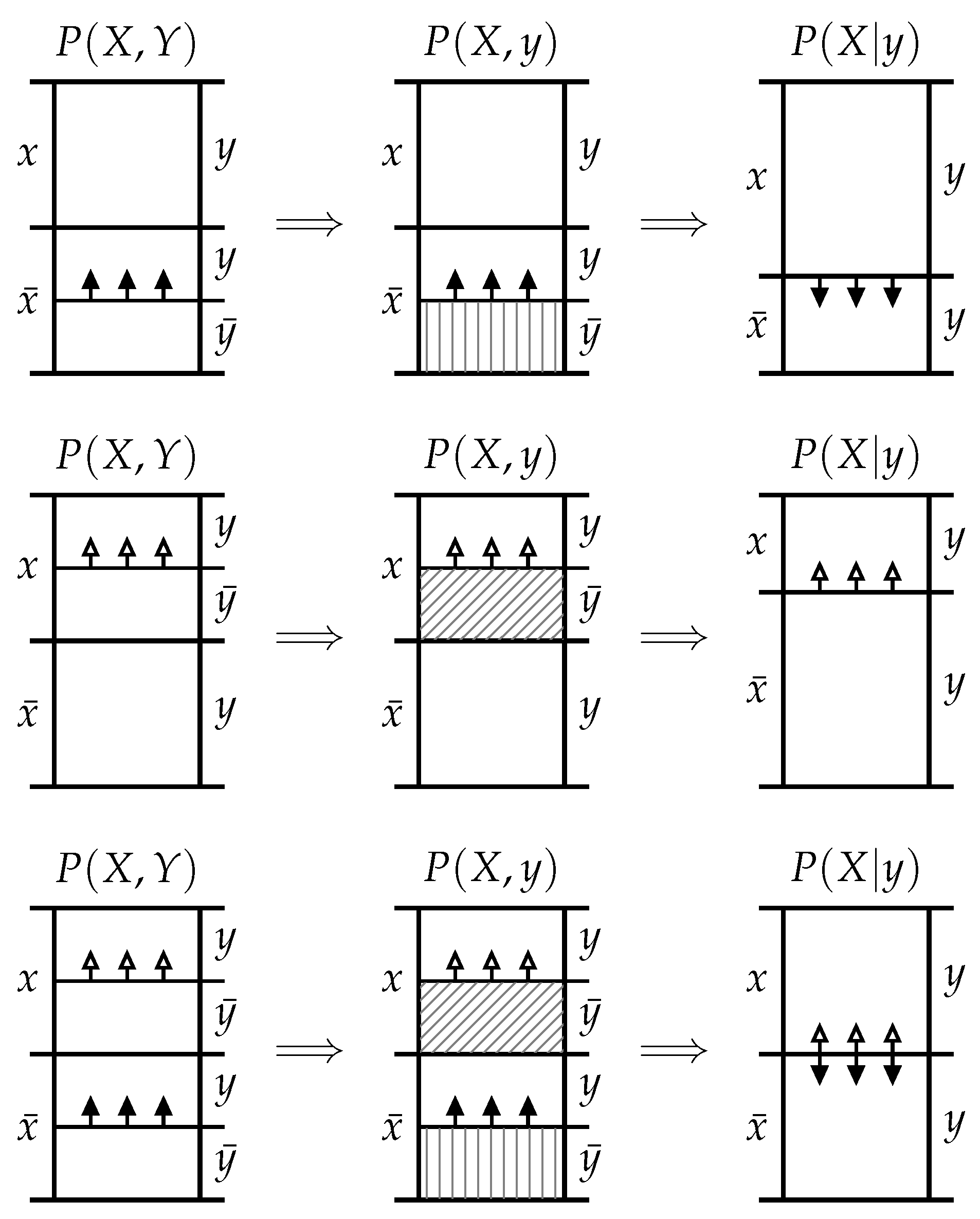
To see why these two types of exclusions are distinct, consider two special cases: The first special case is when the event
y induces exclusions which are confined to the probability mass associated with the complementary event
. This means that the portion of exclusion
is non-zero while the portion
. In this case the posterior
is larger than the prior
and is an increasing function of the exclusion
for a fixed
. This can be seen visually in the
probability mass diagram at the top of
Figure 1 or can be formally demonstrated by inserting
into (
1). In this case, the mutual information
is a strictly positive, increasing function of
for a fixed
. (Note that this is the mutual information between events rather than the average mutual information between variables; depending on the context, it is also referred to as the the information density, the pointwise mutual information, or the local mutual information.) For this special case, it is indeed true that the greater the probability mass exclusion
, the greater the information
y provides about
x. Hence, we define this type of exclusion as follows:
Definition 2 (Informative Probability Mass Exclusion). For the joint event from the random variables X and Y, an informative probability mass exclusion induced by the event y is the portion of the probability mass exclusion associated with the complementary event , i.e., .
The second special case is when the event
y induces exclusions which are confined to the probability mass associated with the event
x. This means that the portion of exclusion
while the potion
is non-zero. In this case, the posterior
is smaller than the prior
and is a decreasing function of the exclusion
for a fixed
. This can be seen visually in the probability mass diagram in the middle row of
Figure 1 or can be formally demonstrated by inserting
into (
1). In this case, the mutual information (
2) is a strictly negative, decreasing function of
for fixed
. (Although the mutual information is non-negative when averaged across events from both variables, it may be negative between pairs of events.) This second special case demonstrates that it is not true that the greater the probability mass exclusion
, the greater the information
y provides about
x. Hence, we define this type of exclusion as follows:
Definition 3 (Misinformative Probability Mass Exclusion). For the joint event from the random variables X and Y, a misinformative probability mass exclusion induced by the event y is the portion of the probability mass exclusion associated with the event x, i.e., .
Now consider the general case where both informative and misinformative probability mass exclusions are present simultaneously. It is not immediately clear whether the posterior
is larger or smaller than the prior
, as this depends on the relative size of the informative and misinformative exclusions. Indeed, for a fixed prior
, we can vary the informative exclusion
whilst still maintaining a fixed posterior
by co-varying the misinformative exclusion
appropriately; specifically by choosing
Although it is not immediately clear whether the posterior
is larger or smaller than the prior
, the general case maintains the same monotonic dependence as the two constituent special cases. Specifically, if we fix
and the misinformative exclusion
, then the posterior
is an increasing function of the informative exclusion
. On the other hand, if we fix
and the informative exclusion
, then the posterior
is a decreasing function of the misinformative exclusion
. This can been seen visually in the probability mass diagram at the bottom of
Figure 1 or can be formally demonstrated by fixing and varying the appropriate values for each case in (
1). Finally, the relationship between the mutual information and the exclusions in this general case can be explored by inserting (
1) into (
2), which yields
If and the misinformative exclusion are fixed, then is an increasing function of the informative exclusion . On the other hand, if and the informative exclusion are fixed, then is a decreasing function of the misinformative exclusion . Finally, if both the informative exclusion and misinformative exclusion are fixed, the is an increasing function of .
Now that a formal relationship between eliminations and information has been established using probability theory, we return to the motivational question—can this understanding of information in terms of exclusions aid in our understanding of how random variables share information?
4. The Directed Components of Mutual Information
The mutual information cannot distinguish between events which induce different exclusions because any given value could arise from a whole continuum of possible informative and misinformative exclusions. Hence, consider decomposing the mutual information into two separate information-theoretic components. Motivated by the strictly positive mutual information observed in the purely informative case and the strictly negative mutual information observed in the purely informative case, let us demand that one of the components be positive while the other component is negative.
Postulate 1 (Decomposition). The information provided by y about x can be decomposed into two non-negative components, such that .
Furthermore, let us demand that the two components preserve the functional dependencies between the mutual information and the informative and misinformative exclusion observed in (
4) for the general case.
Postulate 2 (Monotonicity). The functions and should satisfy the following conditions:
- 1.
For all fixed and , the function is a continuous, increasing function of .
- 2.
For all fixed and , the function is a continuous, increasing function of .
- 3.
For all fixed and , the functions and are increasing and decreasing functions of , respectively.
Before considering the functions which might satisfy Postulates 1 and 2, there are two further observations to be made about probability mass exclusions. The first observation is that an event
x could never induce a misinformative exclusion about itself, since the misinformative exclusion
. Indeed, inserting this result into the self-information in terms of (
4) yields the Shannon information content of the event
x,
Postulate 3 (Self-Information). An event cannot misinform about itself, hence .
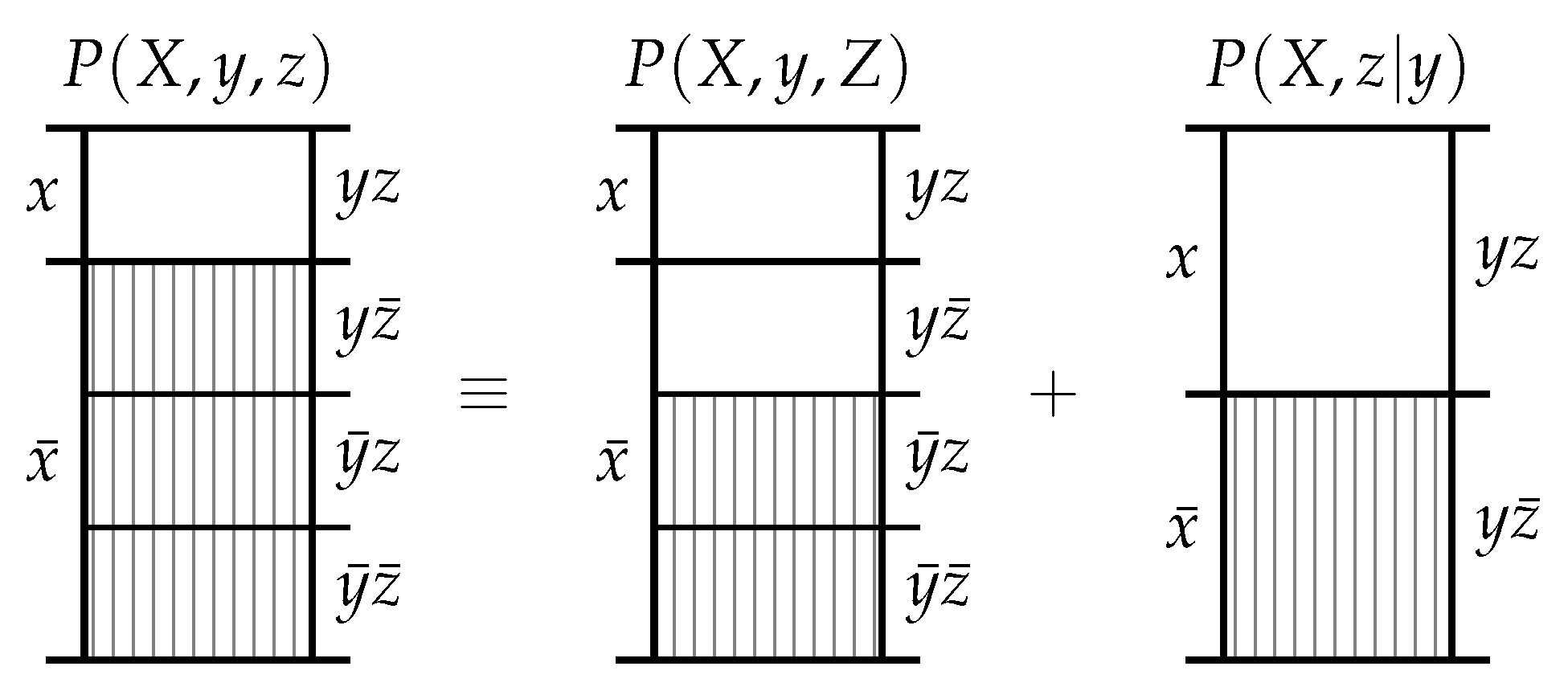
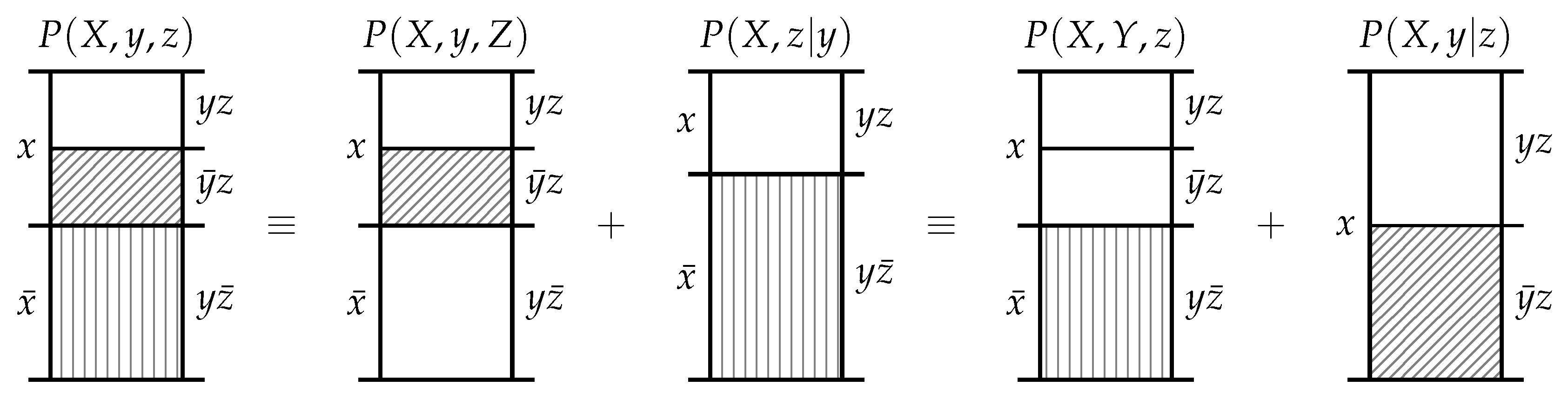
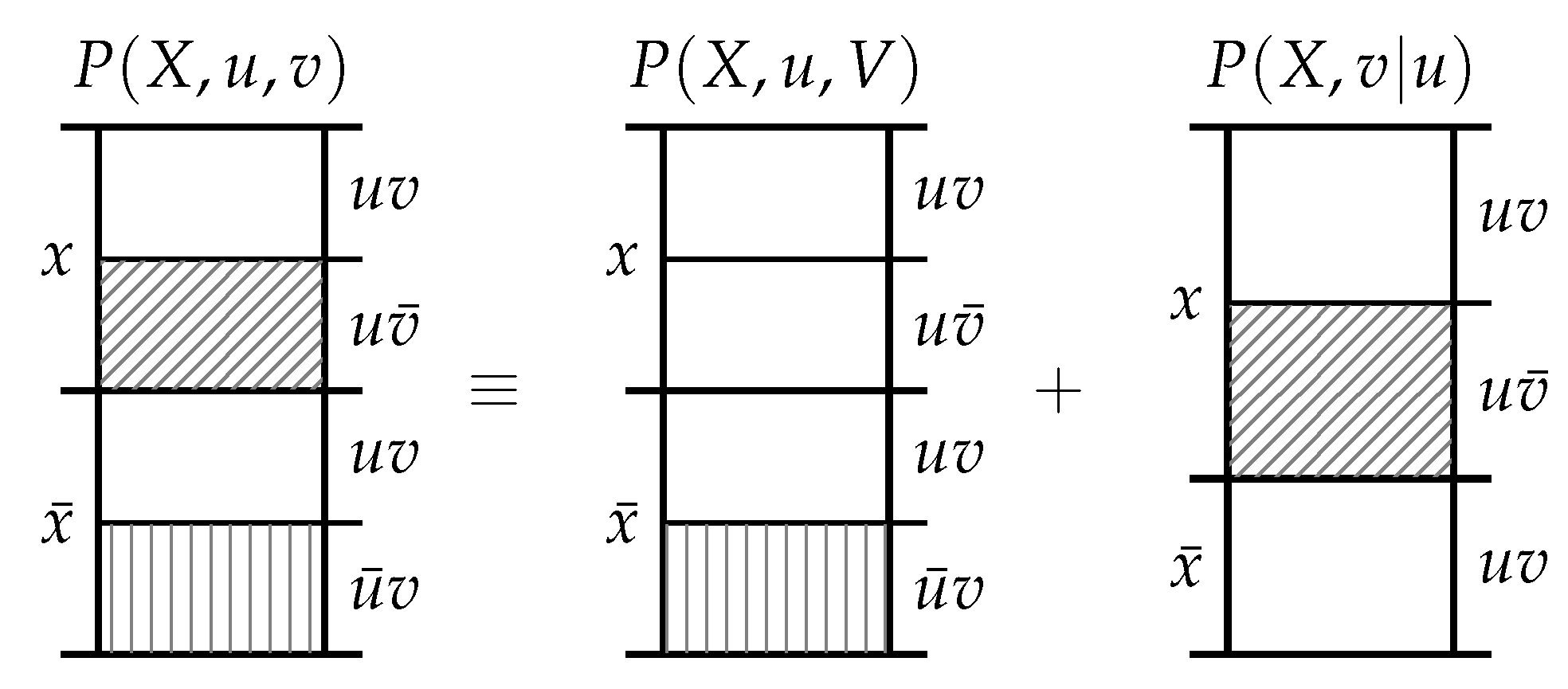
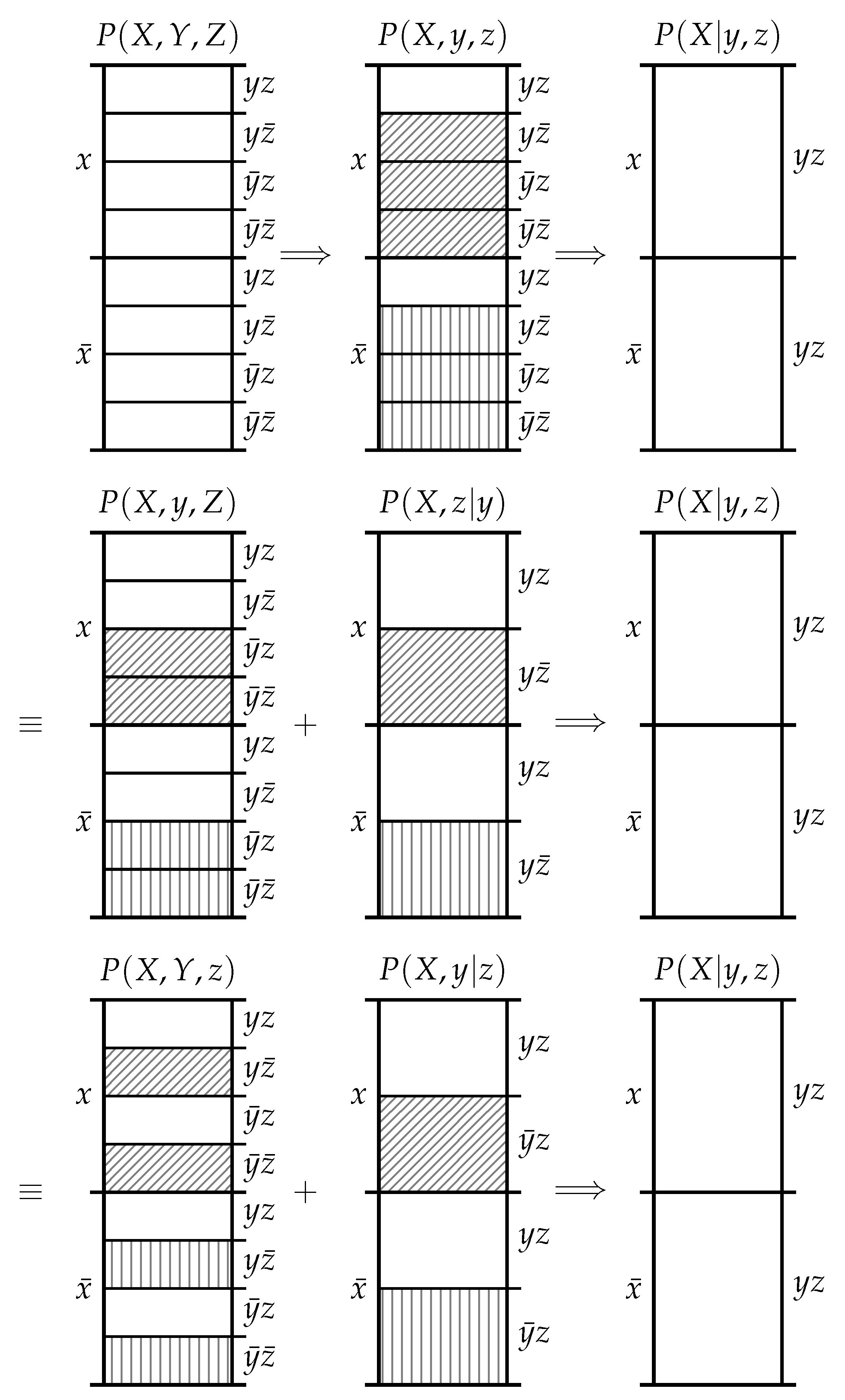
The second observation is that the informative and misinformative exclusions exclusions must individually satisfy the chain rule of probability. As shown in
Figure 3, there are three equivalent ways to consider the exclusions induced in
by the events
y and
z. Firstly, we could consider the information provided by the joint event
which excludes the probability mass in
associated with the joint events
,
and
. Secondly, we could first consider the information provided by
y which excludes the probability mass in
associated with the joint events
and
, and then subsequently consider the information provided by
z which excludes the probability mass in
associated with the joint event
. Thirdly, we could first consider the information provided by
z which excludes the probability mass in
associated with the joint events
and
, and then subsequently consider the information provided by
y which excludes the probability mass in
associated with the joint event
. Regardless of the chaining, we start with the same
and finish with the same
.
Postulate 4 (Chain Rule)
. The functions and satisfy a chain rule; i.e.,where the conditional notation denotes the same function only with conditional probability as an argument. Theorem 1. The unique functions satisfying Postulates 1–4 are By rewriting (
7) and (
8) in terms of probability mass exclusions, it is easy to verify that Theorem 1 satisfies Postulates 1–4. Perhaps unsurprisingly, this yields a decomposed version of (
4),
Hence, in order to prove Theorem 1 we must demonstrate that (
7) and (
8) are the unique functions which satisfy Postulates 1–4. This proof is provided in full in
Appendix A.
5. Discussion
Theorem 1 answers the question posed at the end of
Section 3—although there is no one-to-one correspondence between these exclusions and the mutual information, there is a one-to-one correspondence between exclusions and the decomposition
It is important to note the directed nature of this decomposition—this equation considers the exclusions induced by y with respect to x. It is novel that this particular decomposition enables us to uniquely determine the size of the exclusions induced by y with respect to x, rather than , which would not satisfy Postulate 4. Indeed, this latter decomposition is more typically associated with the information provided by y about x since it reflects the change from the prior to the posterior . Of course, by Theorem 1 this latter decomposition would allow us to uniquely determine the size exclusions induced by x with respect to y.
There is another important asymmetry which can be seen from (
9) and (
10). The negative component
depends on the size of
only the misinformative exclusion while the positive component
depends on the size of
both the informative and misinformative exclusions. The positive component depends on the total size of the exclusions induced by
y and hence has no functional dependence on
x. It quantifies the
specificity of the event
y: the less likely the outcome
y is to occur, the greater the total amount of probability mass excluded by
y and therefore the greater the potential for
y to inform about
x. On the other hand, the negative component quantifies the
ambiguity of
y given
x: the less likely the outcome
y is to coincide with the outcome
x, the greater the misinformative probability mass exclusion and therefore the greater the potential for
y to misinform about
x. This asymmetry between the components is apparent when considering the two special cases. In the purely informative case where
, only the positive informational component is non-zero. On the other hand, in the purely misinformative case, both the positive and negative informational components are non-zero, although it is clear that
and hence
.
Let us now consider how this information-theoretic expression (which has a one-to-one correspondence with exclusion) could be utilised to provide an information decomposition that can distinguish between whether events provide the same information or merely the same amount of information. Recall the example from
Section 3 where
y and
z provide the same amount of information about
x, and consider this example in terms of the decomposition (
11),
In contrast to the mutual information in (
5), the decomposition reflects the different ways
y and
z provide information through differing exclusions even if they provide the same amount of information. As for how to decompose multivariate information using this decomposition? This is not the subject of this paper—those who are interested in seen an operational definition of shared information based on redundant exclusions should see [
12].