The Role of Data in Model Building and Prediction: A Survey Through Examples
Abstract
1. Introduction
First of all, one can construct many mathematical models for the same practical situation, and one has to choose the most appropriate, that which fits the situation as closely as practical aims require (it can never fit completely). At the same time, it must not be too complicated, but still must be mathematically feasible. These are, of course, conflicting requirements and a delicate balancing of the two is usually necessary. […] You have to approximate closely the real situation in every respect important for your purposes, but lay aside everything which is of no importance for your actual aims. A model needs not to be similar to the modeled reality in every respect, only in those which really count. On the other hand, the same mathematical model can be used to fit quite different practical situations. […] In trying to describe such a complicated situation, even a very rough model may be useful because it gives at least qualitatively correct results, and these may be of even greater practical importance than quantitative results. My experience has taught me that even a crude mathematical model can help us to understand a practical situation better, because in trying to set up a mathematical model we are forced to think over all logical possibilities, to define all notions unambiguously, and to distinguish between important and secondary factors. Even if a mathematical model leads to results which are not in accordance with the facts, it may be useful because the failure of one model can help us find a better one [3].
The ideal formal model would be one which would cover the entire universe, which would agree with it in complexity, and which would have a one to one correspondence with it. Any one capable of elaborating and comprehending such a model in its entirety, would find the model unnecessary, because he could then grasp the universe directly as a whole. He would possess the third category of knowledge described by Spinoza. This ideal theoretical model cannot probably be achieved. Partial models, imperfect as they may be, are the only means for understanding the universe. This statement does not imply an attitude of defeatism but the recognition that the main tool of science is the human mind and that the human mind is finite.
2. An Interlude: The Story of Two Seminal Models
2.1. The Lorenz’s Model: How to Obtain Something Interesting with a Crude Assumption
2.2. The Lotka-Volterra Model: The Power of the Analogy
3. The Role of Data and Models for the Prediction
3.1. Prediction When We Know the System State Vector
3.2. Prediction When We Do Not Know the System State Vector
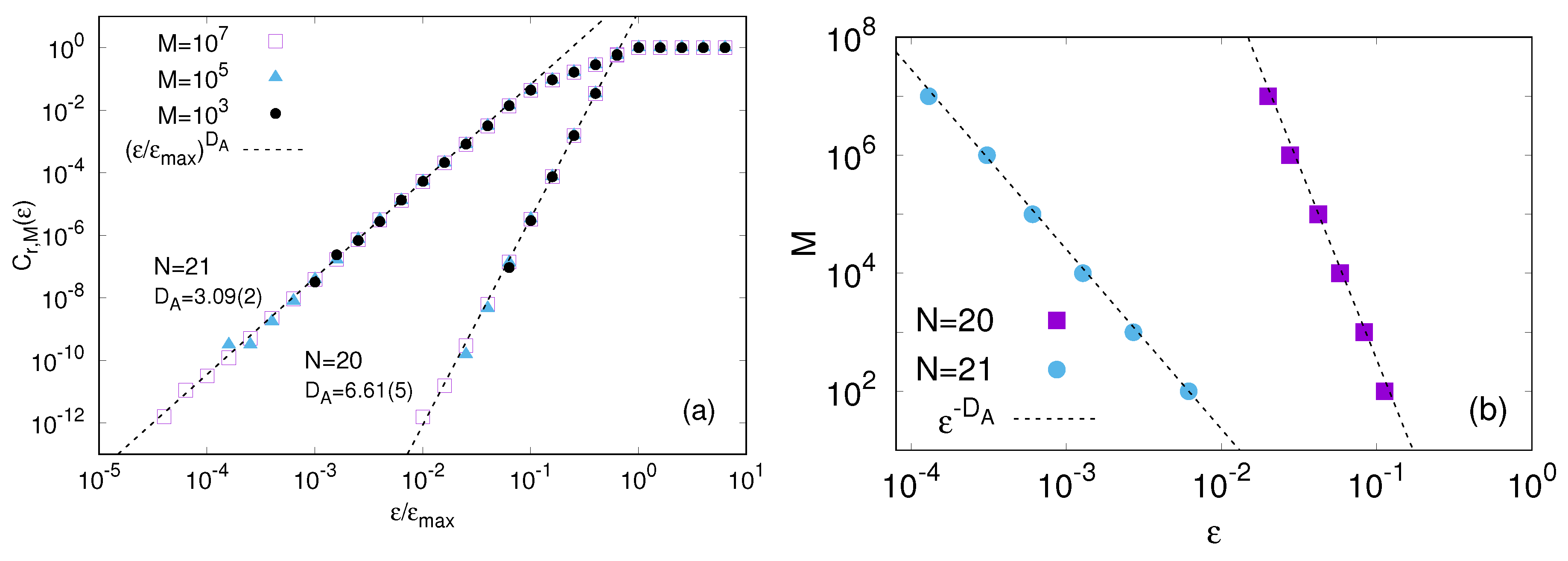
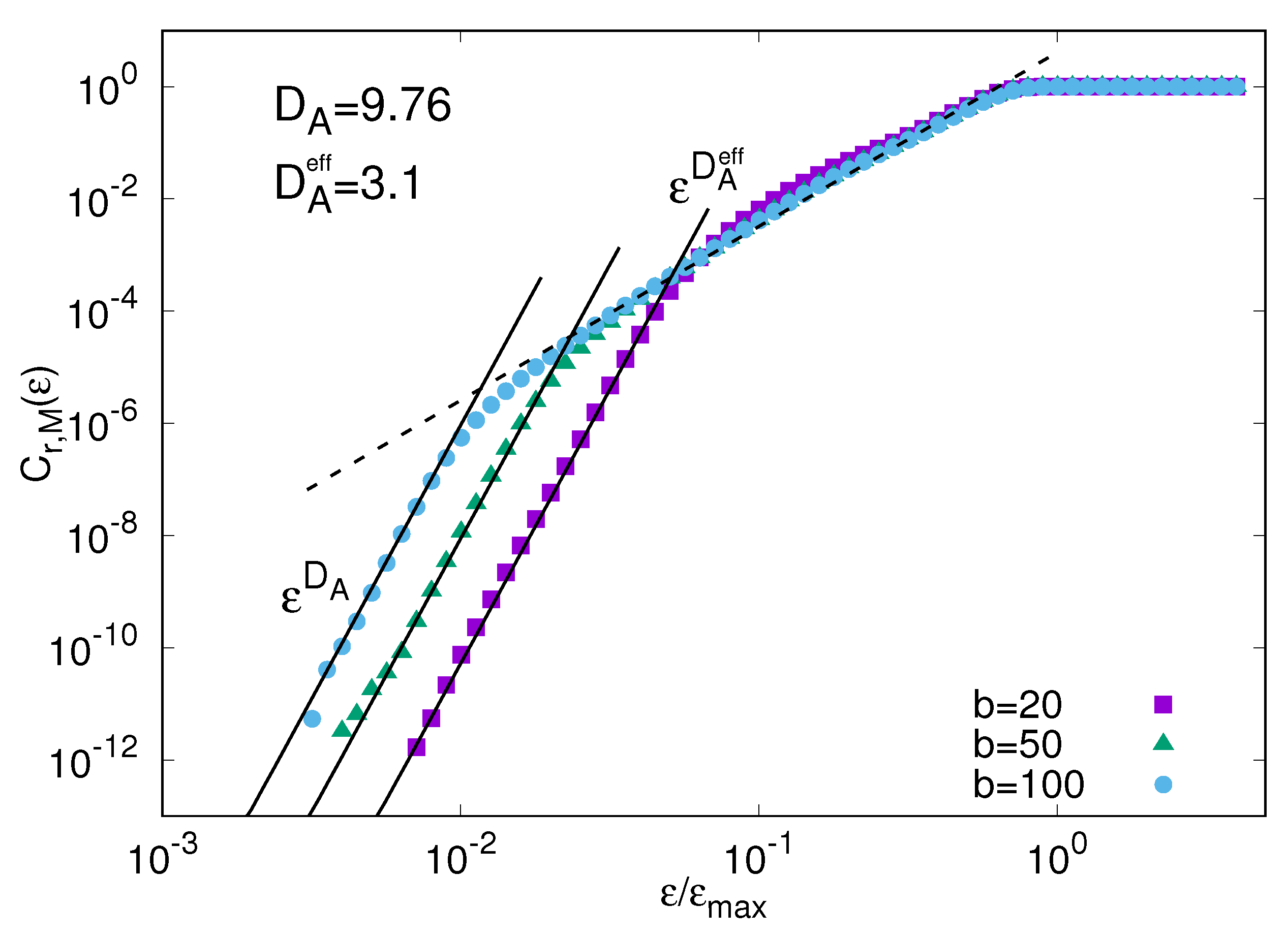
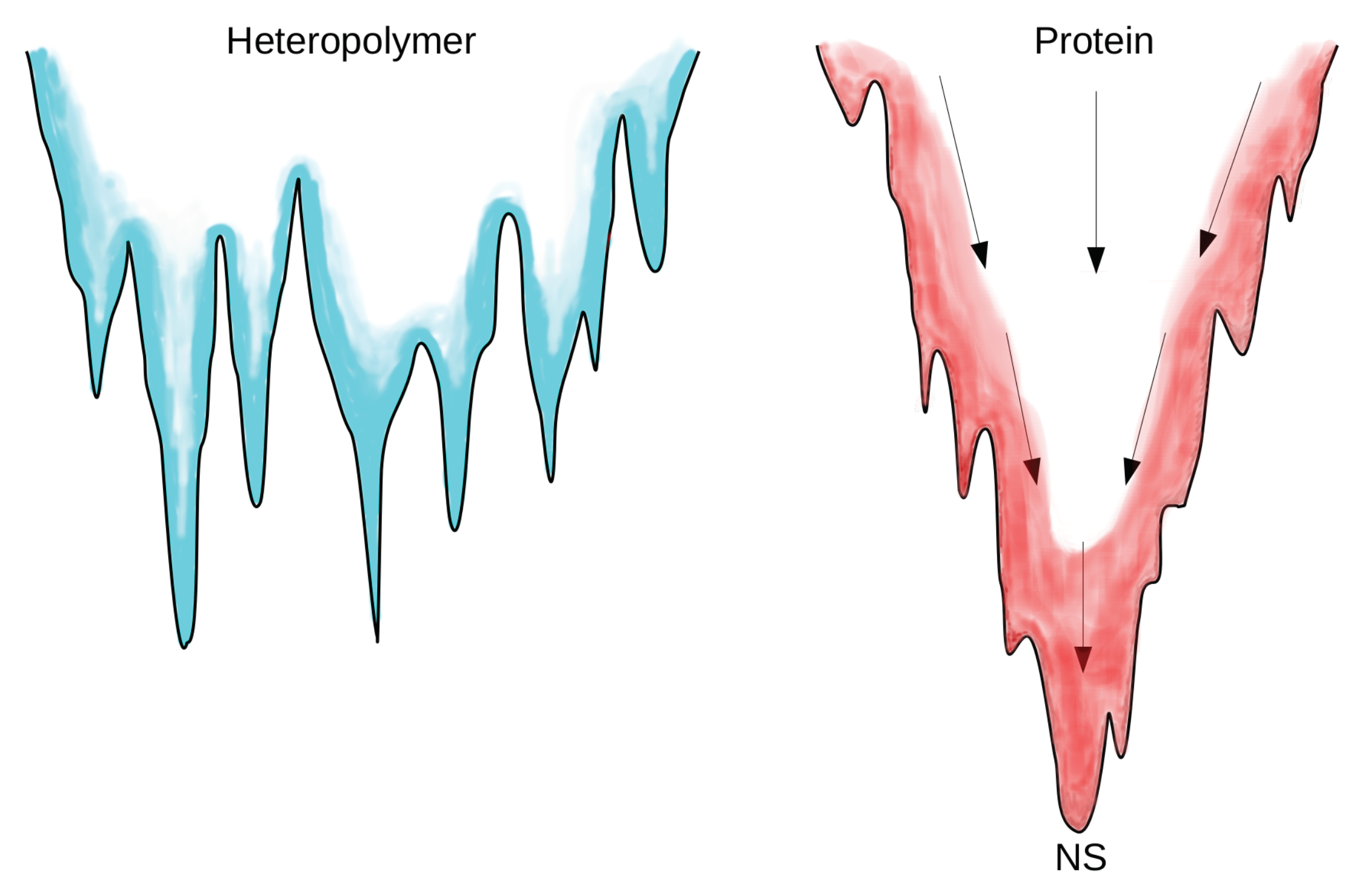
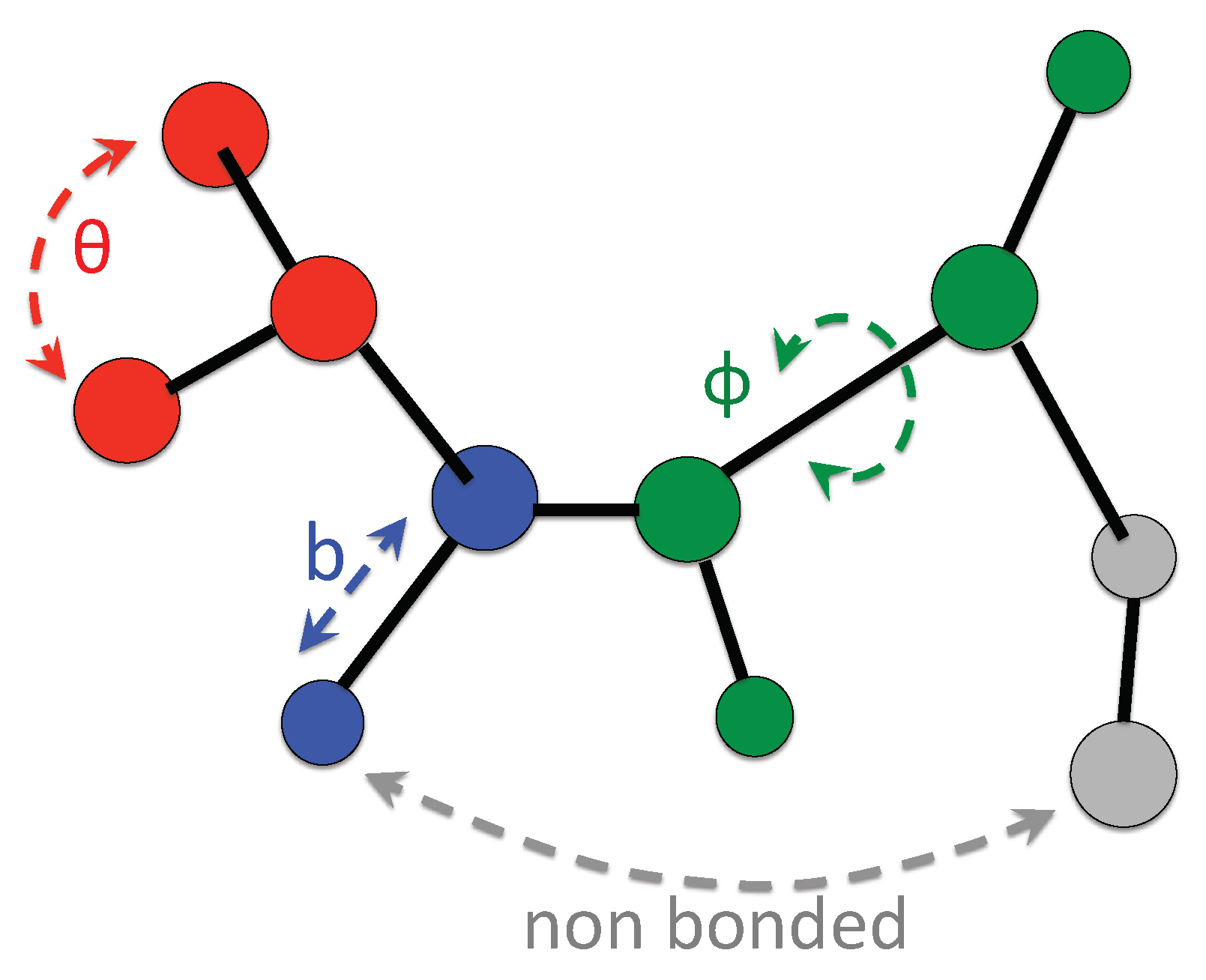
4. Protein Modeling: An Example of Data-Driven Approach
4.1. Knowledge Based Approach
4.2. Structure Based Models
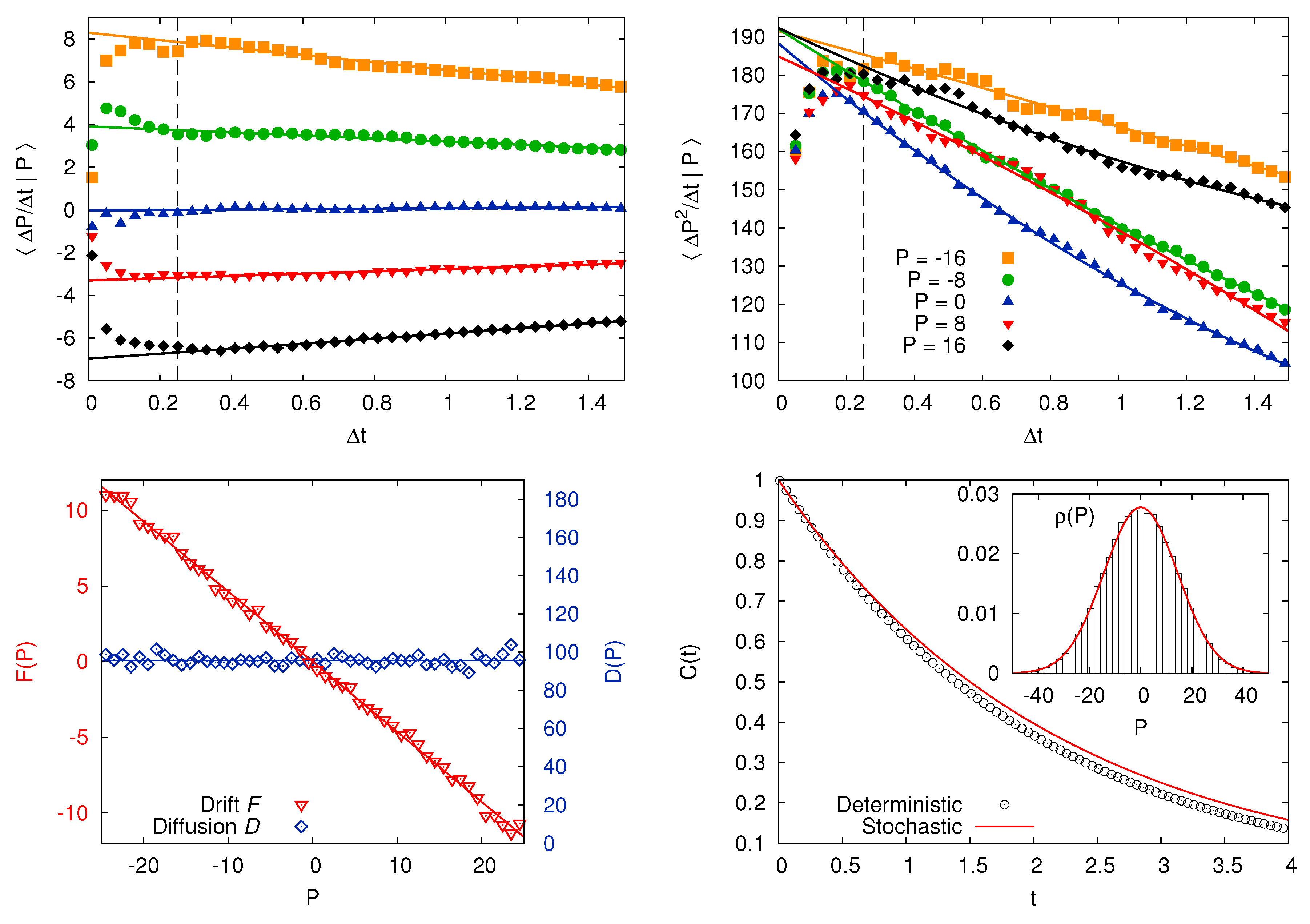
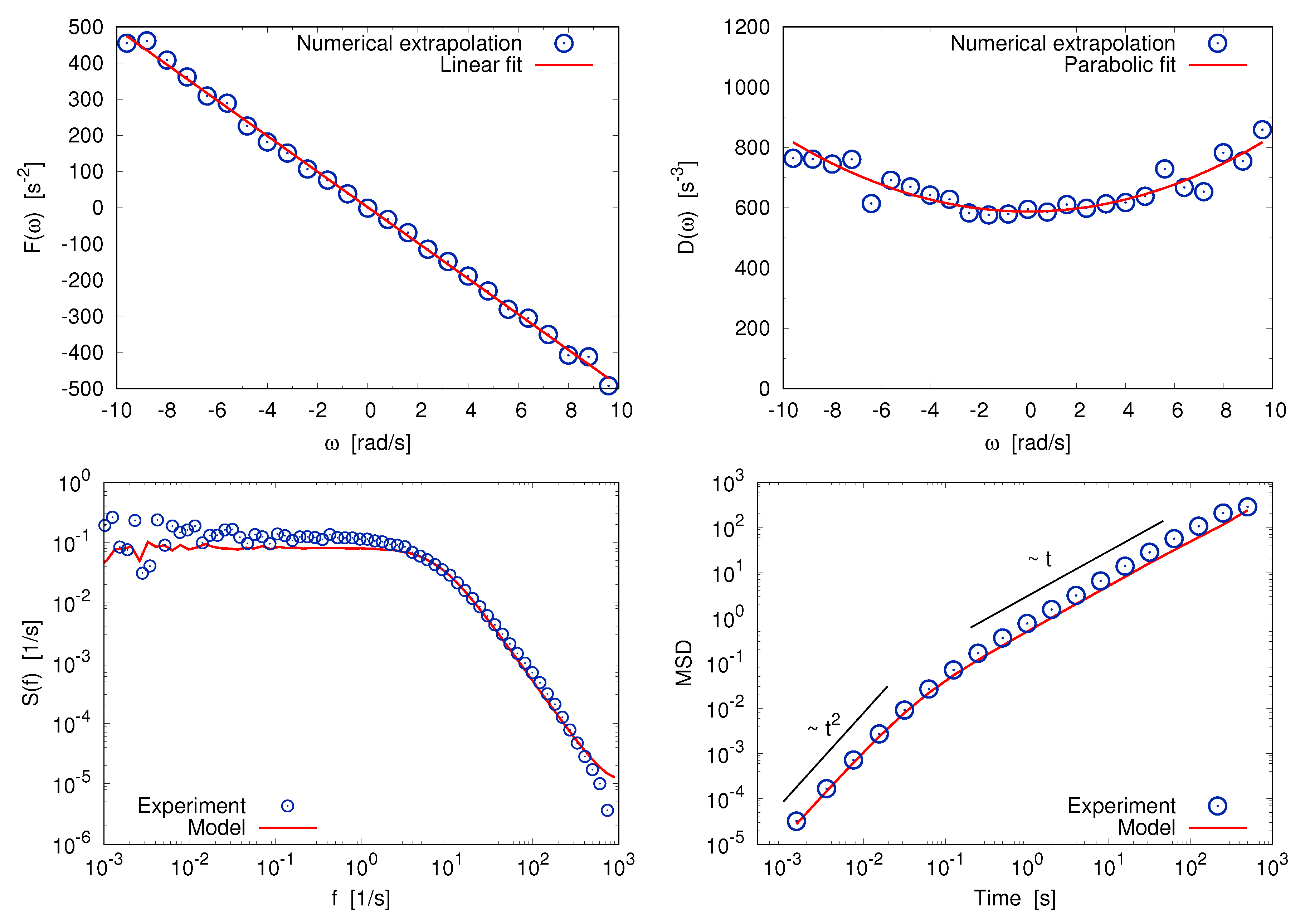
5. Langevin Equation: When a Multiscale Structure Helps
6. Conclusions and Final Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. An Attempt to Build Clever Low Dimensional Sysstems
References
- Rosenblueth, A.; Wiener, N. The role of models in science. Philos. Sci. 1945, 12, 316–321. [Google Scholar] [CrossRef]
- Morgan, M.S.; Morrison, M. (Eds.) Models as Mediators: Perspectives on Natural and Social Science; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Rényi, A. Dialogues on Mathematics; Holden-Day: San Francisco, CA, USA, 1967. [Google Scholar]
- Lorenz, E.N. Deterministic Nonperiodic Flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Tacchella, A.; Mazzilli, D.; Pietronero, L. A dynamical systems approach to gross domestic product forecasting. Nat. Phys. 2018, 14, 861–865. [Google Scholar] [CrossRef]
- Volterra, V. Variazioni e Fluttuazioni del Numero D’individui in Specie Animali Conviventi. Memorie del R. Comitato Talassografico Italiano. Mem. CXXXI; Volterra V. Opere Matematiche: Memorie e Note; Accademia Nazionale dei Lincei: Roma, Italy, 1926; Volume 5, pp. 1926–1940. (In Italian) [Google Scholar]
- Lotka, A.J. Analytical Note on Certain Rhythmic Relations in Organic Systems. Proc. Natl. Acad. Sci. USA 1920, 6, 410–415. [Google Scholar] [CrossRef] [PubMed]
- Holmes, P.; Lumley, J.L.; Berkooz, G.; Rowley, C.W. Turbulence, Coherent Structures, Dynamical Systems and Symmetry; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Ruelle, D.; Takens, F. On the nature of turbulence. Commun. Math. Phys. 1971, 20, 167–192. [Google Scholar] [CrossRef]
- Bacaër, N. Histoires de Mathématiques et de Populations; Cassini: Paris, France, 2009. [Google Scholar]
- Murray, J.D. Mathematical Biology: I. An Introduction, 3rd ed.; Interdisciplinary Applied Mathematics; Springer: New York, NY, USA, 2001; Volume 17. [Google Scholar]
- Cencini, M.; Cecconi, F.; Vulpiani, A. Chaos: From Simple Models to Complex Systems; World Scientific: Singapore, 2009. [Google Scholar]
- Daniels, B.C.; Nemenman, I. Automated adaptive inference of phenomenological dynamical models. Nat. Commun. 2015, 6, 8133. [Google Scholar] [CrossRef] [PubMed]
- Cubitt, T.S.; Eisert, J.; Wolf, M.M. Extracting Dynamical Equations from Experimental Data is NP Hard. Phys. Rev. Lett. 2012, 108, 120503. [Google Scholar] [CrossRef] [PubMed]
- Pikovsky, A. Reconstruction of a random phase dynamics network from observations. Phys. Lett. A 2018, 382, 147–152. [Google Scholar] [CrossRef]
- Stankovski, T.; Duggento, A.; McClintock, P.V.E.; Stefanovska, A. Inference of Time-Evolving Coupled Dynamical Systems in the Presence of Noise. Phys. Rev. Lett. 2012, 109, 024101. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.; Lipson, H. Distilling free-form natural laws from experimental data. Science 2009, 324, 81–85. [Google Scholar] [CrossRef] [PubMed]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, E.N. Atmospheric Predictability as Revealed by Naturally Occurring Analogues. J. Atmos. Sci. 1969, 26, 636–646. [Google Scholar] [CrossRef]
- Lorenz, E.N. Three approachs to atmospheric predictability. Bull. Am. Meteorol. Soc. 1969, 50, 345–351. [Google Scholar]
- Jaeger, H.; Haas, H. Harnessing Nonlinearity: Predicting Chaotic Systems and Saving Energy in Wireless Communication. Science 2004, 304, 78–80. [Google Scholar] [CrossRef] [PubMed]
- Pathak, J.; Lu, Z.; Hunt, B.R.; Girvan, M.; Ott, E. Using machine learning to replicate chaotic attractors and calculate Lyapunov exponents from data. Chaos 2017, 27, 121102. [Google Scholar] [CrossRef] [PubMed]
- Pathak, J.; Hunt, B.; Girvan, M.; Lu, Z.; Ott, E. Model-Free Prediction of Large Spatiotemporally Chaotic Systems from Data: A Reservoir Computing Approach. Phys. Rev. Lett. 2018, 120, 024102. [Google Scholar] [CrossRef] [PubMed]
- Lu, Z.; Pathak, J.; Hunt, B.; Girvan, M.; Brockett, R.; Ott, E. Reservoir observers: Model-free inference of unmeasured variables in chaotic systems. Chaos 2017, 27, 041102. [Google Scholar] [CrossRef] [PubMed]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Sauer, T.; Yorke, J.A.; Casdagli, M. Embedology. J. Stat. Phys. 1991, 65, 579–616. [Google Scholar] [CrossRef]
- Sugihara, G.; May, R.; Ye, H.; Hsieh, C.H.; Deyle, E.; Fogarty, M.; Munch, S. Detecting Causality in Complex Ecosystems. Science 2012, 338, 496–500. [Google Scholar] [CrossRef] [PubMed]
- Cecconi, F.; Cencini, M.; Falcioni, M.; Vulpiani, A. Predicting the future from the past: An old problem from a modern perspective. Am. J. Phys. 2012, 80, 1001–1008. [Google Scholar] [CrossRef]
- Campbell, L.; Garnett, W. The Life of James Clerk Maxwell: With a Selection From His Correspondence and Occasional Writings and a Sketch of His Contributions to Science; Macmillan: London, UK, 1882. [Google Scholar]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2004. [Google Scholar]
- Poincaré, H. Sur le problème des trois corps et les équations de la dynamique. Acta Math. 1890, 13, 1–270. [Google Scholar]
- Kac, M. On the notion of recurrence in discrete stochastic processes. Bull. Am. Math. Soc. 1947, 53, 1002–1010. [Google Scholar] [CrossRef]
- Lorenz, E.N. Predictability: A problem partly solved. ECMWF Semin. Proc. I 1995, 1. [Google Scholar] [CrossRef]
- Karimi, A.; Paul, M.R. Extensive chaos in the Lorenz-96 model. Chaos 2010, 20, 043105. [Google Scholar] [CrossRef] [PubMed]
- Grassberger, P.; Procaccia, I. Characterization of Strange Attractors. Phys. Rev. Lett. 1983, 50, 346–349. [Google Scholar] [CrossRef]
- Ruelle, D. The Claude Bernard Lecture, 1989. Deterministic Chaos: The Science and the Fiction. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1990, 427, 241–248. [Google Scholar] [CrossRef]
- Boffetta, G.; Cencini, M.; Falcioni, M.; Vulpiani, A. Predictability: A way to characterize complexity. Phys. Rep. 2002, 356, 367–474. [Google Scholar] [CrossRef]
- Olbrich, E.; Hegger, R.; Kantz, H. Analysing local observations of weakly coupled maps. Phys. Lett. A 1998, 244, 538–544. [Google Scholar] [CrossRef]
- Bohr, T.; Jensen, M.H.; Paladin, G.; Vulpiani, A. Dynamical Systems Approach to Turbulence; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Anfinsen, C.B. Principles that govern the folding of protein chains. Science 1973, 181, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Finkelstein, A.V.; Ptitsyn, O. Protein Physics: A Course of Lectures, 2nd ed.; Academic Press: Amsterdam, The Netherlands; Boston, MA, USA; Heidelberg, Germany; London, UK, 2016. [Google Scholar]
- Onuchic, J.N.; Luthey-Schulten, Z.; Wolynes, P.G. Theory of protein folding: The energy landscape perspective. Annu. Rev. Phys. Chem. 1997, 48, 545–600. [Google Scholar] [CrossRef] [PubMed]
- Plotkin, S.S.; Onuchic, J.N. Understanding protein folding with energy landscape theory. Part I: Basic concepts. Q. Rev. Biophys. 2002, 35, 111–167. [Google Scholar] [CrossRef] [PubMed]
- Schlick, T. Molecular Modeling and Simulation: An Interdisciplinary Guide, 2nd ed.; Interdisciplinary Applied Mathematics; Springer: New York, NY, USA, 2010. [Google Scholar]
- Gremlich, H.U.; Yan, B. Infrared and Raman Spectroscopy of Biological Materials, 1st ed.; CRC Press: New York, NY, USA, 2000. [Google Scholar]
- Chandler, D. Introduction to Modern Statistical Mechanics; OUP USA: New York, NY, USA, 1987. [Google Scholar]
- Schommers, W. Pair potentials in disordered many-particle systems: A study for liquid gallium. Phys. Rev. A 1983, 28, 3599–3605. [Google Scholar] [CrossRef]
- Tozzini, V. Coarse-grained models for proteins. Curr. Opin. Struct. Biol. 2005, 15, 144–150. [Google Scholar] [CrossRef] [PubMed]
- Clementi, C. Coarse-grained models of protein folding: toy models or predictive tools? Curr. Opin. Struct. Biol. 2008, 18, 10–15. [Google Scholar] [CrossRef] [PubMed]
- Guardiani, C.; Livi, R.; Cecconi, F. Coarse Grained Modeling and Approaches to Protein Folding. Curr. Bioinform. 2010, 5, 217–240. [Google Scholar] [CrossRef]
- Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.C.; Zecchina, R.; Berg, J. Inverse statistical problems: from the inverse Ising problem to data science. Adv. Phys. 2017, 66, 197–261. [Google Scholar] [CrossRef]
- Tanaka, S.; Scheraga, H.A. Medium- and Long-Range Interaction Parameters between Amino Acids for Predicting Three-Dimensional Structures of Proteins. Macromolecules 1976, 9, 945–950. [Google Scholar] [CrossRef] [PubMed]
- Taketomi, H.; Ueda, Y.; Gō, N. Studies on protein folding, unfolding and fluctuations by computer simulation. I. The effect of specific amino acid sequence represented by specific inter-unit interactions. Int. J. Pept. Protein Res. 1975, 7, 445–459. [Google Scholar] [CrossRef] [PubMed]
- Clementi, C.; Nymeyer, H.; Onuchic, J.N. Topological and energetic factors: what determines the structural details of the transition state ensemble and “en-route” intermediates for protein folding? An investigation for small globular proteins. J. Mol. Biol. 2000, 298, 937–953. [Google Scholar] [CrossRef] [PubMed]
- Cecconi, F.; Guardiani, C.; Livi, R. Testing Simplified Proteins Models of the hPin1 WW Domain. Biophys. J. 2006, 91, 694–704. [Google Scholar] [CrossRef] [PubMed]
- Plaxco, K.W.; Simons, K.T.; Baker, D. Contact order, transition state placement and the refolding rates of single domain proteins. J. Mol. Biol. 1998, 277, 985–994. [Google Scholar] [CrossRef] [PubMed]
- Chiti, F.; Taddei, N.; White, P.M.; Bucciantini, M.; Magherini, F.; Stefani, M.; Dobson, C.M. Mutational analysis of acylphosphatase suggests the importance of topology and contact order in protein folding. Nat. Struct. Mol. Biol. 1999, 6, 1005–1009. [Google Scholar]
- Hills, R.D.; Brooks, C.L. Subdomain competition, cooperativity, and topological frustration in the folding of CheY. J. Mol. Biol. 2008, 382, 485–495. [Google Scholar] [CrossRef] [PubMed]
- Guardiani, C.; Cecconi, F.; Livi, R. Stability and kinetic properties of C5-domain from myosin binding protein C and its mutants. Biophys. J. 2008, 94, 1403–1411. [Google Scholar] [CrossRef] [PubMed]
- Kleiner, A.; Shakhnovich, E. The Mechanical Unfolding of Ubiquitin through All-Atom Monte Carlo Simulation with a Gō-Type Potential. Biophys. J. 2007, 92, 2054–2061. [Google Scholar] [CrossRef] [PubMed]
- Li, M.S.; Kouza, M.; Hu, C.K. Refolding upon force quench and pathways of mechanical and thermal unfolding of ubiquitin. Biophys. J. 2007, 92, 547–561. [Google Scholar] [CrossRef] [PubMed]
- Paci, E.; Vendruscolo, M.; Karplus, M. Validity of Gō models: Comparison with a solvent-shielded empirical energy decomposition. Biophys. J. 2002, 83, 3032–3038. [Google Scholar] [CrossRef]
- Clementi, C.; Plotkin, S.S. The effects of nonnative interactions on protein folding rates: Theory and simulation. Protein Sci. 2004, 13, 1750–1766. [Google Scholar] [CrossRef] [PubMed]
- Karanicolas, J.; Brooks, C.L. The origins of asymmetry in the folding transition states of protein L and protein G. Protein Sci. 2002, 11, 2351–2361. [Google Scholar] [CrossRef] [PubMed]
- Khare, S.D.; Ding, F.; Dokholyan, N.V. Folding of Cu, Zn superoxide dismutase and familial amyotrophic lateral sclerosis. J. Mol. Biol. 2003, 334, 515–525. [Google Scholar] [CrossRef] [PubMed]
- Oppenheim, I.; Castiglione, P.; Falcioni, M.; Lesne, A.; Vulpiani, A. Chaos and Coarse Graining in Statistical Mechanics; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- E, W.; Engquist, B.; Li, X.; Ren, W.; Vanden-Eijnden, E. Heterogeneous multiscale methods: A review. Commun. Comput. Phys. 2007, 2, 367–450. [Google Scholar]
- Givon, D.; Kupferman, R.; Stuart, A. Extracting macroscopic dynamics: Model problems and algorithms. Nonlinearity 2004, 17, R55–R127. [Google Scholar] [CrossRef]
- Kampen, N.G.V. Stochastic Processes in Physics and Chemistry, 3rd ed.; North Holland: Amsterdam, The Netherlands; Boston, MA, USA, 2007. [Google Scholar]
- Gardiner, C. Stochastic Methods: A Handbook for the Natural and Social Sciences, 4th ed.; Springer Series in Synergetics; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Langevin, P. Sur la théorie du mouvement brownien. C. R. Acad. Sci. 1908, 146, 530–533. [Google Scholar]
- Lemons, D.S.; Gythiel, A. Paul Langevin’s 1908 paper “on the Theory of Brownian Motion” [“Sur la théorie du mouvement brownien,” C. R. Acad. Sci. (Paris) 146, 530–533 (1908)]. Am. J. Phys. 1997, 65, 1079–1081. [Google Scholar] [CrossRef]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef] [PubMed]
- Livi, R.; Politi, P. Nonequilibrium Statistical Physics: A Modern Perspective; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2017. [Google Scholar]
- Zwanzig, R. Nonequilibrium Statistical Mechanics; OUP USA: Oxford, UK; New York, NY, USA, 2001. [Google Scholar]
- Von Smoluchowski, M. Zur kinetischen Theorie der Brownschen Molekularbewegung und der Suspensionen. Ann. Phys. 1906, 326, 756–780. [Google Scholar] [CrossRef]
- Cecconi, F.; Cencini, M.; Vulpiani, A. Transport properties of chaotic and non-chaotic many particle systems. J. Stat. Mech. Theory Exp. 2007, 2007, P12001. [Google Scholar] [CrossRef]
- Van Kampen, N.G. A power series expansion of the master equation. Can. J. Phys. 1961, 39, 551–567. [Google Scholar] [CrossRef]
- Sarracino, A.; Villamaina, D.; Gradenigo, G.; Puglisi, A. Irreversible dynamics of a massive intruder in dense granular fluids. EPL 2010, 92, 34001. [Google Scholar] [CrossRef]
- Dürr, D.; Goldstein, S.; Lebowitz, J.L. A mechanical model of Brownian motion. Commun. Math. Phys. 1981, 78, 507–530. [Google Scholar] [CrossRef]
- Rubin, R.J. Statistical Dynamics of Simple Cubic Lattices. Model for the Study of Brownian Motion. J. Math. Phys. 1960, 1, 309–318. [Google Scholar] [CrossRef]
- Turner, R.E. Motion of a heavy particle in a one dimensional chain. Physica 1960, 26, 269–273. [Google Scholar] [CrossRef]
- Zwanzig, R. Nonlinear generalized Langevin equations. J. Stat. Phys. 1973, 9, 215–220. [Google Scholar] [CrossRef]
- Krüger, M.; Maes, C. The modified Langevin description for probes in a nonlinear medium. J. Phys. Condens. Matter 2017, 29, 064004. [Google Scholar] [CrossRef] [PubMed]
- Basu, U.; Maes, C.; Netočný, K. How Statistical Forces Depend on the Thermodynamics and Kinetics of Driven Media. Phys. Rev. Lett. 2015, 114, 250601. [Google Scholar] [CrossRef] [PubMed]
- Cerino, L.; Puglisi, A.; Vulpiani, A. A consistent description of fluctuations requires negative temperatures. J. Stat. Mech. 2015, 2015, 12002. [Google Scholar] [CrossRef]
- Puglisi, A.; Sarracino, A.; Vulpiani, A. Temperature in and out of equilibrium: A review of concepts, tools and attempts. Phys. Rep. 2017, 709–710, 1–60. [Google Scholar] [CrossRef]
- Baldovin, M.; Puglisi, A.; Sarracino, A.; Vulpiani, A. About thermometers and temperature. J. Stat. Mech. 2017, 2017, 113202. [Google Scholar] [CrossRef]
- Baldovin, M.; Puglisi, A.; Vulpiani, A. Langevin equation in systems with also negative temperatures. J. Stat. Mech. 2018, 2018, 043207. [Google Scholar] [CrossRef]
- Braun, S.; Ronzheimer, J.P.; Schreiber, M.; Hodgman, S.S.; Rom, T.; Bloch, I.; Schneider, U. Negative absolute temperature for motional degrees of freedom. Science 2013, 339, 52–55. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, R.; Peinke, J.; Sahimi, M.; Reza Rahimi Tabar, M. Approaching complexity by stochastic methods: From biological systems to turbulence. Phys. Rep. 2011, 506, 87–162. [Google Scholar] [CrossRef]
- Kleinhans, D.; Friedrich, R.; Nawroth, A.; Peinke, J. An iterative procedure for the estimation of drift and diffusion coefficients of Langevin processes [rapid communication]. Phys. Lett. A 2005, 346, 42–46. [Google Scholar] [CrossRef]
- Ragwitz, M.; Kantz, H. Indispensable Finite Time Corrections for Fokker-Planck Equations from Time Series Data. Phys. Rev. Lett. 2001, 87, 254501. [Google Scholar] [CrossRef] [PubMed]
- Kifer, Y. Some recent advances in averaging. In Modern Dynamical Systems and Applications; Brin, M., Hasselblatt, B., Pesin, Y., Eds.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- MacKay, R.S. Langevin Equation for Slow Degrees of Freedom of Hamiltonian Systems. In Nonlinear Dynamics and Chaos: Advances and Perspectives; Thiel, M., Kurths, J., Romano, M.C., Károlyi, G., Moura, A., Eds.; Understanding Complex Systems; Springer: Berlin/Heidelberg, Germany, 2010; pp. 89–102. [Google Scholar]
- Jafari, G.R.; Fazeli, S.M.; Ghasemi, F.; Allaei, S.M.V.; Tabar, M.R.R.; zad, A.I.; Kavei, G. Stochastic Analysis and Regeneration of Rough Surfaces. Phys. Rev. Lett. 2003, 91, 226101. [Google Scholar] [CrossRef] [PubMed]
- Renner, C.; Peinke, J.; Friedrich, R. Experimental indications for Markov properties of small-scale turbulence. J. Fluid Mech. 2001, 433, 383–409. [Google Scholar] [CrossRef]
- Siegert, S.; Friedrich, R. Modeling of nonlinear Lévy processes by data analysis. Phys. Rev. E 2001, 64, 041107. [Google Scholar] [CrossRef] [PubMed]
- Takeno, S.; Hori, J.I. Continuum Approximation for the Motion of a Heavy Particle in One- and Three-Dimensional Lattices. Prog. Theor. Phys. Suppl. 1962, 23, 177–184. [Google Scholar] [CrossRef]
- Mazur, P.; Braun, E. On the statistical mechanical theory of brownian motion. Physica 1964, 30, 1973–1988. [Google Scholar] [CrossRef]
- Ford, G.W.; Kac, M.; Mazur, P. Statistical Mechanics of Assemblies of Coupled Oscillators. J. Math. Phys. 1965, 6, 504–515. [Google Scholar] [CrossRef]
- Ma, S. Statistical Mechanics; World Scientific: Singapore, 1985. [Google Scholar]
- Scalliet, C.; Gnoli, A.; Puglisi, A.; Vulpiani, A. Cages and Anomalous Diffusion in Vibrated Dense Granular Media. Phys. Rev. Lett. 2015, 114, 198001. [Google Scholar] [CrossRef] [PubMed]
- Lasanta, A.; Puglisi, A. An itinerant oscillator model with cage inertia for mesorheological granular experiments. J. Chem. Phys. 2015, 143, 064511. [Google Scholar] [CrossRef] [PubMed]
- Onsager, L.; Machlup, S. Fluctuations and Irreversible Processes. Phys. Rev. 1953, 91, 1505–1512. [Google Scholar] [CrossRef]
- Dalmedico, A.D. History and Epistemology of Models: Meteorology (1946–1963) as a Case Study. Arch. Hist. Exact Sci. 2001, 55, 395–422. [Google Scholar] [CrossRef]
- Hosni, H.; Vulpiani, A. Forecasting in Light of Big Data. Philos. Technol. 2017, 1–13. [Google Scholar] [CrossRef]
- Bradshaw, G.F.; Langley, P.W.; Simon, H.A. Studying scientific discovery by computer simulation. Science 1983, 222, 971–975. [Google Scholar] [CrossRef] [PubMed]
- Grabiner, J.V. Computers and the Nature of Man: A Historian’s Perspective on Controversies about Artificial Intelligence. Bull. Am. Math. Soc. 1986, 15, 113–126. [Google Scholar] [CrossRef]
- Hansen, J.P.; McDonald, I.R. Theory of Simple Liquids; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Hey, T.; Tansley, S.; Tolle, K. The Fourth Paradigm: Data-Intensive Scientific Discovery; Microsoft Research: Redmond, WA, USA, 2009. [Google Scholar]
- Anderson, C. The End of Theory: The Data Deluge Makes the Scientific Method Obsolete | WIRED. 2008. Available online: https://www.wired.com/2008/06/pb-theory/ (accessed on 20 October 2018).
- Smith, T.R.; Moehlis, J.; Holmes, P. Low-dimensional modelling of turbulence using the proper orthogonal decomposition: A tutorial. Nonlinear Dyn. 2005, 41, 275–307. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baldovin, M.; Cecconi, F.; Cencini, M.; Puglisi, A.; Vulpiani, A. The Role of Data in Model Building and Prediction: A Survey Through Examples. Entropy 2018, 20, 807. https://doi.org/10.3390/e20100807
Baldovin M, Cecconi F, Cencini M, Puglisi A, Vulpiani A. The Role of Data in Model Building and Prediction: A Survey Through Examples. Entropy. 2018; 20(10):807. https://doi.org/10.3390/e20100807
Chicago/Turabian StyleBaldovin, Marco, Fabio Cecconi, Massimo Cencini, Andrea Puglisi, and Angelo Vulpiani. 2018. "The Role of Data in Model Building and Prediction: A Survey Through Examples" Entropy 20, no. 10: 807. https://doi.org/10.3390/e20100807
APA StyleBaldovin, M., Cecconi, F., Cencini, M., Puglisi, A., & Vulpiani, A. (2018). The Role of Data in Model Building and Prediction: A Survey Through Examples. Entropy, 20(10), 807. https://doi.org/10.3390/e20100807





