Colombian Export Capabilities: Building the Firms-Products Network
Abstract
1. Introduction
2. Data
2.1. Colombian Export Data
2.2. World Trade Web Data
2.3. Data Cleaning Procedure
3. Methods
3.1. Measuring Nodes Similarity
3.1.1. Quantifying the Significance of Nodes Similarity
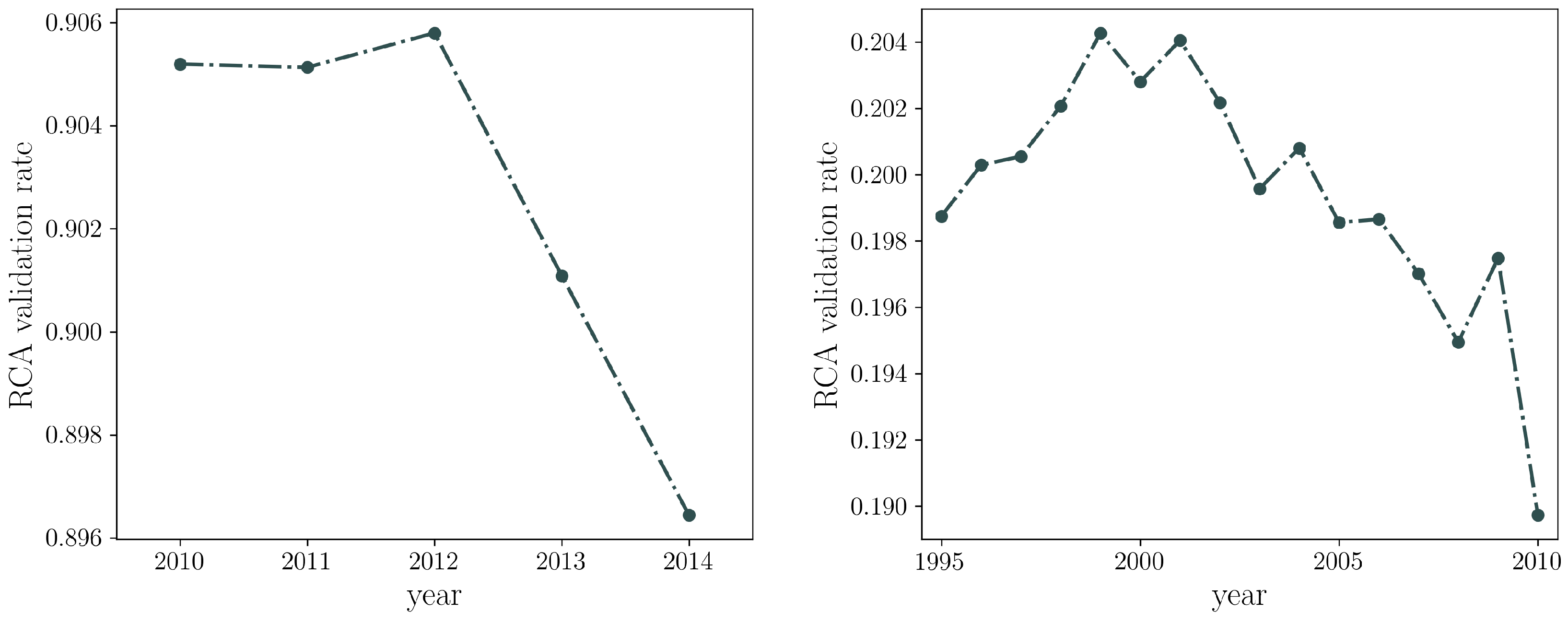
3.1.2. Validating the Projection
3.1.3. Testing the Projection Algorithm
3.1.4. Statistical Analysis
4. Results
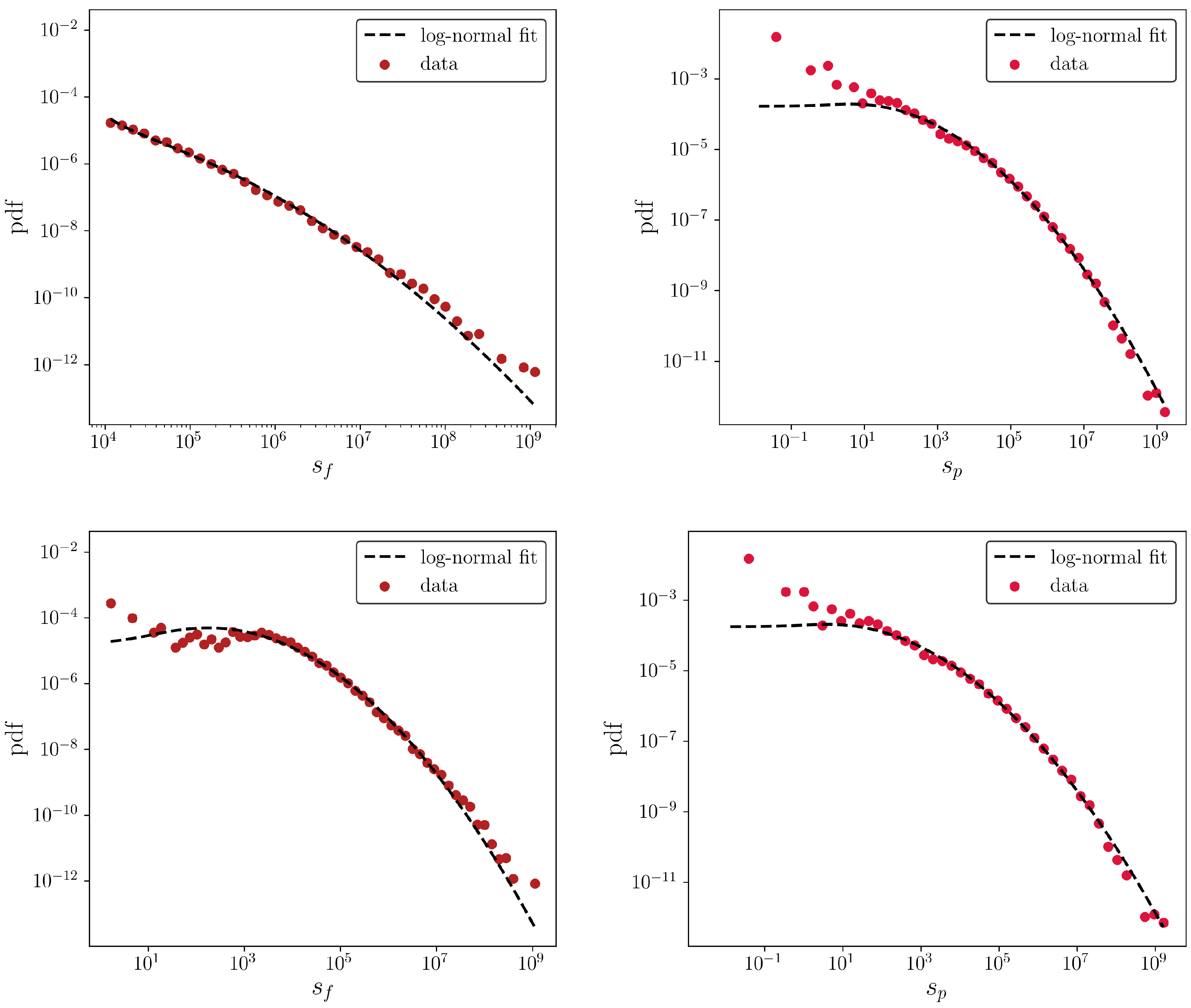
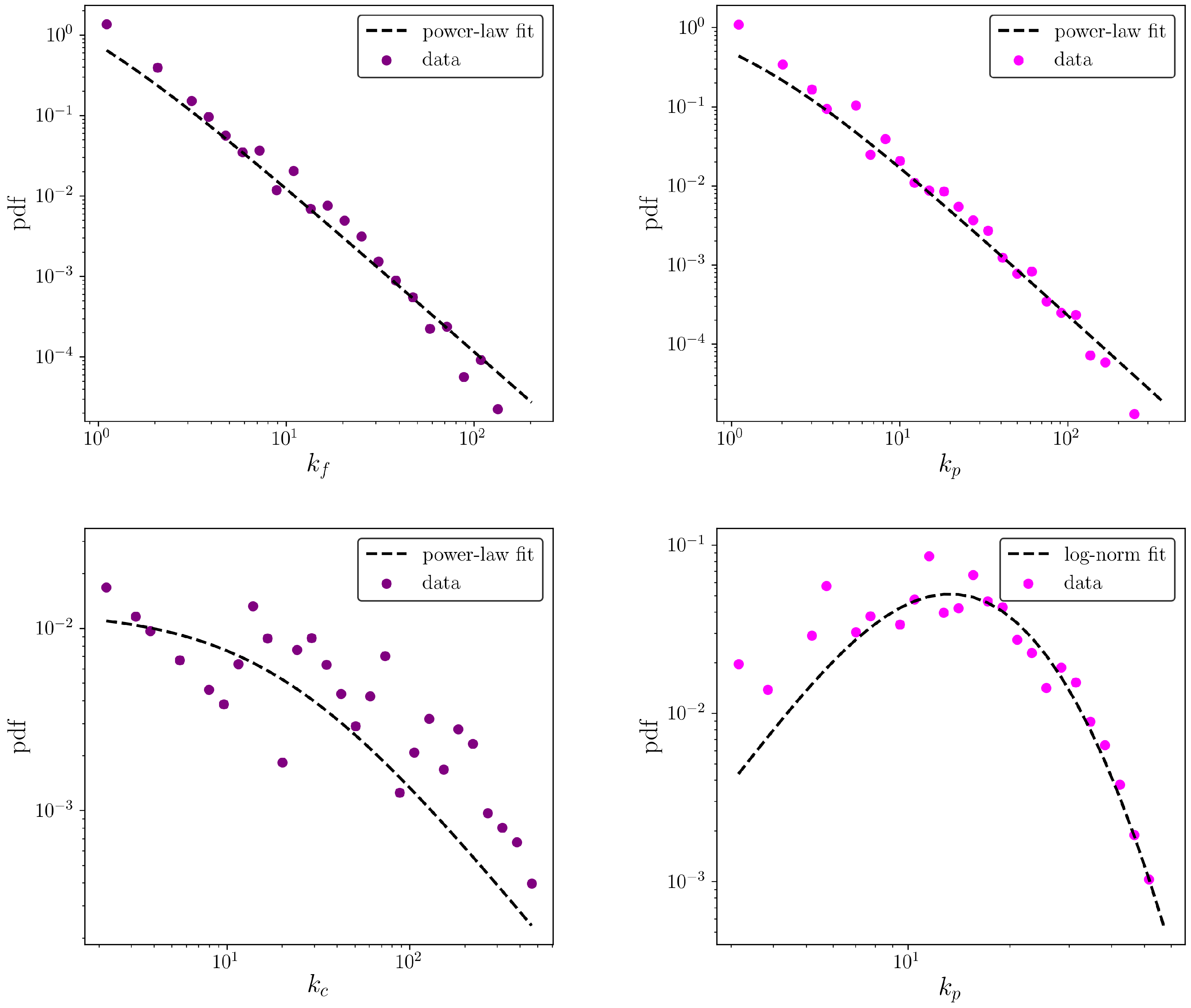
4.1. Node Degree and Strength Distributions
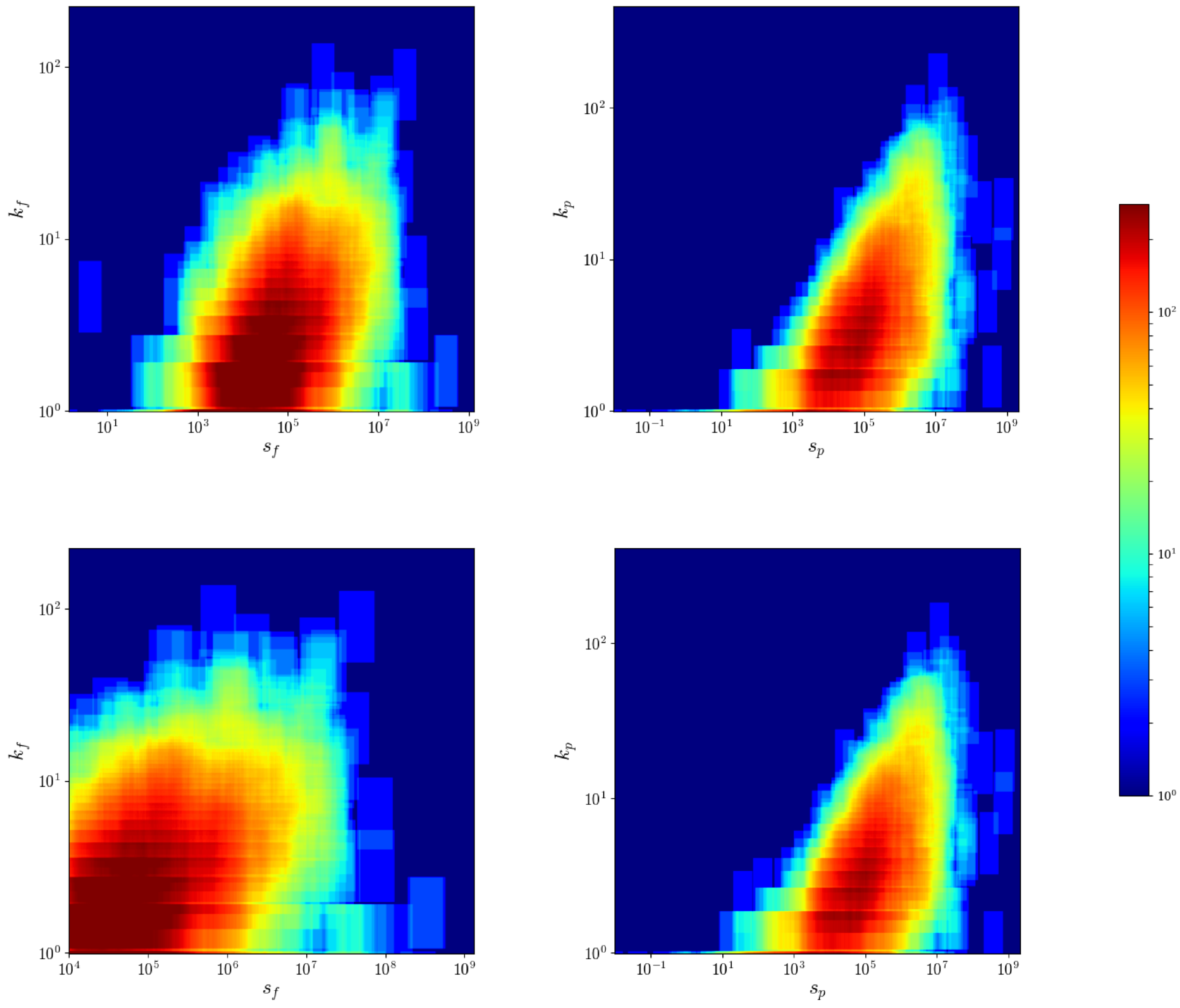
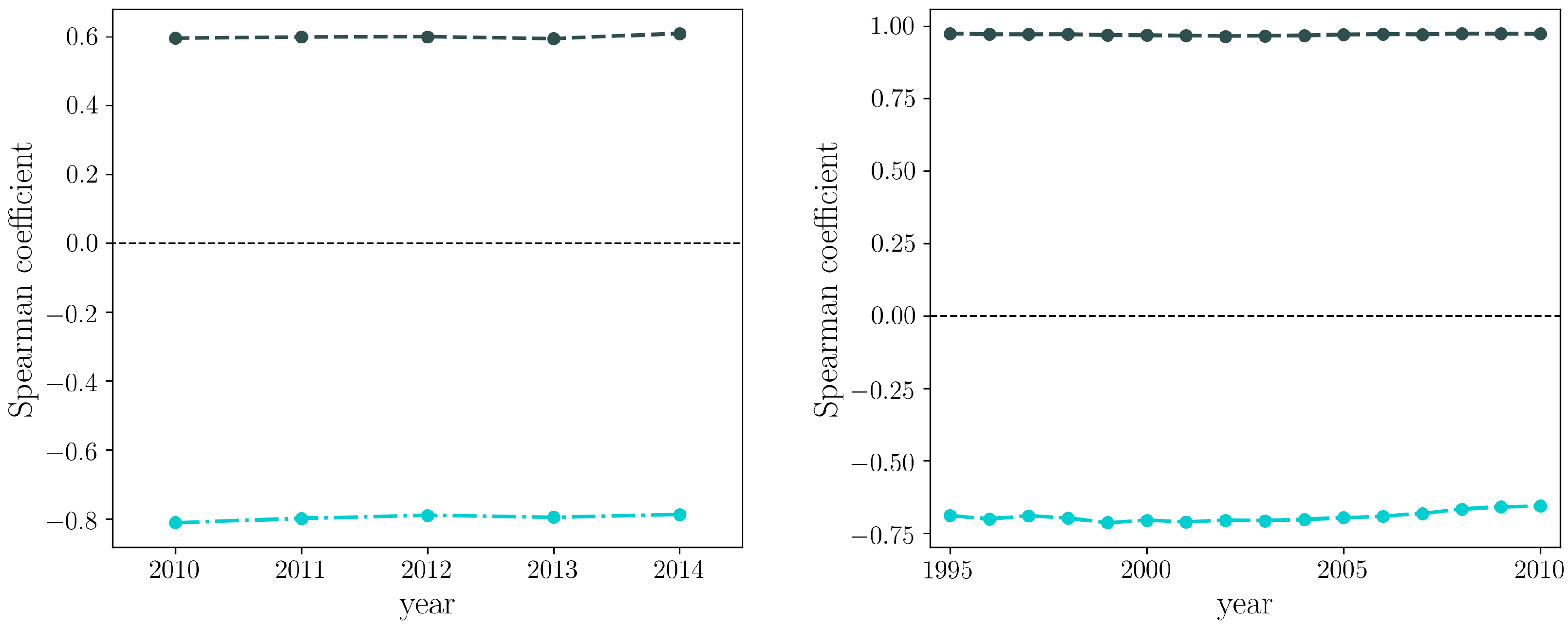
4.2. Nodes Degrees and Strengths Correlation
4.3. Specialization vs. Diversification at a National and International Level
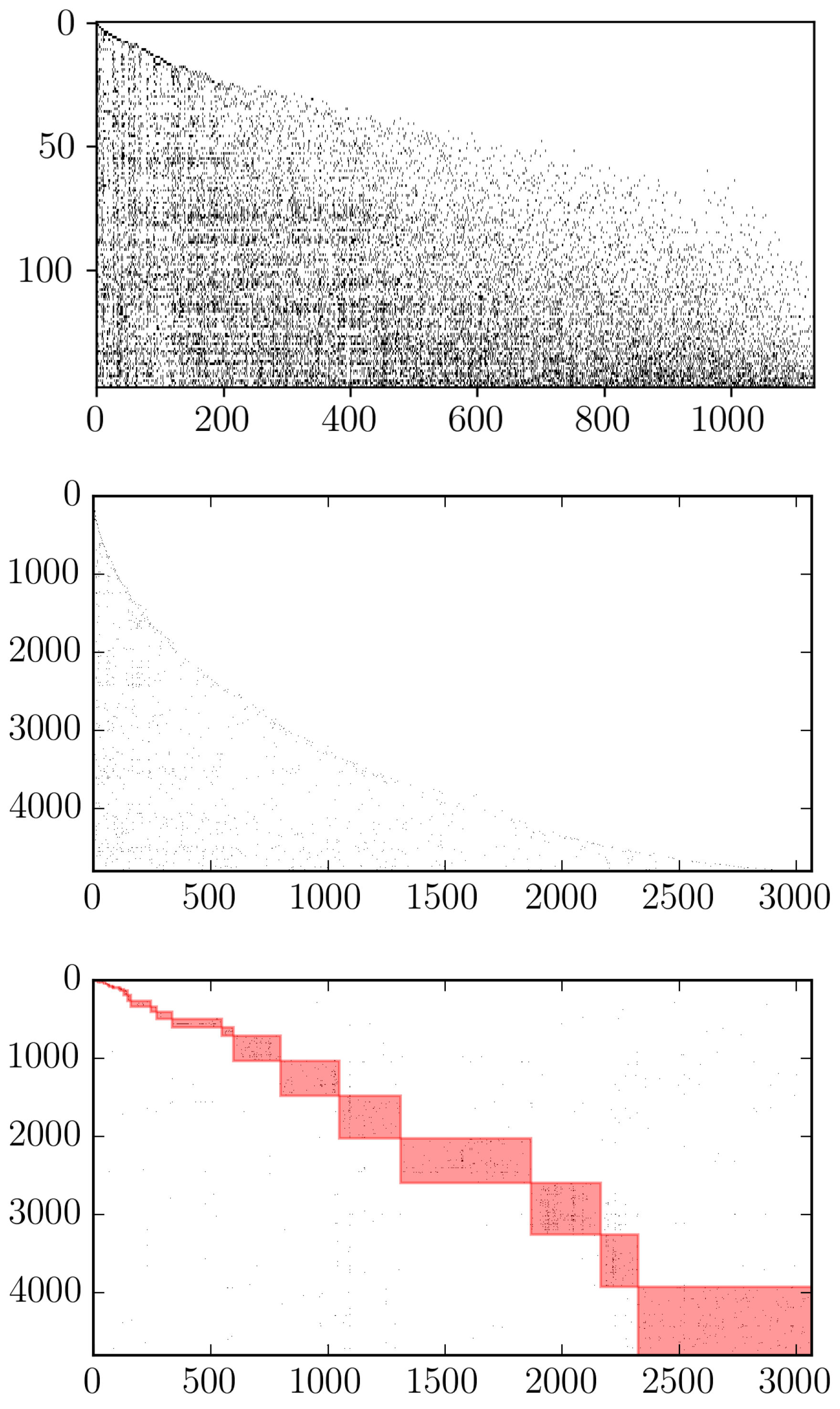
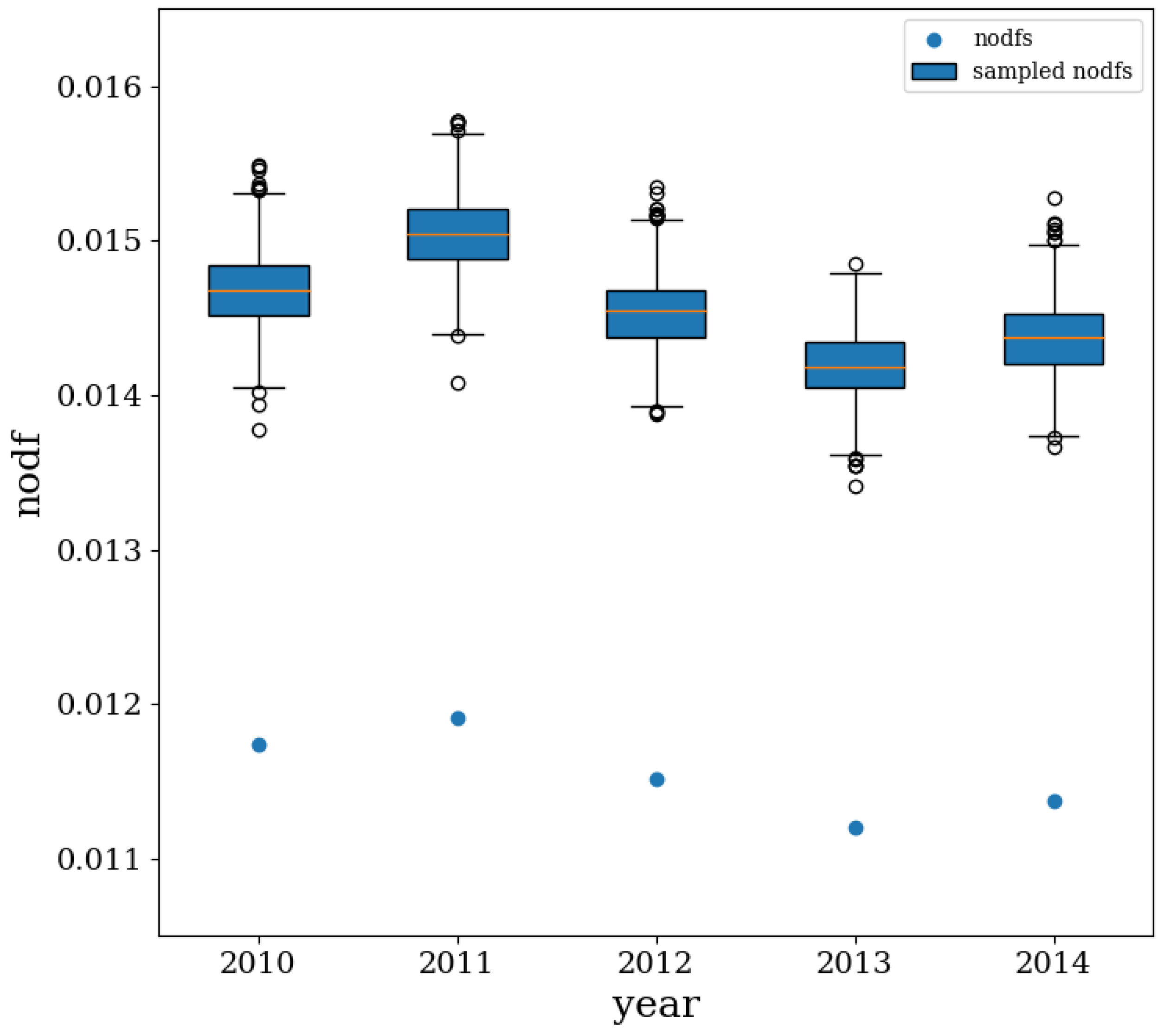
4.4. Nestedness
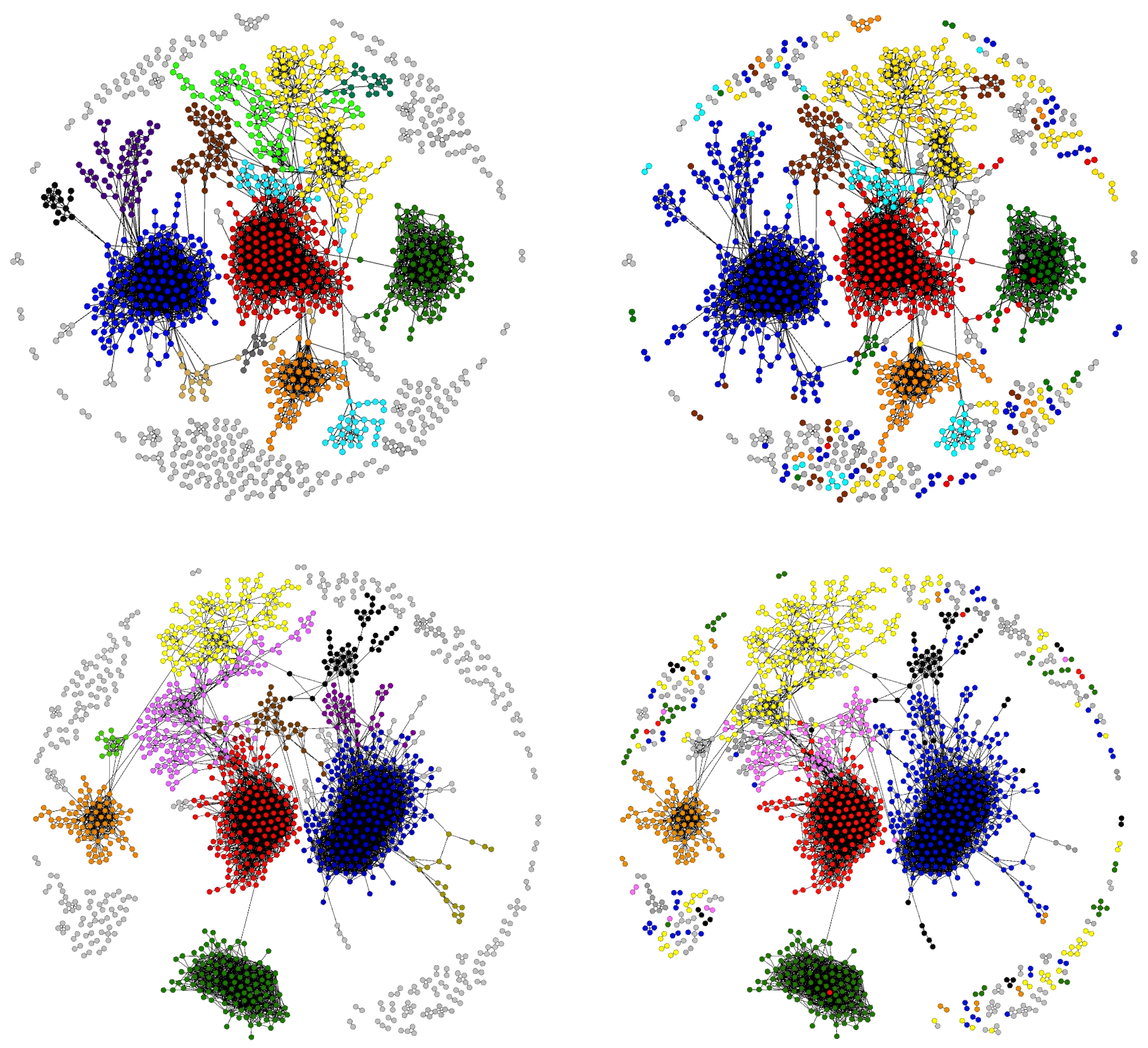
4.5. Projecting the Colombian Firms-Products Network
4.6. Comparison with the WTW
5. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Hidalgo, C.A.; Klinger, B.; Barabási, A.-L.; Hausmann, R. The product space conditions the development of nations. Science 2007, 317, 482–487. [Google Scholar] [CrossRef] [PubMed]
- Caldarelli, G.; Cristelli, M.; Gabrielli, A.; Pietronero, L.; Scala, A.; Tacchella, A. A network analysis of countries’ export flows: Firm grounds for the building blocks of the economy. PLoS ONE 2012, 7, e47278. [Google Scholar] [CrossRef] [PubMed]
- Saracco, F.; Straka, M.J.; di Clemente, R.; Gabrielli, A.; Caldarelli, G.; Squartini, T. Inferring monopartite projections of bipartite networks: An entropy-based approach. New J. Phys. 2017, 19, 053022. [Google Scholar] [CrossRef]
- Penrose, E. The Theory of the Growth of the Firm; Oxford University Press: Oxford, UK, 1959. [Google Scholar]
- Panzar, J.C.; Willig, R.D. Economies of scope. Am. Econ. Rev. 1981, 71, 268–272. [Google Scholar]
- Teece, D.J. Economies of scope and the scope of the enterprise. J. Econ. Behav. Organ. 1980, 1, 223–247. [Google Scholar] [CrossRef]
- Teece, D.J. Towards an economic-theory of the multiproduct firm. J. Econ. Behav. Organ. 1982, 3, 39. [Google Scholar] [CrossRef]
- Teece, D.; Rumelt, R.; Dosi, G.; Winter, S. Understanding corporate coherence: Theory and evidence. J. Econ. Behav. Organ. 1994, 23, 1. [Google Scholar] [CrossRef]
- Hausmann, R.; Hwang, J.; Rodrik, D. What you export matters. J. Econ. Growth 2007, 12, 1–25. [Google Scholar] [CrossRef]
- Tacchella, A.; Cristelli, M.; Caldarelli, G.; Gabrielli, A.; Pietronero, L. A new metrics for countries’ fitness and products’ complexity. Sci. Rep. 2012, 2, 723. [Google Scholar] [CrossRef] [PubMed]
- Cristelli, M.; Gabrielli, A.; Tacchella, A.; Caldarelli, G.; Pietronero, L. Measuring the Intangibles: A Metrics for the Economic Complexity of Countries and Products. PLoS ONE 2013, 8, e70726. [Google Scholar] [CrossRef] [PubMed]
- The latter is the case in which comparative advantages of countries induce specialization in a few products according to their factor and technological endowments.
- Correspondence Tables. Available online: https://unstats.un.org/unsd/trade/classifications/correspondence-tables.asp (accessed on 14th July 2018).
- Gaulier, S.G. BACI: International Trade Database at the Product Level. Available online: http://www.cepii.fr/CEPII/fr/publications/wp.asp (accessed on 5 July 2013).
- Balassa, B. Trade Liberalisation and “Revealed” Comparative Advantage. Manch. Sch. 1965, 33, 99–123. [Google Scholar] [CrossRef]
- Bottazzi, G.; Pirino, D. Measuring Industry Relatedness And Corporate Coherence. Available online: :http://dx.doi.org/10.2139/ssrn.1831479 (accessed on 12 October 2018).
- Park, J.; Newman, M.E.J. Statistical mechanics of networks. Phys. Rev. E 2004, 70, 066117. [Google Scholar] [CrossRef] [PubMed]
- Garlaschelli, D.; Loffredo, M.I. Maximum likelihood: Extracting unbiased information from complex networks. Phys. Rev. E 2008, 78, 015101. [Google Scholar] [CrossRef] [PubMed]
- Squartini, T.; Garlaschelli, D. Analytical maximum-likelihood method to detect patterns in real networks. New J. Phys. 2011, 13, 083001. [Google Scholar] [CrossRef]
- Fronczak, A. Exponential Random Graph Models. In Encyclopedia of Social Network Analysis and Mining; Alhajj, R., Rokne, J., Eds.; Springer: New York, NY, USA, 2014. [Google Scholar]
- Saracco, F.; di Clemente, R.; Gabrielli, A.; Squartini, T. Randomizing bipartite networks: The case of the World Trade Web. Sci.Rep. 2015, 5, 10595. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y. On computing the distribution function for the Poisson binomial distribution. Comput. Stat. Data Anal. 2013, 59, 41–51. [Google Scholar] [CrossRef]
- Deheuvels, P.; Puri, M.L.; Ralescu, S.S. Asymptotic expansions for sums of nonidentically distributed Bernoulli random variables. J. Multivar. Anal. 1989, 28, 282–303. [Google Scholar] [CrossRef]
- Volkova, A.Y. A refinement of the central limit theorem for sums of independent random indicators. Theory Probab. Appl. 1996, 40, 791–794. [Google Scholar] [CrossRef]
- Saracco, F.; di Clemente, R.; Gabrielli, A.; Squartini, T. Detecting early signs of the 2007–2008 crisis in the world trade. Sci. Rep. 2016, 6, 30286. [Google Scholar] [CrossRef] [PubMed]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. B 1995, 57, 289–300. [Google Scholar]
- Our hypotheses, for example, are not independent, since each observed link affects the similarity of several pairs of nodes.
- Blondel, V.D.; Guillaume, J.-L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 174. [Google Scholar] [CrossRef]
- Fagiolo, G.; Schiavo, S.; Reyes, J. World-trade web: Topological properties, dynamics, and evolution. Phys. Rev. E 2009, 79, 036115. [Google Scholar] [CrossRef] [PubMed]
- Bee, M.; Riccaboni, M.; Schiavo, S. Where Gibrat meets Zipf: Scale and scope of French firms. Phys. A Stat. Mech. Appl. 2017, 481, 265. [Google Scholar] [CrossRef]
- Campi, M.; Dueñas, M.; Li, L.; Wu, H. Diversification, economies of scope, and exports growth of Chinese firms. arXiv, 2018; arXiv:1801.02681. [Google Scholar]
- Cimini, G.; Squartini, T.; Garlaschelli, D.; Gabrielli, A. Systemic risk analysis on reconstructed economic and financial networks. Sci. Rep. 2015, 5, 15758. [Google Scholar] [CrossRef] [PubMed]
- Squartini, T.; Almog, A.; Caldarelli, G.; van Lelyveld, I.; Garlaschelli, D.; Cimini, G. Disorder-assisted distribution of entanglement in XY spin chains. Phys. Rev. E 2017, 96, 032315. [Google Scholar] [CrossRef] [PubMed]
- Dixit, A.K.; Stiglitz, J.E. Monopolistic competition and optimum product diversity. Am. Econ. Rev. 1977, 67, 297–308. [Google Scholar]
- Krugman, P. Scale economies, product differentiation, and the pattern of trade. Am. Econ. Rev. 1980, 70, 950–959. [Google Scholar]
- Hummels, D.; Klenow, P.J. The variety and quality of a nation’s exports. Am. Econ. Rev. 2005, 95, 704–723. [Google Scholar] [CrossRef]
- Hausmann, R.; Hidalgo, C. The building blocks of economic complexity. Proc. Natl. Acad. Sci. USA 2009, 106, 10570–10575. [Google Scholar]
- Straka, M.J.; Caldarelli, G.; Saracco, F. Grand canonical validation of the bipartite international trade network. Phys. Rev. E 2017, 96, 022306. [Google Scholar] [CrossRef] [PubMed]
- Cristelli, M.; Tacchella, A.; Pietronero, L. The Heterogeneous Dynamics of Economic Complexity. PLoS ONE 2015, 10, e0117174. [Google Scholar] [CrossRef] [PubMed]
- Johnson, S.; Dominguez-Garcia, V.; Munoz, M.A. Factors determining nestedness in complex networks. arXiv, 2013; arXiv:1307.4685. [Google Scholar]
- In this case, as discussed in [43] the FiCo algorithm does not converge, but the relative rankings are stable. Actually, only the rankings are necessary for reordering the biadjacency matrix.
- Pugliese, E.; Zaccaria, A.; Pietronero, L. On the convergence of the Fitness-Complexity algorithm. Eur. Phys. J. Spec. Top. 2016, 225, 1893–1911. [Google Scholar] [CrossRef]
- Barber, M.J. Modularity and community detection in bipartite networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2007, 76, 066102. [Google Scholar] [CrossRef] [PubMed]
- Almeida-Neto, M.; Guimarães, P.; Guimaraes, J.P.R.; Loyola, R.D.; Ulrich, W. A consistent metric for nestedness analysis in ecological systems: reconciling concept and measurement. Oikos 2008, 117, 1227–1239. [Google Scholar] [CrossRef]
- Meilă, M. Learning Theory and Kernel Machines; Schölkopf, B., Warmuth, M.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 173–187. [Google Scholar]
- Mastrandrea, R.; Squartini, T.; Fagiolo, G.; Garlaschelli, D. Enhanced reconstruction of weighted networks from strengths and degrees. New J. Phys. 2014, 16, 043022. [Google Scholar] [CrossRef]
- Solé-Ribalta, A.; Tessone, C.J.; Mariani, M.S.; Borge-Holthoefer, J. Revealing in-block nestedness: Detection and benchmarking. Phys. Rev. E 2018, 97, 062302. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bruno, M.; Saracco, F.; Squartini, T.; Dueñas, M. Colombian Export Capabilities: Building the Firms-Products Network. Entropy 2018, 20, 785. https://doi.org/10.3390/e20100785
Bruno M, Saracco F, Squartini T, Dueñas M. Colombian Export Capabilities: Building the Firms-Products Network. Entropy. 2018; 20(10):785. https://doi.org/10.3390/e20100785
Chicago/Turabian StyleBruno, Matteo, Fabio Saracco, Tiziano Squartini, and Marco Dueñas. 2018. "Colombian Export Capabilities: Building the Firms-Products Network" Entropy 20, no. 10: 785. https://doi.org/10.3390/e20100785
APA StyleBruno, M., Saracco, F., Squartini, T., & Dueñas, M. (2018). Colombian Export Capabilities: Building the Firms-Products Network. Entropy, 20(10), 785. https://doi.org/10.3390/e20100785





