Link Prediction in Bipartite Nested Networks
Abstract
1. Introduction
2. Methods
2.1. Link Prediction Methods
2.1.1. Preferential Attachment Index (PrefA)
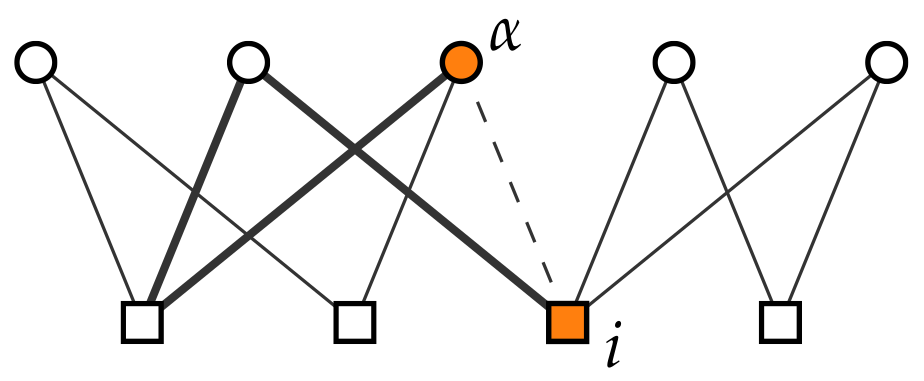
2.1.2. Number of Local Community Links (LCL)
2.1.3. Probabilistic Spreading (ProbS)
2.1.4. Number of Violations of the Nestedness Property (NViol)
2.2. Evaluation Process
3. Data
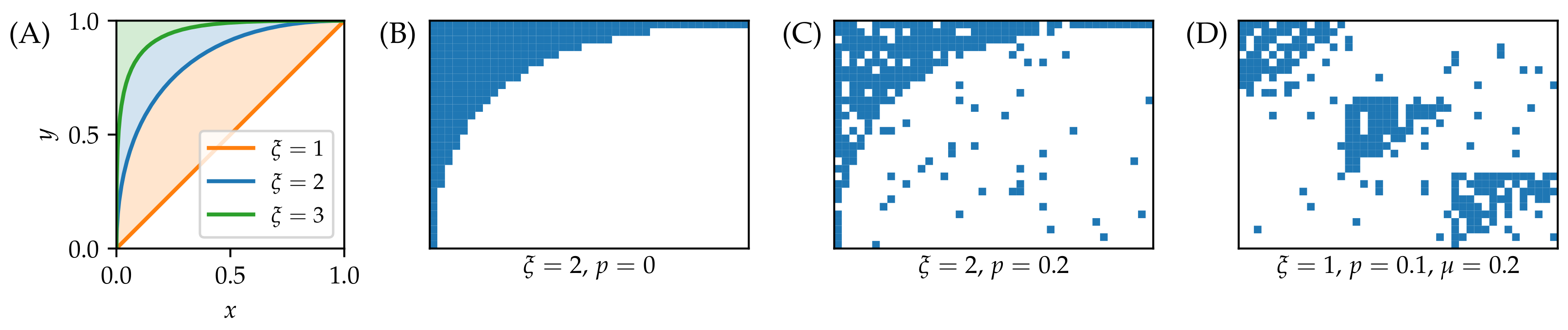
3.1. Synthetic Data
3.2. Real Data
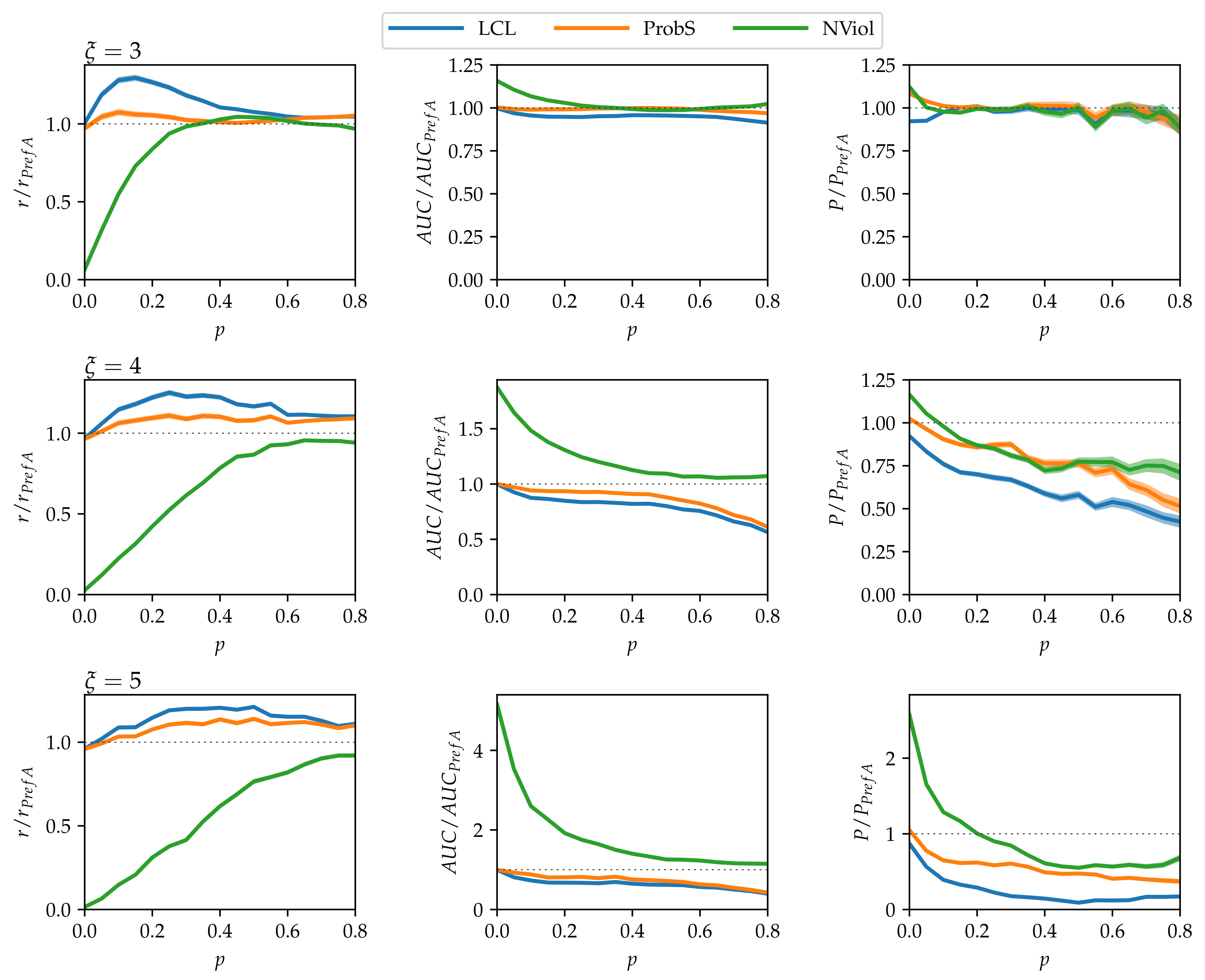
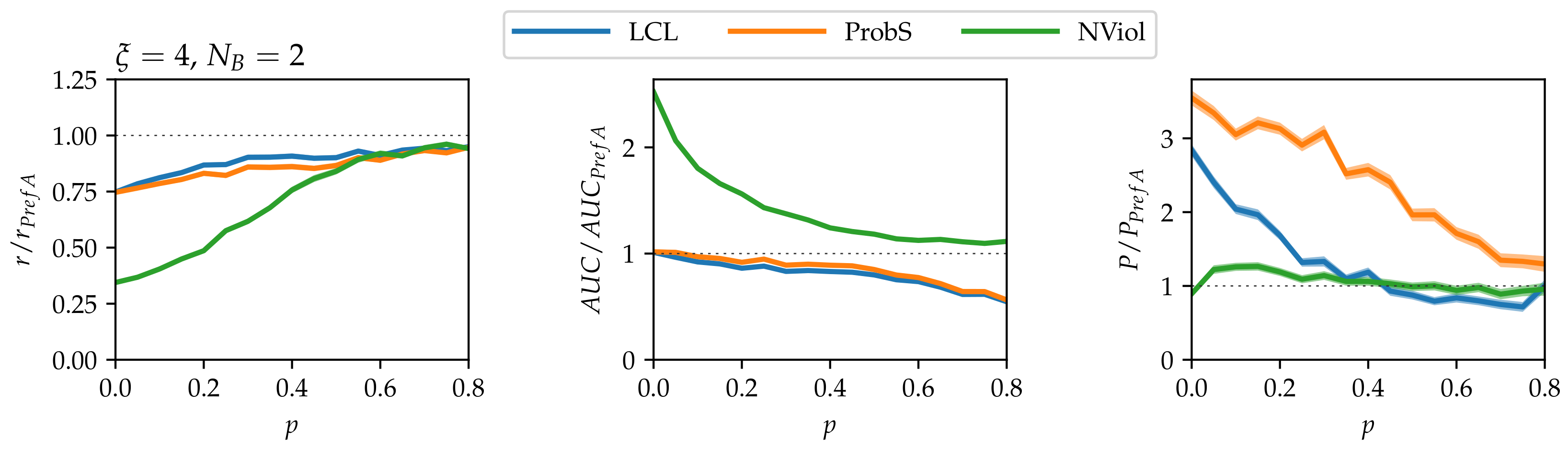
4. Results
- As grows and the networks’ nested structure thus becomes more pronounced, differences between the methods grow.
- NViol is generally the best-performing method with respect to the metrics r and AUC that take the whole link prediction list into account. Upon a closer inspection of link prediction lists produced by the respective methods, the advantage of NViol is due to its ability to place well also links connecting low-degree nodes that the other methods miss due to their general bias towards high-degree nodes. With NViol, though, probe links adjacent to low-degree nodes are not among the top 100 and hence do not contribute to the method’s precision, yet they rank much better than where other methods are used. If we would increase the number of top ranks included in precision evaluation from 100 to 200 or 300, NViol would have an edge also in this metric.
- As the randomization parameter p grows, PrefA eventually outperforms NViol in terms of link prediction precision. High precision improvement with respect to LCL’s precision for are due to the generally low precision achieved for the sparse networks produced at (which is made further worse by introducing the noise when ).
- ProbS outperforms LCL but lacks behind PrefA and NViol. This is expected because ProbS is based on a “personalized” recommendation algorithm; with no communities in the data, there is no place for personalization and thus ProbS’s merits cannot manifest themselves. The situation becomes radically different when there is more than one nested block in the data (see below).
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Getoor, L.; Diehl, C.P. Link mining: A survey. ACM SIGKDD Explor. Newsl. 2005, 7, 3–12. [Google Scholar] [CrossRef]
- Liben-Nowell, D.; Kleinberg, J. The link-prediction problem for social networks. J. Am. Soc. Inf. Sci. Tech. 2007, 58, 1019–1031. [Google Scholar] [CrossRef]
- Guimerà, R.; Sales-Pardo, M. Missing and spurious interactions and the reconstruction of complex networks. Proc. Natl. Acad. Sci. USA 2009, 106, 22073–22078. [Google Scholar] [CrossRef] [PubMed]
- Lü, L.; Zhou, T. Link prediction in complex networks: A survey. Physical A 2011, 390, 1150–1170. [Google Scholar] [CrossRef]
- Warde-Farley, D.; Donaldson, S.L.; Comes, O.; Zuberi, K.; Badrawi, R.; Chao, P.; Franz, M.; Grouios, C.; Kazi, F.; Lopes, C.T.; et al. The GeneMANIA prediction server: Biological network integration for gene prioritization and predicting gene function. Nucleic Acids Res. 2010, 38, W214–W220. [Google Scholar] [CrossRef] [PubMed]
- Holme, P.; Saramäki, J. Temporal networks. Phys. Rep. 2012, 519, 97–125. [Google Scholar] [CrossRef]
- Liao, H.; Mariani, M.S.; Medo, M.; Zhang, Y.C.; Zhou, M.Y. Ranking in evolving complex networks. Phys. Rep. 2017, 689, 1–54. [Google Scholar] [CrossRef]
- Lü, L.; Pan, L.; Zhou, T.; Zhang, Y.C.; Stanley, H.E. Toward link predictability of complex networks. Proc. Natl. Acad. Sci. USA 2015, 112, 2325–2330. [Google Scholar] [CrossRef] [PubMed]
- Al Hasan, M.; Zaki, M.J. A survey of link prediction in social networks. In Social Network Data Analytics; Springer: Berlin/Heidelberg, Germany, 2011; pp. 243–275. [Google Scholar]
- Ren, Z.M.; Zeng, A.; Zhang, Y.C. Structure-oriented prediction in complex networks. Phys. Rep. 2018, 750, 1–51. [Google Scholar] [CrossRef]
- Squartini, T.; Caldarelli, G.; Cimini, G.; Gabrielli, A.; Garlaschelli, D. Reconstruction methods for networks: The case of economic and financial systems. arXiv 2018, arXiv:1806.06941. [Google Scholar] [CrossRef]
- Patterson, B.D.; Atmar, W. Nested subsets and the structure of insular mammalian faunas and archipelagos. Biol. J. Linn. Soc. 1986, 28, 65–82. [Google Scholar] [CrossRef]
- Bascompte, J.; Jordano, P.; Melián, C.J.; Olesen, J.M. The nested assembly of plant–animal mutualistic networks. Proc. Natl. Acad. Sci. USA 2003, 100, 9383–9387. [Google Scholar] [CrossRef] [PubMed]
- Ulrich, W.; Almeida-Neto, M.; Gotelli, N.J. A consumer’s guide to nestedness analysis. Oikos 2009, 118, 3–17. [Google Scholar] [CrossRef]
- König, M.D.; Tessone, C.J. Network evolution based on centrality. Phys. Rev. E 2011, 84, 056108. [Google Scholar] [CrossRef] [PubMed]
- Suweis, S.; Simini, F.; Banavar, J.R.; Maritan, A. Emergence of structural and dynamical properties of ecological mutualistic networks. Nature 2013, 500, 449. [Google Scholar] [CrossRef] [PubMed]
- König, M.D.; Tessone, C.J.; Zenou, Y. Nestedness in networks: A theoretical model and some applications. Theor. Econ. 2014, 9, 695–752. [Google Scholar] [CrossRef]
- Valverde, S.; Piñero, J.; Corominas-Murtra, B.; Montoya, J.; Joppa, L.; Solé, R. The architecture of mutualistic networks as an evolutionary spandrel. Nat. Ecol. Revolut. 2018, 2, 94–99. [Google Scholar] [CrossRef] [PubMed]
- Bastolla, U.; Fortuna, M.A.; Pascual-García, A.; Ferrera, A.; Luque, B.; Bascompte, J. The architecture of mutualistic networks minimizes competition and increases biodiversity. Nature 2009, 458, 1018–1020. [Google Scholar] [CrossRef] [PubMed]
- Allesina, S.; Tang, S. Stability criteria for complex ecosystems. Nature 2012, 483, 205–208. [Google Scholar] [CrossRef] [PubMed]
- Rohr, R.P.; Saavedra, S.; Bascompte, J. On the structural stability of mutualistic systems. Science 2014, 345, 1253497. [Google Scholar] [CrossRef] [PubMed]
- Montoya, J.M.; Pimm, S.L.; Solé, R.V. Ecological networks and their fragility. Nature 2006, 442, 259–264. [Google Scholar] [CrossRef] [PubMed]
- Tacchella, A.; Cristelli, M.; Caldarelli, G.; Gabrielli, A.; Pietronero, L. A new metrics for countries’ fitness and products’ complexity. Sci. Rep. 2012, 2, 723. [Google Scholar] [CrossRef] [PubMed]
- Maron, M.; Mac Nally, R.; Watson, D.M.; Lill, A. Can the biotic nestedness matrix be used predictively? Oikos 2004, 106, 433–444. [Google Scholar] [CrossRef]
- Bustos, S.; Gomez, C.; Hausmann, R.; Hidalgo, C.A. The dynamics of nestedness predicts the evolution of industrial ecosystems. PLoS ONE 2012, 7, e49393. [Google Scholar] [CrossRef] [PubMed]
- Tacchella, A.; Mazzilli, D.; Pietronero, L. A dynamical systems approach to gross domestic product forecasting. Nat. Phys. 2018, 14, 861–865. [Google Scholar] [CrossRef]
- Cristelli, M.; Tacchella, A.; Pietronero, L. The heterogeneous dynamics of economic complexity. PLoS ONE 2015, 10, e0117174. [Google Scholar] [CrossRef] [PubMed]
- Battiston, F.; Cristelli, M.; Tacchella, A.; Pietronero, L. How metrics for economic complexity are affected by noise. Complex. Econ. 2014, 3, 1–22. [Google Scholar]
- Mariani, M.S.; Vidmer, A.; Medo, M.; Zhang, Y.C. Measuring economic complexity of countries and products: Which metric to use? Eur. Phys. J. B 2015, 88, 293. [Google Scholar] [CrossRef]
- Wu, R.J.; Shi, G.Y.; Zhang, Y.C.; Mariani, M.S. The mathematics of non-linear metrics for nested networks. Phys. A Stat. Mech. Appl. 2016, 460, 254–269. [Google Scholar] [CrossRef]
- Olesen, J.M.; Bascompte, J.; Dupont, Y.L.; Elberling, H.; Rasmussen, C.; Jordano, P. Missing and forbidden links in mutualistic networks. Proc. R. Soc. Lond. B Biol. Sci. 2010. [Google Scholar] [CrossRef] [PubMed]
- Bascompte, J.; Jordano, P. Mutualistic Networks; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Vázquez, D.P.; Poulin, R.; Krasnov, B.R.; Shenbrot, G.I. Species abundance and the distribution of specialization in host–parasite interaction networks. J. Anim. Ecol. 2005, 74, 946–955. [Google Scholar] [CrossRef]
- Nielsen, A.; Bascompte, J. Ecological networks, nestedness and sampling effort. J. Ecol. 2007, 95, 1134–1141. [Google Scholar] [CrossRef]
- Grimm, A.; Tessone, C.J. Analysing the sensitivity of nestedness detection methods. Appl. Netw. Sci. 2017, 2, 37. [Google Scholar] [CrossRef]
- Solé-Ribalta, A.; Tessone, C.J.; Mariani, M.S.; Borge-Holthoefer, J. Revealing in-block nestedness: Detection and benchmarking. Phys. Rev. E 2018, 97, 062302. [Google Scholar] [CrossRef] [PubMed]
- Newman, M. Networks: An Introduction; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Kunegis, J.; De Luca, E.W.; Albayrak, S. The link prediction problem in bipartite networks. In Proceedings of the 13th International Conference on Information Processing and Management of Uncertainty in Knowledge-based Systems, Dortmund, Germany, 28 June–2 July 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 380–389. [Google Scholar]
- Daminelli, S.; Thomas, J.M.; Durán, C.; Cannistraci, C.V. Common neighbours and the local-community-paradigm for topological link prediction in bipartite networks. New J. Phys. 2015, 17, 113037. [Google Scholar] [CrossRef]
- Zhou, T.; Ren, J.; Medo, M.; Zhang, Y.C. Bipartite network projection and personal recommendation. Phys. Rev. E 2007, 76, 046115. [Google Scholar] [CrossRef] [PubMed]
- Lü, L.; Medo, M.; Chi, H.Y.; Zhang, Y.C.; Zhang, Z.K.; Zhou, T. Recommender systems. Phys. Rep. 2012, 519, 1–49. [Google Scholar] [CrossRef]
- Yu, F.; Zeng, A.; Gillard, S.; Medo, M. Network-based recommendation algorithms: A review. Phys. A Stat. Mech. Appl. 2016, 452, 192–208. [Google Scholar] [CrossRef]
- Vidmer, A.; Zeng, A.; Medo, M.; Zhang, Y.C. Prediction in complex systems: The case of the international trade network. Phys. A Stat. Mech. Appl. 2015, 436, 188–199. [Google Scholar] [CrossRef]
- Vidmer, A.; Medo, M. The essential role of time in network-based recommendation. EPL 2016, 116, 30007. [Google Scholar] [CrossRef]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 8, 30–37. [Google Scholar] [CrossRef]
- Swets, J.A. Information retrieval systems. Science 1963, 141, 245–250. [Google Scholar] [CrossRef] [PubMed]
- Fortunato, S.; Hric, D. Community detection in networks: A user guide. Phys. Rep. 2016, 659, 1–44. [Google Scholar] [CrossRef]
| Dataset | E | |||
|---|---|---|---|---|
| M_SD_022 | 207 | 110 | 1121 | 0.05 |
| M_PL_015 | 131 | 666 | 2933 | 0.03 |
| M_PL_021 | 91 | 677 | 1193 | 0.02 |
| M_PL_044 | 110 | 609 | 1125 | 0.02 |
| M_PL_057 | 114 | 883 | 1920 | 0.02 |
| M_PL_062 | 456 | 1044 | 15,255 | 0.03 |
| CP-2001 | 169 | 781 | 17,639 | 0.13 |
| CP-2009 | 168 | 774 | 17,739 | 0.14 |
| method | r | AUC | P | method | r | AUC | P | |||
| PrefA | 0.20 | 0.80 | 0.11 | 0.13 | PrefA | 0.38 | 0.61 | 0.12 | 0.10 | |
| LCL | 0.19 | 0.80 | 0.14 | 0.15 | LCL | 0.34 | 0.59 | 0.14 | 0.12 | |
| ProbS | 0.17 | 0.82 | 0.15 | 0.16 | ProbS | 0.33 | 0.61 | 0.16 | 0.13 | |
| NViol | 0.19 | 0.81 | 0.11 | 0.12 | NViol | 0.16 | 0.84 | 0.12 | 0.10 | |
| M_PL_015 | M_PL_062 | |||||||||
| method | r | AUC | P | method | r | AUC | P | |||
| PrefA | 0.23 | 0.77 | 0.12 | 0.09 | PrefA | 0.20 | 0.80 | 0.05 | 0.05 | |
| LCL | 0.19 | 0.80 | 0.20 | 0.14 | LCL | 0.17 | 0.83 | 0.12 | 0.07 | |
| ProbS | 0.18 | 0.82 | 0.25 | 0.18 | ProbS | 0.16 | 0.84 | 0.15 | 0.08 | |
| NViol | 0.24 | 0.75 | 0.13 | 0.08 | NViol | 0.20 | 0.80 | 0.04 | 0.05 | |
| M_PL_021 | CP-2001 | |||||||||
| method | r | AUC | P | method | r | AUC | P | |||
| PrefA | 0.49 | 0.49 | 0.06 | 0.07 | PrefA | 0.23 | 0.78 | 0.05 | 0.10 | |
| LCL | 0.41 | 0.46 | 0.09 | 0.09 | LCL | 0.21 | 0.79 | 0.18 | 0.13 | |
| ProbS | 0.40 | 0.48 | 0.09 | 0.10 | ProbS | 0.19 | 0.81 | 0.14 | 0.12 | |
| NViol | 0.16 | 0.84 | 0.06 | 0.05 | NViol | 0.24 | 0.76 | 0.06 | 0.10 | |
| M_PL_044 | CP-2009 | |||||||||
| method | r | AUC | P | method | r | AUC | P | |||
| PrefA | 0.47 | 0.52 | 0.05 | 0.06 | PrefA | 0.24 | 0.77 | 0.07 | 0.10 | |
| LCL | 0.38 | 0.45 | 0.07 | 0.07 | LCL | 0.22 | 0.79 | 0.22 | 0.13 | |
| ProbS | 0.37 | 0.46 | 0.06 | 0.07 | ProbS | 0.20 | 0.80 | 0.13 | 0.12 | |
| NViol | 0.21 | 0.79 | 0.04 | 0.05 | NViol | 0.25 | 0.75 | 0.08 | 0.10 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medo, M.; Mariani, M.S.; Lü, L. Link Prediction in Bipartite Nested Networks. Entropy 2018, 20, 777. https://doi.org/10.3390/e20100777
Medo M, Mariani MS, Lü L. Link Prediction in Bipartite Nested Networks. Entropy. 2018; 20(10):777. https://doi.org/10.3390/e20100777
Chicago/Turabian StyleMedo, Matúš, Manuel Sebastian Mariani, and Linyuan Lü. 2018. "Link Prediction in Bipartite Nested Networks" Entropy 20, no. 10: 777. https://doi.org/10.3390/e20100777
APA StyleMedo, M., Mariani, M. S., & Lü, L. (2018). Link Prediction in Bipartite Nested Networks. Entropy, 20(10), 777. https://doi.org/10.3390/e20100777






